Ga naar voetnoot1)Ga naar voetnoot2)Ga naar voetnoot3)
5040 circuitus in hora. longitudo circiter 6 poll. cum extenditur angulo 45 gr.Ga naar voetnoot4).
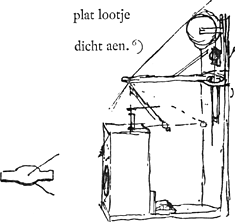
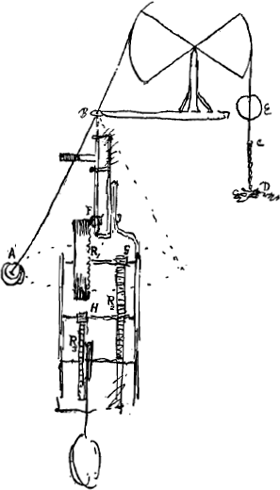
de spil midden uyt de kasGa naar voetnoot7).
het werck dicht aen den bovensten bodem van de kas, of men hem als een schuyf maecktenGa naar voetnoot8).
|
-
voetnoot1)
- Ce texte est emprunté à la p. 175 du Manuscrit A.
-
voetnoot2)
- C.à.d. égal à un fragment de chaîne du même genre que la ‘chaîne CD’.
-
voetnoot3)
- Nous appellerons ‘CD’ la ‘particula catenae quae elevata est..... etc.’, quoique la Fig. 13 ne se rapporte pas au cas considéré dans le texte où le poids A est simplement suspendu sans tourner, le fil AB étant donc vertical. Le fil qui relie les poids E et A (au lieu du double secteur de la Fig. 13 il faut évidemment considérer un cercle entier; voir les Fig. 16 et 17 qui suivent) étant supposé impondérable ou de poids négligeable, il y a équilibre lorsque le poids A, suspendu sans tourner, est égal au poids E augmenté du poids de la partie de la chaîne, CD, qui ne repose pas sur le plan horizontal fixe passant par le point D. Comme Huygens fait entendre qu'une chaîne de ce genre de longueur AB ferait équilibre avec le poids E augmenté du poids nommé CD, il s'ensuit qu'il suppose le poids A (ou, si le ‘fil’ AB est moitié fil moitié verge solide, comme cela semble être le cas dans la Fig. 17 qui suit - voir la note 6 de la p. 91 -, le poids A plus celui de la verge) égal à celui qu'aurait cette chaîne de longueur AB.
-
voetnoot5)
- Le sens de ce passage nous paraît être le suivant: lorsqu'on pense avoir établi l'équilibre dont il est question dans la note 3, mais qu'en réalité le poids A est trop léger, d'où il résulte que la longueur AB diminue et que le poids E descend, de sorte que la partie CD, devenue elle aussi plus petite, pèse p unités moins qu'auparavant, on peut rétablir la longueur AB voulue en augmentant le poids A d'un poids p. Le poids E s'élève alors à son ancienne hauteur, de sorte que le poids p vient de nouveau s'y ajouter.
-
voetnoot6)
- Si dans le cas considéré dans la note précédente, où le poids A est trop léger, de sorte que le poids E descend, on rétablit la longueur AB en faisant descendre le poids A au moyen de l'écrou (p. 91, note 6), de sorte que le poids E ne remonte pas, et qu'on ajoute néanmoins au poids A le poids p mentionné plus haut, il faut également ajouter ce poids au poids E; ce qu'on peut faire alors en raccourcissant la distance EC.
-
voetnoot7)
- Le dispositif de la Fig. 13 a évidemment pour but de maintenir la longueur AB à peu près constante; lorsque cette longueur varie quelque peu, la partie CD augmente ou diminue de longueur (le plan horizontal étant fixe), ce qui a pour conséquence que le poids A revient à sa place. Ceci s'applique en premier lieu au cas considéré dans le texte où il n'y a pas de mouvement rotatoire uniforme. Mais lorsque ce mouvement existe, la tension de la partie supérieure du fil (c.à.d. de la partie au-dessus du point B) sera théoriquement constante tout aussi bien que celle de la partie AB, supposé que le bord de l'ouverture B exerce sur le fil une force horizontale. Dans ce cas aussi, grâce au dispositif de la chaîne, la longueur AB restera à peu près constante, et il en sera de même lorsque la chaîne est remplacée par le cylindre à mercure plongeant dans un deuxième cylindre contenant le même liquide (Fig. 15).
-
voetnoot1)
- Dans ce calcul le chiffre 14 représente le quotient du nombre des dents de la roue R2 par celui du pignon G (voir la Fig. 13 à laquelle nous avons ajouté les lettres F, G, H, R1, R2, R3). Le chiffre 30 représente le nombre de tours que la roue R2 fait par heure; cette roue peut mener une aiguille. Le nombre de tours par heure du pignon G et de la roue R1 est donc 420. Le chiffre 12 est le rapport du nombre des dents de la roue R1 et du nombre correspondant du pignon F. Ce dernier et le pendule tournent par conséquent 5040 fois par heure. Le pignon F étant de 6, c'est 30240 fois par heure qu'une de ses dents engrène avec la roue R1.
-
voetnoot2)
- Le pignon G étant de 6, il en résulte (voir la note 1) que la roue R2 a 84 dents.
-
voetnoot3)
- Les chiffres de ce tableau ne correspondent pas tous à la Fig. 13; en effet, ils supposent que la roue R3 porte sur son axe un pignon I de 8 engrenant avec une roue R4 de 96. On a donc
|
R4 (96 dents) |
| I (8) |
coäxial avec |
R3 (90) |
| H (6) |
coäxial avec |
R2 (84) |
| G (6) |
coäxial avec |
R1 (72) |
| F (6) |
|
La troisième colonne donne les rapports des nombres des dents des différentes roues et des pignons qui engrènent avec elles (12, 15, 14, 12). La quatrième donne les nombres des tours lorsque la roue R4 (roue des heures, menant évidemment une aiguille) en fait 1 par heure. R3 en fait alors 12, R2 180, R1 2520 et le pendule 30240; ces nombres sont six fois plus grands que ceux adoptés plus haut (note 1).
-
voetnoot4)
- Pour qu'un pendule conique, dont le fil est incliné à 45o, fasse 5040 révolutions en une heure, il faut, lorsque l'accélération de la gravité a la valeur de 30 pieds rhénans (941,7 cm) par seconde (ce qui est la valeur adoptée par Huygens avant le 21 octobre 1659; voir plus loin dans le présent Tome) que la longueur du pendule, mesurée - voir à la p. 88 les premières lignes du texte - depuis le point de suspension jusqu'au centre de la sphère (le fil étant impondérable) soit de 4,6 pouces rhénans. Même en adoptant pour l'accélération nommée la vraie valeur de 31,25 pieds par sec. (voir la note 1 de la p. 100) on n'obtient que 4,8 pouces pour la longueur du pendule. Le 5 octobre Huygens ne connaissait pas encore, pensons-nous, les propositions de son Manuscrit ‘De Vi Centrifuga’ (voir la date de la p. 302 du T. XVI). Il a probablement trouvé la longueur de 6 pouces (qui peut s'appliquer à un pendule dont le ‘fil’ n'a pas un poids négligeable; voir la fin de la note 6) par une observation grossière; comparez les §§13 et 14 (p. 307 et 308 du T. XVI), où il parle de ses expériences sur les mouvements circulaires, ainsi que la proposition sur le mouvement du pendule conique qu'il énonce à la p. 173 du Manuscrit A avec les notes que nous y avons ajoutées (p. 319 du T. XVI).
-
voetnoot5)
- La Fig. 16 représente un détail de la figure suivante.
-
voetnoot6)
- On lit à droite de la Fig. 17 qui représente l'horloge à pendule conique, les mots ‘plat lootje’ et ‘dicht aen’ qui signifient respectivement ‘petit plomb plat’ (c'est le poids qui correspond au poids E de la Fig. 13) et ‘proche de’; ces derniers mots indiquent que le double cylindre à mercure doit se trouver très près du montaut vertical. En-dessous du poids du pendule (poids ‘A’) on voit un écrou servant à remonter ou à baisser ce poids; comparez la note 3 de la p. 14.
-
voetnoot7)
- Traduction: ‘la verge [doit sortir] de la cage au milieu’.
-
voetnoot8)
- Traduction: ‘l'ouvrage [doit être placé] près de la paroi supérieure de la cage. Il est désirable qu'on construise cette paroi en guise de tiroir’.
|