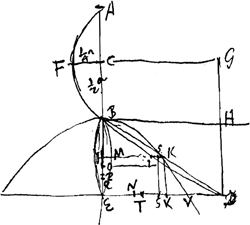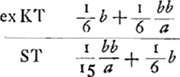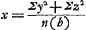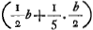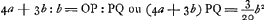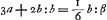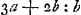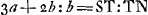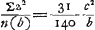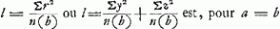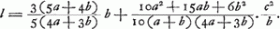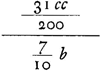
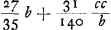 Ga naar voetnoot4) Ga naar voetnoot4) pendulum isochronon conoidi hyperbolico cum latus rectum Ga naar voetnoot5) a ∞ axi b et suspensio ex vertice. |
-
voetnoot1)
- La Pièce est empruntée aux p. 50 et 51 du Manuscrit C.
-
voetnoot2)
- La p. 38 du Manuscrit porte la date du 16 mars 1665 et la p. 65 est datée: juillet 1665.
-
voetnoot3)
- Huygens se propose de calculer la longueur du pendule isochrone avec un segment d'un hyperboloïde de révolution suspendu en son sommet.
-
voetnoot4)
- Il y a deux lettres H dans la figure, ce qui cependant ne peut guère donner lieu à des confusions. Remarquons en même temps que les projections des points S et K sur la droite ED sont désignées par Huygens par les mêmes lettres.
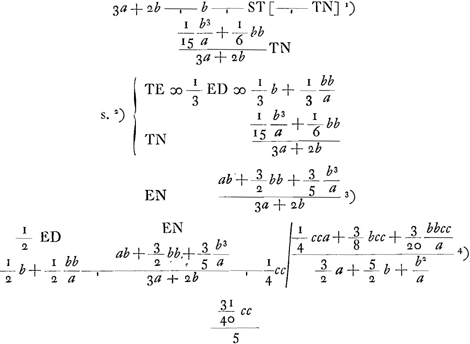
HM est le diamètre de la parabole BME. Cette parabole a été trouvée comme suit. Pour calculer la longueur du pendule isochrone d'après la formule 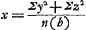 (comparez p.e. la note 7 de la p. 485), où (b) représente la distance de B au centre de gravité du corps considéré, y la distance d'un point pesant quelconque de ce corps à un plan horizontal passant par la droite BH (perpendiculairement au plan du papier), et z la distance de ce point à un plan passant par l'axe AE perpendiculairement au plan du papier, Huygens cherche d'abord Σy2/n(b), ce qui représente la longueur du pendule isochrone avec une surface plane oscillant perpendiculairement à son plan et contenant tous les points pesants de l'hyperboloïde à leurs vraies distances du plan horizontal nommé. Σy2/n(b) représente donc aussi (voir la p. 458 ou le dernier alinéa de la p. 503) la distance du point de suspension B à un plan horizontal passant par le centre de gravité d'un onglet élevé sur cette surface et limité par un plan oblique passant par la droite horizontale BH. Cette surface plane est la figure EHBLDE, où EHB est une droite et BLD (partie de la courbe AFBLD) une parabole (comparez sur cette substitution d'une figure plane à un corps le dernier alinéa de la p. 471 ou la note 2 de la p. 473); le facteur arbitraire qui entre dans la longueur des ordonnées parallèles à l'horizontale BH a été choisi de telle
manière que la parabole passe non seulement par le point B, mais aussi par le point A, AB ou a étant la distance des sommets ou ‘latus transversum’ de l'hyperbole BKV. (comparez p.e. la note 7 de la p. 485), où (b) représente la distance de B au centre de gravité du corps considéré, y la distance d'un point pesant quelconque de ce corps à un plan horizontal passant par la droite BH (perpendiculairement au plan du papier), et z la distance de ce point à un plan passant par l'axe AE perpendiculairement au plan du papier, Huygens cherche d'abord Σy2/n(b), ce qui représente la longueur du pendule isochrone avec une surface plane oscillant perpendiculairement à son plan et contenant tous les points pesants de l'hyperboloïde à leurs vraies distances du plan horizontal nommé. Σy2/n(b) représente donc aussi (voir la p. 458 ou le dernier alinéa de la p. 503) la distance du point de suspension B à un plan horizontal passant par le centre de gravité d'un onglet élevé sur cette surface et limité par un plan oblique passant par la droite horizontale BH. Cette surface plane est la figure EHBLDE, où EHB est une droite et BLD (partie de la courbe AFBLD) une parabole (comparez sur cette substitution d'une figure plane à un corps le dernier alinéa de la p. 471 ou la note 2 de la p. 473); le facteur arbitraire qui entre dans la longueur des ordonnées parallèles à l'horizontale BH a été choisi de telle
manière que la parabole passe non seulement par le point B, mais aussi par le point A, AB ou a étant la distance des sommets ou ‘latus transversum’ de l'hyperbole BKV.
Mais cette surface plane peut être transformée en une autre possédant les mêmes ordonnées parallèles à l'horizentale BH, savoir la surface limitée par les droites BKD et DE et la parabole EMB, où il faut donner à l'axe HM de cette dernière la valeur indiquée dans le texte. L'expression Σy2/n(b) est donc égale à la distance du point B au plan horizontal passant par le centre de gravité d'un onglet élevé sur la surface BKDEMB et limité par un plan oblique passant par l'horizontale BH.
Il est évident qu'on pourrait tout aussi bien prendre une surface plane de forme symétrique, obtenue en ajoutant à la figure considérée une figure pareille à gauche de BE (comparez la Fig. 3 de la Tab. XXVI de l'‘Horologium oscillatorium’; cette figure correspond à la Prop. XXII de la Pars Quarta, mentionnée dans la note de la p. 555).
-
voetnoot5)
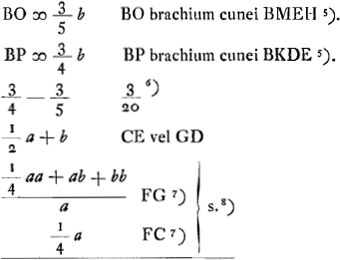
- L'onglet considéré (voir le troisième alinéa de la note précédente) est la différence des onglets BKDEHB (ou BKDE) et BMEHB (ou BMEH), limité l'un et l'autre par un plan oblique passant par la droite horizontale BH. Le premier (BKDE) est une pyramide scalène à base perpendiculaire au plan du papier; il est donc facile de voir que son bras de levier par rapport au point B a la valeur ¾b. Quant au bras de levier correspondant à l'onglet BMEH, la valeur ⅗b ou
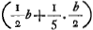 s'accorde avec la valeur de la ‘λ cunei’ de la Pièce XI (voir le huitième alinéa de la p. 472). s'accorde avec la valeur de la ‘λ cunei’ de la Pièce XI (voir le huitième alinéa de la p. 472).
-
voetnoot5)
- L'onglet considéré (voir le troisième alinéa de la note précédente) est la différence des onglets BKDEHB (ou BKDE) et BMEHB (ou BMEH), limité l'un et l'autre par un plan oblique passant par la droite horizontale BH. Le premier (BKDE) est une pyramide scalène à base perpendiculaire au plan du papier; il est donc facile de voir que son bras de levier par rapport au point B a la valeur ¾b. Quant au bras de levier correspondant à l'onglet BMEH, la valeur ⅗b ou
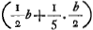 s'accorde avec la valeur de la ‘λ cunei’ de la Pièce XI (voir le huitième alinéa de la p. 472). s'accorde avec la valeur de la ‘λ cunei’ de la Pièce XI (voir le huitième alinéa de la p. 472).
-
voetnoot6)
- La différence 3/20b des deux bras de levier BO et BP est la distance OP.
-
voetnoot7)
- La parabole BLD ayant été choisie de telle manière qu'elle passe par le point
A aussi bien que par le point B (comme
nous l'avons dit dans la note 4), FG et FC doivent avoir les valeurs indiquées dans le texte.
-
voetnoot7)
- La parabole BLD ayant été choisie de telle manière qu'elle passe par le point A aussi bien que par le point B (comme nous l'avons dit dans la note 4), FG et FC doivent avoir les valeurs indiquées dans le texte.
-
voetnoot8)
- s. = subtrahendo. Voir le résultat de la soustraction à la page suivante.
-
voetnoot1)
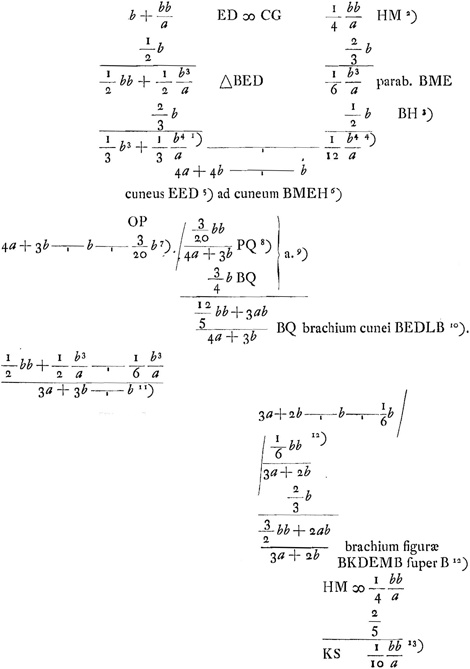
- C'est le moment du triangle BED par rapport au point B.
-
voetnoot3)
- Comparez le premier alinéa de la note 4 de la p. 550. Il s'agit ici du point inférieur H.
-
voetnoot4)
- C'est le moment du segment de parabole BMEHB par rapport au point B.
-
voetnoot6)
- Les volumes des onglets nommés sont dans le rapport des moments de leurs bases (qui sont le triangle BED et le segment parabolique BMEHB) par rapport à l'horizontale BH, d'après la proposition de la p. 501; ce rapport a ici la valeur (4a+4b):b.
-
voetnoot8)
- L'équation
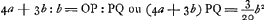 exprime que les moments des onglets à base EMBKDE et à base BMEB par rapport à une droite horizontale passant par le point P (voir la note 6 de la p. 551) sont égaux, vu que le moment de l'onglet à base triangulaire BED par rappert à cette droite est nul. exprime que les moments des onglets à base EMBKDE et à base BMEB par rapport à une droite horizontale passant par le point P (voir la note 6 de la p. 551) sont égaux, vu que le moment de l'onglet à base triangulaire BED par rappert à cette droite est nul.
-
voetnoot10)
- Il ressort de ce que nous avons dit dans le troisième alinéa de la note 4 de la p. 550 que le bras de levier de l'onglet BHEDLB (ou BEDLB) par rapport à l'horizontale BH est identique avec le bras de levier de l'onglet à base EMBKDE par rapport à la même droite. Ce bras de levier est égal à Σy2/n(b) d'après le deuxième alinéa de la même note 4. Les
calculs qui suivent servent à déterminer Σz2/n(b). Voir la note 4 de la p. 554.
-
voetnoot11)
- C'est le rapport de la surface du triangle BED au segment parabolique BMEHB.
-
voetnoot12)
- L'équation
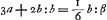 , d'où l'on tire la valeur de β, exprime l'égalité des moments des surfaces EMBKDE et BMEHB par rapport à une horizontale passant par le centre de gravité du triangle BED. En ajoutant ⅔ b à β, on trouve la distance du point B à l'horizontale passant par le centre de gravité de la surface EMBKDE. C'est la longueur (voir la note 4 de la p. 550) que nous avons désignée par (b). , d'où l'on tire la valeur de β, exprime l'égalité des moments des surfaces EMBKDE et BMEHB par rapport à une horizontale passant par le centre de gravité du triangle BED. En ajoutant ⅔ b à β, on trouve la distance du point B à l'horizontale passant par le centre de gravité de la surface EMBKDE. C'est la longueur (voir la note 4 de la p. 550) que nous avons désignée par (b).
-
voetnoot12)
- L'équation
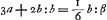 , d'où l'on tire la valeur de β, exprime l'égalité des moments des surfaces EMBKDE et BMEHB par rapport à une horizontale passant par le centre de gravité du triangle BED. En ajoutant ⅔ b à β, on trouve la distance du point B à l'horizontale passant par le centre de gravité de la surface EMBKDE. C'est la longueur (voir la note 4 de la p. 550) que nous avons désignée par (b). , d'où l'on tire la valeur de β, exprime l'égalité des moments des surfaces EMBKDE et BMEHB par rapport à une horizontale passant par le centre de gravité du triangle BED. En ajoutant ⅔ b à β, on trouve la distance du point B à l'horizontale passant par le centre de gravité de la surface EMBKDE. C'est la longueur (voir la note 4 de la p. 550) que nous avons désignée par (b).
-
voetnoot13)
- Les surfaces des segments paraboliques BMEB et BKDLB étant égales (voir le troisième alinéa de la note 4 de la p. 550), leurs diamètres sont aussi égaux (voir la note 4 de la p. 466). En prenant KS = ⅖ (diamètre), on trouve le centre de gravité S du segment parabolique BKDLB. La projection KS a la
même longueur. On a évidemment EK = ½ ED.
-
voetnoot14)
- Le point T est la projection sur ED du centre de gravité du triangle BED. On a donc ET = ⅓ ED et KT = ⅙ ED; or, ED est connue (voir la première ligne de la p. 552).
-
voetnoot1)
- N est la projection sur ED du centre de gravité de la surface BHEDLB.
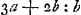 est le rapport des surfaces BHEDLB et BKDLB. L'équation est le rapport des surfaces BHEDLB et BKDLB. L'équation 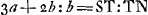 , qui sert à calculer TN, exprime l'égalité des moments des surfaces BHEDLB et BKDLB par rapport à une droite verticale (située dans le plan du papier) passant par le point T (voir la note précédente). , qui sert à calculer TN, exprime l'égalité des moments des surfaces BHEDLB et BKDLB par rapport à une droite verticale (située dans le plan du papier) passant par le point T (voir la note précédente).
-
voetnoot3)
- C'est la distance du centre de gravité de la surface BHEDLB à l'axe BE.
-
voetnoot4)
- La proportion ½ ED:EN = ¼c2:Z, d'où l'on tire la valeur de Z, qui est identique avec Σz2/n (voir la note 4 de la p. 550), correspond à la proportion PΔ:PΦ = ▭BCK:Z, qu'on trouve dans la Prop. XV de la Pars Quarta de l'‘Horologium Oscillatorium’. Cette méthode se rattache à celle de la p. 482 (voir à la p. 483 les sept dernières lignes de la note 4 et aussi la note 2 de la p. 485 et la p. 372 de l'Avertissement). Pour trouver Σz2/n(b) il faut diviser Z par (b), c.à.d. par le ‘brachium figurae BKDEMB super B’ (voir la note 12 de la p. 553).
Huygens pose a = b; le ‘brachium’ en question a alors la valeur 7/10 b, et Z la valeur 31/200 c2. On trouve donc 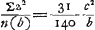 . .
Comme Σv2/n(b), en d'autres termes, comme le ‘brachium cunei BEDLB’ (voir la note 10 de la p. 553) acquiert pour a = b la valeur 27/35b, la longueur cherchée du pendule isochrone avec l'hyperboloïde de révolution 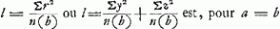 , égale à la somme de 27/35b et de 31/140 c2/b. , égale à la somme de 27/35b et de 31/140 c2/b.
Comparez l'‘Horologium oscillatorium’, où l'on trouve la même valeur de l, calculée à peu près de la même manière (Prop. XXII de la Pars Quarta, au § ‘Centrum oscillationis Conoidis Hyperbolici’). Seulement la parabole BLD y a été choisie de telle manière qu'elle nepasse pas par le point A, mais par le point V (qui coïncide donc avec le point D), et il n'y est pas fait mention de la parabole BME, qui d'ailleurs n'est pas indispensable.
Si l'on ne pose pas a = b, on trouve d'après les formules de Huygens
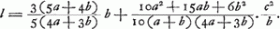
Dans le sommaire de sa lettre à P. Petit du 30 oct. 1664 (T. V, p. 129) Huygens parle déjà du conoïde hyperbolique (‘Des pendules Isochrones... Sphere, conoide hyperbolique. Methode générale’). Comparez la note 1 de la p. 482. Mais comme le présent calcul date de 1665 (comparez la note 2 de la p. 550), il est probable que le calcul primitif, qui nous manque, n'était pas entièrement le même.
-
voetnoot4)
- La proportion ½ ED:EN = ¼c2:Z, d'où l'on tire la valeur de Z, qui est identique avec Σz2/n (voir la note 4 de la p. 550), correspond à la proportion PΔ:PΦ = ▭BCK:Z, qu'on trouve dans la Prop. XV de la Pars Quarta de l'‘Horologium Oscillatorium’. Cette méthode se rattache à celle de la p. 482 (voir à la p. 483 les sept dernières lignes de la note 4 et aussi la note 2 de la p. 485 et la p. 372 de l'Avertissement). Pour trouver Σz2/n(b) il faut diviser Z par (b), c.à.d. par le ‘brachium figurae BKDEMB super B’ (voir la note 12 de la p. 553).
Huygens pose a = b; le ‘brachium’ en question a alors la valeur 7/10 b, et Z la valeur 31/200 c2. On trouve donc 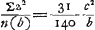 . .
Comme Σv2/n(b), en d'autres termes, comme le ‘brachium cunei BEDLB’ (voir la note 10 de la p. 553) acquiert pour a = b la valeur 27/35b, la longueur cherchée du pendule isochrone avec l'hyperboloïde de révolution 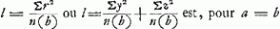 , égale à la somme de 27/35b et de 31/140 c2/b. , égale à la somme de 27/35b et de 31/140 c2/b.
Comparez l'‘Horologium oscillatorium’, où l'on trouve la même valeur de l, calculée à peu près de la même manière (Prop. XXII de la Pars Quarta, au § ‘Centrum oscillationis Conoidis Hyperbolici’). Seulement la parabole BLD y a été choisie de telle manière qu'elle nepasse pas par le point A, mais par le point V (qui coïncide donc avec le point D), et il n'y est pas fait mention de la parabole BME, qui d'ailleurs n'est pas indispensable.
Si l'on ne pose pas a = b, on trouve d'après les formules de Huygens
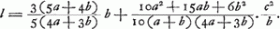
Dans le sommaire de sa lettre à P. Petit du 30 oct. 1664 (T. V, p. 129) Huygens parle déjà du conoïde hyperbolique (‘Des pendules Isochrones... Sphere, conoide hyperbolique. Methode générale’). Comparez la note 1 de la p. 482. Mais comme le présent calcul date de 1665 (comparez la note 2 de la p. 550), il est probable que le calcul primitif, qui nous manque, n'était pas entièrement le même.
-
voetnoot5)
- Lisez ‘latus transversum’, comme Huygens appelle correctement la longueur a dans la Proposition de l'‘Horologium oscillatorium’ citée dans le quatrième alinéa de la note précédente.
|
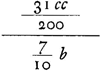
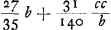 Ga naar voetnoot4) pendulum isochronon conoidi hyperbolico cum latus rectumGa naar voetnoot5) a ∞ axi b et suspensio ex vertice.
Ga naar voetnoot4) pendulum isochronon conoidi hyperbolico cum latus rectumGa naar voetnoot5) a ∞ axi b et suspensio ex vertice.