Oeuvres complètes. Tome XVI. Percussion
(1929)–Christiaan Huygens–
[pagina 545]
| |
XVIIIGa naar voetnoot1).
| |
[pagina 546]
| |
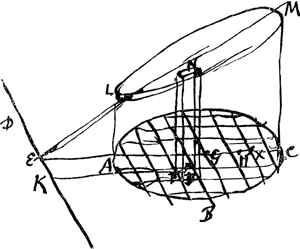
id quod fit ex particula una in numerum particularum in quas divisa est. Itaque omissa utrimque multiplicatione in particulam figurae, apparet summam omnium quadratorum à perpendicularibus super ED aequari producto rectanguli HE, EG in numerum particularum in quas figura divisa estGa naar voetnoot1). 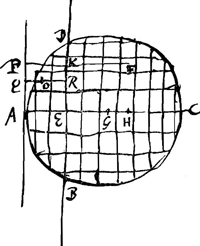 [Fig. 88.]
Sit jam recta DE [Fig. 88] quae figuram secet in partes DAB, DCB et oporteat invenire summam quadratorum a perpendicularibus omnibus quae utrinque è particulis figurae ABC ducuntur in rectam DE ut FK, OR &c. Quod si dentur distantiae centrorum gravitatis partis utriusque ab recta DE, nec non distantiae punctorum superquibus gravitant cunei super dictis partibus abscissi planis per DE ductis, jam quasi duae figurae erunt et extra utramque data linea ED; ac proinde eodem modo quo antea colligentur summae omnium quadratorum à perpendicularibus quae utrinque in rectam ED cadunt à particulis sectae figurae. at non datis illis centrorum distantijs (quae sepe [sic] inventu difficiles aut impossibiles sunt) sed tantum datis ab recta AP, quae tangat figuram sitque parallela ED distantijs AG, centri gravitatis figurae totius, et AH puncti super quo gravitat cuneus abscissus plano per AP, ostendemus tamen dari summam quaesitam omnium quadratorum, quam nempe aequalem esse dicimus rectangulo AGH una cum quadrato EG multiplicibus secundum numerum particularum in quas figura tota dividiturGa naar voetnoot2). Sit enim AE distantia inter rectas ED, AP ∞ a, ductisque ab F et O perpendicularibus in rectam AP, sit FP ∞ b, OQ ∞ c. Est itaque perpendicularis FK ∞ b-a, et perpend.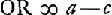 . adeoque quadratum . adeoque quadratum 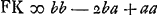 , et , et
| |
[pagina 547]
| |
quadratum 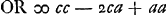 , patetque eadem ratione quadrata singularum perpendicularium tam quae ex particulis portionis DCB quam DAB cadunt in rectam ED, aequari quadrato distantiae particulae cujusque ab recta AP, una cum quadrato AE, minus duplo rectangulo à dicta distantia in ipsam AE. Quare ad colligendam omnium istorum quadratorum summam, appellemus nn summam quadratorum quae fiunt a distantijs singularum particularum ab recta AP. Item appellemus m summam omnium earundem distantiarum; unde dupla omnia rectangula ex distantijs singulis in rectam AE erunt 2ma. Denique et numerum particularum in quas divisa est figura ABCD vocemus θ. unde quad ratum rectae AE toties sumptum quot sunt in figura particulae, erit θaa. ac summa proinde omnium quadratorum à perpendicularibus in rectam ED, fiet , patetque eadem ratione quadrata singularum perpendicularium tam quae ex particulis portionis DCB quam DAB cadunt in rectam ED, aequari quadrato distantiae particulae cujusque ab recta AP, una cum quadrato AE, minus duplo rectangulo à dicta distantia in ipsam AE. Quare ad colligendam omnium istorum quadratorum summam, appellemus nn summam quadratorum quae fiunt a distantijs singularum particularum ab recta AP. Item appellemus m summam omnium earundem distantiarum; unde dupla omnia rectangula ex distantijs singulis in rectam AE erunt 2ma. Denique et numerum particularum in quas divisa est figura ABCD vocemus θ. unde quad ratum rectae AE toties sumptum quot sunt in figura particulae, erit θaa. ac summa proinde omnium quadratorum à perpendicularibus in rectam ED, fiet
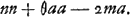 Est autem nn, hoc est, summa omnium quadratorum a perpendicularibus in rectam AP, aequalis rectangulo HAG multiplici secundum θ sive numerum particularum uti parte prima hujus propositionis demonstratum fuitGa naar voetnoot3). θaa vero apparet esse quadratum AE multiplex item secundum dictum particularum numerum. ac denique 2ma aequari dico duplo rectangulo ex GA, AE, multiplici secundum eundem particularum numerum, cum a sit ∞ AE; m vero, sive summa omnium perpendicularium a particulis figurae ABC in rectam AP descendentium, aequalis sit perpend. GA a centro gravitatis figurae descendenti multiplici secundum numerum perpendicularium seu particularum a quibus eductae sunt. Constat itaque nn+θaa-2ma, sive summam omnium quadratorum à perpendicularibus in rectam ED, aequari istis quae dicemus multiplicibus secundum numerum particularum, rectangulo nimirum HAG una cum quadrato AE, minus duplo rectangulo GAE, quae aequalia esse probantur rectangulo AGH una cum quadrato EG. Nam si AH vocetur h: AG vero g: Et AE, ut ante, sit a. Erit quidem rectangulum HAG, una cum quadrato AE, minus duplo rectangulo GAE, aequale hg+aa-2ga. At rectangulum AGH erit hg-gg; et quadratum EG, gg-2ag+aa, quae simul addita efficiunt quoque hg+aa-2ag. Itaque apparet et dictam summam omnium quadratorum aequari rectangulo AGH, unà cum quadrato EGGa naar voetnoot4). quod erat demonstrandumGa naar voetnoot5).
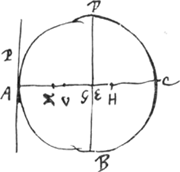
Iisdem positis si recta DE [Fig. 89] transit per G centrum gravitatis sigurae ABC, manifestum est dictam quadratorum summamGa naar voetnoot6) aequalem fore soli ▭o AGHGa naar voetnoot4), | |
[pagina 548]
| |
cum EG nulla sit. Atque hinc porro sequiturGa naar voetnoot1), si DE sit axis figurae ABC [Fig. 89]
 [Fig. 89.]
in duo segmenta aequalia ipsam dividens, AP vero ipsi parallela extra figuram. Et sit uti prius AG brachium figurae totius super AP: AH vero brachium cunei vel trunci abscissi super sigura tota plano per AP. Figurae autem dimidiae DAE brachium super DE sit VG, et XG brachium cunei super eadem dimidia figura abscissi plano per DE. his positis sequitur inquam rectangulum AGH aequale esse rectangulo XGV. Est enim rectangulum XGV multiplex secundum numerum particularum figurae dimidiae DAE, aequale quadratis omnibus perpendicularium à particulis ejusdem dimidiae figurae in rectam DE cadentium. Ac proinde idem rectangulum XGV multiplex secundum numerum particularum figurae totius ABCD, aequale erit quadratis perpendicularium a particulis totius figurae utrinque in rectam DE eductarum, hoc est, per ante ostensaGa naar voetnoot1), rectangulo AGH secundum eundem omnium figurae particularum numerum multiplici. unde patet rectangula ipsa VGX, AGH aequalia esseGa naar voetnoot2).
Data figura plana, et in eodem plano puncto, intra vel extra, divisaque figura in particulas aequales minimas, a quibus singulis ad dictum punctum rectae ducantur. invenire summam omnium quae ab ipsis fiunt quadratorum. sive invenire planum cujus multiplex secundum istarum particularum numerum aequetur dictae quadratorum summae. 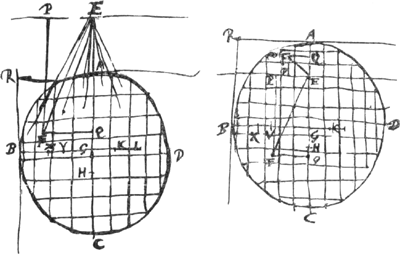 [Fig. 90.]
Sit figura plana ABCD [Fig. 90] et in eodem plano punctum E, divisaque figura in particulas minimas aequales intelligantur a singulis rectae ad punctum E ductae, sicut a particula F ducta FE. Oportetinvenire summam quadratorum ab omnibus hisce rectis. Secetur figura in partes duas, ductâ rectâ quae per datum punctum E perque centrum gravitatis figurae G transeat. Alteraque item per punctum E recta ducatur EP quaesecet EG ad | |
[pagina 549]
| |
angulos rectos. Sit autem data AH subcentrica cunei, super figura abscissi plano per AR tangentem figuram ac parallelam rectae EP. Item BK subcentrica cunei super figura abscissi plano per BR, tangentem figuram extrinsecus ac parallelam EG. Dico summam quadratorum à rectis quae ducuntur ad punctum E ex omnibus figurae particulis aequari rectangulis BGK, AGH una cum quadrato EG multiplicibus secundum numerum particularum in quas secta est figura. Ductis enim ab F perpendicularibus FP, FQ in rectas EP, EG. manifestum est quadratum FE aequari quadratis FP, PE vel FP, FQ. Eademque ratione quadrata singula distantiarum cujusque particulae à puncto E, aequari quadratis binis distantiarum ejusdem particulae ab rectis EP, EG. Quamobrem quadrata omnium distantiarum a puncto E, aequalia erunt summae quadratorum perpendicularium ab omnibus figurae particulis in rectam EP ductarum, una cum summa omnium quae fiunt a perpendicularibus in rectam EG ductis. Est autem summa horum per praeced. aequalis rectangulo BGK multiplici secundum numerum particularum, summa vero istorum aequalis rectangulo AGH una cum quadrato EG, similiter multiplicibusGa naar voetnoot3). Itaque quadrata omnia distantiarum a puncto E aequalia esse liquet rectangulis BGK, AGH cum quadrato EG, multiplicibus secundum quadratorum vel particularum numerum. quod erat demonstrandum.
Quod si autem recta EC sit axis figurae ABCD, in duo aequalia ac similia segmenta eam dividens, deturque GV brachium figurae dimidiae super recta EG, itemque GX brachium cunei super figura eadem dimidia abscissi plano per EG, potest loco rectanguli BGK sumi rectangulum XGV; quemadmodum prop....Ga naar voetnoot4) ostensum est. |
|