Oeuvres complètes. Tome XVI. Percussion

[p. 514]

XVI¹⁾.
[1664]²⁾.

On connaîtra le pendule isochrone avec une figure plane quelconque symétrique par rapport à un axe, suspendue en un point situé sur le prolongement de cet axe et oscillant d'un mouvement plan³⁾, lorsque le pendule isochrone avec la même figure suspendue au même point et oscillant d'un mouvement solide³⁾ est donné, ainsi que le pendule isochrone avec la demi-figure oscillant d'un mouvement solide autour de l'axe de la figure, et encore le centre de gravité de la demi-figure. En effet, la longueur du pendule cherché est égale à celle du premier des pendules donnés augmentée d'une droite, dont le rapport à la longueur du second pendule donné est égal au rapport de la distance du centre de gravité de la demi-figure jusqu'à l'axe de la figure à la distance du centre de gravité de la figure jusqu'au point de suspension.

Soit BAC [Fig. 72] la figure plane symétrique par rapport à l'axe AD. J'appelle symétrique par rapport à un axe toute figure dont les deux moitiés, ayant tourné autour de cet axe jusqu'à ce qu'elles se rencontrent, s'appliquent parfaitement l'une sur l'autre. Et soit E le point sur le prolongement de l'axe auquel la figure qui oscille dans son plan est suspendue. EH est la longueur donnée du pendule isochrone avec la figure lorsqu'elle se meut d'un mouvement solide, étant suspendue au même point; et HK la longueur du pendule isochrone avec la demi-figure ADC lorsque cette dernière oscille d'un mouvement solide autour de l'axe AD. Soit de plus L le centre de gravité de la figure ABC et M celui de la demi-figure DAC. Prenons HN de telle manière que EL:LM = KH:HN. Je dis que EN est la longueur du pendule isochrone avec le mouvement plan de la figure ABC suspendue en E. Appelant QP ou x le pendule isochrone avec la figure, je montrerai donc que ce pendule a une longueur égale à EN.

En effet, supposons la demi-figure ABD divisée en de très petits carrés égaux

1) Manuscrit B p. 200-211.

2) Comparez la note 2 de la p. 435.

3) Comparez sur le ‘motus planus’ (mouvement plan) et le ‘motus solidus’ (mouvement solide) les définitions données à la p. 499.

3) Comparez sur le ‘motus planus’ (mouvement plan) et le ‘motus solidus’ (mouvement solide) les définitions données à la p. 499.

[p. 515]

XVI¹⁾.
[1664]²⁾.

Figurae cuivis planae circa axem ordinatae et a puncto in axe producto suspensae motuque plano³⁾ agitatae pendulum isochronon habebitur, si detur pendulum isochronon figurae eidem ab eadem suspensione motu solido³⁾ agitatum; alterumque item isochronon dimidiae figurae motu solido agitatae circa figurae axem ac praeterea centrum gravitatis figurae dimidiae. Componitur enim quaesiti penduli longitudo, ex priore datorum pendulorum et ex ea linea quae sit ad posterius pendulum datum sicut distantia centri gravitatis figurae dimidiae ab axe figurae, ad distantiam centri gravitatis figurae a puncto suspensionis.

[Fig. 72.]

Sit figura plana BAC [Fig. 72] circa axem ordinata qui sit AD. Intelligo autem circa axem ordinatam figuram omnem, cujus medietates duae circa axem rotatae donec sibi mutuo occurrant, altera alteri congruant. Et sit in producto axe punctum E, unde suspensa figura agitetur motu plano. Ponatur autem EH esse longitudo penduli ipsi isochroni cum motu solido ex eadem suspensione agitatur. HK vero longitudo penduli isochroni dimidiatae figurae ADC, si circa axem AD agitetur motu solido. Sit autem L centrum gravitatis figurae ABC, et M dimidiatae DAC. Et ut EL ad LM ita sit KH ad HN. Dico EN esse longitudinem penduli isochroni motui plano figurae ABC ex E suspensae. Posito enim pendulo QP sive x, quod sit figurae isochronon, ostendam hoc longitudinem habere ipsius EN.

Intelligatur enim dimidia figura ABD secta in quadratula minima aequalia, duc-

1) Manuscrit B p. 200-211.

2) Comparez la note 2 de la p. 435.

3) Comparez sur le ‘motus planus’ (mouvement plan) et le ‘motus solidus’ (mouvement solide) les définitions données à la p. 499.

3) Comparez sur le ‘motus planus’ (mouvement plan) et le ‘motus solidus’ (mouvement solide) les définitions données à la p. 499.

[p. 516]

entre eux, et considérons, après avoir mené la droite EG perpendiculairement à ED, l'un quelconque de ces très petits carrés, p.e. celui dont F est le centre, duquel nous pouvons abaisser sur les droites ED et EG les perpendiculaires FO et FG. Tirons de plus la droite FE.

Or, le pendule x étant par hypothèse isochrone avec la figure ABC, si l'on suppose que l'un et l'autre exécutent une demi-oscillation maximale, c.à.d. d'un quart de cercle, après cette demi-oscillation la vitesse du poids P sera à celle du très petit carré F comme la longueur QP ou x est à la longueur EF que nous désignerons par b. En effet, il est évident que la vitesse du point F dépend de sa distance du point E, de sorte que d'autres points quelconques du plan ABC situés à la même distance du point E acquièrent la même vitesse. Mais comme QP² ou x² est à EF² ou b², ainsi est la hauteur à laquelle s'élève le poids P après avoir exécuté une demi-oscillation à la hauteur à laquelle monterait le petit carré F, si après avoir exécuté avec le plan une demi-oscillation il pouvait ensuite convertir seul son mouvement en ascension. Mais la dite hauteur du poids P est égale à QP ou x même, puisqu'il est certain que ce poids montera à une hauteur égale à celle dont il est descendu. Par conséquent, comme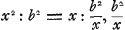 sera la hauteur à laquelle, comme nous l'avons dit, pourrait s'élever le petit carré F. Multipliant le petit carré par cette hauteur, on trouve donc b²f/x, c.à.d. le produit de EF² par le petit carré F, divisé par x. Or, le carré de EF est égal à la somme de FG² et de FO². Par conséquent le produit considéré du carré de EF par le petit carré F, divisé par x, sera égal à la somme des produits de FG², et de FO², multipliés l'un et l'autre par le petit carré F et divisés par x. Pareillement le produit de chacun des autres petits carrés par la hauteur à laquelle il pourrait s'élever si, après avoir exécuté une demi-oscillation, il s'élevait ensuite librement, sera trouvé égal à la somme de deux produits, obtenus en multipliant le petit carré lui-même par les carrés des perpendiculaires abaissées de son centre respectivement sur ED et sur EG, et divisés l'un et l'autre par x. Il s'ensuit donc que la somme de tous les produits des petits carrés par les hauteurs correspondantes auxquelles ils pourraient s'élever, est égale à la somme de tous les carrés des perpendiculaires abaissées des centres des petits carrés sur les droites ED et EG, multipliée par un petit carré tel que F et divisée par x. Nous pouvons représenter cette somme par l'expression , en appelant c² la somme des carrés de toutes les perpendiculaires nommées sur EG et d² celle des carrés de toutes les perpendiculaires sur ED. Mais la somme mentionnée des produits des petits carrés chacun par sa hauteur d'ascension doit être égale au produit de l'ensemble de tous les petits carrés, c.à.d. de la demi-figure ABC, par la hauteur dont son centre de gravité est descendu, c.à.d. par EL; en effet, ceci doit nécessairement avoir lieu

[p. 517]

tâque EG perpendiculari in ED, consideretur unum quoddam dictorum quadratulorum, puta cujus centrum F, a quo in rectas ED, EG, ducantur perpendiculares FO, FG et jungatur FE.

Jam quia pendulum x isochronon ponitur figurae ABC; si tum illud tum haec

[Fig. 72.]

maximam semioscillationem facere concipiantur, hoc est, quadrantalem, erit, in fine ejus, velocitas ponderis P ad velocitatem quadratuli F, sicut longitudo QP sive x ad longitudinem EF, quae dicatur b. Patet enim velocitatem puncti F pendere a distantia ejus à puncto E, adeo ut quaelibet alia puncta plani ABC quae tantundem ab E distant eandem quoque acquirant velocitatem. Sicut vero quadr. QP sive xx ad quadr. EF sive bb ita est altitudo ad quam ascendit peracta semioscillatione pondus P, ad altitudinem ascensus quadratuli F, si peracta cum plano semioscillatione separatim deinde sursum convertat motum suum. Dicta autem altitudo ponderis P est ipsa QP sive x; quum constet ad aequalem ei unde descendit altitudinem ascensurum; ergo quia xx ad bb ut x ad bb/x, erit bb/x altitudo ad quam, uti dictum est, ascenderet quadratulum F. quo itaque ducto in altitudinem istam, fit bbf/x, hoc est, quadratum EF ductum in quadratulum F productumque divisum per x. Est autem quadr. EF aequale quadratis FG et FO. Itaque dictum productum ex quadrato EF in quadratulum F, divisum per x, aequabitur productis duobus ex quadratis FG et FO singulis in quadratulum F, divisisque per x.

Eadem autem ratione productum ex unoquoque reliquorum quadratulorum in altitudinem ad quam ipsum ascenderet, si facta semioscillatione libere deinde sursum moveretur, invenietur aequale productis duobus ex quadratis perpendicularium a centro ejus in ED et EG cadentibus, ductis in ipsum quadratulum, singulisque divisis per x. Unde itaque sequitur summam omnium productorum ex quadratulis in dictas quo ascenderent altitudines, aequari summae omnium quadratorum¹⁾ quae

1) C.à.d. quadratorum perpendicularium.

[p. 518]

afin que le centre de gravité de tous les petits carrés, lorsqu'ils se sont élevés séparément et librement après avoir exécuté une demi-oscillation, se trouve à la même hauteur qu'avant le commencement de la demi-oscillation. Par conséquent la somme mentionnée plus haut sera égale au produit de la demi-figure ABD par la droite EL. Appelons ce produit pg, où la figure plane ABD est désignée par p et la droite EL par g. Comme on a donc , on trouvera, en multipliant

[Fig. 72.]

tous les termes par x, . Or, l'expression d²f, c.à.d. la somme des carrés des perpendiculaires à AD²⁾ qui partent des centres de tous les petits carrés, multipliés chacun par le carré correspondant, est égale au produit de la demi-figure ABD ou CAD²⁾ par le rectangle des deux longueurs KH, ML, parce que ML est la distance du centre de gravité de la figure DAC²⁾ à l'axe AD²⁾, et KH le bras de levier par rapport à AD²⁾ correspondant au centre de gravité du tronc érigé sur la figure CAD²⁾ ou ABD et limité par un plan passant par AD²⁾; c'est ce qui résulte de notre supposition que HK est la longueur du pendule isochrone avec la demi-figure considérée oscillant autour de l'axe AD²⁾. Pour une raison semblable c²f, c.à.d. la somme des carrés des perpendiculaires sur EG, multipliés chacun par un F correspondant, est égale au produit de la demi-figure ABD par le rectangle des deux longueurs HE et EL. En posant HE = k; EL, comme plus haut, = g; KH = m; ML = n, on aura donc



Rayant partout p et divisant par g, on obtient . Par conséquent,

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

[p. 519]

ex centris quadratulorum cadunt in rectas ED et EG ductae in quadratulum unum ut F divisaeque per x. quae summa dicatur , ponendo cc pro quadratis dictarum perpendicularium omnium super EG et dd pro quadratis omnium perpendicularium super ED. Atqui illa productorum summa, ex quadratulis in eas quo ascenderent altitudines, aequalis esse debet producto ex omnibus quadratulis hoc est ex dimidio figurae ABC in altitudinem unde descendit ejus centrum gravitatis, quae est EL; ita enim necesse est fieri quo centrum gravitatis quadratulorum omnium, postquam facta semioscillatione singula deinde liberae¹⁾ sursum ascenderunt, aeque altum inveniatur atque ante coeptam semioscillationem fuerat. Ergo summa praedicta aequabitur producto figurae dimidiae ABD in rectam EL. quod productum vocetur pg, ponendo p pro plano ABD, et g pro recta EL. quia ergo ; ductis omnibus in x, fiet . Est autem ddJ, hoc est summa quadratorum ex perpendicularibus super BD²⁾ quae a centris quadratulorum omnium exeunt, ductorum in singula quadratula, aequalis producto ex dimidia figura ABD seu CBD²⁾ in rectangulum duarum KH, ML, quia ML est distantia centri gravitatis figurae DBC²⁾ ab axe BD²⁾; KH vero distantia ex qua ponderat truncus erectus super figura CBD²⁾ vel ABD, abscissusque plano per BD²⁾; quippe cum ponatur HK longitudo penduli isochroni dictae dimidiae figurae agitatae circa axem BD²⁾. Similemque ob rationem ccf, hoc est summa quadratorum à perpendiculis super EG, ductorum in singula F, aequatur producto ex dimidia figura ABD ducta in rectangulum duarum HE, EL. Ponendo itaque HE ∞ k, EL uti suprà ∞ g; KH ∞ m; ML ∞ n;



Et delendo ubique p ac dividendo per g, fit . Ergo cum k sit EH, et mn/g quarta proportionalis tribus g, n, m, hoc est tribus EL, LM, KH, ac proinde

1) Lisez ‘libere’ ou ‘libera’.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

2) La figure que nous avons désignée par ‘Fig. 72’, se trouve à la p. 200 du Manuscrit; au revers de cette page Huygens reproduit la même figure en intervertissant les lettres A et B. Nous n'avons rien changé dans le texte latin, mais dans le texte français nous nous sommes conformés à la Fig. 72.

[p. 520]

comme k est EH, et que mn/g est quatrième proportionnelle aux trois longueurs g, n, m, c.à.d. aux trois longueurs EL, LM et KH, que mn/g est donc égale par construction à HN, l'expression sera égale à la ligne entière EN. Par conséquent x, c.à.d. QP, sera aussi égale à EN. Ce qu'il fallait démontrer.

Il apparaît donc qu'on peut trouver un pendule isochrone avec une figure plane quelconque suspendue en un point arbitraire du prolongement de l'axe et oscillant d'un mouvement plan, pourvu qu'on connaisse les centres de gravité suivants: 1) celle de la figure entière, 2) celle de la demi-figure, située de part et d'autre de l'axe. Il faut connaître en outre la distance du centre de gravité de l'onglet érigé sur la figure entière et limité par un plan passant par l'axe d'oscillation, jusqu'à un plan mené par le même axe d'oscillation et perpendiculaire au plan de la figure; et enfin la distance du centre de gravité de l'onglet construit sur la demifigure et limité par un plan passant par l'axe de la figure, jusqu'à un plan passant par le même axe et perpendiculaire à la figure¹⁾.

Trouver le pendule isochrone avec un rectangle suspendu en un point qui divise un des côtés en deux parties égales et qui oscille dans son plan.

Supposons le rectangle AB [Fig. 73] suspendu au point C qui divise le côté AE en deux parties égales, et soit CD l'axe du rectangle et F le point milieu de cet axe; F est donc le centre de gravité du rectangle AB, et si l'on tire la droite FH parallèle à CE et égale à la moitié de CE, H sera le centre de gravité du rectangle CB. Et si l'on prolonge la même droite FH jusqu'en K de sorte que FK = ⅔ CE, FK sera la longueur du pendule isochrone avec le rectangle CB, supposé que celui-ci oscille autour de l'axe CD. Pareillement si l'on prend CG = ⅔ CD, CG sera la longueur du pendule isochrone avec le rectangle entier AB oscillant autour de l'axe AE, bien entendu d'un mouvement solide. Soit CE = a et CD = b. Il importe donc de construire une nouvelle longueur FL de telle manière que l'on ait CF:FH, c.à.d. ½b:½a = FK, ou ⅔a:FL, laquelle sera donc ⅔ a²/b. Et en ajoutant cette longueur à CG = ⅔b, on trouve pour la longueur cherchée du pendule isochrone avec le rectangle AB. Or, on trouvera cette longueur par une construction très facile en traçant la diagonale CB du demi-rectangle, et ensuite la droite BN perpendiculaire à CB et rencontrant le prolongement de l'axe CD au point N, enfin en

1) Comparez, à la p. 477, les deux derniers alinéas de la note 2 de la p. 476.

[p. 521]

aequalis ex constructione ipsi HN; aequabitur toti EN. Ideoque et x hoc est QP ipsi EN aequalis erit. quod erat demonstrandum.

Patet igitur cuivis figurae planae a puncto quovis in axe producto suspensae motuque plano agitatae pendulum isochronon inveniri posse, si modo haec centra gravitatis noscantur, nempe figurae totius; figurae dimidiae ab alterutra parte axis. Praeterea distantia centri gravitatis ungulae super figura tota plano per axem oscillationis abscissae, a plano per eundem oscillationis axem ducto quod sit plano figurae ad angulos rectos ac denique distantia centri gravitatis ungulae super figura dimidia plano per axem figurae abscissae, à plano per eundem axem ducto atque ad figuram erecto¹⁾.

Rectangulo suspenso ex puncto quod latus bifariam dividit, motuque plano agitato pendulum isochronon invenire.

[Fig. 73.]

Esto rectangulum AB [Fig. 73] suspensum ex C puncto, latus AE bifariam dividente. sitque axis rectanguli CD, qui bifariam dividatur in F:Est ergo F centrum gravitatis rectanguli AB et ducta FH parallela CE ipsique dimidiae CE aequali, erit H centrum gravitatis rectanguli CB. Eadem vero FH productâ ad K ut sit FK ∞ ⅔ CE; erit FK longitudo penduli isochroni rectangulo CB, si super axi CD agitari concipiatur. similiterque sumta CG ∞ ⅔ CD, erit ea longitudo penduli isochroni rectangulo toti AB agitato circa axem AE, hoc est motu solido. Sit CE ∞ a, CD ∞ b. Oportet igitur facere sicut CF ad FH, hoc est, sicut ½b ad ½a ita FK sive ⅔a ad aliam FL, quae erit ⅔aa/b. quâ addita ad CG ∞ ⅔b, fit longitudo penduli isochroni rectangulo AB quae quaerebatur. Constructione autem facillima invenietur ea longitudo si ducatur CB diagonalis rectanguli dimidij. ipsique CB ad angulos rectos BN quae cum producto axe CD conveniat in N; ac sumatur CM aequalis ⅔ CN. Erit enim tota

1) Comparez, à la p. 477, les deux derniers alinéas de la note 2 de la p. 476.

[p. 522]

prenant CM = ⅔ CN. En effet, la longueur totale CN sera égale à , et par conséquent sera égale à la longueur cherchée. Mais pour trouver le pendule isochrone avec ce même rectangle lorsqu'il est suspendu en un point O situé sur le prolongement de l'axe DC [Fig. 74], nous pouvons poser OF = c et construire la longueur FP de telle manière que OF: FC, c.à.d. c:½b = GF, ou ⅙b:FP, laquelle sera donc 1/12 b²/c. Par conséquent sera le bras de levier du tronc construit sur le rectangle AB et limité par un plan mené par OQ parallèlement à AE, d'après la proposition...¹⁾ et par conséquent la même longueur OP sera la longueur du pendule isochrone avec le rectangle AB oscillant autour de OQ d'un mouvement solide²⁾. D'autre part FK = ⅔a est, comme plus haut, la longueur du pendule isochrone avec le rectangle CB oscillant autour de CD. Et en construisant une longueur de telle manière que OF:FH, c.à.d. c:½a = FK, ou ⅔a:cette longueur, celle-ci sera ⅓ a²/c, et en l'ajoutant à , on obtiendra pour la longueur cherchée du pendule isochrone avec le rectangle AB suspendu en O la formule . Pour construire cette longueur il faut d'abord trouver FN de telle manière que OF:FE, moitié de la diagonale du rectangle AB, = FE:FN, dont il faut prendre le tiers FM; la longueur entière OM sera alors la longueur cherchée du pendule. En effet, comme , on aura , et son tiers ; et par conséquent la longueur entière ; ce qui était la formule donnant la longueur du pendule³⁾.

On trouvera de la même manière le pendule isochrone avec le triangle isoscèle

1) Huygens n'a pas indiqué la proposition qu'il avait en vue. Voir les p. 507-509 (Fig. 67).

2) Voir la p. 509 qui précède.

3) Comparez la p. 469.

[p. 523]

longitudini quaesitae. Rectangulo autem eidem ex puncto O in axe DC [Fig. 74] producto suspenso isochronon pendulum ut inveniatur sit OF ∞ c et fiat ut OF ad FC, hoc est, ut c ad ½b, ita GF hoc est ⅙b ad FP, quae itaque erit 1/12 bb/c. Eritque brachium trunci super rectangulo AC abscissi plano per OQ parallelam AE ducto, per prop....¹⁾ ac proinde eadem OP longitudo penduli isochroni rectangulo AB

[Fig. 74.]

motu solido circa OQ agitato. FK autem ∞ ⅔a, est, ut prius, longitudo isochrona rectangulo CB circa CD agitato²⁾. Quare faciendo ut sicut OF ad FH, hoc est, ut c ad ½a, ita FK ∞ ⅔a ad aliam, ea erit ⅓aa/c, qua addita ad , siet longitudo quaesita penduli isochroni rectangulo AB ex O suspenso aequalis quae longitudo invenietur, si quemadmodum OF ad FE semidiagonium rectanguli AB, ita sit FE ad FN, cujus tertia pars sumatur FM, tota enim OM erit longitudo penduli quaesita. Quia enim , fit , ejusque triens FM ∞ ; ac proinde tota , quae erat inventa penduli longitudo³⁾.

Eadem methodo triangulo isosceli ABC [Fig. 75], suspenso ex puncto D in

1) Huygens n'a pas indiqué la proposition qu'il avait en vue. Voir les p. 507-509 (Fig. 67).

2) Voir la p. 509 qui précède.

3) Comparez la p. 469.

[p. 524]

ABC [Fig. 75] suspendu au point D situé sur le prolongement de l'axe BE. En effet, si l'on pose DE = a, BE = b, EC, moitié de la base, = c, la longueur du pendule isochrone deviendra . Remarquons que a- -⅓b est la longueur DF, c.à.d. la distance du point de suspension au centre de gravité du triangle. Dans le cas a = b, c.à.d. si le triangle est suspendu en son sommet B, il apparaît que la dite longueur sera . Et si en outre c = a, c.à.d. si l'angle ABC est droit, la dite longueur du pendule isochrone devient égale à a, c.à.d. à BE. Mais si le même triangle isoscèle est renversé [Fig. 76], le point de suspension D se trouvant toujours sur le prolongement de l'axe du triangle, et qu'on pose de nouveau DE = a, EB = b, EC ou EA = c, la longueur du pendule isochrone deviendra égale à , où l'on peut remarquer de nouveau que a+⅓b n'est autre que DF, distance du point de suspension au centre de gravité du triangle ABC. On voit aisément d'après cette formule que le triangle, suspendu comme nous l'avons fait ici, sera isochrone avec le triangle suspendu de la manière précédente, si la distance DF est la même dans les deux cas. Mais ceci sera démontré plus loin d'une façon plus générale¹⁾. Si dans le cas considéré a = 0, c.à.d. si le triangle est suspendu en E, point milieu de la base, la longueur du pendule isochrone sera égale à ; en d'autres termes, si l'on tire CN perpendiculairement au côté CB et rencontrant le prolongement de l'axe en N, la moitié de la longueur entière BN sera la longueur du pendule isochrone. Et si de plus c = b, cette longueur sera égale à b, c.à.d. à EB. D'où il apparaît que le triangle droit isoscèle a des oscillations isochrones dans les deux cas où il est suspendu respectivement au sommet et au milieu de la base.

Cette méthode nous permet aussi de trouver le pendule isochrone avec le secteur ABDC [Fig. 77] suspendu en A, centre du cercle dont il fait partie, ou en un point quelconque situé sur le prolongement de son axe AD. Ce qui ne peut être

1) Comparez la note 3 de la p. 461, ainsi que le quatrième alinéa de la note 3 de la p. 462 et les Prop. XII, XIII et XVI de la Pars Quarta de l'‘Horologium oscillatorium’.

[p. 525]

axe producto BE, pendulum isochronon invenietur. Nam positis DE ∞ a; BE

[Fig. 75.]

∞ b; EC dimidia basi ∝ c fit longitudo penduli isochroni . notetur vero quod a-⅓b est DF, quae nempe à puncto suspensionis pertingit ad trianguli gravitatis centrum. Si vero a ∞ b, hoc est si triangulum ex vertice B suspendatur, patet praedictam longitudinem fore . Quod si insuper c∞a, hoc est angulus ABC rectus, fit dicta penduli isochroni longitudo ∞ a, hoc est, ∞ BE.

[Fig. 76.]

Si vero inversum fuerit triangulum idem isosceles [Fig. 76] ut tamen punctum suspensionis D sit in axe trianguli producto; ponendo rursus DE ∞ a; EB ∞ b; EC vel EA ∞ c; fiet longitudo penduli isochroni . ubi notetur rursus a+⅓b esse DF, quae nempe à puncto suspensionis pertingit ad centrum gravitatis trianguli ABC. unde facile perspicitur, triangulum ita ut hic suspensum isochronum fore priorimodo suspenso, si distantia DF utrobique eadem fuerit. sed hoc postea universalius demonstrabitur¹⁾. Quod si hic fuerit a ∞ 0, hoc est, si triangulum ex puncto mediae²⁾ basis E suspendatur, erit longitudo penduli isochroni . hoc est ducta CN perpendiculari super latus CB, quae occurrat axi producto in N, erit semissis totius BN, longitudo penduli isochroni. Si vero insuper sit c ∞ b; erit ea longitudo ∞ b, hoc est, EB. Unde patet triangulum rectangulum isosceles, sive ex vertice sive ex media basi suspendatur isochronas oscillationes habere.

1) Comparez la note 3 de la p. 461, ainsi que le quatrième alinéa de la note 3 de la p. 462 et les Prop. XII, XIII et XVI de la Pars Quarta de l'‘Horologium oscillatorium’.

2) Lisez plutôt ‘medio’.

[p. 526]

calculé d'une autre manière excepté dans le cas de la suspension en A: dans ce dernier cas toutefois on peut aisément trouver le résultat d'après une autre méthode comme nous le montrerons plus loin¹⁾.

Soit AD, le diamètre du secteur, c.à.d. le rayon du cercle, = r; l'arc BD ou DC = p; le sinus BG = b, le sinus versus GD = a.

On a donc (F étant le centre de gravité du secteur ABC) AF = ⅔br/p, parce que ⅔ DA:AF = l'arc BD:sinus BG, comme nous l'avons démontré dans le livre sur la quadrature du cercle²⁾. Or, si nous tirons FO dans une direction parallèle à GC et AP de telle manière qu'elle divise l'angle DAC en deux parties égales, l'intersection des deux droites FO et AP, savoir H, sera le centre de gravité du demi-secteur ADC. Et comme CA:AG = CP:PG, on aura par composition , et par permutation , c.à.d. ; cette dernière longueur sera donc . Supposons construit sur le secteur ABC un onglet limité par un plan passant par AQ parallèle à BC; nous avons déjà trouvé³⁾ que la perpendiculaire abaissée du centre de gravité de l'onglet sur le plan ABC, a son pied en E, où AE = . Considérons encore l'onglet construit sur le demi-secteur ADC, limité par un plan passant par AD; nous avons trouvé que la distance entre la perpendiculaire, abaissée du centre de gravité de cet onglet sur le plan ABC, d'une part et l'axe AD d'autre part, distance que nous désignerons par EK, est égale à ⁴⁾. Si l'on construit donc une autre longueur EL de telle manière que le rapport AF:FH, c.à.d. (car nous avons démontré que c'est là la valeur du rapport AF:FH) soit égal au rapport de EK, ou , à EL, celle-ci sera , en d'autres termes, parce que ⁵⁾, la même longueur EL sera égale à . Et

1) Comparez lez p. 487-488, ainsi que le Theorème XXI de la Pars Quarta de l'‘Horologium oscillatorium (deuxième méthode pour trouver le ‘centrum oscillationis sectoris circuli’).

2) Voir à la p. 309 du T. XI le Theor. VIII des ‘Theoremata de Quadratura Hyperboles, Ellipsis et Circuli ex dato portionum gravitatis centro’.

3) En marge: ‘superius in hoc libro’. Voir la p. 487 qui précède.

4) Cette longueur EK a été trouvée dans le calcul de la p. 481, ou elle s'appelait KC.

5) En marge: ‘Euclid.’ (Prop. XXXV du Lib. III des ‘Elementa’).

[p. 527]

Sectori ABDC [Fig. 77] ex A centro circuli sui suspenso vel ex puncto quovis in producto axe AD pendulum isochronum hoc modo inveniri poterit. quod alio

[Fig. 77.]

fieri non potest, licet ex A suspenso facile inveniatur alia via, ut postea ostendetur¹⁾.

Sit AD diameter sectoris hoc est radius circuli ∞ r arcus BD vel DC ∞ p. sinus BG ∞ b. sinus versus GD ∞ a.

Est igitur AF (posito F centro gravitatis sectoris ABC) ∞ ⅔br/p; quia ut arcus BD ad sinum BG ita est ⅔ DA ad AF, ut demonstravimus in libro de quadratura circuli²⁾. Ducta autem FO parallela GC, et AP quae bifariam dividat angulum DAC, erit intersectio duarum FO, AP, nempe H centrum gravitatis dimidij sectoris ADC. Et quia CA ad AG ut CP ad PG, erit componendo, CA+AG ad AG ut CG ad GP, et permutando CA+AG ad CG hoc est ut 2r-a ad b ita AG ad GP sive AF ∞ ⅔br/p, ad FH, quae erit . Porro si intelligatur cuneus super sectore ABC, abscissus plano per AQ parallelam BC, invenimus³⁾ perpendicularem a centro gravitatis cunei ductam in planum ABC, cadere in E, ut sit . Item si intelligatur cuneus super dimidio sectore ADC, abscissus plano per AD, invenimus distantiam inter perpendiculum à centro gravitatis cunei hujus ductam in planum ABC, interque axem AD, quae distantia sit EK, esse ⁴⁾. Ergo si fiat ut AF ad FH, hoc est, ut 2r-a ad b (nam haec ostensa est ratio AF ad FH) ita EK , ad aliam EL; ca erit ; sive quia 2ar-aa ∞ bb⁵⁾, crit eadem

1) Comparez lez p. 487-488, ainsi que le Theorème XXI de la Pars Quarta de l'‘Horologium oscillatorium (deuxième méthode pour trouver le ‘centrum oscillationis sectoris circuli’).

2) Voir à la p. 309 du T. XI le Theor. VIII des ‘Theoremata de Quadratura Hyperboles, Ellipsis et Circuli ex dato portionum gravitatis centro’.

3) En marge: ‘superius in hoc libro’. Voir la p. 487 qui précède.

4) Cette longueur EK a été trouvée dans le calcul de la p. 481, ou elle s'appelait KC.

5) En marge: ‘Euclid.’ (Prop. XXXV du Lib. III des ‘Elementa’).

[p. 528]

en ajoutant cette longueur à , on obtient AL = ¾pr/b, ce qui est la longueur cherchée du pendule isochrone avec le secteur. C'est-à-dire, si l'on construit une longueur de telle manière qu'on ait: sinus BG: arc BD (ou bien corde BC:arc BDC) = ¾ rayon AD: la dite longueur, cette dernière sera AL, longueur cherchée du pendule. Et l'on déterminera ensuite sans difficulté le pendule isochrone, ou bien le centre d'oscillation, correspondant au même secteur dans le cas de suspension en un point plus éloigné, après que nous aurons démontré d'abord le théorème général qui suit.

Les distances des centres d'oscillation au centre de gravité d'une figure quelconque symétrique par rapport à un axe et oscillant dans son plan, sont inversement proportionnelles aux distances du point de suspension à ce centre de gravité¹⁾. Par conséquent, lorsque le centre d'oscillation d'une figure a été trouvé dans le cas de suspension contigue, ce centre sera aussi connu dans le cas de suspension éloignée, pourvu que l'on suppose le centre de gravité de la figure également connu.

Soit L [Fig. 78] le centre d'oscillation de la figure ABC suspendue en T, c.à.d. soit TL la longueur du pendule isochrone avec la figure. D'autre part soit F le centre de gravité de la figure. Puisse la même figure ensuite être suspendue en V, et qu'on ait VF:FT = LF:FO. Je dis que O est le centre d'oscillation de la figure suspendue en V²⁾.

En effet, soit FH la distance de l'axe AD au centre de gravité de la demi-figure ADC, et EK la distance du même axe à la perpendiculaire passant par le centre de gravité de l'onglet construit sur ADC et limité par un plan passant par AD. Soit E pareillement le pied de la perpendiculaire abaissée du centre de gravité du tronc sur la figure ABC, limité par un plan passant par la droite TX, perpendiculaire à l'axe AD et située dans le plan de la figure. Par conséquent si l'on construit FN de telle manière que VF:FT = EF:FN, N sera le pied de la perpendiculaire abaissée du centre de gravité du tronc limité par un plan passant par VM. Et si l'on construit ensuite EP de sorte que VF:FH = KE:EP, VN ajoutée à la longueur EP constituera la longueur du pendule isochrone avec le secteur suspendu en V. Mais puisque, par hypothèse, le pendule de longueur TL est isochrone avec

1) Comparez la note 1 de la p. 508 où l'on trouve la même proposition pour un autre cas spécial: celui de l'oscillation solide d'une figure plane.

2) Sur une des feuilles collées dans le Manuscrit B (voir la note 2 de la p. 435), plus précisément sur la p. 98 recto d'après la numération nouvelle, on lit la même Proposition dans la forme suivante: ‘Sicut distantiae puncti suspensionis à centro gravitatis figurae suspensae inter se ita distantiae centrorum oscillationis à centro gravitatis figurae cujuslibet contraria ratione respondent distantijs puncti suspensionis ab eodem centro gravitatis. Ideoque invento centro oscillationis figurae in suspensione contigua, idem quoque inventum erit in suspensione remota’. Ici aussi il n'est question que de ‘figurae’ c.à.d. de surfaces planes; plus tard Huygens a étendu ce théorème aux corps oscillants quelconques (‘Horologium oscillatorium’, Pars Quarta, Prop. XIX).

[p. 529]

+⅜pr/b, sit AL ∞ ¾pr/b, longitudo penduli sectori isochroni quae quaerebatur. Hoc est si fiat ut sinus BG ad arcum BD, sive ut subtensa BC ad arcum BDC, ita ¾ radij AD ad aliam ea erit AL longitudo penduli quaesita. Eidem vero sectori in suspensione remota nunc facile pendulum isochronon sive centrum oscillationis assignabitur, demonstrato prius hoc theoremate universali.

Distantiae centrorum oscillationis à centro gravitatis figurae cujuslibet circa axem ordinatae motuque plano agitatae, contraria ratione respondent distantijs puncti suspensionis ab eodem centro gravitatis¹⁾. Ideoque invento centro oscillationis figurae in suspensione contigua, idem quoque centrum habebitur in suspensione

[Fig. 78.]

remota, dummodo et centrum gravitatis figurae datum ponatur.

Sit figurae ABC [Fig. 78] suspensae ex T centrum oscillationis L, hoc est, sit TL longitudo penduli figurae isochroni. F vero sit figurae centrum gravitatis. Deinde eadem figura ex V suspendatur, et sicut VF ad FT, ita sit LF ad FO. Dico O esse centrum oscillationis figurae ex V suspensae²⁾.

Sit enim FH distantia axis AD à centro gravitatis dimidiae figurae ADC, EK vero ejusdem axis distantia à perpendiculari per centrum gravitatis cunei super ADC, abscissi plano per AD. Sitque E similiter sub centro gravitatis trunci super figura ABC, abscissi plano per rectam TX, perpendicularem axi AD, inque plano figurae sitam. Si igitur fiat ut VF ad FT ita EF ad FN, erit N sub centro gravitatis trunci abscissi plano per VM. Rursus si fiat ut VF ad FH ita KE ad EP, constituet VN una cum EP longitudinem penduli isochroni sectori suspenso ex V. Quia autem eidem ex T suspenso isochro-

1) Comparez la note 1 de la p. 508 où l'on trouve la même proposition pour un autre cas spécial: celui de l'oscillation solide d'une figure plane.

2) Sur une des feuilles collées dans le Manuscrit B (voir la note 2 de la p. 435), plus précisément sur la p. 98 recto d'après la numération nouvelle, on lit la même Proposition dans la forme suivante: ‘Sicut distantiae puncti suspensionis à centro gravitatis figurae suspensae inter se ita distantiae centrorum oscillationis à centro gravitatis figurae cujuslibet contraria ratione respondent distantijs puncti suspensionis ab eodem centro gravitatis. Ideoque invento centro oscillationis figurae in suspensione contigua, idem quoque inventum erit in suspensione remota’. Ici aussi il n'est question que de ‘figurae’ c.à.d. de surfaces planes; plus tard Huygens a étendu ce théorème aux corps oscillants quelconques (‘Horologium oscillatorium’, Pars Quarta, Prop. XIX).

[p. 530]

le même secteur suspendu en T, laquelle longueur est la somme de TE et de EL, et que E est le pied de la perpendiculaire abaissée du centre de gravité du tronc limité par un plan passant par TX, il est nécessaire que EL:EK = HF:FT. Or, nous avions EK:EP = VF:FH. Par conséquent, par la règle de la proportion dérangée¹⁾ on aura EL:EP = VF:FT. Mais nous avions aussi EF:FN = VF:FT. Par conséquent aussi la somme LE+EF, c.à.d. LF, est à la somme EP+FN, comme VF est à FT. Mais nous savions que la même longueur LF est à FO, comme VF est à FT. Par conséquent . Et il a été démontré que cette dernière somme constitue la longueur du pendule isochrone lorsque la suspension est en V. La ligne VO sera donc, elle aussi, la dite longueur du pendule, en d'autres termes, O sera le centre d'oscillation. Ce qu'il fallait démontrer. Si l'on pose donc, dans le cas du secteur que nous avons considéré plus haut²⁾, la distance VF, depuis le point de suspension jusqu'au centre de gravité du secteur, = q, et qu'on désigne les autres longueurs par les mêmes lettres qu'auparavant, savoir AD = r, BG = b, l'arc BD = p, la longueur du pendule isochrone VO devient égale à . En effet, nous avions trouvé AL = ¾pr/b. Si nous retranchons de cette longueur AF = ⅔rb/p, il reste . En construisant la longueur FO de telle manière que VF, ou q:FA, ou ⅔rb/p, = FL, ou , cette dernière devient égale à , et en y ajoutant VF = q on obtient , comme nous l'avons dit. Dans le cas où le secteur occupe tout un demi-cercle [Fig. 79], et que de plus le point de suspension est le centre A, on aura AD = BG, c.à.d. r = b, et q = AF = ⅔r²/p, et en substituant partout cette valeur de q, on obtient VO = ¾p. Mais si l'on suppose que le secteur remplit le cercle entier, BG s'annule, et par conséquent , dans quel cas, si q = r, c.à.d. si le cercle est suspendu au point B [Fig. 79] de la circonférence, la longueur du pendule deviendra BO = 3/2r, c.à.d. les trois quarts du diamètre. Mais nous arriverons à ce résultat³⁾ encore par

1) Voir la note 22 de la p. 304 du T. XI.

2) Voir la p. 527.

3) Voir les deux premiers alinéas de la p. 537.

[p. 531]

num est pendulum longitudinis TL, ex hypothesi, compositum nempe ex TE et EL estque E sub centro gravitatis trunci abscissa plano per TX; necesse est EL esse ad EK, sicut HF ad FT. Atqui EK erat ad EP ut VF ad FH. Ergo ex aequali in proportione perturbata¹⁾, erit EL ad EP ut VF ad FT. Sed ut VF ad FT ita quoque erat EF ad FN. Ergo etiam utraque simul LE, EF, hoc est LF ad utraque EP et FN, sicut VF ad FT. Erat autem ut VF ad FT ita eadem LF ad FO. Ergo FO aequalis erit duabus FN et EP; ac proinde tota VO aequalis duabus VN et EP. Quas ostensum est constituere longitudinem penduli isochroni cum suspensio est in V. Itaque et VO erit praedicta penduli longitudo, sive O centrum oscillationis, quod erat demonstrandum.

In sectore igitur de quo ante egimus²⁾, si ponatur distantia VF, a puncto suspensionis usque ad centrum gravitatis sectoris ∞ q; caeteris longitudinibus notatis ut prius, nempe AD ∞ r, BG ∞ b; arcu BD ∞ p; fit longitudo penduli isochroni . Erat enim inventa AL ∞ ¾pr/b. à qua auferendo AF ∞ ⅔rb/p, manet . quare faciendo ut VF, ∞ q, ad FA ∞ ⅔rb/p ita ad FO, fit ea , additaque VF ∞ q, fit VO , uti dictum.

[Fig. 79.]

Quod si sector semicirculum explet [Fig. 79], simulque suspensio sit ex centro A, erit AD ∞ BG, hoc est, r ∞ b: et q ∞ AF ∞ ⅔rr/p, quo ubique substituto in locum q, fit VO ∞ ¾p. Si vero circulum integrum sector explere intelligatur, fit BG nihilo aequalis, ideoque , ubi, si q fuerit aequalis r, hoc est si circulus ex circumferentiae puncto B [Fig. 79] suspendatur, fiet longitudo penduli BO ∞ 3/2r sive tribus quartis diametri. sed haec alijs modis quoque investigabimus³⁾. Dignum vero est animadversione, quod in quolibet sectore, si longitudo VA [Fig. 78] ex qua suspensus est, fit ∞ √½rr, hoc est, quae possit dimidium quadratum radij AB, erit longitudo penduli isochroni VO dupla VA, hoc est aequalis lateri

1) Voir la note 22 de la p. 304 du T. XI.

2) Voir la p. 527.

3) Voir les deux premiers alinéas de la p. 537.

[p. 532]

d'autres procédés. Ce qui mérite d'être remarqué, c'est que, dans le cas d'un secteur quelconque, si la longueur de la ligne VA [Fig. 78] à laquelle le secteur est suspendu, est égale à √½r², c.à.d. si la longueur de cette ligne est telle que son carré est égal à la moitié du carré du rayon AB, la longueur du pendule isochrone VO sera le double de VA, ce qui veut dire qu'elle sera égale au côté d'un carré inscrit dans le cercle du secteur; ce qu'on vérifie en substituant partout q, ou VF, , dans la valeur de VO trouvée auparavant, savoir : on trouvera ainsi VO = √2r². Mais nous avons obtenu ce résultat par une méthode différant de celle que nous avons expliquée ici.

Soit ABG [Fig. 80] une barre impondérable suspendue en A; on demande d'attacher en un point donné B de cette barre deux triangles égaux BC et BD, formant avec l'axe AB des angles égaux (triangles dont les angles B sont par hypothèse très petits ou plutôt infiniment petits), de telle manière que les triangles, suspendus de cette façon en A, ayent leurs oscillations isochrones avec un pendule simple de longueur donnée AL. Je dis que les bases des triangles, D et C (car ces bases peuvent être considérées comme des points), se trouvent sur une circonférence de cercle¹⁾.

En effet, soit AB = a, et la longueur AL = b. Abaissons la perpendiculaire DG sur AG et appelons BG, x et GD, y. Pour trouver maintenant le pendule isochrone avec la figure composée par les triangles BC et BD, suivant la méthode indiquée dans la proposition...²⁾, supposons construit au-dessus de chacun des deux triangles un tronc limité par un plan passant par AM, parallèle à GD. Le centre de gravité commun de ces deux troncs se trouvera sur le diamètre BG, et sera situé de la droite AM à une distance égale à la distance de cette droite du centre de gravité d'un tronc sur le triangle BG, dont l'angle au sommet B est également infiniment petit par hypothèse. Et l'on trouve le centre de gravité de ce tronc en prenant BE = ⅔BG, de sorte que E est le centre de gravité du triangle BG, et ensuite BF = ¾ BG, de sorte que F est le centre de gravité de l'onglet construit audessus du même triangle et limité par un plan passant par B, et en construisant

1) Ou plutôt: que le lieu des points C et D, pour une longueur donnée AL, est une circonférence de cercle.

2) Voir à la p. 515 le premier alinéa de la Pièce XVI.

[p. 533]

inscripti quadrati in circulo sectoris: quod apparet verum esse si in VO, ante reperta , ubique loco q ∞ VF, substituatur , hoc est, VA+AF. fiet enim VO ∞ √2rr. Alia tamen via huc devenimus, quam hic explicavimus. Virga ABG [Fig. 80] ponderis expers suspensa sit in A, oporteatque ad datum in ea punctum B affigere triangula duo paria et paribus angulis ab axe AB recedentia

[Fig. 80.]

BC, BD; quorum anguli ad B tanquam minimi, sive infinitè parvi considerentur; quaeque ita suspensa ab A, oscillationes isochronas habeant pendulo simplici datae longitudinis AL. Dico bases triangulorum D et C, hae enim ut puncta considerantur, esse ad circuli circumferentiam¹⁾. Sit enim AB ∞ a. longitudo AL ∞ b. ductaque DG perpendiculari in AG, vocetur BG, x; GD, y. Ut jam figurae ex triangulis BC, BD compositae pendulum isochronum inveniatur secundum methodum traditam propositione...²⁾ intelligatur super utroque triangulorum truncus erectus abscissus plano per AM ipsi GD parallelam. Horum truncorum centrum gravitatis commune erit in diametro BG, et tantundem distabit ab recta AM, atque centrum gravitatis trunci super triangulo BG cujus item in vertice B minimum esse angulum putandum est. hujus vero trunci centrum gravitatis invenitur, sumendo BE ∞ ⅔ BG, ut E sit centrum gravitatis trianguli BG; deinde BF ∞ ¾ BG, ut sit F centrum gravitatis cunei super triangulo eodem abscissi plano per B; ac faciendo demum ut AE, a+⅔x, ad EB, ⅔x, ita FE, 1/12x, ad EO, . erit enim O centrum gravitatis³⁾ trunci dicti super

1) Ou plutôt: que le lieu des points C et D, pour une longueur donnée AL, est une circonférence de cercle.

2) Voir à la p. 515 le premier alinéa de la Pièce XVI.

3) Voir la note 1 de la p. 535.

[p. 534]

enfin EO de telle manière que AE, ou a+⅔x, soit à EB, ou ⅔x, comme FE, ou 1/12x, est à EO, d'où l'on tire . En effet, O sera alors le centre de gravité¹⁾ du tronc considéré construit sur le triangle BG et limité par un plan passant par AM. est donc la longueur du pendule isochrone avec les triangles BC et BD oscillant d'un mouvement solide autour de l'axe AM. Il faut chercher ensuite la longueur du pendule isochrone avec l'un des deux triangles BD oscillant autour de l'axe BG, laquelle longueur sera FK, ligne tracée parallèlement à GD et rencontrant le triangle BD au point K; en effet, on aura BK = ¾ BD, et par conséquent K sera le centre de gravité de l'onglet construit sur le triangle BD et limité par un plan passant par BG, attendu que l'onglet a ici la forme d'une pyramide. Pareillement, si l'on tire EH parallèle à GD, on aura BH = ⅔ BD, et par conséquent H sera le centre de gravité du triangle BD. Si l'on construit donc une nouvelle longueur de telle manière que AE, ou a+⅔x, soit à EH ou ⅔ GD ou ⅔y, comme KF, qui est égale à ¾ DG ou ¾y, est à la dite longueur, celle-ci sera , et en l'ajoutant à AO qui avait la valeur , on obtiendra la longueur du pendule isochrone avec les triangles BC et BD, oscillant dans leur plan, savoir , qui doit donc être égale à la ligne donnée AL ou b, d'où l'on tire

Cette équation fait voir que l'extrémité de la ligne GD ou y, lorsque BG, ou x, est considérée comme une grandeur variable, se trouve sur une circonférence de cercle, parce que l'on a sous la racine le terme -x². Nous donnerons bientôt une descrip-

1) Ou plutôt la projection de ce centre de gravité sur le plan CBD.

[p. 535]

triangulo BG, abscissi plano per AM. Est igitur longitudo penduli isochroni triangulis BC, BD motu solido agitatis circa axem AM. Insuper vero quaerenda est penduli longitudo quod sit isochronum alteri triangulorum BD agitato circa axem BG, quae quidem longitudo erit FK, quae nempe linea ducta est parallela GD, triangulo BD occurrens in K; erit enim BK ∞ ¾ BD, ideoque K centrum gravitatis cunci super triangulo BD abscissi plano per BG, cum cuneus hic pyramidis formam habeat. Similiter vero ducta EH parallela GD, erit BH ∞ ⅔ BD, ideoque H centrum gravitatis trianguli BD. Itaque si fiat ut AE ∞ a+⅔x ad EH ∞ ⅔GD ∞ ⅔y, ita KF quae est ∞ ¾ DG ∞ ¾y ad aliam , haec addita ad AO, quae erat ∞ faciet longitudinem penduli isochroni triangulis BC, BD, motu plano agitatis, ; quae debet itaque aequari ipsi AL sive b unde fit



Ex hac autem aequatione patet terminum lineae GD sive y, quando BG sive x ut indeterminata consideratur, esse ad circuli circumferentiam quia habetur -xx. Cujus circuli descriptionem mox dabimus, sed prius animadvertendum est, quod si a ∞ 0, hoc est, si punctum B ubi affiguntur trianguli ponatur idem quod A, fore aequationem

[p. 536]

tion de ce cercle, mais il faut remarquer d'abord que, si a = 0, c.à.d. si le point B où sont attachés les triangles est par hypothèse le même que A, l'équation sera

Cela veut dire que, si l'on prend AO = ⅔b = ⅔ AL [Fig. 81], et qu'on décrit par A une circonférence de cercle ADN avec le centre O, l'extrémité de la perpendiculaire GD se trouvera sur cette circonférence.

Par conséquent, comme deux triangles quelconques à sommets A, infiniment aigus et symétriques, placés dans la circonférence ADNC, ont le centre d'oscillation L, où AL = ¾ diamètre AN; et comme le cercle entier est composé de pareilles paires de triangles, et que la même chose est vraie pour une portion quelconque BCDN du cercle, possédant des côtés égaux BC et BD: il est manifeste que le centre d'oscillation est en L, tant pour le cercle entier que pour une portion quelconque de ce genre¹⁾.

Autre cas particulier: si l'on substitue, dans l'équation, 8/3a = 4/3b, en d'autres termes 2a = b, c.à.d. si l'on suppose les triangles attachés en B, point milieu de la longueur AL, on aura [Fig. 82]. Cette équation nous apprend que si l'on décrit du centre B avec un rayon dont le carré est égal au double du carré de BA, une circonférence de cercle CND, deux triangles quelconques infiniment aigus à sommets B, terminés par des bases situées sur la circonférence et symétriques par rapport à AB, auront leur centre d'oscillation au point L, s'ils sont suspendus en A. Il en résulte, puisque le cercle total CND, aussi bien qu'un secteur quelconque de ce cercle symétrique par rapport à la droite AN, sont composés de paires de pareils triangles, que manifestement le point L sera le centre d'oscillation de ce cercle aussi bien que celui de tous ces secteurs. Par conséquent:

Tout secteur de cercle suspendu en un point éloigné du centre de son cercle à une distance égale à la moitié du côté du carré inscrit au cercle, aura un pendule isochrone égal au côté entier du carré nommé. C'est ce que nous avons déjà remarqué plus haut³⁾. Et si l'on pouvait trouver encore dans un autre cas le pendule isochrone avec un secteur sans supposer la longueur de l'arc de ce secteur donnée, de même que nous avons trouvé ici ce pendule sans connaître l'arc, on pourrait au contraire en déduire la longueur de l'arc du secteur. En effet, puisqu'un secteur

1) Comparez la p. 455.

3) Voir la fin de la p. 531.

[p. 537]

[Fig. 81.]

Hoc cst, si sumatur AO ∞ ⅔b ∞ ⅔ AL [Fig. 81], centroque O per A circulus describatur ADN; terminus perpendicularis GD erit ad ejus circumferentiam.

Cum igitur quaelibet duo triangula acutissima quae ex A ad circumferentiam ADNC constituuntur, magnitudine et situ sibi mutuo respondentia, centrum oscillationis habeant punctum L, positâ AL ∞ ¾ diametri AN: cumque circulus totus ex ejusmodi triangulorum paribus componatur, uti et portio ejus quaelibet ut BCND, latera BC, BD aequalia habens: manifestum est, tum circuli totius centrum oscillationis esse in L, tum portionis cujuslibet qualem diximus¹⁾.

Rursus si in aequatione inventa sit 8/3a ∞ 4/3b, hoc est 2a ∞ b, hoc est, si triangula

[Fig. 82.]

affigi intelligantur in B [Fig. 82] quod bifariam dividat longitudinem AL, erit . quae aequatio docet, quod si centro B, radio qui possit duplum BA, circumferentia describatur CND, bina quaelibet triangula acutissima vertices in B habentia, atque ad circumferentiam eam basibus terminata, angulisque aequalibus suber²⁾ AB inclinata, quod inquam suspensa ex A, centrum oscillationis habebunt punctum L. Unde cum et circulus integer CND, et sector ejus quilibet, axem habens rectam AN, ex triangulorum talium paribus componatur, manifestum est circuli et sectorum istorum centrum oscillationis fore punctum L. Itaque

Quilibet circuli sector suspensus à puncto quod distet a centro circuli sui semisse lateris quadrati circulo inscripti, pendulum isochronum habebit aequale integro dicti quadrati lateri. quod etiam supra animadvertimus³⁾. quod si vero aliquo praeterea casu, pendulum sectori alicui inveniri posset isochronon, non supposita

1) Comparez la p. 455.

2) Lisez ‘super’.

3) Voir la fin de la p. 531.

[p. 538]

quelconque BCD suspendu en A, de la même manière que plus haut, savoir en sorte que le carré de BA est égal à la moitié du carré de BC, a son centre d'oscillation en L [Fig. 83], où BL = BA, il suffira, si ce secteur, suspendu en un autre point donné R, a un centre d'oscillation P donné, de diviser la droite RL en Q de telle manière qu'on ait RQ:QL = AR:LP, où ces deux dernières longueurs sont données, pour trouver Q, centre de gravité du secteur BCD, comme cela ressort de la Prop...¹⁾; et, ce centre de gravité étant donné, nous savons que la corde CD est à l'arc correspondant comme BQ est à ⅔ du rayon BC.

Enfin, pour exécuter la construction générale correspondant à l'équation trouvée plus haut , ajoutons et retranchons des quantités qui se trouvent sous le radical les termes ; on obtiendra alors .

Par conséquent il faut diviser la longueur AL en deux parties égales en E [Fig. 84] et ajouter à BE sa tierce partie EF; F sera alors le centre de la circonférence que nous devons décrire. Quant au rayon FO, ce sera la ligne dont le carré est égal au double de la différence des carrés de AE et de EF. Si l'on construit donc du point B deux triangles symétriques extrêmement aigus et s'étendant jusqu'à la circonférence, tels que BD et BC, leur centre d'oscillation sera L lorsqu'ils sont suspendus en A. Par conséquent c'est également en L que se trouvera le centre d'oscillation d'une partie quelconque du cercle CCDD, telle que BCOD ou BCMD, ayant son sommet en B, symétrique par rapport à la droite AL et suspendue en A. Il en sera de même pour les segments de cercle KON et KMN; mais dans tous les autres cas, les centres d'oscillation de pareils segments ne peuvent être trouvés que lorsque la grandeur de l'arc est donnée.

Que si une partie du cercle telle que BCD est donnée, ou un segment de cercle tel que KON, et qu'on demande de trouver son point de suspension A de telle manière que cette partie de cercle ou ce segment soit isochrone avec un pendule de longueur donnée AL, il faut, après avoir déterminé le centre F du cercle correspondant, diminuer la distance FB d'un quart (FE) et prendre les longueurs EA et EL l'une et l'autre égale à une droite dont le carré est égal à la moitié du carré du rayon, augmenté du carré de EF.

1) Voir le deuxième alinéa de la p. 529.

[p. 539]

[Fig. 83.]

arcus longitudine data, sicut hic absque ea invenitur, daretur inde arcus sectoris ejus longitudo. Cum enim sector quivis BCD suspensus ex A, ut modo, ut nempe BA possit ½ quadrati BC, habeat centrum oscillationis L [Fig. 83], ut sit BL ∞ BA. si jam ex alio dato puncto R suspensus habeat centrum oscillationis datum P, oportebit tantum dividere rectam RL in Q, ut sit RQ ad QL ut AR ad LP quae datae sunt, eritque Q centrum gravitatis sectoris BCD, ut constat ex propos...¹⁾. dato autem hoc gravitatis centro scimus esse ut BQ ad ⅔ radij BC, ita subtensam CD ad suum arcum.

Porro ad universalem constructionem aequationis supra inventae y ∞ ; addatur et auferatur, quantitatibus in radice contentis, , fietque

[Fig. 84.]

Itaque dividatur longitudo AL bifariam in E [Fig. 84], et apponatur ad BE pars tertia sua EF, eritque F centrum describendi circuli. Radius autem FO, erit linea quae potest duplum differentiae quadratorum AE et EF. Si itaque ex puncto Bad descriptam circumferentiam triangula duo pariaacutissima constituantur ut BD, BC, illorum ex A suspensorum centrum oscillationis erit L. Quare et portionis cujuslibet circuli CCDD, cujus vertex sit in B axemque habeat in recta AL, quales sunt portiones

1) Voir le deuxième alinéa de la p. 529.

[p. 540]

Considérons encore une barre impondérable AB suspendue en A [Fig. 85] à laquelle on demande d'attacher en son point milieu C une autre barre pondérable

[Fig. 85.]

ED de telle manière que cette barre ainsi suspendue ait des oscillations isochrones avec un pendule de longueur donnée AB. Soit AB = a; appelons AC x et CD y, ces deux longueurs étant regardées comme indéterminées. Le pendule isochrone avec la barre ED suspendue à AC est alors facilement trouvé d'après ce qui a été démontré plus haut au sujet des rectangles²⁾; en effet, on peut considérer la barre ED comme un rectangle de très petite largeur, auquel sera isochrone un pendule de longueur AC augmentée d'un tiers de la troisième proportionnelle à AC et CD. Cette longueur totale sera donc ici ; par hypothèse elle doit être égale à la longueur donnée AB ou a. On en tire . Cette équation nous apprend que le lieu des points D et E est une ellipse, parce nous avons sous le radical le terme -3x². Le centre de cette ellipse sera le point F qui divise la longueur AB en deux parties égales. Et son ‘latus rectum’ par rapport aux ordonnées perpendiculaires à AB sera 3a, c.à.d. le triple de AB, tandis que AB elle-même sera le ‘latus transversum’. Par conséquent dans une ellipse AEBD décrite de cette manière toute droite pondérable ECD attachée en son centre à l'axe AB, le point de suspension restant en A, sera isochrone avec le pendule de longueur AB. Il en résulte que l'ellipse totale aussi bien qu'une partie quelconque de l'ellipse comprise entre une ou deux droites perpendiculaires à l'axe AB est isochrone avec le même pendule AB³⁾.

2) Voir la p. 523.

3) Voir sur cette ellipse la p. 446 qui précède. Dans la note 3 de cette p. 446 nous donnons le sens précis de l'expression ‘latus rectum... secundum quod possunt ordinatim applicatae’.

[p. 541]

BCOD, BCMD, ex A suspensi¹⁾, centrum oscillationis erit in L. atque adeo etiam segmentorum circuli KON et KMN; quorum alijs quibuscunque casibus, centrum oscillationis non nisi supposita arcus dimensione inveniri potest.

Quod si data sit circuli portio ut BCD vel segmentum circuli ut KON oporteatque invenire illius punctum A, unde suspensum isochronum sit pendulo notae longitudinis AL; invento circuli cujus datum est segmentum centro F; minuenda est distantia FB parte sui quarta FE; sumendaeque EA, EL singulae aequales ei quae potest dimidium quadratum radij una cum quadrato EF.

Sit rursus virga sine pondere AB suspensa in A [Fig. 85], cui alia virga ponderans, ED, affigenda sit puncto sui medio C. quae sic suspensa oscillationes isochronas habeat pendulo datae longitudinis AB. Sit AB ∞ a. AC vero vocetur x. CD, y: quae ambae tanquam indeterminatae considerantur: Pendulum itaque isochronum virgae ED ex AC suspensae, facile invenitur ex ijs quae supra de rectangulis ostensa sunt²⁾, potest enim ED virga ut rectangulum minimae latitudinis considerari, cui isochronum pendulum aequale erit AC una cum triente tertiae proportionalis duabus AC, CD: quae igitur tota longitudo hic erit , quae ex hypothesi aequari debet datae AB ∞ a. Unde fit ; sive y ∞ . Quae aequatio docet locum puncti D vel E esse ad ellipsin, quia habetur -3xx. cujus ellipsis centrum erit F punctum quo longitudo AB bifariam dividitur. Latus rectum vero secundum quod possunt ordinatim applicatae ad AB erit 3a sive triplum AB, atque ipsa AB latus transversum. Itaque in Ellipsi AEBD secundum ista descripta, quaelibet recta ponderans ECD axi AB medio sui puncto affixa, manente puncto suspensionis A, isochrona erit pendulo longitudinis AB. unde patet et Ellipsin totam et quamlibet ejus partem abscissam recta una vel duabus axi AB perpendicularibus, eidem pendulo AB isochronum esse³⁾.

1) Lisez ‘suspensae’.

2) Voir la p. 523.

3) Voir sur cette ellipse la p. 446 qui précède. Dans la note 3 de cette p. 446 nous donnons le sens précis de l'expression ‘latus rectum... secundum quod possunt ordinatim applicatae’.