Oeuvres complètes. Tome XVI. Percussion
(1929)–Christiaan Huygens–
Auteursrecht onbekend
[pagina 498]
| |
XVGa naar voetnoot1).
| |
[pagina 499]
| |
XVGa naar voetnoot1).
| |
[pagina 500]
| |
Considérons l'onglet AFC [Fig. 63] ou le tronc AEFC [Fig. 64] construit au-dessus de la surface plane ABCD [Fig. 63 et 64] et terminé par le plan oblique FE passant par la droite GH située dans le même plan que la figure ABCD. Soit K le centre de gravité de la figure ABCD et puisse une perpendiculaire à cette figure élevée en son centre de gravité rencontrer le plan oblique en L. Soit AMNC le prismatoïde à hauteur KL construit au-dessus de la même figure ABCD. Je dis que ce prismatoïde est égal au tronc ou à l'onglet mentionné. En effet, si l'on divise le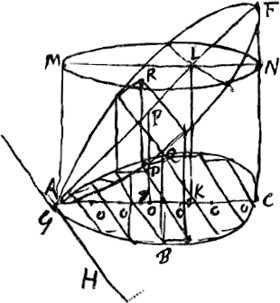 [Fig. 63.]
plan ABCD en de très petits rectangles OOO par des lignes parallèles à la droite GHGa naar voetnoot1), il est établi que si l'on multiplie chacun de ces rectangles par la distance de son centre de gravité à la droite GH (distances représentées par les droites OG) la somme des produits sera égale à celui de la droite GK par l'ensemble des dits rectangles O. Or, si GK = KL, il apparaît que chaque distance OG est égale à la parallèle à KL partant du point O correspondant et terminée par le plan oblique de l'onglet ou du tronc. Partant la somme des produits de chacune de ces hauteurs par le rectangle O correspondant sera égale au produit de KL par l'ensemble des rectangles O. Or, ces produits sont des parallélépipèdes à bases rectangulaires O, tels que BDRQ, produit de la hauteur OP par le rectangle DB; et ces parallélépipèdes composent le corps entier de l'onglet AFC ou du tronc AEFC. D'autre part il est évident que le produit de KL par l'ensemble des rectangles O est égal au prismatoïde AMNC; celui-ci sera donc égal à l'onglet AFC ou au tronc AEFC. Mais si KL est plus grande ou plus petite que KG, la hauteur de chacun des prismes de hauteur inégale considérés sera augmentée ou diminuée dans le rapport GK:KL, et la hauteur du prismatoïde pareillement. Par conséquent la somme de tous ces prismes, c.à.d. l'onglet, ou le tronc, AFC sera égale au prismatoïde AMNC, ce qu'il fallait démontrerGa naar voetnoot2). | |
[pagina 501]
| |
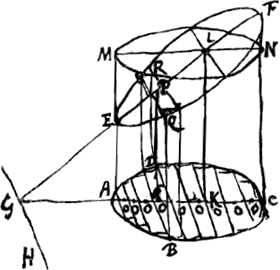 [Fig. 64.]
Sit super figura plana ABCD [Fig. 63 et 64] cuneus AFC [Fig. 63] vel truncus AEFC [Fig. 64], abscissus plano obliquo FE transeunte per rectam GH quae in eodem plano cum figura ABCD sita sit. Sitque figurae ABCD centrum gravitatis K, unde super ipsam perpendicularis educta occurrat plano obliquo in L. et intelligatur prismatoides AMNC super eadem figura ABCD altitudinem habens KL. dico hoc trunco vel cuneo praedicto aequale esse. Diviso enim plano ABCD in minima rectangula OOO, lineis rectae GH parallelisGa naar voetnoot1), constat singula horum rectangulorum ducta in distantias centrorum suorum gravitatis à recta GH, (quae distantiae denotentur rectis OG) summam productorum facere aequalem ei quod fit ex recta GK in omnia dicta rectangula O. Quod si jam GK aequalis sit KL, apparet etiam singulas distantias OG aequari singulis rectis ex punctis ijsdem O parallelis ipsi KL eductis usque ad planum cunei vel trunci obliquum. Quare et summa productorum ex singulis his altitudinibus in sua rectangula O ductis aequabitur producto ex KL in omnia rectangula O. Atqui ista producta sunt parallelepipeda super basibus rectangulis O, quale unum est BDRQ productum ex altitudine OP in rectangulum DB: quae parallelepipeda componunt cuneum totum AFC vel truncum AEFC; productum vero ex KL in omnia rectangula O, aequari manifestum est prismatoidi AMNC; ergo hoc cuneo AFC vel trunco AEFC aequale erit. Quod si vero KL major vel minor fuerit quam KG, priorum prismatum inaequalis altitudinis singulorum altitudo aucta erit vel diminuta secundum rationem GK ad KL, quemadmodum et prismatoidis altitudo. Ideoque rursus summa illorum omnium, hoc est, cuneus vel truncus AFC prismatoidi AMNC aequalis erit, quod erat demonstrandumGa naar voetnoot2). | |
[pagina 502]
| |
Lemme.Considérons [Fig. 65] une figure plane quelconque ABC et en dehors d'elle dans le même plan une ligne droite ED, et divisons cette figure en de très petits carrés égaux par des lignes droites se coupant à angles droits. Supposons encore que des perpendiculaires soient abaissées sur la dite ligne en dehors de la figure à partir des centres de gravité des différents petits carrés, p.e. la perpendiculaire FK partant du petit carré F. Élevons ensuite au-dessus de la figure ABC le tronc à angle demi-droit ALMC, limité par un plan passant par ED. Et soit EH la distance entre cette droite ED et le pied de la perpendiculaire abaissée du centre de gravité du tronc sur le plan ABC; EG la distance de cette même droite ED au centre de gravité de la figure ABC. Je dis que la somme des produits obtenus en multipliant chacun des carrés par le carré de la perpendiculaire abaissée de son centre de gravité sur la droite ED est égale au produit de la figure ABC par le rectangle des droites HE et EG. En effet, si nous considérons un des petits carrés en question tel que F, au-dessus duquel nous supposons construit le parallélépipède FN limité par le même plan que le tronc ALNC, il appert que la hauteur de ce parallélépipède est égale à la perpendiculaire FK, et que la même chose est vraie pour chacun des parallélépipèdes élevés sur les autres petits carrés; et il est évident que l'ensemble de ces parallélépipèdes n'est autre que le tronc ALMC. Or, si nous multiplions le parallélépipède NF par la perpendiculaire FK, tirée de la base du parallélépipède à la droite ED, c.à.d. si nous formons le produit du petit carré F par le carré de FK, et que nous multiplions de même chacun des parallélépipèdes par la perpendiculaire à ED correspondante, c.à.d. si nous formons le produit de chacun des petits carrés par le carré de la perpendiculaire à ED partant de ce petit carré: la somme des produits sera égale au produit de l'ensemble des parallélépipèdes, c.à.d. du tronc ALMC, par la distance EH, lorsque le tronc a son centre de gravité audessus du point H. Or, le tronc ALMC est égal au produit du plan ABC par la distance EG. Il apparaît donc que la somme des produits considérés des différents petits carrés par les carrés des perpendiculaires à ED correspondantes est égale au produit du plan ABC par le rectangle des distances HE et EG. Ce qu'il fallait démontrer.
Le pendule simple isochrone avec une figure plane quelconque, oscillant d'un mouvement solide, a une longueur égale à la distance entre l'axe d'oscillation et la perpendiculaire, abaissée sur la figure, du centre de gravité d'un onglet ou tronc construit sur cette figure et limité par un plan passant par l'axe d'oscillationGa naar voetnoot1). | |
[pagina 503]
| |
Lemma.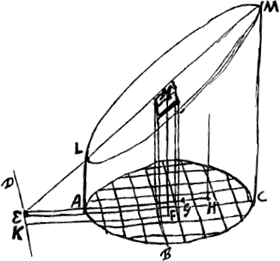 [Fig. 65.]
Sit figura quaevis plana ABC [Fig. 65], et extra eam in eodem plano linea recta ED, seceturque figura in quadrata minima aequalia lineis rectis sese ad rectos angulos secantibus. Et in dictam lineam extra figuram sitam ex centris gravitatis singulorum quadratulorum perpendiculares ductae intelligantur sicut ex quadratulo F ducta est perpendicularis FK. Porro super figura ABC, erigatur truncus anguli semirecti ALMC, abscissus plano per ED transeunte. Sitque EH distantia inter ipsam ED et terminum perpendicularis a centro gravitatis trunci in planum ABC dimissae. EG vero distantia ejusdem ED a centro gravitatis figurae ABC. Dico summam productorum quae fiunt ductis quadratulis singulis in quadrata perpendicularium ex suis centris gravitatis in rectam ED dimissarum, aequari producto ex figura ABC in rectangulum linearum HE, EG. Considerando enim unum dictorum quadratulorum ut F, super quod intelligatur parallelepipedum erigi FN, eodem plano quo truncus ALNC abscissum, apparet altitudinem ejus aequalem esse perpendiculari FK. idemque accidere singulis parallelepipedis super reliquis quadratulorum erectis; quae etiam simul sumpta aequalia liquet esse trunco ALMC. Ducto autem parallelepipedo NF in perpendicularem FK, à basi sua ad rectam ED ductam, hoc est ducto quadratulo F in quadratum ipsius FK: similiterque ductis parallelepipedis singulis in suas perpendiculares super ED, hoc est, quadratulis singulis in quadrata suarum perpendicularium super ED: summa productorum aequalis erit producto ex parallelepipedis omnibus, hoc est ex trunco ALMC in distantiam EH, quum truncus graviter super H. Est autem truncus ALMC aequalis producto ex plano ABC in distantiam EG. Patet igitur summam dictorum productorum ex quadratulis singulis in quadrata suarum perpendicularium super ED aequari producto ex plano ABC in rectangulum distantiarum HE, EG. quod erat demonstrandum.
Planae cuivis figurae, motu solido agitatae, isochronum est pendulum simplex cujus longitudo aequalis distantiae inter axem oscillationis et perpendicularem quae in figuram demittitur ex centro gravitatis cunei vel trunci super eadem figura erecti abscissique plano per axem oscillationis ductoGa naar voetnoot1). | |
[pagina 504]
| |
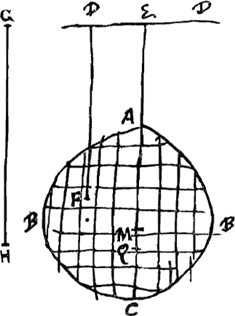
Considérons une figure plane quelconque ABC [Fig. 66], mise en mouvement autour de l'axe d'oscillation ED situé dans le même plan qu'elle. Et soit Q le point sous le centre de gravité du tronc ou de l'onglet construit sur la figure et limité par le plan passant par l'axe ED; QE étant une perpendiculaire à ce dernier. Je dis que cette perpendiculaire est la longueur du pendule isochrone avec la figure ABC. En effet, si GH représente le pendule isochrone avec la figure, je ferai voir que ce pendule est égal à EQ. Pour démontrer cette proposition, supposons la figure ABC divisée en de très petits carrés égaux entre euxGa naar voetnoot1); considérons un de ces carrés, p.e. celui qui a son centre en F, et abaissons de ce point une perpendiculaire sur la droite ED. Or, puisque le pendule GH est par hypothèse isochrone avec la figure ABC, le poids H et un point quelconque de la figure parcourront dans le même temps des arcs semblables, s'ils ont été écartés l'un et l'autre d'un même angle de la position verticale; et après une demi-oscillation le point H et un point de la figure à distance HG de l'axe ED auront la même vitesse. Admettons que l'un et l'autre accomplissent une demi-oscillation aussi grande que possible, nous voulons dire une demi-oscillation d'un quart de circonférence de cercle. Au bout de cette demi-oscillation la vitesse du poids H sera donc à la vitesse du petit carré F comme la longueur GH est à DF. Appelons GH, x; et DF, b. Nous savons que la hauteur à laquelle peut monter le poids H après avoir accompli une demi-oscillation est à la hauteur à laquelle pourrait s'élever le petit carré F si, après avoir accompli avec la figure une demi-oscillation, il était libre de monter séparément aussi haut que possible, comme le carré de GH, ou x2, est au carré de DF, ou b2. Mais la dite hauteur à laquelle peut s'élever le poids H n'est autre que GH ou x, puisqu'il est évident qu'il montera à une hauteur égale à celle dont il est descendu. Par conséquent, comme on a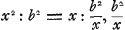 sera la hauteur à laquelle pourrait s'élever le petit carré F, comme nous venons de le dire. On obtient donc cette hauteur en divisant le carré de FD par la longueur GH. Le même raisonnement fera voir que la hauteur à laquelle pourrait s'élever l'un quelconque des autres petits carrés si, après avoir accompli une demi-oscillation, il pouvait employer son mouvement à monter aussi haut que possible, se calcule en divisant le carré de la distance du petit carré à la droite ED par la longueur GH ou x. Par conséquent, si l'on appelle c2 la somme de tous les carrés des distances des différents petits carrés à la droite ED, la somme de toutes ces hauteurs sera c2/x.
Or, si l'on multiplie chacune des hauteurs par le petit carré correspondant, la somme de tous les produits sera c2f/x. Et cette somme de produits doit être égale au produit de l'ensemble des petits carrés, c.à.d. de la figure ABC, par la hauteur | |
[pagina 505]
| |
 [Fig. 66.]
Sit plana figura quaevis ABC [Fig. 66], agitata circa axem oscillationis ED in eodem cum ipsa plano existentem. Sit autem punctum Q sub centro gravitatis trunci vel cunei super figura erecti abscissique plano per ED ducto; in quam perpendicularis sit QE. Dico hanc ipsam esse longitudinem penduli isochroni figurae ABC. Posito enim pendulo GH quod sit figurae isochronon ostendam hoc ipsi EQ aequale esse. Intelligatur enim figura ABC secta in quadrata minima aequaliaGa naar voetnoot1) quorum unum consideretur puta cujus centrum F, à quo in rectam ED perpendicularis ducatur FD. Jam quia pendulum GH isochronon ponitur figurae ABC, si aequalibus angulis a situ perpendiculari extrahantur, aequali tempore similes arcus pondus H et quodlibet figurae punctum percurrent, peractaque semioscillatione eadem erit celeritas ponderis H atque puncti figurae quod longitudine HG ab axe ED distabit. Ponamus autem utrumque facere semioscillationem maximam sive quadrantulae. Itaque in fine ejus erit celeritas ponderis H ad celeritatem quadratuli F sicut longitudo GH ad DF. Vocetur GH, x; DF, b. Est autem ut quadr. GH, hoc est, xx, ad quadratum DF, hoc est bb, ita altitudo quo ascenderet peracta semioscillatione pondus H, ad altitudinem quo ascenderet quadratulum F si peracta cum figura semioscillatione, separatim deinde motum suum sursum converteret. Dicta autem altitudo quo ascenderet pondus H est ipsa GH sive x, quum constet ad aequalem ei unde descendit altitudinem ascensurum. Ergo quia xx ad bb ut x ad bb/x, erit bb/x altitudo ad quam, uti dictum est, ascenderet quadratulum F. quam altitudinem itaque haberi constat applicando quadratum ex FD ad longitudinem GH. Eodem modo autem invenietur altitudo ad quam ascenderet unumquodque quadratulorum reliquorum si peractâ semioscillatione sursum suum motum converteret, oriri ex applicatione quadrati distantiae singulorum ab recta ED ad longitudinem GH sive x. Quare si summa omnium quadratorum, quae fiunt à distantijs singulorum quadratulorum ab recta ED, dicatur cc, erit summa omnium altitudinum illarum cc/x. Si vero singulae altitudines in quadratula sua ducantur, summa omnium producto- | |
[pagina 506]
| |
dont le centre de gravité de cette figure est descendu, laquelle hauteur est EMGa naar voetnoot1) à cause de l'amplitude maximale de la demi-oscillation; en effet, il faut admettre cette égalité qui exprime que le centre de gravité de tous les petits carrés, après que chacun d'eux a converti en ascension la vitesse acquise par la demioscillation, est situé à une hauteur égale à celle dont le centre de gravité est descendu par hypothèse. Par conséquent, si nous appelons p la figure ABC et g la distance ME, la somme en question c2f/x sera égale à pg; et en multipliant les deux membres par x, on obtiendra: c2f = pgx. Nous savons en outre que l'expression c2f, c.à.d. la somme des produits qu'on obtient en multipliant chacun des petits carrés par le carré de sa distance à la droite ED, est égale au produit du rectangle de ME et de QE par la figure ABC, bien entendu en considérant un tronc à angle demi-droit sous le centre de gravité duquel se trouve le point Q. Posant QE = k, nous aurons donc gkp = c2f. Mais nous avons démontré que c2f = pgx. Par conséquent on a aussi gkp = pgx. Et, en divisant de part et d'autre par gp, on aura k = x, c.à.d. EQ = GH, ce qu'il fallait démontrer. Il importe donc de connaître le centre de gravité de l'onglet construit sur la figure plane ou du moins la distance entre l'axe d'oscillation et le plan parallèle à cet axe perpendiculaire à la base de l'onglet et passant par le centre de gravité de ce dernier, pour qu'on puisse trouver le pendule isochrone avec la figure oscillant d'un mouvement solide autour d'un axe qui la touche. Et pour trouver le pendule isochrone correspondant au cas où l'oscillation a lieu autour d'un axe extérieur à la figure et ne la touchant pas, il faut trouver d'abord le centre de gravité du tronc ou du moins la dite distance au plan passant par ce centre. Lorsque cette dernière distance est connue pour l'onglet, et qu'on connaît aussi le centre de gravité de la figure donnée, base de l'onglet, la distance correspondante pour le tronc sera toujours, elle aussi, connue: on la déterminera de la manière suivante. Considérons le tronc AKLC [Fig. 67] construit au-dessus d'une figure plane quelconque, représentée, lorsqu'on la regarde de côté, par la ligne AC. Le tronc est limité par un plan passant par la droite EE située dans le même plan que la figure; la droite CAE passant par M, centre de gravité de la figure, est par hypothèse perpendiculaire à EE. Quant à la longueur AC il faut savoir qu'elle est égale à la distance de deux droites parallèles à EE et comprenant entre elles la base du tronc AKLC. Or, si nous divisons le tronc considéré par un plan KT passant par K et parallèle à AC en un onglet KLT et un prismatoïde AKTC, et qu'un plan passant par le centre de gravité de l'onglet KLT coupe la droite AC en S perpendiculairement; et qu'on construise MQ de telle manière que EM: MA = SM:MQGa naar voetnoot2); je dis que Q se trouve dans un plan perpendiculaire à AC et passant par le centre de gravité du tronc AKLC. | |
[pagina 507]
| |
rum erit ccf/x. Haec vero productorum summa aequalis esse debet producto ex omnibus quadratulis, hoc est, ex figura ABC in altitudinem unde descendit ipsius centrum gravitatis; quae est EMGa naar voetnoot1), propter semioscillationem maximam; ita enim fieri necesse est, quo centrum gravitatis quadratulorum omnium, postquam singula celeritatem semioscillatione acquisitam sursum converterunt, aeque altum inveniatur atque unde descendisse ponitur. Ergo, ponendo p pro figura ABC, et g pro distantia ME, erit summa praedicta ccf/x ∞ pg; ac ducendo utraque in x, fiet ccf ∞ pgx. Jam porro ccf, hoc est, summam productorum, quae fiunt ducendo singula quadratula in quadrata suarum distantiarum ab recta ED, scimus aequari producto ex rectangulo ME, QE in figuram ABC, si nempe truncum anguli semirecti ponamus sub cujus centro gravitatis est punctum Q; ergo ponendo QE ∞ k, erit gkp ∞ ccf. Sed ccf ostendimus aequari pgx. Ergo et gkp ∞ pgx. Et, dividendo utrinque per gp, erit k ∞ x, hoc est EQ ∞ GH, quod erat ostendendum. Oportet igitur novisse centrum gravitatis cunei supra plana aut saltem distantiam inter axem oscillationis et planum ipsi parallelum quod per centrum gravitatis cunei in basin ejus perpendiculare est ut figurae agitatae motu solido circa axem qui ipsam contingat, pendulum isochronon reperiri possit. Ut autem habeatur agitatae circa axem remotum, oportet trunci centrum gravitatis aut dictam distantiam plani per ipsum ducti prius invenire. Semper autem data illa distantia in cuneo, itemque centro gravitatis figurae propositae quae basis ejus est, etiam distantia in trunco ea dabitur, reperieturque hoc modo. 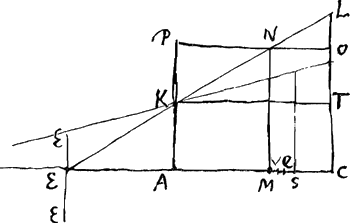 [Fig. 67.]
Sit super plana figura qualibet, quae a latere inspecta referatur linea AC [Fig. 67], erectus truncus AKLC, abscissus plano ducto per rectam EE in eodem figurae plano jacente et ad quam recta CAE, per figurae centrum gravitatis quod sit M, transiens, perpendicularis intelligitur. longitudo autem AC tanta putanda est quanta est distantia duarum rectae EE parallelarum quae basin trunci AKLC comprehendunt. Quod si jam ducto per K plano KT ipsi AC parallelo dividatur truncus propositus in cuneum KLT et prismatoides AKTC; perque centrum gravitatis cunei KLT transiens planum secet rectam AC | |
[pagina 508]
| |
En effet, prolongeons le prismatoïde AKTC [Fig. 67] jusqu'en PO de telle manière que le corps entier APOC soit égal au tronc AKLC, savoir en faisant passer un plan parallèle à ACGa naar voetnoot2) par le point N où la perpendiculaire élevée au centre de gravité M rencontre le plan KL. Il en résultera aussi que le prismatoïde KPOT est égal à l'onglet KLTGa naar voetnoot3). Or, le prismatoïde APOC est à KPOT comme CO est à OT, c.à.d. comme EN est à NK, c.à.d. comme EM est à MA, c.à.d. comme SM est à MQ. C'est pourquoi le même prismatoïde APOC sera aussi à l'onglet KLT comme SM est à MQ; d'où l'on tire par partage que le rapport du prismatoïde AKTC à l'onglet KLT est égal à SQ:QM. Or, l'onglet KLT a son centre de gravité au-dessus du point S et le prismatoide AKTC a son centre de gravité au-dessus du point M, puisque M est le centre de gravité de sa base. Par conséquent comme SM est divisée de telle manière en Q que les distances QS et QM sont inversement proportionnelles aux poids qui se trouvent au-dessus de S et de M, Q sera le point d'équilibre du poids composé de ces deux poids, l'équilibre étant considéré par rapport à la ligne EEGa naar voetnoot4). Par conséquent EQ sera la distance cherchée et en même temps la longueur du pendule isochrone avec la figure AC oscillant autour de l'axe EE. Lorsqu'un rectangle tel que ABCD [Fig. 68] oscille d'un mouvement solide autour d'un de ses côtés AB, la longueur du pendule isochrone EF sera donc égale à deux tiers du côté AD perpendiculaire à l'axe; en effet, un onglet étant construit sur le rectangle ABCD, onglet limité par un plan passant par AB, l'extrémité d'une perpendiculaire abaissée sur le plan AC et passant par le centre de gravité de l'onglet est située à une distance de AB égale à deux tiers ducôté AD. On en conclut aisément que le centre d'oscillation d'une barre ou ligne pesante, en d'autres termes l'extrémité du pendule isochrone avec elle et suspendu au même point,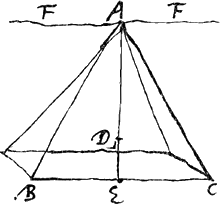 [Fig. 69.]
est éloigné de ce point à une distance de deux tiers de la longueur de la barre. Mais lorsqu'un triangle isoscèle BAC [Fig. 69] suspendu à son sommet A oscille d'un mouvement solide, son centre d'oscillation D se trouvera à une distance de A égale à trois quarts du diamètre AE. En effet, l'onglet construit au-dessus dutriangle ABC et limité par un plan passant par FAF qui est parallèle à la base BC, n'est autre chose qu'une pyramide scalène ayant son sommet en A et dont la perpendiculaire du sommet sur la base est le diamètre AE du triangle donné. Or, le plan passant par | |
[pagina 509]
| |
ad angulos rectos in S. Et fiat sicut EM ad MA, ita SM ad MQGa naar voetnoot1). Dico Q esse in plano per centrum gravitatis trunci AKLC transeunte ad AC recto. Extendatur enim prismatoides AKTC (Fig. 67) usque in PO, ut totum APOC sit trunco AKLC aequale, ducto nempe plano opposito OCGa naar voetnoot2) per N punctum, ubi perpendicularis a centro gravitatis M occurrit plano KL. Erit igitur et prismatoides KPOT aequale cuneo KLTGa naar voetnoot3). Est autem prismatoides APOC ad KPOT ut CO ad OT, hoc est, ut EN ad NK, hoc est ut EM ad MA, hoc est, ut SM ad MQ. Quare idem prismatoides APOC erit quoque ad cuneum KLT ut SM ad MQ, et dividendo proinde, sicut prismatoides AKTC ad cuneum KLT ita SQ ad QM. Incumbit autem gravitas cunei KLT super S, et gravitas prismatoidis AKTC super M, quia M est centrum gravitatis baseos ipsius. Ergo cum SM ita divisa sit in Q ut distantiae QS, QM gravitatibus super S et M contraria ratione respondeant, erit Q punctum aequilibrij gravitatis ex utrisque compositae, saltem respectu lineae EEGa naar voetnoot4). ideoque EQ erit quaesita distantia, eademque longitudo penduli quod figurae AC circa axem EE agitatae isochronum sit. 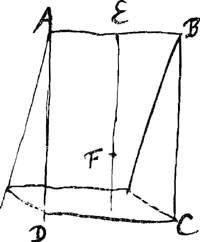 [Fig. 68.]
Si igitur rectangulum ut ABCD [Fig. 68] circa unum laterum AB agitetur motu solido, erit longitudo penduli isochroni EF aequalis ⅔ lateris pendentis AD, quia nempe cuneo existente super rectangulum ABCD, abscisso plano ducto per AB, terminus perpendicularis per centrum gravitatis cunei in planum AC ductae abest ab AB duabus tertijs lateris ABGa naar voetnoot5). Unde facile intelligitur etiam virgae seu lineae ponderantis centrum oscillationis seu terminum penduli isochroni ab eodem puncto suspensi, distare ab hoc puncto duabus tertijs longitudinis virgae. Si vero triangulum isosceles BAC [Fig. 69] ab angulo verticis A agitetur motu solido, centrum oscillationis ejus D distabit ab A tribus quartis diametri AE. quia nempe cuneus super triangulo ABC, abscissus plano per FAF basi BC parallelam, nihil aliud est quam pyramis scalena verticem habens A, perpendicularem | |
[pagina 510]
| |
le centre de gravité de cette pyramide et parallèle à sa base, perpendiculaire par conséquent au plan du triangle ABC, coupera la droite AE en D, de sorte que les trois quarts de AE constitueront la longueur AD, comme on sait. Lorsqu'au contraire le triangle isoscèle BAC oscille autour de sa base CB [Fig. 70], je dis que son centre d'oscillation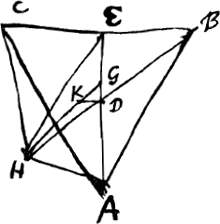 [Fig. 70.]
divise le diamètre EA en deux parties égales. En effet, l'onglet construit audessus du triangle ABC et limité par un plan passant par CB est alors une pyramide ayant le triangle donné ABC pour base et un côté AH perpendiculaire à ce triangle, et si du sommet H de cette pyramide on tire une droite jusqu'au point G, centre de gravité du triangle ABC, et qu'on prend sur cette droite GK = ¼ GH, K sera le centre de gravité de la pyramide. Abaissons de ce point une perpendiculaire KD sur le plan du triangle, laquelle aura son pied sur le diamètre du triangle attendu que le sommet H est au-dessus du point A, alors on aura GD = ¼ GA, vu que KD est parallèle à HA. Puisque EG est égale à ⅓ EA et CD à ¼ GA ou ½ EG, ou ⅙ EA, il est manifeste que la somme de EG et de GD est égale à la moitié de la longueur totale EA. Or, ED est la longueur du pendule isochrone avec le triangle ABC, attendu que D est le pied de la perpendiculaire partant du centre de gravité de l'onglet construit sur le triangle et limité par un plan passant par CB. Quant à un cercle AB [Fig. 71] oscillant autour d'une tangente DA, il sera isochrone avec un pendule AE égal à ⅝ du diamètre AB. En effet, considérons l'onglet AFB construit sur ce cercle et limité par un plan passant par AD, et en même temps le cône scalène AFB construit sur la même base et ayant son sommet en F. Puisqu'alors, si l'on découpe ce cône et en même temps l'onglet en des tranches très minces par des plans perpendiculaires à la base AB et parallèles à la droite AD, les sections sont des rectangles dans l'onglet, mais dans le cône des paraboles inscrites à ces rectangles dont la surface est égale aux deux tiers de celle du rectangle correspondant, il est évident que le cône et l'onglet ont leurs | |
[pagina 511]
| |
vero a vertice in basin, ipsam AE trianguli diametrum. planum autem per centrum gravitatis pyramidis actum basi suae parallelum hoc est erectum ad planum trianguli ABC, secabit rectam AE in EGa naar voetnoot1) ut AE sint ¾ AEGa naar voetnoot2) ut satis notum est. Rursus si circa basin CB [Fig. 70] agitetur triangulum isosceles BAC, centrum oscillationis ejus bifariam secare aio diametrum EA. Est enim cuneus, super triangulo ABC, plano per CB abscissus, pyramis basin habens ipsum triangulum ABC, latus vero AH triangulo ad angulos rectos à cujus pyramidis vertice H, si ducatur recta ad punctum G quod pono esse centrum gravitatis trianguli ABC, sumaturque in ea GK aequalis ¼ GH, erit K centrum gravitatis pyramidis; cadat autem ab ipso KD perpendicularis in planum trianguli, quae quidem incidet in diametrum ejus cum vertex H sit supra A, eritque GD ∞ ¼ GA, cum KD ipsi HA sit parallela. Quia igitur EG est ⅓ EA, et GD ¼ GA sive ½ EG, sive ⅙ EA, manifestum est EG una cum GD efficere dimidium totius EA. Est autem ED longitudo penduli triangulo ABC isochroni, cum in D cadat perpendicularis a centro gravitatis cunei super triangulo abscissi plano per CB. 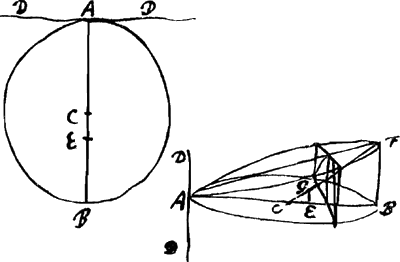 [Fig. 71.]
Circulus autem AB [Fig. 71] agitatus circa tangentem DA isochronus erit pendulo AE aequali ⅝ diam. AB. Sit enim super ipsum cuneus AFB abscissus plano per AD. simul autem et conus scalenus AFB super eadem basi intelligatur constitutus verticem habens F. Quia igitur secando conum hunc simulque cuneum in solida minima planis super AB basi erectis parallelisque rectae AD, in cuneo quidem sectiones sunt rectangula in cono vero parabolae singulis rectangulis istis inscriptae, | |
[pagina 512]
| |
centres de gravité au-dessus d'un même point de la droite AB. Mais si l'on réunit F, sommet du cône, par une droite FC au centre de la base, et qu'on prend CG = ¼ CF, G sera le centre de gravité du cône; et si de là on abaisse une perpendiculaire GE sur AB, E sera le point au-dessus duquel se trouve le centre de gravité du cône, partant aussi celui de l'onglet AFB. Et comme GE est parallèle à FB, on aura CE = ¼CB, et par conséquent AE = ⅝ AB. Telle sera donc aussi la longueur du pendule isochrone avec le cercleGa naar voetnoot1). | |
[pagina 513]
| |
quae ubique eorum sunt subsesquialterae, manifestum est conum cuneumque centro gravitatis suae incumbere eodem puncto rectae AB. Ducta autem FC a vertice coni F ad centrum baseos, sumtaque CG ∞ ¼ CF, erit G centrum gravitatis coni; unde si cadat in AB perpendiculum GE, erit punctum E super quo incumbit centrum gravitatis coni ac proinde et cunei AFB. Et quia GE est parallela FB erit CE ∞ ¼ CB. ideoque AE ∞ ⅝ AB. Ergo tanta quoque erit longitudo penduli circulo isochroniGa naar voetnoot1). |
|
