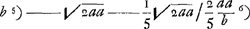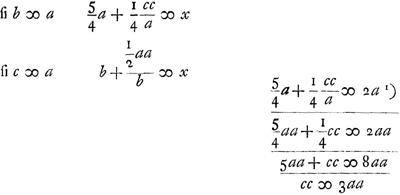|
-
voetnoot1)
- Cette Pièce est empruntée aux p. 165-168 et 174 du Manuscrit B, à une des feuilles collées dans ce Manuscrit mentionnées dans la note 2 de la p. 435, et à une autre feuille collée dans le même Manuscrit (voir la note 1 de la p. 475).
-
voetnoot2)
- Voir la note 2 de la p. 435, et la note 3 de la p. 462, où nous avons fait mention de la découverte du centre d'oscillation de la sphère.
-
voetnoot3)
- La Première Partie est empruntée à une des feuilles collées dans le Manuscrit, plus précisément à la p. 99 recto.
-
voetnoot4)
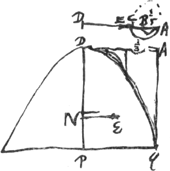
- Il y a deux points E dans la figure. Ici il s'agit du point inférieur E. Plus haut, à gauche, on voit une troisième lettre qui ressemble à un E, mais qui est en réalité un M tourné de 90o.
-
voetnoot4)
- Il y a deux points E dans la figure. Ici il s'agit du point inférieur E. Plus haut, à gauche, on voit une troisième lettre qui ressemble à un E, mais qui est en réalité un M tourné de 90o.
-
voetnoot6)
- Le présent calcul doit être antérieur à celui de la Deuxième Partie qui suit; en effet, ce dernier fait voir que la restriction ‘AD vero major quam latus quadrati in circulo BCE’ est superflue. Pour pouvoir expliquer les raisonnements de Huygens de la Première et de la Deuxième Partie, nous devons admettre qu'il avait trouvé en ce moment la formule générale pour la longueur du pendule isochrone avec un corps oscillant quelconque.
On peut en effet déduirecette formule générale de considérations qui se rattachent aux calculs précédents (Pièces VI et VII; voir pour ce qui suit la Fig. 23 à la p. 441). Le centre de gravité M du corps oscillant, situé à une distance MA = b de l'axe de suspension, s'élève à la hauteur MW = c. Posons AN (longueur du pendule isochrone) = x. Ce pendule s'élève donc à la hauteur SN = xc/b. Si vn est la vitesse du point N et v celle d'un point P quelconque du corps, situé à une distance r de l'axe d'oscillation, au moment où les points M et N se trouvent sur la verticale passant par A, on aura, pour déterminer la hauteur h à laquelle le point P pourra s'élever librement, l'équation  . En supposant le corps divisé en un nombre n de points ou globules égaux de ‘masse’ m, la somme des produits des masses par les hauteurs h correspondantes sera cm/xb Σr2 et le produit de la masse totale M par l'ascension du centre de gravité sera mnc. On a donc . En supposant le corps divisé en un nombre n de points ou globules égaux de ‘masse’ m, la somme des produits des masses par les hauteurs h correspondantes sera cm/xb Σr2 et le produit de la masse totale M par l'ascension du centre de gravité sera mnc. On a donc  . .
Il faut remarquer en outre que pour une surface plane oscillant perpendiculairement à son plan cette même formule peut être déduite des considérations de la Pièce IX. Dans ce cas toutes les distances r sont parallèles et la formule n'est autre chose que la mise en équation de la règle de l'onglet ou du tronc (voir à la p. 458 la Deuxième Partie de la Pièce IX).
Si l'on donnait aux points des masses quelconques, égales ou inégales, la formule prendrait la forme x = Σmr2/Mb.
Lorsque toutes les masses sont égales, on peut écrire (Σr2)m = bMx. Sous cette forme l'équation correspond à l'équation  qu'on trouve à la p. 519 de ce Tome: c'est là l'équation générale trouvée par Huygens et publiée plus tard sous une autre forme et pour un corps oscillant quelconque (à la p. 519 il n'est question que d'une surface oscillant dans son plan) à la p. 100 de l'édition originale de l'‘Horologium oscillatorium’ (Pars Quarta, Prop. V). Comparez aussi la Huitième Partie de cette Pièce (note 7 de la p. 485), où l'on voit clairement que dans la pensée de Huygens l'équation générale s'applique à des corps. qu'on trouve à la p. 519 de ce Tome: c'est là l'équation générale trouvée par Huygens et publiée plus tard sous une autre forme et pour un corps oscillant quelconque (à la p. 519 il n'est question que d'une surface oscillant dans son plan) à la p. 100 de l'édition originale de l'‘Horologium oscillatorium’ (Pars Quarta, Prop. V). Comparez aussi la Huitième Partie de cette Pièce (note 7 de la p. 485), où l'on voit clairement que dans la pensée de Huygens l'équation générale s'applique à des corps.
Lorsque le corps considéré posséde un centre et est symétrique par rapport à un plan passant par ce centre perpendiculairement à la verticale AD [Fig. 43] on peut écrire (voir cependant, à la p. 474, le dernier alinéa de la note 2 de la p. 473)  (Prop. XIV de la Pars Quarta de l'‘Horologium oscillatorium’), y étant la distance d'un point quelconque du corps au plan horizontal passant par son centre et z la distance du point à un plan vertical passant par l'axe d'oscillation et le centre du corps, perpendiculaire par conséquent au plan du papier. (Prop. XIV de la Pars Quarta de l'‘Horologium oscillatorium’), y étant la distance d'un point quelconque du corps au plan horizontal passant par son centre et z la distance du point à un plan vertical passant par l'axe d'oscillation et le centre du corps, perpendiculaire par conséquent au plan du papier.
Dans le cas de la sphère on peut écrire  . Et si l'on considère, au lieu de la sphère donnée de rayon a, une sphère concentrique de rayon √2a2, on peut écrire . Et si l'on considère, au lieu de la sphère donnée de rayon a, une sphère concentrique de rayon √2a2, on peut écrire  , le dernier signe Σ s'appliquant à la sphère agrandie, dont EH représente le diamètre. On a donc , le dernier signe Σ s'appliquant à la sphère agrandie, dont EH représente le diamètre. On a donc  . Si l'on désigne ensuite par y1 la distance d'un point de la sphère agrandie au plan horizontal passant non pas par le centre D mais par le point A, on aura x = Σy21/nb, c.à.d. x, la longueur cherchée du pendule isochrone avec la sphère de rayon a, sera égale à la longueur du pendule isochrone avec une surface plane, oscillant perpendiculairement à son plan et contenant tous les points pesants de la sphère agrandie, chacun à sa vraie distance du plan horizontal passant par A. Tous ces points doivent donc être transportés horizontalement de la sphère agrandie à une surface plane, et si l'on veut que cette dernière (KLMN) ait une forme symétrique par rapport à un axe vertical MK (coïncidant en
réalité avec EH) et que la densité des points y soit partout la même, il faut nécessairement composer son contour de deux paraboles comme le texte et la Fig. 44 l'indiquent. En effet, si l'on découpe la sphère agrandie et la surface plane KLMN ainsi construite en tranches par des plans horizontaux, les tranches ou éléments de surface de KLMN seront proportionnels aux tranches correspondantes de la sphère agrandie. Comparez sur cet artifice de calcul, la réduction d'un corps à une surface plane, la note 2 de la p. 282 du T. XIV. Voir aussi la réduction d'un tronc à une surface plane, expliquée dans la note 1 de la p. 464, dans la Troisième Partie de la Pièce X qui précède. Cette Troisième Partie est d'ailleurs probablement postérieure au présent calcul, puisqu'elle date du 13 oct. et que Huygens connaissait le centre d'oscillation de la sphère le 10 octobre, d'après la note 3 de la p. 462. . Si l'on désigne ensuite par y1 la distance d'un point de la sphère agrandie au plan horizontal passant non pas par le centre D mais par le point A, on aura x = Σy21/nb, c.à.d. x, la longueur cherchée du pendule isochrone avec la sphère de rayon a, sera égale à la longueur du pendule isochrone avec une surface plane, oscillant perpendiculairement à son plan et contenant tous les points pesants de la sphère agrandie, chacun à sa vraie distance du plan horizontal passant par A. Tous ces points doivent donc être transportés horizontalement de la sphère agrandie à une surface plane, et si l'on veut que cette dernière (KLMN) ait une forme symétrique par rapport à un axe vertical MK (coïncidant en
réalité avec EH) et que la densité des points y soit partout la même, il faut nécessairement composer son contour de deux paraboles comme le texte et la Fig. 44 l'indiquent. En effet, si l'on découpe la sphère agrandie et la surface plane KLMN ainsi construite en tranches par des plans horizontaux, les tranches ou éléments de surface de KLMN seront proportionnels aux tranches correspondantes de la sphère agrandie. Comparez sur cet artifice de calcul, la réduction d'un corps à une surface plane, la note 2 de la p. 282 du T. XIV. Voir aussi la réduction d'un tronc à une surface plane, expliquée dans la note 1 de la p. 464, dans la Troisième Partie de la Pièce X qui précède. Cette Troisième Partie est d'ailleurs probablement postérieure au présent calcul, puisqu'elle date du 13 oct. et que Huygens connaissait le centre d'oscillation de la sphère le 10 octobre, d'après la note 3 de la p. 462.
On trouve la longueur cherchée AO ou x (voir la Pièce IX qui précède) en calculant la distance de A à O, pied de la perpendiculaire abaissée sur le plan du papier du centre de gravité du tronc EFGH, situé en réalité au-dessus de la surface KLMN, c.à.d. obtenu en érigeant un cylindre sur cette surface (placée de telle manière que le point M coïncide avec le point H et le point K avec le point inférieur E) et en coupant ce cylindre obliquement par un plan passant par la droite horizontale située dans le plan du papier et passant par le point A.
Or, pour déterminer cette distance AO, Huygens considère d'abord l'onglet (voir la Pièce IX, et la p. 499) découpé dans le même cylindre par un plan oblique parallèle au plan oblique mentionné et passant par une tangente en H à la sphère agrandie.
On a généralement, lorsque la figure plane a un contour quelconque symétrique par rapport à son axe vertical (HE, c.à.d. MK) et qu'on construit sur cette base un ‘truncus’ et un ‘cuneus’ limités par des plans obliques parallèles passant par des droites horizontales du plan de la base situées respectivement à la distance b et à la distance b' du centre de gravité de la base:
(Vol. cunei) (b+λcunei)+(vol. trunci-vol.cunei).b = (vol. trunci) (b+λ trunci) où ‘λ cunei’ et ‘λtrunci’ désignent les distances du centre de gravitéde la base, respectivement aux pieds des perpendiculaires abaissées sur cette base des centres de gravité de l'onglet et du tronc (on a donc  trunci): c'est l'équation des moments autour de la droite du plan de la base correspondant au tronc. Elle peut s'écrire trunci): c'est l'équation des moments autour de la droite du plan de la base correspondant au tronc. Elle peut s'écrire
b+λ trunci

Connaissant la ‘λ cunei’ on peut donc trouver la ‘λ trunci’ (et ensuite la longueur cherchée AO) d'après l'équation b:b' = (λcunei):(λ trunci).
Cette dernière équation correspond à la proportion EM:MA = SM:MQ de la p. 509 (première ligne).
Dans le cas considéré la λ cunei a la valeur ⅕ √2a2, comme on peut s'en convaincre par le calcul; Huygens n'indique pas comment il a calculé cette longueur. Quant à b', elle est ici égale à √2a2.
La longueur cherchée s'obtient donc à l'aide de l'équation
 trunci, qui donne: λ trunci trunci, qui donne: λ trunci  . .
Remarquons encore que la distance AD doit d'après le texte être plus grande que √2a2, parce que sinon le point de suspension A ne serait plus extérieur à la sphère agrandie.
Huygens annonce la découverte du centre d'oscillation de la sphère dans sa lettre à Moray du 10 oct. 1664 (voir la p. 120 du T. V), et il lui communique le résultat du calcul dans sa lettre du 21 nov. 1664 (p. 149 du T. V).
Dans l'‘Horologium oscillatorium’ on ne trouve pas le calcul du centre d'oscillation de l'ellipsoïde de révolution (voir la Deuxième Partie de cette Pièce), mais seulement celui du centre d'oscillation de la sphère (Prop. XXII de la Pars Quarta); la méthode de calcul de ce centre, basée sur al formule  , n'y est pas cependant identique à la méthode de la Première Partie, ni aux méthodes de la Deuxième Partie de cette Pièce. , n'y est pas cependant identique à la méthode de la Première Partie, ni aux méthodes de la Deuxième Partie de cette Pièce.
-
voetnoot1)
- Cette Partie est empruntée à la p. 165 du Manuscrit B.
-
voetnoot2)
- Pour expliquer le calcul du centre d'oscillation de l'ellipsoïde de révolution suspendu en un point quelconque de son axe, calcul d'une brièveté imposante, il faut, comme dans la Première quelconque de son axe, calcul d'une brièveté imposante, il faut, comme dans la Première Partie de cette Pièce, partir de la formule x = Σr2/nb. On peut décomposer r2 en y 2+z2, y étant la distance d'un point du corps à un plan horizontal passant par l'axe d'oscillation A perpendiculaire au plan du papier, et z la distance de ce point au plan vertical passant par l'axe AD perpendiculairement au papier.
Pour calculer Σy2 il faut, comme dans le cas précédent (voir la note 6 de la p. 470), réduire le corps à une surface plane:c'est la surface limitée par les paraboles BED et BCD tracées par Huygens à l'intérieur de l'ellipse. Comme la formule l = Σy2/nb à elle seule représenterait la longueur d'un pendule isochrone avec la surface BCDE oscillant perpendiculairement à son plan, on sait, d'après le théorème de la Deuxième Partie de la Pièce IX (p.458), que Σy2 est le produit de nb par une longueur égale à la distance entre l'axe d'oscillation et le pied de la perpendiculaire, abaissée sur la figure BCDE, du centre de gravité d'un tronc construit sur cette figure et limité par un plan passant par le nouvel axe d'oscillation qui est la droite horizontale située dans le plan du papier et passant par le point A. Pour trouver cette distance Huygens se sert de la méthode décrite dans la note à la p. 472: l'équation du texte

qui sert à calculer la longueur ⅕ a2/b, est analogue à l'équation  de la Première Partie de cette Pièce. À ⅕ a2/b il faut ensuite ajouter la longueur b. de la Première Partie de cette Pièce. À ⅕ a2/b il faut ensuite ajouter la longueur b.
Comme le texte l'indique, Huygens trouve Σz2 = ⅕ nc2 en multipliant l'une par l'autre (abstraction faite du nombre n) les expressions ⅜c et 8/15c. La méthode de calcul est donc la suivante. Au lieu des paraboles BED et BCD, on peut considérer maintenant les deux paraboles CBE et CDE: les courbes tracées à l'intérieur de l'ellipse peuvent tout aussi bien ètre censées représenter ces deux dernières paraboles. Remarquons en passant que ces figures BCDE sont analogues aux figures auxiliaires qu'on trouve à la p. 114 de l'édition originale de l'‘Horologium oscillatorium’ (Prop. XIV de la Pars Quarta). Pour obtenir Σz2, il faut maintenant diviser l'ellipsoïde et la nouvelle figure plane BCDE par des plans verticaux parallèles à BD et perpendiculaires au plan du papier: les éléments de surface ou tranches de la figure plane seront proportionnels aux volumes des tranches correspondantes de ellipsoïde. Reste donc à calculer Σz2 pout la nouvelle figure plane BCDE. À cet esset, on élève sur la demi-figure BED, ayant un point saillant en E, un cylindre perpendiculairement au plan du papier et on coupe ce cylindre par un plan oblique passant par BD, l'inclinaison de ce plan pouvant être quelconque. Si l'on appelle F le centre de la figure BCDE, G le centre de gravité de la demi-figure considérée BED et H le pied de la perpendiculaire abaissée sur le plan de la figure du centre de gravité de l'onglet limité par le plan oblique nommé on aura pour la demi-figure Σz2 =
n/2 FG. FH d'après le théorème de la p. 546 qui suit, donc Σz2 = = n FG. FH pour la figure CBED entière. Or, on a ici FG = ⅜c et FH = 8/15c.
Pour la première longueur (FG = ⅜c), on peut consulter la lettre de Huygens à Fr. van Schooten du 10 déc. 1653 (T. I, p. 254). Pour la deuxième (FH = 8/15c) voir la Troisième Partie de cette Pièce.
Après avoir formé le produit  , il faut le diviser parnb, ce qui donne ⅕c2/b. On a alors x(longueur du pendule isochrone) , il faut le diviser parnb, ce qui donne ⅕c2/b. On a alors x(longueur du pendule isochrone)  . .
Huygens ne se sert donc pas de l'équation  , déjà mentionnée dans la note 6 de la p. 470, valable pour le corps considéré dont CE est un plan de symétrie et où Σz2 a la même signification que plus haut (somme des carrés des distances à un plan passant par AD perpendiculairement au plan du papier), tandis que Σy2 représente la somme des carrés des distances au plan horizontal passant par CE. Remarquons en passant que, si l'on voulait se servir de cette équation, on pourrait aussi trouver la nouvelle somme Σy2 (outre d'après la méthode qui a servi à calculer Σz2), à l'aide du théorème de la p. 548 qui suit; d'après ce théorème on aurait Σy2 = n.BF.FK, FK étant la ‘λ cunei’ (voir la p. 472) ⅕a. On aurait donc Σy2 = ⅕na2, et on trouverait de nouveau , déjà mentionnée dans la note 6 de la p. 470, valable pour le corps considéré dont CE est un plan de symétrie et où Σz2 a la même signification que plus haut (somme des carrés des distances à un plan passant par AD perpendiculairement au plan du papier), tandis que Σy2 représente la somme des carrés des distances au plan horizontal passant par CE. Remarquons en passant que, si l'on voulait se servir de cette équation, on pourrait aussi trouver la nouvelle somme Σy2 (outre d'après la méthode qui a servi à calculer Σz2), à l'aide du théorème de la p. 548 qui suit; d'après ce théorème on aurait Σy2 = n.BF.FK, FK étant la ‘λ cunei’ (voir la p. 472) ⅕a. On aurait donc Σy2 = ⅕na2, et on trouverait de nouveau  . .
Le fait que Huygens se sert de deux méthodes différentes pour calculer les deux sommes Σy2 et Σz2 pourrait faire croire qu'il ne connaissait pas encore l'équation  de l'alinéa précédent (bien facile d'ailleurs à dériver de l'équation primitive pour Σr2. Dans la note 6 de la p. 470 nous supposions que cette équation lui était connue, mais il est possible que son raisonnement différait quelque peu du nôtre. de l'alinéa précédent (bien facile d'ailleurs à dériver de l'équation primitive pour Σr2. Dans la note 6 de la p. 470 nous supposions que cette équation lui était connue, mais il est possible que son raisonnement différait quelque peu du nôtre.
-
voetnoot1)
- Cette Partie, où Huygens détermine le centre de gravité de deux onglets, est empruntée à une feuille séparée collée dans le Manuscrit B entre les p. 117 et 118 (numération ancienne). Le texte se trouve sur la p. 60 recto, d'après la numération nouvelle (voir la note 2 de la p. 435).
Dans la Deuxième Partie de cette Pièce (voir, à la p. 474, le troisième alinéa de la note 2 de la p. 473) Huygens fait usage de la valeur trouvée ici [Fig. 47] pour le ‘brachium cunei super PDQ abscissi per DP’.
-
voetnoot2)
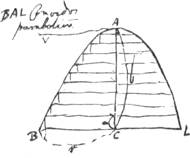
- Les ‘paraboloïdes’ de Huygens sont les courbes ya = kxb; comparez les p. 197-198 du T. XIV. Dans le cas considéré ici l'équation de la ‘paraboloïdes’ DLM est y2 = kx3.
-
voetnoot3)
- C.à.d. le plan DPM et l'onglet élevé sur DQP ont le même bras de levier par rapport à la droite ADV.
-
voetnoot4)
- Voir les p. 280-282 du T. XIV. On trouve que le ‘brachium’ TE a la valeur
 DP, c.à. d.dans le cas considéré ici 5/7 DP. DP, c.à. d.dans le cas considéré ici 5/7 DP.
-
voetnoot5)
- Pour trouver le ‘brachium’ en question d'après la méthode de Huygens il faut faire usage, comme dans le cas précédent, d'une ‘paraboloïdes’. On peut considérer l'onglet en question [Fig. 47] comme la différence d'un onglet élevé sur la base DAQP et d'un onglet élevé sur la base DAQ, l'un et l'autre étant terminé par un même plan oblique passant par DP. L'onglet sur la base DAQP a évidemment un centre de gravité situé à une distance ⅓ AD de la droite AQ. En remplaçant les sections droites de l'onglet sur DAQ (sections faites par des plans parallèles à DP et perpendiculaires au plan du papier) par des ordonnées (perpendiculaires à DA, dans le plan du papier) proportionnelles à ces sections on trouve une ‘paraboloïdes’ y = kx3, dont le centre de gravité est situé à une distance ⅕ AD de la droite AQ.
Ce sont là, paraît-il, les longueurs AC et AB indiquées dans la figure. On peut démontrer en outre que les volumes des deux onglets partiels qui constituent l'onglet élevé sur la base DAQP sont égaux. Pour trouver le ‘brachium’ de l'onglet élevé sur la base DQP, il faut donc prendre une distance CE = CB; de cette façon l'onglet sur DQP ‘suspendu’ en E, et l'onglet sur DAQ ‘suspendu’ en B, seront équivalents à l'onglet total ‘suspendu’ en C. On trouve finalement: DE ou NE = 8/15 AD.
-
voetnoot2)
- Pour calculer la longueur x du pendule isochrone avec une surface plane de forme elliptique suspendue en un point situé sur le prolongement de l'axe DB et oscillant dans son plan, Huygens doit calculer, comme dans le cas de l'ellipsoïde (voir la note 2 de la p. 473), l'expression
 , où b est la distance du point de suspension A au centre de l'ellipse, et où Σy2+Σz2 représentent les sommes des carrés des distances resp. à la droite horizontale et à la droite verticale passant par le point A et situées dans le plan du papier. , où b est la distance du point de suspension A au centre de l'ellipse, et où Σy2+Σz2 représentent les sommes des carrés des distances resp. à la droite horizontale et à la droite verticale passant par le point A et situées dans le plan du papier.
Pour trouver Σy2 il se sert de la même méthode que dans les deux cas précédents (sphère et ellipsoïde). Si l'on construit un onglet ou ‘cuneus’ au-dessus de l'ellipse, limité par un plan oblique passant par la tangente en B, la ‘λ cunei’ (p. 472) de cet onglet est ¼a, et la λ du tronc correspondant, limité par un plan passant par la droite horizontale en A, sera déterminée par l'équation
b:a = ¼a:λ trunci,
d'où l'on tire: ‘λ trunci’ = ¼ a2/b, de sorte que  . .
Pour calculer Σz2, Huygens remplace, comme la Fig. 48 l'indique, la demi-ellipse BGD par un demi-cercle, ce qu'on peut faire, puisque la circon férence de ce cercle s'obtient en multipliant toutes les ordonnées de l'ellipse (parallèles à DB) par un facteur constant, de sorte que, si l'on distribue les points pesants qui constituent la surface de la demi-ellipse sur le demicercle, sans que leur distance à l'axe BD change, la densité des points dans le demi-cercle pourra être elle aussi constante. En élevant ensuite un cylindre sur le demi-cercle et en coupant celui-ci par un plan oblique passant par BD, on obtient un onglet tel que le pied de la perpendiculaire abaissée de son centre de gravité sur le plan de la base se trouve à une distance ⅜q de l'axe BD, où q désigne le quart de la circonférence de cercle (voir la Cinquième Partie de cette Pièce, en particulier la note 4 de la p. 480). Comme le centre de gravité du demi-cercle se trouve à une distance ⅔ c2/q de l'axe BD, on obtient Σz2 (comme dans le calcul de Σz2 dans le cas de la note 2 de la p. 473; voir à la p. 474 le deuxième alinéa de cette note) en formant le produit de ⅔ c2/q par ⅜ q et par n, non pas par n/2, puisqu'il s'agit de calculer Σz2 pour la surface elliptique entière. L'expression ¼nc2 doit ensuite être divisée par nb. On trouve
donc finalement  . .
Mais quoique le calcul se rattache absolument au calcul précédent de la Deuxième Partie, comme nous venons de le faire voir, et qu'il paraisse vraisemblable que Huygens l'ait exécuté après avoir fait ce calcul pour l'ellipsoïde de rotation (Deuxième Partie), qui se trouve à la page précédente du Manuscrit, il faut cependant remarquer que le calcul pour l'ellipse (ce qui évidemment ne s'applique pas au calcul pour l'ellipsoïde) est entièrement conforme (abstraction faite de la substitution du demi-cercle à la demi-ellipse) à la méthode générale pour les surfaces planes symétriques oscillant dans leur plan qu'on trouve à la p. 515 et suiv. de ce Tome.
Il ne paraît donc pas improbable que Huygens ait formulé cette méthode générale (dont il annonce la découverte, en même temps que celle de la méthode pour les corps oscillants, à de Sluse dans sa lettre du 28 oct. 1664; voir la p. 127 du T. V) après l'avoir appliquée dans le cas de l'ellipse, et à l'instar de ce calcul.
-
voetnoot1)
- Huygens cherche quel doit être le rapport des axes pour que le centre d'oscillation se trouve au point D, lorsque la surface elliptique est suspendue en B. Le résultat (c2 = 3a2) confirme celui obtenu précédemment (voir le calcul de la p. 446).
-
voetnoot2)
- Manuscrit B, p. 167-168.
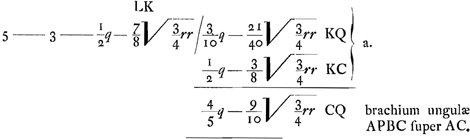
Huygens calcule d'abord le bras de levier de l'onglet APBC, où AB est un arc de 60o, par rapport à AD. Ensuite il fait le même calcul pour un arc AB quelconque. Voir aussi la note 4 de la p. 480.
L'onglet APBC ‘suspendu’ en Q, et la pyramide CPBD ‘suspendue’ en L, doivent être équivalents à la somme APBD de ces deux corps ‘suspendus’ en K (Le bras de levier KC du corps APBD est égal aux trois quarts de celui de la ‘surface ongulaire’ ABP). Connaissant K et L, on trouve Q:
-
voetnoot3)
- Voir sur le théorème d'Archimède le deuxième livre ‘De sphaera et cylindro’, cap. II, où on lit dans la traduction de J.L. Heiberg (Arch. Op. omn. 1910, Lipsiae in aed. Teubneri, I, p. 175): ‘Cuiuis segmento sphaerae aequalis est conus basim habens eandem, quam segmentum, altitudinem autem rectam, quae ad altitudinem segmenti eam rationem habet, quam radius sphaerae una cum altitudine reliqui segmenti ad altitudinem reliqui segmenti.’
-
voetnoot2)
- La distance KQ est obtenue, comme précédemment, en multipliant la longueur LK trouvée plus haut par le rapport du volume de la pyramide PBCD à celui de l'onglet APBC; rapport qui a ici la valeur
 . .
-
voetnoot3)
- Nous supprimons le calcul (substitution de la valeur de r) qui conduit à cette dernière expression pour KC.
-
voetnoot4)
-
 . Nous supprimons le calcul. Lorsque l'arc AB ou p devient égal à un quart de circonférence (AE), on trouve AC = a = r; et CB = b = r, donc CQ = ⅜p. C'est donc là la longueur du bras de levier par rapport à AD de l'onglet obtenu en coupant un cylindre, élevé sur le quart de cercle AED, par un plan oblique passant par la droite AD. On trouve évidemment le même bras de levier lorsque la base du cylindre est la moitié du cercle: ce qui est confirmé par la substitution b = o, p = 2p dans la formule pour CQ. . Nous supprimons le calcul. Lorsque l'arc AB ou p devient égal à un quart de circonférence (AE), on trouve AC = a = r; et CB = b = r, donc CQ = ⅜p. C'est donc là la longueur du bras de levier par rapport à AD de l'onglet obtenu en coupant un cylindre, élevé sur le quart de cercle AED, par un plan oblique passant par la droite AD. On trouve évidemment le même bras de levier lorsque la base du cylindre est la moitié du cercle: ce qui est confirmé par la substitution b = o, p = 2p dans la formule pour CQ.
Dans la Quatrième Partie de cette Pièce il est fait usage de la valeur CQ = ⅜ p (ou ⅜ q); voir, à la p. 477, le troisième alinéa de la note 2 de la p. 476.
-
voetnoot6)
- C.à.d. ±. Comparez la note 1 de la p. 426.
-
voetnoot7)
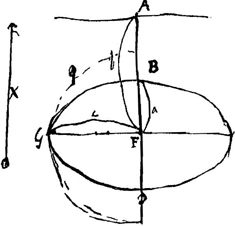
- Ce calcul est analogue à celui de la p. 446 qui précède. Huygens considère d'abord un cercle horizontal suspendu au point A de la verticale qui passe parson centre; le fil a la longueur x, et le rayon du cercle esty. La longueur a du pendule isochrone avec ce cercle est donnée par l'équation
 , qui découle de l'équation générale: longueur du pendule isochrone = Σr2/nb, comme on peut s'en convaincre, p.e. en se servant de la méthode des onglets exposée dans les notes précédentes (voir les p. 474 et 477). , qui découle de l'équation générale: longueur du pendule isochrone = Σr2/nb, comme on peut s'en convaincre, p.e. en se servant de la méthode des onglets exposée dans les notes précédentes (voir les p. 474 et 477).
Le lieu de tous les cercles ainsi suspendus et possédant un même pendule isochrone, c.à.d. une même période d'oscillation, est donc l'ellipsoïde engendré par la rotation autour de AC de l'ellipse ABCD ou  , dont l'axe horizontal BD est le double de l'axe vertical AC. , dont l'axe horizontal BD est le double de l'axe vertical AC.
On peut vérifier ce résultat à l'aide de la formule générale trouvée pour l'ellipsoïde de révolution à la p. 473 qui précède.
-
voetnoot1)
- Manuscrit B, p. 174. C'est sans doute à ce morceau que Huygens fait allusion dans sa lettre du 30 oct. 1664 à P. Petit (T. V, p. 129), où il dit avoir trouvé la ‘Methode generale’. Comparez la fin de sa lettre du 31 oct. à Moray (T. V, p. 131).
-
voetnoot2)
- ‘Ungula’ = ‘cuneus’ (comparez la note 3 de la p. 498).
-
voetnoot3)
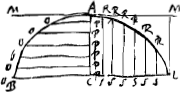
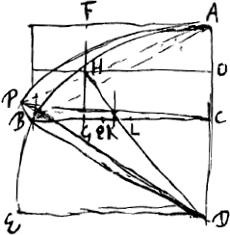
- D'après la p. 515 (comparez à la p. 477 l'avant-dernier alinéa de la note 2 de la p. 476) on a: longueur du pend. isochr. avec la figure BAL oscillant dans son plan = (longueur l1 du pend. isochr. avec la figure BAL oscillant perpendiculairement à son plan)+l'z'/b', où l' désigne la longueur du pendule isochrone avec la demi-figure ACB oscillant autour de l'axe AC, z la distance du centre de gravité de la demi-figure à l'axe AC, et b la distance du centre de gravité de la figure entière au point de suspension A.
Pour déterminer l', il faut connaître le centre de gravité de l'onglet ‘super ACB, plano per AC abcissae’ (voir la p. 458), ce qui conduit à évaluer Σ(OP)3; pour déterminer l1 il faut connaître le centre de gravité de l'onglet ‘super BAL abscissi plano per MA ducto’. Huygens fait mention en outre de b', mais il ne parle pas de z'.
Connaissant le centre de gravité de l'onglet ‘super CLA (ou “super BLA”) abcissae plano per CL ducto’, - ou plutôt la distance à BL de la projection de ce centre sur la base BLA - on connaîtra en effet également la distance à BL ou à MM de la projection sur cette même base du centre de gravité de l'onglet ‘super BAL abscissi plano per MA ducto’; ces deux onglets, qu'on peut supposer, pour fixer les idées, limités par des plans inclinés à 45o, peuvent former ensemble un cylindre à base BAL, et en prenant alors l'équation des moments autour de la droite BL p.e., on trouve que, la somme des moments des deux onglets étant égale au moment du cylindre, on a  , où a désigne la distance à BL de la projection du centre de gravité de l'onglet, dont le plan oblique passe par MM, et a' la distance à BL de la projection du centre de gravité de l'onglet, dont le plan oblique passe par BL. , où a désigne la distance à BL de la projection du centre de gravité de l'onglet, dont le plan oblique passe par MM, et a' la distance à BL de la projection du centre de gravité de l'onglet, dont le plan oblique passe par BL.
-
voetnoot4)
- Il faut déterminer
 , où b désigne la distance à A du centre de gravité du corps, y la distance d'un point quelconque du corps à un plan horizontal passant par MM, et z la distance de ce point à un plan passant par le point C et l'axe d'oscillation A perpendiculaire au plan du papier. Pour trouver Σy2 on peut transformer le corps, découpé en tranches horizontales, en une surface plane située dans le plan du papier (voir, à la p. 471, l'avantdernier alinéa de la note 4 de la p. 470), élever ensuite sur cette surface plane un onglet dont le plan oblique passe par MM, et calculer le moment de cet onglet par rapport à MM, donc la ‘summa quadratorum OP in quadrata distantiarum PA’. Pour trouver Σz2, on peut également diviser le corps en tranches circulaires horizontales et prendre les moments par rapport aux axes P (perpendiculaires au plan du papier) des onglets élevés sur les demicercles et limités par des plans obliques passant par les axes P, ce qui conduit en effet à évaluer Σ(OP)4; ce qu'on peut démontrer en se servant de la méthode d'‘intégration’ dans laquelle on remplace les sections droites de l'onglet considéré par des ordonnées (voir le deuxième alinéa de la note 1 de la p. 464). , où b désigne la distance à A du centre de gravité du corps, y la distance d'un point quelconque du corps à un plan horizontal passant par MM, et z la distance de ce point à un plan passant par le point C et l'axe d'oscillation A perpendiculaire au plan du papier. Pour trouver Σy2 on peut transformer le corps, découpé en tranches horizontales, en une surface plane située dans le plan du papier (voir, à la p. 471, l'avantdernier alinéa de la note 4 de la p. 470), élever ensuite sur cette surface plane un onglet dont le plan oblique passe par MM, et calculer le moment de cet onglet par rapport à MM, donc la ‘summa quadratorum OP in quadrata distantiarum PA’. Pour trouver Σz2, on peut également diviser le corps en tranches circulaires horizontales et prendre les moments par rapport aux axes P (perpendiculaires au plan du papier) des onglets élevés sur les demicercles et limités par des plans obliques passant par les axes P, ce qui conduit en effet à évaluer Σ(OP)4; ce qu'on peut démontrer en se servant de la méthode d'‘intégration’ dans laquelle on remplace les sections droites de l'onglet considéré par des ordonnées (voir le deuxième alinéa de la note 1 de la p. 464).
-
voetnoot5)
- Manuscrit B, P. 174. Pour trouver la longueur du pendule isochrone avec un segment d'un paraboloïde de révolution, suspendu au point A, Huygens se sert de la formule générale. Voir la note précédente et la note 7 de la p. 485; comparez aussi la note 1 de la p. 369.
-
voetnoot1)
- Le calcul de ¼ r2n, où r = BC, est identique au calcul de ¼nc2 dans le cas considéré dans la Quatrième Partie de cette Pièce et q a la même signification (voir, à la p. 477, le troisième alinéa de la note 2 de la p. 476). La Fig. 53 représente un onglet élevé sur le demi-cercle. On a Σz2 = ¼ r2n, où z a la même signification que dans la note nommée, et où le signe Σ s'applique au demi-cercle considéré (il est évident qu'on peut faire le calcul en considérant les demicercles et le demi-paraboloïde tout aussi bien qu'en considérant le paraboloïde entier), ou plutôt à un segment infiniment petit (appelé ‘segmentum BC’) de hauteur déterminée a [Fig. 52] ayant le demi-cercle pour base. Sil'on étend l'intégration à un cylindre de hauteur AC élevé sur la même base, on trouve Σz2 = ¼ r2nb, nb étant le nombre des particules dans le demi-cylindre entier.
-
voetnoot2)
- Pour le demi-paraboloïde de révolution Σz2 est le tiers de la somme Σz2 pour le demi-cylindre. En effet, pour chaque tranche horizontale le Σz2 (comparez les six dernières
lignes de la note 4 de la
p. 483) est proportionnel à la 4iéme puissance du rayon de cette tranche, donc au carré de sa distance au plan AV. Cette relation est représentée par une parabole, et la considération de l'aire de cette parabole conduit au résultat cherché.
-
voetnoot5)
- C.à.d. le Σy2 (où y désigne la distance d'un point quelconque au plan horizontal passant par A) du demi-paraboloïde par rapport à ce plan AV est égal au quart du Σy2 pour le demi-cylindre.
On peut aussi trouver le Σy2 cherché, en formant le produit du nombre de particules contenues dans le demi-paraboloïde par la distance du point A au centre de gravité du paraboloïde et par la distance du point A au pied de la perpendiculaire abaissée sur le plan BAL du centre de gravité d'un onglet construit sur une figure plane S (comparez la p. 282 du T. XIV) contenant dans chaque tranche horizontale autant de particules que la tranche correspondante du paraboloïde et limité par un plan oblique passant par la droite AV. C'est la formule n.FG.FH de la note qui occupe la p. 474.
Le nombre de particules dans le demi-paraboloïde est ½ nb, si l'on désigne toujours par n le ‘numerus particularum in segmento BC’. Mais le nombre de particules pour le paraboloïde entier sera ½ nb, si l'on désigne par n le nombre de particules dans le segment BL entier. C'est ce qui résulte du théorème d'Archimède (‘de Conoidibus et Sphaeroidibus’, XXI) d'après lequel le volume du paraboloïde de révolution est égal à 1 ½ fois celui du cône BAL; car le volume de ce dernier corps est ⅓nb, n étant le ‘numerus particularum’ dans le segment BL.
La distance du centre de gravité du paraboloïde au point A est ⅔p (voir la dernière ligne de la p. 282 du T. XIV).
Reste à savoir si ¾p est la distance de A au pied de la perpendiculaire abaissée sur le plan BAL du centre de gravité de l'onglet nommé, élevé sur la figure plane S. Or, la figure S est un triangle isoscèle, tel que BAL, et l'onglet par conséquent une pyramide scalène à base perpendiculaire au plan du papier. On trouve donc en effet ¾p.
-
voetnoot5)
- C.à.d. le Σy2 (où y désigne la distance d'un point quelconque au plan horizontal passant par A) du demi-paraboloïde par rapport à ce plan AV est égal au quart du Σy2 pour le demi-cylindre.
On peut aussi trouver le Σy2 cherché, en formant le produit du nombre de particules contenues dans le demi-paraboloïde par la distance du point A au centre de gravité du paraboloïde et par la distance du point A au pied de la perpendiculaire abaissée sur le plan BAL du centre de gravité d'un onglet construit sur une figure plane S (comparez la p. 282 du T. XIV) contenant dans chaque tranche horizontale autant de particules que la tranche correspondante du paraboloïde et limité par un plan oblique passant par la droite AV. C'est la formule n.FG.FH de la note qui occupe la p. 474.
Le nombre de particules dans le demi-paraboloïde est ½ nb, si l'on désigne toujours par n le ‘numerus particularum in segmento BC’. Mais le nombre de particules pour le paraboloïde entier sera ½ nb, si l'on désigne par n le nombre de particules dans le segment BL entier. C'est ce qui résulte du théorème d'Archimède (‘de Conoidibus et Sphaeroidibus’, XXI) d'après lequel le volume du paraboloïde de révolution est égal à 1 ½ fois celui du cône BAL; car le volume de ce dernier corps est ⅓nb, n étant le ‘numerus particularum’ dans le segment BL.
La distance du centre de gravité du paraboloïde au point A est ⅔p (voir la dernière ligne de la p. 282 du T. XIV).
Reste à savoir si ¾p est la distance de A au pied de la perpendiculaire abaissée sur le plan BAL du centre de gravité de l'onglet nommé, élevé sur la figure plane S. Or, la figure S est un triangle isoscèle, tel que BAL, et l'onglet par conséquent une pyramide scalène à base perpendiculaire au plan du papier. On trouve donc en effet ¾p.
-
voetnoot6)
- C'est le ‘moment’ du paraboloïde (produit de sa ‘masse’ par la distance de son centre de gravité à A [Fig. 52]).
-
voetnoot6)
- C'est le ‘moment’ du paraboloïde (produit de sa ‘masse’ par la distance de son centre de gravité à A [Fig. 52]).
-
voetnoot7)
- C'est l'équation générale de la longueur du pendule isochrone (voir, à la p. 471, le premier alinéa de la note 6 de la p. 470)
 , tandis que , tandis que  . .
-
voetnoot1)
- Même calcul qu'à la p. 484, où le nombre de particules n est remplacé par l'élément de volume sa renfermant ce nombre de particules. Voir sur s le texte de la p. 483, et sur a la note 1 qui commence à la p. 484.
|

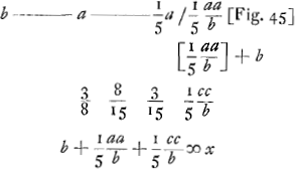
 .
.
 .
.