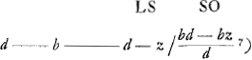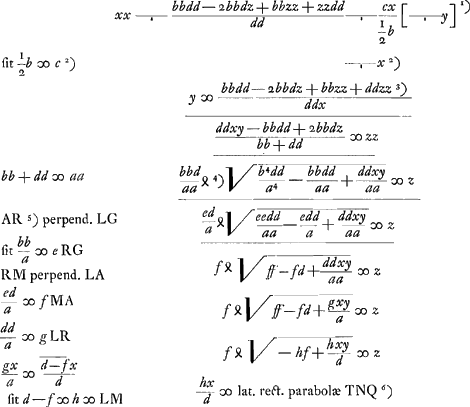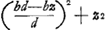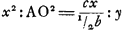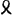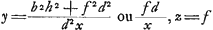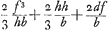Oeuvres complètes. Tome XVI. Percussion
(1929)–Christiaan Huygens–
[pagina 449]
| |
VIIGa naar voetnoot4).
| |
[pagina 450]
| |
[pagina 451]
| |
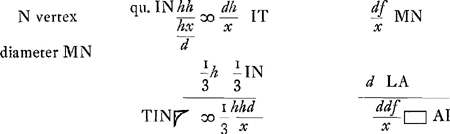 | |
[pagina 452]
| |
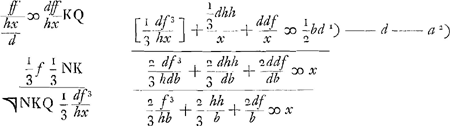 Ga naar voetnoot1)Ga naar voetnoot2) Ex dictis pag. praecedentiGa naar voetnoot3) constat esse 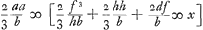 . vide pag. praeced. . vide pag. praeced.
| |
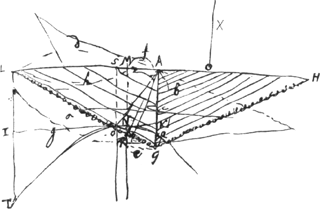
[Deuxième Partie]Ga naar voetnoot4).29 Sept. 1664. Prius scripta quae pag. sequenti habentur. 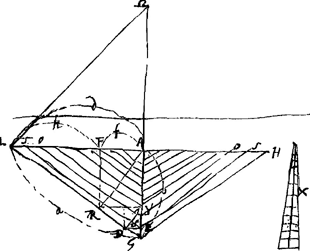 [Fig. 31].
Invenire pendulum simplexisochronas oscillationes habens triangulo isosceli suspenso ex puncto quod basin bifariam dividit. Sit AL ∞ d [Fig. 31]. AG ∞ b. LG ∞ a. Cum pendulum x isochronon virgis LG, GH inventum sit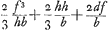 Cogitemus virgis LGH parallelas virgas SSS, OOO &c. aequalibus intervallis distantes, atque ita compo- | |
[pagina 453]
| |
nentes totum triangulum LGH. Quibus singulis si inveniantur pendula isochrona, certum est ex aequalibus differentijs decrescere debereGa naar voetnoot5). Quare si longitudo penduli x in totidem aequales partes dividatur atque ad singulas divisiones affigi intelligantur pondera ab imo aequaliter decrescentia quemadmodum et virgae LGH, SSS, OOO &c. quae triangulum LGH componunt. pendulum ita oneratum necessario isochronon erit dicto trianguloGa naar voetnoot6). Tale autem pendulum isochronon esse scimus triangulo eandem cum ipso longitudinem habenti, atque ex vertice suspenso, hoc est pendulo simplici quod habeat ¾ ejus longitudinis. Ergo Δlo LGH isochronon erit pendulum habens ¾ inventae quantitatis 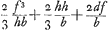 , hoc est , hoc est 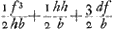 . Has quantitates aliter exprimemus. Est enim h ad f ut LR ad RG, hoc est, ut qu. LA ad qu. AG. Ergo f/h∞bb/dd. Ergo ½f3/hb∞½ffbb/ddb ∞ ½ffb/dd. Sed d ad f ut LG ad GR, hoc est ut qu. LG ad qu. GA, hoc est ut aa ad bb, ergo . Has quantitates aliter exprimemus. Est enim h ad f ut LR ad RG, hoc est, ut qu. LA ad qu. AG. Ergo f/h∞bb/dd. Ergo ½f3/hb∞½ffbb/ddb ∞ ½ffb/dd. Sed d ad f ut LG ad GR, hoc est ut qu. LG ad qu. GA, hoc est ut aa ad bb, ergo 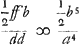 . Ergo quantitas prima . Ergo quantitas prima 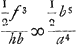 . Porro . Porro 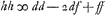 . Ergo . Ergo 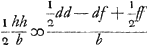 . huic adde tertiam quantitatem . huic adde tertiam quantitatem 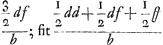 . Ergo tres propositae quantitates aequantur . Ergo tres propositae quantitates aequantur
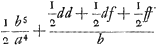 , quas dico aequari simul ½aa/b. adeoque inventâ duabus AG, GL tertia proportionali GΩ, hujus semissem esse longitudinem penduli isochroni triangulo LGH ex A suspenso , quas dico aequari simul ½aa/b. adeoque inventâ duabus AG, GL tertia proportionali GΩ, hujus semissem esse longitudinem penduli isochroni triangulo LGH ex A suspenso
| |
[pagina 454]
| |
et in plano suo agitato. ducantur enim RV perpend. AG. VD perpend. LG. DE perpend. AG. Fit ergo GE ∞ b5 / a4. EV ∞ ff/b. VA ∞ df/b. AΩ ∞ dd/b. Istae vero quatuor constituunt rectam GΩ. Ergo
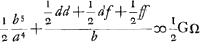 |
|