Oeuvres complètes. Tome XVI. Percussion

[p. 434]

V¹⁾.
[1664]²⁾.

[Fig. 20.]

Dato pendulocomposito ex duabus gravitatibus in lineam inflexibilem conjunctis, invenire in ea punctum quod in transitu penduli per cathetum, eadem celeritate feratur qua pondus penduli simplicis cujus longitudo aequalis distantiae dicti puncti a puncto suspensionis. et ostendere quod pendulum hoc simplex composito isochronum est.

Sit compositum pendulum ABC [Fig. 20] suspensum in A, pondera habens B et C. idque cadere intelligatur ex AE in AC. Manifestum igitur est pondus B minorem celeritatem in B acquisivisse quam si solum pendulo longitudinis AB annexum fuisset, quia pondus C ex longitudine AC agitatum, celeritatem brevioris penduli non a ssequitur, ideoque ex parte remoratur. At rursus pondus C celeritatem majorem in C acquisivit quam pondus penduli simplicis longitudinis AC, quia a pondere B celeriorem motum affectante aliquatenus impellitur, idque tanto magis quanto ipsum B respectu C majus erit. Itaque inter B et C punctum aliquod reperiri necesse est ut D quod perveniente pendulo ABC ex AE in AC, tantam celeritatem

1) Manuscrit B, p. 188-190.

2) La p. 171 est datée: 7 oct. 1664, et la p. 214 porte la date du 28 oct. 1664. Entre la p. 187 et la p. 188 quelques feuillets ont été collés dans le Manuscrit; le premier de ces feuillets (voir la p. 467) porte la date du 13 oct. 1664.
En 1928, les feuillets qui constituent le Manuscrit B ont été numérotés de nouveau. Cette numération nouvelle embrasse aussi les feuillets collés dans le Manuscrit. Nous continuerons cependant à citer le texte d'après la numération ancienne, sauf dans les cas où il s'agit d'un des feuillets collés dans le Manuscrit.

[p. 435]

acquisiverit quantam haberet pondus simplicis penduli longitudinis AD peracto arcu simili MD. Quod itaque punctum D ut inveniatur, sit AC ∞ d, AB ∞ e; quantitas ponderis C vocetur c; quantitas ponderis B vocetur b. ductisqué FH, LG et MK perpendicularibus in AC, vocetur altitudo HC, h. Quaesita vero longitudo AD sit x.

Quum igitur sit AC ad CH ut AD ad DK, itemque ut AB ad BG, erit DK ∞ hx/d, BG ∞ he/d. Jam quia punctum D eam celeritatem acquirit quam haberet pondus penduli simplicis AD post descensum per arcum MD, hoc est eam, qua id pondus ad eandem unde venerat altitudinem per arcum DO ascensurum esset, hoc est ad altitudinem DK ∞ hx/d, cumque celeritas puncti D ad celeritatem ponderis C sit sicut AD ad AC hoc est sicut x ad d. sicut autem quadratum celeritatis puncti D ad quadr. celeritatis ponderis C, ita altitudo ad quam ascenditur celeritate puncti D, hoc est altitudo DK ∞ hx/d ad altitudinem ad quam ascenderet pondus C si post descensum per arcum EC a pendulo composito liberum evaderet. Si igitur fiat ut xx ad dd ita hx/d ad aliud, nempe dh/x, hoc designabit altitudinem ad quam ascenderet pondus C. Eadem ratione altitudo ad quam ascenderet pondus b invenitur ∞ e²h/dx. ductis autem utrisque altitudinibus hisce in sua pondera, summa productorum, quae erit 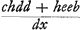, aequalis sit oportet summae productorum ex altitudine HC in pondus C, et ex altitudine BG in pondus b, quae est , quia nimirum posterior summa aequatur producto ex descensu centri gravitatis communis ponderum C et B in ipsa pondera, prior vero producto ex ascensu centri gravitatis dictorum ponderum in eadem pondera, quae producta aequalia inter se esse necesse est, cum ascensus centri communis gravitatis aequalis sit descensui suo. Itaque

[p. 436]

In qua aequatione deleto ubique h et reliquis ut opus est transpositis fit

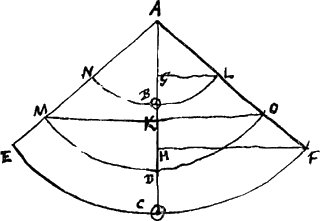
Oportet itaque singulas gravitates ducere in longitudines à quibus affixae sunt; et ut summa horum productorum ad producta singula, ita facere singulas longitudines, respective ad alias; hae enim simul additae constituent distantiam inter A et punctum D¹⁾.

Quod si vero quaeratur in dicto pendulo composito punctum D quod descensu penduli ex AE in AC, ita ut EC sit pars tantum arcus descendentis, velocitatem

[Fig. 21.]

eam acquirat quam pondus penduli simplicis longitudinis AD acquireret peracto arcu simili: notatis rursus altitudinibus arcuum EC, MD, NB, quae sint CH, DK, BG, quaeque eandem et hic inter se ratiónem servant quam longitudines CA, DA, BA: Eodem quo prius ratiocinio, literis eadem denotantibus, invenietur longitudo AD eadem quae et ante reperta fuit, nempe .

Quum igitur punctum D in pendulo ABC ita ut supra repertum, quolibet loco arcus per quemtransit, ea velocitate feratur qua ponduspendulisimplicis longitudine AD, perspicuum est pendulum hujus longitudinis eodem tempore cum pendulo composito ABC semioscillationem persicere per arcum similem. Unde et per arcum ascendentem eadem celeritate feretur. ut ex prop...²⁾ manifestum. Adeoque pendulo composito isochronon erit. Atque hoc de quibuslibet pendulis compositis

1) C.à.d. on a: et . Comparez la quatrième ligne de la p. 419.

2) Huygens n'avait apparemment pas encore mis par écrit la proposition qu'il jugeait à propos de citer.

[p. 437]

eadem ratione verum est. unde et vice versa constat, pendulum simplex quod composito isochronon est, si aequali angulo cum pendulo composito removeatur a perpendiculari, atque inde cadere permittatur, semper plumbum penduli simplicis peractis ijsdem angulis cum composito, eam celeritatem habere quam punctum in composito quod longitudine penduli simplicis distat a suspensione.

Virgae ponderanti sive lineae rectae gravitate praeditae, alteroque capite suspensae, pendulum simplex isochronon reperire³⁾.

[Fig. 22.]

Sit virga ponderans AB [Fig. 22] suspensa in A, cui isochronon quaeratur pendulum simplex RS. Sit AB ∞ a. divisaque intelligatur virgae longitudio in partes aequales BK, KL, LM &c. quarum singulae vocentur e. sintque centra gravitatis dictarum partium O, P, Q &c; itaque aequaliter quoque sese excedent

3) Toute cette partie jusqu'à la fin de la Pièce IV a été biffée par Huygens, comme on peut le voir dans la Fig. 22. Nous la reproduisons néanmoins parce qu'elle conduit pour le cas considéré de la barre ou ligne pesante d'une façon très simple à l'équation qui donne la longueur x du pendule simple isochrone, savoir .

[p. 438]

lineae AO, AP, AQ &c. quae dicantur, b, c, d, &c. Penduli vero simplicis quaesiti longitudo RS sit x; quod cum isochronon debeat esse virgae AB, eodem igitur tempore peragent arcus similes, quos quadranti integro aequales ponamus, ita ut virga AB cadat ex AC in AB, posito angulo BAC recto. Eritque celeritas puncti O ubi virga venerit in AB ad celeritatem ponderis penduli S similiter per quadrantem moti, sicut longitudo OA, sive b, ad x. similiterque celeritas puncti P ad celeritatem ponderis penduli S ut AP, sive c, ad x, atque ita porro. Sicut autem

[Fig. 22.]

quadratum xx ad quadratum AO hoc est bb, ita erit altitudo ad quam ascendet pondus S ad altitudinem qua ascendere poterit pars virgae BK si libera atque a virga reliqua separata fieri intelligatur postquam cum ipsa venit ex AC in AB. Atqui pondus S ascendit ad eandem unde venit altitudinem quae est SR ∞ x. Ergo quia ut xx ad bb ita x ad bb/x, erit bb/x altitudo dicta ad quam pars virgae BK uti diximus ascenderet. Simili ratione altitudo ad quam ascenderet pars KL invenitur ∞ cc/x, et altitudo ad quam ascenderet pars LM eodem modo fit dd/x. et sic de caeteris. ductis porro singulis hisce altitudinibus in partes virgae aequales e, quarum centra gravitatis sunt O, P, Q, fit summa productorum quae quidem summa aequalis esse debet producto ex distantia centri gravitatis virgae à puncto suspensionis quae est ½ a in ipsam virgam a, quia ita centrum gravitatis

[p. 439]

partium omnium e, sursum motarum postquam a virga liberae sunt, tantundem ascendisse reperietur atque centrum gravitatis virgae, hoc est partium earundem omnium, descendit, quod necessario fieri debere ostensum est supra prop...¹⁾. Est itaque




ductisque omnibus in x, fi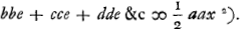t



²⁾.

Sit jam BD aequalis AB cui insistat ad angulos rectos, et sit AN aequalis distantiae centri gravitatis trianguli ABD ab recta AC, hoc est, sit AN ∞ ⅔ a³⁾.

1) Même remarque que plus haut, note 2 de la p. 436.

2) Ce qu'on pourrait écrire (comparez la note 3 de la p. 437) .

3) Huygens n'a pas achevé ce morceau. On peut tronver la limite de la somme considérée en multipliant la surface du triangle ABD par le double de la distance de son centre de gravité à la droite AB, c.à.d. par AN, suivant le théorème de Pappus, mieux connu sous le nom de théorème de Gulden ou Guldin, dont Huygens fait mention en 1653 (voir la note 5 de la p. 280 du Tome XIV): il faut considérer le cône engendré par la révolution du triangle ABD autour de AB. On trouve ainsi x = ⅔a.