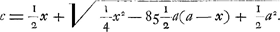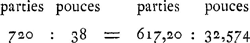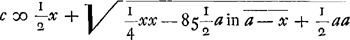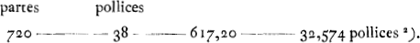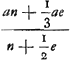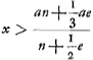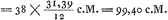Oeuvres complètes. Tome XVI. Percussion
(1929)–Christiaan Huygens–
[pagina 414]
| |
IVGa naar voetnoot1).
| |
[pagina 415]
| |
IVGa naar voetnoot1).
| |
[pagina 416]
| |
globes B et C. En effet, il ne peut être plus élevé. Mais il ne peut pas non plus être moins élevé parce que les globes G et F en retombant des hauteurs acquises mettent les globes E et D en mouvement avec une force qui les fait monter jusqu'en B et C, comme nous l'avons dit. Ceci est évident d'après la mécaniqueGa naar voetnoot1). Supposons maintenant que le pendule linéaire AED oscille aussi rapidement que le pendule simple HK. Appelons cette longueur HK x, et prenons AD = a, AE = b, le poids D = e, le poids E = c, et la hauteur CS (de laquelle celle de C surpasse celle de D) = d. Or, comme le pendule linéaire AED se meut par hypothèse avec la même vitesse avec laquelle se mouvrait le pendule simple HK, la vitesse du poids D sera à celle du poids K après que celui-ci aura parcouru, dans son pendule HK, un arc semblable, comme AD est à HK, c.à.d. comme a est à x. Mais le poids K s'élève par la force de son mouvement à la hauteur QP qui est dx/a. Par conséquent le poids D avec sa vitesse déjà mentionnée, ou bien le poids F qui reçoit toute la vitesse de D, peut monter à une hauteur qui sera à la hauteur QP comme le carré de cette vitesse est au carré de la vitesse acquise par le poids K. Or, ces carrés sont dans le rapport a2:x2 et la hauteur QP = dx/a; par conséquent, en prenant x2:a2 = (dx/a):(une autre quantité, savoir ad/x), cette dernière sera la hauteur, au-dessus de la ligne horizontale DS évidemment, à laquelle peut monter le globe frappé F. En d'autres termes, si l'on prendGa naar voetnoot2) (HK ou x):(AD ou a) = (la hauteur CS ou d):(une quatrième longueur, savoir ad/x), celle-ci (appelons-la RN) sera la dite hauteur; et ceci doit être considéré comme un théorème. Par ce théorème on apprend aussi à connaître la hauteur à laquelle montera le globe frappé G. En effet, comme HK ou x est à AG ou b, ainsi sera la hauteur BO ou bd/a à b2d/ax, hauteur à laquelle G s'élève au-dessus de la ligne horizontale EO; appelons cette hauteur MV. Pour que le centre de la gravité composée de G et de F, après qu'ils ont atteint les dites hauteurs, se trouve aussi haut que le centre de la gravité composée de B et de C, il faut maintenant que le produit de la hauteur NR par le poids F ou D, augmenté du produit de la hauteur MV par le poids G ou E, c.à.d. l'expression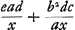 , il faut, dis-je, que cette somme de deux produits soit égale à celle des deux produits qu'on obtient en multipliant la hauteur CS par le poids D et la hauteur BO par le poids E, ce qui fait , il faut, dis-je, que cette somme de deux produits soit égale à celle des deux produits qu'on obtient en multipliant la hauteur CS par le poids D et la hauteur BO par le poids E, ce qui fait 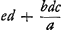 . .
| |
[pagina 417]
| |
lius quoniam recidentes sphaerae G, F ab acquisitis altitudinibus dant motum sphaeris E, D, cujus vi ascendant in B et C, uti dictum fuit: haec enim ex mechanicis clara suntGa naar voetnoot1). 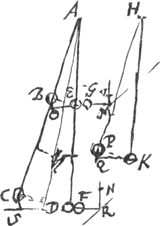 [Fig. 16.]
Ponamus jam perpendiculum AED aequè celeres vibrationes habere ac perpendiculum HK, quae longitudo vocetur x, et AD sit a; AE ∞ b, gravitas D ∞ e; gravitas E ∞ c, altitudo CS nempe qua altius est C quam D ∞ d. Quia ergo perpendiculum AED movetur celeritate eadem qua moveretur perpendiculum simplex HK, erit velocitas ponderis D ad velocitatem ponderis K in perpendiculo HK per similem arcum vibrati, ut AD ad HK, hoc est ut a ad x. Sed pondus K vi motus sui ascendit ad altitudinem QP quae est dx/a. Ergo pondus D dicta velocitate sua, vel pondus F omnem ejus velocitatem accipiens, potest ascendere ad altitudinem quae sit ad altitudinem QP sicut quadratum hujus velocitatis ad quadratum velocitatis acquisitae ponderi K. sunt autem haec quadrata ut aa ad xx et altitudo QP ∞ dx/a, ergo faciendo ut xx ad aa ita dx/a ad aliud nempe ad/x, erit haec altitudo, nempe supra horizontalem DS, ad quam poterit ascendere percussa sphaera F. nempe si fiatGa naar voetnoot2) ut HK, x ad AD, a, ita altitudo CS, d, ad aliam, ad/x, ea quae sit verbi gratia RN, erit altitudo dicta, atque hoc theorematis loco habendum, quo similiter innotescit altitudo ad quam ascendet percussa sphaera G. ut enim HK, x, ad AG, b, ita altitudo BO, bd/a ad bbd/ax altitudinem quo ascendet G supra horizontem EO, quae sit MV. Jam ut centrum gravitatis compositae ex G et F, postquam ita ascenderunt, sit aeque altum ac centrum gravitatis compositae ex B et C, oportet, ut NR altitudo ducta in gravitatem F seu D, una cum producto altitudinis MV in gravitatem G sive E, hoc est, 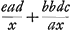 , ut inquam haec duo producta aequentur productis duobus ex altitudine CS in gravitatem D, et ex altitudine BO in gravitatem E, quae sunt , ut inquam haec duo producta aequentur productis duobus ex altitudine CS in gravitatem D, et ex altitudine BO in gravitatem E, quae sunt 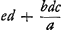 . .
| |
[pagina 418]
| |
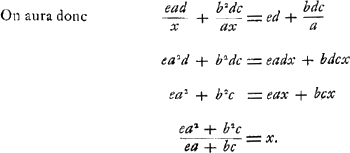 C'est donc là la règle universelle par laquelle on calculera aisément la longueur d'un pendule simple isochrone avec un pendule composéGa naar voetnoot1). Par exemple lorsque AE = ½ AD et que les poids D et E sont égaux, on aura 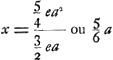 .
Mais si, étant donnée la longueur du pendule linéaire AD et le poids D ainsi que le poids E, il faut fixer ce dernier à un certain point du pendule linéaire de .
Mais si, étant donnée la longueur du pendule linéaire AD et le poids D ainsi que le poids E, il faut fixer ce dernier à un certain point du pendule linéaire de
 [Fig. 16.]
sorte que le pendule linéaire composé soit isochrone avec un pendule simple de longueur donnée HK, on aura d'après l'équation précédente 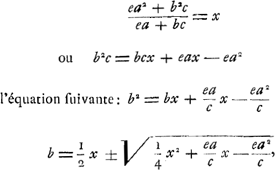 , équation dans laquelle le terme ea2/c est plus grand que eax/c, parce que a est plus grand que x. Par conséquent l'équation a deux racines vraiesGa naar voetnoot2) dont chacune représente une longueur AE = b. Cependant si la longueur donnée HK ou x est plus grande que a, l'équation aura une autre forme et ne possédera qu'une seule racine vraieGa naar voetnoot2), savoir 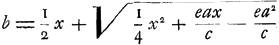 , ce qui fait voir que la longueur b est plus grande que x et par conséquent aussi plus grande que a. , ce qui fait voir que la longueur b est plus grande que x et par conséquent aussi plus grande que a.
| |
[pagina 419]
| |
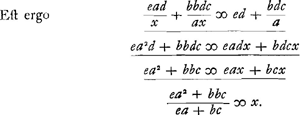 Haec igitur est regula universalis, per quam longitudo penduli simplicis quod compositoGa naar voetnoot1) isochronum sit facile supputabitur. Ex. gratia si AE sit ∞ ½AD et pondera D et E aequalia, erit 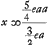 , hoc est ⅚a.
Quod si vero data longitudine perpendiculi AD et pondere D, itemque pondere E oporteat hoc affigere ad certum perpendiculi punctum, ita ut perpendiculum compositum sit isochronum perpendiculo datae longitudinis HK, dabitur ex aequatione praecedenti , hoc est ⅚a.
Quod si vero data longitudine perpendiculi AD et pondere D, itemque pondere E oporteat hoc affigere ad certum perpendiculi punctum, ita ut perpendiculum compositum sit isochronum perpendiculo datae longitudinis HK, dabitur ex aequatione praecedenti
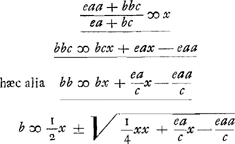 in qua aequatione eaa/c major est quam eax/c quia a major quam x; habet igitur duas radices verasGa naar voetnoot2) quarum utraque dat longitudinem AE ∞ b. Quod si vero HK, x, major data sit quam a, erit aequatio alterius formae, tantumque unam veram radicemGa naar voetnoot2) habebit, nempe 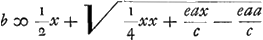 , ubi b majorem fieri apparet quam x, ac proinde majorem quoque quam a. , ubi b majorem fieri apparet quam x, ac proinde majorem quoque quam a.
| |
[pagina 420]
| |
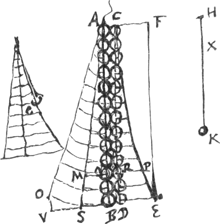
Pour trouver le pendule simple isochrone avec une barre ou un cylindre (que je considère toutefois comme une ligne droite seulement sans avoir aucun égard à son épaisseur) j'imagine au lieu de ce cylindre un nombre infini de petits globes formant une ligne droite rigide telle que AB [Fig. 17]. Si celle-ci se trouve d'abord en AO et parvient par une demi-oscillation en AB, et que là chaque globule frappe un des globules de la série CD lesquels ne sont pas attachés les uns aux autres, chacun de ces derniers prendra tout le mouvement du globule de la série AB par lequel il a été frappé, et la barre AB demeurera immobile. Pour la même raison que plus haut il est donc nécessaire que le centre commun de gravité de tous les globules CD, après qu'ils ont reçu le mouvement de la part des globules AB et qu'ils se sont élevés par ce mouvement aussi haut que possible, soit à la même hauteur que le centre de gravité des globules AB lorsque ceux-ci se trouvaient sur la droite AO. Supposons maintenant que la barre AB ait ses oscillations isochrones avec le pendule simple HK, dont la longueur soit appelée x. Posons aussi AB = a, et appelons d la hauteur OV à laquelle la droite BS est égale par construction. Par conséquent, d'après le théorème susmentionnéGa naar voetnoot1) la hauteur à laquelle s'élèvera par le choc le globe inférieur D sera da/x. Soit DE cette hauteur et supposons tracée la parabole EC dont l'axe CF soit parallèle à DE et dont le point C soit le sommet. Je dis que si du centre de chaque globule de la série CD on tire une droite parallèle à DE jusqu'à la parabole EC, ces droites représenteront les hauteurs auxquelles monteront les globules correspondants. En effet, joignons les points S et A par une droite. Comme OV, égale à SB, représente la hauteur de laquelle le globule le plus bas D est descendu, NM parallèle à SB et tracée à partir du centre d'un autre globule N sera, dis-je, la hauteur dont le globule N est descendu. Mais pour trouver, en partant de ces données, la hauteur RP à laquelle montera le globule R frappé par N, il faut d'après le théorème nommé construire RP d'après l'équation HK:AN = NM:RP. Par conséquent HK×RP = AN×NM. Mais HK×DE = AB×BS, puisque d'après le même théorème HK:AB = BS:DE. On a donc AN×NM:AB×BS = HK×RP:HK×DE, c.à.d. = RP:DE. Mais AN×NM:AB×BS = AN2:AB2. Par conséquent RP est à DE comme AN2 est à AB2 ou comme CR2 est à CD2, d'où il apparaît que le point P se trouve sur la dite parabole EC. Or, pour que le centre commun de gravité des globules CD, après que ceux-ci se sont élevés chacun à sa propre hauteur, soit aussi haut que le centre commun des globules AB lorsqu'ils se trouvaient sur la droite AO, il est nécessaire que lorsqu'on multiplie chaque hauteur par le poids du globule correspondant la somme de ces produits soit la même dans les deux cas. Mais comme le poids de tous les globules | |
[pagina 421]
| |
Ad inveniendum perpendiculum isochronon baculo seu cylindro, (quem tamen ut rectam lineam tantum considero nulla habita ratione crassitudinis) imaginor ejus loco infinitum numerum sphaerularum in rectam lineam rigidam conjunctarum velut AB [Fig. 17]. Haec si primum sit in AO, ac semivibra tione perveniat in AB, ibique singuli globuli occurrant singulis seriei CD, qui non connexi sint, accipiet horum quisque motum omnem a globulo seriei AB
 [Fig. 17.]
à quo impulsus erit, manebitque virga AB immota. Hinc eadem ratione qua suprà, necesse est centrum gravitatis commune globulorum omnium CD, postquam a globulis AB motum accepere, eumque sursum quousque possunt converterunt, aeque altum esse ac centrum gravitatis globulorum AB cum essent in recta AO. Ponamus jam virgam AB isochronas vibrationes habere perpendiculo simplici HK, cujus longitudo vocetur x. Et AB sit a. altitudo OV cui aequalis ponatur BS linea, vocetur d. Itaque per theorema superiusGa naar voetnoot1), erit altitudo ad quam ascendet percussa sphaera infima D, da/x, quae sit DE, descripta autem intelligatur parabola EC, cujus axis CF aequidistans DE, vertex vero C punctum. Dico si à centro cujusque globuli seriei CD ducantur rectae ipsi DE parallelae usque ad parabolam EC, eas singulas exhibere altitudines ad quas ascendent globuli unde eductae fuere. Jungatur enim recta SA. Cum igitur SB aequalis OV sit altitudo unde descendit globulus imus D, erit NM, quae parallela est SB atque educta ex centro globuli alterius N, erit inquam illa altitudo unde descendit globulus N. Hinc vero ut inveniatur altitudo RP ad quam ascendet globulus R percussus ab N, oportet per theorema dictum facere ut HK ad AN ita NM ad RP. Itaque ▭ HK, RP aequale ▭o AN, NM. sed ▭ HK, DE aequale est ▭o AB, BS, quia per idem theorema HK ad AB ut BS ad. DE. Ergo ▭ AN, NM ad ▭ AB, BS ut ▭ HK, RP ad ▭ HK, DE, hoc est ut RP ad DE. Sed ▭ AN, NM est ad ▭ AB, BS ut quadratum AN ad quadratum AB. Ergo ut quadr. AN ad quadr. AB sive ut quadr. CR ad quadr. CD ita est RP ad DE, unde liquet punctum P esse ad parabolam dictam EC. Jam vero ut centrum gravitatis commune globulorum CD postquam singulae ad suas altitudines ascenderunt sit aeque altum ac centrum gravitatis commune globulorum AB cum essent in recta AO, necesse est ut ductis singulis altitudinibus in suorum globulorum gravitatem aggregatum productorum utrobique aequale efficiatur. Quia autem aequalis omnium globulorum est gravitas, concipiamus singu- | |
[pagina 422]
| |
est le même, nous pouvons supposer que le poids de chacun d'eux est exprimé par la ligne de grandeur constante qui sépare les centres de deux globules adjacentsGa naar voetnoot1). Toutes ces petites lignes étant donc de part et d'autre multipliées par les hauteurs adjacentes, il apparaît qu'on obtient d'un côté pour somme des produits le triangle ABS, et de l'autre l'espace CPED compris entre la parabole CPE et les droites ED et DC. Ces espaces doivent donc être égaux entre eux. Or, le triangle ABS est égal à ½ ad ou ½ edGa naar voetnoot2), parce que AB = a et BS = d. Et l'espace CPED est égal à ⅓ da2/x ou ⅓ dae/x, parce que ED = da/x et CD = a; on en conclut que le rectangle CDEF est égal à da2/x, et la surface CPED est le tiers de ce rectangle. 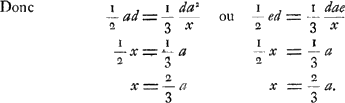 Ga naar voetnoot2) Le pendule simple HK doit donc avoir une longueur égale à deux tiers de celle de la barre AB pour que les deux pendules se meuvent avec des oscillations isochrones. Le centre d'oscillation de la barre se trouve donc à ⅔ du point de suspension, et lorsqu'on attache à la barre en ce point un poids quelconque, ses va-et-vient n'en deviendront ni plus rapides ni plus lents. Mais si l'on suspend un poids à l'extrémité inférieure de la barre, ou du moins en dessous dudit centre d'oscillation, son mouvement en sera ralenti; et le contraire se produira si l'on attache un poids à un endroit plus élevé. Supposons d'abord qu'un poids Q soit suspendu à l'extrémité inférieure D [Fig. 18] d'une barre pesante CD, le rapport de la gravité de ce poids à celle de la barre étant donné. Si l'on désigne comme plus haut la longueur de la barre par a et que la gravité de chacun des globules dont elle est composée par hypothèse est représentée par les petites parties de la droite CD ou eGa naar voetnoot2), parties que les globules considérés occupent sur cette droite, le poids total de la barre sera évidemment représenté par sa longueur entière, c.-à.-d. par aGa naar voetnoot3). C'est pourquoi si l'on prend une certaine droite telle que n qui soit à la longueur CD comme le poids Q est au | |
[pagina 423]
| |
lorum gravitatem exprimi lineis aequalibus quae inter binorum contiguorum centra interjacentGa naar voetnoot1). Quibus itaque utrinque in adjacentes altitudines ductis, apparet ex una parte pro summa productorum haberi triangulum ABS, ex altera vero spatium CPED parabola CPE et rectis ED, DC comprehensum. quae itaque spatia inter se aequalia esse oportet. Est autem triangulum ABS ∞ ½ad vel ½edGa naar voetnoot2), quia AB ∞ a, et BS ∞ d. Spatium vero CPED ∞ ⅓ daa/x vel ⅓ dae/x, quia ED ∞ da/x et CD ∞ a; hinc enim rectangulum CDEF fit ∞ daa/x, cujus tertia pars est spatium CPED.  Ga naar voetnoot2) Oportet igitur perpendiculum HK duas tertias habere longitudinis baculi AB ut vibrationibus isochronis moveantur. Igitur centrum oscillationis baculi est ⅔ à puncto suspensionis, quo loco quodcunque pondus baculo affigatur, nihilo velociores reditus aut tardiores acquiret. Quod si autem in ima baculi extremitate pondus aliquod appendatur, vel tantum infra dictum oscillationis centrum, eo lentior motus evadet, et contra si loco superiore quid ponderis addatur. 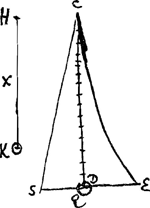 [Fig. 18.]
Ponamus primum in parte ima D [Fig. 18] baculi ponderantis CD, appensam gravitatem Q, cujus ad gravitatem baculi data sit ratio. cum autem baculi longitudo ponatur ut modo ∞ a, et singulorum quibus constare ponitur globulorum gravitas exprimatur particulis rectae 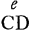 Ga naar voetnoot2) quas in ea singuli globulorum occupant, totius proinde baculi gravitas per totam sui ipsius longitudinem, nempe a, exprimeturGa naar voetnoot3). quare si quae recta sumatur, ut n, quae sit ad longitudinem CD sicut gravitas Q ad gravitatem baculi, ea recta n referet gravitatem Q, haud aliter ac singulae particulae quas in recta CD unusquisque globulorum baculum componentium occupat, sui globuli gravitatem refert. Ga naar voetnoot2) quas in ea singuli globulorum occupant, totius proinde baculi gravitas per totam sui ipsius longitudinem, nempe a, exprimeturGa naar voetnoot3). quare si quae recta sumatur, ut n, quae sit ad longitudinem CD sicut gravitas Q ad gravitatem baculi, ea recta n referet gravitatem Q, haud aliter ac singulae particulae quas in recta CD unusquisque globulorum baculum componentium occupat, sui globuli gravitatem refert.
Eadem itaque qua prius repetita ratiocinatione | |
[pagina 424]
| |
poids de la barre, cette droite n représentera le poids Q de la même manière que chacune des petites parties qu'occupe sur la droite CD chacun des globules qui composent la barre, représente le poids du globule correspondant. On trouve donc en répétant le raisonnement précédent que d'une part à la somme des produits considérée, qui était représentée par le triangle CQS, il faut ajouter le produit de n par QS, c.à.d. nd, et que de l'autre il faut, là où il y avait la surface CDE, y ajouter le produit de n par DE, savoir nda/x.  [Fig. 18.]
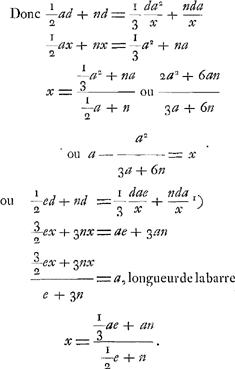 Ga naar voetnoot1) Autre application: si outre le poids inférieur Q [Fig. 19] un autre poids dont la gravité est représentée par la droite h est attaché à la barre ou perche pesante CD, il faudra ajouter de plus à la somme des produits d'une part le produit de LH par h, de l'autre celui de HG par h. En d'autres termes, posant CH = c, il faudra ajouter d'une part cdh/a et de l'autre c2dh/ax. En effet, cette dernière expression est le produit de HG par h, parce qu'à cause de la forme parabolique de EGC on peut poser (DC ou a2):(HC ou c2) = (ED ou da/x):HG, d'où l'on tire HG = c2d/ax. | |
[pagina 425]
| |
invenitur ad summam productorum ex una parte, quae erat triangulum CQS, addendum productum ex n in QS, hoc est, nd; ex altera vero ubi erat spatium CDE, addendum productum ex n in DE, nempe nda/x. 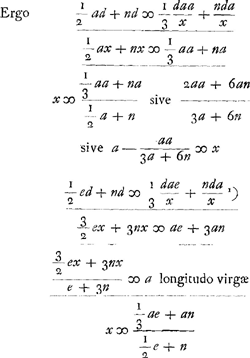 Ga naar voetnoot1) 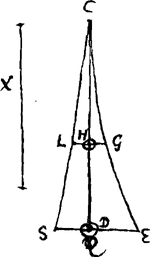 [Fig. 19.]
Porro autem si virgae vel baculo ponderanti CD [Fig. 19], praeter pondus infimum Q affixum sit aliud pondus H cujus gravitas exprimatur recta h, addendum erit insuper ad summam productorum ex una parte productum ex LH in h; ex altera vero productum ex HG in h. hoc est, posita CH ∞ c, inde addendum erit cdh/a; hinc ccdh/ax; hoc enim est productum ex HG in h, quia propter parabolam EGC, si fiat ut quadratum DC ∞ aa, ad quadr. HC ∞ cc, ita ED ∞ da/x ad HG, fit hinc ccd/ax. | |
[pagina 426]
| |
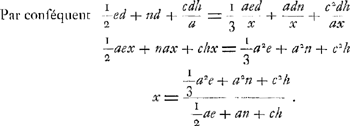 De la même équation on peut aussi tirer c, lorsque x et les autres grandeurs sont données. On aura en effet 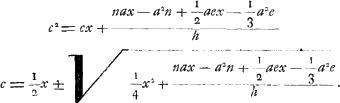 On peut également, lorsque toutes les grandeurs excepté h sont données, trouver cette dernière. On aura en effet 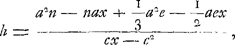 dans le cas où la longueur x est plus grande que cGa naar voetnoot2). Dans l'équation 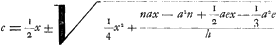 il apparaît que l'expression nax+½aex doit être plus petite que a2n+⅓a2e parce qu'autrement l'équation ne peut avoir deux racines vraiesGa naar voetnoot3). il apparaît que l'expression nax+½aex doit être plus petite que a2n+⅓a2e parce qu'autrement l'équation ne peut avoir deux racines vraiesGa naar voetnoot3).
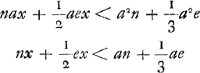 | |
[pagina 427]
| |
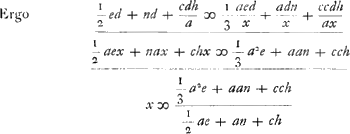 Ex eadem vero aequatione datis ipsa x et reliquis invenietur c: erit enim 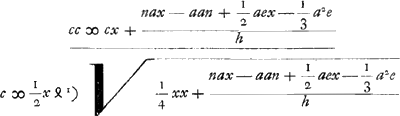 Ga naar voetnoot1) Rursus datis omnibus praeter h invenietur et ipsa. Erit enim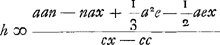 si nempe x major quam cGa naar voetnoot2). 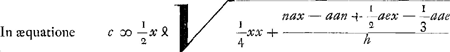 apparet nax+½aex minus esse debere quam aan+⅓a2e, quia alias duas veras radicesGa naar voetnoot3) aequatio habere nequit. 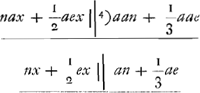 Ga naar voetnoot4) | |
[pagina 428]
| |
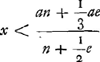 Ga naar voetnoot1) Considérons un pendule d'horloge dont les demi-oscillations dénotent les secondes, lequel est donc isochrone avec un pendule simple de 38 pouces du pied de RhynlandeGa naar voetnoot2). Supposons le poids de la barre égal à 1/28 de celui du plomb quiy est suspendu; et qu'il y ait en outre un petit poids en plomb mobile possédant une gravité égale à ⅓ de celle de la barre. On demande où il faut placer ce petit poids sur la barre pour que le pendule fasse avancer l'horloge d'une minute en 24 heuresGa naar voetnoot3). En multipliant 24 par 60 on obtient 1440; c'est le nombre des minutes comprises dans 24 heures. Retranchez-en une puisqu'on désire une marche plus rapide d'une minute, il en reste 1439. Or le carré du rapport 1440/1439 est à peu près 1440/1438 ou 720/719. Par conséquent si l'on suppose la longueur du pendule simple qui était de 38 pouces divisée en 720 parties égales et qu'on donne 719 de ces parties à un autre pendule simple, l'horloge mise en mouvement par ce pendule devancera l'autre d'une minute en 24 heuresGa naar voetnoot4). Mais comme nous supposons le pendule linéaire, composé d'un poids et d'une barre d'airain, isochrone avec le pendule simple de 720 parties, il faut | |
[pagina 429]
| |
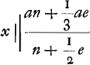 Ga naar voetnoot1)  [Fig. 19.]
Sit perpendiculum horologij quod singulis vibrationibus secunda scrupula denotet, nempe aequipollens perpendiculo simplici 38 pollicum pedis RhenolandiciGa naar voetnoot2). Gravitas virgae sit 1/28 gravitatis appensi plumbi; exiguum vero plumbum mobile sit ⅓ gravitatis virgae. quaeritur quo loco hoc virgae imponendum sit ut uno scrupulo primo citius spatio 24 horarum perpendiculum incedatGa naar voetnoot3). Ductis 24 in 60 fiunt 1440, quot nempe scrupula prima horis 24 continentur, ex his unum aufer quia uno scrupulo citius petitur, supersunt 1439. Ratio autem 1440 ad 1439 duplicata proxime est ea quae 1440 ad 1438, sive 720 ad 719. Ergo si perpendiculi longitudo quae erat 38 unc. divisa intelligatur in partes aequales 720, earumque 719 alij perpendiculo tribuantur, hoc perpendiculo horologium agitatum praecedet alterum illud in 24 horis uno scrupulo primoGa naar voetnoot4). Quia autem perpendiculum, compositum ex pondere et virga aenea isochronum ponitur perpendiculo simplici partium 720, inveniendum primum est virgae | |
[pagina 430]
| |
d'abord trouver la longueur de la barre à l'aide de l'équation susmentionnée 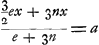 . Or, nous avons ici . Or, nous avons ici
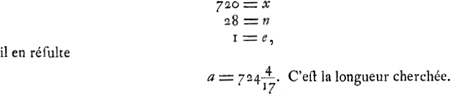 Calculons maintenant la longueur c en nous servant de l'équation qu'on trouve plus haut 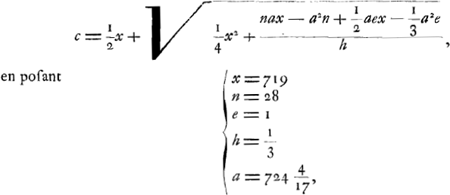 c.à.d. cherchons la place du poids mobile h par la vertu duquel le pendule considéré, composé d'une barre d'airain et d'un poids de plomb à son extrémité inférieure, puisse avancer d'une minute en 24 heures. L'équation 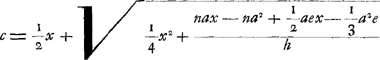 est maintenant équivalente à la suivante: 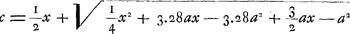 ou(pour a = 724¼) 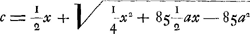 | |
[pagina 431]
| |
longitudo per aequationem superius positam, 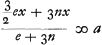 . Est nempe hic . Est nempe hic
720 ∞ x 28 ∞ n 1 ∞ e fitque a ∞ 724 4/17. longitudo quaesita ∞ a. Jam ex aequatione superiori 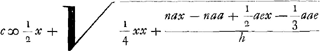 inveniamus quantitatem c positis x ∞ 719 n ∞ 28 e ∞ 1 h ∞ ⅓ a ∞ 724 4/17, hoc est quaeramus locum plumbi mobilis h cujus ope pendulum dictum, compositum ex virga aenea et plumbo in ima extremitate uno 1' citius incedat spatio 24 horarum. Idem autem nunc valet aequatio 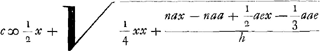 atque haec 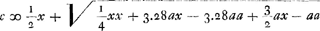 sive (a ∞ 724¼) 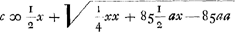 | |
[pagina 432]
| |
[pagina 433]
| |
|