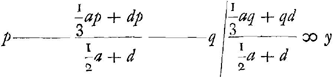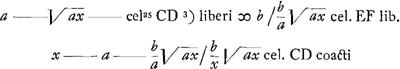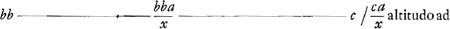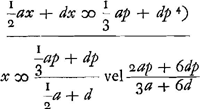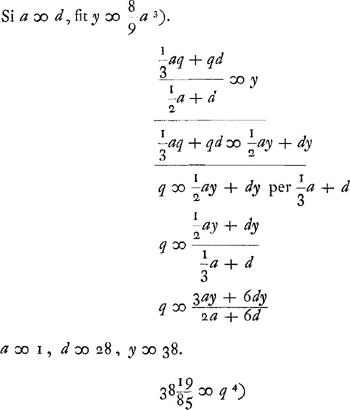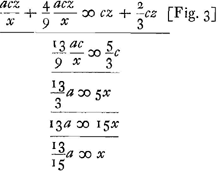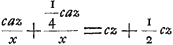
[Fig. 5.]
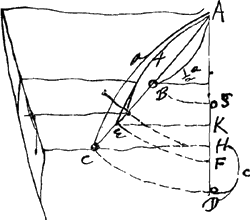
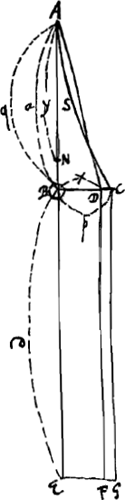
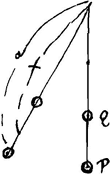
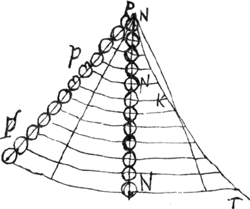
altitudines ad quas ascendent globi NNN [Fig. 5] impulsi a globis PPP, erunt ad parabolam aliquam PKT cujus vertex in P. Ex eo quod ca/x inventa est altitudo [Fig. 4] ad quam impellit CD coactumGa naar voetnoot4). nempe coactum incedere celeritateGa naar voetnoot5) penduli AE ∞ xGa naar voetnoot6). |
-
voetnoot2)
- La p. 176 porte la date du 15 nov. 1659, et la p. 188 celle du 15 déc. 1659.
-
voetnoot3)
- En choisissant convenablement la longueur qui représente l'unité de poids.
-
voetnoot4)
- Il est possible que le feuillet précédent du Manuscrit A, que nous ne possédons plus (comparez la note 1 de la p. 318 de ce Tome), contenait l'explication de ce calcul. D'ailleurs la p. 178 du Manuscrit (voir la suite de cette Pièce) donne également une partie de cette explication. Huygens suppose le pendule considéré en mouvement de telle manière que le point corporel B possède en son point le plus bas une vitesse qui lui permettrait d'atteindre une hauteur BC ou p s'il était libre. Cette hauteur est donc proportionnelle au carré de cette vitesse. Si l'on représente également par des lignes horizontales les hauteurs auxquelles pourraient s'élever les différents points pesants qui composent la barre AB, il est évident que les extrémités de ces lignes horizontales se trouveront sur la parabole considérée. Huygens part du principe que le centre commun de gravité doit monter autant dans le cas où tous les points sont libres que dans celui où ils composent un corps unique (comparez à ce propos l'alinéa qui commence en bas de la p. 415). De là il s'ensuit que, si l'on multiplie chaque hauteur par le poids correspondant, la somme sera la même dans les deux cas, bien entendu si les vitesses angulaires correspondant à la position verticale de la barre sont les mêmes dans les deux cas. Il en résulte que la surface ABC de la parabole (limite de la somme des produits des hauteurs par les poids), augmentée de la surface BCGE qui correspond au ‘pondus appensum’, doit être égale à la surface du triangle ABD augmentée de celle du rectangle BDFE, où BD = x représente la hauteur qu'atteignent en
réalité le point B de la barre et le ‘pondus appensum’. La ligne AD est bien une droite parce que les hauteurs auxquelles deux points de la barre s'élèvent simultanément sont proportionnelles à leurs distances du point A.
-
voetnoot1)
- C.à.d. p:x = q:y, où y représente la longueur cherchée du pendule simple isochrone avec le pendule composé considéré. En effet, le point pesant du pendule simple isochrone et le point B décrivent des arcs semblables et le point pesant du pendule simple monte donc à une hauteur h déterminée par l'équation h:x = y:q; on en tire h = xy/q. Mais les vitesses angulaires du point B et du point pesant du pendule isochrone sont toujours les mêmes; les hauteurs auxquelles le point B supposé libre d'une part et le point pesant du pendule isochrone d'autre part peuvent monter en vertu des vitesses qu'ils possèdent au point le plus bas étant proportionnelles aux carrés de ces vitesses, seront donc aussi proportionnelles aux carrés de leurs distances à leurs points de suspension respectifs. On a donc xy/q:p = y2:q2, ou py = qx, ce qu'il fallait démontrer. Huygens donne cette démonstration plus loin (voir la p. 417).
-
voetnoot2)
- Pour d = o, on trouve y = ⅔q. Comparez la note 1 de la p. 388.
-
voetnoot4)
- Nous supprimons le calcul numérique. Lorsque le ‘pondus appensum’ est 28 fois plus lourd que la barre et qu'on veut que le pendule composé soit isochrone avec un pendule simple de longueur 38, il faut donc donner au pendule composé une longueur 38 19/85. Le ‘pondus appensum’ est considéré, tant ici que plus haut, comme un point matériel.
-
voetnoot5)
- Huygens considère ici un pendule idéal dont le fil ou la barre est impondérable et porte deux points matériels de même poids, l'un en bas, l'autre un tiers de la longueur de la barre plus haut.
La longueur du pendule simple isochrone est appelée x. Le poids de chacun des points matériels s'appelle z. La hauteur que le poids P atteint réellement est désignée par la lettre c; la hauteur correspondante pour le poids Q est donc ⅔c.
Si nous appelons p la hauteur que le poids P pourrait atteindre, s'il était libre, avec la vitesse qu'il possède au point le plus bas de sa course, on a d'après la première équation de la note 1 de la p. 386 p:c = a:x,
a étant la longueur de la barre impondérable comme on le voit dans la Fig. 3. On en tire
p = ac/x.
Pour le poids Q la hauteur correspondante est 4/9p.
L'équation de Huygens exprime donc ici aussi que si l'on multiplie chaque hauteur par le poids correspondant, la somme sera la même dans le cas où tous les points sont libres que dans celui où ils composent un corps unique.
-
voetnoot1)
- La dernière partie de cette phrase exprime le résultat trouvé dans le cas précédent lorsque le ‘pondus appensum’ est supprimé (comparez la note 2 de la p. 386 et les p. 423 et 439).
-
voetnoot3)
- Dans la fig. 4 D et S désignent, comme l'on voit, deux globules contre lesquels les globules C et B vont choquer, tous les globules étant égaux entre eux. ‘Celeritas CD’ désigne la vitesse que le globule C communique au globule D. De même ‘celeritas BS’ serait la vitesse que le globule B communique au globule S. Mais Huygens écrit par inadvertance ‘celeritas BO’ au lieu de ‘celeritas BS’ et désigne encore une fois le globule S par la lettre O. La lettre S de la Fig. 4 a d'ailleurs plus ou moins la forme d'une lettre O corrigée en S.
-
voetnoot5)
- C'est ce qu'exprime l'équation
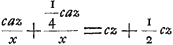 qui suit. Cette équation correspond à celle du cas précédent représenté par la Fig. 3; seulement comme le poids supérieur se trouve cette fois, non pas à un tiers de la longueur du pendule mais au milieu du fil ou de la barre impondérable, le facteur 4/9 du premier membre est remplacé ici par ¼ et le facteur ⅔ du second membre par ½. Supposer, comme Huygens le fait ici, que les globules B et C viennent choquer contre d'autres globules égaux et libres en leur communiquant toute leur vitesse, cela revient évidemment au même que de supposer que les globules B et C euxmêmes sont mis en liberté au point le plus bas de leur parcours. Mais Huygens dérive ici l'expression ca/x que l'on rencontre dans cette formule par un raisonnement différent de celui que nous avons suivi dans la note 5 de la p. 387 et qui correspondait à celui de Huygens dans le cas de la Fig. 2. qui suit. Cette équation correspond à celle du cas précédent représenté par la Fig. 3; seulement comme le poids supérieur se trouve cette fois, non pas à un tiers de la longueur du pendule mais au milieu du fil ou de la barre impondérable, le facteur 4/9 du premier membre est remplacé ici par ¼ et le facteur ⅔ du second membre par ½. Supposer, comme Huygens le fait ici, que les globules B et C viennent choquer contre d'autres globules égaux et libres en leur communiquant toute leur vitesse, cela revient évidemment au même que de supposer que les globules B et C euxmêmes sont mis en liberté au point le plus bas de leur parcours. Mais Huygens dérive ici l'expression ca/x que l'on rencontre dans cette formule par un raisonnement différent de celui que nous avons suivi dans la note 5 de la p. 387 et qui correspondait à celui de Huygens dans le cas de la Fig. 2.
Voici le nouveau raisonnement. Comme AE ou AF représente la longueur x du pendule simple isochrone avec le pendule considéré, le temps d'une oscillation est le même pour le point E qu'il soit ‘liberum’ ou ‘coactum’, c.à.d. libre ou attaché au pendule composé. L'expression ‘celeritas EF lib.’, égale à ce qu'on peut appeler la ‘celeritas EF coacti’, désigne la vitesse que le point E possède en atteignant l'endroit F. ‘Celeritas CD liberi’ la vitesse que posséderait à l'endroit D le globule C, si AC était lui aussi un pendule simple. On aura:
√a:√x = celas CD liberi:celas EF liberi,
ce qu'on peut écrire si l'on veut (comparez la note 1 de la p. 300)
a:√ax = b:celas EF liberi,
en désignant par b la ‘celas CD liberi’. On en tire
celas EF liberi = b/a√ax,
donc aussi celas EF coacti = b/a√ax.
Mais la figure fait voir que
celas EF coacti:celas CD coacti = x:a.
On en tire celas CD coacti = b/a√ax.
‘Altitudo ad quam impellit C D lib.’ veut dire: la hauteur à laquelle D parvient après avoir reçu de C la ‘celas CD liberi’; ‘altitudo ad quam impellit C D coact.’ veut dire: la hauteur à laquelle D (qui est toujours libre) parvient après a voir reçu de C la ‘celas CD coacti’. On a donc
(cel. CD lib.)2:(cel. CD coacti)2 = la première hauteur:la deuxième.
Or la première hauteur n'est autre que celle dont le globule C, parvenu en D, est descendu; c'est la hauteur DH ou c. On a donc:
b2:b2a/x = c:la hauteur à laquelle D parvient a vec la ‘cel. CD coacti’.
Cette dernière hauteur est donc ca/x, ce qu'il fallait trouver.
-
voetnoot3)
- Dans la fig. 4 D et S désignent, comme l'on voit, deux globules contre lesquels les globules C et B vont choquer, tous les globules étant égaux entre eux. ‘Celeritas CD’ désigne la vitesse que le globule C communique au globule D. De même ‘celeritas BS’ serait la vitesse que le globule B communique au globule S. Mais Huygens écrit par inadvertance ‘celeritas BO’ au lieu de ‘celeritas BS’ et désigne encore une fois le globule S par la lettre O. La lettre S de la Fig. 4 a d'ailleurs plus ou moins la forme d'une lettre O corrigée en S.
-
voetnoot3)
- Dans la fig. 4 D et S désignent, comme l'on voit, deux globules contre lesquels les globules C et B vont choquer, tous les globules étant égaux entre eux. ‘Celeritas CD’ désigne la vitesse que le globule C communique au globule D. De même ‘celeritas BS’ serait la vitesse que le globule B communique au globule S. Mais Huygens écrit par inadvertance ‘celeritas BO’ au lieu de ‘celeritas BS’ et désigne encore une fois le globule S par la lettre O. La lettre S de la Fig. 4 a d'ailleurs plus ou moins la forme d'une lettre O corrigée en S.
-
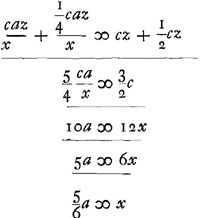
voetnoot5)
- C'est ce qu'exprime l'équation caz/x + ¼caz/x = cz + ½ cz qui suit. Cette équation correspond à celle du cas précédent représenté par la Fig. 3; seulement comme le poids supérieur se trouve cette fois, non pas à un tiers de la longueur du pendule mais au milieu du fil ou de la barre impondérable, le facteur 4/9 du premier membre est remplacé ici par ¼ et le facteur ⅔ du second membre par ½. Supposer, comme Huygens le fait ici, que les globules B et C viennent choquer contre d'autres globules égaux et libres en leur communiquant toute leur vitesse, cela revient évidemment au même que de supposer que les globules B et C euxmêmes sont mis en liberté au point le plus bas de leur parcours. Mais Huygens dérive ici l'expression ca/x que l'on rencontre dans cette formule par un raisonnement différent de celui que nous avons suivi dans la note 5 de la p. 387 et qui correspondait à celui de Huygens dans le cas de la Fig. 2.
Voici le nouveau raisonnement. Comme AE ou AF représente la longueur x du pendule simple isochrone avec le pendule considéré, le temps d'une oscillation est le même pour le point E qu'il soit ‘liberum’ ou ‘coactum’, c.à.d. libre ou attaché au pendule composé. L'expression ‘celeritas EF lib.’, égale à ce qu'on peut appeler la ‘celeritas EF coacti’, désigne la vitesse que le point E possède en atteignant l'endroit F. ‘Celeritas CD liberi’ la vitesse que posséderait à l'endroit D le globule C, si AC était lui aussi un pendule simple. On aura:
√a:√x = celas CD liberi:celas EF liberi,
ce qu'on peut écrire si l'on veut (comparez la note 1 de la p. 300)
a:√ax = b:celas EF liberi,
en désignant par b la ‘celas CD liberi’. On en tire
celas EF liberi = b/a√ax,
donc aussi celas EF coacti = b/a√ax.
Mais la figure fait voir que
celas EF coacti:celas CD coacti = x:a.
On en tire celas CD coacti = b/a√ax.
‘Altitudo ad quam impellit C D lib.’ veut dire: la hauteur à laquelle D parvient après avoir reçu de C la ‘celas CD liberi’; ‘altitudo ad quam impellit C D coact.’ veut dire: la hauteur à laquelle D (qui est toujours libre) parvient après a voir reçu de C la ‘celas CD coacti’. On a donc
(cel. CD lib.)2:(cel. CD coacti)2 = la première hauteur:la deuxième.
Or la première hauteur n'est autre que celle dont le globule C, parvenu en D, est descendu; c'est la hauteur DH ou c. On a donc:
b2:b2a/x = c:la hauteur à laquelle D parvient a vec la ‘cel. CD coacti’.
Cette dernière hauteur est donc ca/x, ce qu'il fallait trouver.
-
voetnoot2)
- ‘Altitudo ad quam impellit BO coactum’ (comparez la note 4 de la p. 389) désigne la hauteur à laquelle le globule B ‘coactum’ fait monter par son choc le globule O (ou plutôt S, voir la note 3 de la p. 389) qui est toujours libre.
-
voetnoot4)
- Comparez la note 2 qui précède. C'est le globule C qui est ‘coactum’ et qui donne sa vitesse au globule D qui est libre.
-
voetnoot6)
- Voir pour la signification de x, de c et de a la Fig. 4. L'expression ca/x déduite plus haut est indépendante, comme le montre cette déduction, de la distribution des poids du pendule composé linéaire. Dans la figure qui accompagnait cette déduction, le globule C était placé tout en bas du pendule composé, mais le raisonnement reste entièrement le même si l'on considère un globule placé plus haut. Or, dans la formule ca/x la longueur x est une constante, pour un pendule composé donné, mais lorsque la distance a du globule considéré au point de suspension varie, la longueur c variera dans le même rapport, de sorte que le produit ca, et la hauteur ca/x, seront proportionnels au carré de la distance du globule considéré au point de suspension. Si l'on suppose tracées dans la figure dans le sens horizontal les hauteurs ca/x, chacune à partir du globule N correspondant, les extrémités se trouveront donc sur une parabole. C'est la parabole déjà tracée dans la
Fig. 2 de la p. 385 au début de cette Pièce.
|