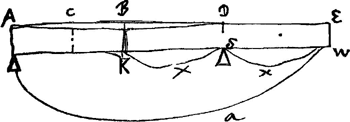
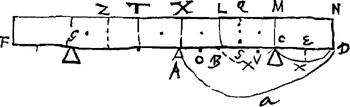
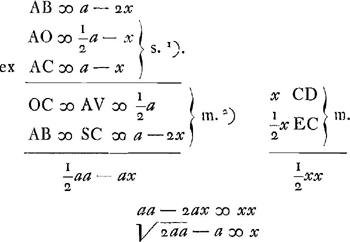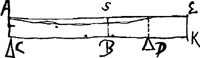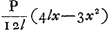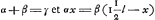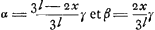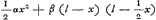Quaeritur ubi ponenda fulcra G C sub trabe FN [Fig. 4], ut tantundem sit periculi rupturae in AGa naar voetnoot3) atque in C vel in G.
[Fig. 4.]
Sit DC ∞ x. AD vel AF ∞ a. Sit CB ∞ ∞ CD. Ergo pars BN cum aequilibret super C, nequaquam incumbit medio A, ac similiter pars TF. Sed sola incumbit pars BT. AEquipollet autem pars BX ad rupturam faciendam in A non fultum parti QC ad rumpendum super fulcrum in A, positis his partibus inter se aequalibus, quia ex utravis ruptura in C vel A par gravitatis fit descensusGa naar voetnoot4).
Ergo momentum ad rupturam in A fit multiplicando AB in distantiam OC. At momentum rupturae in C, fit multiplicando CD in dist. CE. quae momenta aequalia esse oportetGa naar voetnoot5).
Partis TB momentum ad faciendam rupturam in positis fulcris GC, idem est ac momentum duarum simul partium QC, ZG super fulcro in A. Quarum unam QC tantum considerare opus ac si ad alteram partem A fulcri plane fixum esset librae brachiumGa naar voetnoot6).
| |
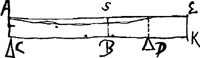
[Fig. 7.]
pars AB [Fig. 7] solum gravitatem habet, reliqua BE nihilGa naar voetnoot6). fulcra in C et D. quaeritur ubi rumpi debeat CE. Resp. ibi, ubi sumto aequali angulo rupturae, plurimum descendat gravitas composita è partibus ipsius ABGa naar voetnoot7). |
-
voetnoot2)
- La p. 107 est datée: août 1662, et la p. 125 porte la date du 15 sept. 1662.
-
voetnoot3)
- Il n'y a pas de ‘fulcrum’ en ce point, comme la figure pourrait le faire croire. Lorsque plus loin Huygens parle d'un ‘fulcrum in A’, il s'agit d'un support imaginaire.
-
voetnoot4)
- C. à d. (comparez la suite de cette Pièce) ‘posito angulo disjunctionis aequali’. Huygens suppose que, lorsqu'une rupture se produit p.e. en MC, la partie MNDC de la poutre tourne autour de C d'un certain ‘angle de disjonction’. Lorsque la rupture se produit en A, on peut considérer, si l'on veut, la rotation de la partie XNDA (ou de la partie XLBA) autour de C comme une rotation virtuelle. Par ‘gravitatis descensus’ il faut entendre le produit du poids du corps considéré par la descente verticale de son centre de gravité. La thèse de Huygens (comparez la note 4 de la p. 383) d'après laquelle dans le cas considéré les deux ruptures en A et en C sont également probables lorsque le ‘travail’ de la pesanteur est le même dans les deux cas, l'angle de disjonction (égal dans ce cas-ci à l'angle de rotation virtuelle; comparez la note 6) étant supposé le même, est correcte: ces ‘travaux’ sont proportionnels aux moments de rupture. Si une rupture se produit en A, la demi-poutre AN aura la tendance de tourner autour du point C avec un moment égal à celui de la partie BX par rapport au point C, puisque le moment de la partie BN par rapport au point C est nul.
-
voetnoot5)
- Les équations qui suivent expriment l'égalité de ces deux moments.
-
voetnoot6)
- Si une rupture se produit en A et que les deux moitiés de la poutre descendent simultanément en tournant d'un même angle (infiniment petit) resp. autour des supports G et C, l'angle de disjonction sera le double de cet angle de rotation. Mais si la partie droite descend seule, l'angle de disjonction sera égal à l'angle de rotation, comme nous l'avons déjà dit dans la note 4.
-
voetnoot3)
- On peut en effet, au lieu de considérer le moment de la partie BX [Fig. 4] par rapport au point C, considérer directement le moment de la demi-poutre AN par rapport au point C: c'est le même moment sous une autre forme (comparez la note 4 de la p. 381).
-
voetnoot4)
- On trouve en effet que le moment de rupture en K est la moitié du moment de rupture en S.
Si une rupture se produit en K, la partie AK aura la tendance de tourner autour du support gauche; si au contraire une rupture se produit en S, la partie DW tournera autour du support S. Le travail de la pesanteur est égal dans les deux cas en supposant les angles de rotation égaux, mais il n'est pas permis d'en conclure à l'égalité des moments de rupture: ce cas diffère du cas considéré à la p. 381 en ce que les parties AK et BW de la poutre exercent l'une sur l'autre dans la section BK une force verticale qui faisait défaut dans la section AX de la Fig. 4.
Néanmoins la règle indiquée dans la note 4 de la p. 381 est encore applicable au cas actuel, si l'on admet qu'en cas de rupture en A ce n'est pas la partie AK seule qui tourne d'un petit angle, mais que la partie BW tourne également (autour du point S) de telle manière que les deux parties continuent à cohérer au point B; l'angle de rotation de la partie AK est alors la moitié de l'angle de disjonction. Comparez les p. 335 et 336 de l'Avertissement qui précède.
-
voetnoot5)
- C.à.d. le moment de DW par rapport à S est égal au moment de rupture qui existerait en K si la partie DW de la poutre était supprimée et que seule la partie AK, KD subsistait. En effet, dans ce deruier cas le moment de rupture en K serait égal au moment de la partie AK par rapport au support gauche, d'après les considérations de la p. 381. Mais, comme la partie DW existe, le moment en K doit avoir une valeur différente, que Huygens ne détermine pas.
-
voetnoot6)
- C.à.d. la partie AB seule a un moment par rapport au point D, le moment de BE par rapport à D est nul.
-
voetnoot7)
- Cette solution peut ne pas paraître évidente, mais le calcul la confirme. Si nous admettons, comme la figure l'indique, que CB = BK et BD = DK, nous pouvons poser CK = 2l, CB = l, BD = DK = ½l. Le moment de rupture à une distance x du point C est alors
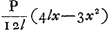 , où P est le poids de la poutre. Ce moment a une valeur maxima pour x = = ⅔l. Or, on trouve cette même valeur en appliquant la règle que Huygens énonce dans ce paragraphe. En effet, si une rupture se produit entre C et B de sorte qu'à une distance x du point C un angle de disjonction (infiniment petit) γ apparaît, les parties gauche et droite de la poutre, qui cohèrent encore en haut, auront tourné resp. autour de C et de D d'angles α et β, , où P est le poids de la poutre. Ce moment a une valeur maxima pour x = = ⅔l. Or, on trouve cette même valeur en appliquant la règle que Huygens énonce dans ce paragraphe. En effet, si une rupture se produit entre C et B de sorte qu'à une distance x du point C un angle de disjonction (infiniment petit) γ apparaît, les parties gauche et droite de la poutre, qui cohèrent encore en haut, auront tourné resp. autour de C et de D d'angles α et β, 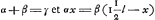 ; il en résulte ; il en résulte 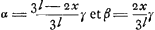 . Les centres de gravité des parties gauche et droite de la partie AB de la poutre sont descendus resp. de ½αx et de β(l-½x), et le travail correspondant de la pesanteur est le produit de
P/2l par . Les centres de gravité des parties gauche et droite de la partie AB de la poutre sont descendus resp. de ½αx et de β(l-½x), et le travail correspondant de la pesanteur est le produit de
P/2l par 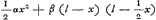 , ce qui se réduit à Pγ/12l(4lx-3x2). Ce travail est maximum pour x = ⅔l. Comparez la démonstration plus générale donnée dans l'Avertissement (note 2 de la p. 335). , ce qui se réduit à Pγ/12l(4lx-3x2). Ce travail est maximum pour x = ⅔l. Comparez la démonstration plus générale donnée dans l'Avertissement (note 2 de la p. 335).
|