Oeuvres complètes. Tome XVI. Percussion

II²⁾.
[Oct. 1659]³⁾.

[Fig. 1.]

1. AH ∞ EC⁴⁾. HE, AC sunt lineae⁵⁾ [Fig. 1].

Ostendendum quod ⁶⁾.

Sit EL parallela CA.

2) Manuscrit A, p. 156. Les §§ 1, 2, et 3 sont purement géométriques, mais le § 4 qui fait suite au § 3 traite un cas de statique.

3) La p. 155 porte la date du 11 oct. 1659 et la p. 157 est datée: oct. 1659.

4) Le signe ∞ indique l'égalité. Comparez la note 3 de la p. 7 du T. XI.

5) C. à d. des lignes droites.

6) C. à d. EG:GH = AD:DC. Comparez la note 19 de la p. 13 du T. XI.

[p. 380]

Ergo ut AD ad DC ita LD ad DE, et AL ad EC, sive AL ad AH, nam AH ∞ EC.

Sed ut LA ad AH ita EG ad GH. Ergo EG ad GH ut AD ad DC. quod erat demonstrandum.

2. Conversum quoque verum est; nempe si intra angulum ADE ducantur duae HE, AC, fueritque ut AD ad DC ita EG ad GH, etiam HA, EC aequales erunt.

Nam quia ut AD ad DC ita AL ad CE, erit ergo AL ad CE ut EG ad GH, hoc est ut LA ad AH. ideoque EC aequalis AH.

[Fig. 2.]

3. Secent rursus se mutuo AC HE in G [Fig. 2], sitque ut AD ad DC ita EG ad GH. Et sumatur HM aequalis EN; et jungatur MN. dico eam secari à recta AC in O, ut sit NO ad OM sicut EG ad GH sive ut AD ad DC.

Est enim AH ∞ EC per 2. Ergo has auferendo ab aequalilibus HM, EN, relinquuntur aequales AM, CN. Ergo per 1. ut AD ad DC ita NO ad OM, sive ut EG ad GH. quod erat ostendendum.

[Fig. 3.]

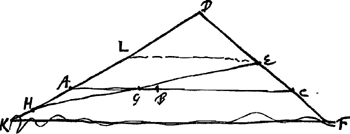
[4.] Si fuerit triangulum ABC [Fig. 3] cujus latus AC horizonti parallelum, pendeantque super ejus lateribus pondera fune colligata, D, E. quorum D ad E gravitas sit sicut latus AB ad BC; pondera quemcunque datum situm servabunt.

Quia centrum ipsorum gravitatis commune G non descendit etiamsi pondera moveri incipiant, sed eadem semper manet altitudine, ut ex praecedentibus facile ostenditur.