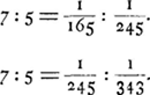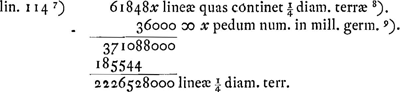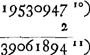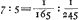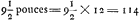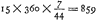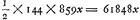Ga naar voetnoot3)
Ga naar voetnoot3)
aliquanto erit quam calculo praecedenti inventa est Ga naar voetnoot4). |
-
voetnoot1)
- Cet Appendice est emprunté au Manuscrit C, p. 89 et 90.
-
voetnoot3)
- La p. 79 porte la date du 20 nov. 1665, et la p. 92 est datée ‘à Paris 1666’.
-
voetnoot4)
- Comme la suite le fait voir, Huygens se propose de calculer la vitesse de rotation que la terre devrait avoir pour qu'un mobile placé sur l'équateur éprouvât une force centrifuge égale à sa gravité. Suivant la Prop. V du Traité (p. 275), il faut à cet effet calculer la vitesse qu'un mobile d'abord en repos acquiert en parcourant d'un mouvement uniformément accéléré, avec l'accélération g, une distance égale à ¼ du diamètre de la terre. En prenant le pied rhénan pour unité de longueur et l'heure pour unité de temps, il trouve par un calcul que nous supprimons, et qui revient à calculer √gR, R étant le rayon de la terre, la vitesse 103005000. Ce nombre est beaucoup trop grand; comme Huygens n'avait apparemment pas sous la main la mesure de Snellius (p. 304 de ce Tome), il prend pour le diamètre de la terre une valeur plus de 50% trop grande (voir p. 324, note 1). Pour ½g il prend la valeur 13.4.1 pieds. Il est vrai que plus tard il indique sur la même feuille la vraie valeur de ½g(15.7½) et la mesure de Snellius, mais sans corriger le calcul. Voir à ce sujet la note 4 de la p. 326.
-
voetnoot5)
- Huygens veut dire que le nombre 103005000 représente la vitesse d'un mobile ayant parcouru d'un mouvement accéléré (accélération g) ¼ du diamètre de la terre.
-
voetnoot1)
- Ici aussi Huygens annote plus tard: ‘verius 22800’. C'est cette erreur dans la longueur du mille germanique (p. 88 du Manuscrit: ‘36000 ped. mill. germ. ut puto’) qui conduisit Huygens à une valeur excessive pour le diamètre de la terre; voir la note 4 de la p. 323.
-
voetnoot3)
- Cette fraction fut corrigée en 1/162. Une valeur beaucoup meilleure (1/265) avait déjà été trouvée par Huygens en 1659 (p. 304).
-
voetnoot3)
- Cette fraction fut corrigée en 1/162. Une valeur beaucoup meilleure (1/265) avait déjà été trouvée par Huygens en 1659 (p. 304).
-
voetnoot4)
- Pour trouver ce nombre, il faut multiplier la fraction 1/165 deux fois de suite par ½√2 ou 5/7, une fois parce que le rayon de la circonférence décrite est 5/7 de celui de l'équateur, et une fois parce que la direction de la force centrifuge fait un angle de 135o avec celle de la gravité.
Dans l'équation 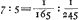 il y a une erreur de calcul. On trouverait 1/245 si la fraction précédente était 1/175. il y a une erreur de calcul. On trouverait 1/245 si la fraction précédente était 1/175.
-
voetnoot6)
- Consultez la p. 281 de ce Tome. On ne trouve plus dans le Manuscrit A le calcul en question; comparez à ce sujet l'Appendice V, note 4, p. 320, quatrième alinéa de cette note.
-
voetnoot8)
- Huygens prend ici pour le rayon de la terre
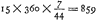 mill. germ. Si l'on appelle x le nombre de pieds rhénans contenus dans un mille germanique, le demi-rayon de la terre devient mill. germ. Si l'on appelle x le nombre de pieds rhénans contenus dans un mille germanique, le demi-rayon de la terre devient 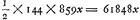 lignes rhénanes. lignes rhénanes.
-
voetnoot9)
- Nombre trop grand; comparez la note 1 et la note 11 qui suit.
-
voetnoot11)
- Le nombre 39061894 (beaucoup trop grand) résulte donc de la division de la longueur du rayon terrestre, exprimée en pouces, par 9½. Voir pour la correction de ce nombre la p. 326, note 4.
-
voetnoot2)
- Les lignes qui suivent ont été ajoutées plus tard (encre différente).
-
voetnoot3)
- ‘Eratosthenes Batavus’, 1617, Lib. II, Cap. XII.
-
voetnoot4)
- Pour corriger le nombre 39061894 trouvé plus haut (voir p. 325) il faut donc le multiplier par 22800/36000, ce qui donne 24739200. La force centrifuge à l'équateur serait donc égale à 24739200 fois la pesanteur si la terre tournait en une seconde.
En divisant ce nombre par (24×3600)2, on trouve que la force centrifuge à l'équateur est égale à 1/302 fois la pesanteur. Cette fraction est plus petite que la fraction 1/265 obtenue en 1659 (p. 304) parce qu'à la p. 281 la valeur de ½g est correcte (15 pieds 7½ pouces), tandis qu'à l'endroit considéré à la p. 304 Huygens avait pris ½g = 13 pieds 8 pouces. (Voir la note 5 de la p. 305).
Dans ce calcul nous avons pris avec Huygens le rayon terrestre égal à 859×22800 = = 19585200 pieds rhénans. A la p. 304 de ce Tome Huygens avait pris avec Snellius, qui se sert d'une valeur plus exacte du nombre π, le rayon terrestre = 19595160 pieds. À la p. 91 du Manuscrit C Huygens écrit: ‘3264500 perticae in diam. terrae.’ Le rayon terrestre serait alors de 19587000 pieds. En ce cas la force centrifuge à l'équateur serait égale à 24741474 fois la pesanteur si la terre tournait en une seconde. La fraction qu'il s'agit de calculer devient de nouveau 1/302. On trouve la même valeur en corrigeant le calcul de la première Partie de cet Appendice.
Plus tard, dans le ‘Discours de la Cause de la Pesanteur’ de 1690 Huygens prend avec Picard le rayon de la terre = 19615800 pieds parisiens = 144/139×19615800 = 20321404 pieds rhénans. Il trouve alors (en appliquant cette fois la Prop. XIII, p. 291 de ce Tome) pour la fraction considérée 1/172 ou 1/289 à peu près. D'après les méthodes du présent Appendice on trouve, pour cette valeur du rayon terrestre, la fraction 1/291; mais en prenant plus exactement (comme Huygens le fait aussi dans le Discours nommé) la durée de la rotation de la terre = 23 h. 56 m., on trouve précisément 1/289.
|