Vid. fig. pag.ae praeced.is primam.
| (1) | Sit ∠ BAE = 45o. |
| (2) | mobile B vim centrifugam gravitati suae aequalem debet habere. ea celeritate debet circumferri quam habet post casum ex dimidia AE vel EB. |
| (3) | tempus per AK ad tempus per BE ut VAGa naar voetnoot3) ad circumferentiam EB. |
| (4) | sed tempus per BE ad tempus per K hoc est per circulum omnium minimum ut KA ad VA. |
| (5) | tempus per AK ad tempus per K ut KA ad circumferentiam EB. |
| (6) | sed tempus per ½AK ad tempus per AK ut BE vel EA ad AK. |
| (7) | tempus per ½AK ad tempus per K ut BE ad circumferentiam BE, hoc est, ut radius ad circumferentiam. |
| (8) | Itaque tempus minimae gyrationis penduli AK aequale est minimae ejusdem oscillationiGa naar voetnoot4). |
|
-
voetnoot1)
- Cet Appendice est emprunté au Manuscrit A, p. 177. Le feuillet sur lequel se trouvait la figure fait défaut, ainsi que les quatre feuillets précédents.
-
voetnoot2)
- La p. 176 porte la date du 15 nov. 1659, et la p. 188 celle du 15 déc. 1659.
-
voetnoot3)
- Voir (au quatrième alinéa de la p. 322) la note qui suit.
-
voetnoot4)
- La Proposition (8) correspond à la Prop. XII du Traité (p. 289) où il est dit: ‘Si pendulum motu conico latum circuitus minimos faciat, eorum singulorum tempora... aequalia sunt tempori duarum oscillationum lateralium ejusdem penduli minimarum’. Dans (8) il faut donc entendre par ‘minima oscillatio’ le temps d'une petite oscillation double.
La Prop. XII du Traité, comme nous l'avons dit aux pp. 281 note 4 et 317 note 6, a été empruntée par les éditeurs à l'‘Horologium oscillatorium’; ce sont eux qui y ont ajouté une démonstration.
Or, le texte de la Prop. (8) du présent Appendice ressemble davantage à celui du Th. 10 du Manuscrit No. 13 (p. 313): ‘tempus circuitus (c.à.d. le temps de révolution dans des “circuli omnium minimi”) proinde aequale est oscillationi minimae ejusdem penduli, qua ultro citroque moveretur’: ici aussi le temps d'une oscillation double est désigné par l'expression peu exacte: ‘oscillatio minima’. Il est peut-être permis d'en conclure que les propositions du Manuscrit No. 13 ont été rédigées plus tôt que les propositions de l'‘Horologium oscillatorium’.
Le présent Appendice qui contient la démonstration de la Proposition (8) - les chiffres (1)....(8) y ont été ajoutés par nous - fut sans doute précédé par d'autres démonstrations. Comparez p. 325 note 6. Il est possible que les feuillets qui font défaut (les p. 177 et 178 contiennent encore d'autres calculs et peuvent avoir été laissées dans le livre pour cette raison) furent enlevés par de Volder et Fullenius, et qu'ils s'en sont servi pour rédiger leurs démonstrations des Prop. VII, XII, XIII, XIV et XV du Traité.
Quoi qu'il en soit, le texte du présent Appendice et la démonstration de la Prop. XII (p. 289-291) ont entre eux une forte ressemblance.
La Fig. 20 (p. 293) qui accompagne la démonstration des éditeurs sert aussi à celle des propositions suivantes; sinon, elle aurait dû avoir la forme de la Fig. 1 de la présente note qui correspond au texte de Huygens. Les points C et D de la Fig. 20 correspondent à nos points
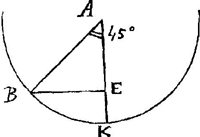
B et E. Le point le plus bas doit être désigné ici par la lettre K comme dans la Fig. 19 (p. 289).
Si nous appelons r le rayon BE et l la longueur du fil AK, l'équation (6) nous apprend que
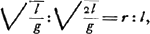
donc l = r√2, conformément à la Fig. 1.
L'équation (5), savoir 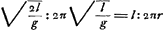 , est satisfaite: l'expression ‘tempus per K’ est expliquée dans l'équation (4) et l'expression ‘circumferentia EB’ désigne la circonsérence dont EB est le rayon. , est satisfaite: l'expression ‘tempus per K’ est expliquée dans l'équation (4) et l'expression ‘circumferentia EB’ désigne la circonsérence dont EB est le rayon.
L'équation (7) est également satisfaite. Pour pouvoir conclure de l'équation (7) à l'équation (8) il faut supposer connue l'équation:
(9) tempus per ½AK ad tempus minimae oscillationis (oscillation double) ut radius ad circumferentiam,
qui peut aussi s'écrire:
(9') ¼ tempus minimae oscillationis (½ oscillation simple) ad tempus per ½AK = semicircumferentia ad diametrum.
Sous cette forme elle correspond à la Prop. XXV de la Pars Secunda de l'‘Horologium Oscillatorium’, où il est dit à propos de l'oscillation cycloïdale:
‘tempora descensus... ad punctum imum verticis... sunt inter se aequalia, habentque ad tempus casus perpendicularis per totum axem cycloïdis eam rationem, quam semicircumferentia circuli ad diametrum’. En effet, l'axe de la cycloïde est égal à la moitié du rayon de courbure au point le plus bas. Nous savons d'ailleurs par une observation de Huygens à la p. 188 du Manuscrit A que la Prop. XXV de la Pars Secunda de l'‘Horologium Oscillatorium’ lui était connue avant le 15 décembre 1659.
L'équation (4) peut s'écrire 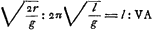
et l'équation (3) 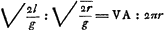 . .
De chacune de ces équations l'on tire
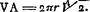
La longueur VA, égale à celle d'une circonférence de rayon 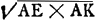 , était probablement représentée dans la figure de Huygens par une droite auxiliaire en dehors de la Figure 1, ou plutôt par une droite ayant une de ses extrémités au centre A. , était probablement représentée dans la figure de Huygens par une droite auxiliaire en dehors de la Figure 1, ou plutôt par une droite ayant une de ses extrémités au centre A.
Considérons maintenant les équations (2).. (8) dans l'ordre du texte.
L'équation (2) correspond à la Prop. V (p. 275) du Traité, ou bien au Th. 1 du Manuscrit No. 13 (p. 312). Les éditeurs (p. 289-291) commencent également leur démonstration de la Prop. XII en partant de la Prop. V.
L'équation (3) peut s'écrire:
tempus per AK ad tempus per BE ut ∜2 ad 1
ou bien: tempus per ½BE: tempus per 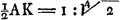 . .
Elle correspond donc à la phrase suivante des éditeurs: ‘Est autem DC ad CA [Fig 20] ut 1 ad √2, adeoque tempus casus perpendicularis ex dimidia DC ad tempus casus perpendicularis ex dimidia CA, quae tempora sunt in subduplicata ratione DC ad CA, erit in ratione 1 ad √√2.’
L'équation (4) peut s'écrire, en divisant le premier et le troisième terme par √2:
tempus per ½ BE: tempus per 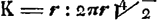 . .
Sous cette forme elle correspond à la phrase suivante des éditeurs (p. 291): ‘tempus ergo casus perpendicularis ex dimidia DC, est ad tempus circuitus minimi, ut radius ad circumferentiam ductam in √√2.’
L'équation (5), qui se déduit des équations (3) et (4), peut s'écrire, en multipliant deux termes par √2:
tempus per K: tempus per 2AK = 2πr:2r
ou bien: tempus per K: tempus per 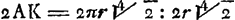 . .
Elle correspond donc à la phrase suivante des éditeurs: ‘tempus igitur circuitus minimi penduli AC ad tempus casus perpendicularis ex dupla penduli altitudine, ut circumferentia ducta in √√2 ad duplum radii ductum in √√2, sive ut circumferentia ad diametrum.’
L'équation (7), qui se déduit de l'équation (5) au moyen de l'équation évidente (6), est à peu près identique à l'équation (5).
Enfin les éditeurs supposent connue la Prop. XXV de la Pars Secunda de l'‘Horologium Oscillatorium’ (voir p. 291 note 2 et p. 282 note 3) et concluent de la même manière que Huygens à l'égalité du temps de révolution suivant une très petite circonférence d'une part et du temps d'une très petite oscillation double d'autre part.
|

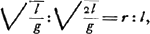
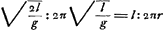 , est satisfaite: l'expression ‘tempus per K’ est expliquée dans l'équation (4) et l'expression ‘circumferentia EB’ désigne la circonsérence dont EB est le rayon.
, est satisfaite: l'expression ‘tempus per K’ est expliquée dans l'équation (4) et l'expression ‘circumferentia EB’ désigne la circonsérence dont EB est le rayon.
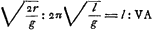
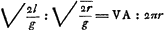 .
.
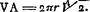
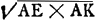 , était probablement représentée dans la figure de Huygens par une droite auxiliaire en dehors de la Figure 1, ou plutôt par une droite ayant une de ses extrémités au centre A.
, était probablement représentée dans la figure de Huygens par une droite auxiliaire en dehors de la Figure 1, ou plutôt par une droite ayant une de ses extrémités au centre A.
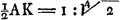 .
.
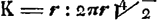 .
.
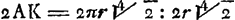 .
.

