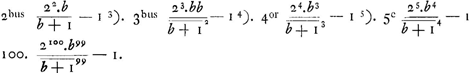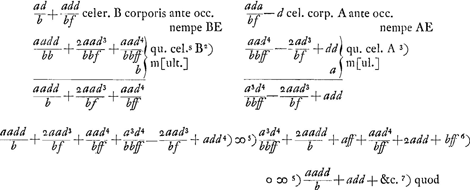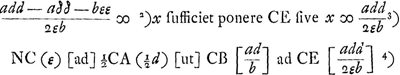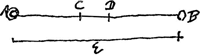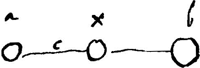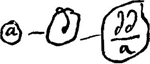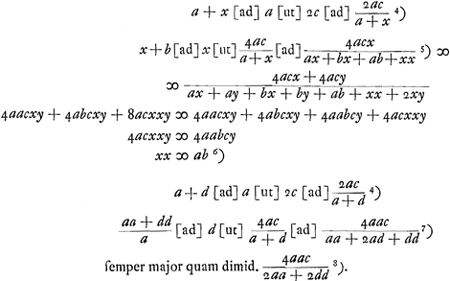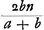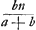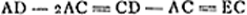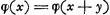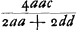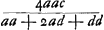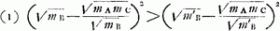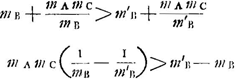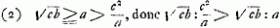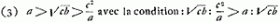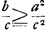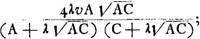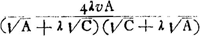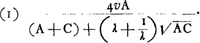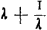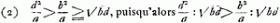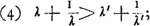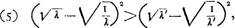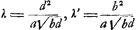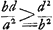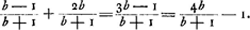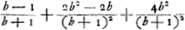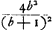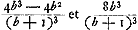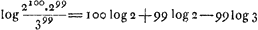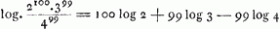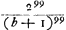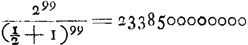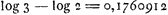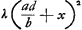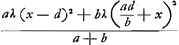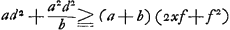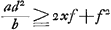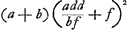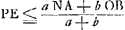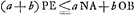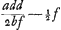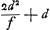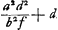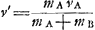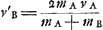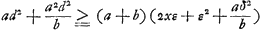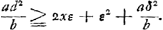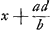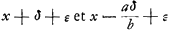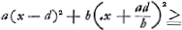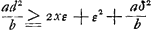|
| |
| |
| |
Appendice IIIGa naar voetnoot1)
À l'ouvrage: ‘De motu corporum ex percussione’.
[1656-1667?]
Quae pag. 11 ad signum...Ga naar voetnoot3). ubi de utilitate in Physicis addendum, Nam si natura universa corpusculis quibusdam constat à quorum motu omnis rerum diversitas oriatur, quorumque celerrimo impulsu lux momento temporis propagetur et per immensa caeli spatia defluat, ut probabile esse multi philosophi existimarunt; non parum adjuvari haec contemplatio videbitur si verae motus leges innotuerint quaque ratione de corporibus in corpora transferaturGa naar voetnoot4). Quam vero sublimis sit atque ardua in hisce comtemplatio quam difficilis ad haec naturae penetratioGa naar voetnoot5). Quantaque animi contentione veritas occulta eruatur, ex aliorum potius qui ante nos eidem disquisitioni incubuere quam nostra opinione intelligi cupimusGa naar voetnoot6). Itaque omnino locum eum ex dialogis viri perspicacissimi Galilei de Galil. quos de motu Italica lingua conscripsit adducendum existimavi, atque interpraetandum, ubi difficultatem rei et inpensum in ea studium suum aperte testaturGa naar voetnoot7).
| |
| |
16.17.Ga naar voetnoot8) Caeterum et in libris de Mundi SystemateGa naar voetnoot9) idem Galileus pluribus in locis motus naturam persequitur quae &c. p. 11 in fin.Ga naar voetnoot10)
| |
Sint corpora a et b. Celeritas corporis a ∞ p. Celeritas corporis b ∞ q. Celeritas quam habent respectu mutuo (hoc est, summa celeritatum utrarumque, si in contrarias partes moveantur, differentia vero, si in easdem) sit n. Eritque celeritas corporis a post impulsum, aequalis differentiae inter p et 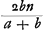 Ga naar voetnoot12) Ga naar voetnoot12), vel uno casu eorum summae cum nempe a in motu praecedit, quo casu etiam manifestum est
| |
| |
semper moveri a in eandem partem quam prius. alijs vero omnibus, si p major sit quam 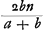 feretur a in eandem quoque partem. at si p minor sit quam 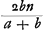 , referetur a in partem contrariam. si denique aequalia, restabit a immotum.
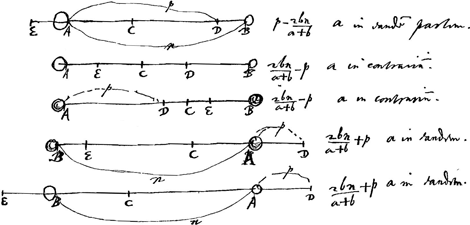
Sit AD celeritas corporis A. BD celeritas corporis B. quae itaque convenient in puncto D. dividatur AB in C, ut sit sicut A ad B ita CB ad CA. Et sumatur CE aequalis CD. Erit celeritas corporis A post impulsum, EA. corporis B vero EB, idque in partem eam quam demonstrat ordo punctorum EA; EB. quod si E cadat in A aut B restabit tunc A aut B immotumGa naar voetnoot2).
| |
| |
| |
| |
| |
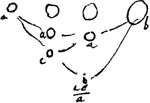
[Fig. 6.]
a, c, a, b minor quam a, a, a, bGa naar voetnoot1) quia c minor quam a. Sed a, c, cc / a, b minor quam a, c, a, b, quia cc / a magis recedit à medio prop. inter c et b quam aGa naar voetnoot2). Etenim cc/a minor quam c. Ergo a, c, cc/a, b minor quam a, a, a, b.
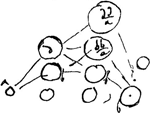
[Fig. 7.]
Ostend.Ga naar voetnoot3) quod a, d, dd/a, b minorem dat quam a, b, bb/a, b.
a, d, bb/a, b minor quam a, b, bb/a, bGa naar voetnoot4). sed a, d, dd/a, b minor quam a, d, bb/a, b quia dd/a magis
| |
| |
recedit à medio prop. inter d, b quam bb/aGa naar voetnoot5): Etenim d major quam b.
| |
| |
| |
pag. 194 Epist. Cartesij 2 vol.Ga naar voetnoot3) Alias leges motus tradit quam in Principijs Philos.Ga naar voetnoot4).
| |
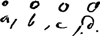
[Fig. 8.]
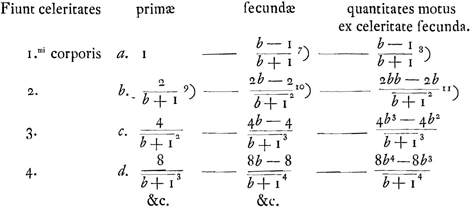
Positis corporibus duris a, b, c, d &c. [Fig. 8] continue proportionalibus, motoque solo a minimo et per ipsum successive b, c, d &c. Invenitur motus singulorum primus, item alter postquam percusserint corpus sequens, hoc modo. Sit a ∞ 1. et corpus secundum sit b ut positum est. Ergo c ∞ bb. d ∞ b3 &c. Sit etiam celeritas corporis primi a ∞ 1.
| |
| |
| |
| |
Si a sit maximus proportion.lium primae celeritates exprimuntur eodem modoGa naar voetnoot1), secundae mutatis signis +-Ga naar voetnoot2).
Quantitas motus in corporibus postquam ultimum fuerit impulsum.
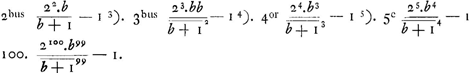 Ga naar voetnoot3)Ga naar voetnoot4)Ga naar voetnoot5)
Ga naar voetnoot3)Ga naar voetnoot4)Ga naar voetnoot5)
Si proportio corporum sit dupla, quantitas motus in corporibus 100 augetur secundum rationem 1 ad 4677000,000,000 proximèGa naar voetnoot6).
Si tripla, 1 ad 542100,000,000,000,000, prox.Ga naar voetnoot7)
Cum autem a maximo corpore incipit motus non augetur unquam nec minuitur motus quantitasGa naar voetnoot8). Celeritas vero minimi ad maximi celer.m in proportione dupla et corporibus 100 fit proxime quae 14760000000Ga naar voetnoot9) ad 1Ga naar voetnoot10).
| |
| |
| |
| |

[Fig. 10.]
A, B, C egales. Posons que ces corps soient durs parfaitement, et que A et B se touchent et reposent. C vient a les frapper. A partira seul, et B et C demeureront joints et en repos. Cela arrive aux corps les plus durs que nous ayons, et d'autant plus precisement qu'ils sont plus durs. Or si B ne s'est point meu, il ne peut pas avoir men A. car de l'avoir meu sans mouvement,
| |
| |
il n'est pas possible, car si B estoit inesbranlable comment est ce que le costè D se resentiroit du coup. B s'est donc meu et A necessairement en mesme temps, et pour le moins aussi viste que B, de sorte qu'ou ils sont allè joints ensemble ou A a devancè B, d'ou s'ensuit que A n'a pu empescher B de continuer son chemin vers le costè A. Toutefois B se trouve en repos le coup estant fait. il est donc retournè sans que rien l'y ait obligè. ce qui est absurde. Et la mesme chose se conclurait quand B seulement iroit plus lentement que A. donc il faut conclure que ces corps se touchant immediatement, ils ne peuvent pas estre parfaitement durs et faire l'effect qu'ils font, et que par consequent ils font ressortGa naar voetnoot1). Ou bien il faut dire que si ces corps sont parfaitement durs ils ne se touchent pas immediatement. Et il y a des experiences avec les verres convexes qui semblent le prouuerGa naar voetnoot2).
Quand un corps dur en rencontre un autre egal qui est en repos, on peut dire que l'un acquiert en un instant le mouvement, et que l'autre en un instant le perd. Mais de dire que le corps B en mesme instant acquiert et perd le mouuement, c'est dire qu'il demeure en repos, car le mouuement ne se fait que dans le temps, et il n'y en a point dans un instant.
S'ils ne se touchent pas immediatem.t il faut qu'ou bien les corps qui sont entre deux se retirent promptement et s'echappent, ou qu'ils fassent ressort eux mesmes, comme l'air.
[Fig. 11.]

[Fig. 12.]
[Fig. 13.]
[Fig. 14.]
| |
Sunt corpora quaedam quae in se mutuo impingentia non recedunt a contactu, qualia sunt quae prae mollitie figuram aliquatenus mutant cum percutiuntur, nec omnino in eandem se restituere conantur, ut argilla humida plumbum et alia.
| |
| |
Alia vero quae in se mutuo impingentia à contactu resiliunt: quod quidem non illis solum quae dura nobis vocantur, ut ebori vitro lapidibus plerisque chalibi et alijs accidit sed et ijs quae dum colliduntur figuram nonnihil mutare constat sed continuo vi quadam eandem sibi restituere, veluti suber spongia, vesica aere inflata, et alia multa. Nec immerito dubitari potest annon etiam illa quae apud nos ex materia durissima constant, hac restitutionis vi a se invicem resiliant.
Cum vero appareat in occursu mutuo hujusmodi corporum non extingui sed conservari quodammodo motum, idque tanto melius quanto perfectior fuerit eorum sive durities sive restitutionis vis, proinde eas in summa perfectione considerari volumus in corporibus de quibus in sequentibus agetur. de quorum motu ex percussione sequentia supponimusGa naar voetnoot5).
| |
A et B corpora mollia, A movetur celeritate AC [Fig. 15] B celeritate BC. quae sunt reciproce ut ipsa corpora. dico post concursum in C, manere utrumque immotumGa naar voetnoot8).
| |
| |
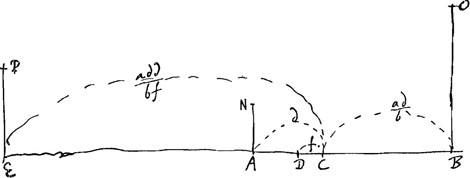
[Fig. 15.]
Sit ut DC (f)Ga naar voetnoot1) ad CB (ad/b) ita CA (d) ad CE (add/fb), sitque haec celeritas navis, quae talis ponitur ad formandam demonstrationem.
hic navis ponitur sinistrorsum ferri celeritate CE.
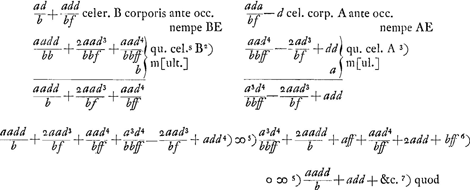 Ga naar voetnoot2)Ga naar voetnoot3)Ga naar voetnoot4)Ga naar voetnoot5)Ga naar voetnoot6)Ga naar voetnoot5)Ga naar voetnoot7)
Ga naar voetnoot2)Ga naar voetnoot3)Ga naar voetnoot4)Ga naar voetnoot5)Ga naar voetnoot6)Ga naar voetnoot5)Ga naar voetnoot7) esse nequit.
Si enim fieri potest moveantur post conjunctionem celeritate CD versus partem
| |
| |
A. Ponantur haec in navi fieri quae feratur celeritate CE, fient haec ergo eodem modo respectu navigantis ac respectu stantis in ripa. movebitur corpus A ante occursum celeritate AE, et corpus B celer. BE. Et post conjunctionem utrumque simul movebitur celeritate ex CE et CD composita. Quare etiam, si stans in terra hos motus corporum efficiat, idem quoque evenire necesse est. hoc autem fieri non posse ostendetur.
Sit NA altitudo ex qua corpus A cadens acquisiverit celeritatem AE. Ergo faciendo sicut qu.AE ad qu.EB ita AN ad BO, erit BO altitudo ex qua decidens B acquisivit cel. BE. Et rursus si fiat ut qu. AE ad qu. utriusque simul EC, CD, ita AN ad EP, erit EP altitudo ad quam corpora A, B, juncta ascendere poterunt celeritate ex EC, DC composita. Atqui ostendetur PE altitudinem ductam in magnitudinem utramque A et B majus facere productum quam
| |
| |
sint duo quae fiunt ducendo NA in A, et OB in B, quod fieri nequitGa naar voetnoot1). ErgoGa naar voetnoot2)
Haec fortasse optima erit demonstr.o et melior ea quae in fin. pag. praec.Ga naar voetnoot3)
ita est: sed sufficit ponere CE ∞ add/2bfGa naar voetnoot4).
Des ChalesGa naar voetnoot5). Sunt qui satis demonstrasse se putant veritatem hujus Theorematis ex eo quod quantitas motus in utroque corpore est aequalisGa naar voetnoot6). Est probabilis ratio sed non sufficit. SicGa naar voetnoot7) demonstraretur corpus quiescens a diversis corporibus impulsum quorum eadem quantitas motus aequalem celeritatem acquirere quod tamen falsumGa naar voetnoot8).
| |

A et B concurrunt in C, celeritatibus BC, AC, quae sunt reciprocè ut corpora. Sint discessura spatio ST, sed quo diviso in N, in proportione reci- | |
| |
proca ponderum, non cadat N in C si potest, et intervallum NC dicatur ε.
| |
| |
Fiant haec in navi quae feratur celeritate CEGa naar voetnoot1) à C versus N. quae celeritas CE ita inventa sit ut sit sicut ε sive NC ad ½CA ita CB ad CE.
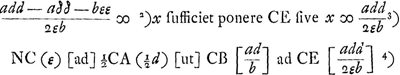 Ga naar voetnoot2)Ga naar voetnoot3)Ga naar voetnoot4)
Ga naar voetnoot2)Ga naar voetnoot3)Ga naar voetnoot4)
qualiscunque sit discessus resilientium ST, necesse est reflexiones singulorum A et B, esse inter se in proportione reciproca corporum, uti fuere celeritates occurrentium, aut alioqui devenietur hac demonstratione ad absurdum, nempe ut altius fiat centr. commune gravitatis post occursum quam ubi fuerat cum deciderent corpora A et B ex ijs altitudinibus unde celeritates concursus nacta sunt. Etenim ad inveniendam celeritatem adventitiam CE, non opus est considerare δ nec aδ/b, nec proinde discessus quantitatem ST, sed tantum distantiam CN sive ε, qua centrum grav.is recessit post occursum, nempe in fine temporis secundiGa naar voetnoot5).
Centrum gravitatis igitur si ad occursum tendentibus quiescebat, quiescet etiam post occursum, in hujusmodi semiduris aeque ac in perfecte duris et mollibus.
| |
| |
unde ostenditur, quod si ante occursum movebatur, etiam post eodem motu perget.
que la mesme reflexion se fait quand l'un des corps seroit tout a fait dur ou d'un ressort parfait, pourvu que le mouvement respectif soit le mesmeGa naar voetnoot6).
Corpora quaedam in se mutuo impingentia resilire, idque ita ut recedant mutuo respectu aeque celeriter atque accesserunt, qualiscunque fuerit celeritas illa respectivaGa naar voetnoot7). deinde fiet propositio. non posse ulla corpora celerius recedere quam accesserunt.
Item. Si fuerit eadem celeritas respectiva accedentibus etiam eandem fore celeritatem respectivam recedentibus.
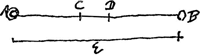
[Fig. 17.]
sit corporibus A et B celeritas respectiva accedentibus AB [Fig. 17]. Et propria celeritas corporis A sit AC, corporis B celeritas BC. Vel sit A celeritas AD, ipsi vero B celeritas BD. Dico utroque casu eandem fore celeritatem respectivam recedentibus ab occursu. Sit priore casu celeritas respectiva recedentium E. Et fiant quae in casu posteriore in navigio, quod feratur celeritate DC. Jam stantis in ripa respectu movebitur A celeritate AC et B celeritate BC. Quare ejusdem spectatoris respectu debent A et B recedere celeritate respectiva E. Ergo et vectoris respectu, eadem celeritate respectiva AB moventur. ut autem in navigio ita in terra.
| |
| |
| |
An corpora dura quae figuram non mutant, sequuntur leges nostrorum durorum, de quibus demonstrari potest restitutioni et flexioni obnoxia esse.
Non video quid impediat. Non enim impossibile videtur motum in instanti vel indivisibili tempore communicari (quod necesse est) quandoquidem quo duriora sunt corpora quae habemus, hoc est quo minus a figura recedunt minusque restituuntur, hoc est, quo minori tempore motum communicant, eo melius leges nostras reflexiones serventGa naar voetnoot2).
| |
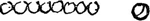
[Fig. 18.]
Si une boule d'yvoire venant choquer un rang de boules d'acier trempè ou de verre dont chacune soit plus legere qu'elle, rejalira pourtant quelque peu. a cause que son ressort est plus lent. |
-
voetnoot1)
- Dans cet Appendice nous avons réuni plusieurs Pièces et Annotations qui se rattachent au Traité ‘De Motu’. Nous les avons arrangées, autant qu'il nous était possible, dans l'ordre chronologique, mais leur date est souvent plus ou moins incertaine.
-
voetnoot2)
- Cette annotation se rencontre à la première page du Manuscrit de 1656, auquel nous avons emprunté l'Appendice II (p. 137-149).
-
voetnoot3)
- Il y a ici dans le Manuscrit présent un signe de renvoi qu'on retrouve à la page indiquée du Manuscrit qui a servi pour l'Appendice I, savoir en marge du texte reproduit (p. 104) dans le deuxième alinéa de la Cinquième Partie.
-
voetnoot4)
- Comparez les allusions aux règles du choc, qu'on trouve aux pp. 11, 12, 14, 16 et 20 du Chap. I de l'édition originale du ‘Traité de la lumiere’ (1690). On connaît d'ailleurs le rôle important que ces règles ont joué plus tard dans la théorie cinétique des fluides.
-
voetnoot7)
- Comparez le premier alinéa de la p. 105.
-
voetnoot8)
- Il s'agit encore du Manuscrit d'où nous avons emprunté l'Appendice I. Voir pour le contenu des p. 16-17 de ce Manuscrit la Sixième Partie de cet Appendice depuis le sixième alinéa de la p. 111 jusqu'au début du quatrième alinéa de la p. 113 y inclus.
-
voetnoot9)
- Voir l'ouvrage cité dans la note 8 de la p. 101.
-
voetnoot10)
- Comparez l'avant-dernier alinéa de la p. 106 qui en effet se trouve dans le Manuscrit en question vers la fin de la page numérotée 11.
-
voetnoot11)
- Cette Pièce empruntée à une feuille détachée nous fait connaître comment la belle solution par construction du problème le plus général du choc direct des corps durs (voir l'alinéa qui commence en bas de la p. 65) a été trouvée par Huygens, savoir en combinant dans une formule unique les résultats de cinq cas différents que sa méthode géométrique le forçait de distinguer.
En même temps elle explique l'indication du calcul numérique qu'il ajouta plus tard au texte de son Traité (voir la note 4 de la p. 69). En effet la vitesse C dont il est question dans cette indication n'est autre que celle indiquée dans la Pièce présente par 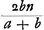 . .
-
voetnoot12)
- Évidemment ce résultat a été obtenu en appliquant l'un ou l'autre des Théorèmes cités dans la note 1 de la p. 148. En effet, lorsqu'on ajoute aux vitesses p et q de a et b une vitesse commune qui réduit le corps a en repos, il est clair que le corps b se mouvra avec la vitesse n. Appliquant ensuite l'un de ces Théorèmes on trouve
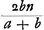 pour la vitesse de a aprèsle choc, laquelle vitesse doit encore être composée avec la vitesse ajoutée p. pour la vitesse de a aprèsle choc, laquelle vitesse doit encore être composée avec la vitesse ajoutée p.
-
voetnoot1)
- Dans tous les cas indiqués dans la Fig. 3, AC et AD représentent respectivement
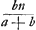 et p en grandeur. Or, considérons p.e. le premier cas. D'après le raisonnement que nous avons exposé dans la note précédente la vitesse du corps a après le choc sera représentée par et p en grandeur. Or, considérons p.e. le premier cas. D'après le raisonnement que nous avons exposé dans la note précédente la vitesse du corps a après le choc sera représentée par 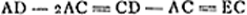 . Dans tous les autres cas on arrive au même résultat final, savoir que la vitesse du corps a après le choc est représentée par EA en grandeur et en direction. Quant à la vitesse du corps b après le choc elle est représentée par EB puisque la vitesse d'éloignement doit être égale à celle d'approchement. . Dans tous les autres cas on arrive au même résultat final, savoir que la vitesse du corps a après le choc est représentée par EA en grandeur et en direction. Quant à la vitesse du corps b après le choc elle est représentée par EB puisque la vitesse d'éloignement doit être égale à celle d'approchement.
-
voetnoot2)
- Comparez, p. 65-66, les deux premiers alinéas de la discussion de la Prop. IX du Traité.
-
voetnoot3)
- La Pièce, empruntée à une feuille détachée, nous montre comment Huygens a calculé quelle doit être la masse du corps intermédiaire en repos, afin que le corps a [Fig. 4.] qui se meut avec la vitesse c, donne le maximum de vitesse au corps b en repos. Comparez, p. 81, la Prop. XII du Traité. De même on y trouve la déduction du résultat mentionné dans la note 8 de la p. 136 et quelques considérations sur le cas de deux intermédiaires.
-
voetnoot4)
- Vitesse du corps intermédiaire après le premier choc, calculée d'après les théorèmes biffés, mentionnés dans la note 1 de la p. 148.
-
voetnoot5)
- Vitesse du corps b après les chocs, de laquelle vitesse il s'agit de déterminer la valeur maximum. À cet effet Huygens emploie la méthode de Fermat, telle qu'il l'avait simplifiée. Cette méthode consiste à poser
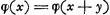 , sauf à omettre dans le calcul les termes sans y et ceux qui contiennent les puissances de y au-dessus de la première; voir la note 30 de la p. 19 de notre T. XI. , sauf à omettre dans le calcul les termes sans y et ceux qui contiennent les puissances de y au-dessus de la première; voir la note 30 de la p. 19 de notre T. XI.
-
voetnoot4)
- Vitesse du corps intermédiaire après le premier choc, calculée d'après les théorèmes biffés, mentionnés dans la note 1 de la p. 148.
-
voetnoot7)
- Vitesse du corps de masse dd / a après les chocs.
-
voetnoot8)
- Vitesse de ce même corps frappé par le corps de masse a sans l'intervention du corps intermédiaire. Huygens veut dire que
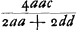 est toujours plus grand que la moitié de est toujours plus grand que la moitié de 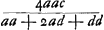 , ce qu'on vérifie aisément. , ce qu'on vérifie aisément.
-
voetnoot1)
- Huygens compare les vitesses obtenues par le dernier corps après les chocs dans les deux cas mentionnés où les vitesses initiales du premier corps a sont supposées égales.
-
voetnoot2)
- Suivant la première formule à la p. 81 de la note 2 de la p. 80 on doit démontrer pour conclure à l'inégalité en question, qui peut s'écrire (c, cc/a, b) < (c, a, b):
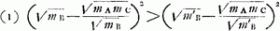
où ma = c, mc = b, mb = cc/a, m'b = a.
Or, cette inégalité se réduit successivement à
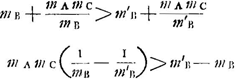
et enfin, divisant par la différence, ici positive, m'b-mb, à mamc > mbm'b, savoïr bc > cc. Or, cette condition est remplie lorsque, comme dans la figure, b > c.
En écrivant: ‘cc / a magis recedit à medio prop. inter c et b quam a’, Huygens semble vouloir dire qu'on a soit 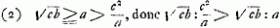 , soit , soit 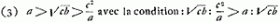 qui conduit également à la relation b > c, apparemment admise par lui. Dans le cas (2) on a: cb ≧ a2, ou qui conduit également à la relation b > c, apparemment admise par lui. Dans le cas (2) on a: cb ≧ a2, ou 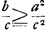 , donc également (puisque a > c):b > c. Comparez la note 5 de la page suivante. , donc également (puisque a > c):b > c. Comparez la note 5 de la page suivante.
-
voetnoot3)
- Il s'agit peut-être encore cette fois d'un problème que Huygens se proposait de joindre à son Traité ‘De Motu’; comparez la note 10 de la p. 133. De même l'alinéa qui précède pouvait donner lieu à un tel problème.
-
voetnoot4)
- Puisque b est moyen proportionnel entre a et bb/a, mais d ≠ b.
-
voetnoot5)
- Pour saisir plus ou moins la pensée de Huygens (comparez sa démonstration de la Prop. XII du Traité ‘De Motu’ où il considère d'abord, p. 83, fig. 20, trois corps tels que la masse du corps intermédiaire est moyenne proportionnelle entre les masses des corps extrêmes, et remplace ensuite, p. 85 fig. 21 et p. 83 dernière ligne, ce corps intermédiaire par un corps de masse X, dont il considère le rapport à la masse d'un des trois corps) concevons trois globes tels qu'il les suppose, de masses A, λ√AC et C respectivement. Le corps A pousse le corps λ√AC, celui-ci pousse ensuite le corps C. Nous savons déjà que pour une vitesse donuée υ du corps A la vitesse du corps C sera la plus grande possible pour λ = 1. La vitesse du corps C sera généralement, d'après la formule de la page 153,
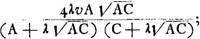
cette expression se réduit à
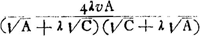
et ensuite à
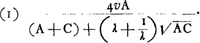
Comme l'expression 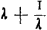 ne change pas quand on remplace λ par 1/λ, il est évident que la vitesse du corps C sera la même lorsque la masse du corps intermédiaire est p.e. trois fois plus grande que √AC, que lorsqu'elle est au contraire trois fois plus petite que √AC. L'on peut dire que dans les deux cas la masse du corps intermédiaire ‘recedit’ d'une même quantité de la moyenne proportionnelle √AC. Comme l'expression ne change pas quand on remplace λ par 1/λ, il est évident que la vitesse du corps C sera la même lorsque la masse du corps intermédiaire est p.e. trois fois plus grande que √AC, que lorsqu'elle est au contraire trois fois plus petite que √AC. L'on peut dire que dans les deux cas la masse du corps intermédiaire ‘recedit’ d'une même quantité de la moyenne proportionnelle √AC. Comme l'expression 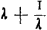 croît uniformément lorsque λ croît de 1 à ∞ (et aussi lorsque λ diminue de 1 à o), il s'ensuit que la vitesse du corps C diminue de plus en plus à mesure que la masse du corps intermédiaire ‘magis recedit à medio prop. √AC’. croît uniformément lorsque λ croît de 1 à ∞ (et aussi lorsque λ diminue de 1 à o), il s'ensuit que la vitesse du corps C diminue de plus en plus à mesure que la masse du corps intermédiaire ‘magis recedit à medio prop. √AC’.
Dans le cas considéré (d > b), on aura ‘dd/a magis recedit a medio prop. inter d, b quam bb/a’ lorsque 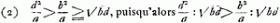 , ou bien lorsque , ou bien lorsque  . .
La formule (1) fait voir que, si la masse du corps intermédiaire est d'abord λ√AC et ensuite λ'√AC, la vitesse du corps C sera la plus petite dans le premier de ces deux cas, lorsque
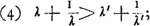
c'est donc là, sous une forme moderne, la condition de Huygens qui peut également s'écrire
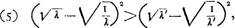
formule équivalente à la formule (1) de la note (2) de la p. 154.
En substituant dans la formule (4) les valeurs de λ et de λ' qui correspondent aux cas où la masse du corps intermédiaire est d2/a ou b2/a (savoir 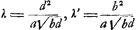 ), on trouve que, pour d > b, la formule (4) se réduit à bd > a2, conformément aux sormules (2) et (3) (De la formule (2) on tire ), on trouve que, pour d > b, la formule (4) se réduit à bd > a2, conformément aux sormules (2) et (3) (De la formule (2) on tire 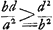 , où d > b, donc bd > a2). , où d > b, donc bd > a2).
Huygens aurait donc dû observer que, pour pouvoir affirmer que ‘dd/a magis recedit à medio prop. inter d, b quam bb’/a, il faut admettre la relation bd > a2.
-
voetnoot1)
- La Pièce est empruntée à la p. 140 du Manuscrit A.
-
voetnoot2)
- D'après le lieu que la Pièce occupe au Manuscrit A.
-
voetnoot3)
- Il s'agit des deux premiers volumes de l'édition de Clerselier des ‘Lettres de Mr. Descartes’; voir la note 1 de la p. 515 de notre T. I et la note 11 de la p. 334 du T. II.
-
voetnoot4)
- Voici le passage en question qu'on trouve au deuxième volume, publié en 1659, dans une lettre à Mersenne du 25 décembre 1639 (p. 627 du T. II de l'édition d'Adam et Tannery des OEuvres de Descartes): ‘Pour l'inertie, ie pense auoir desia escrit qu'en vn espace qui n'est point du tout empeschant, si vu corps de certaine grandeur, qui se meut de certaine vitesse, en rencontre vn autre qui luy soit esgal en grandeur, & qui n'ayt point de mouuement, il luy communiquera la moitié du sien, en sorte qu'ilz iront tous deux ensemble de la moitié aussy viste que faisoit le 1er; mais, s'il en rencontre vn qui luy soit double en grandeur, il luy communiquera les deux tiers de son mouuement, & ainsy ils ne feront tous deux ensemble pas plus de chemin en trois momentz, que le 1er faisoit en vn moment. Et generalement, plus les corps sont grands, plus ilz doibuent aller lentement, lors qu'ilz sont poussez par vne mesme force.’
Or, ces deux exemples, qui seraient à leur place dans la Théorie de la percussion des corps mous, sont en contradiction flagrante avec deux des règles énoncées par Descartes dans les ‘Principia’, savoir le premier avec la sixième règle, sur laquelle on peut consulter la note 18 de la p. 139 de ce Tome, et le second avec la quatrième règle que nous avons reproduite dans la note 1 de la p. 38.
-
voetnoot5)
- La Pièce, empruntée à une feuille détachée, se rapporte au dernier alinéa (p. 91 ci-dessus) du Traité ‘De Motu’.
-
voetnoot6)
- L'alinéa mentionné dans la note précédente, manque dans le Manuscrit de 1656. La Pièce doit donc être postérieure à cette année. Or dans les notices de Huygens qui lui ont servi pour ses discours à l'Académie des Sciences du 4, 11 et 18 janvier 1668 (que nous publierons plus loin dans le Tome présent; voir les p. 182-186) on rencontre aux numéros 14 et 13 (p. 184) une allusion aux résultats et calculs de la présente Pièce. Puisque entre ces deux époques Huygens, comme du moins sa Correspondance le fait présumer, ne semble pas s'être occupé de nouvelles recherches sur la percussion des corps, nous avons cru pouvoir choisir 1667 pour la date probable de cette Pièce V.
-
voetnoot7)
- Vitesse du premier corps dans la direction ba (voir la Fig. 8) après le premier choc, calculée à l'aide du premier théorème de la note 1 de la p. 148, lequel calcul Huygens désigne sur une autre feuille, traitant du même sujet d'une manière moins complète, comme ‘per regulam nostram’.
-
voetnoot8)
- Quantité de mouvement du premier corps dans la direction ba après le premier choc.
-
voetnoot9)
- Vitesse du deuxième corps dans la direction ab après avoir reçu son premier choc, calculée à l'aide du théorème mentionné dans la note 7.
-
voetnoot10)
- Vitesse définitive du deuxième corps dans la direction ba.
-
voetnoot11)
- Quantité de mouvement définitive du deuxième corps dans la direction ba.
-
voetnoot1)
- Voir le deuxième théorème de la note 1 de la p. 148.
-
voetnoot2)
- C'est-à-dire dans les numérateurs, qu'on doit alors écrire 1-b, 2-2b, etc. Ces vitesses et les quantités de mouvement qui en résultent dans la der nière colonne sont alors dans la direction ab.
-
voetnoot3)
- En sommant à la manière de Descartes, savoir sans avoir égard à leur direction, les quantités de mouvement définitives des deux premiers corps supposés seuls présents, on trouve:
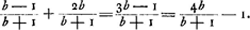
-
voetnoot5)
- Cette sois il sera plus facile de soustraire du résultat obtenu dans la note précédente le terme
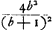 et d'y ajouter les termes et d'y ajouter les termes 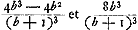 après quoi on obtient le résultat annoncé par Huygens. après quoi on obtient le résultat annoncé par Huygens.
-
voetnoot6)
- Comparez la note 6 de la p. 91. Sur une autre feuille détachée on retrouve le calcul de Huygens par les logarithmes d'après la formule:
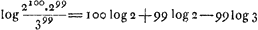 . .
-
voetnoot7)
- On trouve sur la feuille mentionnée dans la note précédente le calcul par la formule:
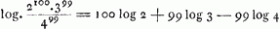 . .
-
voetnoot8)
- Puisqu'alors toutes les vitesses sont dirigées dans le même sens.
-
voetnoot9)
- En continuant la première colonne du petit tableau de la p. 157 l'on voit que pour le centième et dernier corps la vitesse après les chocs est égale à
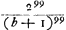 , ou dans le cas présent à , ou dans le cas présent à 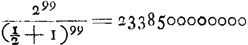 , et non pas 14760000000; comparez la note 4 de la p. 90. , et non pas 14760000000; comparez la note 4 de la p. 90.
Or, nous avons retrouvé sur une autre feuille détachée le calcul qui a amené le résultat erroné de Huygens. Il y suppute le logarithme du nombre cherché en soustrayant 99 (log 3-log 2) de 99 log 2; mais il commet une simple erreur de calcul dans la multiplication de 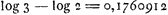 par 99, trouvant 19,6330288 au lieu de 17,4330288. par 99, trouvant 19,6330288 au lieu de 17,4330288.
-
voetnoot10)
- On trouve encore sur la même feuille une ‘Regula universalis’ qui correspond presque textuellement avec le premier alinéa de la Pièce II, p. 151-152. Cela semble prouver que les deux principales additions au Traité ‘De Motu’ après 1656 (date du Manuscrit dont nous avons tiré l'Appendice II (p. 137-149)), savoir celle des p. 69-71 (voir la note 4 de la p. 69) et celle du dernier alinéa du Traité (voir la note 1 de la p. 90), ont été conçues à la même époque. En effet, la première addition correspond bien à la Pièce II et à la ‘Regula Universalis’, tandis que la deuxième se retrouve à la fin de la Pièce V(p. 158).
-
voetnoot11)
- La Pièce a été empruntée à la même feuille détachée qui contient les calculs dont il est question dans les notes 6 et 7 qui précèdent.
-
voetnoot12)
- La Figure, où nous avons ajouté les lettres A, B, C, D semble représenter une machine pour saire des expériences sur le choc des corps. Il est clair que lorsqu'on pousse en bas le bout D du levier AD les vitesses communiquées aux plateaux qui portent les billes seront dans le rapport de AB à AC et il en sera peut-être de même pour celles reçues en conséquence par les billes. On pourrait constater alors quels sont les sens dans lesquels se menvent les billes après le choc ou si l'une d'elle est alors en repos, oui ou non. Comparez encore la note 13 de la p. 185 où l'une des Figures représente une machine analogue ou identique.
-
voetnoot13)
- La Pièce est écrite sur une feuille détachée.
-
voetnoot14)
- La Pièce date probablement de l'année 1667 puisqu'on trouve dans les notices pour les discours mentionnées dans la note 6 de la p. 157 au numéro 6.1 (p. 184) l'annotation suivante: ‘Experience belle des boules ou dames rangees et frappees par 2 ou 3 autres [voir la Fig. 14, p. 160]. Et que la communic.n de mouvement s'y fait de mesme que si les boules avoient quelque petite distance.’
-
voetnoot1)
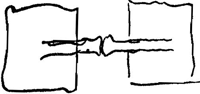
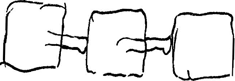
- Les Fig. 11-13, p. 160, se rapportent sans doute à cette pensée: que les corps ne sont jamais parfaitement durs, mais qu'ils font ressort.
-
voetnoot2)
- De même on lit dans les notices publiées dans ce Tome à la p. 183, au numéro 6: ‘Experience de deux verres convexes, ou l'on voit qu'il y reste de l'air entre deux’.
-
voetnoot3)
- La Pièce fut écrite sur une feuille détachée.
-
voetnoot4)
- Puisqu'au revers de la feuille on trouve des calculs qui se rapportent au même sujet que ceux qu'on trouve dans la Pièce V (p. 156-158) il est à présumer que cette Pièce et la présente furent conçues dans la même année.
-
voetnoot5)
- Comme les suppositions dont il s'agit ici Huygens désigne successivement (dans une rédaction parfois un peu différente): les Hypothèses II (p. 31 ci-dessus) et IV (p. 39) du Traité ‘De Motu’, l'Hypothèse: ‘Si vero corpus minus occurrat majori quiescenti non posse ei dare celeritatem majorem sua’, sur laquelle on peut consulter le troisième alinéa de la p. 129, et enfin les Hypothèses V(p. 41) et III (p. 33) du même Traité.
-
voetnoot6)
- La Pièce est empruntée à une feuille détachée.
-
voetnoot7)
- Parmi les notices mentionnées dans la note 6 de la p. 157 on trouve au numéro 15 (p. 184) la suivante: ‘de la rencontre des corps moux et la commun.n de mouvement qui s'y fait’. Il est donc bien probable que la présente Pièce concernant la théorie du choc des corps mous fut écrite avant les premiers jours de janvier 1668.
-
voetnoot8)
- Il semble utile de faire précéder ici un aperçu de la démonstration par l'absurde que Huygens va donner de ce théorème. Supposons donc avec lui que les corps mous A et B de masses a et b se meuvent à leur rencontre avec les vitesses AC [Fig. 15] = d et BC = ad/b et soit f = = CD la vitesse avec laquelle ils se meuvent ensemble après le choc; ajoutons la vitesse commune CE que nous représentons provisoirement par x, et convertissons les nouvelles vitesses, qui sont supposées horizontales, en des vitesses verticales; alors les hauteurs auxquelles les corps a et b pourront monter avant le choc seront respectivement λ(x-d)2 et
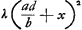 (où λ = 1/2g), après quoi leur centre de gravité composé se trouvera à la hauteur (où λ = 1/2g), après quoi leur centre de gravité composé se trouvera à la hauteur 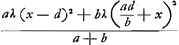 , tandis qu'après le choc ce centre pourra monter jusqu'à la hauteur λ(f+x)2. Or, d'après le Principe adopté par Huygens (consultez la p. 57): que le centre de gravité ne peut pas
monter par l'effet seul de la gravité, il faut donc que la première de ces hauteurs soit supérieure ou égale à la seconde; ce qui mène à la condition , tandis qu'après le choc ce centre pourra monter jusqu'à la hauteur λ(f+x)2. Or, d'après le Principe adopté par Huygens (consultez la p. 57): que le centre de gravité ne peut pas
monter par l'effet seul de la gravité, il faut donc que la première de ces hauteurs soit supérieure ou égale à la seconde; ce qui mène à la condition 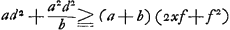 ou bien, en divisant par a+b, à ou bien, en divisant par a+b, à 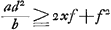 , condition qui ne peut pas être remplie pour chaque valeur de x (et e.a. pas pour celle x = ad2/bf choisie par Huygens) sans qu'on ait f = 0; ce qu'il fallait prouver. , condition qui ne peut pas être remplie pour chaque valeur de x (et e.a. pas pour celle x = ad2/bf choisie par Huygens) sans qu'on ait f = 0; ce qu'il fallait prouver.
-
voetnoot1)
-
f est la vitesse commune des deux corps mous après le choc, vitesse dont Huygens va prouver qu'elle doit être égale à zéro.
-
voetnoot2)
- Grandeur proportionnelle à la hauteur BO à laquelle le corps pourrait monter après la conversion de sa vitesse horizontale en une vitesse verticale.
-
voetnoot4)
- Cette grandeur est proportionnelle à la hauteur à laquelle peut monter le centre de gravité commun des deux corps avant le choc, multipliée par a+b.
-
voetnoot5)
- Lisez plutôt ≧; consultez la note 8 de la p. 161.
-
voetnoot6)
- Cette grandeur, égale à
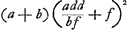 , est proportionnelle à la hauteur à laquelle peut monter le centre de gravité commun des deux corps après le choc, multipliée par a+b. Nous avons supprimé le calcul. , est proportionnelle à la hauteur à laquelle peut monter le centre de gravité commun des deux corps après le choc, multipliée par a+b. Nous avons supprimé le calcul.
-
voetnoot5)
- Lisez plutôt ≧; consultez la note 8 de la p. 161.
-
voetnoot1)
- De par le principe que le centre de gravité ne peut pas monter par l'effet seul de la gravité. En effet d'après ce principe
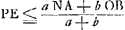 , ou bien , ou bien 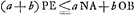 . Or les calculs qui précèdent montrent que cette condition n'est pas remplie. . Or les calculs qui précèdent montrent que cette condition n'est pas remplie.
Ajoutons encore que Huygens se rendait parfaitement compte de ce que, le théorème dont il s'agit dans cette Pièce étant prouvé, toute la théorie du choc direct des corps mous en peut être facilement déduite. Voici, en effet, ce qu'on lit sur une autre feuille détachée, qu'il n'a pas semblé nécessaire de reproduire: ‘Primo ostendi potest quod si hoc ita fiat, tunc alijs casibus omnibus, velut si A [voir la Fig. 15] moveatur celeritate aliqua AE et B celeritate BE, post occursum in E, centrum grav. commune quod motum est à C in E perrecturum eadem celeritate versus V [où V se trouve dans le prolongement de AE]’.
En effet pour obtenir cette belle solution géométrique du cas général du choc direct des corps mous, il suffit d'ajouter aux vitesses AC du corps A, BC du corps B (où AC:BC=b:a) et à celle égale à zéro des deux corps réunis par le choc la vitesse commune CE.
-
voetnoot2)
- Nous empruntons encore à une autre feuille détachée, concernant le choc des corps mous, l'annotation suivante: ‘mirabilis est haec demonstratio, qua evincitur si corpora mollia sibi occurrunt mutuo celeritatibus quae sint reciproce ut corpora, nec post occursum maneant immota sed vel tantillum in alterutram partem progrediantur jam motum perpetuum daturum iri. augeri enim posse constabit vim ascensivam; idque quantum libet, aucta scilicet CE. quae saltem major debet esse quam
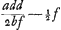 ’. ’.
-
voetnoot3)
- On trouve la démonstration indiquée au revers de la feuille à laquelle nous avons emprunté cette Pièce et qui visiblement a fait partie d'un des livres des ‘Adversaria’. D'ailleurs cette démonstration sut biffée et ne se distingue de celle de notre texte que par le choix de la vitesse attribuée au navire, cette vitesse étant choisie successivement égale à
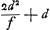 et à et à 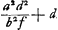 . Or, la première réduction à l'absurde, fondée sur la première valeur, réussit lorsqu'on a b > a et la deuxième lorsque b < a (consultez la note 8 de la p. 161) tandis qu'il est clair qu'on peut faire à volonté l'une ou l'autre de ces suppositions. . Or, la première réduction à l'absurde, fondée sur la première valeur, réussit lorsqu'on a b > a et la deuxième lorsque b < a (consultez la note 8 de la p. 161) tandis qu'il est clair qu'on peut faire à volonté l'une ou l'autre de ces suppositions.
-
voetnoot4)
- Comparez les dernières lignes à la p. 163 de la note 8 de la p. 161. Il est clair que pour x = ad2 / 2bf la condition mentionnée n'est pas remplie non plus sans prendre f = 0. On trouve d'ailleurs la déduction de cette valeur de x sur la seuille mentionnée dans la note 2 de la p. 164.
-
voetnoot5)
- Il s'agit du ‘Cursus seu Mundus mathematicus’ de Claude François Dechales, ouvrage de 1674, cité dans la note 4 de la p. 347 de notre T.V. En effet l'état du Manuscrit semble indiquer que l'annotation présente fut faite après coup.
-
voetnoot6)
- Voici, en effet, la démonstration de Dechales de sa Prop. VII: ‘Si duo mobilia sibi invicem occurrant cum velocitatibus, quae sint ipsis corporibus reciprocae, cessabit utriusque motus’ du ‘Lib. VII’ du ‘Tractatus octavus. Mechanica’ (voir la p. 199 du T. II de la deuxième édition, de 1690, de son ‘Cursus’): ‘Demonstr. Eadem supponitur esse ratio A ad B, quae lineae BC ad lineam AC [voir p.e. la Fig. 16]; ergo productum ex multiplicatione primi termini A per quartum AC, seu quantitas motus corporis A, aequale erit producto multiplicatione secundi termini B, per tertium BC, seu quantitati motus corporis B; ergo sicut prius sunt hinc inde motus contrarii aequales, ergo pariter erit aequilibrium, & neutrum praevalebit, nam mobile B compensat suâ velocitate, id quod deerat in mole.’
-
voetnoot7)
- C.à.d. si l'on voulait admettre que généralement l'influence exercée par un corps qui en rencontre un autre sur ce dernier ne dépend que de la quantité de mouvement du premier corps.
-
voetnoot8)
- Dans le cas de deux corps mous A et B de masses ma et
mb, dont A possède la vitesse va et B est en repos, on trouve pour la vitesse commune après le choc
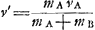 , de sorte que cette vitesse ne dépend pas seulement de mava mais aussi du rapport entre les masses. Il en est de même dans le cas des corps durs de Huygens où les formules de la note 1 de la p. 67 sont applicables; on a alors , de sorte que cette vitesse ne dépend pas seulement de mava mais aussi du rapport entre les masses. Il en est de même dans le cas des corps durs de Huygens où les formules de la note 1 de la p. 67 sont applicables; on a alors 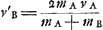 . .
-
voetnoot9)
- La Pièce est empruntée à une feuille détachée.
-
voetnoot10)
- Il y a tant d'analogie entre cette Pièce et la précédente qu'il semble permis de supposer qu'elles datent de la même époque.
-
voetnoot11)
- A et B sont les corps semi-durs de masses a et b qui se rencontrent en C de sorte que leurs vitesses peuvent être supposées égales à AC et BC. Après leur rencontre ces corps sont supposés rejaillir avec les vitesses CS et CT et Huygens va prouver que si l'on a AC:CB = =b:a, savoir si primitivement les vitesses des corps A et B étaient en raison réciproque de leurs masses, il en sera de même après le choc. Il en va donner une démonstration par l'absurde. À cet effet il suppose que le point N (à peine lisible dans la figure) qui divise ST dans la raison de b à a diffère du point C. Posant ensuite SN = δ, de sorte que TN = aδ / b, il suppose NC = ε et va démontrer que nécessairement ε = 0.
Afin de réussir dans cette démonstration il emploie de nouveau la méthode que nous avons expliquée dans la note 8 de la p. 161, c'est-à-dire: convertissant toutes les vitesses horizontales en vitesses verticales il montre que, par un choix approprié de la vitesse CE=x à ajouter à toutes les autres vitesses, la hauteur du centre de gravité commun pourrait devenir plus grande après le choc qu'elle ne l'était avant cet événement, excepté lorsque l'on prend ε = 0.
Par des calculs tout-à-fait analogues à ceux que nous avons exposés dans la note citée on arrive à la relation: 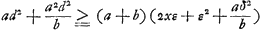 ou bien ou bien 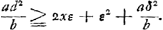 Or, cette condition, qui indique que la hauteur du centre de gravité commun avant le choc est supérieure ou égale à celle après le choc, et qui est exigée par le Principe que ce centre ne peut pas monter, n'est évidemment pas remplie lorsque x ≧ add / 2εb, à moins qu'on n'ait ε = 0; ce qu'il fallait prouver. Or, cette condition, qui indique que la hauteur du centre de gravité commun avant le choc est supérieure ou égale à celle après le choc, et qui est exigée par le Principe que ce centre ne peut pas monter, n'est évidemment pas remplie lorsque x ≧ add / 2εb, à moins qu'on n'ait ε = 0; ce qu'il fallait prouver.
Remarquons encore que lorsqu'ainsi la coïncidence de N avec C a été prouvée, de sorte que SC/AC = CT/CB, la solution par construction du problème général du choc direct des corps semidurs s'ensuit facilement. En effet, il suffit d'ajouter aux vitesses avant et après le choc une vitesse commune CE de grandeur arbitraire. On voit alors que si AE et BE représentent les vitesses avant le choc, celles après le choc seront données par SE et TE, où SC:AC dépend de la nature des corps A et B.
-
voetnoot1)
- Cette vitesse est représentée par x dans les calculs qui suivent dans le Manuscrit mais que nous croyons pouvoir supprimer après les renseignements fournis par la Pièce précédente et par les notes 8 et 11 des pp. 161 et 165. Remarquons seulement que les vitesses des corps A et B par rapport à la rive sont respectivement avant le choc x-d et
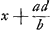 et après le choc et après le choc 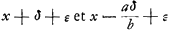 , d'où il suit: , d'où il suit:
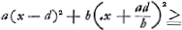
-
voetnoot2)
- Lisez plutôt ≧. La formule se déduit immédiatement de celle-ci:
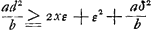 qui résulte de la dernière formule de la note précédente après division par a+b; comparez la note 10 de la p. 165. qui résulte de la dernière formule de la note précédente après division par a+b; comparez la note 10 de la p. 165.
-
voetnoot3)
- Savoir pour obtenir que la condition précédente (NC ≠ 0) n'est pas remplie.
-
voetnoot4)
- Détermination de la valeur indiquée de x.
-
voetnoot5)
- Huygens vent dire que la vitesse supplémentaire add/2εb, qui est nécessaire pour la réduction à l'absurde, ne dépend pas de δ, c'est-à-dire qu'elle est indépendante de la nature des corps qui se choquent et par suite la même pour les corps mous, durs ou semi-durs.
-
voetnoot6)
- Cette remarque peut avoir été ajoutée après coup.
-
voetnoot7)
- Comparez (p. 43) la Prop. IV du Traité ‘De Motu’. Évidemment cette Proposition n'est valable que pour les corps durs, savoir dans le cas particulier de la Fig. 16 où CS = CA et, par suite CT = CB. Huygens va indiquer ensuite comment elle doit être modifiée dans le cas des corps semi-durs.
-
voetnoot1)
- La Pièce est empruntée à une feuille détachée.
-
voetnoot3)
- La Pièce est empruntée à une feuille détachée. Sur la même feuille Huygens se pose quelques autres questions qui appartiennent à la physique.
-
voetnoot4)
- On trouve cette date au revers de la feuille détachée.
|
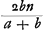 feretur a in eandem quoque partem. at si p minor sit quam
feretur a in eandem quoque partem. at si p minor sit quam 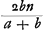 , referetur a in partem contrariam. si denique aequalia, restabit a immotum.
, referetur a in partem contrariam. si denique aequalia, restabit a immotum.