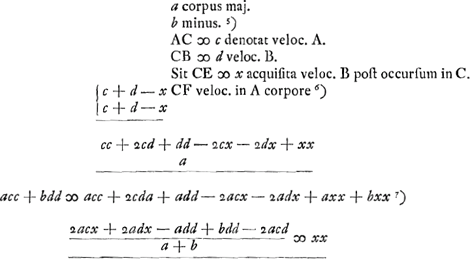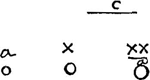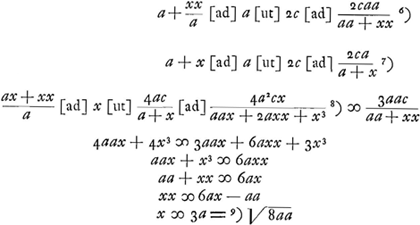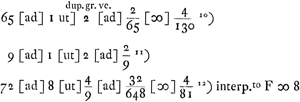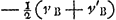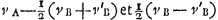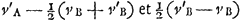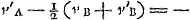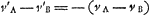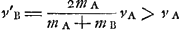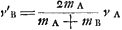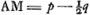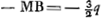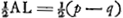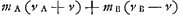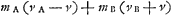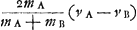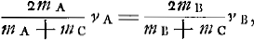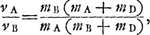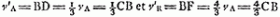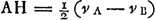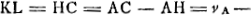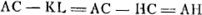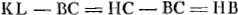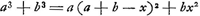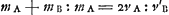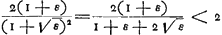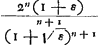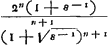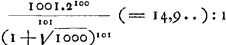Oeuvres complètes. Tome XVI. Percussion
(1929)–Christiaan Huygens–
[pagina 92]
| |
Appendice IGa naar voetnoot1)
| |
[pagina 93]
| |
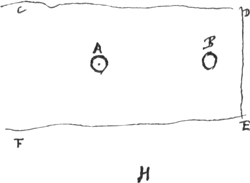
Ga naar margenoot+ Si A et B sint aequalia [Fig. 2] A autem quiescat: et B ad ipsum pergat.
 [Fig. 2.]
restabit B in loco concursus immotum, at A movebitur sinistram versus, tanta celeritate quantam prius habuit BGa naar voetnoot8). Eadem erit vis collisionis ac si B dimidia celeritate quam habet sinistrorsum motum occurrat corpori A, eâdem dimidia celeritate moto dextrorsum. Itaque imaginemur haec ita contingere in spatio CDEF. Sed hoc ipsum ferri interea sinistram versus eâdem quam diximus celeritate dimidiâ corporis B. quibus fiet ut respectu eorum qui extra spatium CDEF constituti sunt ut H, videatur A quiescere et B moveri, ut | |
[pagina 94]
| |
utrumque ab initio positum fuit. Itaque post collisionem ijs qui cum spatioGa naar voetnoot1) CDEF una veherentur videbitur B dextrorsum reflecti, A vero sinistrorsum et utrumque cum dimidia celeritate ejus quam corpori B tribuimus respectu H. Sed quia eâdem dimidia celeritate navis posita est tendere sinistram versus, apparebit spectanti ex H, corpus B quiescere, at A moveri sinistrorsum ea celeritate qua prius movebatur B. Axioma. [Quae vis corpori quiescenti certam dat velocitatem, eadem corpori quod prioris duplum sit dimidium istius celeritatis conferre potis est.Ga naar voetnoot2)] Si A quiescat [Fig. 3] et B ipsi allidatur, sitque B quantumvis majus, non dabit corpori A velocitatem quae sit dupla suae, sed semper minoremGa naar voetnoot3).  [Fig. 3.]
Necesse enim est corpora A et B post collisionem aeque celeriter a se mutuo separari, atque prius accedebant. (atque hoc patebit si corpus B quiescere intelligatur, et A versus B moveri. paulum enim tantum movebit corpus B dextram versus, at A penè eadem celeritate quâ venit resiliet.) sed B corpori A occurrens paulum tantum de celeritate sua amittit et pergit sinistrorsum moveri, itaque necessario debebit A sinistrorsum moveri paulo minore quam dupla celeritate, ejus quam B habuit ab initio. nempe ut eadem sit separationis celeritas post duorum corporum occursum, quae fuit appropinquandi. | |
[Deuxième Partie.]Ga naar voetnoot4)
| |
[pagina 95]
| |
[ax. 1Ga naar voetnoot2)] Iis qui in navi sunt quae progreditur, corporum sibi in navi occurrentium motus non alius apparet quam si navis immota staret, vel ipsi una cum ijs extra navem essent. Idem de motu terrae. Hinc demonstraturGa naar voetnoot7) quod si corpora sint duo aequalia alterum quiescens alterum quiescenti impactum, omnis motus transibit in id quod quiescebat, et illud quod movebatur restabit immotum in loco concursus. Majus corpus quiescens ab eodem corpore eadem celeritate impulsum minorem celeritatem acquirit quam corpus minusGa naar voetnoot8). Ex his demonstrari potest non semper post duorum corporum collisionem, tantundem motus remanere quantum erat antea, eo videlicet sensu, ut corporum magnitudines cum velocitatibus multiplicatae, eundem numerum producant quem prius producebantGa naar voetnoot9). [ax. 2Ga naar voetnoot1)] Sed necesse est quadrata velocitatum ducta in magnitudinem corporum semper eundem numerum producereGa naar voetnoot10). Ex hoc et primo ax.Ga naar voetnoot11) regula conficiturGa naar voetnoot12). | |
[pagina 96]
| |
Si corpus 2 cum celeritate 3 impactum corpori 1 quiescenti, concedatur ipsi dare velocitatem 4 et sibi retinere veloc. 1 in eandem partem. Ostendi potest, quod corpus 1 cum celeritate 3 impactum corpori 2 quiescenti, dabit ipsi velocitatem 2, et sibi retinebit velocitatem 1 sed resiliens in partem contrariamGa naar voetnoot1). [ax. 3.Ga naar voetnoot2)] Si corpus A majus occurrat B minori, sed velocitas in B sit ad velocitatem in A reciprocè ut magnitudo A ad B, tum utrumque cum eadem qua venit celeritate resilietGa naar voetnoot3). Hoc concesso omnia demonstrari possuntGa naar voetnoot4). Cartesius autem concedere cogiturGa naar voetnoot5). Sed videndum an demonstrari per notiora queat.
Axioma. Si duo corpora ex adverso sibi mutuo occurrant, unumque eorum eadem qua venit celeritate retro feratur nihil de motu suo amittens, etiam alterum eâ quâ venit celeritate resilietGa naar voetnoot6).
Duo corpora ex adverso sibi mutuo occurrentia pari celeritate separantur qua et appropinquantGa naar voetnoot7). 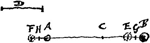 [Fig. 4.]
Sunto duo corpora A et B [Fig. 4] sibi mutuo ex adverso occurrentia in puncto C; ad quod pervenisse ponantur ex locis A et B in tempore D. post occursum vero ad C venerint rursus in tempore D ad E et FGa naar voetnoot8). dico spatium FE spatio AB aequale esse. Ponamus enim corpora A B praeter motus istos quos jam ipsis tribuimus, adhuc alij motui esse simul obnoxia quo versus partem B ferantur, in tempore D per spatium aequale GB, hoc est dimidio | |
[pagina *1]
| |
 | |
[pagina 97]
| |
EB. vel imaginemur motus corporum A et B quos primò dedimus, in navi contigisse quae dextram versus feratur celeritate GBGa naar voetnoot9). IgiturGa naar voetnoot10) eorum respectu quibus navis ita movetur, videtur corpus in tempore D percurrisse spatium ipsi GC aequale; repercussum verò, cum intra navem tempore D dextram versus feratur per spatium CE, videbitur ijs qui extra navem sunt, moveri per spatium aequale ipsi CG, quoniam navis interea temporis dextrorsum quoque perrexit per spatium aequale EG. Itaque extra navem positis aequali celeritate ante et post occursum corpus B moveri videbitur. Quare et corpus A aequè celeriter ante et post occursum moveri apparere debebit, per axiom. at corpus A ante occursum necessario visum fuit ipsis moveri celeritate HC (posita vl.Ga naar voetnoot11) AH aequali EG vel GB.). hoc est visum fuit in tempore D transire spatium HC, ergo et resiliens apparet ijsdem moveri per spatium aequale HC in tempore D. Quare in navi transijsse necesse est per spatium aequale duobus HC et HA sive EG. at positum fuit in navi transijsse spatium FC. igitur FC aequale HC et GB. Quare HF ∞ GB. sed et HA. Ergo FA ∞ EB. additaque communi AE, erit FE aequalis AB. quod erat demonstrandum. | |
[pagina 98]
| |
[Troisième Partie.]Ga naar voetnoot1)
| |
[pagina 99]
| |
librum tuum de locis planis quem dudum perlegere desidero si commodum est velim ut mittas nunc mihi, vel si excurrere huc vacat ut ipse adferas, sunt enim quaedam quae ostendere invicem tibi praesenti cupiam ex inventis meis et non pauca narrare habeo de itinere gandavensi unde nunc primum reverti. diu cum P. Gregorio collocutus sum cujus quadraturam licet ab ipso confessionem exprimere non satis potuerim, Gotscovius condemnavit dixitque mea opera eversam funditus, Ita nobis retulit D. Edelheer Antverpiensium Syndicus. valeGa naar voetnoot6). | |
[Quatrième Partie.]Ga naar voetnoot7)
| |
[pagina 100]
| |
tamen definivit quod ad nos perveneritGa naar voetnoot1) nisi quod immensam percussionis potentiam dixerit. Verba ipsius operae pretium interpretari quia simul sententiam ipsius de contemplationis hujus difficultate exhibent diligentiamque ab eo adhibitam testantur. ut et momentumGa naar voetnoot2). verba Galilei. Post hunc autem alijGa naar voetnoot3) quoque impulsus regulas tradidere sed paucas tantum veritati consentaneas quas ab experimentis edocti fuere neque tamen ratione ulla evidenti demonstrarunt. Cartesius vero contra experimentorum fidem novas condere ausus estGa naar voetnoot4) quas nulla demonstratione egere dixit principia sua intelligentibusGa naar voetnoot5). Cujus sententiam nonnullos amplecti videoGa naar voetnoot6). Sed cum in plerisque à veritate abeat quo major est tradentis autoritas eo utilius ut error redarguatur. Non autem ideo sententiam circa haec nostram illius sententiae praeferendam contendemus quod omnibus cum experimentis accuratè consentiat cum ipsius manifesto adversetur. sed demonstrationibus primum omnia firmabimus evidentissimis, quae si experientia comprobentur tum hoc quoque evicisse credemus non omnino inutilia esse duritiei defectu corpora quaedam, neque à circumfuso aere ita impediri ipsorum motum, quin ad experimenta sufficiant. nam hanc causam adfert quo minus exhiberi Theorematum suorum veritas possitGa naar voetnoot7). | |
[pagina 101]
| |
Necesse est autem principia quaedam deligere quae motus naturae conveniant et non aegrè fidem inveniant Quibus concessis circa reliquas demonstrationes nulla supersit dubitatio. Quae quidem eadem fere cum Cartesio statuemus paucis tamen discrepantesGa naar voetnoot8). Primum itaque cum Cartesio dura omnino corpora esse fingemus quae sibi mutuo occurrant, tum eo loci librata ubi corpora circumambientia nihil motum ipsorum retardent neque adjuventGa naar voetnoot9). Ubi denique nec gravitas sursum nec levitas deor- | |
[pagina 102]
| |
sum tendere cogat. ad haec quod corpus motum, pergit eadem velocitate moveri secundum lineam rectam usque donec ab alio impediatur. Sed hoc quoque cum ipso statuemus eandem motus quantitatem corporibus post impulsum conservari, non in singulis semper sed una sumptisGa naar voetnoot1). Quod quidem principium cum non in omni casu eodem modo accipi debeat neque possit, primum ad eos referemus casus in quibus nullam habet dubitationem, atque inde ea efficiemus quibus postea probetur non ubique eodem modo hoc principium interpretandum esse sed nonnunquam longè aliter quam à Cartesio fieri soleat adhibendumGa naar voetnoot2).
Primum hoc statuemus. Si corpus aliquod secundum rectam lineam moveatur &c. deinde motum corporum non interire mutua ipsorum collisione nec augeri sed remanere debere ut si alteri quid decedat id accedat alteri, quod tamen quoniam non semper evidens est, tantum in manifestis hisce casibus ita contingere ponemus. Primùm si corpora duo aequalia pari celeritate ex adverso sibi mutuo occurrant omnem ijs motum servari, ideoque utrumque eadem servata celeritate revertiGa naar voetnoot3). Cum enim aequalia sint et aequali celeritate delata non potest dispar esse utriusque reflexio. Jam omnia de aequalibusGa naar voetnoot4). deinde, si corpus majus minori occurrat quiescenti, et motum aliquem huic conferre, et motum proinde suum aut aliquid certe de suo motu amittereGa naar voetnoot5). denique quod duobus corporibus collisis si alterum eorum omnem motum suum servet, etiam alterum nihil deperdere. in aequalibus patuit. sed et in inaequalibus fieri esse [sic]Ga naar voetnoot6).
Corpora dura. Nullum aeris impedimentum nec gravitatis attractionem. tum sequens. deinde quod ad motus naturam spectet. hoc cum ipso statuemus corpus in linea recta motum in eadem pergere moveri eadem semper velocitate donec ab alio impediatur. | |
[pagina 103]
| |
Quod autem movetur aliorum corporum respectu moveri intelligitur quibuscum distantiam situmve commutat. Itemque quod quiescit eorum respectu quiescere quibuscum distantiam situmque servat eundem. Nam si quis naturam motus in uno corpore absque aliorum respectu investigare contendat operam se ludere inveniet. Itaque cum corpora quaedam moventur possumus motum eorum expendere cujusvis corporis aliùs respectu quod tanquam quiescens spectamus. Neque enim corpus aliquod aut punctum in universo ostendi potest ad quod omnium reliquorum motus referre necesse sit. Itaque cum corpora duo respectu partium terrae moventur sibi mutuo occurrunt certaque lege reflectuntur, constat utique omnia hic similiter contingere debere atque eadem ratione sese habere, sive quiescere terram aliquis existimet sive noverit alijs ipsam motibus obnoxiam esse. Item si in navigio quod aequabili motu provehatur, respectu partium ipsius navigij corpora duo ex adverso moveantur atque invicem sibi occurrant, certum est post impulsum perinde sese habere debere utriusque motum respectu ejusdem navigij ac si eadem omnia in quiescente peracta fuissent. Et hoc experientia quoque comprobat, sive super mensa in navigio immota globuli concurrantGa naar voetnoot7) sive in aere a navigante projecti invicem fiant obviam. Si enim aequales fuerint et aequali celeritate motum adacti, cum eadem unusquisque resilietGa naar voetnoot3).
PriusGa naar voetnoot8) de navigio in universumGa naar voetnoot9) tum exemplum sphaerarum aequaliumGa naar voetnoot10). Tum si quis dubitet an hoc ita evenire debeat terrae exemplo probandum. Dubitatio ejus à praejudicio quod terram magis quam navigium quiescere existimet. Sed Cartesius recte dicet non magis terram quiescere quam navim quae flumine deferturGa naar voetnoot11). quod majus minori non conjunctum manet. sed eadem celeritas sit separandi quae adveniendiGa naar voetnoot12). Inde quod semper hoc contingat. Falsus ergo CartesiusGa naar voetnoot13) tum quod majus à minori movetur. | |
[pagina 104]
| |
Imo quod etiam repellitur occurrens. Hinc quod eadem motus quantitas non semper conservaturGa naar voetnoot1). Quod augetur quoties minus majori quiescenti occur[rat]Ga naar voetnoot1). Quod minuitur quoties post impulsum majus quiescatGa naar voetnoot1). | |
[Cinquième Partie.]Ga naar voetnoot2)
| |
[pagina 105]
| |
adeo ut si vel terrae universae aequalis sphaera detur unus homo mallei percussu eam loco pulsurus sit. Aliquibus hoc absurdum prima specie existimatum iri credo, et tamen satis evidentes fore demonstrationes nostras ut perceptis ijs certi reddantur non aliter fieri posseGa naar voetnoot8). Neque primi nos ita sensimus sed ante hoc idem subtilissimus Galileus scivisse videtur, licet nulla ejus circa haec extet demonstratioGa naar voetnoot9). In dialogis qui hucusque Italico tantum idiomate circumferuntur sequentia prodidit, e quibus praeter praedictam ejus sententiam impensum quoque in hanc rem studium colligere licebitGa naar voetnoot10), atque adeo ipsius contemplationis difficultatem et praetium. Sic igitur Sagredum confabulationem &cGa naar voetnoot11). Haec Galileus neque alibi quidquam de percuss. aut impulsu. Motus autem naturam pluribus locis consideravit in systemateGa naar voetnoot12). Et haec omnia perpendisse utile fuerit haec nostra lecturis, quoniam varijs inveteratis praejudicijsGa naar voetnoot13) mentem solvant. Sed et praecipue quae ab Illustri Cartesio de motu tradita sunt in Principijs philos.Ga naar voetnoot14). Quamvis enim contraria ipsi tradituri sumus in his, attamen &c. et praeclare multa explicasse et multum eo nomine ipsi nos debere fatemur.
Princip. CartesijGa naar voetnoot14) quod diu nobis verisimileGa naar voetnoot15) visumGa naar voetnoot16). Postea falsum inventum est. Principio recte cavisseGa naar voetnoot17) videtur perfectam corporum sese impellentium duritiem animo concipiendam esse, eaque moveri in spatio quasi vacuo in quo nulla alia corpora motum eorum juvare possint aut imminuere. Ergo haec etiam nos supponemus sed neque gravitatis proprietateGa naar voetnoot18) deorsum trahi ipsa, aut prae levitate sursum efferri fingemus. Statuemus porro unumquodque corpus natura ferri secundum lineam rectam, quâque celeritate semel motum est ea pergere moveri nisi ab alio impediatur; quod praeter CartesiumGa naar voetnoot19) GalileusGa naar voetnoot20) quoque et alij dixere. Porro ad duritiem | |
[pagina 106]
| |
corporum et proprietatem motus attendentes, ponemus occursu mutuo duorum corporum motum tamen eorum non omnino interverti atque ad nihilum redigi sed superstitem remanere. Qua verò quantitate nondum definiemus nisi tantum in casibus his manifestis. Nimirum si contingat alterum eorum omnem celeritatem suam servare post impulsum, etiam alterius celeritati nihil decedereGa naar voetnoot1). Et si aequalia duo corpora aequali celeritate invicem occurrunt, utrumque eadem illa celeritate revertiGa naar voetnoot2). Ad haec quoties corpus majus minori quiescenti occurrit aliquem ei motum conferre, ac proinde de sua celeritate aliquid amittereGa naar voetnoot3). Denique concedi postulamus cum minori mole corpus majori quiescenti occurret, celeritatem ei minorem dare sua ipsius celeritateGa naar voetnoot4); utique si per praecedentia prius aliquam dare demonstratum fuerit. Haec digna nobis visa sunt quae concedantur neque ipsius Cartesij Principijs aut regulis adversantur. Caeterum una etiamnum circa motus naturam praemittenda est consideratio, longe maximi in hisce momenti quam nemo adhuc quod sciam adhibuitGa naar voetnoot5). Pendet autem ex eo quod circa compositum motum à pluribus animadversum fuit. Constat nimirum, quod in navi constitutis, quae aequabili cursu progrediatur, perinde contingunt motus omnes ac in quiescente, aut super terram agentibusGa naar voetnoot6), idque cuivis experiri obvium est. Videmus enim globulum plumbeum e summitate mali dimissum ad pedem ejusdem decidere neque retro deseri. Et si quis in puppe consistens stanti in prora eundem globulum projiciat non majorem ei vim adhibendam, quam alteri eundem rejicere volenti; planè sicut navi quiescenteGa naar voetnoot7) contingeret, adeoque nulla rationeGa naar voetnoot8) in navi ipsa navis motum aut quietem discerni posse, nisi ad terram respiciamus. Et haec quidem prolixius à Galileo in Systemate MundiGa naar voetnoot9) explicata sunt, et ratione confirmata. Ut autem ad id quod nobis declarare propositum est accedamus cogitemus intra | |
[pagina 107]
| |
navem uti dictum est aequabili motu incedentem, ludum eum exerceri quo super mensam planam ad libellam aequatam globuli eburnei clavulis ex eadem materia confectis pellunturGa naar voetnoot10). Equidem neminem dubitare arbitror quin aeque commode omnia hic ludentibus successura sint, quam si aut navis conquiesceret aut domi suae mensam constituissent. Et si sint duo quorum alter ad eam mensae partem stet quae proram spectat, alter ex adverso, simulque globulos suos impellant ita ut hi in media mensa invicem sibi occurrant, certum quoque pariter suum sibi quemque reversurum esse, et nullam quidem celeritatis partem amissuros, si perfecteGa naar voetnoot11) duri fuissent, ac inter se aequales, mensaeque superficies omni inaequalitate et scabritie careret essetque ad libellam exquisitè complanata. Praeterea haec omnia eodem modo eventura scimus, si supra navis tectum mensa collocetur. Quid si vero validiore percussu ut saepe fit supra mensae planum globuli efferantur aequaliter utrinque ut diximus impulsi? Sane si vel sic directe sibi mutuo obviam fiant aequaliter quoque ut antea repercutientur. Nam licet prius mensae planitiem semper contigerint, certum tamen hanc nihil globulorum motibus conferre aut officere nisi quatenus aspera est et inaequalis. Ergo remotâ quoque mensa si tantum à prora et puppi ijdem globuli projiciantur aequali vi ita ut supra mediam navem in aere concurrant, pari quoque celeritate reflectentur. Atque hinc porro facile intelligimus quod etiamsi non projecti forent à stantibus in prora et puppi, sed alia quavis ratione contingeret ut pari celeritate ex adverso sibi deferrentur respectu sedentis in navi; idem tamen eventurum sit, nimirum ut ejusdem respectu pari quoque celeritate resiliant. | |
[pagina 108]
| |
[Sixième Partie.]Ga naar voetnoot1)
| |
[pagina 109]
| |
sum observabunt. Eadem plane est ratio quae in superiori exemplo, neque reliqui corporum horum motus quos cum navigio communes habent, quidquam rationem
 [Fig. 5.]
eam interturbant. Sed et experientia hoc docet si [Ga naar voetnoot6) enim binos ex [Fig. 5.] ebore vel duriore materia globulos] e funiculis in navi pendentes [Fig. 5], vel alia ratione collidi facias, haud aliter quam si navis consisteret impellere invicem animadvertes. Haec etsi levis consideratio videri queat, omne tamen impulsus fundamentum continet.
Quiescere unumquodque dicitur eorum respectu quibuscum eandem distantiam situmque servat. Moveri vero respectu eorum quibuscum distantiam situmve non servat. Ita quidem puppis quiescit respectu prorae quocunque modo navis moveatur. Haec vero navigans movetur respectu terrae. et rursus quiescit eorum respectu qui in ipsa sedent. Adeo ut corpus idem moveri et quiescere possit, ad diversa scilicet alia corpora attendendo. MoveaturGa naar voetnoot7) ergo navigium HK [Fig. 6] à parte A versus B. et sedeat in eo vector e regione puncti C, cujus respectu aequali celeritate et motu aequabili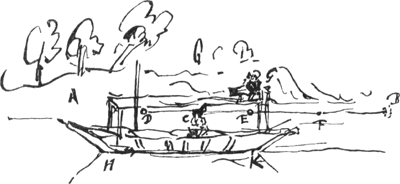 [Fig. 6.]
Ga naar voetnoot8) ferantur ad se mutuo corpora aequalia D et E. Quae quidem (aequalibus spatijs existentibus DC, CE) concurrent in C. et post impulsum mutuum aequali rursus celeritate à C discedent respectu vectoris et partium navigiiGa naar voetnoot9). Quod si eodem tempore puta scrupuli unius quo corpora D et E venere ad occursum in C, navigium et cum ipso unà homo sedens confecit spatium CE. necesse est corpus E immotum mansisse respectu ripae G aut spectatoris ibi sedentis. corpus verò D confecisse spatium DE. Nam non aliter fleri potest ut vectori corpora D et E aequali celeritate mutuo occurrisse appareant. Post concursum autem, qui contingit in E, ut aequali celeritate rursus ab se invicem corpora recedant respectu vectoris qui post alterum tem- | |
[pagina 110]
| |
poris scrupulum pervenit e regione F puncti transijtque spatium EF ipsi CE aequale, id aliter fieri nequit quam ut corpus D post impulsum in E eodem in loco E subsistat respectu G. atque ut corpus E perveniat usque in B, ità ut spatium EB ipsi ED aequale fiat. Apparet itaque quod si respectu hom.is G. quiescat corpus E et ab aequali corpore D impellatur, omnem ab eo motum accipiet, ipsumque D corpus relinquet immotum in loco E. Hinc autem porro quidquid ad occursum aequalium corporum spectat facile determinabitur. Et primum si scire libeat quid futurum sit si inaequali celeritate mutuo sibi occurrant facile probabitur permutata invicem celeritate recessura hoc est ut quod celerius fertur omnem motum suum lentiori conferat contraque omnem tardioris motum sibi accipiatGa naar voetnoot1). Ferantur enim ex adverso corpora aequalia A, B [Fig. 7]. sed celeritas corporis A ad celeritatem corporis B sit ut AE ad EB respectu spectatoris in G manentis.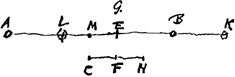 [Fig. 7.]
Convenient igitur in E. nam si scrupulo temporis corpus A transeat spatium AE eodem tempore B transibit BE spatium. Dico igitur post occursum in E altero temporis scrupulo corpus A confecturum ab E spatium EL et B spatium EK, ut sit EL aequ. EB et EK ipsi EA. dividatur enim EL bif. in M et sit C punctum e regione M et sumatur utraque harum CF, FH aequ. EM. Sedenti itaque in navigio et praetervecto celeritate CF, dum corpus A fertur celeritate AE et B celeritate BE, necesse est ut videatur utrumque corpus aequali celeritate nimirum AM properare ad occursum in EGa naar voetnoot2) qui fiet cum C pervenerit in F. Quamobrem ejusdem quoque spectatoris respectu aequali quoque celeritate recedent. Quod | |
[pagina 111]
| |
quidem non aliter fieri potest, quam ut altero temp. scrupulo, quo navigans spectator pervenit ad H, corpus B conficiat spatium EK et A spatium EL.
Qui terram quiescere credunt solent corpora respectu ipsius quiescentia tamquam revera quiescant considerare, et reliquorum motum ad ipsa referre. Sed conveniat hoc inter nos ut corporibus duobus mutuo sibi occurrentibus etiamsi alteri praeterea motuiGa naar voetnoot3) utrumque simul obnoxium sitGa naar voetnoot4), haud aliter invicem repellant respectu ejus qui eundem quoque motum sequiturGa naar voetnoot5), quam si omnibus alterGa naar voetnoot6) iste motus abesset.
Quod movetur ita pergere moveri nisi ab alio impediatur. Sciendum autem de motibus ijs tantum nos agere qui sunt secundum lineam rectam et aequabiles.
Simpliciter autem nulliusque corporis alterius respectu corpus aliquod moveri vel quiescere.
Nam qui motum corporis definiunt loci mutationem locum certum universi respectu definiri posle credunt. Si dicant igitur terram revera quiescere rogabo quid sit revera quiescere, dicent locum eundem constanter obtinere; loci igitur quem terra, tenet definitio ab aliquibus celiGa naar voetnoot7) punctis pendet aut superficie quae revera quiescat. sed hujus rursus quietem apparet aliunde aut à terra ipsa definiri debere.
Quidnam in corporibus quies sit aut motus nisi aliorum corporum respectu non videtur intelligi posse. Nihil enim de motu nobis imaginari aliud possumus quam quod permutet corporum ad se invicem distantiam et dispositionem. Itaque corpus quod movetur aliorum corporum respectu moveri dicatur quibuscum situm mutat et quiescere respectu eorum quibuscum situm servat. Neque nobis necesse sit quaerere an aliquid in universo hoc revera quiescat aut quidnamGa naar voetnoot8) illud sit. An terra consistet an caelum stellarum. Sed et hic et ubicunque abiat inter bina | |
[pagina 112]
| |
aut plura corpora motus. animadvertitur quodlibet eorum tanquam quiescens reputare liceat. respectu nimirum corporis cujusdam alterius quocum situm servat eundem. de impulsu corporum scientiam haberi utile. nam et percussionis vires simul innotescunt. Quas maximi ad Mechanica opera momenti esse certum est, neque minus necessarium videtur harum leges intelligere quam rationes ponderum. AEque enim ad omnes fabricas adhibentur et sepeGa naar voetnoot1) quod ponderibus exequi non possemus, percussione perficimus. Difficilem autem contemplationem habet propterea quod motus natura perplexa est, et considerare non assuetis perobscura. Galileus in dialogis de motu locali et difficultatem rei indicat et ea scribit ex quibus aliquid in ea vidisse existimari potest. Verba ipsius interpretari operae praetium visum est atque hic subjicere. Sic enim Sagredum Confabulatorem inducit loquentem dialogo 4o ante prop. 5Ga naar voetnoot2). PercussionisGa naar voetnoot3) istius atque ictuum mentio meminisse denuo me cogit Problematis cujusdam, imo quaestionis potius Mechanicae, quam qui explicaverit adhuc inveni neminem, nec qui quidquam memoriae prodiderit quo aut admirationem mihi eximat, aut ulla saltem ratione satisfaciat Hinc autem dubitatio mihi nascitur et stupor, quod minimè intelligam quae sit origo aut causa efficaciae istius et vis immensae quae in percussione cerniturGa naar voetnoot4). Siquidem unico mallei ictu cujus gravitas 8 aut 10 pondo non excedat, non posse ea resistere videmus quae nec cedant impositae gravitati prementi tantum nulloque ictu illisae etiam si centena aliquot pondo adaequet. Vellem tantum doceri me qua ratione vim istiusmodi plagae metiri possem, quam sane infinitam esse non arbitror, sed certo termino contineriGa naar voetnoot5) ut exaequari quoque possit, et cum alijs, prementium ponderum, aut vectis, aut cochleae viribus comparari quarum potentiae in quantum multiplicentur optime mihi compertum est. SALVIATUS. Non soli tibi admirationem parit tam stupendi effectus consideratio neque soli causa ejus obscura est. Nam et ipse aliquantum temporis hic contrivi, et frustra quidem, crescente in dies rei perplexitate. Donec convento forte Academico nostro (Galileum intellige) geminam cepi consolationem. Primum namque et sese diu mecum in eadem caligine fuisse versatum dicebatGa naar voetnoot6); tum hoc addebat, | |
[pagina 113]
| |
multis millibus horarum in hanc contemplationem absumptis, tandem aliqua perspexisseGa naar voetnoot7) longe ab ijs quae prima facie videri soleant diversa atque esse nova omnino, eoque magis mirabilia. &c. In fine autem dialogi ubi in aliud tempus differendam hujus rei disquisitionem constituunt ita SagredusGa naar voetnoot8). Equidem lubens tibi assentio nam saepe numero quoque à perfamiliaribus Academici nostri id audivisse meminiGa naar voetnoot9), obscurissimam esse hanc de Percussione tractationem, nemo nempe adhuc eorum qui explicandam susceperint ad intimos ejus recessus penetrare potuisse densis quippe tenebris obseptos et planè alios quam mens humana sibi figurare soleat. Inter caetera autem effata istud unum recitari mihi memini mirum prorsus, vim scilicet Percussionis interminatam esse ne dicam infinitam. Haec Galileus, qui quousque materiam hanc penetraverit non mihi constatGa naar voetnoot10). hoc quod refert de immensa percussionis potentia cum nostris demonstrationibus apprime convenit, ostendemus enim maximum quodque corpus minimi corporis impulsu moveriGa naar voetnoot11).
Experimenta ad demonstrationem non bene adhiberi scimus, eoque omnia certis ex principijs probanda fore, neque tamen parum id videtur quod Cartesij regulis experimenta omnia contrarium ostendunt, nostris vero adamussim consentiunt. Nam quod aitGa naar voetnoot12) corporum quorumcunque imperfectam duritiem praetereaque circumfusum aerem in causa esse quo minus exhiberi Theorematum suorum veritas possit id nequaquam verisimile est. si enim tantum impedimenti ista adferunt et praeterea falsa sunt Theoremata nostra, mirum esset ita semper error alio errore aut defectu materiae compensariGa naar voetnoot13), ut quod praedicimus eventurum in occursu corporum id eveniat. AttamenGa naar voetnoot14), et nos perfectam singemus corporum duritiem ijsque in spatijs librata sumemus quibus neque impediatur eorum motus a circumfusis corporibus neque adjuvetur. | |
[pagina 114]
| |
[Septième Partie.]Ga naar voetnoot1).
| |
[pagina 115]
| |
Itaque toto tempore AB motu accelerato majus spatium transijt quam omnia simul crescentia Eι, Sη cum intermedijs, hoc est majus quam xbGa naar voetnoot7). Igitur quod celeritate aequabili subdupla maximae tempore AG peregit simul majus est et minus quam quod tempore AB fecit motu accelerato. quod est absurdum. Jam si fieri potest celeritate aequabili dimidiâ maximae percurrerit spatium minus in tempore AB. ergo in majori tempore aequale percurret &c. Motus diversos unius mobilis separatim considerare licere. AEquali tempore eandem celeritatem acquiri duobus corporibus, quorum unum à quiete moveri incipiat, alterum quolibet motu. Si quamlibet in partem mobile prius feratur motu aequabili, deinde vero et naturali accelerationi obnoxium esse incipiat, duo motus in eo separatim considerari debent, aequabilis qui durat in partem eandem quam prius, et acceleratus cujusmodi spectatur in mobili quod e quiete moveri incepit. Eo demonstrato vel posito quod spatia peracta sunt in duplicata ratione temporum alteroque assumpto quod demonstratum est nempe quod duobus corporibus duris mutuo sibi ex adverso occurrentibus, separationis eorum eadem quae appropinquandi est celeritasGa naar voetnoot8), demonstrari potest, quod si corpora duo sibi mutuo occurrant, sitque velocitas unius ad velocitatem alterius ut magnitudo hujus estad magnitudinem illius, utrumque cum eadem velocitate resiliet qua venitGa naar voetnoot9). | |
[pagina 116]
| |
Ex quo solo et hoc demonstrari potest falsum esse quod Cartesius putat; semper nimirum eandem motus quantitatem in natura remanereGa naar voetnoot1), eo sensu ut tantundem motus intelligatur in corpore quod duobus gradibus celeritatis movetur, quantum in corpore duplo quod moveatur gradu celeritatis uno. Nam si hoc verum, consequitur inde ista corporum singulorum in recedendo et accedendo aequalis celeritas, nempe cum celeritates corporum occurrentium reciproce sunt ut eorundem magnitudines. sed hoc posito si porro adhibeatur consideratio motus extranei ut navis, rursus falsum deprehenditur quod ille pro principio posuitGa naar voetnoot2). Possunt et alio quoque modo procedere demonstrationes nostrae, positis hisce, nempe corpus tantundem aliquò versus moveri intelligi, quantum ejus centrum gravitatis movetur. tum duo corpora vel plura tanquam unum ex ijs compositum considerari posse. et quod movetur, in eandem partem pergere moveri eadem velocitate donec ab alio impediatur, vel (inita ratione motus secundum Cartesij mentem) semper tantundem motus manere in partem eandem quantum fuit anteaGa naar voetnoot3). Corpus corpori celeritatem tribuens de sua deperdit. Demonstrabuntur autem haec. Corpus quantumvis magnum a quamlibet parvo moveri potest licet quiescatGa naar voetnoot4). Eadem est celeritas appropinquandi in corporibus occurrentibus quae et separationis. hoc autem jam demonstratum fuitGa naar voetnoot5). Tum illud de revenientibus ea celeritate qua post occursum resilieruntGa naar voetnoot6). Et illud de aequali accessu et recessu in singulisGa naar voetnoot7). Item quod quantumvis magnum corpus alij minori quiescenti nunquam velocitatem tribuit quae sit dupla suaeGa naar voetnoot8). Quod aequale aequali omnem suum motum transfert et quod eum recipit quem alterum habebat, si habuit ullumGa naar voetnoot9). Corpus majus minori occurrens jam ad eandem partem moto, minorem ipsi celeritatem dabit quam si quiescenti occurrissetGa naar voetnoot10). | |
[pagina 117]
| |
Varios casus in corporibus inaequalibusGa naar voetnoot11). Item problemataGa naar voetnoot12). Quod quum duo diversa corpora varia celeritate lata idem corpus quiescens aequaliter commovent, aliud corpus non aeque commovebuntGa naar voetnoot13). 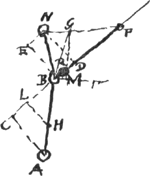 [Fig. 9.]
Quod celeritatis quadrata ducta in quantitatem corporum semper eandem summam producunt ante corporum occursum et postGa naar voetnoot14).
De occursu globorum non directo. Esto A [Fig. 9] globus duplus R cui quiescenti occurrat in B. ducatur CBRF per centra utriusque et cadat in eam perpend. AC. et sit BF 4/3 BC, erit F locus globi R post tempus ab occursu aequale tempori quo A venerat ex A in B. Sit BD ∞ ⅓ CB vel ¼ BF, et sit perpend. DN aequalis AC | |
[pagina 118]
| |
 [Fig. 9.]
erit N locus globi A, simul atque R est in F. et BN transitus ex B in NGa naar voetnoot1). potest ad horum demonstrationem etiam consideratio motus extranei adhiberiGa naar voetnoot2). apparet etiam NF, AB aequalesGa naar voetnoot3) esse. nam ND aeq. AC et DF aeq. CB, et triang.a sunt rect.laGa naar voetnoot4) imo HBG linea recta. BGFΔ isoscelesGa naar voetnoot5). De occursu indirecto quando uterque movetur sive in partes contrarias, sive in easdem. et vel directè vel indirectè in partes contrarias vel easdem, hoc est in lineis parallelis vel non parallelisGa naar voetnoot6). Cur globus aequali impactus in tabula non quiescat, in causa est motus circa cent. [Fig. 10.]  [Fig. 10.]
Ga naar voetnoot7 | |
[Huitième Partie.]Ga naar voetnoot8)
| |
[pagina 119]
| |
spatio ex utrisque AE et BH composito manifestum lineam utrique simul AE et BH aequalem mensuram esse celeritatis qua corpora A B mutuo respectu feruntur, cum nimirum AE linea celeritatem denotat corporis A et BH corporis B. At si eandem partem corpora feranturGa naar voetnoot12) quoniam quo tempore A corpus transit spatium AE et B spat. BH, eodem tempore diminuitur rursus vel augetur distantia corporum A B spatio quod aequale sit differentiae duarum AE, BH. Evidens est hanc eandem differentiam mensuram esse velocitatis qua corpora mutuo respectu moventur, cum AE et BH mensuram referunt velocitatum in corporibus A et B.
Corporis cujusvis velocitas, alterius corporis respectu quod in eadem recta movetur aestimetur secundum augmentum vel diminutionem ejus quae inter utrumque est distantiae. | |
[pagina 120]
| |
Atque adeo aeque velociter aliorum respectu moveri dicantur quae eodem vel aequali tempore pari quoque spatio ab alijs recedant vel accedant. 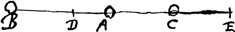 [Fig. 12.]
Etiam cum alterum ei corpori ad quod refertur appropinquat, alterum recedit. Veluti positis in eadem recta corporibus A, B, C [Fig. 12]. Si aequali temporis intervallo peragat corpus B spatium BD accedendo ad A, corpus vero C spatium ipsi aequale CE, sed ab A recedens; dicentur tamen respectu corporis A pari velocitate moveri corpora B et C. | |
Theorema.Si corpora duo in eadem recta inaequali celeritate ferantur, dummodo utrumque motu aequabili, etiam alterum alterius respectu aequabili motu procedet.
Ponantur corpora A et CGa naar voetnoot1) [Fig. 11] quae in eadem recta ferantur motu aequabili. A versus E et B versus H.  [Fig. 11.]
Quatuor autem sunt casusGa naar voetnoot2); nam vel in contrarias partes motus contingit, idque vel accedendo vel recedendo. Vel in partem eandem, ubi rursus differentia est, quod vel praecedens corpus tardius subsequente moveatur vel celerius. Dicimus itaque quibuscunque aequalibus temporis intervallis etiam spatijs aequalibus diminui vel augeri distantiam inter corpora A, B. Sumatur quaecunque temporis pars quâ corpus A transiverit spatium AC, corpus B verò spatium BD. Sequente igitur parte temporis quae priori aequalis sit, peraget A spatium CE ipsi AC aequale quoniam motu fertur aequabili, atque item corpus B spatium DH aequ. BD. Unde apparet aequalibus temporibus in primo quidem casu decessisse distantiae corporum AB partes aequales quantum nimirum efficiant duae simul AC et BD. Sequenti vero casu tantundem singulis temporibus accessisse distantiae AB. Rursus tertio casu singulis temporibus tantum illam diminui quanta est difserentia duarum AC, BD. Eandem denique differentiam postremo casu singulis temporibus accrevisse. | |
[pagina 121]
| |
[Neuvième Partie.]Ga naar voetnoot3)
| |
Theorema 1.Si corpori quiescenti occurrat aliud ipsi aequale post occursum quiescet hoc, omnisque motus alteri acquireturGa naar voetnoot4) Quiescenti corpori A [Fig. 13] occurrat aequale corpus B, dico post occursum 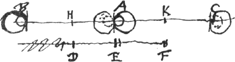 [Fig. 13.]
quiescere hoc debere, celeritatemque qua advenerat omnem transferre in corpus A. Ideoque si unam temporis partem insumpsit B dum pergit B ad A, alteram illi aequalem insumet A dum percurrat spatium AC ipsi AB aequ. Dividantur enim distantiae BA, AC utraque bifariam in H et K ductaque DF parall. BA, sint puncta D, E, F e regione punctorum H, A, K. Igitur motu aequabili et celeritate dimidia corporis B navi deferatur secundum lineam DF, is quidem dum B pervenit ad A conficiet spatium DE distantiae BA dimidium. Atque ipsius respectu aequali velocitate corpora B et A sibi mutuo occurrent. Ergo quoniam mole etiam aequalia sunt debebunt ejusdem spectatoris respectu, ea qua venerunt velocitate utraque revertiGa naar voetnoot5). Ideoque si unam temporis partem impenderunt priusquam sese mutuo attingerent, post alteram tantam unumquodque in locum pristinum revertisse debebit, dicti scilicet spectatoris respectu qui interea transijt spatium EF ipsi DE aequale. Quod quidem non aliter fieri potest quam si corpus A confecerit spatium AC ipsi BA aequale et B restiterit ad occursum corporis A. sicut enim spectator in D constitutus erat e regione puncti H medij inter corpora BA, ita rursus in F e regione puncti K quod medium est inter corpus B restantisGa naar voetnoot6) ad occursum A et corpus A delatum in C. Itaque sic fieri necesse est quemadmodum fuit propositum. Caeterum quia sequentium quoque demonstrationum vis omnis in huiusmodi | |
[pagina 122]
| |
relatione motus ad diversa corpora consistit idcirco paulo manifestius ob oculos ponenda videtur demonstratio primi hujus theor.is. Esto igitur navigium HK [Fig. 14] quod aequabili motu pergat dextram versus. Inque eo sedeat vector e regione punctu D. Cujus respectu aequali celeritate ferantur ad se mutuo corpora aequalia B, A. Quae quidem aequalibus spatijs exsistentibus DB, DA, concurrent in D, vectoris respectu et post mutuum impulsum, ejusdem respectu, aequali rursus celeritate digredientur. Quod si vero eodem tempore (puta secundi unius)
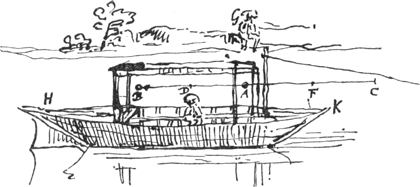 [Fig. 14.]
quo corpora B et A venere ad occursum in D, navigium et cum ipso unâ vector confecit spatium DA, necesse est corpus A immotum permansisse respectu ripae G aut spectatoris ibi consistentis; corpus verò B confecisse omne spatium BA. Nam non aliter fieri potest, istis positis, ut vectori corpora B et A aequali celeritate sibi invicem occurrisse appareant. Post concursum autem qui contingit in A respectu ripae, ut aequali rursus celeritate à se invicem corpora recedant respectu vectoris, qui altero temporis secundo transijt spatium AF ipsi DA aequale, id aliter fieri nequit quam si corpus B quiescat post impulsum in A respectu spectatoris G, atque ut corpus A percurrat dicto temporis secundo spatium AC ipsi BA aequale. Itaque respectu spectatoris G, primo temporis scrupulo pervenit corpus B ad A quiescens altero autem scrupulo confecit corpus A spatium AC ipsi AB aequale, et B restitit omnis motus expers ad occursum in A. | |
[pagina 123]
| |
Theorema 2.Si corpora duo aequalia inaequali celeritate moveantur et vel à contrarijs partibus venientia inter se collidantur, vel in eandem partem tendente utroque tardiùs praecedens à subsequente propellatur; permutata invicem celeritate exinde ferenturGa naar voetnoot1). 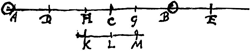 [Fig. 15.]
Tendant primo in partes contrarias corpora aequalia A et B. Et A quidem celeritate AC: B verò celeritate minore BC. Occurrent igitur sibi mutuo in C. Dico reversurum inde corpus A celeritate CD ipsi BC aequali corpus verò B celeritate CE aequali AC. Hoc est si prima temporis parte corpora A et B venere in C, post alteram temporis partem priori aequalem invenietur corpus A in D, et B in E. Dividatur enim distantia AB bifariam in H, sitque CG aequalis CH, et ducta KM parallela AB sint puncta K L M e regione punctorum H, C, G. Qui igitur praetervehitur celeritate KLGa naar voetnoot2), dum A fertur celeritate AC et B celeritate BCGa naar voetnoot3), is perveniet in L cum utrumque corpus ad C convenerit, et respectu ipsius aequali celeritate procedent corpora A et B. cum enim aequali prius spatio corpus utrumque ab ipso fuerit remotum, eodem tempore utrumque ex adverso ipsi factum est in CGa naar voetnoot4). Sed mole quoque aequalia sunt corpora, ergo pari rursus celeritate a se invicem recedere ea necesse est, ejus quem diximus respectuGa naar voetnoot5) Quare si unam temporis partem insumpsere ante mutuum contactum, debebunt ab occursu post alteram temporis partem ad pristinum locum quodque revertisse, dicti spectatoris respectu, qui interea confecit spatium LM. Id vero fieri non potest nisi, quod corpus A transierit spatium CD, et B spatium CE. Est enim distantia DE aequalis ipsi AB, quoniam utraque seorsim CD, CE aequales utrique CB, CA. Verum et CG aequalis est CH; ergo tota quoque GD aequalis HB. Sed HB dimidia est ipsius AB, ergo et GD dimidia DE; ideoque distantia DE bifariam dividitur in G. Unde manifestum est situm corporum in D et E, respectu spectatoris in M quod est e regione puncti G eundem esse qui fuerat corporum in A et B constituto ipso in K. | |
[pagina 124]
| |
Sed nunc corpus utrumque in eandem partem moveri intelligatur, B [Fig. 16] quidem celeritate BC, et A celeritate AC. hoc igitur attinget corpus BCGa naar voetnoot1) in
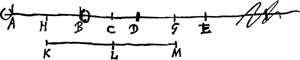 [Fig. 16.]
puncto C. Dico autem utrumque in eandem partem uti prius delatum iri sed permutata invicem celeritate, ut A feraturceleritate CD ipsi BC aequali; B vero celeritate CE aequali AC quantam scilicet prius habuit corpus A. Positis enim sicut in casu praec. punctis H, G et K, L, MGa naar voetnoot2). Evidens est ei qui praeterveheretur celeritate KL dum A fertur celeritate AC, et B celeritate BC, ei inquam pari celeritate utrumque corpus moveriGa naar voetnoot3), et conjungi utrumque in C cum ipse est in L. AEquali igitur celeritate utrumque recedere necesse est ejusdem spectatoris respectuGa naar voetnoot4), qui secundo tempore conficit spatium LM. ideoque ipso in M perveniente debet punctum e regione G eodem modo sese habere ad corpora in D et E, uti punctum H ad eadem in A et B. Quod sane fieri non potest nisi quo tempore spectator venit ab L ad M, corpus B peragat CE ipsi CA aequale et A corpus spatium CD aequale CB. Ergo sic fieri necesse est ut fuit prop.
ExGa naar voetnoot5) quovis impulsu corpora non nisi aequabilem motum nancisci. hoc est quo aequalibus temporibus aequalia spatia percurrant. [Etsi in alijs quoque corporibus locum habeant quae demonstraturi sumus, sphaeras tamen adhiberiGa naar voetnoot6).] Sphaeras quidem quarum centra in eadem recta moventur propter mutuum impulsum lineâ non excedere, quoniam absurdum dictu esset magis ad unam quam ad aliam partem deflectere. Reliquis vero corporibus idem evenire quando contactus punctum in eam rectam incidit, secundum quam utriusque gravitatis centra moventurGa naar voetnoot7).
Quoniam spatia à diversis corporibus aequali tempore peracta motu aequabili, | |
[pagina 125]
| |
in eadem qua velocitates sunt ratione. Ideo velocitatum rationem ratione spatiorum metiemur quae ijsdem vel aequalibus temporibus percursa sunt. Veluti cum
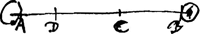 [Fig. 17.]
simul corpus A [Fig. 17] moveri dicetur celeritate AC, et corpus B celeritate BC, intelligendum est eodem temporis intervallo percurrisse corpus A spatium AC et corpus B spatium BC. Velocitatibus eam inter se rationem tenentibus quae est linearum AC ad BC. Praeterea ex ordine quo terminos linearum appellabimus, intelligatur in quam partem motus contingat. Veluti cum corpus A dicetur moveri celeritate AC id significabit certo temporis intervallo pervenisse aequabili motu ab A ad C, non à C ad A. Similiter cum dicetur postea ferri celeritate CD, significatur alia temporis parte quae sit priori aequalis pervenisse ex C in D. Ut enim possit ratio lineae AC ad CD proportionem designare velocitatum, oportet spatia AC, CD equalibus temporibus decursa fuisse. | |
[Dixième Partie.]Ga naar voetnoot8)
| |
[pagina 126]
| |
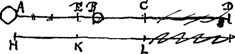
temporis partem rursus intervallo ipsi AB aequali sejuncta fore corpora. Quod ut fiat manifestum sciendum est imprimis, corpus quidem B ab A majore propelliGa naar voetnoot1).
 [Fig. 18.]
ipsi vero A de tribus unum contingere debere, ut post impulsum vel omnino conquiescat, vel retro feratur, vel denique ut prorsum ire pergat. E quibus hoc posterius semper verum esse in sequentibus ostendeturGa naar voetnoot2), sed in presens quodcunque è tribus statuatur propositum comprobabimus. Primo igitur ponamus pulso corpore B corpus A tamen pergere moveri in partem eandem. Quia autem motum dedit corpori B aliquid de sua celeritate remisitGa naar voetnoot1). Itaque cum primo tempore confecerit spatium AB, sequenti tempore ponatur confecisse BC spatium ipso AB minus. dico corpus B eodem secundo percurrisse spatium BD ita ut distantia corporum CD aequalis sit ipsi AB. Dividatur enim AC bifariam in E, sintque puncta H, K, L ex adverso punctorum A E C in linea ipsi AB aequidistante. Si quis igitur praetervehatur celeritate HK, dum corpus A fertur celeritate AB eum primo tempore praetervertet corpus A spatio EB sequenti verò exacto tempore cum ipse pervenerit in L rursus ex adverso ipsi continget corpus A, pervenit enim in C. Itaque respectu ejus qui sic praetervehitur eandem celeritatem habet corpus A ante et post impulsum. Quare neque corpus B quidquam de motu aut celeritate sua amisisse oportetGa naar voetnoot3). dicti autem spectatoris respectu qui vehebatur celeritate HK, habuit corpus B tempore primo cum quiesceret eam ipsam celeritatem HK. Ergo tantam quoque altero tempore conservasse ipsum necesse est. Ergo vel in eandem partem servavit celeritatem omnem vel in contrariam, spectatoris scilicet respectu. Sed non in partem eandem, quia debuisset semper quietum remansisse in B, quod non fieri jam ab initio dictum fuitGa naar voetnoot4). Ergo in contrariam. quum igitur primo tempore appropinquarit ad spectatorem celeritate HK, sequenti tempore pari celeritate ab ipso recedere necesse est. Quamobrem cum primi temporis initio praecesserit corpus B spectatorem in H | |
[pagina 127]
| |
constitutum spatio AB, eundem exacto secundo tempore cum in L constitutus est, aequali spatio CD praecedere debet. ergo constat propositum. Dicatur nunc corpus A postquam pepulit B quiescens, retrorsum agi, celeritate [Fig. 19.]
BC, [Fig. 19] quae quidem minor erit celeritate AB qua veneratGa naar voetnoot1), quia aliquam contulit corpori B. Cum igitur secundo tempore exacto pervenerit corp. A in C, dico corpus B fore in D, ita ut distantia CD ipsi AB aequalis sit. Estque demonstratio eadem quae in casu praecedente. 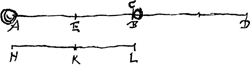 [Fig. 20.]
Denique fingamus corpus A pulso B quiescere. Dico necesse esse ut corpus B currat celeritate BD ipsi AB aequali. Neque hic diversa est demonstrationis ratio, coeuntibus in unum punctis B et C.
Quoties duo corpora inter se colliduntur, eadem est, mutuo respectu, discedentibus celeritas, quae fuit appropinquantibusGa naar voetnoot5). AEqualibus corporibus jam antea accidere demonstratum fuitGa naar voetnoot6). Sed et inaequalibus eo casu quo minus quiescit. Unde quatuor adhuc casus supersuntGa naar voetnoot7). Nam vel majus e duobus quiescit, vel ex adverso ad se invicem feruntur, vel celeriori motu minus insequitur majus, vel contra. Quos simul omnes proponemus demonstrabimusque. [Fig. 21.]
Sit ergo corpus A [Fig. 21] minùs quam B. Et feratur A celeritate AC, B verò vel omnino quiescat vel habeat celeritatem BC. Cum igitur ante occursum mutuo respectu corpora habuerint celeritatem AB dico et post occursum mutuo respectu parem ipsi AB celeritatem habitura. hoc est, si una pars temporis intercesserit priusquam | |
[pagina 128]
| |
corpora A et B in C convenirent dico sequente altera aequali temporis parte exactâ, rursus intervallo quod ipsi AB aequale sit sejuncta fore. Si quis enim pretervehaturceleritate
 [Fig. 21.]
DE ipsi AC aequali quâ fertur corpus A, ejus respectu ipsum A quiescit, et solum B movetur celeritate BA. Est autem A minus quam B. Ergo per anteced.Ga naar voetnoot1) ejusdem praetervecti respectu etiam eadem celeritate AB corpora post occursum a se invicem recedent, adeo ut finito aequali post impulsum tempore cum ipse confecerit spatium EH aequale DE distent rursus intervallo ipsi AB aequali. Hoc autem fieri nequit nisi revera et cujusvis alterius respectu eo spatio distent. Ergo sicut propositum est continget. | |
Theorema.Corpus omne quiescens à quamlibet exiguo corpore et celeritate qualibet impacto moveturGa naar voetnoot2). Quiescat corpus A [Fig. 22], et occurrat ei qualibet celeritate corpus B ipso A  [Fig. 22.]
minus. Dico hoc ab illo moveri. Sumatur AK aequ. AB sintque puncta C, D, E ex adverso punctorum B, A, K in linea ipsi BA parallela. Si ergo praetervehatur quis celeritate ea qua fertur corpus B, ut quo tempore B conficit spatium BA, ipse percurrat aequale spatium CD, | |
[pagina 129]
| |
ejus respectu quiescit corpus B, totaque hujus celeritas attribuiturGa naar voetnoot3) corpori A. Quare post impulsum, debet ejusdem spectatoris respectu qui secunda temporis parte priori aequali confecit sp. DE, moveri corpus B, A vero remisisse aliquid de sua celeritate aut omnem amisisseGa naar voetnoot4). Horum vero utrumvis non aliter fieri potest quam si aliquid spatij percurrat ab A versus K, puta spatium AH. Nam si in A quietum maneret, tum dicti spect.is respectu nihil de celeritate sua amisisset quod esse nequit. Itaque motum accepit corpus A occursu corporis minoris B. Caeterum spatium AH minus esse debere quam AB vel AK manifestum est quia minorem celeritatem à corpore B accepit A quam ipsum B habuerit.
Cartesij vero falsas esse regulas praeter primam omnes ex hac et praecedentibus propositionibusGa naar voetnoot5) manifestum est. Nam huic quidem contrarium plane statuit, corpus scilicet majus quiescens nullo ictu vel tantillo minoris moveri posseGa naar voetnoot6).
Axioma sit. quod minus corpus majori quiescenti occurrens dabit ei minorem quam habet ipsum celeritatemGa naar voetnoot7), nam quod aliquam conferet ex ijs quae hic antea posita sunt probabiturGa naar voetnoot8). Corpus quiescens à diversae magnitudinis corporibus singulis seorsim impulsum, majorem celeritatem à majori accipere quam à minori si eadem celeritate utrumque occurratGa naar voetnoot9). Inde quod majus minori quiescenti occurrens continuat motum suum in eandem partemGa naar voetnoot10). Tum theorema in principio phyliraeGa naar voetnoot11): Si majus &c.Ga naar voetnoot12) | |
[pagina 130]
| |
tum sequensGa naar voetnoot1). Tum quod minus à majori resilitGa naar voetnoot2), si non potest aliter. Quod majus minori quiescenti minorem quam duplum sui datGa naar voetnoot3). Hactenus demonstratum est quod non tantum minus à majore corpore moveri potest, sed et à minore majusGa naar voetnoot4). item quaecunque ad corporum aequalium impulsum pertinent explicata fueruntGa naar voetnoot5). Data autem corporum inaequalium magnitudine et celeritate, ut definiri possit quatenus haec ab impulsu mutuo immutetur atque ab alio in aliud transeat praeter ea quae in praecedentibus adhibuimus aliud adhuc circa motus naturam inveniendum est quod principij loco habeatur. Solebat mihi unicum hic videri minimeque dubiumGa naar voetnoot6) id quod à Cartesio primò omnium consideratum fuit, Eandem scilicet motus quantitatem in corporibus simul sumptis post impulsum conservari quae prius ineratGa naar voetnoot7). Quantitatis ratione sic inita ut aequalis celeritas majorem motus quantitatem in majore corpore quam in minore constitueret, idque pro ratione molisGa naar voetnoot8). Veluti si corpus A [Fig. 23] duplum  [Fig. 23.]
esset corporis B, eique quiescenti occurreret cum tribus celeritatis partibus, dicebat utrumque in eandem partem deinceps moveri cum partibus celeritatis duabus; eaque ratione motus quantitati nihil decedere, quoniam et corpori A duae celeritatis partes relictae essent, et corpori B totidem acquisitae, quae tamen non majorem motus quantitatem hic efficerent, quam una pars celeritatis in corpore duplo A, [Id quidem non verisimile existimabam conjuncta invicem post impulsum manere corpora, uti fieri hic necesse est cum utrumque pari celeritate motum continuet in eandem partem: videbam tamen eodem retento axiomate veriores erui posse, quaeque nihil nostris legibus obessent: veluti in casu proposito si corpus B quatuor partes celeritatis accipere dicatur A vero retinere unam quacum subsequatur corpus B praecedens. Ita enim | |
[pagina 131]
| |
et cum tribus celeritatis partibus à se invicem separantur sicut appropinquarunt secundum Theor.....Ga naar voetnoot1) et motus quantitate omni integra servata salvum est axioma praedictum. Et sane in hoc casu rectè sic definiri postea ostendemusGa naar voetnoot9)]Ga naar voetnoot10). Neque tamen eo magis dictum axioma admitti potest. Quod ut manifestum fiat. Ponamus corpus A quiescere esseque duplum ut ante corporis B, quod ipsi occurrat. B igitur movebit A atque aliquam ipsi celeritatem imprimetGa naar voetnoot4); Esto ea pars quantumvis exigua, decima ex. gr. celeritatis ipsius B. ut si hoc habeat celeritatis partes decem, unam accipiat A. Ut igitur eadem celeritate separentur corpora qua et appropinquarunt, necesse est corpus B retrorsum agi cum partibus celer. novem; pars autem celeritatis una in corpore duplo A tantam motus quantitatem constituit quantam duae partes in corpore B. Ergo post impulsum ea jam motus quantitas existit quantam constituunt partes undecim celeritatis in corpore B. cum prius decem tantummodo fuerint. Aucta est hic igitur contra princip. Cartesij motus quantitas idque semper fieri necesse est cum corpus majus quiescens à minore impelliturGa naar voetnoot11). Contra verò alijs casibus minui motus quantitatem ostendere possemGa naar voetnoot12), sed supersluum id esset quum ex hoc solo quod jam dictum fuit satis manifesta sit Principij istius infirmitas atque impossibilitas. Veruntamen mirabile hoc videri potest quantitatem motus ea ratione multiplicari rursusque diminui, et me quidem diu suspensum tenuit, ita ut quid certi statuerem non invenirem. Tandem veròGa naar voetnoot13) et principium quidem illud non omnino rejiciendum esse sed convenienti interpretatione emendandum. Eandem nimirum motus quantitatem servari vult natura, sed in eandem quoque partem, idque hoc modo est intelligendumGa naar voetnoot14).
Sint corpora. Hoc fieri naturae consentaneum quae determinationem quidem singulorum corporum diversam concedere debuit ne pereatGa naar voetnoot15). sed determinationem quantitatis motus hoc est quae in corporum summa resideret cum nihil impediat nequaquam immutari convenitGa naar voetnoot16). unumquodque enim uti est ita manet donec &c. ut recte disserit CartesiusGa naar voetnoot17), huic autem determi.i corporum simul sumptorum | |
[pagina 132]
| |
nihil contrarii est, utique postquam aeque majus a minori quam hoc ab illo moveri demonstratum estGa naar voetnoot1). Notandum autem quod secundum haec quae diximus, centrum grav. corporum simul sumptorum aequabili semper motu eodem versus pergit neque impulsu corporum ullo desistitGa naar voetnoot2). | |
Onzième PartieGa naar voetnoot3).
| |
[pagina 133]
| |
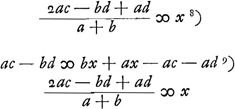 Ga naar voetnoot8)Ga naar voetnoot9) Datum corpus quiescens dato alio corpore movere ut celeritatem acquirat aequalem dataeGa naar voetnoot10).  [Fig. 25.]
Datum sit corpus quiesc. a [Fig. 25] et alterum b, et celeritas c. Sicut duplum corporis b ad b et a simul, ita sit c ad d. erit d velocitas requisita in corpore b quâ impactum corpori a, dabit ei velocitatem cGa naar voetnoot11). 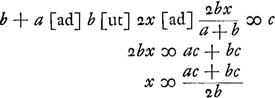 Ga naar voetnoot12) Mirandum est quod magnum corpus quiescens à parvo celerius movetur per interposita corpora proportionalia, quam si immediatè à parvo impulsum fuissetGa naar voetnoot13). | |
[pagina 134]
| |
Videndum quousque illud extendatur, nam pluribus sumptis medijs, plus motus dat magno corpori quam si pauciora sumantur. et tamen nunquam tantum motus dabit corpori majori quantum ipsum habetGa naar voetnoot1). 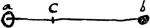 [Fig. 26.]Ga naar voetnoot2)
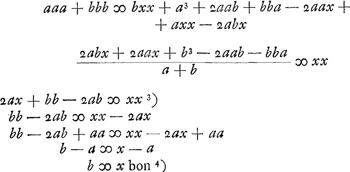 Ga naar voetnoot3)Ga naar voetnoot4) | |
[pagina 135]
| |
[pagina 136]
| |
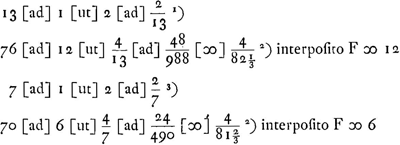 Ga naar voetnoot1)Ga naar voetnoot2)Ga naar voetnoot3)Ga naar voetnoot2) interpositis omnibus 2 4 8 &c.Ga naar voetnoot4) dabit corpori G 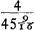 Ga naar voetnoot5). Ga naar voetnoot5).
HincGa naar voetnoot6) videtur quod si uno corpore intermedio velimus maximum motum magno corpori conciliare, opus erit illud medium proportionale sumere inter minimum et maximumGa naar voetnoot7). Unum intermedium non potest duplum dare immediati, quantumvis exigua sit proportio minimi ad maximumGa naar voetnoot8). plura vero intermedia non duplum tantum sed octuplum, et decuplum et infinities multiplex immediatiGa naar voetnoot9). duo intermedia non possunt dare quadruplum immediati. 1 dabit τω 1000 per interpositum 100 paulo plus quam triplum immediatiGa naar voetnoot10). |
|