Oeuvres complètes. Tome XV. Observations astronomiques

[p. 553]

V¹⁾.
[1660]²⁾.

Oporteat quaerere in eclipticae quadrante AE, particulam HD, quam sol motu apparente minima quapiam temporis particula peragit, quaeque ita sit posita, ut ductis ex polo AEqu. ^sP meridianis PDC, PHL, hi comprehendant arcum LC aequatoris, aequalem motui medio solis per similem temporis particulam.

Ponatur arcus PD jam inventus esse sitque ejus sinus ∞ x. arcus autem PE (qui datus est, cum sit complementum declinationis eclipticae EB) sinus vocetur s. Radius ad quem sinus referuntur sit r.

Jam quia in triangulo sphaerico rectangulo PDE, datur hypotenusa PD et latus PE; si fiat ut sinus lateris PD, hoc est, ut x, ad sinum lateris PE qui est s ita radius r ad aliud, orietur sinus anguli PDE ∞ rs/x, per regulas triang.^orum sphaer.^orum

1) La Pièce a été empruntée aux p. 246-249 du Manuscrit A. Huygens s'y applique à déterminer dans le premier quadrant de l'écliptique (celui du printemps) le lieu où doit se trouver le Soleil, afin que le rapport des petits intervalles correspondants du temps vrai et du temps moyen soit égal à l'unité. Ce lieu correspond comme Huygens le remarque (voir la l. 6 d'en bas de la page suivante) à un maximum de l'équation du temps. Il trouve la longitude: 25^o0′ ♉ = 55^o0′.

2) D'après le lieu que la Pièce occupe au Manuscrit A.

[p. 554]

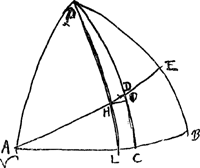
unde et anguli HDO sinus erit rs/x. sit autem HO arcus parallelus LC, hoc est, eodem polo aequatoris P descriptus. Itaque in triangulo HOD angulus O rectus est, quod triangulum tanquam rectilineum censeri debet cum HD sit particula minima quaepiam eclipticae. Cum igitur latus HD sit ad latus HO, ut sinus anguli HOD, hoc est, ut radius r ad sinum anguli HDO qui erat rs/x: Erit ergo HD ad HO ut r ad rs/x hoc est ut xr ad rs, hoc est, ut x ad s. Porro nunc, si ponamus HD ad LC, hoc est, celeritatem motus solis apparentis circa D ad celeritatem motus sui medij notam habere rationem, puta eam quam a ad r; habebit proinde HD ad HO rationem eam quam a ad x. Nam quia arcus LC ad arcum HO, sicut sinus quadrantis LP sive radius ad sinum arcus HP sive sinum arcus DP (hi enim arcus nihil differre censendi sunt, cum HD sit particula minima) hoc est sicut r ad x; HD autem ad LC ut a ad r; Erit ex aequo HD ad HO ut a ad x. Erat autem HD ad HO ut x ad s. Ergo a ad x ut x ad s, Ideoque xx = as. Si solem ponamus progredi in ecliptica motu medio aequali, hoc est, si inaequalitatis dierum unam tantum causam ponamus, nempe inaequalitatem arcuum eclipticae et aequatoris qui simul meridianum transeunt, erit hîc a aequalis r, ideoque xx ∞ rs. Quod significat, ad inveniendum tunc arcum eclipticae AD, ab A intersectione verna vel autumnali, qui arcus ab ascensione sua recta, AC plurimum differat; debere sumi à polo P arcum PD eclipticae occurrentem, cujus sinus sit medius proportionalis inter radium et sinum arcus PE, complementi videlicet declinationis eclipticae. Quae est regula Gebri Arabis¹⁾, quam ex illo habuit Regiomontanus, ex hoc Stevinius, qui putat

1) Geber, astronome arabe, vécut à Séville dans l'onzième siècle. Ses oeuvres furent traduites en latin dans le douzième siècle par Gérard de Crémone et cette traduction fut publiée à Nurenberg en 1533.

[p. 555]

non esse hanc Arabicam inventionem, sed ex reliquijs ejus, quod sibi fingit, sapientis aevi²⁾. Idem vero punctum D sic inventum, est illud, ubi sol positus



diem apparentem aequabili sive medio aequalem efficit. Et tempus dierum apparentium qui effluxere dum sol arcum AD emensus est, quam maximo excessu superatur à tempore totidem dierum aequabilium, in illo scilicet eclipticae quadrante. quia si punctum D ulterius distans ab A accipiatur, jam arcus exiguus CL major fiet eo quem sol medio motu percurreret eo tempore quo conficit arcum HD motu apparente. Posito autem solis motu apparente, sicut est, inaequali, non datur proportio a ad r, de qua modo, quamdiu punctum D in incerto est atque ubi sit quaeritur. Ideo regula ill xx ∞ as, hunc usum legitimum tantum habet, ut dato vel posito puncto aliquo D inquiratur, an sit ejusmodi quod diem apparentem medio aequet cum sol ibi positus fuerit, et consequenter tempus dierum apparentium plurimum deficere faciat a tempore totidem dierum mediorum, à termino A. Ut exempli gratia ponamus D punctum in gr. 27 ♉³⁾. motus solis apparens diurnus hîc est 57′,34″ ut ex ephemer. colligitur. qui ad motum diurnum medium 59′.8″. se habet ut 3454 ad 3548. Si igitur fiat ut 3548 ad 3454 ita radius r ∞ 100000 ad aliud, invenietur 97350 ∞ a. Est autem s sive sinus complementi declinationis eclipticae ∞ 91686, positâ cum Tuchone declinatione gr. 23.31′30″. ergo as ∞ ∞ 8925729450 cujus radix 94476 ∞ x; estque sinus gr. 70.52′, hoc est arcus PD.

2) On trouve le passage en question dans la première Partie des ‘Wisconstige Gedachtenissen’ (1608) de Simon Stevin (voir l'ouvrage cité dans la note 10 de la p. 7 de notre T. I). Cette première Partie est divisée en trois Volumes à pagination indépendante. Le passage se trouve à la p. 157 du troisième Volume ‘Van den Hemelloop’ (Du cours des corps célestes). Nous le faisons suivre dans la traduction qui en a été donnée par Albert Girard dans son édition des ‘OEuvres Mathématiques de Simon Stevin, Augmentées par Albert Girard’ (voir les p. 250-251 du deuxième Volume de l'ouvrage (de 1634), cité dans la note 2 de la p. 517 de notre T. I):

‘Theoreme. Proposition XVII.

Estant mené un arc du pole de l'equateur jusques en l'ecliptique, ainsi que son sinus soit moyen proportionel, entre le raid de la Sphere, & le sinus de complement de la majeure declinaison de l'ecliptique: iceluy arc marquera l'ecliptique au poinct, dont l'ascension droite differe au plus de l'arc de l'ecliptique.

La difference entre les jours naturels, & les egaux, est trouvée par les 15 & 16 propositions en nombre [voir les p. 152-157 de l'ouvrage de Stevin, p. 248-250 de la traduction de Girard]; mais joignant cela, la Theorie est parvenue plus avant, où c'est que telle difference est la majeure; premierement à cause de l'obliquité de l'ecliptique, puis apres à cause de l'eccentricité du deferant du Soleil, desquelles choses la présente dixseptiesme proposition & la suivante [p. 164 de l'ouvrage de Stevin, p. 254 de la traduction] traitent.
Notez que combien que cette matiere soit profonde, qu'elle n'est pas en Ptolemée, mais és escrits de Regiomontanus à la 25 proposit. du troisiesme livre de l'Epitome de l'Almageste, ce qu'il dit avoir extrait de Geber Arabe: tontesfois elle ne semble estre des Arabes, mais plustost une relique du siècle sage, comme aussi les ecrits de Hyparchus & Ptolemée, leur sont venus entre les mains.’
Ajoutons que Stevin a exposé dans le deuxième Volume de la première Partie de ses ‘Wisconstige Gedachtenissen’, p. 9-18 (p. 106-110 de la traduction de Girard) ses idées sur le siècle sage ‘auquel les hommes ont eu une cognoissance admirable des sciences, ce que nous remarquons infailliblement par certains signes, toutesfois sans sçavoir qui se sont esté, où à quel lieu, ny quand.’

3) Savoir 57^o de longitude.

[p. 556]

Cujus complementum gr. 19.8′. est arcus DC qui arcus est declinatio grad. 25.13′. ♉ Quod si autem fuisset hic gr. 27. ♉, idem nempe qui erat assumti puncti D, id indicio fuisset locum solis in g. 27 ♉ recte assumtum ut illa quae dixi circa dierum aequationem efficiat. Nunc autem non recte assumtum esse constat. Attamen hoc pacto verum locum dicti puncti accuratissime inveniri sciendum est; Certum enim est si punctum D ponamus secunda vice in gr. 25.13′. ♉ qui ex priore calculo extitit, eodemque modo hinc calculum instituamus, exoriturum quam proxime eundem gr. 25.13 ♉. Quia enim in hoc loco eclipticae motus diurnus solis proxime idem est atque in gr. 27 ♉ antea assumto, quippe 57′,36″; hoc solum à calculo superiori secundus calculus differet, quod loco rationis 3548 ad 3454 nunc habebitur ratio 3548 ad 3456, quae cum parum adeo differant, et reliquus calculus eodem modo utrobique se habeat, necesse est quemadmodum ex priore prodit 25.13′ ♉ ita quoque eundem fere locum ex posteriori prodire, exiguo scilicet anteriorem, quia a nunc major erit ideoque et as cui aequatur xx. Et hic quidem qui ultimo invenietur locus qui quidem erit 25.0′. ♉¹⁾ pro vera determinatione puncti D retineri poterit, quem notandum est revera adhuc ulteriorem fore loco verissimo, sed nullius momenti differentia, nec enim exactitudo summa praestari utique hic potest, cum motus solis per tabulas etiam proxime tantum cognoscatur. alioqui ex posteriore loco denuo alius multo accuratior reperiri posset repetita simili operatione²⁾.

1) En effet, nous avons vérifié qu'on obtient ce résultat, si l'on applique de nouveau le même procédé, partant cette fois de la longitude 25^o13′ ♉ = 55^o13′.

2) Soient ε l'inclinaison de l'écliptique sur l'équateur, λ et δ la longitude et la déclinaison du Soleil, 1 + φ (λ) (où φ (λ) est une fraction relativement petite) le rapport de la vitesse du Soleil vrai à la vitesse moyenne. On trouve alors facilement que la position cherchée du Soleil est déterminée par l'équation:

cos² δ = (1 + φ(λ)) cos ε, où sin δ = sin ε. sin λ.

Or, la méthode appliquée par Huygens pour résoudre cette équation consiste, partant d'une valeur λ₁ pas trop éloignée de la quantité cherchée, dans le calcul des quantités λ₂, λ₃, λ₄, etc. déterminées successivement par les équations:

cos²δ₂ = (1 + φ(λ₁)) cos ε; sin λ₂ = sin δ₂: sin ε cos²δ₃ = (1 + φ(λ₂)) cos ε; sin λ₃ = sin δ₃: sin ε
etc.,

jusqu'à ce que λ_n + 1 ne diffère plus sensiblement de λ_n.
Remarquons que pour φ(λ) = 0 la formule cos²δ = cos ε est identique avec l'équation ‘xx ∞ rs’ de la p. 554.