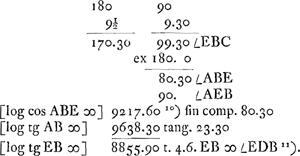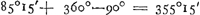
[Fig. 3.]
|
-
voetnoot1)
- L'Appendice qui suit est emprunté à la p. 82 du Manuscrit A. Il contient la détermination de l'angle entre la ligne des anses de Saturne et une ligne parallèle à l'équateur terrestre dans les deux cas suivants: 1o celui où la largeur apparente de l'anneau est un maximum par rapport à son diamètre apparent, 2o celui où l'angle en question est maximum lui-même. Nous avons apporté une division en trois paragraphes.
-
voetnoot2)
- La pièce date probablement de février 1659 d'après de lieu qu'elle occupe.
-
voetnoot3)
- Huygens indique ici que lorsque Saturne, dont le plan de l'orbite est censé coïncider avec l'écliptique, se trouve dans les points de longitude 170o30′ et 350o30′, ses anses font avec l'écliptique un angle de 23o30′; comparez la p. 317.
-
voetnoot4)
- Parce que Saturne se trouve alors, sur la sphère céleste, à une distance de 90o des points où l'écliptique est coupée par un plan parallèle à l'équateur de Saturne. D'ailleurs ‘20.30 ⇸ vel ♊’ = 260o30′ ou 80o30′ de longitude. Ajoutons que dans ces positions de Saturne le rapport de la largeur apparente de l'anneau à son diamètre apparent devrait être maximum.
-
voetnoot6)
- Consultez le sixième alinéa de la note 1 de la p. 372. Les longitudes des points en question sont 175o15′ et 355o15′.
-
voetnoot9)
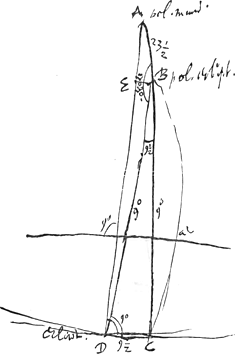
- Dans cette figure A ‘pol. mundi’ représente le pôle de l'équateur, B celui de l'écliptique, C le solstice d'hiver, D la position de Saturne où la ligne des anses est parallèle à l'écliptique. Quant à l'arc EB, il appartient au grand cercle dont D est le pôle. On a donc DE = BD = BC = 90o, AB = 23o30′, DC = 9o30′, ∠ EBC = 99o30′, ∠ ABE = 80o30′, et par suite dans le triangle sphérique ABE (rectangulaire en E): tg. EB = tg 23o30′ cos 80o30′; voir maintenant les calculs du § 2.
-
voetnoot11)
- Évidemment cet angle est égal à celui entre une parallèle à l'équateur et la ligne des anses, qui coïncide au point D avec la tangente à l'écliptique.
-
voetnoot1)
- Dans ce paragraphe Huygens s'occupe de la valeur maximum de l'angle entre la ligne des anses et la parallèle à l'équateur terrestre. Avant d'expliquer le calcul de Huygens il sera utile de considérer le problème auquel la détermination de cette valeur se réduit.
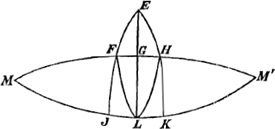
Soit donc E (voir la figure en bas de la p. 373) le pôle de l'écliptique, H le pôle de l'équateur terrestre, F celui d'un plan parallèle à l'équateur de Saturne, passant par le centre de la sphère céleste, N une position quelconque (non indiquée dans la figure) de Saturne, position qu'on doit supposer sur l'écliptique MK puisque Huygens identifie, comme nous l'avons déjà remarqué, le plan de l'orbite de Saturne à celui de l'écliptique. Il s'agit alors en premier lieu de placer sur l'écliptique le point N de sorte que l'angle FNH soit maximum.
Or, ce problème dont la solution dans le cas général, où les points F et H seraient placés arbitrairement sur la sphère, amènerait des calculs assez compliqués, se simplifie singulièrement dans le cas supposé par Huygens où les points F et H se trouvent à une distance égale de 23o30′ du pôle E de l'écliptique.
Dans ce cas il est assez évident qu'on doit placer le point cherché au point L situé à égale distance des points J et K, ou bien au point L′ (non marqué) diamétralement opposé à L. La longitude du point K, qui n'est autre que le solstice d'été, étant 90o et celle du point J 80o30′ (comparez la note 4, p. 370), on trouve pour les longitudes des points L et L′ respectivement 85o15′ et 265o15′, ou, si l'on veut, 25o15′ ♊ et 25o15′ ⇸ (comparez le dernier alinéa du § 1).
Quant à l'angle cherché FLH on trouve successivement à l'aide des triangles rectangles EGH et LHG (où GEH = 4o45′, EH = 23o30′): GH = 1o53′30″ (et par suite FH, qui mesure l'angle entre l'équateur terrestre et l'équateur de Saturne = 3o47′), EG = 23o25′40″, GL = 66o34′20″, GLH = = 2o3′40″ et enfin FLH = 4o7′.
Cherchons encore, à l'exemple de Huygens (voir la première phrase du dernier alinéa du § 1), les points où la ligne des anses est parallèle à l'équateur terrestre. À cet effet il suffit de prolonger l'arc FH jusqu'aux points d'intersection M et M′ avec l'écliptique. Or, puisqu'évidemment l'angle FGL est droit, on a ML = = LM′ = 90o. La longitude des points M et M′, où ce parallélisme se présente, est donc respectivement 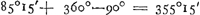 et 175o15′, ou bien 25o15′ ♓ et 25o15′ ♍. et 175o15′, ou bien 25o15′ ♓ et 25o15′ ♍.
Passons maintenant aux calculs qui ont conduit Huygens pour l'angle maximum en question à la valeur de 4o8′ qu'on retrouve dans le ‘Systema Saturnium’ (voir la p. 315 qui précède).
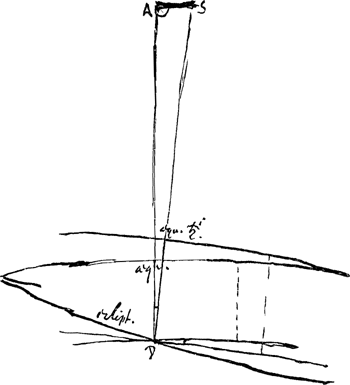
Considérons à cet effet la Fig. 2. S y représente le pôle d'un plan parallèle à l'équateur de Saturne; A le pôle de
l'équateur terrestre. L'arc AS mesure donc l'angle entre ces équateurs, pour lequel Huygens a trouvé auparavant (voir l'Appendice V, p. 368) 3o48′.
Or, le point D correspond évidemment au point L′ nommé plus haut qui se trouve à une distance de 4o45′ du solstice d'hiver. Il s'agit donc d'évaluer l'angle ADS. À cet effet Huygens se sert du triangle ADS. Il considère que l'angle DAS ne peut pas différer beaucoup d'un angle droit. Quant au côté SD on a SP = 90o, puisque P se trouve sur le plan parallèle à l'équateur de Saturne (consultez la Fig. 3) et il évalue DP à 23o environ. Partant de ces suppositions un peu arbitraires il trouve par les calculs qui suivent une valeur qui ne diffère que d'une minute de celle trouvée par nous plus haut.
|