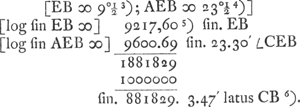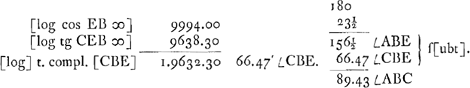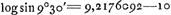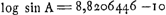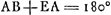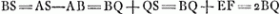
Cum in ∆o EBA ex datis ang.o A et E et lat. EB quaero latus BAGa naar voetnoot5), fit hoc 83.14′. cum autem in ⊿ rectang. BCA ex datis ∠o CBA et latere CB, quaero idem latus BA, fit 85.43′Ga naar voetnoot6). an error in tabulis sin.Ga naar voetnoot7)

Ga naar voetnoot8)
|
-
voetnoot1)
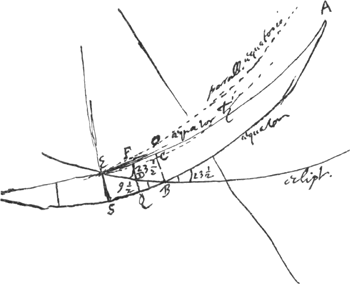
- Partant de certaines données qu'on retrouve dans le ‘Systema Saturnium’ Huygens s'applique dans cet Appendice, emprunté aux p. 78-79 du Manuscrit A, à déterminer la situation de l'équateur de Saturne par rapport à l'équateur terrestre.
Remarquons encore qu'afin de faciliter la discussion nous avons ajouté les lettres D et F à la figure de Huygens.
-
voetnoot2)
- D'après le lieu qu'elle occupe dans le Manuscrit A la Pièce doit dater de janvier, ou du commencement de février 1659.
-
voetnoot3)
- Comparez la p. 315 qui précède d'après laquelle le grand cercle parallèle à l'équateur de Saturne couperait, sur la sphère céleste, l'écliptique à une distance de 9o30′ des équinoxes.
-
voetnoot5)
- Nous écririons plutôt 9.21760-10 et ainsi de suite pour les autres logarithmes.
-
voetnoot6)
- Le calcul qui précède est peu exact. D'abord il aurait mieux valu écrire respectivement 9217.61 et 9600.70 au lieu de 9217.60 et 9600.69 puisqu'on a en sept mantisses
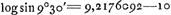 et log sin 23o30′ = 9,6006997. Alors on trouve CB = 3o46′24″. Et en tout cas la valeur 3o47′, donnée par Huygens est trop grande de plus d'une demi-minute. et log sin 23o30′ = 9,6006997. Alors on trouve CB = 3o46′24″. Et en tout cas la valeur 3o47′, donnée par Huygens est trop grande de plus d'une demi-minute.
-
voetnoot1)
- Remarquons que la valeur 9,9990472-10 pour log cos EAB correspond à
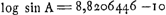 . .
-
voetnoot2)
- Ce nombre représente la somme des derniers deux des trois qui précèdent.
-
voetnoot3)
- Ce nombre est obtenu en soustrayant de la dite somme (voir la note qui précède) le premier nombre (8821.3425) de la colonne. Huygens applique ici au triangle ABE la règle des sinus.
-
voetnoot5)
- Voir l'avant-dernier calcul de la page précédente. Ce calcul donne EA = 96o46′ (comparez la note 4); mais on a
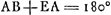 (comparez la note 8), donc BA = 83o14′. (comparez la note 8), donc BA = 83o14′.
-
voetnoot6)
- Voir le dernier calcul de la p. 368, qui, en effet, amène cette valeur.
-
voetnoot7)
- La contradiction apparente à laquelle les calculs de Huygens l'ont conduit s'explique par les inexactitudes indiquées dans la note 6 de la p. 367 et la note 1 de la p. 368. Quant à la valeur de CB, il est vrai que la page 79 du Manuscrit contient encore l'annotation ‘3.46.26 lat. CB’; mais les calculs sont faits avec la valeur 3o47′.
Voici d'ailleurs les valeurs des grandeurs en question telles qu'on les trouve par des calculs plus exacts: BC = 3o46′; ∠CBE = 66o47′; ∠A = 3o47′; AB = 85o39′.
-
voetnoot8)
- Les petits calculs qui suivent encore ont servi probablement à vérifier la valeur trouvée pour AB par le dernier des calculs qui précèdent. Pour le montrer nous commencerons par considérer les propriétés de la figure dessinée par Huygens. Prolongeons à cet effet les arcs AE et AB et soit A′ le point où ils se coupent pour la seconde fois. On a alors AE = A′B; AB = A′E à cause de la congruence des triangles AEB et A′BE; par suite
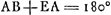 . Tirons ensuite l'arc ADA′ passant par le point D qui se trouve au milieu de l'arc EB. À cause de la congruence des triangles ABD et A′DE on a AD = A′D = 90o. Par conséquent l'arc FDQ peut être considéré comme appartenant au grand cercle dont A et A′ sont les pôles et qui coupe orthogonalement les arcs AEA′, ADA′ et ABA′; on a donc, posant AS = AE, . Tirons ensuite l'arc ADA′ passant par le point D qui se trouve au milieu de l'arc EB. À cause de la congruence des triangles ABD et A′DE on a AD = A′D = 90o. Par conséquent l'arc FDQ peut être considéré comme appartenant au grand cercle dont A et A′ sont les pôles et qui coupe orthogonalement les arcs AEA′, ADA′ et ABA′; on a donc, posant AS = AE, 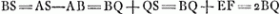 , où BQ peut être calculé de la manière indiquée par le dernier calcul de cet Appendice et devrait se trouver égal à ½ BS. , où BQ peut être calculé de la manière indiquée par le dernier calcul de cet Appendice et devrait se trouver égal à ½ BS.
Ajoutons encore que DQ mesure la moitié de l'angle A; de sorte que cet angle peut être supputé facilement à l'aide de la formule: sin ½ A = sin DQ = sin BD. sin DBQ = sin 4o45′. sin 23o30′; mais on ne trouve pas de traces d'un tel calcul dans le Manuscrit en question.
|