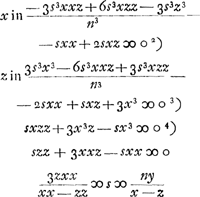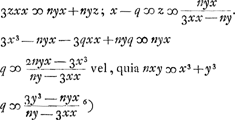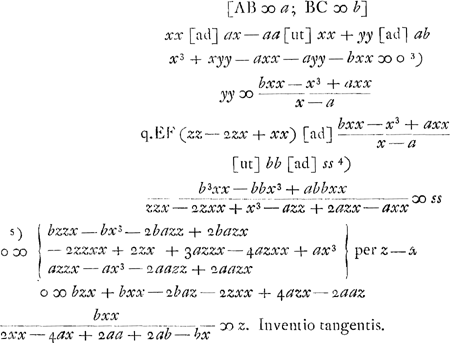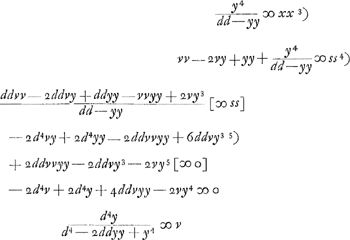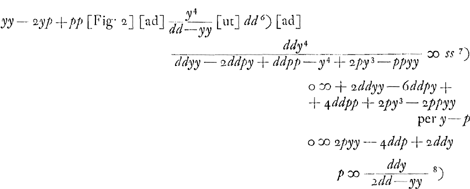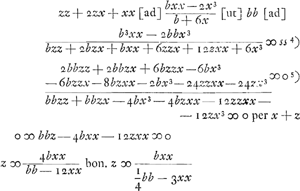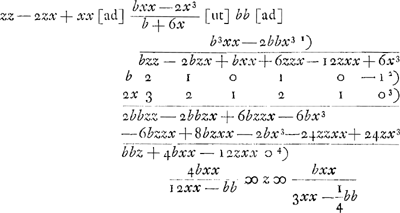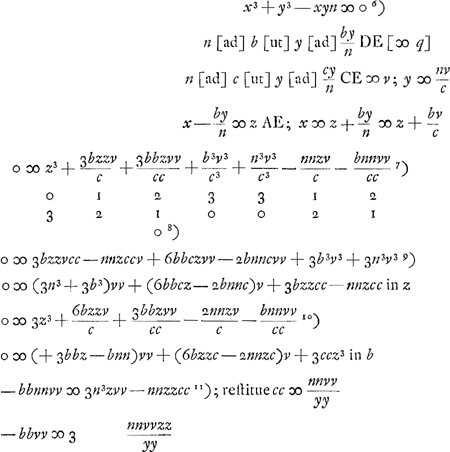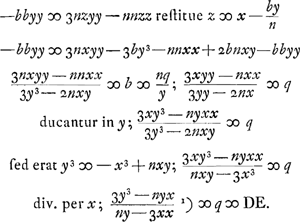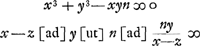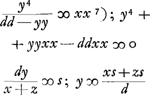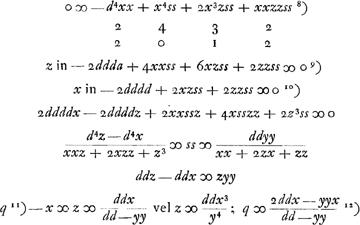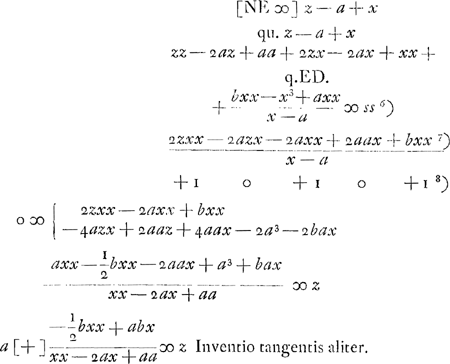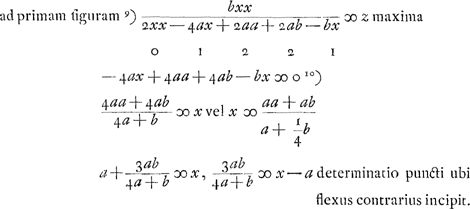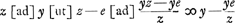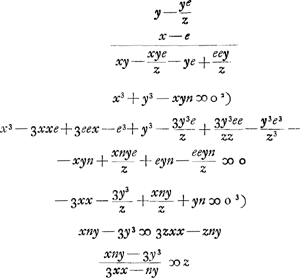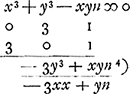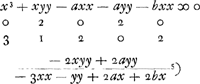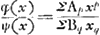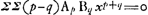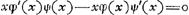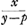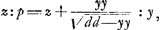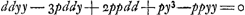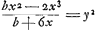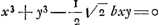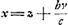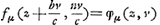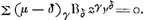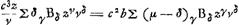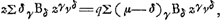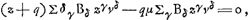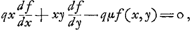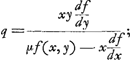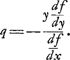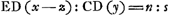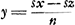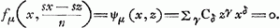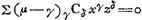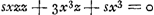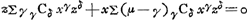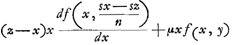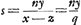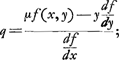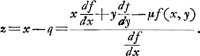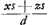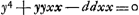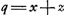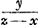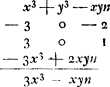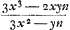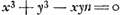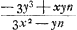|
-
voetnoot1)
- La Pièce est empruntée aux pp. 125-139 du Manuscrit B; nous l'avons divisée en paragraphes. D'après le lieu qu'elle occupe au Manuscrit B, elle doit dater de 1662. Consultez encore la note 8.
-
voetnoot2)
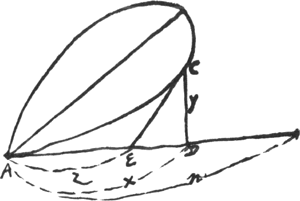
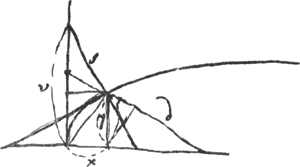
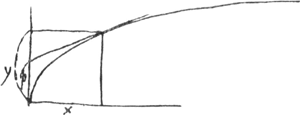
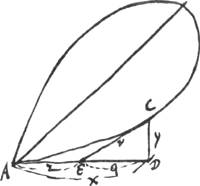
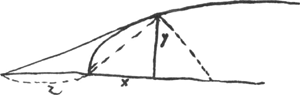
- Ce paragraphe contient la détermination de la tangente à la courbe de Gutschoven de deux manières différentes.
-
voetnoot3)
- Équation de la courbe de Gutschoven; comparez le deuxième alinéa de la Pièce No. VI. p. 501.
-
voetnoot4)
-
s représente donc la longueur d'un segment de la normale depuis le point sur la courbe jusqu'à l'intersection avec l'axe des y. Or, si l'on fixe ce point d'intersection, dont la distance à l'origine est désignée par v et qu'on déplace l'autre extrémité du segment le long de la courbe, il faut que la longueur du segment soit stationnaire (c'est-à-dire en général maximum ou minimum) lorsque le segment reprend sa position primitive. Il s'agit donc dès ici de trouver la valeur de y qui rend maximum ou minimum l'expression pour ss. À cet effet Huygens emploie la méthode de Hudde, exposée dans son ‘Epistola secvnda de Maximis et Minimis’ (voir la note 5 de la p. 360 du T. II), pour déterminer le maximum ou minimum d'une fraction rationnelle
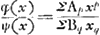 par la résolution de l'équation par la résolution de l'équation 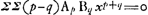 ; équation qu'on déduit facilement de la relation (en notation moderne) ; équation qu'on déduit facilement de la relation (en notation moderne) 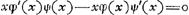 . .
-
voetnoot5)
- Cette première ligne contient les termes pour lesquels q = 0, celle qui suit ceux qui correspondent à q = 2; voir la note précédente.
-
voetnoot6)
- Au lieu de dd Huygens aurait pu choisir (voir la note 7 qui suit) le carré de toute autre ligne de longueur constante; il ne choisit d que parce qu'elle représente la seule ligne de cette nature qui entre dans l'équation de la courbe de Gutschoven.
-
voetnoot7)
-
s est donc proportionnel au quotient
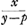 . Or, il est évident que lorsqu'on déplace, le long de la courbe, le point où elle est touchée par la tangente, sans changer la longueur p, ce quotient sera stationnaire et dans le cas présent un minimum. Par suite, on peut appliquer la méthode de Hudde à l'expression pour ss. Divisant en même temps par ddy4, Huygens obtient de cette manière l'équation qui suit, dont il écarte ensuite le facteur y-p. . Or, il est évident que lorsqu'on déplace, le long de la courbe, le point où elle est touchée par la tangente, sans changer la longueur p, ce quotient sera stationnaire et dans le cas présent un minimum. Par suite, on peut appliquer la méthode de Hudde à l'expression pour ss. Divisant en même temps par ddy4, Huygens obtient de cette manière l'équation qui suit, dont il écarte ensuite le facteur y-p.
-
voetnoot8)
- C'est probablement à propos des deux méthodes de ce paragraphe que Huygens écrivit à de Sluse dans la lettre du 25 septembre 1662, mentionnée dans la note 4 de la p. 502: ‘Nam illius quidem curvae Gutschovianae quam proponis tangentem nullo negotio investigavi varijs modis calculoque brevissimo, qui vix duos hujusmodi versiculos occupet’.
Ajoutons que, auparavant, Huygens avait essayé, p. 113 du Manuscrit B, une méthode analogue à la deuxième avec cette différence que pour la quantité qui doit être minimum il choisit la longueur du segment z situé sur l'axe des x entre l'origine des coordonnées et le point d'intersection avec la tangente. Employant au reste les notations de la Fig. 2 (différentes de celles de la page citée du Manuscrit), on a donc
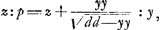
d'où Huygens déduit:
 À cette fraction il applique ensuite la méthode de Hudde; ce qui donne l'équation quadratique en p:
À cette fraction il applique ensuite la méthode de Hudde; ce qui donne l'équation quadratique en p:
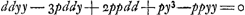 Après avoir obtenu cette équation Huygens ne continue pas le calcul. Il semble ne pas avoir aperçu que l'équation est divisible par y - p. Or, après l'écartement de ce facteur on arrive à la valeur de p indiquée dans le texte.
Après avoir obtenu cette équation Huygens ne continue pas le calcul. Il semble ne pas avoir aperçu que l'équation est divisible par y - p. Or, après l'écartement de ce facteur on arrive à la valeur de p indiquée dans le texte.
-
voetnoot1)
- Ce paragraphe contient la détermination de la tangente au folium de Descartes de trois manières différentes. En effet, l'équation
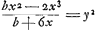 , qui suit, correspond à l'équation , qui suit, correspond à l'équation 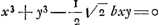 , pour laquelle les tangentes au point A sont les axes des coordonnées. Or, dans cette dernière équation on reconnaît celle du folium de Descartes. Ainsi dans sa lettre à de Sluse, déjà citée dans les notes 4 de la p. 502 et 8 de la p. 505 Huygens pouvait écrire à propos du folium: ‘Hujus tangentem in dato puncto ego quidem non nisi mediocriter prolixo calculo inveni (ex hac nempe aequatione, nam potest alioqui ad aliam multo commodiorem res deduci)’. Ajoutons que le ‘calcul prolixe’ était probablement celui du § 3, ou du § 4. , pour laquelle les tangentes au point A sont les axes des coordonnées. Or, dans cette dernière équation on reconnaît celle du folium de Descartes. Ainsi dans sa lettre à de Sluse, déjà citée dans les notes 4 de la p. 502 et 8 de la p. 505 Huygens pouvait écrire à propos du folium: ‘Hujus tangentem in dato puncto ego quidem non nisi mediocriter prolixo calculo inveni (ex hac nempe aequatione, nam potest alioqui ad aliam multo commodiorem res deduci)’. Ajoutons que le ‘calcul prolixe’ était probablement celui du § 3, ou du § 4.
-
voetnoot2)
- Cette première méthode est identique à la première du § 1, p. 504. Huygens va donc appliquer l'algorithme de Hudde (voir la note 4 de la p. 505) pour trouver le minimum ou maximum de ss. Dans ce calcul il n'a pas besoin de s'occuper du terme vv, puisque v est considéré comme une constante.
-
voetnoot3)
- Détermination du lieu de largeur maximum de la boucle. Comparez les p. 301 et 302 du Tome présent.
-
voetnoot4)
-
s est donc proportionnel à
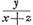 ; sa valeur doit donc être un maximum lorsqu'on déplace le point de contact le long de la courbe en fixant la valeur de z. ; sa valeur doit donc être un maximum lorsqu'on déplace le point de contact le long de la courbe en fixant la valeur de z.
-
voetnoot5)
- Application de l'algorithme de Hudde accompagné de la division de tous les termes par b2x2. La première ligne correspond au premier terme du dénominateur, l'autre au deuxième terme.
-
voetnoot1)
- Fraction qu'il s'agit de rendre maximum à l'aide de l'algorithme de Hudde.
-
voetnoot2)
- Cette ligne donne les coefficients p - q (voir la note 4 de la p. 505) par lesquels on doit multiplier tous les termes qui correspondent au premier terme du numérateur. D'ailleurs, puisque Huygens se propose de diviser tous les termes par bbxx on doit multiplier ceux du dénominateur par (p - q)b et non par (p - q)b3xx comme l'algorithme de Hudde l'exige.
-
voetnoot3)
- On doit pour la même raison nuiltiplier les termes correspondant à - 2bbx3 par - 2(p - q)x; c'est pourquoi Huygens change les signes des termes du dénominateur en même temps qu'il les multiplie par 2(p - q)x.
-
voetnoot4)
- Cette équation est obtenue après division de l'expression qui précède par 2(z - x).
-
voetnoot5)
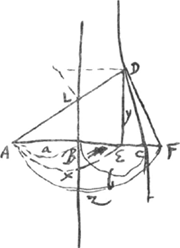
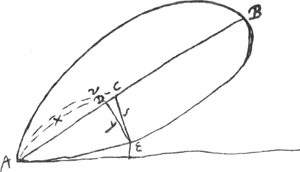
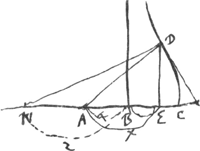
- Ce paragraphe et le suivant nous montrent qu'avant de trouver, dans le cas d'une courbe algébrique quelconque, la règle exposée dans la lettre à de Witt du 25 février 1663 (voir les p. 312-317 du T. IV), Huygens s'est occupé d'autres méthodes très curieuses pour déterminer les tangentes d'une telle courbe. Afin de faire connaître la portée de ces methodes, nous croyons utile de les appliquer au cas général d'une courbe algébrique fμ(x, y) = ΣαΑβ xαyβ = 0 du degré μ. Commençons donc par la méthode utilisée dans le présent paragraphe et remarquons d'abord que la forme du triangle ECD (Fig. 6) est définie par les rapports entre ses côtés, en posant v : c = y : n = q : b, où l'une des trois grandeurs c, n, b peut être choisie égale à une constante arbitraire, p.e. à la constante n de l'équation de la courbe. On a alors
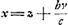 ; y = nv/c; où z = AE. ; y = nv/c; où z = AE.
Or, la substitution de ces expressions pour x et y dans l'équation de la courbe, donne:
| (1) |
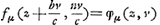 |
Si maintenant nous supposons un instant que les valeurs de z, c, n et b soient données et invariables, et que v soit l'inconnue de l'équation (1), les solutions de cette équation correspondront aux points d'intersection de la droite EC avec la courbe fμ (x, y) = 0; mais puisqu'il saut qu'au point C correspondent deux racines égales de l'équation en v, on aura:
Cela explique le premier algorithme, représenté dans le texte par les nombres 0, 1, 2, 3, 3, 1, 2, qui amènent l'équation 0 ∞ 3bzzvcc - nnzccv + etc.
Pour expliquer le deuxième algorithme, représenté par les nombres 3, 2, 1, 0, 0, 2, 1, il suffit de remarquer que des équations (1) et (2) on déduit facilement:
| (3) |
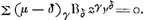 |
C'est cet algorithme qui conduit dans le texte à l'équation 0 ∞ 3z3 + 6bzzv/c + etc.
-
voetnoot6)
- Équation du folium de Descartes; comparez la p. 301.
-
voetnoot7)
- C'est l'équation qui correspond à l'équation (1) de la note 5.
-
voetnoot8)
- La signification de ce zéro nous échappe.
-
voetnoot9)
- C'est l'équation qui correspond à l'équation (2) de la note 5; mais elle a été multipliée par c3.
-
voetnoot10)
- C'est l'équation qui correspond à l'équation (3) de la note 5.
-
voetnoot1)
- Cette expression pour DE s'accorde avec la construction de la tangente indiquée par de Sluse dans sa lettre du 6 octobre 1662, p. 246 du T. IV.
-
voetnoot2)
- Dans ce paragraphe une méthode différente de celle du § 3 est appliquée, d'abord au folium de Descartes, ensuite à la courbe de Gutschoven. Ainsi que nous l'avons fait dans les notes 5 de la p. 508 et 11 de la p. 509 pour la méthode précédente, nous appliquerons cette nouvelle méthode à son tour au cas d'une courbe algébrique quelconque fμ (x, y) = ΣαAβxαyβ = 0.
Posant 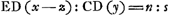 , on a ici , on a ici 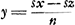 , et par suite: , et par suite:
| (1) |
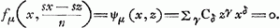 |
Si l'on ne change pas les valeurs de z, ni de s, de sorte que la forme du triangle CED et la situation du point E ne varient pas, il est clair qu'en changeant la valeur de x, on verra le point C se déplacer le long de la tangente et que les racines de l'équation ΣγCδxγzδ = 0 correspondront aux points d'intersection de cette tangente avec la courbe. Or, puisque le point de contact de la tangente doit correspondre à une racine double, on aura:
Cela explique le deuxième algorithme (p. 512), qui conduit à l'équation qui, plus bas, est multipliée par z. De même l'équation:
| (3) |
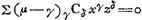 |
explique le premier algorithme.
De cette façon l'équation 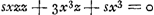 du texte est remplacée dans le cas général par: du texte est remplacée dans le cas général par:
| (4) |
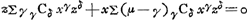 |
ou bien:
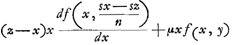 d'où résulte, puisque
d'où résulte, puisque 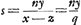 : :
| (5) |
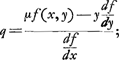
|
relation qui est équivalente à la relation connue:
| (6) |
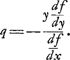
|
La deuxième méthode de Huygens conduit donc, elle aussi, à une expression pour la sous-tangente équivalente à l'expression (6), mais de forme différente.
-
voetnoot1)
- La grandeur de s détermine donc la forme du triangle ECD, puisque n est une constante donnée.
-
voetnoot2)
- Cette équation correspond donc à l'équation (3) de la note 2 de la page précédente.
-
voetnoot3)
- Équation qui correspond à l'équation (2) de la note mentionnée.
-
voetnoot4)
- Équation qui correspond à l'équation (4) de la note mentionnée.
-
voetnoot5)
- Plus généralement, on trouve:
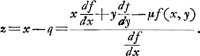
Or, le terme 0Aμ yμ de l'équation de la courbe n'entre pas dans le dénominateur et il disparaît dans le numérateur après réduction.
-
voetnoot7)
- Équation de la courbe de Gutschoven; comparez le deuxième alinéa de la Pièce No. VI, p. 501. Voir, pour l'exposition générale de la méthode suivie, la note 2 de la p. 511. La quantité constante n est remplacée ici par d.
-
voetnoot8)
- Huygens substitue
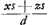 pour y dans l'équation pour y dans l'équation 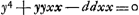 , mais il omet le terme y4, puisqu'il sait que ce terme n'a pas d'influence sur l'expression qu'il trouvera pour z; comparez la note 5. , mais il omet le terme y4, puisqu'il sait que ce terme n'a pas d'influence sur l'expression qu'il trouvera pour z; comparez la note 5.
-
voetnoot9)
- Comparez la note 3; mais Huygens omet partout, ici et dans l'équation qui suit, deux facteurs x.
-
voetnoot12)
- Nous supprimons l'application de la même méthode à la détermination de la tangente à la parabole ‘2ny - yy - xx - 2xy ∞ 0’, qu'on trouve à la même page, parce que cette application ne présente rien de particulier. On rencontre la même courbe dans la lettre de de Sluse du 6 octobre 1662, p. 247 du T. IV. La construction de la tangente indiquée par lui correspond à la solution de Huygens.
-
voetnoot1)
- Détermination de la tangente à la conchoïde de de Sluse de deux manières différentes et détermination du point d'inflexion de cette courbe.
-
voetnoot2)
- Comparez la lettre de de Sluse du 6 octobre 1662 (p. 247 du T. IV) où il donne la définition de sa conchoïde, dont il dit avoir trouvé la construction de la tangente et du point d'inflexion.
-
voetnoot4)
- Huygens applique la dernière des trois méthodes employées dans le § 2. Puisque s est proportionnelle à
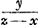 , il faut que sa grandeur soit maximum ou minimum lorsque DF est tangente à la courbe et lorsque z est considérée comme une constante tandis que le point D est déplacé le long de la courbe. , il faut que sa grandeur soit maximum ou minimum lorsque DF est tangente à la courbe et lorsque z est considérée comme une constante tandis que le point D est déplacé le long de la courbe.
-
voetnoot5)
- Application de l'algorithme de Hudde pour déterminer la valeur maximum ou minimum d'une fraction (voir la note 4 de la p. 505), accompagnée de la division de chaque terme par b2x2. Chaque ligne correspond à l'un des termes du numérateur.
-
voetnoot6)
- Huygens se sert ici de la première méthode du § 1; consultez la note 4 de la p 505.
-
voetnoot7)
- Il s'agit de déterminer le maximum ou minimum de ss; mais puisque a est une quantité constante et que z doit être considérée comme telle, les trois premiers termes de l'expression précédente n'importent pas et peuvent être négligés dans la formation de la fraction à laquelle Huygens va appliquer l'algorithme de Hudde.
-
voetnoot8)
- Ces coefficients ont servi pour former la première ligne (dépendant du premier terme x du numérateur) de l'équation qui se construit suivant l'algorithme de Hudde en divisant toutefois tous les termes par x.
-
voetnoot10)
- Application de l'algorithme de Hudde avec division des termes par bxx.
-
voetnoot1)
- Ce paragraphe nous fait connaître les calculs qui ont servi à déduire l'algorithme simple pour déterminer la sous-tangente d'une courbe algébrique donnée, que Huygens expose dans sa lettre à de Witt du 25 février 1663 (p. 312-317 du T. IV) et qui fut publié en 1693 dans les ‘Divers ouvrages de Mathématique et de Physique. Par Messieurs de l'Académie Royale des Sciences’ (voir la p. 331 de l'ouvrage cité dans la note 1 de la p. 91 de notre T. IX). Probablement cette découverte fut mandée à de Sluse dans une lettre du 10 décembre 1662, que nous ne connaissons pas (voir la seconde note 1 de la p. 291 du T. IV), puisqu'on lit dans la réponse de de Sluse, du 12 janvier 1663 (voir la p. 292 du T. IV): ‘Gaudeo Te ac Clarissimum Huddenium in tangentium methodum meae non absimilem incidisse: an vero eadem sit necue, hoc τεϰμηϱίῳ colliges’.
-
voetnoot3)
- Il s'agit du coefficient de e dans l'équation qui précède.
-
voetnoot4)
- L'algorithme employé ici pour la détermination de la sous-tangente ne diffère de celui exposé dans la lettre à de Witt, citée dans la note 1, que par le signe attaché à chaque terme du numérateur et du dénominateur.
Ajoutons qu'à la même page du manuscrit on trouve encore d'autres petits calculs dans lesquels on reconnaîtra facilement l'algorithme inventé par Hudde tel qu'il est exposé dans la note 6 de la p. 446 de notre Avertissement.
En voici le premier:
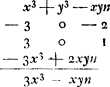
Or, la règle de Hudde exige qu'on multiplie la fraction obtenue par - x, de sorte qu'elle donne pour la sous-tangente l'expression 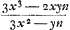 , qui se réduit, si l'on applique la relation , qui se réduit, si l'on applique la relation 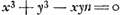 , à , à 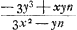 ; expression que ne diffère de celle trouvée par Huygens que par le signe qui dépend de la convention qu'on a adoptée. ; expression que ne diffère de celle trouvée par Huygens que par le signe qui dépend de la convention qu'on a adoptée.
Les autres petits calculs présentent les coefficients:

conformes à l'algorithme de Hudde avec cette différence que, dans l'une des deux lignes, les signes des coefficients sont renversés; ce qui change le signe de l'expression pour la sous-tangente.
-
voetnoot5)
- Application de l'algorithme à la conchoïde de de Sluse; comparez le § 5 qui précède.
|