|
-
voetnoot1)
- À cause du lieu occupé par la Pièce, p. 112 du Manuscrit B.
-
voetnoot2)
- La proportion s'ensuit de la similitude des triangles isocèles ABC et AED; on a
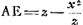 , puisque EC = x2/z à cause des triangles semblables BEC et ABC. , puisque EC = x2/z à cause des triangles semblables BEC et ABC.
-
voetnoot3)
- La construction de l'heptagone régulier est donc réduite à la solution d'une équation cubique, dont il faut choisir la racine positive plus grande que l'unité. Pour indiquer la signification des autres racines, soit d la longueur de la diagonale qui sous-tend p côtés de l'heptagone (de sorte qu'on a d4 = d3, d5 = d2, etc.); alors les trois racines de l'équation sont égales à d3/d1, à d1/d2 et à - d2/d3.
Ajoutons que quelques années auparavant van Schooten s'était occupé, non sans succès, de la détermination des équations algébriques dont dépend la construction des polygones réguliers. Il appliqua à cette détermination plusieurs méthodes qui, toutefois, pour l'heptagone et pour les cas plus compliqués, amènent des équations d'un trop haut degré, qu'il réussit à simplifier en écartant les facteurs inutiles. Aiusi dans le cas de l'heptagone il trouve, comme de juste, 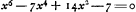 et dans celui du tétradécagone et dans celui du tétradécagone 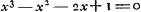 , où x représente chaque fois le rapport du côté au rayon du cercle circonscrit (voir les p. 464-475 de l'ouvrage de 1657 de van Schooten dont nous avons reproduit le titre général et celui du ‘Liber V’ aux pp. 50 et 52 du Tome présent, ou bien les p. 433-443 de l'édition hollandaise sur laquelle on peut consulter les pp. 51 et 53 du même Tome). , où x représente chaque fois le rapport du côté au rayon du cercle circonscrit (voir les p. 464-475 de l'ouvrage de 1657 de van Schooten dont nous avons reproduit le titre général et celui du ‘Liber V’ aux pp. 50 et 52 du Tome présent, ou bien les p. 433-443 de l'édition hollandaise sur laquelle on peut consulter les pp. 51 et 53 du même Tome).
D'ailleurs, puisque l'angle BAC de la Fig. 1 est égal à l'angle central que sous-tend le côté du tétradécagone, il est clair que le rapport AB : BC, cherché par Huygens, est le réciproque du rapport du côté du tétradécagone au rayon du cercle circonscrit.
On sait que ce fut Gauss qui, le premier, apprit à indiquer d'avance le degré des équations dont dépend la construction d'un polygone régulier d'un nombre donné de côtés; voir la ‘Sectio septima: De aequationibus circuli sectiones definientibus’ de ses ‘Disquisitiones arithmeticae’ de 1801 (p. 412-474 du T. I, 1863, de ses oeuvres complètes: ‘Carl Friedrich Gauss Werke. Herausgegeben von der Königlichen Gesellschaft der Wissenschaften zu Göttingen’).
-
voetnoot4)
- Réduction de l'équation à une équation sans second terme.
-
voetnoot5)
- Après avoir trouvé l'équation réduite, Huygens applique dans la Fig. 2 les règles données par Descartes dans sa ‘Géométrie’ (voir les p. 470-473 du T. VI de l'édition d'Adam et Tannery) pour la construction des racines d'une équation cubique par les intersections d'une parabole et d'un cercle passant par son sommet.
-
voetnoot1)
- Nous n'avons pas voulu supprimer les petits calculs qui suivent. Huygens y cherche à réduire la résolution de l'équation cubique, trouvée plus haut, à la détermination des intersections d'autres courbes, qu'on obtient en supposant connues dans les équations qui suivent, x, y ou z. Ajoutons encore que la construction au bas de la Fig. 1 nous est incompréhensible.
|