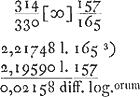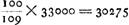|
-
voetnoot1)
- L'Appendice fut écrit, en 1673, sur une partie, restée primitivement vide, de la p. 101 du Manuscrit B, laquelle page suit immédiatement celles dont nous avons emprunté la Pièce No. IV. Il contient l'application de la théorie de Huygens, exposée dans cette Pièce, à une expérience de Cassini qui avait trouvé qu'à une altitude de 1070 pieds le baromètre avait baissé de 16 lignes. Posant 27 1/2 pouce = 330 lignes pour la hauteur du baromètre au niveau de la mer, on en déduit que la densité de l'air avait diminué dans la raison de 330 à 314.
Ajoutons qu'on trouve à la p. 38 du Manuscrit F des renseignements sur l'expérience de Cassini. D'après la date où ce Manuscrit fut mis en usage, il est presque certain que ces renseignements plus précis ne furent reçus par Huygens que vers 1680:
de M. Cassini, Nostredame de la garde montagne a Toulon a de hauteur 1070 pieds. au haut le mercure du barometre avait 27 pouces 1/3 de ligne. au bas 28 po. 4 2/3 de ligne. la difference est donc 1 p. 4 2/3 de ligne. la pente de la montagne 41 degr. l'horizon sous le niveau 32′30″.
-
voetnoot2)
- Dans cette première partie Huygens commence par calculer, en appliquant sa théorie, la hauteur fictive de l'atmosphère si la densité était partout égale à celle au niveau de la mer, telle qu'elle résulte de l'expérience de Cassini; ensuite il en déduit quel rapport de la densité de l'air à celle de l'eau correspondrait à cette hauteur.
-
voetnoot3)
- Comparez, pour le calcul qui suit l'algorithme de la p. 486.
-
voetnoot1)
- Voir le calcul à côté. D'après l'algorithme mentionné dans la note précédente on doit soustraire du ‘log spatij’ la différence entre les logarithmes de 100000 et du nombre qui indique la hauteur de l'atmosphère fictive d'égale densité, afin de trouver le logarithme de l'altitude du lieu en question. Or, pour faire concorder l'expérience de Cassini et la théorie de Huygens, il faut que le résultat soit égal au logarithme de 1070. Ce résultat peut donc servir maintenant à calculer la hauteur de l'atmosphère fictive exprimée en pieds de Paris.
-
voetnoot3)
- Comme l'on voit ce nombre diffère beaucoup de celui:
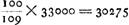 qui résulte des suppositions faites dans la partie de l'Appendice I qu'on trouve aux p. 492-494.
-
voetnoot4)
- Comparez le ‘num. perp. ad mensuram Paris.’ de la p. 492.
-
voetnoot5)
- Partant de la hauteur de la colonne barométrique au niveau de la mer, Huygens calcule ici la hauteur, en pouces de Paris, d'une colonne d'eau de pesanteur égale. Nous ne savons pas d'ailleurs pourquoi Huygens a remplacé les 27½ pouces, mentionnés plus haut, par 27,35 pouces.
-
voetnoot6)
- Le nombre 3 1/2 indique évidemment le nombre des lignes, supposées égales chacune à la dixième partie d'un pouce; comparez la note 5 de la p. 492.
-
voetnoot7)
- Hauteur de l'atmosphère fictive en pouces de Paris.
-
voetnoot8)
- Ce rapport est trouvé en divisant 258780 par 427. Consultez sur sa véritable valeur la note 1 de la p. 494. En effet la théorie de Huygens devait amener une densité trop grande de l'air.
-
voetnoot9)
- Dans cette Partie Huygens calcule, d'après les données obtenues dans la Partie précédente, l'abaissement du baromètre à une altitude de 28 toises. Peut-être se proposait-t-il de faire vérifier ce résultat expérimentalement.
-
voetnoot10)
- Comparez cet algorithme à celui au bas de la p. 487.
-
voetnoot11)
- En pouces: 27 1/2; hauteur supposée du baromètre au niveau de la mer.
|
Auteursrecht onbekend
