Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666

[p. 483]

IV.
1662.

17 Jul. 1662.

De altitudine Atmosphaerae¹⁾.

In Toricelliano experimento altitudo Hydrargyri in tubo, cum bene ab aere purgatus est, inventa est a Boilio 2 ped. 6 poll. Londinensium sive unciarum 30²⁾. Quae nempe hydrargyri altitudo aequiponderat cylindro aeris usque ad extremam atmosphaeram, cujus eadem sit crassitudo quae tubi diametri. Proportio autem gravitatis Hydrargyri ad aquam est quae 13 4/7³⁾ ad 1 proximè unde cylindrus aqueus dictis 30 uncijs hydrargyri sive cylindro aereo aequiponderans erit altus circiter 34 pedibus. Proportio rursus gravitatis aeris ad aquam a me inventa est circiter quae 1 ad 960⁴⁾ Aeris videlicet ita ut hîc compressus est. Itaque altitudo 32640 pedum aeris ita compressi aequiponderaret aquae pedibus 34, vel uncijs 30 argenti vivi, quanta nempe altitudo fit ductis 960 in 34. Sumamus autem rotundum numerum 33000 pedum.

1) Quoique cette Pièce n'appartienne pas aux mathématiques pures, nous n'avons pas voulu la séparer de celle qui précède et dont elle constitue une application. Elle la suit immédiatement aux p. 96-100 du Manuscrit B et y est datée du lendemain du jour où l'autre Pièce fut composée.
Une version plus récente assez différente se trouve aux p. 27-33 du Manuscrit N^o. 13; nous la reproduisons dans l'Appendice I, p. 491-494, pour autant qu'elle diffère notablement de la version du texte présent.

2) On rencontre cette donnée dans l'‘Experimentum XXXVI’ des ‘Nova experimenta physico-mechanica’; ouvrage de 1660, cité dans la note 4 de la p. 295 de notre T. III. Dans l'‘Experimentum XVII’ Boyle avait trouvé ‘triginta digitos & supra octavam digiti partem’.

3) Boyle dans l'‘Experimentum XXXVI’ avait trouvé 13 19/28.

4) Comparez la lettre au frère Louis du 22 février 1662, p. 64 du T. IV. On trouve les expériences, du 20 février 1662, qui ont amené cette donnée, à la p. 57 du Manuscrit B. Nous les publierons dans un autre Tome.

[p. 484]

Porro compertum est Boilianis experimentis, spatia ab eadem quantitate aeris occupata contrariam rationem servare ponderum quibus premitur¹⁾. Ita si aeris particulam tubo vitreo inclusam 60 unciae hydrargyri premant, is aer duplo minus spatium occupabit quam si tantum 30 uncijs hydrargyri prematur. Ubi tamen semper aeris quoque gravitas in censum venire debet, ut nempe aer tubo inclusus, cum nullus hydrargyrus adfusus est, tamen quasi a 30 uncijs hydrargiri premi intelligatur, quia tantum est pondus aeris superstantis. At cum 30 unciae hydrargiri injectae sunt, quasi a 60 uncijs premi credendus. Uncias pedis Lond.^is non vero gravitatis intelligimus. Hisce igitur positis omnia quae ad Atmosphaerae altitudinem, diversamque aeris in qualibet ejus regione densitatem pertinent, explicari possunt.

Ponamus cylindrum quendam aeris ab ima terra ad supremam atmosphaeram divisum esse sectionibus horizon.^bus in partes minimas quarum unaquaeque aequalem aeris quantitatem et pondus contineat, quas partes extensione admodum inaequales fore perspicuum est, cum quanto quaeque altior est tanto minus aeris pondus sustineat ideoque amplius se extendat. Quantitates autem aeris aequales istis partibus comprehensae designentur per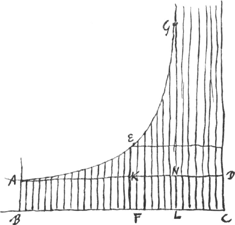

[Fig. 1.]

particulas aequales in quas sectum est rectangulum ABCD. Quarum quae proxima est AB, referat particulam aeris infimam, et sequentium quaeque sequentes ordine eodem particulas aeris. Quod si igitur recta AB referat altitudinem ad quam sese extendit particula aeris infima, facile jam et reliquarum extensio reperietur. Consideremus enim quamlibet earum ut FK; quae cum sustineat tantùmmodo reliquarum pondus quae efficiunt rectangulum KFCD, tanto proinde latius se expandet quam particula infima ad AB, quanto graviores sunt quae toto

1) Huygens reçut le premier avis de cette découverte de Boyle par l'intermédiaire de Moray dans une lettre du 13 mars 1662: voir les p. 84-85 du T. IV. Après avoir pris connaissance ensuite de la ‘Defensio Doctrinae de Elatere et Gravitate Aeris’ (ouvrage cité dans la note 2 de la p. 171 du T. IV), où Boyle communique les expériences qui l'on conduit à sa loi, Huygens fut pleinement convaincu de l'exactitude de cette loi puisqu'il écrivit à Moray le 14 juillet 1662 (voir la p. 171 du T. IV): ‘J'ay estè sur tout bien aise d'y trouver les deux experiences touchant la condensation et rarefaction de l'air, qui prouvent assez clairement cette proprietè remarquable a sçavoir que la force de son ressort suit la proportion contraire des espaces ou il est reduit’.

[p. 485]

rectangulo ABCD continentur ijs quae efficiunt rectangulum KFCD. Hoc est sicut BC ad CF ita erit EF altitudo extensionis particulae KF ad AB altitudinem extensionis particulae infimae. Ergo rectangulum AB, BC, aequale erit rectangulo EF, FC, ideoque punctum E ad hyperbolen, quae per punctum A describitur ad asymptotos BC, CD. Singularum itaque prout ordine exhibentur in rectangulo ABCD, extensiones determinat hyperbola AEG, utque EF est extensio particulae KF, ita GL est extensio particulae NL atque ita de caeteris.

Extensiones autem omnium simul quae rectangulo ABFK continentur, efficient spatium AEFB, et omnium quae rectangulo ABLN extensiones efficient spatium AEGLB. atque ita quanto majus est ex. gr. spatium AEGLB rectangulo ABLN tanto major erit altitudo extensarum partium hujus rectanguli quam si omnes aeque atque infima ad AB compressae jacerent. Et quae proportio spacij AEGLB ad rectangulum totum ABCD, eadem erit altitudinis partium extensarum rectanguli ABLN ad altitudinem omnium rectanguli ABCD, ita ut infima est, compressarum; hoc est ad altitudinem 33000 pedum.

Hic itaque primo animad vertendum est, cum spatium quale AEGLB possit majus majusque sumi in infinitum (nam spatium inter hyperbolen et asymptotos est infinitae magnitudinis) sequi infinitam esse aeris sive atmosphaerae altitudinem. utique si in quantalibet aeris extensione sibi constare sumamus Boilianum experimentum. Sed si ex corporeis partibus aer constat sese mutuo tangentibus, nam contactum hunc arguere videtur vis illa aeris elastica, non potest fieri ut in infinitum cylindrus aliquis aereus extendatur, cum definitum pondus habeat et quantitatem. Credibilius itaque est post ingentem aeris expansionem non amplius proportionem illam servari quam ostendit Experimentum Boilij. Verum, quia quousque se extendit experientia, successus semper egregiè respondisse inventus est haud aberraturos puto si eodem principio imposterum utamur ad illa quae sequuntur supputanda. namque etsi forte pars centiesmillesima quantitatis aeris, quae in suprema regione sita est, non secundum istam rationem extenditur, id nihil impedit quo minus in reliquo omni aere exacte satis observetur. Praedicta igitur hypothesi, veluti si per omnia certum sit Boilij experimentum, innixi, sequentia Problemata solvemus. Veluti si scire velim⁺ ad quantam altitudinem ascendendum sit ut tantum pars decima aeris, hoc est secundum quantitatem aut pondus, supra caput extet. quo nempe loco hydrargyrus in tubo Toricelliano tantum 3 pollices altus restabit.

Ac rursus si inquirendum sit, datâ loci altitudine supra terrae superficiem, quanta aeris portio, seu gravitas supra atque infra resideat, et ad quantam proinde altitudinem hydrargyrus in tubo suspensus manebit²⁾. Itaque primò sit inveniendum,

+ Problema 1.

2) Après avoir mentionné à son frère Lodewijk, dans une lettre du 17 août 1662, sa solution de ce dernier problème, Huygens communiqua le lendemain à Moray les règles pour la solution des deux problèmes; voir les pp. 198, 202 et 205-206 du T. IV.

[p. 486]

Data aeris portione seu gravitate a loco aliquo sursum, invenire quanta sit loci ejus altitudo.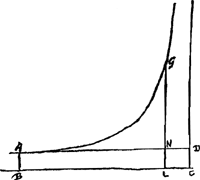

[Fig. 2.]

Sit sursum pars decima aeris. Ergo ponatur LC [Fig. 2] ∞ 1/10 BC. Hinc ducta LG parallela asymptoto CD, fiet et LN seu AB ∞ ∞ 1/10 LG¹⁾. Jam itaque data ratione GL ad AB inveniatur magnitudo spatij ABLG in partibus primò qualium quadr.^m hyperbolae seu rectangulum ABCD 100000. idque per Regulam superius descriptam²⁾.

³⁾

Sed quia patet ad logar. 5,00000 addendum fuisse num. perpetuum 36222, et rursus à summa 5,36222 auferendum 0,48149 qui et ipse hic semper est idem, poterit brevitatis gratia in hac regula esse numerus perpetuuso, 11927, quae scilicet est differentia duorum 0,48149 et 0,36222. adeo ut hoc modo tantum operatio instituatur.

1) Puisqu'on a AB : LG = LC : BC; comparez le premier alinéa de la p. 485.

2) On trouve cette règle à la p. 476. Remarquons toutefois qu'elle fait connaître le rapport de l'aire cherchée (ici celle de l'espace ABLG) au rectangle (AC) sur l'abscisse et l'ordonnée d'un point quelconque de l'hyperbole. On a donc dans le cas présent: log spat. ABLG = log (log 10 - log 1) + log 100000 + num. perp. Consultez la note 2 de la p. 476.

3) C'est-à-dire après avoir ajouté log ABCD = log 100000 = 5; voir la note 1 de la p. 476.

[p. 487]

³⁾

3) C'est-à-dire après avoir ajouté log ABCD = log 100000 = 5; voir la note 1 de la p. 476.

Exempl. 2.

Sit sursum pars aeris quae se habeat ad totius altitudinis pondus ut 36789 ad 100000. Ea pars putetur NLCD. Cum sit ergo BC ad CL ut 100000 ad 36789, eadem erit et proportio GL ad AB.

³⁾

Quando igitur in ea sumus altitudine, ubi finiret atmosphaera si aer ubique compressus esset ut ille in quo hic vivimus; tunc adhuc paulo plus tertia parte aeris supra caput habemus. Sed quae tertia pars ad immensam porro altitudinem extendi queat. Hydrargyrus in tubo hic 11 pollices occupabit; quia ut 100000 ad 36789 ita 30 poll. ad 11.

Data loci altitudine supra terrae aequabilem superficiem, invenire quanta ibi gravitas seu portio aeris desuper incumbat, et ad quantam proinde altitudinem hydrargyrus in tubo Toricelliano consistet.

Sit altitudo data pedum 1,00000. Regula itaque est contraria praecedentis.

⁴⁾

3) C'est-à-dire après avoir ajouté log ABCD = log 100000 = 5; voir la note 1 de la p. 476.

4) C'est-à-dire le nombre qui correspond au logarithme qu'on obtient en retranchant du nombre précédent log ABCD = 5.

[p. 488]

Proportio igitur aeris totius ad portionem desuper incumbentem est quae 100000 ad 4831 hoc est fere 21 ad 1.

100000 [ad] 4831 [ut] 30 pollices [ad] 1 45/100 altitudo pollicum hydrargyri in tubo.

Sit data altitudo pedum 33000.

aer ergo totus ad aerem superextantem ut 100000 ad 36789.

Sit data alt.^o pedum 380010.

Hic ergo aer totus ad superextantem ut 100000 ad 1.

Sit data alt. pedum 100,00000.

[p. 489]

Hic aer totus ad superextantem ut 100000 ad 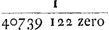dixi 122 zero, nam quia characteristica logar.ⁱ est 126 debet eius numerus constare characteribus 127 quorum 5 primi sunt 40739. Praestaret autem in tantis altitudinibus uti logarithmis 10 characterum.

Sciendum est inventa altitudine loci ubi 1/10 aeris adhuc supra est, velut in primo exemplo Problematis prioris¹⁾, facile etiam inveniri altitudines ubi superextet 1/100 vel 1/1000 vel 1/10000 atque ita porro. Altitudo enim pedum 75986 illic inventa, bis sumpta conveniet proportioni 1/100 sive 100 ad 1, ter sumpto vero conveniet proportioni 1/1000 atque ita porro. Atque hoc in quavis proportionali progressione locum habet²⁾.

Sit data pars aeris sursum dimidia totius.

1) Voir les p. 486 et 487.

2) C'est là, en effet, une conséquence immédiate de la règle, puisque, p.e. dans le cas où le rapport est 1/1000, on doit remplacer dans le calcul du premier exemple (p. 487) le premier et le troisième des six nombres par 3,00000 et le quatrième par 5 + log 3 (voir la note 3 de la p. 486), de sorte que le sixième nombre est augmenté de log 3 et que, par conséquent, la hauteur résultante est triplée.

[p. 490]

Sit data alt.^o pedum 100.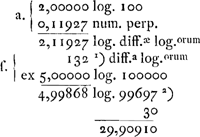

¹⁾²⁾

Ergo in turri pedum 100 altitudinis, descendet hydrargyrus in tubo Torricelij 1/10 unc. pedis Londinensis.

1) 0,00132 est le nombre qui correspond au logarithme: 2,11927-5; comparez la note 4 de la p. 487.

2) La quantité d'air qui se trouve au-dessus de la tour est donc à la quantité totale comme 99697 à 100000, et la hauteur de la colonne de mercure du baromètre, qui est censé être de 30 pouces au pied de la tour, devient donc au sommet: 99697/100000 × 30 pouces.