Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666

[p. 460]

II.¹⁾
1661.

10 Sept. 1661.

[Fig. 1.]

1) La Pièce est empruntée aux p. 175-183 du Manuscrit B. Avec l'Appendice qui l'accompagne, elle a été publiée par Uylenbroek dans ses ‘Christiani Hugenii aliorumque seculi XVII virorum celebrium exercitationes mathematicae et philosophicae’, ouvrage cité dans la note 2, p. 500 du T. VII. Elle y occupe les p. 172-183 du ‘Fasciculus II.’
La Pièce traite des propriétés de la courbe appelée plus tard par Huygens ‘Logarithmique’ ou ‘Logistique’; voir la p. 169 de l'édition originale de 1690 du ‘Discours de la pesanteur’, qui accompagne le ‘Traité de la lumiere’. Les résultats obtenus furent publiés sans démonstrations aux p. 176-178 du même ‘Discours’.

[p. 461]

In recta AE sunt partes aequales sumtae AB, BC, CD &c. et erectae perpendiculares AK, BF, CG, DH, EI &c. quarum unaquaeque est praecedentis dupla. transit autem curva KGIL per extrema dictarum perpendicularium, quae eadem per extrema etiam transit perpendicularium LM, NO &c. quae e punctis bisectionum partium AB, BC &c. erectae sunt, ac mediae proportionales inter binas utrimque proximas. crescunt autem et hae secundum duplam proportionem. ac rursus per extrema aliarum perpendicularium quae bisecant partes ultimo effectas in recta AE, suntque item proximarum suarum mediae proportionales et in dupla proportione crescentes; atque ita in infinitum per omnes enim ejusmodi perpendicularium extremitates linea curva versus AE convexa transit²⁾. Et patet quotlibet puncta per quae describenda sit in linea facile invenire. Habet autem proprietates insignes. Primo ad inveniendas quotcunque medias proportionales inter duas datas. Sint ex. gr. PR, QR. Statuantur ad curvam perpendiculares ijs aequales ST, VX, et intervallum TX quo inter se distant dividatur in partes aequales unâ plures quam quot medias quaerimus. Veluti si duas, oportet dividi in tres partes, ut hic punctis ΔZ, e quibus eductae ad lineam perpendiculares ΔΓ, ZY erunt mediae duae quaesitae inter ST, VX sive LR³⁾, QR. Quod facile demonstratur quia inter XV, TS cadit series infinita proportionalium ex natura lineae, earumque totidem inter XV, ZY quot inter ZY, ΔΓ, ac inter ΔΓ, TS; totidem inquam, quia partes XZ, ZΔ, ΔT sunt aequales, innumeraeque illae proportionales aequalibus intervallis a se mutuo distant.

TA, XA considerandae sunt ut logarithmi linearum TS, XV⁴⁾, et intervallum TX ut differentia logarithmorum. Ubicunque binae perpendiculares intervallo eodem dissitae erunt, habebunt eandem inter se rationem. Sic sicubi duae distiterint intervallo aequali AB earum major minoris dupla erit, quia nempe BF est dupla AK.

2) Prenant AR pour l'axe des x et AΞ pour celle des y, on a donc pour l'équation de la courbe , ou, si l'on veut, y = ka^x, où k = AK, .

3) Lisez: PR.

4) Posant AK = 1, et prenant pour base du système des logarithmes le nombre b = 2^AK/AB, on a, en effet, log TS = AT; mais la conception de Huygens est un peu différente. D'après les calculs qui suivent il considère les abscisses AT non pas comme égales mais seulement comme proportionnelles aux logarithmes des ordonnées TS. Soit donc log TS = m.AT. Or, puisque l'addition de AB aux abscisses double les ordonnées on aura nécessairement log 2 = m.AB et, par suite, AT = log TS/log 2. AB, ou bien, si l'on suppose AB égal à 10ⁿ log 2, AT = 10ⁿ log TS.

[p. 462]

Recta RA est curvae asymptotos.

Spatia duo quaevis a binis perpendicularibus intercepta quae aequalibus intervallis distant ut sunt spatia TSΓΔ, YZXV, eam inter se rationem habent quam major unius perpend.^is ad majorem perpend.^em alterius vel quam minor ad minorem facillime demonstratur.

Spatium quodvis a binis perp.^bus interceptum est ad spatium deinceps decrescens in infinitum ut differentia perpendicularium ad perpend.^m minorem. Sic spatium STΔΓ est ad spatium infinitum ΓHKΩΔ ut SΘ ad ΓΔ. Si enim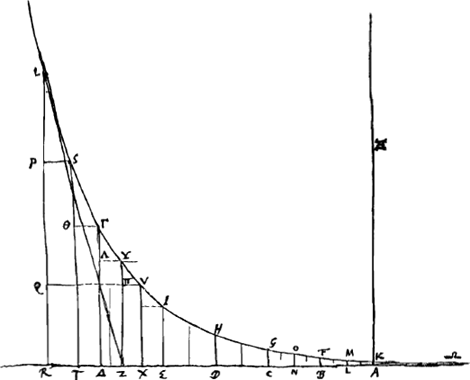

[Fig. 1.]

aequalibus intervallis ipsi TΔ constituantur perpendiculares YZ, VX, IE &c. in infinitum. Quia spatium STΔΓ ad spatium ΓZ ut ST ad ΓΔ per praeced.^m hoc est ut SΘ ad ΓΛ quia tres ST, ΓΔ, YZ sunt prop.^es; Et rursus spatium ΓZ ad YX sicut ΓΛ ad YΠ, Ideoque spatium SΔ ad YX sicut SΘ ad YΠ; atque ita porro, Erit proinde spatium SΔ ad omnia spatia ΓZ, YX, &c. in infinitum ut SΘ ad omnes ΓΛ, YΠ &c. quae simul efficiunt ipsam ΓΔ. Ergo &c.

Spatia quaevis duo a duabus perpend.^bus intercepta ut CE [Fig. 2], GN sunt inter se sicut perpendicularium differentiae, hoc est hic ut CH ad GL, ducatur enim et GK parall. AB.

Quia ergo per praeced. spatium CE est ad spatium infinitum DEA ut CH

[p. 463]

[Fig. 2.]

ad HB. Spatiumque similiter DF ad spatium infinitum GFA ut DK ad KE, Et invertendo et componendo spatium infinitum GFA una cum spatio DF, hoc est spatium infinitum DEA ad spatium DF ut DE sive HB ad DK, Erit ex aequo spatium CE ad spatium DF ut CH ad DK. Eodem modo autem ostenditur spatium DF ad spat. GN ut DK ad GL. Ergo ex aequo erit spatium CE ad spatium GN ut CH ad GL. quod erat ost.

Si curvam linea recta contingat et a puncto contactus in asymptoton perpendicularis ducatur; erit pars asymptoti inter perpendicularem et tangentem intercepta, eidem semper lineae rectae aequalis.

[Fig. 3.]

Sint hic [Fig. 3] tangentes AE, BF, et a punctis A, B perpendiculares in asymptoton, AC, BD. dico partes CE, DF esse aequales. Vel potius sic; sit AE tangens, sitque ipsi CE aequalis DF; dico et FB tangentem esse in B.

Sumatur enim in recta BF quodlibet punctum praeter B, ut O, per quod ducatur perpendicularis POQ, et, sumta ipsi DQ aequali CS in eandem partem, erigatur perpendicularis SHG, secans tangentem AE in H, curvam vero in G. Erit itaque GS major quam HS¹⁾. Est autem ut AC ad HS hoc est ut CE ad SE, sive ut DF ad QF, ita BD ad OQ. Et invertendo est HS ad AC ita OQ ad BD. Sed ut AC ad GS ita est BD ad PQ, propter intervalla aequalia CS, DQ. Ergo ex aequo erit ut HS ad GS ita OQ ad PQ. Erat autem GS major quam HS. ergo et PQ major quam OQ. Unde apparet punctum O esse a parte convexa curvae AB. Eodem modo autem et punctum N sumtum ab altera parte puncti B ostendetur cadere ad partem convexam curvae AB. Ergo tangit eam recta NBOF in puncto B. quod erat dem.

Longitudo lineae CE vel DF cujus ope tangens in quovis puncto duci posset,

1) Puisque la courbe est partout convexe du côté où se trouve l'axe TF; voir la p. 461.

[p. 464]

[Fig. 3.]

non potest ratione ulla geometrica, ut puto, inveniri¹⁾ sed ex logarithmis quamlibet proximè. Nam si consideremus triangulum minimum AVX, cujus latus AX tam curvae AB quam tangentis AE portio censendum est, et perpendiculares AC, XY duos numeros esse putemus minimo quodam excessu sese superantes ut 100000 et 99999. Erit VX vel CY, logarithmorum ipsorum differentia²⁾ quae inter istos est 43430, ut patet ex tabulis. Jam si igitur fiat ut AV quae est 1 ad VX 43430 ita AC 100000 ad CE, fiet haec 4343000000, qualium nempe differentia inter logarithmos numerorum 100000 et 99999 est 43430, qualiumque logarithmus binarij est 3010299957. linea autem quae referat logarithmum binarij facile invenitur, applicando tantum duas perpendiculares inter curvam et asymptoton quarum altera sit alterius dupla velut GS, MR, nam SR intervallum referet logarithmum binarij. Ergo si fiat ut 30102 ad 43430 hoc est proxime ut 3 ad 4 1/3 ita SR ad aliam ea erit linea CE vel DF, quam latus rectum curvae hujus appellabimus. Invenitur autem adhuc accuratius si loco numerorum 100000 et 99999, quaeritur per numeros 1 et 1 1/10000000000000000, fit enim CE 434294481903251804³⁾ qualium logarithmus binarij est 301029995663981195⁴⁾. Patebit autem usus hujus lateris recti in sequentibus.

[Fig. 4.]

Si a puncto quolibet in curva sumpto ut A [Fig. 4] demittatur in asymptoton perpendicularis, AB, dico rectangulum ab AB et latere recto BF comprehensum nempe ABFE aequari spatio infinito inter curvam, perpendicularem AB et asymptoton BZ interjecto.

Fiat enim primò in eodem latere AB, rectangulum quoddam AH quod majus sit rectangulo AF. dico illud majus quoque esse dicto spatio infinito. Ductis enim diagonijs AF, AH rectangulorum utrorumque, constat quidem AF tangere curvam in A, quia BF ponitur esse latus rectum. Unde pars quaedam lineae AH cadet intra curvae cavam partem, puta AK. dividatur AH in partes tot aequales punctis

1) On a , où e représente la base des logarithmes népériens et AB (voir la Fig. 1, p. 460) la différence des abscisses qui correspond au rapport de 2 à 1 des ordonnées.

2) Voir la note 4 de la p. 461. On a ici n = 10.

3) On retrouve cette donnée, avec le même nombre de chiffres, à la p. 11 de l'‘Arithmetica Logarithmica’, ouvrage mentionné dans la note 5 de la p. 455. Ajoutons qu'on a log e = 0,434294481903251827 (Adams, Proc. Roy. Soc. of London, vol. 42, 1887, p. 25).

4) Ce nombre, qui indique les premiers 18 mantisses de log 2, se retrouve à la p. 14 de l'‘Arithmetica Logarithmica’.

[p. 465]

L, M, N, ut earum quaelibet sit minor quam AK. Et ductis per ea puncta rectis parallelis AB, divident eae rectang.^m AH in rectangula aequalia ut sunt AR, QT &c. ab ijsdem vero punctis si ducantur parallelae asymptoti lineae LO, MΛ, NC, et a punctis ubi hae occurrunt curvae AC, demittantur perpendiculares in asymptoton velut OY, ΛΠ, CZ, fient etiam spatia inter binas quasque earum interjecta inter se aequalia ut sunt AOYB, OΛΠY, ΛCZΠ ac denique etiam insimum spatium infinitum CZD, ut constat ex praecedentibus⁵⁾, quia nempe differentiae duarum perpendicularium dicta spatia comprehendentium sunt ex constr.^e aequales. Jam vero rectang.^m AR majus esse liquet spatio AOYB, cum hoc illius pars sit, nam OY necessario cadet inter AB et LR. Ergo et ▭SR majus erit spatio OYΠΛ, quippe quod aequale est spatio AOYB. Item ▭VT majus erit spatio ΛΠZC atque ita singula rectangula si plura forent, singulis sequentibus spatijs quum par utrorumque sit numerus, ac denique ultimum ▭VH majus quoque spatio infimo ac infinito CZD. Itaque omnia rectangula omnibus simul spatijs;

[Fig. 5.]

hoc est rectangulum ABHG spatio infinito ABDC majus erit.

Esto rursus ▭ quoddam ABHG [Fig. 5] quod sit minus rectangulo ABFE; dico illud minus quoque esse spatio infinito ADB. Ductis enim ut ante diagonijs AF, AH, cum AF tangat curvam in A, secabit eam recta HA versus A producta; productaque pars cadet intra cavitatem curvae ut AK. Dividatur AH in tot partes aequales ut earum unâ appositâ in producta HA, velut AL, non pertingat ad K. Constructis porro reliquis ut prius. patet rectangulum AR minus nunc esse spatio AOYB cujus nempe pars est, nam LR manifesto nunc cadit inter OY et AB. Hinc ergo et rectang. AT minus

5) Voir les p. 462-463.

[p. 466]

[Fig. 5.]

erit spatio AΛΠB, cum et rectangulum rectangulo et spatium spatio priori sit aequale. eadem ratione rectang.^m QT minus erit spatio ΛΩΘΠ, et ▭^m QX spatio ΩCZΘ, et ▭GX spatio CDZ infinito, quod nempe et ipsum reliquis spatijs aequale est. Itaque totum rectang.^m ABHG minus esse patet spatio omni AΩCDBA infinito.

Cum igitur ostensum sit rectangulum quodlibet quod majus est rectangulo ABFE, majus quoque esse spatio ACDB infinito; item rectangulum quodvis quod minus est rectangulo ABFE minus quoque esse praedicto spatio; necesse est rectangulum ipsum ABFE eidem spatio infinito aequale esse. quod erat dem.

[Fig. 6.]

Nota vero hunc modum demonstrandi sine deductionè ad absurdum, quae videtur hoc pacto alibi quoque devitari posse¹⁾.

Si ergo ab eodem puncto curvae perpendicularis in asymptoton, et tangens ducatur ut sunt hic [Fig. 6] AB, AF, erit semper triangulum ABF dimidium spatij totius infiniti ABD.

Spatium quodvis inter duas perpendiculares interceptum ut ABLH [Fig. 7], equale erit rectangulo sub latere recto et differentia dictarum perpendicularium, ut hic rectangulum

[Fig. 7.]

AK. Nam cum spatium infin. ABD sit aequale ▭^lo AF; spatium vero infin. HLD aequale ▭^lo CF; eritreliquum spatium ABLH aequale ▭^lo reliquo AK.

Alia praecedentis demonstratio datur, ostendendo ABDC [Fig. 8] terminatum duabus perpendicularibus AB, CD, duplum semper esse spatij inter duas tangentes AF, CE, ab ijsdem punctis eductas, intercepti.

Basis BD in partes aequales dividatur BH, HN &c. unde perpend.^es ad curvam

1) Comparez, à la p. 338 du Tome présent, la description de Huygens de la méthode archimédienne de la réduction à l'absurde; il lui semble donc que cette méthode peut être remplacée quelquefois par celle suivie dans la démonstration qu'il vient d'achever.

[p. 467]

erigantur, HK, NP &c. Et a punctis A, K, P &c. tangentes ducantur AF, KM &c.

[Fig. 8.]

et compleantur rectangula BG, BK, KN, PH &c. et tangentes binae quaeque proxime sibi occurrant in punctis L, Q &c. Jam quia BF, HM, NR &c sunt aequales fient et FM, MR, &c aequales et singulae singulis BH, HN, NO &c. Itaque triang.FLM minus erit 1/2 rectang.^o AH, majus vero 1/2 ▭^lo KB. Itidem triang.^m MQR, minus erit 1/2 ^lo KN, majus vero 1/2 ▭^lo PH. Atque ita composita figura ex omnibus triang. minor erit 1/2 figurâ ex circumscriptis rectang.^lis major vero dimidia figura ex rectangulis inscriptis. Unde facile ostendetur spatium ACEF dimidium esse spatij ACDB. Quod cum ubique contingat, ubicunque perpend.^is CD statuatur patet cum CD infinite parva erit, spatium ACEF, fore infinitum inter curvam et asymptoton interjacens rectaque AF terminatum; spatium vero ACDB, fore infinitum inter curvam et asymptoton, atque linea AB terminatum. Itaque illud spatium infinitum hujus infiniti spatij dimidium erit, ac proinde et triangulum reliquum AFB ejusdem spatij infiniti ACXEB dimidium esse constabit.

Hinc et de solido spatij infiniti circa axem BE demonstrabitur, esse sequialterum coni ex conversione trianguli AFB circa BF.

Nempe cum solidum a triang.^o FLM sit minus quam 1/3 cylindri a ▭^lo AH, majus vero quam 1/3 cylindri a ▭^lo KB, atque ita de ceteris; facile ostendetur solidum a spatio ACEF, esse 1/3 solidi a spatio ACDB idque ubicunque terminus CD statuatur. Unde solidum ab infinito spatio ACXEFA erit 1/3 solidi ab infinito spatio ACXEBA. ac proinde conus a reliquo triangulo AFB aequabitur 2/3 solidi ab eodem spatio ACXEBA.

Hinc porro et distantia centri grav.^is spatij infiniti ABEXA, ab asymptoto BE ostenditur esse quarta pars perpendicularis AB.

[p. 468]

Sumta enim BD [Fig. 9] ∞ duplae BF et BO ∞ 1/2 AB, et completo ▭^lo

[Fig. 9.]

BOCD, erit hoc duplum trianguli ABF ac proinde aequale spatio infinito ABEXA. Sed et cylindrus a ▭ BOCD circa BD aequabitur solido ex conversione spatij dicti infiniti circa BE. Est enim cylindrus e conversione ▭BOCD sexcuplus coni a conversione triang.ⁱ OFB circa BF, ideoque sesquialter coni à triang.^o AFB circa eandem BF, cujus coni et solidum a spatio infinito ABEX sesquialterum ostendimus. Itaque centra gr. solidi infiniti et ▭! BOCD aequaliter distare necesse est a linea BE¹⁾; utraque igitur distat dimidiâ BO, hoc est quarta parte AB. q. e. d.

[Fig. 10.]

Potest idem hoc de centro gr.^is aliter quoque ostendi descriptis intra spatium infinitum ABEX [Fig. 10] rectangulis quorum unumquodque aequali altitudinis excessu sibi proximum superet. haec enim si multitudine infinita imaginemus poterunt haberi pro aequalibus inter se²⁾, altissimi autem centrum gr. distabit ab asymptoto BE per dimidiam AB, et sequentium deinceps centra gr. aequalibus semper intervallis propiora fient ipsi BE, quae scilicet, intervalla erunt dimidia excessus altitudinum proximorum rectangulorum. Cum igitur aequalium magnitudinum centra gravitatis in aequalia intervalla dividant lineam BT, dimidiam ipsius AB: erit commune omnium gravitatum centrum in medio ipsius BT, hoc est, distabit per 1/4 AB ab asymptoto BE.

Nullius spatij a curva et asymptoto et duabus perpendicularibus comprehensi centrum grav. ulterius distat a majori earum perpendicularium quam est longitudo lateris recti.

Sit ejusmodi spatium ABCD [Fig. 11], dico ejus centr. gr. non alterius distare ab AB quam est longitudo lateris recti³⁾. Si enim fieri potest sit ejus centr. gr. in G ita ut GM major sit latere recto. possum ergo ab ea abscindere particulam ut MR ut residua RG adhuc major sit latere recto. ducatur MRO⁴⁾

1) D'après le théorème de Guldin.

2) Voir l'avant-dernier alinéa de la p. 462.

3) L'analyse moderne nous donne facilement pour cette distance: , où r représente le ‘latus rectum’ de la courbe. C'est d'ailleurs le résultat obtenu plus loin par Huygens lui même; voir le troisième alinéa de la p. 471.

4) Lisez: NRO.

[p. 469]

[Fig. 11.]

parall. BA, et per O ubi occurrit curvae, agatur AOM recta⁵⁾. fietque necessario NM minor latere recto, quia OM non tangit sed secat curvam in O. Sit OP parall. BC. et ipsi OP vel BN sumatur aequalis CF versus partem acutam spatij infiniti, et ducatur FE parall. BA. quia igitur portionis OEFN basis FN aequalis est basi CB portionis ADCB, erit quoque ON ad EF ut AB ad DC⁶⁾. unde quum portio utraque constare concipi possit ex innumeris rectang.^is aequales bases habentibus atque eadem proportione decrescentibus, manifestum est (sed et acurate ostendi posset) utriusque centra grav. similiter dividere distantiam utriusque extremarum perpendicularium; quae distantia cum sit utrobique aequalis, aequaliter ergo utriusque centra gr. aberunt a perpendicularibus majoribus AB, ON. Ergo cum centr. gr. spatij ADCB ponatur G, erit (sumpta RH ∞ MG) punctum H centr. gr. spatij ONFE⁷⁾. a quo si auferatur spatium DEFC, cujus intra seipsum est centr. gr.; apparet spatij reliqui ODCN centr. gr. inter H et G cadere, puta in K. Jam vero quia spatium AONB est ad spatium ODCN ut AP ad OQ, ex praecedentibus²⁾, hoc est ut OP ad XQ; si fiat ut OP ad XQ ita KG ad GL, erit L centr. gravitatis spatij AONB, quia nempe G ponitur centr. gr. spatij totius ABCD et K centr. gr. spatij ONCD. Erit autem GL minor quam XQ cum et KG sit minor quam OP; nam tota HG ipsi OP aequalis erat. atqui XQ minor est quam MN, et haec minor latere recto, ut supra dictum fuit. Ergo GL omnino minor erit latere recto. Sed GR ipso major erat: Ergo GL minor quam GR. Itaque L centr. gr. spatij AONB caderet extra spatium ipsum, atque ita ut ducta per L linea recta⁸⁾ totum caderet ad partem unam quod esse non potest.

Hinc itaque patet, ubicunque CD perpend.^is statuatur, etsi in infinitum distans ab AB, semper spatij ab utraque terminati centr. gr. non ulterius ab AB remotum fore, quam longitudine lateris recti atque adeo recte de spatio infinito concluditur esse ei centr. aliquod gr., idque non alterius quam dictum est distare ab AB.

Ostendam autem neque minus distare ab AB, dicta longitudine lateris recti, ac proinde ipsa hac longitudine inde abesse⁹⁾.

5) Remarquez le double emploi de la lettre M dans la figure. Il s'agit cette fois du point M situé sur l'asymptote BC.

6) Consultez, p. 461, le premier alinéa de la présente Pièce.

7) En vérité on doit considérer II, K et L non pas comme les centres de gravité eux mêmes des espaces en question, mais comme les projections de ces centres sur la droite MG.

2) Voir l'avant-dernier alinéa de la p. 462.

8) Savoir une droite parallèle à AB.

9) Comparez la note 3. En effet, on constate facilement que le deuxième terme de l'expression pour la distance en question s'approche indéfiniment de zéro lorsque le point C s'éloigne de plus en plus vers la droite.

[p. 470]

[Fig. 12]

Sit enim spatij infiniti AECB [Fig. 12] centr. gr. G, sitque si potest GM minor latere recto. Abscindam igitur ab ea partem MR, ita ut GM una cum MR minor adhuc sit latere recto; constat enim fieri posse. ducatur NRO ut supra, itemque recta AOM, et OP: et sumatur RK aequalis MG, unde et GK aequalis fiet MR.

Cum igitur duas portiones quaslibet quarum bases aequales, centra gravitatis suae ita dividunt, ut aequaliter distent a perpendiculari majori, sicut modo de portionibus ABCD, ONFE [Fig. 11] ostendimus. sequitur et de infinitis portionibus quales sunt hic ABCE, ONCE idem verum esse, cum ergo G ponatur centr. gr. spatij infin. ABCE, sitque MG aequalis RK erit K centr. gr. spatij infiniti ONCE¹⁾. Si jam ergo fiat, sicut portio AONB ad dictum spatium infin. ONCE, hoc est, ut AP ad ON, hoc est ut PO sive BN ad NM, ita KG ad GL, erit in L centr. gr. portionis AONB: eritque GL aequalis NM, quum KG sit aequalis BN. Est autem BM major latere recto, (aequalis enim huic esset, si AM tangeret curvam in A, cujus pars AO nunc arcum curvae subtendit, ideoque angulus PAO fit major quam si AO in A tangens esset). Sed GM una cum MR minor est latere recto ex constructione. Ergo ablatis utrimque aequalibus hinc MR, inde BN, relinquetur NM major quam GM. Sed ipsi NM aequalis ostensa est GL. Ergo et GL major quam GM. Itaque L, centr. gr. portionis ABNO cadit extra portionem ipsam, ita ut recta per illud duci possit cui tota portio jaceat ad partem eandem, quod est absurdum. Itaque in spatio infinito ABCE centr. gr. nec magis, nec etiam minus distat ab AB quam longitudinem lateris recti, ergo hac ipsa longitudine ab ea remotum est. qu. erat dem.^m.

1) Comparez la note 7 de la p. 469.

[p. 471]

[Fig. 13.]

Hinc et de solido spatij infiniti ex conversione ejus circa perpendicularem pronuntiare poterimus. Etenim si intra angulum perpendicularis cum asymptoto rectangulum applicetur, ut OBDC [Fig. 13], cujus altitudo OB dimidia sit AB, basis vero BD dupla lateris recti. manifestum est ejus rectanguli centrum gr. P incidere in centr. gr. spatij infiniti ABEX; cui spatio quoque dictum rectangulum aequale est²⁾. Unde constat conversione ejus circa OB cylindrum gigni aequalem solido infinito ex conversione spatij infiniti circa eundem axem AB. Sicut de cylindro qui sit ejusdem rectanguli conversione circa BD, ostensum antea est³⁾, esse eum aequalem solido alteri infinito ex circumvolutione spatij ABEX circa asymptoton BE.

Est ergo solidum ex spatio infinito ABEX circa asymptoton BE ad solidum infinitum ex eodem spatio circa AB perpendicularem, sicut PF ad PS, hoc est sicut 1/4 perpend.^is AB ad latus rectum lineae AX. ad solidum vero circa rectam AZ asymptoto parallelam ut 1 ad 3. Quod postremum solidum calicem refert infinitae capacitatis, licet exigui ponderis, quod et in Cissoide contingit⁴⁾.

Portionis a binis perpendicularibus terminatae centrum gravitatis distat a perpendiculari majore longitudine lateris recti demta linea quae se habeat ad basin portionis sicut minor perpendicularis ad excessum quo ipsa a majori superatur⁵⁾. Si igitur detur portionis cujusvis terminatae centrum grav. inveniri poterit latus rectum.

Centrum gr. solidi infiniti circa asymptoton distat a perpendiculari sive a basi ipsius solidi per dimidium lateris recti⁶⁾.

Ergo et centr. gr. solidi infiniti circa perpendicularem distabit per 1/8 ipsius perpendicularis, quae est axis solidi⁷⁾.

2) Voir le deuxième alinéa de la p. 464 et le dernier de la p. 467.

3) Voir le premier alinéa de la p. 468.

4) Comparez la note 17 de la p. 199 du Tome présent.

5) Comparez la note 3 de la p. 468. On arrive facilement à ce résultat en considérant l'espace en question comme la différence des deux espaces qui s'étendent à l'infini depuis chacune des deux ordonnées. On connaît, en effet, par ce qui précède, la situation des centres de gravité et les aires de ces deux espaces.

6) Plus tard Huygens ajouta ici: ‘demonstrationem multo post scripsi in libro G’. Voir l'Appendice qui suit.

7) Ce résultat semble reposer sur le théorème suivant: Soit Q une figurè située entièrement dans un des quadrants du système XOY de coordonnées rectilignes rectangulaires; soit Q_x le solide engendré par la rotation de cette figure autour de l'axe des x, Q_y celui qui résulte de la rotation de la même figure Q autour de l'axe des y; la distance du centre de gravité de Q_x à l'axe des y est alors à la distance du centre de gravité de Q à l'axe des x, comme la distance du centre de gravité de la figure Q à l'axe des y à la distance de ce même centre à l'axe des x.
Afin de démontrer ce théorème, considérons en premier lieu l'anneau décrit par la révolution d'un élément dQ de la figure Q autour de l'axe des x. Évidemment le moment de cet anneau par rapport à un plan perpendiculaire au plan de la figure et passant par l'axe des y est égal à 2πxy dQ. Or, on trouve la même expression pour le moment de l'anneau décrit par dQ autour de l'axe des y, pris par rapport à un plan perpendiculaire au plan de la figure et passant par l'axe des x. Il en résulte que le moment du solide Q_x par rapport au plan passant par l'axe des y est égal au moment du solide Q_y par rapport au plan passant par l'axe des x. Par suite, les volumes des solides Q_x et Q_y sont en raison inverse des distances de leurs centres de gravité respectivement à l'axe des y et à l'axe des x. Mais, en vertu du théorème de Guldin, ces mêmes volumes sont en raison directe des distances du centre de gravité de la figure Q aux axes des x et des y; d'où s'ensuit le théorème en question.
Or, il n'y a rien dans cette démonstration qui, sous une forme un peu modifiée, n'ait été facilement accessible à Huygens. On peut donc présumer que le théorème lui était connu; comme la dernière phrase du texte le semble prouver.
Ajoutons qu'on retrouve le même théorème dans l'ouvrage suivant de Guido Grandi, qu'il publia en 1701: ‘Geometrica demonstratio theorematum Hugenianorum circa logisticam, seu logarithmicam lineam, Qua occasione plures Geometricae Methodi exhibentur circa Tangentes, Quadraturas, Centra gravitatis, Solida, &c. variarum curvarum, uti infinitarum Parabolarum, Hyperbolarum, Spiralium, &c. Aliaeque Geometricae Veritates illustrantur. Addita epistola geometrica ad P. Thomam Cevam S.J. Auctore D. Guidone Grando Cremonensi, Monacho Camaldulensi, & in Almo Pisano Lyceo Publ. Phylosophiae Professore’.
Cet ouvrage fut réimprimé par G.J. 's Gravesande dans les ‘Christiani Hugenii Zuilichemi Dum viveret. Zelhemii Toparchae. Opera reliqua. Tomus primus. Amstelodami, Apud Janssonio-Waesbergios, M.DCC.XXVIII’, p. 137-315.
Guido Grandi, né à Crémone en 1671, mort à Pise en 1742, démontre le théorème d'une manière analogue à celle que nous avons suivie, quoiqu'un peu plus compliquée, et il l'emploie de même pour démontrer la conclusion à laquelle Huygens était arrivée, voir les p. 266-268 de la réimpression de son ouvrage.