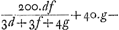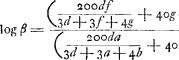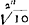Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 458]
| |
AppendiceGa naar voetnoot1) à la pièce No I.
| |
[pagina 459]
| |
- 3f - 3d, qui numerus vocetur n. (In hoc exemplo est 545869542830178.) Hic numerus n ducatur in a - ad/f productusque inde vocetur s, qui hic est 12569535892606 &c. Jamque erit sicut numerus v ad s, ita logarithmus denarij ad logarithmum propositi numeriGa naar voetnoot4), nempe hic, 0,30102999567. Pro characteristica praeponendum scimus 0, quia datus num. minor est denario. Si dati numeri, qui denario major sit, invenire logarithmum libeat, extrahatur toties continuè radix ejus, donec ultimo extracta minor sit radice sexta ex 10 nempe 10366 &c. voceturque ultimo extracta g, penultima f, sicut prius; omnia deinceps eodem modo peragantur, et invenietur hac ratione logarithmus radicis quae septima ab ultimâ numeratur, sive quae sex locis ultimam praecedit; idque aeque accurate atque modo logarithmum binarij invenimus, nempe ad 10 characteres veros. Inventum deinde logarithmum duplicando existet logarithmus radicis octavae ab ultima; et rursus duplicando, nonae; atque ita porro, donec existit ipsius numeri propositi logarithmus, duplicatio continuabitur. In vulgari logarithmorum inventione, necesse erat ex 32 characteribus cum totidem zero adjunctis, quadragies circiter radicem extrahereGa naar voetnoot5), ut fieret logarithmus 10 verarum notarum. sed en alia multa praeterea peragenda erant summae prolixitatis. Demonstratio horum in libro BGa naar voetnoot6). |
|


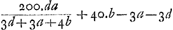 , qui numerus vocetur p, est autem 559661035184532, idemque ducatur in a - d, ac productus inde vocetur v. Qui numerus ad omnes logarithmos inveniendos adhibebitur, estque 4175509443116778, &c, sed hos priores characteres adhibere sufficit.
, qui numerus vocetur p, est autem 559661035184532, idemque ducatur in a - d, ac productus inde vocetur v. Qui numerus ad omnes logarithmos inveniendos adhibebitur, estque 4175509443116778, &c, sed hos priores characteres adhibere sufficit.