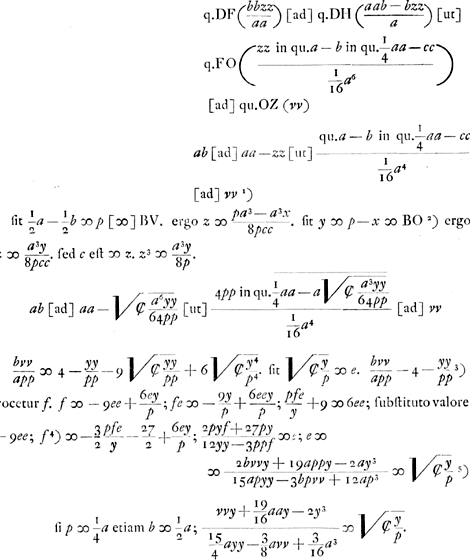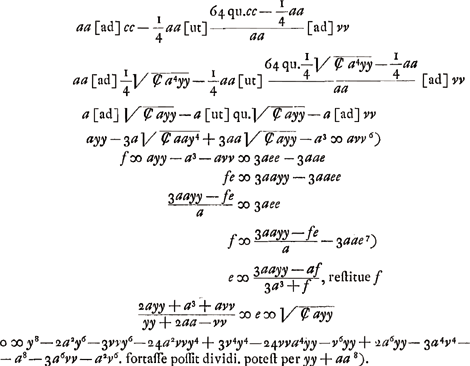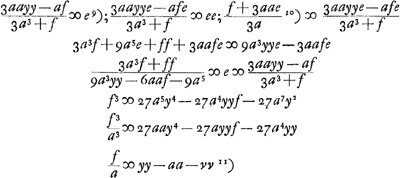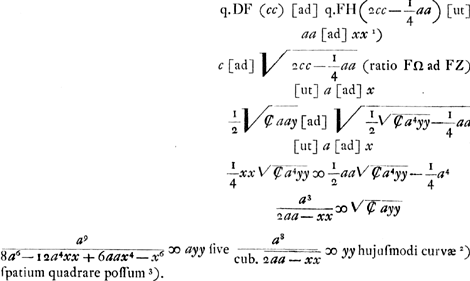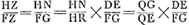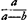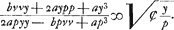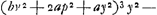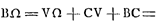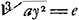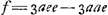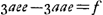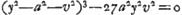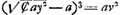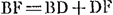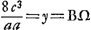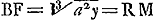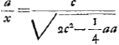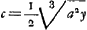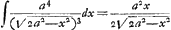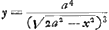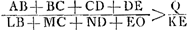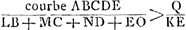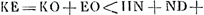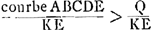|
| |
| |
| |
[Recherches sur la théorie des développées.]
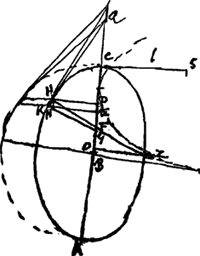
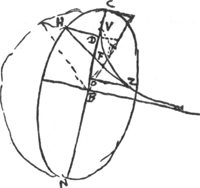
[Fig. 1].
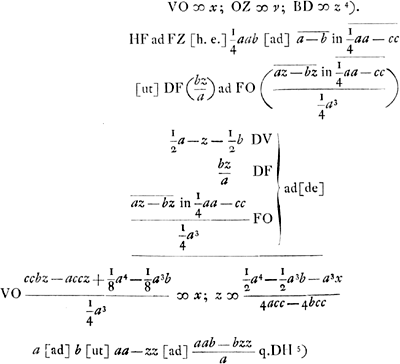
AC ∞ a; l. r. CS ∞ b; BD ∞ c; BE ∞ d.
ABGa naar voetnoot3) (a) [ad] CS (b) [ut] BD (c) [ad] DF (bc/a)Ga naar voetnoot4)
ABGa naar voetnoot3) (a) [ad] CS (b) [ut] BE (d) [ad] EG (bd/a)
DF (bc/a) s[ubtr]. DE (c - d); EF (bc/a - c + d) ex EG (bd/a); FG (bd/a - bc/a + c - d)
| |
| |
DE (c - d) [ad] FG (bd/a - bc/a + c - d) [ut] ac - ad [ad] bd - bc + ac - ad [i.e. ut] a [ad] a - b.

[Fig. 1.]
DC (1/2 a - c); DA (1/2 a + c). [DA - DC] (2 c) [ad] DC (1/2 a - c) [ut] AC ( a) [ad] CQ ( 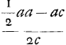 ) Ga naar voetnoot1); CQ 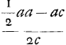 ad[de] CD 1/2 a - c; QD 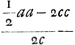 [adde] DF bc/a; QF 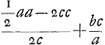 .
ratio HZ ad ZF componitur ex rationibus QF ( 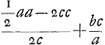 ) [ad] QD ( 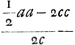 ) et DE ad FG [h.e.] a ad a - bGa naar voetnoot2). Ergo est ea quae 1/2 a3 - 2 acc + 2 bcc [ad] 1/2 a3 - 2 acc - 1/2 aab + 2 bcc. Ergo HF ad FZ ut 1/2 aab [ad] 1/2 a3 - 2 aac - 1/2 aab + 2 bcc [h.e.] [ut] 1/2 aab [ad] 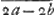 in 1/4 aa - cc.
HF ad FZ [componitur] ex 1/4 aa [ad] 1/4 aa - cc [et] b [ad] a - bGa naar voetnoot3).
| |
| |
| |
| |
| |
| |
| |
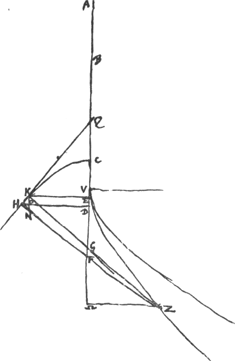
[Fig. 3.]
l. tr. ∞ aGa naar voetnoot7); l. r. ∞ b; BD ∞ c; BE ∞ d.
DF ∞ bc/aGa naar voetnoot8) a[dde] DE ∞ c - d, EF [∞] bc/a + c - d s[ubtr]. bd/a [∞] EG; GF [∞] bc/a - bd/a + c - d.
GF (bc/a - bd/a + c - d) [ad] DE (c - d) [ut] b + a [ad] a
BD ( c) [ad] BC (1/2 a) [ut] BC (1/2 a) [ad] BQ 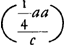 Ga naar voetnoot9) Ga naar voetnoot9)
DQ [∞] c - 1/4 aa/c a[dde] DF [∞] bc/a; QF [∞] 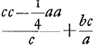
ratio KN ad GF sive KZ ad ZG componitur ex rationibus NK ad KO [sive] QF [ad] QD [sive] cc - 1/4 aa + bcc/a [ad] cc - 1/4 aa et DE [ad] GF [sive] a [ad] a + b.
ergo ratio KZ [ad] ZG [ut] acc - 1/4 a3 + bcc [ad] acc - 1/4 a3 + bcc -
| |
| |

[Fig. 3.]
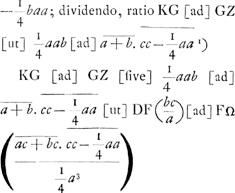
Ga naar voetnoot1)
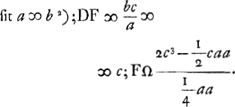
Ga naar voetnoot2)
DV ∞ BD - BC - CV [∞] c - 1/2 a - 1/2 aGa naar voetnoot3) ∞ c - a [adde] DF ( c) [et] FΩ (8 c3/ aa - 2 c) [fit] 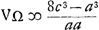 ; 8 c3/ aa ∞ y ∞ BΩ Ga naar voetnoot4); c ∞ 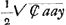 ∞ BD ∞ DF
qu.DF (cc) [ad] q.DH (cc - 1/4 aa)Ga naar voetnoot5) [ut] q.FΩ (64cc/a4 in qu.cc - 1/4 aa)
[ad] q.ΩZ (vv)
| |
| |
| |
| |
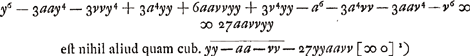
Ga naar voetnoot1)
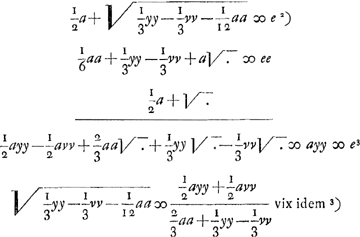
Ga naar voetnoot2)Ga naar voetnoot3)
haec methodus hic optime adhibetur quia sine Huddenij regulaGa naar voetnoot4) pervenitur ad aequationem 6 dimensionum tantumGa naar voetnoot5).
| |
| |
[Fig. 4.]
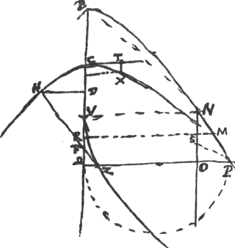
BNP est curva HeuratijGa naar voetnoot6), ejus lat. r. ∞ ∞ a ∞ BVGa naar voetnoot7) ∞ VN. NO parall. BΩ. VZ est curva ejus naturae ut qu.ΩZ in ΩO sive a, sit ∞ cub OP. dico cuivis ejus parti rectam aequalem inveniri posse. Sit BR
media proportionalis inter BV, BΩ, hoc est ∞ √ay, ergo applicata RM erit √Ȼaay. Sumatur BF ∞ RMGa naar voetnoot8), vel sumatur VF ∞ SM, erit FZ tangens in Z. divisâ BF bifariam in D, sit DH perpendicularis CF. et occurrat ei producta ZH in H. Erit ZH minus CV ∞ VZ curvaeGa naar voetnoot9).
nota CV ∞ CB ∞ 1/2 a.
linea flexilis CVZ evoluta per C describit hyperbolam CH cujus lat. r. et transv. ∞ 2VC vel VB.
Si sumatur CT ∞ OP fiet TX ∞ ΩZGa naar voetnoot10), unde facile erit curvam VZ describere.
| |
| |
| |
| |
[Fig. 5.]
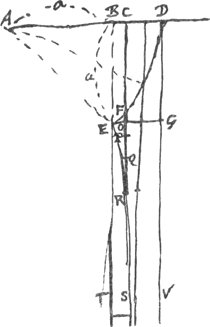
EDGa naar voetnoot4) est 1/8 circf.; AB ∞ BE [∞ a]; EG parall. BD. CF, CO, CP, CQ, CR sunt continue proport.es
ERS curva per puncta ita inventa ut R descripta est. dico spatij inter hanc et rectam ET, vel GV interjacentis partem quamvis quadrari posse.
AC ∞ x; CR ∞ y; 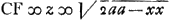 .
| |
[Fig. 6.]
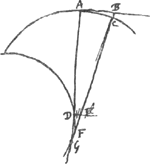
∠ DAB est rectusGa naar voetnoot6). AD est tangens in D. CG tang. in G.
DF + FG ‖Ga naar voetnoot7) DG. AF + FG ‖ ADG sive CG
aufer utrinque FG. Ergo FA ‖ FC.
Ergo FB ‖ FC.
Ergo punctum C citra B.
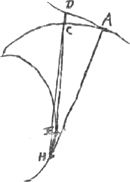
[Fig. 7.]
HCD est recta.
∠ DAH rectus.
HE recta ‖ HE curva.
HE recta + EC ‖ ‖ HE curva + EC, hoc est HA. HC recta ‖ HA. HC ‖ ‖ HD.
C citra AD rectam.
| |
| |
| |
[Theorema I.]
Si sit curva quaedam AB [Fig. 9], et alia item curva CD illa
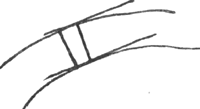
[Fig. 8.]
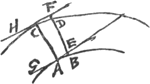
[Fig. 9.]
exterior, hoc est cujus cavitas respiciat convexitatem curvae AB. Sit autem CD curva ita comparata ad curvam AB, ut si ducantur à quibuslibet hujus punctis velut A et B rectae AC, BD quae curvae AB insistant ad angulos rectos, atque ex alia parte occurrant curvae CD, ut inquam, hae omnes ita ductae inter se aequales sint. dico easdem etiam curvae CD ad rectos angulos occurrereGa naar voetnoot1).
Ut hoc demonstretur de quavis linea ita ducta, puta AC, ducatur GAE ipsi AC ad angulos rectos, quam quidem constat tangere curvam AB in A. per C autem agatur HCF ipsi GAE aequidistans, ac proinde quoque ipsi AC ad angulos rectos. Si igitur ostendatur hanc HCF contingere curvam CD in C, manifestum erit eidem curvam ad rectos angulos occurrere rectam AC. Sumatur in CD punctum aliud D quamlibet propinquum ipsi C, per quod ducta intelligatur FDB quae occurrat curvae AB ad angulos rectos; rectae autem HCF in F. Erit ergo DB per hypothesin aequalis CA. Et cum curva AB jaceat tota ad partem alteram tangentis GAE, curva autem CD ad alteram, necesse est rectam GAE secari à DB. esto in E. Itaque ED minor erit quam BD, hoc est quam AC ideoque minor etiam ipsâ EF, interceptâ inter parallelas AE, CF; quia videlicet AC est interceptarum omnium brevissima. Itaque apparet punctum D cadere ad partem rectae HCF quae est versus curvam AB. Eadem autem ratione hoc ostendetur de quovis puncto in curva CD sumtoGa naar voetnoot2). Ergo tota curva CD est ad partem eandem sita rectae HCF, ac proinde ab hac contingitur in C. quod erat dem.
| |
| |
| |
[Lemma I.]
dato puncto A in curva qualibet versus eandem partem cava,

[Fig. 10.]
dico aliud insuper punctum in ea sumi posse ut B, in quo si recta curvam contingat ut BC, atque occurrat tangenti in A, angulum cum ea faciat ACB quovis dato majoremGa naar voetnoot3).
datus enim sit angulus GHA. Ducatur AD quae faciat super tangentem AC angulum acutum DAC minorem complemento anguli dati GHA ad duos rectos. Manifestum itaque est curvae partem quandam ut AB incedere intra angulum CAD, in qua parte accipi possit punctum ut B quod magis distet àb recta AD, omni alio curvae puncto inter ipsum B et A sumto. quare ab eo puncto si ducatur BE parallela AD occurrensque tangenti AC in E, ejus pars BE tota cadet extra curvam, ac proinde vel ipsa tangens erit in B, vel si in B tangens alia fuerit ut BC ea incedet inter curvam BA et rectam BE. Si ergo BE tangens fuerit erit angulus BEA una cum EAD duobis rectis aequalis quia BE parallela AD. atqui angulus EAD cum sit minor complemento anguli GHA ad 2 rectos, additus proinde ang.o GHA minor erit compositus duobus rectis, ergo angulus BEA major erit angulo GHA. Atque ita constabit jam propositum, quoniam BE, AE sunt tangentes curvae. At si BC demum tangens fuerit, erit ang. BCA major adhuc angulo BEC erit enim aequalis ambabus simul BEA et EBC, quoniam C cadit necessario inter A et E. Ergo sic quoque constat propositum.
| |
[Lemma II.]
Si fuerit curva in easdem partes cava, et angulo tangentium
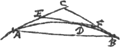
[Fig. 11.]
contenta; ab eaque pars abscindatur; comprehendetur pars reliqua angulo tangentium majori quam sit angulus totam comprehendensGa naar voetnoot4).
Sit curva ADB tangentium AC, BC angulo comprehensa ACB. abscindatur autem pars BD et sit FDE tangens in D. Ergo angulus comprehendens partem reliquam DA est DEA. dico itaque hunc esse majorem angulo ACB.
Cum enim D punctum sit intra triangulum ACB; et per punctum Drecta transeat EF necesse est eam utrinque productam occurrere duobus trianguli ACB lateribus, vel uni lateri occurrentem parte alia incidere in angulum aliquem A,
| |
| |

[Fig. 11.]
C, aut B. Non potest autem in angulum A incidere, quia rectae ex D in A aut B ductae non tangunt curvam in D quod tamen ponitur. Sed neque omnino occurrere potest EF lateri AB, quia cum tangat curvam ADB versus eandem partem cavam, debet tota esse ad eandem partem curvae ad quam tangentes AC, CB. Itaque nec in angulum C parte altera incidere poterit EF, quia scilicet tunc altera parte occurreret lateri AB. Necessario itaque occurrit lateribus AC, CB. efficitque triangulum EFC. Hujus autem angulum exteriorem DEA majorem esse constat angulo interiori opposito C. quod erat dem.
| |
[Theorema II.]
datâ curvae portione in easdem partes cava et tangentium
[Fig. 12.]
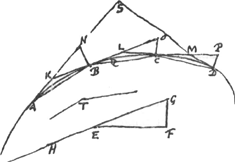
ang. comprensâ ut AQD potest ea in tot partes dividi, ut si unicuique parti subtensa recta ducatur ut AB, BC, CD et ab unoquoque divisionis puncto ducatur recta tangens curvam, ut AN, BO, CP, occurrensque ei quae curvae in puncto divisionis sequenti ad angulos rectos insistit, nempe lineis BN, CO, DP, ut inquam subtensa quaeque habeat ad sibi adjacentem curvae perpendicularem, velut AB ad BN, BC ad CO &c. rationem majorem quavis ratione propositaGa naar voetnoot1).
Sit data ratio lineae EF ad FG; quae recto angulo ad F jungantur; et ducatur recta GEH. Sumatur autem angulus obtusus T major angulo HEF, idemque major angulo tangentium quae curvam comprehendunt, ASD. itaque angulus T si super curvae AQC convexitatem moveri intelligatur, ita ut lineae ipsum comprehendentes tangant perpetuo curvam; constat semper minorem curvae portionem comprehensurum quam sit tota AQD; sit autem minima curvae portio quam comprehendere dictus angulus possit, aequalis AQ curvae. nam vel ubique aequalem portionem comprehendere eam certum est, velut, si curva fuerit circuli circumferentia, vel aliquam portionem fore minimam quam possit comprehendere. Jam si dividatur curva AQD in partes AB, BC, CD quarum singulae sint minores quam
| |
| |
AQ, et in divisionum punctis ducantur tangentes, quibus curvae figura quaedam rectilinea circumscribatur AKLMD necesse est angulos singulos AKB, BLC, &c. majores esse angulo T. quoniam si partes AB, BC, CD singulae aequales forent ipsi AQ, anguli tangentium ipsas comprehendentium singuli vel aequales vel minores essent angulo T, nunc autem partes dictae sunt ipsa AQ minores; ideoque angulos K, L, M ipsas comprehendentes majores esse necesse est angulo T per praec.Ga naar voetnoot2) Iidem anguli itaque multo majores erunt singuli angulo HEF; Ac proinde productis AK, BL, CM donec conveniant cum rectis BN, CO, DP, quae super curvam AQC sive super tangentes BK, CL, DM positae sint perpendiculares, erunt anguli NKB, OLC, PMD, priorum nempe residui ad 2 rectos minores singuli angulo FEG. habent autem ∆la KBN, LCO, MDP angulos rectos B, C, D. itaque ratio KB ad BN, item LC ad CO, et MD ad DP major erit quaeque ratione EF ad FG. Sed AB est major quam BK, quia in triangulo AKB angulus K cui subtenditur AB est obtusus; itaque major multo erit ratio AB ad BN quam EF ad FG. Eademque ratione major ratio BC ad CO, et CD ad DP quam EF ad FG. Quare constat propositum.
| |
[Theorema III.]
Duae curvae existere nequeunt quae sint in easdem partes cavae alterumque communem terminum habeant, sintque ita ad se invicem comparatae ut recta omnis quae alteram earum ad rectos angulos secet eadem producta etiam reliquam ad rectos angulos secetGa naar voetnoot3).
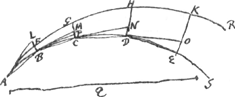
[Fig. 13.]
Sint enim si fieri potest ejusmodi lineae curvae ABCDES et AFGHKR videlicet quae sint in easdem partes cavae, et communem habeant terminum A, atque ita sint comparatae ut quaelibet rectae BF, CG quae alteri ad rectos angulos occurrunt, etiam alteri sic occurrant.
Quoniam ergo ab A termino diversae incedunt, poterit in exteriori curva punctum aliquod sumi ut KGa naar voetnoot4)
| |
| |
| |
[Lemma III.]
Si fuerint duae curvae communium perpendicularium atque
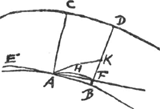
[Fig. 14.]
in easdem partes cavae CD, AB [ Fig. 14]. Interiorem autem duarum AB tangat recta EAF in puncto A unde ducatur perpend. AC ad curvam exteriorem: per aliud vero punctum sumtum in recta EF eaque ejus parte quae inter utramque curvam interjacet ut F, ducatur alia recta curvis perpendicularis DFB. dico hujus partem FD, inter rectam EF et curvam exteriorem interceptam minorem esse recta AC.
Si enim non, erit DF vel aequalis vel major recta AC. Sit primo aequalis, et intelligatur per A procedere curvam AHF parallelam curvae CDGa naar voetnoot1); fieri enim potest cum CA, DB non concurrerint adhucGa naar voetnoot2), nam occurrunt curvae AB, in easdem partes cavae in quas CD. Transibit ergo curva AHF per F. eritque tota ad partes rectae AF ubi et CD cum sit cava versus easdem partes atque CD. Itaque recta AF nequaquam continget curvam AHF in A: quod est contra propositionem ...Ga naar voetnoot3) Cum enim AHF curva sit parallela curvae CD, huic vero occurrat AC ad ang. rectos, eadem AC etiam curvae AHF ad rectos angulos occurrere deberetGa naar voetnoot4).
| |
| |
Si sint duae curvae communium perpendicularium et cavae in eandem partem nullae duae perpendiculares earum sese secabunt intra spatium quod inter curvam utramque interjacetGa naar voetnoot2).

[Fig. 15.]
linea curva in easdem partes cava vocetur quam tangentes omnes rectae ab eadem parte continguntGa naar voetnoot5).
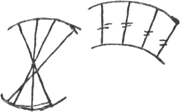
[Fig. 16.]
curvae parallelae vocentur quae ita ad se mutuo sunt comparatae ut, rectae omnes quae alteri earum ad angulos rectos insistunt, et ad reliquam terminantur, sint inter se aequalesGa naar voetnoot6).
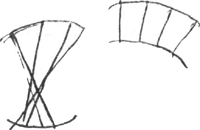
[Fig. 17].
Curvae communium perpendicularium dicantur quae ita ad se mutuo sunt comparatae, ut rectae omnes quae uni earum occurrunt ad angulos rectos etiam alteri ad angulos rectos occurrant.
| |
| |
| |
[Première Partie.]
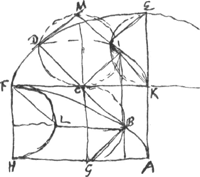
[Fig. 18.]
Si ABF sit dimidia cycloides, cui circum applicatum sit filum seu linea flexibilis ABF, caque firmata in A, capite altero ab F recedens curvam quandam describat semper tensa manens, ea curva, puta FDE, erit dimidia item cycloides ipsi FBA aequalis similisque.
BCD tangens in B. CD ∞ CBGa naar voetnoot2). ostend. D esse in cycloide FE. Sit BL parall. AH, et jungatur LF. Ergo haec parall. BCGa naar voetnoot3) et aequalis. Ergo ▱ est FCBL. Sed LB ∞ arcui LFGa naar voetnoot4). ergo et CF ∞ arcui LF.
Sit circulus genitor MDC tangens in C rectam FK, ubi et circulus BG. Ergo punctum D est in circumferentia MDC. Sed et arcus CD ∞ CB vel FL, hoc est rectae CF. unde punctum D necessario in cycloide FDE.
Porro cum BD sit dupla BC siv FL rectae, cujus dupla quoque est curva FBGa naar voetnoot5) apparet, rectam BD una cum curva BA aequari curvae ABF. hoc est rectae AE.
| |
| |
| |
[Deuxième Partie.]
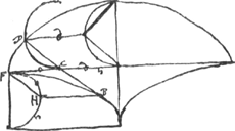
Ex eo quod BD ∞ BFGa naar voetnoot7), hoc est per Wrennij inv.mGa naar voetnoot8) ∞ 2BC, et BCD tangens, ostenditur D punctum in cycloide FDGa naar voetnoot9).
Ex eo quod tangens est BCD, ostenditur occurrere alteri cycloidi ad angulos rectosGa naar voetnoot10) hinc ex nostra methodo sequitur describi cycloidem.
|
-
voetnoot1)
- La Pièce, que nous avons divisée en paragraphes, est empruntée aux pp. 181-185, 192-208 et 226 du Manuscrit A.
-
voetnoot2)
- Dans ce paragraphe Huygens s'occupe de la développée de l'ellipse. La méthode suivie pour déterminer cette courbe est expliquée par lui dans la ‘Prop. XI’ de la ‘Pars tertia’ de son ‘Horologium Oscillatorium’ (p. 81-82 de l'édition originale). Pour l'exposer en quelques mots, soit R le point où les lignes KE et HN (parallèle à l'axe BC) de la Fig. 1 se coupent, Z le point d'intersection des normales consécutives HF et KG; on a alors
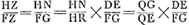 . Par suite, afin de connaître le point Z de la développée, qui correspond au point H de l'ellipse, il suffira de déterminer les deux rapports QG/QE et DE/FG. Or, dans la présente Pièce, Huygens commence par chercher le deuxième rapport, qu'il trouve égal à . Par suite, afin de connaître le point Z de la développée, qui correspond au point H de l'ellipse, il suffira de déterminer les deux rapports QG/QE et DE/FG. Or, dans la présente Pièce, Huygens commence par chercher le deuxième rapport, qu'il trouve égal à 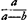 ; ensuite il remplace le premier rapport par QF/QD dont il ne diffère qu'insensiblement à cause de la situation rapprochée des points K et H. ; ensuite il remplace le premier rapport par QF/QD dont il ne diffère qu'insensiblement à cause de la situation rapprochée des points K et H.
-
voetnoot4)
- Calcul de la sous-normale. La formule se déduit facilement de celle pour FC de la p. 317 en substituant b pour r, a pour q et 1/2 a - c pour x.
-
voetnoot1)
- Cette proportion résulte immédiatement de celle (DA : DC = QA : QC) qu'on trouve formulée dans la ‘Prop. XXXVI’ du ‘Lib. I’ des ‘Con.’ d'Apollonius; voir la p. 26 verso de l'édition de Commandin.
-
voetnoot2)
- Consultez la note 2 de la page précédente.
-
voetnoot3)
- À l'aide de cette relation il est possible de construire la développée de l'ellipse point par point; mais Huygens désire connaître l'équation de cette courbe afin de savoir si elle est algébrique et jusqu'à quel degré son équation s'élève. À cet effet il prend pour origine le point V de la Fig. 2, posant VO = x, OZ = v. Or, afin de trouver le point V, il suffit de remarquer que CV est égal à la limite de DF = bc/a pour BD = c = 1/2 a. On a donc CV = 1/2 b.
-
voetnoot4)
- Le segment BD est déjà représenté par c (voir la première ligne du présent paragraphe). Or, il semble que Huygens n'a remarqué cette double représentation que beaucoup plus bas (l. 7 de la p. 390), où il pose c = z.
-
voetnoot5)
- Huygens applique ici la ‘Prop. XXI’ du ‘Lib. I’ des ‘Con.’ d'Apollonius (voir la note 3 de la p. 340); malheureusement il écrit pour le troisième terme de la proportion aa -zz, au lieu de 1/4 aa - zz, et cette erreur fausse les calculs qui suivent. Ainsi l'équation finale à laquelle il arrive dans le cas général devient, après correction:
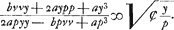
On en déduit:
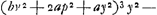 Il est vrai que cette équation est du huitième degré tandis que la développée de l'ellipse est une courbe du sixième degré, comme Huygens lui-même l'a trouvé plus tard (comparez la note 5 de la p. 394); mais, lorsqu'on y substitue - p2 pour y2, on voit qu'elle est divisible par y2 + p2, et l'équation qui reste est alors, en effet, identique à l'équation bien connue de la développée de l'ellipse.
Il est vrai que cette équation est du huitième degré tandis que la développée de l'ellipse est une courbe du sixième degré, comme Huygens lui-même l'a trouvé plus tard (comparez la note 5 de la p. 394); mais, lorsqu'on y substitue - p2 pour y2, on voit qu'elle est divisible par y2 + p2, et l'équation qui reste est alors, en effet, identique à l'équation bien connue de la développée de l'ellipse.
Ajoutons que Huygens a été plus heureux dans le cas de l'hyperbole, qui est traité dans le paragraphe qui suit.
-
voetnoot1)
- Nous supprimons, ici et ailleurs, quelques calculs intermédiaires.
-
voetnoot2)
- B peut donc être considéré comme l'origine des coordonnées y et v.
-
voetnoot3)
- Lisez: + yy/pp. Nous n'indiquons pas les corrections qui devraient résulter de cette inadvertance. Le résultat final resterait inexact à cause de l'erreur signalée dans la note 5 de la p. 389.
-
voetnoot4)
- Ici Huygens reprend l'équation f ∞ - 9ee + 6ey/p pour y substituer la valeur de ee déduite de l'équation qui précède.
-
voetnoot5)
- Consultez sur ce résultat erroné la note 5 de la p. 389.
-
voetnoot6)
- Dans ce paragraphe Huygens s'occupe de la développée de l'hyperbole.
-
voetnoot7)
- On a donc, dans la Fig. 3, AB = BC = 1/2 a. Si dans cette figure la distance AB est prise plus courte que BC, c'est parce que la figure s'approchait trop du bord de la page du manuscrit pour pouvoir prendre BA égal à BC.
-
voetnoot8)
- Cette expression pour la sous-normale se déduit aisément de celle de la p. 315 en posant r = b; q = a; x = c - 1/2 a.
-
voetnoot9)
- Voir la proposition d'Apollonius citée dans la note 4 de la p. 341.
-
voetnoot1)
- La construction point par point de la développée est donc trouvée. Il s'agit dans la suite de la détermination de son équation.
-
voetnoot2)
- Huygens ne continue pas les calculs pour le cas général. Dès ici il se borne à celui de l'hyperbole équilatère.
-
voetnoot3)
- On a CV = 1/2 a, puisque CV est égale à la valeur limite de DF pour c = 1/2 a.
-
voetnoot5)
- Valeur de l'ordonnée de l'hyperbole équilatère correspondant à l'abscisse BD = c.
-
voetnoot6)
- L'équation de la développée de l'hyperbole équilatère est donc trouvée. Il s'agit maintenant de la rendre rationnelle. À cet effet Huygens pose
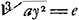 . .
-
voetnoot7)
- Cette équation est obtenue en substituant la valeur de ee, déduite de l'équation précédente, dans la première équation
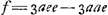 . .
-
voetnoot8)
- Comparez la note 4 de la p. 394 qui suit sur la méthode de Hudde par laquelle ce facteur peut avoir été découvert.
-
voetnoot9)
- Huygens reprend l'équation qu'il a trouvée quatre lignes plus haut.
-
voetnoot10)
- Cette expression pour ee est déduite de l'équation
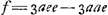 qu'on trouve plus haut. qu'on trouve plus haut.
-
voetnoot11)
- Voir, plus haut, au lieu où la lettre f est introduite pour la première fois.
-
voetnoot1)
- Huygens mentionne ce résultat dans la ‘Prop. X’ de la ‘Pars III’ de l'‘Horologium oscillatorium’, p. 80 de l'édition originale, seulement on y doit lire ‘DN, x’ au lieu de ‘CN, x’.
-
voetnoot2)
- On obtient ce résultat par la résolution de l'équation quadratique
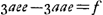 qu'on trouve au lieu indiqué dans la note 11 de la p. 393. Le choix de la racine est motivée probablement par ce que dans la partie VZ de la développée, que Huygens considère, on a toujours BΩ = y > BC = 1/2 a. qu'on trouve au lieu indiqué dans la note 11 de la p. 393. Le choix de la racine est motivée probablement par ce que dans la partie VZ de la développée, que Huygens considère, on a toujours BΩ = y > BC = 1/2 a.
-
voetnoot3)
- Comparez le résultat
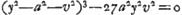 , obtenu quelques lignes plus haut; mais on vérifie aisément que les deux résultats sont identiques. , obtenu quelques lignes plus haut; mais on vérifie aisément que les deux résultats sont identiques.
-
voetnoot4)
- Il s'agit de l'article de Hudde ‘Epistola prima de reductione aequationum’, qui occupe les p. 406-506 de la seconde édition (de 1659) de la ‘Geometria Renati Des Cartes opera Fr. à Schooten’, citée dans la note 5, p. 360 du T. II. C'était surtout la ‘III Regula’, p. 414 de cet article qui a pu servir à découvrir le facteur y2 + a2 par laquelle l'équation du huitième degré de la p. 393 peut être divisée. Voici la suscription de cette règle: ‘Regula, Quae modum docet reducendi omnem aequationem, quae produci potest ex multiplicatione duarum aliarum, quarum una literam aliquam comprehendit, quae in altera non continetur; & quae litera non habet eundem dimensionum numerum in diversis Terminis’. Or, en posant v = 0, la règle amène les expressions y - a, y + a et y2 + a2 comme facteurs possibles de l'équation du huitième degré.
-
voetnoot5)
- Remarquons que dans le cas de l'ellipse et dans celui d'une hyperbole quelconque la méthode conduit également à une équation qui ne s'élève pas au dessus du sixième degré. C'est donc bien probablement en appliquant cette méthode que Huygens a obtenu ce même résultat, qu'il formule dans la ‘Prop. X’ de la ‘Pars III’ de l'‘Horologium oscillatorium’, p. 80 de l'édition originale, sans faire connaître les calculs dont il l'a
déduit.
-
voetnoot6)
- Afin d'expliquer ce qui suit, nous devons remonter à l'équation ayy - 3a√Ȼaay4 + + 3aa√Ȼaay - a3 ∞ aav (voir la ligne 4 de la p. 393), qu'on peut écrire:
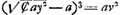 . Dans cette équation a représente l'axe réel de l'hyperbole équilatère CH des Fig. 3 et 4, y l'abscisse BΩ et v l'ordonnée ΩZ d'un point quelconque de sa développée VZ. Posant donc ΩP = √Ȼay2, ΩO = a, on aura, comme dans le texte, OP3 = aΩZ2. Mais, puisque ΩP3 = a. BΩ2, la courbe BNP, décrite par le point P, sera la ‘curva Heuratij’, c'est-à-dire la courbe dont van Heuraet avait fait connaître la rectification dans l'article ‘Epistola de transmutatione curvarum linearum in rectas’, publié par van Schooten p. 517-520 de l'édition de 1659 de l'ouvrage mentionné dans la note 4. . Dans cette équation a représente l'axe réel de l'hyperbole équilatère CH des Fig. 3 et 4, y l'abscisse BΩ et v l'ordonnée ΩZ d'un point quelconque de sa développée VZ. Posant donc ΩP = √Ȼay2, ΩO = a, on aura, comme dans le texte, OP3 = aΩZ2. Mais, puisque ΩP3 = a. BΩ2, la courbe BNP, décrite par le point P, sera la ‘curva Heuratij’, c'est-à-dire la courbe dont van Heuraet avait fait connaître la rectification dans l'article ‘Epistola de transmutatione curvarum linearum in rectas’, publié par van Schooten p. 517-520 de l'édition de 1659 de l'ouvrage mentionné dans la note 4.
-
voetnoot7)
- Puisque CB = 1/2 a, comme demi-axe de l'hyperbole, et CV = 1/2 a d'après la note 3 de la p. 392.
-
voetnoot8)
- Il s'agit de construire à l'hyperbole CH la normale HZ, qui touche la développée au point Z. Or, on a
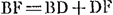 , où BD = c (voir la première ligne de la p. 391) et où DF est dans le cas de l'hyperbole équilatère = BD, par suite BF = 2c; mais on a trouvé plus haut (voir la troisième ligne d'en bas de la p. 392) , où BD = c (voir la première ligne de la p. 391) et où DF est dans le cas de l'hyperbole équilatère = BD, par suite BF = 2c; mais on a trouvé plus haut (voir la troisième ligne d'en bas de la p. 392) 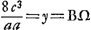 ; donc ; donc 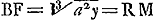 . .
-
voetnoot9)
- À cause de la théorie des développées dont Huygens venait de découvrir les principes.
-
voetnoot10)
- On a CT3 = OP3 = a.ΩZ2 = a.TX2; au lieu d'exécuter la construction à l'aide de l'hyperbole, Huygens aurait donc dû se servir de la courbe BNP, comme c'était évidemment son intention. De cette manière, en considérant la courbe BNP comme donnée, Huygens était en possession d'une méthode très simple de construire la courbe VZ par points.
-
voetnoot1)
- Afin d'expliquer cette dernière partie du présent paragraphe, remarquons d'abord que la rectification d'une courbe donnée entraîne nécessairement la quadrature d'une autre courbe. Or, il est clair que la développée de l'hyperbole est algébriquement rectifiable puisque sa longueur VZ (Fig. 4) est égale à la différence HZ - VC. Quelle est donc la courbe correspondante dont la quadrature dépend de la rectification de cette développée? Voilà la question que Huygens se pose pour le cas de l'hyperbole équilatère.
Soit ds un élément de la développée; on a alors ds/dy = FZ/FΩ, où BΩ = y. Posant donc ds/dy = x/a = φ (y), il est évident qu'on peut carrer la courbe x = aφ (y), parce que pour cette courbe xdy = ads. Il s'agit donc, pour trouver la courbe cherchée, d'exprimer x en fonction de y à l'aide de la relation a/x = dy/ds = FΩ/FZ = DF/FH, c'est-à-dire, en employant les notations indiquées au commencement de ce paragraphe, 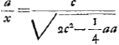 , puisque dans le cas de l'hyperbole équilatère , puisque dans le cas de l'hyperbole équilatère  , tandis que , tandis que 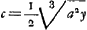 d'après la note 8 de la page précédente. d'après la note 8 de la page précédente.
-
voetnoot2)
- Voir plus loin (Fig. 5) la construction de cette courbe.
-
voetnoot5)
- Dans ce paragraphe nous réunissons les renseignements que les manuscrits nous donnent sur l'invention, en 1659, de la théorie générale des développées et des courbes parallèles. En partie ils ont servi d'avant-projet pour les ‘Definitiones I-IV’ et les ‘Prop. I-IV’ de la ‘Pars III’ de l'‘Horologium oscillatorium’ (voir les p. 59-65 de l'édition originale de 1670), desquelles elles s'écartent toutefois sur quelques points.
-
voetnoot6)
- Comparez à cette première partie, qui se rapporte aux figures 6 et 7, la Prop. I (p. 60 de l'‘Hor. osc.’) dont elle constitue l'avant-projet. Ainsi les courbes DG et EH représentent une même développée; la courbe AC (dans les deux figures) deux parties consécutives (celle à droite et celle à gauche du point A) de la développante. En effet, Huygens démontre que ces deux parties se trouvent du même côté de la droite AB ou AD, qui est perpendiculaire à DA ou AH, d'où il conclut dans la proposition citée, que la développante est coupée orthogonalement par la tangente à la développée.
-
voetnoot7)
- Ce signe est équivalent au signe moderne >.
-
voetnoot1)
- On ne retrouve pas ce théorème dans l'‘Horologium oscillatorium’.
-
voetnoot2)
- Voir la figure à gauche sans lettres à laquelle la même démonstration est applicable.
-
voetnoot3)
- Dans l'‘Horologium Oscillatorium’ Huygens n'a pas reproduit la démonstration de ce ‘Lemma’. Quand il applique dans la ‘Prop. II’ (p. 62 de l'édition originale) la construction indiquée, il se contente de faire suivre: ‘quod quidem sieri posse evidentius est quam ut demonstratione indigeat’.
-
voetnoot4)
- On ne rencontre pas ce ‘Lemma’ dans l'‘Hor. osc.’.
-
voetnoot1)
- Comparez la ‘Prop. II’ de la ‘Pars III’ de l'‘Horologium oscillatorium’, p. 62-63 de l'édition originale.
-
voetnoot2)
- Voir le ‘Lemma II’ qui précède, p. 399. On lit encore dans le manuscrit au bas de la page: ‘Lemma quod major angulus minorem portionem complectitur’.
-
voetnoot3)
- Comparez la ‘Prop. III’ de la ‘Pars III’ de l'‘Horologium oscillatorium’, p. 63 de l'édition originale.
-
voetnoot4)
- Huygens arrête ici la démonstration parce qu'il s'aperçoit que pour l'achever il a besoin du lemme qu'il fait suivre (voir la p. 402). Or, en admettant que ce lemme soit prouvé, on peut facilement reconstituer la suite de la démonstration à l'aide des indications que la ‘Prop. III’, citée dans la note précédente, nous donne. À cet effet nous supposons que le segment Q soit choisi de sorte qu'on a Q > courbe ABCDE. Ensuite, d'après la proposition précédente, on divise la courbe ABCDE en tant de parties qu'on a partout: AB/LB, BC/MC, CD/ND, DE/EO > Q/KE, où AL, BM, CN, DO sont des tangentes à la courbe AS et LB, GC, HD, KE des perpendiculaires aux deux courbes.
On a donc 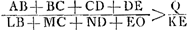 , et à fortiori , et à fortiori 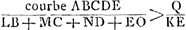 . Mais, d'après le lemme, on a . Mais, d'après le lemme, on a 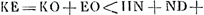 . On en déduit . On en déduit 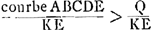 , et par suite courbe ABCDE > Q, ce qui est absurde, puisqu'on a, par supposition, Q > courbe ABCDE. , et par suite courbe ABCDE > Q, ce qui est absurde, puisqu'on a, par supposition, Q > courbe ABCDE.
Ajoutons qu'il nous semble que Huygens n'a pas été satisfait de la démonstration du lemme en question, qu'il n'a pas achevée non plus. En effet, dans la démonstration de la ‘Prop. III’, citée dans la note 3 de la p. 401, il a su éviter l'emploi de ce lemme et sur la dernière des deux pages d'où nous avons emprunté le lemme, Huygens a ébauché quelques figures où l'on retrouve les lignes auxiliaires dont il s'est servi dans cette démonstration.
-
voetnoot1)
- Voir au troisième alinéa de la p. 403 qui suit la définition des ‘curvae parallelae’, dont la propriété principale avait déjà été démontrée dans le ‘Theorema I’ de la p. 398 sans que Huygens leur avait appliqué cette dénomination.
-
voetnoot2)
- Voir à propos de cette remarque les Fig. 16.
-
voetnoot3)
- Il s'agit du ‘Theorema I’ cité dans la note 1.
-
voetnoot4)
- Huygens n'achève pas la démonstration, mais il est évident que la ligne AK représente la courbe parallèle à CD, passant par A, dans le cas où FD > AC.
-
voetnoot2)
- Voir à propos de cette remarque les Fig. 16.
-
voetnoot5)
- Comparez la ‘Definitio I’ de la ‘Pars III’, p. 59 de l'édition originale de l'‘Hor. oscil.’
-
voetnoot6)
- Cette définition et la suivante ne se retrouvent pas dans l'‘Horologium oscillatorium’.
-
voetnoot1)
- Dans son ‘Horologium oscillatorium’ (voir la Prop. XI de la ‘Pars tertia’, p. 82 de l'édition originale) Huygens nous dit expressément qu'il avait appliqué en premier lieu à la cycloïde la méthode, décrite dans la note 2 de la p. 387, pour déterminer la développée d'une courbe donnée. Il avait trouvé que pour la cycloïde on a HN = 2FG (voir la Fig. 1 de la p. 388) lorsque AC représente la base de la cycloïde, d'où il suit que pour cette courbe FZ devient égal à HF.
Cette assertion de Huygens est encore confirmée par une lettre du 10 février 1662 à Moray où l'on lit (voir la p. 51 du T. IV): ‘La propriété de la Cycloïde, de ce que par son evolution, il se décrit une courbe pareille n'estoit pas difficile a demontrer apres que Monsieur Wren a decouvert la dimension de cette ligne, mais a trouver methodiquement la dite proprietè comme j'ay fait, il y avoit plus de peine’.
Or, cette première application méthodique de la théorie générale des développées, qui doit donc avoir précédée les calculs des §§ 1 et 2 (p. 387-397), est perdue pour nous, puisqu'on ne la retrouve pas dans les manuscrits que nous possédons.
Ce qu'on y trouve sur la détermination de la développée de la cycloïde, nous l'avons reproduit dans les deux parties qui composent ce § 4.
La Première Partie que nous croyons antérieure à l'autre est empruntée à une feuille détachée, la Deuxième à la p. 226 du Manuscrit A.
-
voetnoot2)
- Cette supposition était donc probablement suggérée par le résultat dont nous avons parlé dans la note précédente.
-
voetnoot4)
- Comparez le § 1 de la Pièce No. XI, p. 347.
-
voetnoot6)
- Nous avons ajouté à cette figure la lettre H.
-
voetnoot7)
- La courbe FD est donc, par définition, une développante de la cycloïde FB.
-
voetnoot8)
- Il s'agit de la rectification de la cycloïde par Wren; comparez la note 5 de la p. 367.
-
voetnoot9)
- Puisqu'on a évidemment arc CD = arc FH = HB = FC.
-
voetnoot10)
- Par la théorie générale des développées; comparez la note 6 de la p. 397.
|

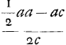 )Ga naar voetnoot1); CQ
)Ga naar voetnoot1); CQ 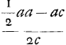 ad[de] CD 1/2 a - c; QD
ad[de] CD 1/2 a - c; QD 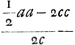 [adde] DF bc/a; QF
[adde] DF bc/a; QF 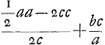 .
.
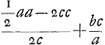 ) [ad] QD (
) [ad] QD (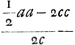 ) et DE ad FG [h.e.] a ada - bGa naar voetnoot2). Ergo est ea quae 1/2 a3 - 2acc + 2bcc [ad] 1/2 a3 - 2acc - 1/2 aab + 2bcc. Ergo HF ad FZ ut 1/2 aab [ad] 1/2 a3 - 2aac - 1/2 aab + 2bcc [h.e.] [ut] 1/2 aab [ad]
) et DE ad FG [h.e.] a ada - bGa naar voetnoot2). Ergo est ea quae 1/2 a3 - 2acc + 2bcc [ad] 1/2 a3 - 2acc - 1/2 aab + 2bcc. Ergo HF ad FZ ut 1/2 aab [ad] 1/2 a3 - 2aac - 1/2 aab + 2bcc [h.e.] [ut] 1/2 aab [ad] 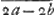 in 1/4 aa - cc.
in 1/4 aa - cc.

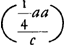 Ga naar voetnoot9)
DQ [∞] c - 1/4 aa/c a[dde] DF [∞] bc/a; QF [∞]
Ga naar voetnoot9)
DQ [∞] c - 1/4 aa/c a[dde] DF [∞] bc/a; QF [∞] 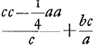

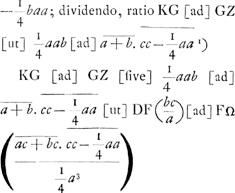
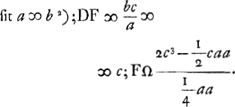
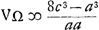 ; 8c3/aa ∞ y ∞ BΩGa naar voetnoot4); c ∞
; 8c3/aa ∞ y ∞ BΩGa naar voetnoot4); c ∞ 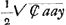 ∞ BD ∞ DF
∞ BD ∞ DF
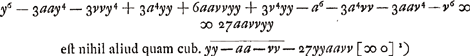
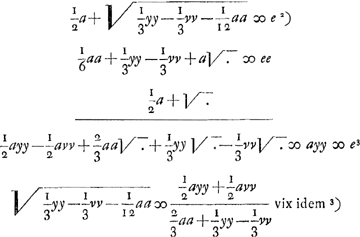


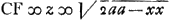 .
.