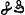heeft in als 3570 x, hetwelc geseght wert soo veel meer te sijn dan hetgeen hij sijn meester most geven, dat aen hem te weten de knecht noch 40 gl. komt. Ergo
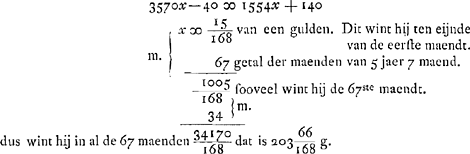
In 36 maenden nu geeft hij sijn meester 666x + 60 dat is 20070/168 gl. hoe veel in 67 maenden? komt 222 157/168Ga naar voetnoot1); hier dan afgetrocken hetgeen sijn meester hem schuldigh is te weten 203 66/168, Rest 19 91/168Ga naar voetnoot2) gl. dat de knecht aen de meester schuldigh is.
Traduction:
ou 84 mois, est égal à 3570x, somme qui surpasse, ainsi qu'il a été dit, ce que le valet doit donner à son maître de tant qu'il lui (savoir au valet) revient encore 40 florins. Par suite, on a 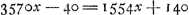 . On trouve x (c'est-à-dire ce que le valet gagne dans le premier mois) égal à 15/168 d'un florin. Multipliant par 67 le nombre de mois des 5 années et 7 mois, il suit qu'il gagne 1005/168 dans le 67ième mois. Par suite, multipliant par 34, on voit que dans les 67 mois ensemble il gagne 34170/168, ou 203 66/168 fl. . On trouve x (c'est-à-dire ce que le valet gagne dans le premier mois) égal à 15/168 d'un florin. Multipliant par 67 le nombre de mois des 5 années et 7 mois, il suit qu'il gagne 1005/168 dans le 67ième mois. Par suite, multipliant par 34, on voit que dans les 67 mois ensemble il gagne 34170/168, ou 203 66/168 fl.
Or, en 36 mois il donne à son maître 666x + 60, savoir 20070/168 fl. Combien donc en 67 mois? Il vient 222 157/168Ga naar voetnoot1). Si l'on diminue cette somme de ce que son maître lui doit, savoir 203 66/168, il reste 19 91/168Ga naar voetnoot2) fl. que le valet doit au maître.
|
-
voetnoot1)
- La Pièce est empruntée à la p. 153 du Manuscrit A.
-
voetnoot2)
- Voici cette question avec la traduction que nous en donnons: ‘Een Meester neemt een knecht aen voor 7 jaren; onder conditie dat hij hem ten eynde des tijdts, voor sijnen dienst, betalen sal (boven sijne mont-kosten &c.) 40
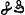 . Maer in-dien hij op 't eynde van 't derde jaer begheert te vertrecken, soo sal hij aan sijnen Meester betalen 60 . Maer in-dien hij op 't eynde van 't derde jaer begheert te vertrecken, soo sal hij aan sijnen Meester betalen 60 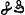 . overmidts sijnen dienst gerekent wert te verbeteren van 't beghin tot den eynde toe, gelijck eene Arithmetische Progressie; Het ghebeurt nu na 5 jaren en 7 maenden dat sy-lieden, met beyder bewilliginghe, van malkanderen scheiden, midts betalende naer advenant van de eerste conditie; De vrage is, hoe dat het met de rekeninghe staet? Antw. de Knecht moet aen sijn Meester betalen 18 317/336 . overmidts sijnen dienst gerekent wert te verbeteren van 't beghin tot den eynde toe, gelijck eene Arithmetische Progressie; Het ghebeurt nu na 5 jaren en 7 maenden dat sy-lieden, met beyder bewilliginghe, van malkanderen scheiden, midts betalende naer advenant van de eerste conditie; De vrage is, hoe dat het met de rekeninghe staet? Antw. de Knecht moet aen sijn Meester betalen 18 317/336 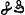 .’ [Un Maître prend un valet pour 7 années; sous condition qu'il lui payera (en dessus de ses vivres, &c.) à la fin de cette période la somme de 40 .’ [Un Maître prend un valet pour 7 années; sous condition qu'il lui payera (en dessus de ses vivres, &c.) à la fin de cette période la somme de 40 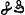 . Mais s'il désire partir à la fin de la troisième année, il payera à son Maître 60 . Mais s'il désire partir à la fin de la troisième année, il payera à son Maître 60 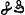 . parce qu'il est supposé que son service s'améliore du commencement jusqu'à la fin d'après une Progression Arithmétique. Or, il arrive, après 5 années et 7 mois, qu'ils veulent se quitter de consentement mutuel, pourvu que le paiement aura lieu suivant la condition prémentionnée; On demande comment ce payement
doit être réglé. Rép. Le Valet doit payer à son Maître 18 317/336 . parce qu'il est supposé que son service s'améliore du commencement jusqu'à la fin d'après une Progression Arithmétique. Or, il arrive, après 5 années et 7 mois, qu'ils veulent se quitter de consentement mutuel, pourvu que le paiement aura lieu suivant la condition prémentionnée; On demande comment ce payement
doit être réglé. Rép. Le Valet doit payer à son Maître 18 317/336 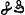 .] .]
On trouve ce problème à la p. 460 de l'ouvrage suivant: ‘Arithmetica Van Mr. Johan Coutereels Van Antwerpen; Nu nieuwelijcx oversien, alle Questien na-gerekent, en van ontallicke fauten gesuyvert; Item vermeerdert met d'Algebraïsche werckingen, uyt het Fransche Exempelaer over-geset; met by-voeginghe van verscheiden andre fraeye Questien, en noodige annotatien. Door Cornelis Fr. Eversdyck, Reken-meester's Lants ende Graeffelijckheyts van Zeelant. Tot Middelburgh, Bij Jaques Fierens, Anno MDCLVIII. Met privilegie voor tien jaren.’
-
voetnoot3)
- Cornelis Fransz. Eversdyck appartenait à une famille distinguée de la Zélande. Il naquit à Goes le 20 mai 1586 et mourut à Middelbourg le 19 décembre 1666. Élève de Johan Coutereels, il était l'auteur de plusieurs traités d'arithmétique pratique.
-
voetnoot4)
- Johan Coutereels d'Anvers s'établit, vers 1594, à Middelbourg en Zélande, où il enseigna les mathématiques. De son traité d'arithmétique, publié en 1599 chez Symon Moulert à Middelbourg, des réimpressions hollandaises parurent en 1606 et en 1610, tandis que l'édition française, mentionnée dans le titre de l'édition de Eversdyck, citée dans la note 2, parut en 1620.
-
voetnoot2)
- Voici cette question avec la traduction que nous en donnons: ‘Een Meester neemt een knecht aen voor 7 jaren; onder conditie dat hij hem ten eynde des tijdts, voor sijnen dienst, betalen sal (boven sijne mont-kosten &c.) 40
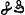 . Maer in-dien hij op 't eynde van 't derde jaer begheert te vertrecken, soo sal hij aan sijnen Meester betalen 60 . Maer in-dien hij op 't eynde van 't derde jaer begheert te vertrecken, soo sal hij aan sijnen Meester betalen 60 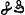 . overmidts sijnen dienst gerekent wert te verbeteren van 't beghin tot den eynde toe, gelijck eene Arithmetische Progressie; Het ghebeurt nu na 5 jaren en 7 maenden dat sy-lieden, met beyder bewilliginghe, van malkanderen scheiden, midts betalende naer advenant van de eerste conditie; De vrage is, hoe dat het met de rekeninghe staet? Antw. de Knecht moet aen sijn Meester betalen 18 317/336 . overmidts sijnen dienst gerekent wert te verbeteren van 't beghin tot den eynde toe, gelijck eene Arithmetische Progressie; Het ghebeurt nu na 5 jaren en 7 maenden dat sy-lieden, met beyder bewilliginghe, van malkanderen scheiden, midts betalende naer advenant van de eerste conditie; De vrage is, hoe dat het met de rekeninghe staet? Antw. de Knecht moet aen sijn Meester betalen 18 317/336 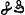 .’ [Un Maître prend un valet pour 7 années; sous condition qu'il lui payera (en dessus de ses vivres, &c.) à la fin de cette période la somme de 40 .’ [Un Maître prend un valet pour 7 années; sous condition qu'il lui payera (en dessus de ses vivres, &c.) à la fin de cette période la somme de 40 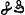 . Mais s'il désire partir à la fin de la troisième année, il payera à son Maître 60 . Mais s'il désire partir à la fin de la troisième année, il payera à son Maître 60 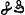 . parce qu'il est supposé que son service s'améliore du commencement jusqu'à la fin d'après une Progression Arithmétique. Or, il arrive, après 5 années et 7 mois, qu'ils veulent se quitter de consentement mutuel, pourvu que le paiement aura lieu suivant la
condition prémentionnée; On demande comment ce payement doit être réglé. Rép. Le Valet doit payer à son Maître 18 317/336 . parce qu'il est supposé que son service s'améliore du commencement jusqu'à la fin d'après une Progression Arithmétique. Or, il arrive, après 5 années et 7 mois, qu'ils veulent se quitter de consentement mutuel, pourvu que le paiement aura lieu suivant la
condition prémentionnée; On demande comment ce payement doit être réglé. Rép. Le Valet doit payer à son Maître 18 317/336 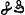 .] .]
On trouve ce problème à la p. 460 de l'ouvrage suivant: ‘Arithmetica Van Mr. Johan Coutereels Van Antwerpen; Nu nieuwelijcx oversien, alle Questien na-gerekent, en van ontallicke fauten gesuyvert; Item vermeerdert met d'Algebraïsche werckingen, uyt het Fransche Exempelaer over-geset; met by-voeginghe van verscheiden andre fraeye Questien, en noodige annotatien. Door Cornelis Fr. Eversdyck, Reken-meester's Lants ende Graeffelijckheyts van Zeelant. Tot Middelburgh, Bij Jaques Fierens, Anno MDCLVIII. Met privilegie voor tien jaren.’
-
voetnoot1)
- En vérité on trouve à l'aide de la proportion indiquée: 222 113/336.
-
voetnoot2)
- Lisez: 18 317/336. La solution d'Eversdyck (voir la note 2 de la p. 384) est donc exacte. Si celle de Huygens en diffère, c'est à cause d'une erreur de calcul.
-
voetnoot1)
- En vérité on trouve à l'aide de la proportion indiquée: 222 113/336.
-
voetnoot2)
- Lisez: 18 317/336. La solution d'Eversdyck (voir la note 2 de la p. 384) est donc exacte. Si celle de Huygens en diffère, c'est à cause d'une erreur de calcul.
|
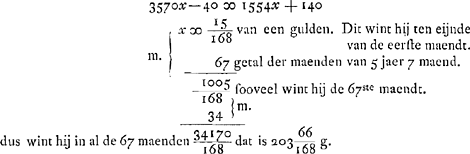


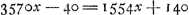 . On trouve x (c'est-à-dire ce que le valet gagne dans le premier mois) égal à 15/168 d'un florin. Multipliant par 67 le nombre de mois des 5 années et 7 mois, il suit qu'il gagne 1005/168 dans le 67ième mois. Par suite, multipliant par 34, on voit que dans les 67 mois ensemble il gagne 34170/168, ou 203 66/168 fl.
. On trouve x (c'est-à-dire ce que le valet gagne dans le premier mois) égal à 15/168 d'un florin. Multipliant par 67 le nombre de mois des 5 années et 7 mois, il suit qu'il gagne 1005/168 dans le 67ième mois. Par suite, multipliant par 34, on voit que dans les 67 mois ensemble il gagne 34170/168, ou 203 66/168 fl.