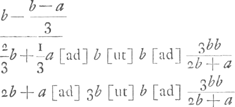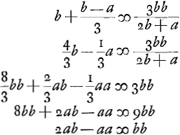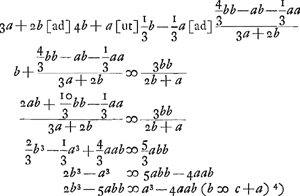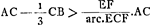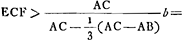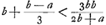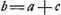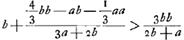|
-
voetnoot2)
- Nous reproduisons dans cette Pièce un théorème de cyclométrie et quelques annotations qui s'y rapportent. On les trouve aux p. 75 et 76 du Manuscrit A, lesquelles pages suivent immédiatement celles dont nous avons emprunté les §§ 3 et 4 de la Troisième Partie de la Pièce No. XI (p. 368-374), qui traitent de la détermination du centre de gravité d'un arc cycloïdal. En effet, on verra qu'il s'agit d'une application cyclométrique de cette détermination.
-
voetnoot3)
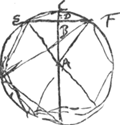
- Dans ce premier paragraphe Huygens calcule la valeur approximative qu'on trouverait pour le nombre π en supposant que le centre de gravité D [Fig. 1] d'un arc de 60o coïncide avec celui d'un arc cycloïdal possédant la même flèche, auquel cas on aurait CD = 1/3 CB.
-
voetnoot4)
- Nous supprimons les calculs. On trouve en vérité 104675.
-
voetnoot1)
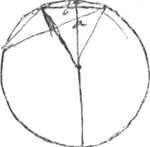
- Dans les premières trois lignes de ce paragraphe Huygens se borne encore au cas particulier où EF est le côté d'un hexagone et qu'on a par suite CA = EF = b, et BA égal à la ligne a de la Fig. 2 Ensuite il généralise tout-à-coup le résultat qu'il a trouvé pour l'approprier au cas où b est la corde et a le sinus d'un arc quelconque et il le précise en même temps en indiquant que la valeur approximative qu'on obtient pour l'arc ECF est plus petite que la valeur exacte.
Afin d'arriver à cette conclusion Huygens a dû se rendre compte de ce que le centre de gravité de l'arc de cercle se trouve toujours au-dessous de celui de l'arc cycloïdal correspondant. À cet effet il peut p.e. avoir considéré l'arc cycloïdal EBF de la Fig. 36 de la p. 373, afin de le comparer à l'arc de cercle GBL. En ce cas le rapport des longueurs des éléments de l'arc de cercle aux longueurs des élements correspondants de l'arc cycloïdal, qui se trouvent à la même distance de la corde, est de 1 à 2cos 1/2 φ, où φ est l'angle au centre de l'arc de cercle compté depuis le sommet B jusqu'à l'élément circulaire en question. Par suite, ce rapport (comme on peut aussi le démontrer facilement par des considérations purement géométriques) augmente de plus en plus à mésure que cette distance diminue; ce qui doit amener évidemment un abaissement du centre de gravité de l'arc de cercle par rapport à celui de l'arc cycloïdal.
En effet, si l'on choisit le poids spécifique de la cycloïde de manière que les éléments des deux courbes qui sont à la distance de 2/3 BM de la corde ont le même poids, tous les élements du cercle qui se trouvent à plus grande distance seront plus légers et les autres plus pesants que les éléments correspondants de la cycloïde.
Enfin, la situation réciproque des deux centres de gravité une fois admise, on obtient facilement le théorème énoncé. On a alors [Fig. 1] 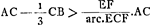 ; c'est-à-dire arc. ; c'est-à-dire arc. 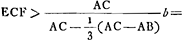 , puisqu'évidemment AF : AB = b: a. , puisqu'évidemment AF : AB = b: a.
-
voetnoot2)
- Le théorème est équivalent à la ‘Prop. XXVIII’ du ‘Cyclometricus’ de Snellius (voir l'ouvrage cité dans la note 6 de la p. 94 du T. XII) et, par suite, au ‘Theorema XIII, Prop. XVI’ de l'ouvrage ‘De circuli magnitudine inventa’ (voir la p. 159 du T. XII). Cela résulte de la comparaison des notes 27, p. 99-100, et 33, p. 159, du T. XII; mais il est probable que Huygens ne s'en est pas aperçu à cause de la dissemblance des énoncés.
-
voetnoot3)
- Dans ce paragraphe et dans le suivant, qui se trouve à côté, Huygens compare l'approximation nouvellement obtenue à celles énoncées dans le ‘Theor. XVI, Prop. XIX’ de son ouvrage ‘De circuli magnitudine inventa’, p. 169 du T. XII.
Or, la dernière équation du § 3 doit être remplacée évidemment par 2ab - aa < bb (puisque o < (b - a)2). Remontant ensuite la chaîne des équations, on trouve 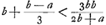 , d'où il suit (parce qu'il s'agit d'une limite inférieure) que la nouvelle formule donne une meilleure approximation que celle à laquelle elle est comparée. , d'où il suit (parce qu'il s'agit d'une limite inférieure) que la nouvelle formule donne une meilleure approximation que celle à laquelle elle est comparée.
Appliquant le même raisonnement au § 4, on trouve d'abord (en posant 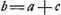 , comme Huygens l'indique) 2b3 - 5abb > a3 - 4aab, d'ou il suit , comme Huygens l'indique) 2b3 - 5abb > a3 - 4aab, d'ou il suit 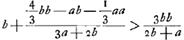 ; résultat qui était à prévoir, puisque la première expression représente une limite supérieure et l'autre une limite inférieure. ; résultat qui était à prévoir, puisque la première expression représente une limite supérieure et l'autre une limite inférieure.
Ajoutons ici que l'article de M.F. Schuh, dont nous avons fait mention dans la note 51 à la p. 174 du T. XII, a paru en 1913 et 1914 dans le T. III (Série IIIa) des Archives Néerlandaises (p. 1-178 et 229-323). On y trouvera une étude approfondie, d'après une méthode nouvelle, des diverses approximations qu'on a proposées pour l'arc de cercle.
-
voetnoot4)
- Outre les annotations que nous venons de reproduire, on trouve encore aux p. 75 et 76 du Manuscrit A des calculs qui se rapportent à l'application du théorème nouveau aux cas des polygones à 16 et à 60 côtés.
|