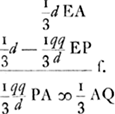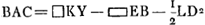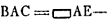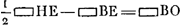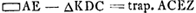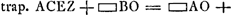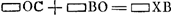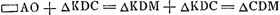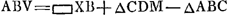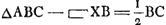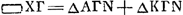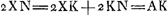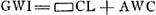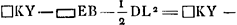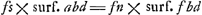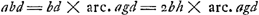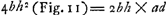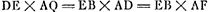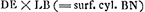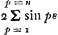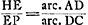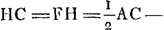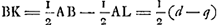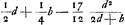Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 347]
| |
XIGa naar voetnoot2).
| |
[pagina 348]
| |
§ 2Ga naar voetnoot1).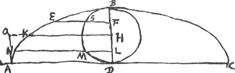 [Fig. 2.]
Sit HL ∞ HF. et ducantur FE, LN. Erunt duae simul GE et MN ∞ DA. nam GE ∞ arc.GB. Et MN ∞ arc.MB sive GD. Ergo GE + MN ∞ arc.BGD, hoc est ∞ DA. Quod cum semper contingat, hinc facile ostenditur quod spatium AEBGMDA ∞ ▭ HA, hoc est ∞ circ.oBD. Unde totum cycloidis spatium ABC, triplum erit circuli genitoris BD. 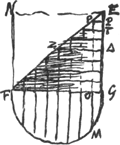 [Fig. 3.]
 [Fig. 4.]
FNEG [Fig. 3] cylindrus cujus basis circulus FG ∞ BD [Fig. 4] et GE ∞ ∞ FG. Hic sectus est plano EF in duo aequalia. BH [Fig. 4] ∞ GO [Fig. 3]; KL ∞ arc.BK vel GM vel PQGa naar voetnoot2). sit HR ∞ KL et sic porro. fit ergo ▭ RS aequale superficiei curvae QT [Fig. 3], et sic in singulis. Unde spatium totum BRVCD ∞ superficiei curvae FGE. Sed spatium BRVCD ∞ BKXDAL ex constructione quasi. Ergo spatium BKXDAL ∞ superf. FGE. hoc est duplo semicirculo FMG vel BXD. Unde rursus patet quod supra demonstratum fuit. Itaque spatium BLADXB reductum ad BRVCD nihil aliud est quam dimidium involucrum FGE expansum in superficiem planam. Et si fuerit E∆ ∞ BY, et planum ∆Z parall. plano basis FG, erit semi involucrum Z∆E ∞ spatio XΓBKX, vel YVRB. Quod si autem E∆ fuerit ∞ 1/2 EG, ideoque ΓXY per centrum circuli BD. | |
[pagina 349]
| |
erit [spat. BLΓXKB ∞] involucrum Z∆E ungulae cylindricae; quadratoque aequabitur à latere E∆ vel ∆Z vel BYGa naar voetnoot3). Itaque spatium BLΓY aequatur quadranti BXY + qu.oBY. Hoc est, si ΓX (∞ XKB) dividatur bifariam in Ξ, et compleatur ▭ BΞ; hoc aequale erit spatio BLΓY. | |
§ 3Ga naar voetnoot4).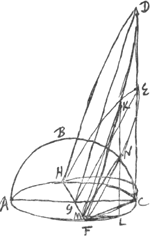 [Fig. 5.]
AHCFB semisphaera. CD ∞ CBA. FHDC ungula cylindrica ∞ semisphaerae AHCFB. Et superficies superficiei, curva nimirum curvaeGa naar voetnoot5). Sit ungula minus alta HEFC. EC ∞ CA. Ergo superf. ungulae FCDH ad superf. FCEH ut CD ad CE, hoc est ut ABC vel AHC ad AC. h.e. ut circulus ad inscr. quadratum. Sed superf. FCDH ∞ 2 circ. AHCF. Ergo superf. FCEH ∞ 2 qu.inscr. h.e. ∞ 2 qu.FC. sit frustum KMLF abscissum plano KML parall.o DGC, erit superf. FKL ∞ circ. rad. FL, ut in abscissis superficiebus sphaericisGa naar voetnoot6). At superf. FNL ∞ ∞ qu.FL. | |
§ 4Ga naar voetnoot7).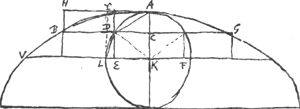 [Fig. 6.]
Sit BC [Fig. 6] basi parallela. dico spatium ABC datum esse.
Sit enim ungula TQR | |
[pagina 350]
| |
 [Fig. 6.]
[Fig. 7]. TQ, QR ∞ KA [Fig. 6]. Itaque involucrum RQM ∞ spatio ABVLDAGa naar voetnoot1). Sit QS vel PX ∞ AC. Ergo involucrum OPR ∞ spatio ADBGa naar voetnoot2). Datum autem est OPR involucr. Ergo et ABD spatium. Datum esse OPR hinc patet. Datur superficies MON ∞ 1/2 qu.NMGa naar voetnoot3). Sed et superf.  [Fig 7.]
ONQP datur quae non differt a ▭ BE. Ergo ablatis MON et ONQP ab involucro RQM (quod datum est ∞ qu.QT vel AK) reliquum quoque involucrum OPR datum erit, hoc est ADB spatium. Huic addito segmento ADC, quod datum est (quippe sector ADK datur ∞ 1/2 ▭ EH) datum erit totum spatium ABC. quod erat ostend.
Jam si AC ∞ CK [Fig. 6]. dico spatium ABC esse triplum trianguli ACDGa naar voetnoot4). Oportet enim auferre à qu.oKA, ▭m EB et 1/2 qu.DL (∞ MN [Fig. 7]) ut fiat reliquum ∞ spatio ADB. Item ut fiat segmentum ADC, oportet à sectore ADK hoc est 1/2 ▭o HE, h.e. ▭o BE auferre ∆KCD. Ergo ut fiat | |
[pagina 351]
| |
otum spatium ABC oportet ab additis simul qu.oAK et ▭ BE auferre ▭ EB et 1/2 qu.DL, et ∆KCD. Sed ▭ BE se ipsum tollit. Ergo qu.AK - 1/2 qu.DL - ∆KCD ∞ spatio ABC. Sed 1/2 qu.DL ∞ ▭ EY. Ergo qu.ex AK sive q.ALGa naar voetnoot5) - ▭ EY - ∆KCD ∞ spatio ABC, hoc est ▭ AE - ∆KCD; hoc est 3 ∆ADC ∞ spatium ABC. quod erat ostend.  [Fig. 8.]
Si ACGa naar voetnoot6) major quam CK. Erit spatium ABC ∞ ∞ trapezio ACEZ + ▭ BOGa naar voetnoot7). (dividitur ZE in O bifariam.) h.e. ▭ XB + + ∆CDMGa naar voetnoot8). segm. ABV ∞ ∞ ∆DCM - ∆CBKGa naar voetnoot9).
Si AC minor quam CKGa naar voetnoot10). Erit spatium ABC ∞ trapezio ACEZ - ▭BO. h.e. ∆CDM - ▭XB. segm. abscissum rectâ AB ∞ ∆DCM - ∆CBK nam si ad ∆DCM - ∆CBK addatur ∆ABC fit ∆DCM - ▭XB quia CK ∞ AC + 2CX. | |
[pagina 352]
| |
Si ANGa naar voetnoot1) major AK [Fig. 9.] Erit spatium AΓN ∞ trapez. AZTN + ▭ OΓ h.e. ∞ ▭XΓ + ∆ADC (idem enim est sive ▭oOΓ addatur trapez.
 [Fig. 9.]
AZTN, sive addatur ▭AO + ▭ON - ∆NTS. est autem ▭OΓ + ▭ON ∞ ∞ ▭XΓ. Et ▭AO - ∆NTS ∞ ∆ADC vel NSM, nam ▭AO ∞ ∆ADK quia AK ∞ 2AX. sed ∆NTS ∞ ∆CDK. Ergo ▭AO - ∆NTS ∞ ∆ADC vel NSM) h.e. ∞ ∆AΓN + ∆KΓNGa naar voetnoot2) + ∆NSM. Ergo segmentum AΓB ∞ ∞ ∆KΓN + ∆NSM.  Ga naar voetnoot3)Ga naar voetnoot4)Ga naar voetnoot5)Ga naar voetnoot6)Ga naar voetnoot7) | |
[pagina 353]
| |
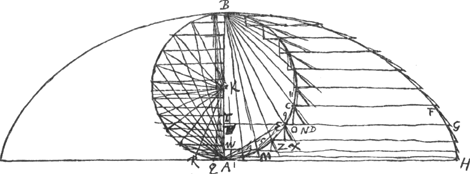
§ 5Ga naar voetnoot8). [Fig. 10.]
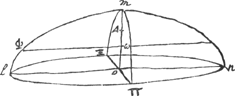
Centrum gravitatis 1/2 circuli BGD est in HG. Si itaque centrum grav. spatij BGDAEB sive BFADBGa naar voetnoot9) inventum fuerit altitudine tenus. dabitur totius spatij | |
[pagina 354]
| |
 [Fig. 10.]
 [Fig. 11.]
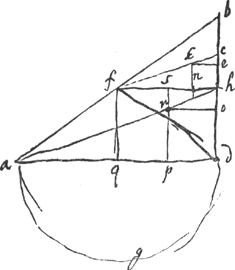
BEAD centr. gr. altitudine tenus. quia et spatiorum ad se mutuo ratio data estGa naar voetnoot1). spatium BFADB est involucrum semicylindri bad [Fig. 11]Ga naar voetnoot2). Ergo hujus centr. gr. altitudine tenus quaerendum est. superficiei cylindricae bfd centrum gr. est in fhGa naar voetnoot3): puta nGa naar voetnoot4), quod postea invenietur. superficiei cyl. afd centr. gr. est in fq. Sicut involucrum abd ad fbd ita sit nf ad fs. et sp parall. bd. Ergo totius involucri abd centr. gr. erit. in spGa naar voetnoot5). Sed et in ah. Ergo in intersectione r. Sit ro parall. ad. Ergo sicut bd dividitur in o, ita centrum gr. spatij AFBKC [Fig. 10] dividet diametrum BD. Ad inveniendum vero centr. gr. supert. | |
[pagina 355]
| |
 [Fig. 12.]
cyl.ae bfd vel bfh, comparo hanc superficiei sphaericae minimae ABC [Fig. 12] nam sicut DE, quae per centrum gr. hujus secat AC, ita necessario punctum n dividet fhGa naar voetnoot6). semisphaerae superficiei FLC centr. grav. Q dividit AL bifariam, ut ostendetur posteaGa naar voetnoot7). Sit ut FC ad FLC ita AQ ad AM. Erit Q centr. grav. 1/2 circumf. SME. Sed et Q centrum gravit. est superf. sphaericae FLC. Ergo singularum partium superficiei ut ABC centrum gravit. debet esse in circumf.a SME. Sed AQ ad AM ut FC ad FLC, ideoque AL ad AM ut 2FC ad FLC, h.e. ut AL ad 1/4 FLC. Ergo AM vel AE ∞ 1/4 FLC. Unde et fn [Fig. 11] ∞ 1/4 agdGa naar voetnoot8). Sit fc quae bifariam secet bh; nk parall. hb; ke parall. fh. Quia ergo ch ∞ 1/2 bh vel 1/2 hf, erit kn, sive eh ∞ 1/2 nf. h.e. ∞ 1/8 agd. Itaque sumptâ in super[iore] fig. [Fig. 10] He ∞ 1/4 arc. BG, erit e centr. gr. spatij FBK. sive duorum BGE. BMLGa naar voetnoot9). Porro quia ut involucr. abd [Fig. 11] ad fbd h.e. ut agd ad adGa naar voetnoot10) ita nf ad fs; estque nf ∞ 1/4 agd. Erit et fs ∞ 1/4 ad sive ∞ 1/2 fh. Unde et hr ∞ 1/4 ha. Ergo et ho ∞ ∞ 1/4 hd. Ideoque bo ad od ut 5 ad 3. Ergo in super. fig. [Fig. 10] sumpta Bo partium 5 qualium BD est 8, erit o centr. gr. spatij AFBKC. sive utriusque BEADGB, BLCDMB. haec vero aequantur duplo circ.o BDGa naar voetnoot11); Ergo divisa Ho in z ut sit Hz dupla zo, erit z centrum grav. spatij cycloidis totiu ABC. Do est 3/8 sive 9/24 BD et oz ∞ 1/24 BD. Ergo Dz ∞ 10/24 sive 5/12 BDGa naar voetnoot12). | |
[pagina 356]
| |
Ratio solidi a Cycloide facti circa axem AC ad cylindr. à ▭AR circa axem eundem componitur ex ratione spatij cycloidis ad spatium ▭i AR, hoc est ex ratione 3 ad 4; et ex ratione Dz ad DH, quae est 5 ad 6. Ergo solidum cycloidis ad dictum cylindrum crit ut 15 ad 24 hoc est ut 5 ad 8.  [Fig. 10.]
Ratio solidi à spatio FBK (ungulae nimirum involucro) circa FK axem ad cylindrum à ▭FW, componitur ex ratione spatij FBK ad ▭FW, hoc est ex ratione HG ad FH (nam spatium FBK ∞ 2 qu.HGGa naar voetnoot1)), et ex ratione eH ad cH, hoc est ex ratione 1/4 [arc.] GB vel 1/4 FH ad 1/2 HG h.e. FH ad 2HG. Ergo eadem est quae HG ad 2HG, hoc est quae 1 ad 2. Est autem solidum ab FBK aequale ei quod à duobus spatijs BGE, BML. Ergo si solido ab FBK hoc est cylindro à ▭oFB addatur sphaera BD, vel cylindrus ipsi aequalis, oritur solidum ab EBL circa axem EL. | |
§ 6Ga naar voetnoot2).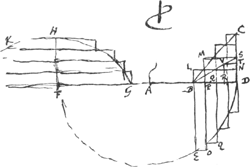 [Fig. 13.]
BDC est frustum cylindri cujus cylindri basis est circulus FED. frusti basis est segmentum EBD vel potius hujus duplum. Oporteat invenire centrum gravitatis involucri BDC. ut DE arcus ad EB ita est AD radius ad AQGa naar voetnoot3) ut Q sit centrum gr. arcus DE (dupli scilicet), ideoque et involucri LD. Quare si▭BO suspendatur ex F, illud suspensa libra ex A, aequiponderabit invo- | |
[pagina 357]
| |
lucro LD ut positum estGa naar voetnoot4). Similiter ▭PQGa naar voetnoot5) ex F suspensum aequiponderabit (ex A) involucro MN, atque ita totum segmentum BDE ex F suspensum aequiponderabit involucro BCD et duplum duplo. Sicut igitur involucrum BCD ad segmentum BDE ita si siat FA ad AR. Erit R centr gr. vel certè sub centro grav.is involucri BDC. Est autem et in BS quae bifar. secat DC idem gr. centrum. Ergo datum erit in intersectione V. Et facta VT parall.a BD dabitur quoque ratio CT ad TD. 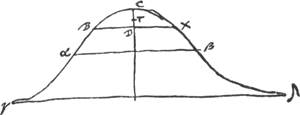 [Fig. 14.]
Si igitur involucrum BDC exporrectum fuerit in plano [Fig. 14], faciens partem quamlibet involucri semicylindrici ut BCX, ejus centrum gr. in diametro CD inveniri poterit. Et haec methodus brevior meliorque est quam qua paulo ante totius involucri centrum gr. ut et involucri ungulae, quod est αCβ, quaerebamusGa naar voetnoot6).  [Fig. 15.]
Cumque centr. gr. involucri BCX hoc est duorum spatiorum CRL, CNO [Fig. 15] inveniri possit, itemque centr. gr. segmenti circularis RCN. datum igitur est partis LCO centr. gr. quae qualitercunque lineâ LO basi parallela à cycloide abscinditur. Sed et dimensio data est partis ejusmodi per antecedentiaGa naar voetnoot7). Ergo et solidum quod ab ea efficitur circa axem LO conversione factâGa naar voetnoot8). | |
[pagina 358]
| |
[Deuxième PartieGa naar voetnoot1)].§ 1Ga naar voetnoot2). [Fig. 16.]
 [Fig. 17.]
Iisdem positis quae in propositione  (hoc signo notataGa naar voetnoot3)) aequiponderat, (ex k suspensa librâ [Fig. 16]) segmentum def (aequale abc), involucro agbc ut positum estGa naar voetnoot4). Involucrum hoc expansum in plano sit lmn [Fig. 17], nempe ln ∞ arcus abc. superque ea basi parallelopipedumGa naar voetnoot5) intelligatur, idque plano lpn sectum esto, ut fiat ungula seu cuneus lmnp, minimus quasi. (hoc signo notataGa naar voetnoot3)) aequiponderat, (ex k suspensa librâ [Fig. 16]) segmentum def (aequale abc), involucro agbc ut positum estGa naar voetnoot4). Involucrum hoc expansum in plano sit lmn [Fig. 17], nempe ln ∞ arcus abc. superque ea basi parallelopipedumGa naar voetnoot5) intelligatur, idque plano lpn sectum esto, ut fiat ungula seu cuneus lmnp, minimus quasi.
| |
[pagina 359]
| |
Oportet invenire quomodo hujus centrum gr. s dividat diametrum om. super basi circulo abch, conus intelligatur maximus cujus latera hz, bz. hujus coni pars quam cum ungula acbg communem habet si ab ungula auferri intelligatur, supererit solidum quoddam cavum minimum; quod solidum (si fuerit angulus gbz ∞ pom in cuneo) nihil aliud erit quam ipse ille cuneus inflexus veluti. Sit etiam super segmentum def extructa ungula defht, ut sit angulus eht ∞ mop vel gbz. tum inscriptis ▭is aequalis altitudinis in segmento def super ijs parallelopipeda intra ungulam excitentur, et totidem annularia solida intra solidum cavum aucbg formentur. horum singula singulis dictis parallelopipedis aequiponderabunt, quia involucra (ex propos.  Ga naar voetnoot3)) basibus parallelopipedorum aequiponderant et utraque in eandem altitudinem ducuntur. Ergo apparet ungulam ipsam defht aequiponderare solido cavo aucbg. Quare si fiat ut solidum cavum Ga naar voetnoot3)) basibus parallelopipedorum aequiponderant et utraque in eandem altitudinem ducuntur. Ergo apparet ungulam ipsam defht aequiponderare solido cavo aucbg. Quare si fiat ut solidum cavum
 [Fig. 18.]
aucbg ad ungulam defht ita kh radius ad ko [Fig. 18] erit o sub centro gr. dicti solidi cavi. Sed quaenam est ratio solidi cavi, sive cunei lmnop [Fig. 17] ad ungulam defht? Eam dico datam esse. Est enim eadem quae solidi ex conversione involucri expansi lmn circa ln [Fig. 17], ad solidum ex conversione segmenti def circa df. Illud solidum ex ijs quae ex Prop. 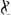 deduximus datum estGa naar voetnoot6). alterum similiter datum est quoniam segmentum def magnitudine datur datâ cycloideGa naar voetnoot7), itemque segmenti centr. grav. Ergo quum utraque solida sint data etiam ratio ad se invicem data erit. quare itaque et ratio kh ad ko [Fig. 18]. ducta ergo oq parall. bg in ea erit centr. gr. solidi cavi aucbg [Fig. 16], sed et in recta ir [Fig. 18], quae ita dividit bg ut br sit dupla rg. quia videlicet ex triangularibus solidis, quale
gbβ, totum cavum solidum aucbg deduximus datum estGa naar voetnoot6). alterum similiter datum est quoniam segmentum def magnitudine datur datâ cycloideGa naar voetnoot7), itemque segmenti centr. grav. Ergo quum utraque solida sint data etiam ratio ad se invicem data erit. quare itaque et ratio kh ad ko [Fig. 18]. ducta ergo oq parall. bg in ea erit centr. gr. solidi cavi aucbg [Fig. 16], sed et in recta ir [Fig. 18], quae ita dividit bg ut br sit dupla rg. quia videlicet ex triangularibus solidis, quale
gbβ, totum cavum solidum aucbg
| |
[pagina 360]
| |
[Fig. 16] componi intelligi potest. quorum singulorum centra gr. in plano per ri [Fig. 18] ductoGa naar voetnoot1). Ergo centrum ipsius grav. datum erit in intersectione q. Sit qy parall. ib. Ergo sicut y secat gb similiter s [Fig. 17] secabit cunei diametrum om. | |
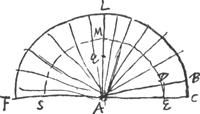
§ 2Ga naar voetnoot2).Examinemus casum illum cum lmnGa naar voetnoot3) totius semicylindri est involucrum.  [Fig. 19.]
 [Fig. 20.]
hic ratio solidi quod ex involucro lmn [Fig. 20], ad solidum ex circulo mo circa ln, sive solidum ex circulo de [Fig. 19] circa hb, ea est quae 3 ad 2 ut ex superioribus facile colligiturGa naar voetnoot4). Ergo ea quoque ratio erit cunei lmnop, sive solidi cavi ibgβ ad ungulam detfh. Ergo etiam kh ad ko ut 3 ad 2. Ergo hb ad bo item hr ad rq, item br ad ry ut 6 ad 1. sed br erat ad rg ut 6 ad 3. Ergo erit gy ad yb ut 4 ad 5. Ideoque et ms [Fig. 20] ad so ut 4 ad 5: et s centr. gr. cunei lpnmGa naar voetnoot5). | |
[pagina 361]
| |
Sit nunc super basi tota cycloide lpn cuneus constitutus lγpnom. Ejus cunei duae partes lγpδ, pεnζ habent punctum sub centro gr. in mo quam ita dividit quemadmodum ungulae oπmρp centro gr.is suppositum. cum nihil aliud sint quam haec ungula diducta. Ergo id centr. gr. θ [Fig. 20 et 21] ita dividit rectam om ut pars versus m sit 3, reliqua 5Ga naar voetnoot6). ex ms ∞ 4/9 [mo] aufer mθ ∞ 3/8 [mo], relinquitur θs ∞ 13/72
 [Fig. 21.]
(5/72)Ga naar voetnoot7) mo. haec θs dividatur in λ [Fig. 21] ut sit θλ duplaGa naar voetnoot8) (sesquialt.) ipsius λs, fit λs ∞ 13/216 (1/36)[mo] cui additâ so ∞ 5/9 [mo] fit λo ∞ 133/216 (7/12) totius mo. λ autem est centr. gr. cunei lγpζnom [Fig. 20]. Sit solidum ex cycloide ortum circa axem ln [Fig. 20] eoque per axem eundem ln sectoGa naar voetnoot9) quaerendum sit hujus medietatis centr. gr. Sectio quae bifariam hanc medietatem dividit, sit circulus σmφ [Fig. 22] et sumpta oλ ∞ 133/216 (7/12)om sit designata circumferentia χλξ. in hac 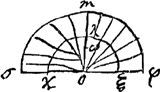 [Fig. 22.]
quia centr. gr. sunt omnium cuneorum cycloidalium dicti semisolidi; erit proinde periferiae χλξ centr. gr. idem quoque semisolidi dicti. Ergo ut semiperiferia circuli ad diametrum, hoc est ut dimidia basis cycloidis lo [Fig. 23] ad ejusdem altitudinem om ita sit λo nempe 133/216 (7/12)om ad oω, eritque ω centr. gr. semisolidi | |
[pagina 362]
| |
 [Fig. 23.]
dicti. sive ut lo ad om ita sit haec ad aliam oΔ, et sumatur oω ∞ 133/216Ga naar voetnoot1) (7/12) ipsius oΔ. Eritque ω centr. gr. ut prius solidi cycloidalis dimidij. Itaque ducta ωΦ parallela ol, in ipsa erit centrum gr. medietatis lΞmπ, cujus centr. gravitatis Gallus postulatGa naar voetnoot2). (HocGa naar voetnoot3) est si fiat ut tota ln, sive circumferentia genitoris ad ejus diam. mo ita haec ad aliam; hujus 7/6 aequantur ipsi oω. Hoc est ut 6 circumf.a ad 7 diam. ita erit diameter mo ad oω.)
(duplicem calculi errorem commiseramGa naar voetnoot4). methodus rectè se habebat.) | |
[pagina 363]
| |
[Lemma].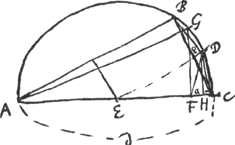 [Fig. 24.]
[AC ∞ d]; BD ∞ DC; DH perpend. AC; HC ∞ HF [∞ a]. 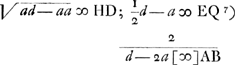 Sed et AF ∞ d - 2a; Ergo AB ∞ AF. Sed AG media prop. inter FA et AC. Ergo AG media prop. inter AB, AC. Ergo ▭BA, AC ∞ qu.AG sive ∞ ∞ ▭FAC hoc est ∞ qu.AC - 2qu.CD.
Curvae pars AS [Fig. 25] ad AN rectam ut quadr.AC - 2qu.CD, hoc est | |
[pagina 364]
| |
 [Fig. 25.]
▭BAC ex lemm. praec., ad 1/2 qu. AB, hoc enim demonstraboGa naar voetnoot1). atqui AN ad AB ut 1/2 qu.AB ad 1/2 ▭BAC. Ergo ex aequo erit curva AS ad AB ut ▭BAC ad 1/2 ▭BAC hoc est ut 2 ad 1.
facilius hoc demonstr. in sequentibusGa naar voetnoot2). | |
§ 2Ga naar voetnoot3).Lemma [I.]Ga naar voetnoot4) [Fig. 26.]
CD arcus ∞ DB; DH perpend. AC. HF ∞ HC. Ostend. AF ∞ AB.
Dem. quia HF ∞ HC et DH perpend. erit DF ∞ DC hoc est ∞ DB. est autem in triang. ABD, AFD, ∠ABD ∞ ∞ ∠AFD quia hic una cum ∠DFC, ille cum ∠DCF (ipsi DFC aequali) aequatur 2 rectisGa naar voetnoot5). Sed et latus AD triangulis ABD, AFD commune, ergo et latus AF ∞ AB. qu. erat dem. | |
Lemma [II.] [Fig. 27.]
in ∆ECD, ∠D + ABD ∞ ang.  . ∠C + ∠ECA sive + ∠EBA ∞ ∠ . ∠C + ∠ECA sive + ∠EBA ∞ ∠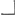 . Ergo ∠C superat ∠D angulo EBD. . Ergo ∠C superat ∠D angulo EBD.
| |
[pagina 365]
| |
 [Fig. 28.]
CD est parallela tangenti FGGa naar voetnoot6). ducendo autem CN ita ut ang. DCN sit aequ. dimidio CBE, fit ∆NEC isosceles, cruribus aequalibus EN, ECGa naar voetnoot7). Omnes autem CN habeantur pro longitudine curvae BFHGa naar voetnoot8). Quaero jam quam rationem habeant omnes CN ad omnes CO, quae sunt perpend.es in Δlis ECN. ista enim ratio inveniri potest, et dupla esse ostenditur. Ergo curva BFH dupla rectae BA. Quod autem omnes CN ad omnes CO duplae sunt sic ostenditur. Anguli E triangulorum CEN aequaliter crescunt ut numeri 1, 3, 5, 7, 9, 11 &c. Habent autem singuli crura eidem EC aequalia. sunt ergo omnes CN subtensae arcuum aequaliter crescentium usque ad semicircumfer.m in circulo cujus radius EC. Perpendiculares verò CO sunt eorundem arcuum omnium sinus. atqui omnium arcuum istorum subtensas omnium sinuum suorum duplos esse constat, infinitâ consideratâ multitudine. nam sinus quidem omnes tantundem efficiunt atque duplum sinuum arcuum omnium usque ad circuli quadrantem; subtensae autem omnes duplae sunt sinuum omnium ad quadrantem, sed duplo plurium numero; qui sinus duplo plures, quum simul dupli sint duplo pauciorum; hinc et subtensae omnes ad semicirculum duplae erunt omnium sinuum qui ad eosdem arcus pertinentGa naar voetnoot9). | |
[pagina 366]
| |
 [Fig. 28.]
Ad inveniendam rectam aequalem parti curvae ut HG, ductâ GE parall.a HA, inveniendum est quaenam sit ratio omnium subtensarum usque ad arcum AE ad omnes sinus ab eodem demissos, infinita multitudine utrorumque. haec enim ratio eadem est illi quam habent omnes EX deinceps usque ad A ad omnes pendiculares EZ. Dictam autem rationem omnium subtensarum ad omnes sinus eam dico esse [Fig. 29.]
quam habet quadrupla AW sinus versus dimid. arcus AE, ad ATGa naar voetnoot1). Ostendit Archimedes omnes sinus ab arcu AE in aequales partes diviso demissos esse ad AT ut AR [Fig. 29] ad RB subtensam unius partisGa naar voetnoot2). Similiter ergo omnes sinus ab arcu AS demissi erunt ad AZ ut AR ad RB. Itaque omnes sinus ab arcu AE ad AT, sicut omnes sinus ab arcu AS ad AZ. Et permutando, omnes sinus ab arcu AE ad omnes sinus ab arcu AS ut AT ad AZ, sive etiam ut qu.AE ad qu.AS. | |
[pagina 367]
| |
 [Fig. 30.]
Omnes subtensae crescentes in arcu AE [Fig. 30] aequantur duplo omnium FP rectarum quae parallelae sunt ipsi AE et bina quaeque sectionum puncta conjunguntGa naar voetnoot3). quum illae in eodem circuli segmento duplo plures sinus quam hae constituant. Harum verò (ipsi AE parallelarum) dimidiae omnes, sive sinus ab arcu ME demissi, ita se habent ad omnes sinus ET demissos ab arcu AME ipsius ME duplo, sicut MO vel AW ad AT per praeced. Ergo ex aequo omnes subtensae in arcu AE ad omnes sinus ab eodem arcu AE demissos eam habent rationem quam quadrupla AW ad AT. Quum ergo superius dictum sit eam fore rationem curvae partis HG [Fig. 28] ad rectam TA quam omnium subtensarum in arcu AE ad omnes sinus ab eodem demissos, quam nunc invenimus esse eam quam quadruplae AW ad AT, apparet ipsam curvam HG aequari quadruplae AW. Nimirum ad inveniendam rectam curvae HG aequalem oportet ducere GE parall. basi cycloidis, et diviso arcu EA bifariam in M ducere MW parall. eidem basi. Eritque quadrupla AW aequalis curvae HG. Jam verò quoniam BA aequatur dimidiae curvae BHGa naar voetnoot4), et AW bis (ut ostendimus) aequ. [dimidiae] curvae parti HG hinc 1/2 reliqua pars GB aequabitur BA - 2AW. hoc est ipsi BE rectaeGa naar voetnoot5). nam haec aequatur BA - 2AW ex lemm. superioriGa naar voetnoot6). Notandum item quod WK semper aequalis 1/4 curvae GB. | |
[pagina 368]
| |
§ 3Ga naar voetnoot1).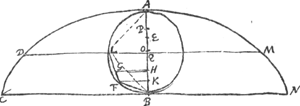 [Fig. 31.]
22 Jan. 1659. BE est 2/3 BA. E est centr. gr. totius lineae cycloidis CAN. AO ∞ OB. D punctum datum. DL parall. CB. LF ∞ FB. FG ∞ 1/3 FL. GH parall. CB. H est centr. grav. curvarum CD, NM. Ratio constructionum in sequentibus explicatur pag. versa et sequGa naar voetnoot2). Si fiat ut OK ad KB ita HE ad EP erit P centr. grav. curvae DAMGa naar voetnoot3).
AL ∞ q; AB ∞ d; AQ [∞] qq/d. 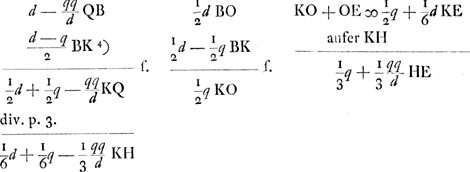 | |
[pagina 369]
| |
§ 4Ga naar voetnoot1).Lemma ad ea quae in fin. pag. sequentisGa naar voetnoot6).
in ∆ABC, BD perp. AC. dico majorem habere rationem AD ad DC quam ang.ACB ad ang.CAB. 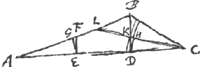 [Fig. 32.]
Sit AE ∞ DC, et EF perp. AC, et ∠ACL ∞ ∞ ∠BAC. AD ad DC ut AD ad AE, h.e. ut BD ad EF vel DK. Sed BD ad DK major ratio quam ang.i BCD ad ∠KCD sive A. ut facile est ostendere. Ergo et AD ad DC major quam ∠BCA ad A.
Circumfer.a divisa est in partes aequales [Fig. 33]. Omnes CN parallelae et aequales tangentibus cycloidem respondentibusGa naar voetnoot7). hoc est ipsi curvae. Et singulae in eadem | |
[pagina 370]
| |
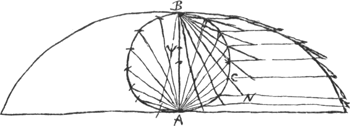 [Fig 33.]
altitudine similiter sitae. Ergo centr. gr. cycloidis lineae erit in eadem altitudine atque centr. gr. omnium CN. Superius autem apparuit, pag. 78Ga naar voetnoot1), singulas CN esse inter se sicut quae ipsis adjacent CA. Unde sequitur, si in singulis punctis C suspenderentur singulae CA, fore centrum gr. omnium CA ita suspensarum eadem altitudine atque centr. gr. omnium CN uti positae sunt, vel certè si singulae CN suspenderentur itidem è punctis C. quod nihil refert. Oportet igitur invenire centrum gr. omnium CA ex punctis C suspensarum. Sit  [Fig. 34.]
primo propositum invenire centr. gr. omnium CA suspensarum ex C punctis per arcum ACBGa naar voetnoot2) [Fig. 34] quemcunque. dividatur hic bifariam in C, à quo bina quaeque reliquorum punctorum C aequaliter utrinque distent; quae jungantur rectis ef, kl &c. et ducatur item CD. Quia ergo AC dividit bifariam angulum eAf, erit ut eA ad Af ita eg ad gf, vel ita quoque fh ad heGa naar voetnoot3). Ergo h centr. gr. erit ipsarum Ae, Af suspensarum ex e et f. Eodem modo ostendetur centr. gr. duarum kA et lA suspensarum ex k et l esse in n; atque ita de caeteris quibusque binis apparebit centr. ipsarum gr. esse in recta CD. Ergo omnium AC ex punctis C suspensarum per totum arcum ACD erit centr. gr. in CD. dividatur ABGa naar voetnoot4) in s ut sit As dupla sB. dico centr. gr. omnium AC, per totam circumferen- | |
[pagina 371]
| |
tiam suspensarum, centr. gr. esse s punctum. Sit enim primo magis versus A ut in t. Et sumatur arcus Aq tam exiguus ut omnium AC ex ipso suspensarum gravitas minorem rationem habeat ad omnes AC ex tota circumf.a suspensarum, quam ts ad sA. arcus ACBq dividatur bifariam in o. et ducatur oq secans AB in r. Erit ang. roA duplus ang.irAo, ideoque rA major quam dupla rBGa naar margenoot*. unde r inter s et B. Est autem centr. gr. omnium AC suspensarum per arcum ACBq in recta oqGa naar margenoot† et quidem in parte or, quoniam suspensarum ex arcu Aq est ad partes diametri AB quae versus q. Sit ergo p centr. gr. omnium suspensarum ex arcu ACBq. Ergo pt recta major quam st. unde si producatur pt, ut fiat sicut gravitas omnium ex tota circumferentia suspensarum ad suspensas ex arcu Aq ita yp ad pt. cadet y extra circulum longè, quia As ad st majorem rationem habere posita est. esset autem centrum gr. suspensarum ex arcu Aq in y quod fieri non potest. Jam si fieri potest, sit centr. gr. omnium AC per totam circumf.m suspensarum magis versus B quam punctum s velut in u. Sumatur arcus Aq tam exiguus ut reliquo qDBCA bifariam diviso in o, ductâque qo, secet haec diam. BA inter u et s, potest enim fieriGa naar voetnoot6). Quum ergo suspensarum omnium AC ex arcu qDBCA, centr. gr. sit in recta qo, inque ejus parte ro ut modo etiam dictum fuit, puto in p: omnium autem suspensarum per totam circumf.m centr. gr. ponatur u; cadet necessario centr. gr. suspensarum ex arcu reliquo Aq in producta pu, quod esse non potest quoniam producta pu non potest unquam transire vel arcum vel segmentum circuli AqGa naar voetnoot7), intra quod necesse est dictum centr. gr. suspensarum per arcum Aq [Fig. 35.]
reperiri. Est ergo punctum s centr. gr. omnium AC suspensarum per totam circumferentiam. Quare etiam centr. gr. curvae cycloidis ψ [Fig. 33] ita secat axem BA ut Aψ sit dupla ψB. Esto rursus quicunque arcus ACD [Fig. 35] per quem suspensae sint rectae aequales subtensis AC. dividatur bifariam in C et ducatur CD. Ostensum est centr.gr. omnium dictarum suspensarum fore in recta CD. dico autem ipsum ita hanc dividere in s ut sit Ds dupla sC. Sit enim si fieri potest primum inter s et D, velut in t. et sumatur arcus Dq tam exiguus ut omnium AC ex ipso suspensarum ad omnes suspensas ex reliquo arcu | |
[pagina 372]
| |
 [Fig. 35.]
qCA, minor sit ratio quam st ad tD. arcus qCA bifariam dividatur in o, et ducatur qo. erit arcus Co subduplus ad arcum Dq, unde intersectio r cadet inter s et C per lemma adjectumGa naar voetnoot1). Erit autem centr. gr. suspensarum ex arcu qoA in recta qo, at non in parte qrGa naar margenoot*, nam si ibi sit puta in x, debebit in producta xt esse centr. gr. suspensarum per arcum Dq, quod absurdum est quia xt producta non transit per segmentum circuli Dq. Sed neque in parte ro erit centrum gr. suspensarum per arcum qoA, nam si fuerit inibi puta in p; ergo quia omnium ex toto arcu DCA suspensarum centr. gr. est in t, erit reliquo ex arcu Dq suspensarum centr. gr. in producta pt ulterius quam ubi ea sic terminatur (ut sit pt ad adjectam sicut st ad tD)Ga naar voetnoot3), sed pt major est quam st. Ergo longe ultra circulum caderet centr. gr. suspensarum per arcum Dq quod absurdum. non ergo inter s et D potest cadere centrum gravitatis suspensarum per arcum ACD. Jam fi fieri potest sit centr. gr. idem inter s et C, puta in u. Sumatur arcus Dq tam parvus, ut, diviso bifariam arcu reliquo qCA in o, ductâque qo, secet haec rectam DC in r inter s et u: potest enim fieri quia Cu minor est quam 1/3 CDGa naar margenoot*. Cum ergo suspensarum ex arcu qoA centr. gr. sit in recta qo, et in parte ejus ro per ea quae modo dicta suntGa naar voetnoot5). sit igitur in p. Ergo centr. gr. suspensarum ex reliquo arcu Dq esset in producta upGa naar voetnoot6), quod esse nequit, quia haec non potest transire per segmentum Dq, ubicunque fuerit p in ro. Ergo neque inter s et C cadet centr. gr. omnium suspensarum per arcum ACD. quamobrem reliquum est ut sit ipsum punctum s. quod erat demonstr. Est autem demonstratio prorsus similis praecedenti qua de suspensis per totam circumf.m ostensum est. Atque ex his manifesta est ratio constructionis pag. 81 | |
[pagina 373]
| |
qua partium curvae DC, MN [Fig. 31] centr. gr. inveniturGa naar voetnoot7). Unde deinde deduciturGa naar voetnoot8) centr. gr. partis DAM esse in P ut sit AP ∞ 1/3 AQ. 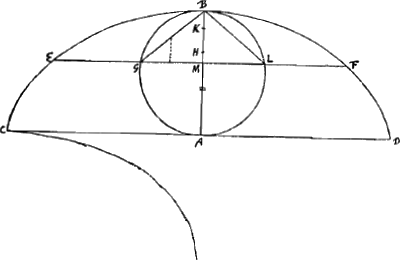 [Fig. 36.]
Est ergo haec proprietas Cycloidis et miranda profecto, quod sicut centrum grav. totius curvae axem ejus dividit, ita quoque centra gr. cujusque partis recta basi parallela abscissae suos axes dividunt, nempe ut pars ad verticem triens sit axis totiusGa naar voetnoot9). Ita hic BK [Fig. 36] est 1/3 BM, ideoque K centrum gr. curvae EBF. Cum autem BG semper sit dimidia curvae BE, hinc jam superficiei magnitudinem quae fit conversione curvae EBF circa basin EMF facile inveniemus. habet enim superficies ejusmodi ad superficiem ad eam quae fit conversione utriusque rectae GB, BL, circa GL, rationem compositam ex ratione curvae EBF ad utrumque simul GB, BL et ex ratione KM ad dimidiam BM, cum in media BM sit centr. gr. duarum GB, BL. Erit igitur superficiei ex curva EBF genitae ad superficiem è duabus GB, BL, hoc est ad duplicem conicam superficiem, rationem compositam ex 2 ad 1 et ratione 4 ad 3, nam curva est ad dictas duas rectas ut 2 ad 1, et KM ad 1/2 BM ut 4 ad 3. Est ergo ratio ea quae 8 ad 3. Idque perpetuo. unde superficies a tota curva CBD circa basin ad superficiem circuli genitoris erit ut 64 ad 3Ga naar voetnoot10), sive ut 21 1/3 ad 1. | |
[pagina 374]
| |
[Lemma]Ga naar voetnoot1). [Fig. 37.]
arcus Dq duplus co dico Dr ad rc majorem esse quam duplam. sit rf perp. oD. Ergo Df major quam dupla fo per lemm. superius. pag. 81Ga naar voetnoot2) et multo magis ergo Dr major quam dupla rc, cum sit ∠ Dco obtusus. | |
Lemma I.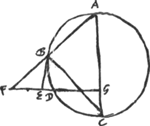 [Fig. 38.]
GDF perp. AC diametro. cui occurrit ABF. Demonstrandum rectam DF majorem esse arcu DB.
∆aABC, AGF similia sunt. ∠F ∞ ∠ACB. sit BE tangens in B. Ergo ∠FBE ∞ ∠BCAGa naar voetnoot4). Ergo ∠FBE ∞ ∞ ∠BFE. Et latus BE ∞ EF. Et BE + ED ∞ FD. Sed BE + ED majores sunt arcu BD. Ergo et FD maj. arcu BD. | |
[pagina 375]
| |
Lemma II.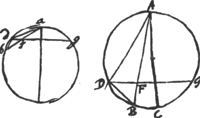 [Fig. 39].
AC diam. AB linea. DFG perp. AC. demonstrandum arcum BD majorem recta DF.
ducatur subtensa DB. arcus AG ∞ AD, Ergo ∠ADG ∞ ABD. ∠ autem DFB ∞ ∞ ADG + DAF. Ergo ∠DFB ‖ ∠ABD. Ergo in ∆DFB latus DB ‖ latere DF. quare multo magis arcus BD major recta DF. | |
[Theorema.]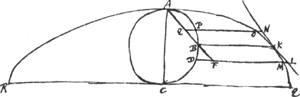 [Fig. 40.]
Sit RAQ Cycloides. K datum in ipsa punctum in quo tangens sit ducenda. ABC est circulus genitor intra cycloidem constitutus. Sit KB parall. basi QC, et jungatur BA, cui parallela sit NKL. dico eam tangere cycloidem in puncto K.
Sumatur enim in NKL punctum quodvis praeter K, ac primo altius ut N, unde agatur NQ parall. BK, quae occurrat cycloidi in O circulo ABC in P. Quia ergo PO est ∞ arcui PA ut superius dem.Ga naar voetnoot5) erit QO ∞ arc.PA + PQ. hisce autem duobus major est arc.APB, quia arc.PB major rectâ PQ per lemm. secund. Estque arcui APB aequalis BK sive QN. Ergo QN major quam QO. Ergo punctum N est extra cycloidem. deinde infra K sumatur in KL punctum L et ducatur LD parall. KB. occurrens cycloidi in M, productaque AB in F. Ergo quia DM ∞ arcui DBA. DF autem major arcu DB per lemma I. Erit FM minor arcu BA, hoc est rectâ BK sive FL. Ergo punctum L extra cycloidem. Est ergo NKL tangens in K. | |
[pagina 376]
| |
|


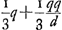 ) [ad] (
) [ad] (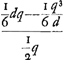 ) EP.
) EP.