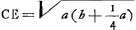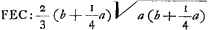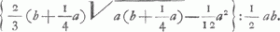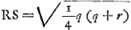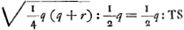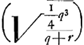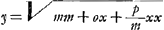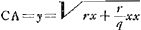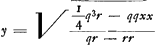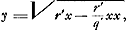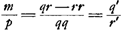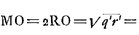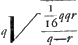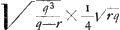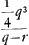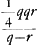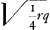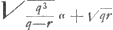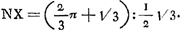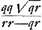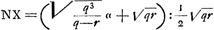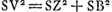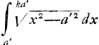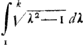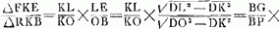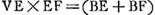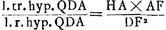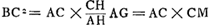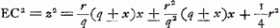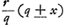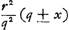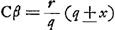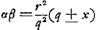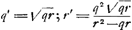|
| |
| |
| |
[Réduction de la quadrature de la surface du conoïde elliptique allongé à la quadrature du cercle, et réduction de celle des surfaces du conoïde elliptique aplati et du conoide hyperbolique à la quadrature de l'hyperbole.]
[Fig. 1.]
BA est parab. lat. rect. a.
Superficies ex tangentibus HG, GV &c. ad circulum ex CA semidiam. sunt ut omnia ▭ sub AC, HG; SQ, GV; &c. ad ▭ACO, sive 1/2 qu.AC.
CE est ∞ AD quae occurrit in A ad angulos rectos. Et ut AD sive EC ad AC ita HG ad LK sive NR. Ergo ▭ EC, NR ∞ ▭ AC, HG. Ergo ut omnia ▭ CE, NR. MQ, WL, &c. hoc est ut parabolae frustum EXBC (sunt enim puncta E, M, &c. ad parabolam cujus lat. rect. item a. sed vertex in F, sumpta BF ∞ 1/4 aGa naar voetnoot4)) ad ▭ ACO, ita superficies conoidis BAC ad circulum baseos CA. Ergo ut (4 b + a) 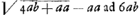 Ga naar voetnoot5) Ga naar voetnoot5).
| |
| |
| |
[Fig. 2.]
Superficies conoidis hyperbolici BA ad circulum basis suae, ut spatium EXBC ad 1/2 qu.ACGa naar voetnoot7).
[latus rectum ∞ r; latus transversum BF ∞q; BS ∞ ∞ 1/2 BF; BC ∞ x; AD ∞ EC ∞ z.]
CD ∞ 1/2 r + rx/qGa naar voetnoot8)
| |
| |
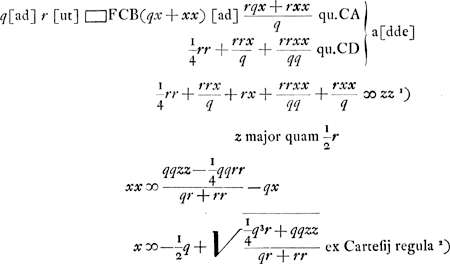
Ga naar voetnoot1)Ga naar voetnoot2)

Fig. 2.]
T vertex hyperb. TE. ST sumenda ∞ m hoc est 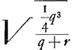 . Ergo sit BY ∞ 1/2 r et SR media prop. inter SY, SB. Et ut RS ad BS ita sit BS ad TS Ga naar voetnoot3).
p [ad] mGa naar voetnoot4) [hoc est] qq [ad] qr + rr [ut] 2 m [h.e.]  [ad] 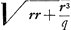 latus rect. hyperb. TE. Ergo media prop. inter hoc et l. transv. erit 2SO ∞ √ rq ∞ diam. conjugatae hyperb. TE. Ergo cum hyperbolae TE, BA habeant eandem diam. conjug. m habebunt latera recta reciproce rationem laterum transversorum Ga naar voetnoot5).
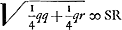 Ga naar voetnoot6) Ga naar voetnoot6); R est focus hyperb. BA, OB ∞ SR. RG ∞ 1/2 r.
| |
| |
| |
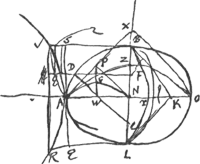
[Fig. 3.]
[latus rect. ∞ r; latus transv. BL ∞ q; BF ∞ x; DC ∞ EF ∞ z.]
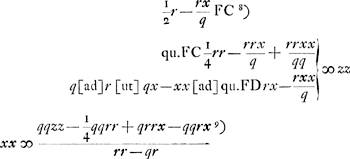
Ga naar voetnoot8)Ga naar voetnoot9)
| |
| |

(Fig. 3.]
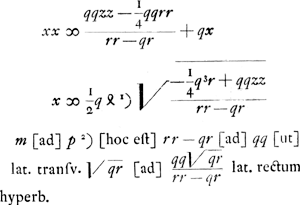
Ga naar voetnoot1)
m [ad] pGa naar voetnoot2) [hoc est] rr - qr [ad] qq [ut]
lat. transv. √qr [ad] qq√qr/rr - qr lat. rectum hyperb.
Ergo diam. conjugata 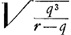 Ga naar voetnoot3) Ga naar voetnoot3).
AE est hyperb. centrum ejus N. vertex A.
Superficies sphaeroidis dimidij ABO est ad circ. AO ut spatium RAVBL ad qu. ANGa naar voetnoot4).
Sit AP + PN ∞ BV ∞ 1/2 lat. rect.Ga naar voetnoot5) AGN parab. ut GW sit ∞ 1/2 PWGa naar voetnoot6).
Erit ut linea parabolica AGN ad 1/4 lateris recti ellipsis ita superficies spheroi- | |
| |
dis dimidij ABO ad circulum AO. Vel sumpta parabola dupla, ut sint AX, XO singulae ∞ 1/2 latus rectum, erit curva AZO ad 1/4 lat. rect. sicut tota spheroidis superficies ad dictum circulum AO.
Applicato spatio RAVBL ad lineam BL ∞ q fit longitudo parabolae AGN. applicato vero quadr.o AN ad lin. BL, fit 1/4 rGa naar voetnoot7).
NO ∞ BK ( 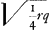 ) [ad] BN (1/2 q) [ut] XA (1/2 r) [ad] AN ( 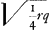 ) hinc video mutari posse constructionem ut pro ∆ oAXO sumatur BKL. et pro 1/4 lat. recti sumatur 1/4 AO Ga naar voetnoot8).
| |
Constructio.
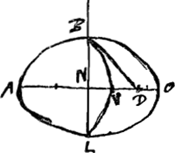
[Fig. 4.]
Sphaeroidis lati axis est BL, sectio per axem ellipsis ABOL cujus diam. maxima AO. BD ∞ NO, sive D est focus.
NV ∞ 1/2 ND. BVL est parab. axis VN. Sicut linea parabolica ad 1/4 AO ita superf. sphaeroidis ad circulum OA.
Circulus cujus semidiam. est media proport. inter OA et curvam BVL, aequalis est superficiei sphaeroidisGa naar voetnoot9).
| |
| |
| |
3 Febr. 1658.
AT ∞ q. lat. rect. Ellipsis A[N]T[X] ∞ r. [AB ∞ x; BWGa naar voetnoot2) ∞ z]. Superficies QAZ partis sphaeroidis, ad circulum QZ, vu spatium WFACY ad qu. QBGa naar voetnoot3).
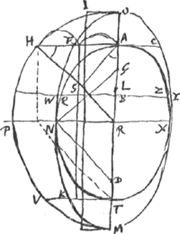
[Fig. 5.]
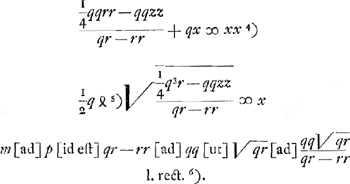
Ga naar voetnoot4)Ga naar voetnoot5)Ga naar voetnoot6).
Ergo dupla  Ga naar voetnoot7) Ga naar voetnoot7).
AL Ga naar voetnoot8) ∞ 1/2 r. RG media inter RL, RA, ergo 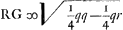 . Ut RG ad RA ita haec ad RO, ergo RO ∞ 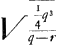 ∞ RH ∞ RP.
| |
| |
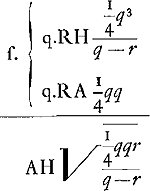
quia qu. RH ad qu.AH ut q ad r, ideo RH ad HA ut q ad √rq, hoc est ut RA ad RN. Sit ND ∞ RT, et RH parall. DN. Est autem D focusGa naar voetnoot9).
Superficies sphaeroidis dimidij NAX ad circulum NX ut spatium AFNKT ad qu.NRGa naar voetnoot10).
fiatut AFNKT [ad] AHPVT, [idest] NR ( 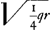 ) [ad] RP ( 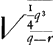 ) [ita]
| |
| |
qu.NR (1/4 qr) [ad] aliud spatium 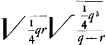 , h[oc] est 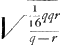 Ga naar voetnoot1) Ga naar voetnoot1).
hoc applica ad OM ∞ 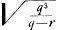 fit 1/4 √ rq ∞ OI ∞ 1/2 RN.

[Fig. 5].
itaque jam superfic. sphaeroidis dimidij NAX ad circulum NX ut spatium AHPVT ad ▭ IM. sit AS perpend. in RH. Itaque spatium AHPVT aequatur ▭o sub RP et HPGa naar voetnoot2) + AS, quarum AS aequalis supra ostensa est ipsi RNGa naar voetnoot3). Ergo dicta superf. ad dictum circulum ut ▭ sub PR et HP + NR ad ▭ IM, hoc est ▭ sub RO, sive RP, et RN. Unde abjecta communi altitudine PR, erit dicta superficiei ad circulum ratio ea quae HP + NR ad NR. Et duplicatis antecedentibus erit tota sphaeroidis superf. ad circulum NX ut HPV + NX ad NR.
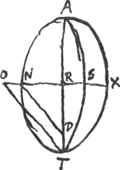
Ergo constructio est haec [Fig. 6]. Sphaeroidis oblongi axis est AT. sectio per axem Ellipsis ANTX, minor axis NX. ND ∞ RT sive D est focus Ellipseos.
| |
| |
[Fig 6.]
TO parallela DN Ga naar voetnoot4). TSA estarcus circuli descriptus centro O radio OT. Sicut TSA + NX ad RX, ita superficies sphaeroidis NAXT ad circulum NX.
Vel, sit D focus, superque AT arcus AST semidiametro tertia proport.i duabus RD, RT.
Vel potius, sit TO tertia prop. duabus RD, RT.
Circulus cujus semidiam. media est proport. inter RN et lineam aequalem AST + NX, aequatur superf.ei spheroidisGa naar voetnoot5).
Sphaeroidis sectio per axem est ellipsis [NAXT]Ga naar voetnoot6) ejusmodi ut latus transv. [AT] sit sesquitertium lateris recti. Dico superficiem conoidis ad circulum per centrum cujus diam. [NX] esse ut triens peripheriae circuli una cum sua subtensa ad ejusdem subtensae semissemGa naar voetnoot7).
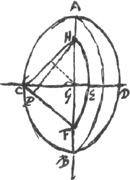
[Fig. 7].
HGa naar voetnoot8), F sunt foci, sive CH ∞ GA. FEH circumf. centro C. Semisuperf. sphaeroidis ad maximum circulum CD ut sector CFEH cum ∆CFH ad ∆CFHGa naar voetnoot9). vel ut arcus HEF cum perpendiculari HP ad HP.
Ergo si axis sphaeroidis oblongi ad diametrum eam habeat rat.m quam radius circuli ad perpend. quae ex centro in latus cadit alicujus polygoni ordinati circulo inscripti; Erit dimidia sphaeroidis superf. ad maximum in eo circulum sicut circulus una cum illo polygono inscripto ad ipsum polygonum.
| |
| |

[Fig. 6.]
Si [AST]Ga naar voetnoot1) sextans peripheriae erit 1/2 superficies sphaeroidis ad circulum maximum [NX], ut circulus cum inscripto sibi hexagono ad ipsum hexagonum. atqui ita porro, si peripheria [AST] metiatur circumferentiam.
Ut autem fiat commensurabilis debet [TA] ad [NX] eam habere rationem quam radius circuli ad perpendicularem quae ex centro cadit in latus polygoni alicujus inscripti. quia videlicet [AT] ad [NX] ut [TR] sive [ND] ad [NR], hoc est [OT] ad [OR].
Sive [AST] peripheria non sit commens. circumferentiae; erit semisuperficies sphaeroidis ad circulum [NX] ut sector [OAST] cum ∆[OAT] ad ∆[OAT].
| |
§ 1.

[Fig. 8.]
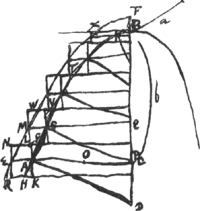
Dato sphaeroide quovis lato seu compresso, potest inveniri conoides hyperbolicum, vel dato hyperbolico potest inveniri sphaeroides, et utriusque simul superficiei inveniri circulus aequalisGa naar voetnoot3). Huc pertinent quae hac et proxima pagina continenturGa naar voetnoot4).
SO, ST, OX debent esse proportionales sive OX ∞ 1/2 l. rect.Ga naar voetnoot5) TX est hyperbola cujus centr. S vertex TGa naar voetnoot6). Ergo data est. datumque ideo hyperbolae lat. rectum et diam. conjugataGa naar voetnoot7).
Invenienda autem est alia BG, quae idem habeat centrum S et eandem diam.m conjuga- | |
| |
tam cum hyp. TX. utque, posito V foco hyp. BG, sint proportionales ST, SB, SV.
His enim factis, serviet hyperb.TX, tam superficiei sphaeroidis dimid. LOT dimetiendae quam superficiei conoidis hyperbolici BGGa naar voetnoot8).
Oportet autem ad hoc, ducta BA tangente, ducere ex A rectam AR quae abscindat portionem AXR ∞ XAT. quod fieri posse docetur pag. sequentiGa naar voetnoot9).
Eo autem facto, erit superf. ex BGH hyperb. ad circulum TL ut spat. RXABK ad 1/2 qu.STGa naar voetnoot10). Superf. autem dimidij sphaeroidis TOL ad circulum TL ut spatium TAXOS ad 1/2 qu.STGa naar voetnoot11). Ergo utraque simul dictarum superfic.m ad utrumque simul spatium RXABK, TAXOS, hoc est ad duo trapezia RABK, XTSO, ut circulus TL ad 1/2 qu.ST. Et permutando. quare duarum superfic.m ad circ. TL data erit ratio.
| |
| |
| |
| |
| |
[Problema I.]
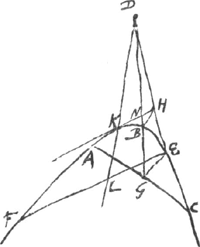
[Fig. 9.]
ABC est portio hyperb. centr. D. diam. BG. E est punctum in hyperb. datum. Oportet ducere EF, quae abscindat portionem EKF ∞ ABC.
Constr. ut DB ad BG ita sit DH ad HE. Et sit tangens HKGa naar voetnoot6), et EF parall. HK.
Ducta enim DKL, erit DK ad KL ut DH ad HE, hoc est, ut DB ad BG. Ergo portio FKE ∞ ABC ut
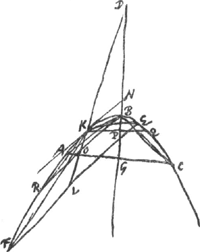
[Fig. 10.]
hic demonstrabitur Ga naar voetnoot7).
Jungatur KB [Fig 10]. Et sit BR parall. KN. KQ paral. AC. Ergo quia NK est tangens, erunt proportionales DN, DB, DP, ut in hac pag. supra ostenditurGa naar voetnoot8).
Ergo DK ad DO ut DB ad DP. Ergo ∆KBO ∞ ∆KBPGa naar voetnoot9). Ergo et portio KBQ ∞ portioni BKR. Nam haec consequ. ostendi potestGa naar voetnoot10).
Sed ∆FKE ad ∆RKB ut ∆ABC ad ∆KBQ quia DL similiter divisa in K, O, ac DG in B et PGa naar voetnoot11) Ergo ∆FKE ∞ ∆ABC. Ergo et portio FKE ∞ portioni ABCGa naar voetnoot12).
| |
| |
| |
[Problema II.]

[Fig. 11.]
AB est hyperb. D centrum. C punctum datum non extra asymptotosGa naar voetnoot1). CB ducenda tangens.
Constr.o DCA lin. recta. DC, DA, DF proportionales. AG tangens, FB parall. AG. CB est tangens quaesita.
Quia enim FB ordin. appl. ad AFGa naar voetnoot2), suntque proportionales DF, DA, DC. Erit CB tangensGa naar voetnoot3).
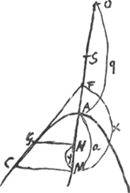
[Fig. 12.]
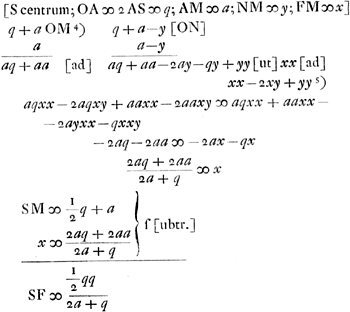
Ga naar voetnoot4)Ga naar voetnoot5)
| |
| |
SM (1/2 q + a) [ad] SA (1/2 q) [ut] SA (1/2 q) [ad] SF ( 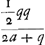 ) Ga naar voetnoot6) bon.
| |
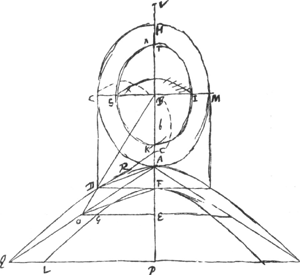
[Fig. 13.]
Axis sphaeroidis CMGa naar voetnoot8).
Ut conveniat hyperbola AD Ellipsi AC debent esse prop.es CB, BA, CD sive CD ∞ 1/2 l. rect.Ga naar voetnoot9) Ut autem conveniat hyperbola AD hyperbolae FGL, debet sumptis BA, BF, BE propor.bus, esse E focus hyperb. FGLGa naar voetnoot10). B centr. FD vel CB ∞ 1/2 l. rect.Ga naar voetnoot11)
| |
| |
BA [ad] BF h[oc] e[st] BF ad BEGa naar voetnoot1) ut BD ad BOGa naar voetnoot2). Ergo OGE recta lineaGa naar voetnoot3). DA paral. OFGa naar voetnoot4).
Spatium QDFP ∞ QODRAP quia QDO ∞ ODRA ∞ DRAF Ga naar voetnoot5). Spatium

[Fig. 13.]
rectilin. QODFP ∞ ∆QAP quia ∆ODA ∞ ∆DAF Ga naar voetnoot6).
Sicut spatium QDFP (∞ ∞ QODRAP) ad 1/2 qu. BA ∞ 1/2 bb ita superf. LGF conoidis ad circulum à rad.bGa naar voetnoot7).
Sicut spat. DRABC ad 1/2 qu.BA ℞ 1/2 bb ita 1/2 superf. sphaeroidis HCAM cujus axis CM (vel ita superficies tota sphaeroidis KSTI sumtis BK et BS potentia subduplis ad BA et BC) ad circ. à rad.bGa naar voetnoot8).
Ergo sicut totum spat. QODCBAP ad superf. conoidis FL et sphaeroidis KS ita 1/2 bb ad circ. à rad.b. Et permutando spat. QODCBAP ad 1/2 bb ut superf. conoidis FL + superf. sphaeroid. KS ad circul. à rad. b.
| |
| |
| |
| |
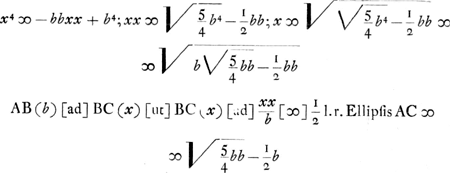

[Fig. 14.]
BA ∞ b 1/2 lat. tr. Ellipsis AC. BA divisa in N [Fig. 14] secundum extremam et mediam rationem. major pars NA est 1/2 lat. rectum Ellipsis AC.
Hyperbolae AQ lat. rect. aequale transv.oGa naar voetnoot1) nimirum bGa naar voetnoot2).

Ga naar voetnoot3)
Ergo 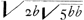 ∞ rad. circ. duabus superf. bus aequalis. Haec melius in adjuncta paginaGa naar voetnoot4).
| |
| |
BE [Fig. 13] secta est in A secundum extremam et mediamGa naar voetnoot5). BA ad AE ut BA ad 1/2 l. rect. ellipsis ACGa naar voetnoot6). Ergo AP ∞ l. r. Ellipsis AC ∞ 2xx/b quae ante inventa fuit 2b3/xx - 2bGa naar voetnoot7).
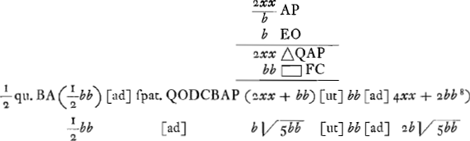
Ga naar voetnoot8)
Ergo 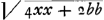 h. est  aequatur radio circuli qui aequalis est superficiebus sphaeroidis STK et conoidis hyp. i FLP.
Vel sumatur potius  Ga naar voetnoot9) Ga naar voetnoot9).
Constr.oGa naar voetnoot10) Sit [Fig. 15] datum sphaeroides cujus centrum O, axis SI, diameter TK.
Sumatur BC potentia dupla ad OS. Et BA potentia dupla
| |
| |

[Fig. 15.]
ipsius OK. Et sint quatuor hae continue proportionales BC, BA, BF, BEGa naar voetnoot1). et ponatur EP ∞ ∞ EA. Et intelligatur conoides hyperbolicum FQN, cujus axis FP axi adjecta sit FB sive 1/2 l. tr.; 1/2 latus vero rectum BC Ga naar voetnoot2). Dico hujus conoidis superficiei una cum superficie sphaeroidis TK aequare circulum cujus semidiam. possit quadr. TK cum duplo qu. o SI.
E est umbilicus hyperb. QFNGa naar voetnoot3).
Nota quod etiam BC ad BF hoc est lat. rectum hyperb. QF ad latus transversum eam habet rationem quam lat. rect. ellipsis SK ad suum lat. transv. TKGa naar voetnoot4). hoc est quam major pars ad totam linea divisam ἄϰρον ϰαὶ μέσον λόγονGa naar voetnoot5).
| |
3 Feb. 1658.
Sphaerae superficiei Archimedes circulum aequalem deditGa naar voetnoot7), nos superficiei conoidis paraboliciGa naar voetnoot8).
| |
| |
Si vero detur circulus aequalis superficiei sphaeroidis cujusvis data erit quadratura circuli, et hyperbolae quadratura. Nam si sphaeroidis oblongi superficiei circulus aequalis detur, data erit circuli quadratura, et contraGa naar voetnoot9). Si autem superficiei conoidis lati circulus aequalis detur, data erit quadratura hyperbolae, et contraGa naar voetnoot10). Data autem hyperbolae quadratura, datur longitudo lineae parabolicae, et contraGa naar voetnoot11). Ergo data hic longitudine lineae parabolicae datur etiam circulus aequalis superficiei sphaeroidis lati. Rursus, dato circulo qui aequalis sit superficiei conoidis hyperbolici, datur quadratura hyperbolaeGa naar voetnoot12), ergo et longitudo parabolicae lineae; et circulus aequalis superficiei sphaeroidis lati. Et contra ex superficie sphaeroidis lati innotescit superficies conoidis hyperbolici. Data autem unius sphaeroidis conoidisve hijperbolici superficie datur infinitorum aliorum dissimilium; quoniam &c.
dato sphaeroide lato potest conoides hyperbolicum inveniri, vel dato conoide hyperbolico potest sphaeroid. latum adinveniri et utriusque simul superficiei circulus aequalis effici exactèGa naar voetnoot13).
Sphaeroidis omnis oblongi superficies aequalis est circulo, cujus semid. media proportionalis inter semidiametrum sphaeroidis (hoc est dimidium ejus quae per centrum ducitur axi ad angulos rectos) et lineam aequalem utrisque, diametro sphaeroidis et arcui peripheriae descriptae super axe sphaeroidis, cujus peripheriae diameter sit ad dictum axem ut axis ad distantiam umbilicorum in sectione per axemGa naar voetnoot14).
Sphaeroidis omnis lati superficies aequalis est circulo, cujus semidiam. est media proportionalis inter diametrum sphaeroidis et lineam parabolicae portionis rectam cujus basis sit axis sphaeroidis, altitudo verò aequalis quartae parti distantiae umbilicorum in sectione per axemGa naar voetnoot15).
| |
| |
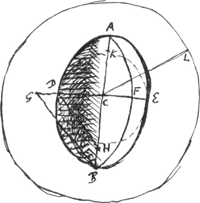
[Fig. 16.]
DH ∞ CB. H umbilicus. BG parall. HD. CL media inter CD et DE + AFB.
superfic. sphaeroidis ad superfic. sphaerae inscr. ut DE + AFB ad 2DE.
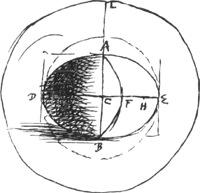
[Fig. 17.]
H umbilicus. CF = 1/2 CH. AFB parab. CL media inter DE et AFB.
superficies sphaeroidis ad superf. sphaerae circumscr. ut AFB ad DE.
ad superf. cylindri circumscr. ut AFB ad AB.
3 Feb. 1658.
| |
| |
| |
Aliqui per indivisibilia. Sed falluntur si pro demonstratione ea venditentGa naar voetnoot2). Caeterum ad fidem faciendam apud peritos haud multum interest, an demonstratio absoluta tradatur an fundamentum ejus demonstrationis, quo conspecto non dubitent demonstrationem perfectam dari posse. fateor tamen etiam in hac rite instituenda ut clara concinna omniumque aptissima sit, peritiam et ingenium elucere, uti in Archimedis omnibus operibus. verum et prior et longe praecipua est inveniendi ratio ipsa, hujus cognitio potissimè delectat atque a doctis expetitur, quamobrem magis etiam haec methodus sequenda videtur qua brevius clariusque comprehendi et ob oculos poni potest. Tum verò et nostro labori parcimus in scribendo, et aliorum in legendo, quibus vacare tandem amplius non poterit, ut ingentem multitudinem Geometricorum inventorum quae augetur in dies doctoque hoc saeculo in immensum porro exitura videtur, evolvant, si quidem prolixam illam ac perfectam veterum methodum scriptores usurpant.
In praecedentibus tamen hanc retinuimus jam olim ita perscriptisGa naar voetnoot3) ut argumento ac quodammodo exemplo sint quo appareat etiam reliqua ad hunc modum perfici potuisseGa naar voetnoot4).
Egregia est illa er subtiliter reperta veterum ratio demonstr. per inscripta er circumscripta ad absurdum deductio et certitudine mirabili. Et in illo Geometriae exortu cum novum etiamnum et pene incredibile videretur res tantas tamque reconditas ex parvis initijs confirmari, omnino necessaria.
| |
| |

[Fig. 18.]
dicoGa naar voetnoot1) esse AB ad C ut DE ad F. Sit enim primò AB ad C minor quam DE ad F. Et sit si potest GA ad C ut ED ad F et circumscribatur HA simulque DK.
Quia ergo ponitur GA ad C ut ED ad F erit minor ratio HA ad C quam ED ad F. Sed ut HA ad C ita KD ad F. Ergo minor quoque ratio KD ad F quam ED ad F. Ergo KD minor quam ED quod absurdum.
Sit jam si potest ratio BA ad C major quam ED ad F, eademque quae SD ad F, et circumscribatur KD, simulque HA. Ergo KD at F habet minorem quam BA ad C. Sed KD ad F ut HA ad C. Ergo et HA ad C minorem quam BA ad C. Ergo HA minor quam BA quod absurdum.
[Fig. 19.]
in omnibus fieri posse. in parabola ex. gr. sic.Ga naar voetnoot2).
fig. adjuncta voceturGa naar voetnoot3).
describatur simul ordinatè circumscriptaGa naar voetnoot4) et ex ea adjuncta.
| |
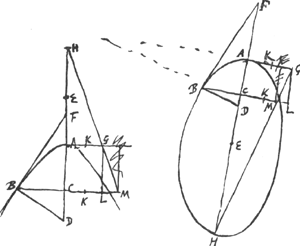
[Theorema I.]
Si a quovis in parabola puncto [Fig. 20] recta linea ad axem parabolae terminata ducatur, perpendic. ei quae in adsumto puncto parabolam contingit perque idem punctum quaedam ordinatim ad axem applicetur quae sit aequalis lineae prius ductae. Terminus illius ordinatim applicatae parabolam aliam continget positionè datamGa naar voetnoot5).
| |
| |
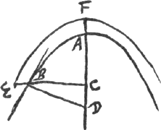
[Fig. 20.]
Sit parabola AB, cujus axis AD, vertex A, et sumto in ea puncto B, ducatur BD quae parabolae vel parabolam in puncto B contingenti sit ad angulos rectos, sitque CBE ordinatim ad axem AD applicata et aequalis ipsi BD. dico hujus terminum E contingere parabolam aliam FE, cujus quidem latus rectum idem sit quod parabolae AB, axisque FD cum axe AD conveniat, vertex vero F altior sit vertice A intervallo AF quod aequet quartam partem lateris recti.
Constat enim CD aequalem esse semissi lateris rectiGa naar voetnoot6). Quia ergo quadr. EC sive BD aequale est quadratis duobus BC et CD quorum BC qu, aequale est ▭ a latere recto et AC comprehenso, quadr. vero CD aequale quartae parti quadrati à latere recto. hoc est ▭ ex AF et latere recto. Erit igitur qu.EC aequale rectangulo quod tota CF et latere recto parabolae FE continetur. quare punctum E in parabola FE esse liquet.
| |
[Theorema II.]
[Fig. 21.]
Si à quovis puncto in hyperbola aut ellipsi duae rectae ad axem sectionis ducantur, quorum altera sit applicata ordinatim, altera perpend. ei quae in eodem puncto sectionem contingit, Erit pars axis ab utraque intercepta in hyperbola quidem aequalis hisce utrisque, dimidio lateri recto, et ei lineae quae sit ad portionem axis inter verticem et ordina-
| |
| |

[Fig. 21.]
tim applicatam interceptam, sicut latus rectum sectionis ad latus transversum. In ellipsi vero aequalis ei quo prior harum alterum exceditGa naar voetnoot1).
Sit hyperbola vel ellipsis AB. cujus axis AC, diameter transversa AH. centrum sectionis E. Et à puncto B in sectione sumpto ducatur BC ad axem ordin. appl.a, BD vero perpend. tangenti sectionem in puncto B, quae sit BF.
Sit porro latus rectum sectionis AG insistens axi ad angulos rectos, et ducatur HGM, occurrens ordinatim applicatae BC in M. eidemque occurrat GL parallela AC. Et secetur CL bifariam in K. Est igitur LK dimidio lateri recto aequalis, LM vero ei lineae quae est ad LG sive portionem axis AC sicut latus rectum GA ad latus transversum AH, et MK in hyperbola utrique illarum aequalis: in ellipsi vero ei quo KL ipsam LM superat. Dico itaque utrobique KM esse aequalem parti axis CD a duabus BC, BD interceptaeGa naar voetnoot2).
Quia enim ▭ AC, CM aequale est quadr.o CB..... Conic.Ga naar voetnoot3) itemque ▭ DCF aequale eidem qu.o CB, propter angulos rectos DBF, DCB. Erit ergo ▭ AC, CM aequ. ▭o FCD, ideoque AC ad CF ut CD ad CM. Quia autem BF sectionem in B contingit, erunt per... Con.Ga naar voetnoot4) proportionales EF, EA, EC. ideoque ut EA ad EC, hoc est HE ad EC, ita FA ad AC; et componendo ut HC ad EC ita FC ad AC. Sed ut FC ad AC ita erit CM ad CD. Ergo CM ad CD ut HC ad EC sed ut HC ad EC ita quoque est CM ad KM. quoniam CM similiter divisa est in L atque HC in A, sectaque bifariam est LC in K et AH in E. Itaque est sicut CM ad CD ita CM ad KM; Quare CD aequalis KM. quod erat demonstr.
| |
| |
| |
[Theorema III.]
Iisdem positis si ea quae ordinatim applicata est extra sectionem producatur donec aequalis fiat illi quae ducta est contingenti perpendicularis, productae terminus aliam coni sectionem continget positione datam in hijperbola hyperbolenGa naar voetnoot5) in ellipsi vero ellipsin aut hyperbolen, prout ad majorem aut minorem ellipsis axem ordinatim applicata fueritGa naar voetnoot6).
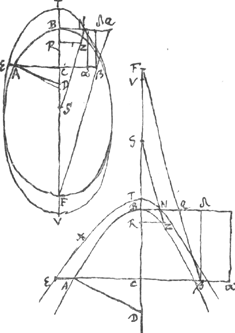
[Fig. 22.]
Sic sectio hyperbolae aut ellipsis AB, cujus axis transvers. BF (sit autem primum BF axis major ellipseos) latus rectum BQ ad axem perpendiculare. Centrum sectionis S. Et à puncto A in sectione sumto, ducta sit AD, occurrens sectioni sive tangenti sectionem in A ad angulos rectos, et applicetur ad axem ordinatim CAE ipsi AD aequalis, dico terminum ejus E contingere sectionem aliam positione data TX. quae hyperbole erit si sectio BA sit hyperbole, si vero ellipsis ellipsis; centrum idem habens cum sectione AB axemque axi convenientem, latera vero transversum et rectum reciproce proportionalia lateribus sectionis AB. Et latus quidem transversum VT quod ad latus transversum FB sit potentia, sicut latus transversum FB, ad compositam ex ipsa FB et latere recto BQ in Hyperbolae in Ellipsi vero ad utriusque differentiamGa naar voetnoot7).
| |
| |

[Fig. 22.]
Jungatur enim FQ, et producatur occurratque rectae AC in β, et sit duabus FC, Cβ tertia proportionalis βα addenda ipsi Cβ in hyperb. in ellipsi vero auferendaGa naar voetnoot1). et compleatur rectangulum CβδB itemque ▭ δα. Sit etiam duabus ST, SB tertia prop.is SR; et ducatur RZ parallela BQ itemque SZ parall. FQ quae secabit latus rectum bifariam in N.
Quia igitur ut VT ad FB sive ut ST ad SB ita ponitur reciproce esse BN dimidium lat. rect. sectionis BA ad 1/2 l. rect. sectionis TX: sicut autem ST ad SB, hoc est, sicut SB ad SR ita BN ad RZ: Erit proinde RZ dimidium lat. rect. sectionis TXGa naar voetnoot2). Quamobrem si ostensum fuerit sicut ST ad RZ ita esse ▭ VCT ad qu. AD seu qu.CE, constabit punctum E contingere sectionem TXGa naar voetnoot3). Illud vero sic ostendemus.
Quoniam aequales sunt BT, FV erit ▭ VCT aequale duobus rectangulis FCB et VBT: In hyperbole per prop. 24. lib. 7 PappiGa naar voetnoot4). In Ellipsi vero per prop. 57 ejusdem libriGa naar voetnoot5). quia autem ut ST ad TB ita SB [ad] BR, erit etiam ut utraque simul ST, SB sive ut VB ad utrumque simul TB, BR hoc est ad
| |
| |
TR ita ST ad TB: ideoque ▭ VBT ∞ ▭ STR. Itaque ▭ VCT aequabitur ▭ FCB + ▭ STR.
Jam vero quoniam est ST ad SB potentia, hoc est ST ad SR longitudine ut SB ad utramque simul SB, BN in hyperbole; in ellipsi vero ad harum differentiamGa naar voetnoot6), Erit dividendo in hyperb., in ellipsi autem per conversionem rationis, ST ad TR ut SB ad BN. hoc est ut FC ad Cβ. Sed quia Cβ ad βα ut FC ad Cβ ex constr. hoc est ut SB ad SN, hoc est ut ST ad TR: Erit Cβ ad Cα ut ST ad SR, hoc est ut TR ad RZ; nam ST erat ad TR ut SB ad BN, hoc est, ut SR ad RZ, ideoque permutando ST ad SR ut TR ad RZ. Quia igitur ostendimus esse ut ST ad TR ita FC ad Cβ. utque TR ad RZ ita Cβ ad Cα. Erit ex aequo ut ST ad RZ ita FC ad Cα. atque ita ▭ FCB ad ▭ αC, CB. seu Bα rectangulum.
Rursus quia ut ST ad TR ita SB ad BN erit ▭i STR ad ▭ SB, BN duplicata ratio ejus quam ST ad SB, ac propterea eadem quae ST ad SR. Sed ▭ SB, BN est ad qu.BN ut SB ad BN, h.e. ut SR ad RZ, ergo ex aequo ▭ STR erit ad qu.BN ut ST ad RZ. Sed et ▭ FCB ostensum est ad ▭ Bα esse ut ST ad RZ, Ergo ut ST ad RZ ita utrumque simul et ▭ FCB et ▭ STR, hoc est ita ▭ VCT, ad utrumque horum, ▭ Bα et qu.BN.
Haec autem utraque simul aequalia esse qu.oAD vel CE deinceps ostendemus. Nam primo quidem in hyp. ▭ Bα aequale est ▭ Bβ et ▭ δα e quibus ▭ Bβ aequatur qu.oACGa naar margenoot*. ▭ vero δα ▭o BδQGa naar margenoot*, quoniam videlicet latera reciproce
| |
| |

[Fig. 22.]
proportionalia sunt scil. ut βδ ad δQ, hoc est ut FC ad C β ita C β ad βα ex constr. Ergo ▭ B α + qu.BN aequalia sunt qu.AC. et ▭ B δQ et qu.BN, sed ▭ B δQ + qu.BN aequantur quadr. oδN per .... secundi Elem. Ga naar voetnoot1) hoc est qu.CD per anteced. mGa naar voetnoot2). Ergo ▭ B α + + qu.BN aequalia qu. is ex AC et CD hoc est qu.AD sive EC.
In ellipsi vero idem sic ostenditur. qu.BN ∞ ∞ ▭ BδQ + qu.Nδ. per 2. Eucl.Ga naar voetnoot3) sed ▭ BδQ ∞ ▭ δβ, βα, quia ut βδ ad δQ hoc est ut FC ad Cβ, ita Cβ sive Bδ ad βα, ex constr. Quadr. igitur BN ∞ qu.Nδ + ▭ δα hoc est qu.CD + ▭ δα, nam CD ∞ Nδ per antecedendemGa naar voetnoot2). Addito jam utrinque ▭ αB, fiet qu.BN + ▭ αB ∞ qu.CD + ▭ δα + ▭ αB, hoc est qu.CD + ▭βB. Sed ▭ βB ∞ ∞ qu.ACGa naar voetnoot4). Ergo qu.BN + ▭ αB ∞ qu. CD + qu.CA, hoc est qu.oDA. sive qu.CE. sicut in hyperbola quoque ostensum est. Erat autem utrobique sicut ST ad RZ, hoc est ut latus transversum sectionis TX ad ejusdem latus rectum, ita ▭ VCT ad ▭ Bα + qu.BNGa naar voetnoot5). Ergo ut dictum latus transversum ad latus rectum ita apparet esse ▭ VCT ad qu.CE. Ideoque punctum E contingere sectionem TX. quod erat dem.
AccipiaturGa naar voetnoot6) jam pro latere rectoGa naar voetnoot7) minor ellipseos axis BF [Fig. 23] ad quae ordinatim applicata sit AC. ductaque ut prius AD quae contingenti Ellip-
| |
| |
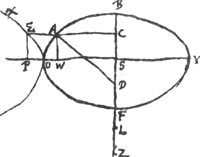
[Fig. 23.]
sim in A occurrat ad ang. rectos. Ipsique AD aequalis statuatur CAE. dico terminum ejus E contingere hyperbolen OX positione datam. cujus nimirum latus transversum axi adjacens sit ipse major ellipseos axis OY. latus rectum autem quod ad latus transversum OY eam habeat rationem quam qu. lateris transversi Ellipseos BF, ad id quo qu. lateris recti ellipseos excedit ▭ ab lateribus recto et transv. contentum Ga naar voetnoot8), hoc est (ponendo SZ ∞ 1/2 lat. recti ellips., sumtisque quantitatum dictarum quartis partibus) eam quam qu.BS ad ▭ SZF. Est enim ▭ SZF ∞ ei quo qu.SZ superat ▭ ZSF, hoc est quartae parti ejus quo qu. lateris recti ellipsis superat ▭ a latere transverso et recto comprehensum.
Ducantur enim à punctis A, E axi majori OY ad ang. rectos, AW, EP. Sit CL ∞ SZ. Quoniam igitur per praeced.Ga naar voetnoot2) pars axis CD rectis AC, AD intercepta aequalis est ei quo 1/2 latus rectum ellipseos excedit lineam quae sit ad BC ut latus rectum ad latus transversum: Est autem CL ∞ 1/2 lateri recto. Ergo DL erit praedicta linea, quae nimirum erit ad BC sicut latus rectum ellipseos ad latus transv. sive sumtis horum dimidijs, ut CL ad SB. quare et perm.o et convertendo erit CL ad LD ut SB ad BC. Et per conv.m rationis LC ad CD ut BS ad SC; et permut.o rursus, LC sive ZS ad SB ut DC ad CS. Sicut autem ZS ad SB, ita est qu.OSGa naar voetnoot9) ad qu.SB, utque qu.OS ad qu.SB ita est ▭ OWY ad qu.WAGa naar voetnoot10). Ergo etiam ut DC ad CS ita ▭ OWY ad qu.WA. Sed ut DC ad CS ita ▭ DCS ad qu.CS sive ad qu.WA. Ergo ▭ DCS ∞ ∞ ▭ OWY.
Est autem qu.DC ad ▭ DCS ut DC ad CS. Ergo etiam qu.DC ad ▭ OWY ut DC ad CS hoc est ut ZS ad SB hoc est ut qu.ZS ad ▭ ZS, SB. Itaque et divid.o erit qu.DC ad qu.DC - ▭ OWY ut qu.ZS ad qu.ZS - ▭ ZSB h.e. ad ▭ SZF. Est autem qu.DC - ▭ OWY ∞ ▭ YPO. nam ▭ YPO ∞ qu.PS - qu.SO, hoc est qu.CD + qu.AC - qu.SO; sed qu.SO ∞
| |
| |

[Fig. 23.]
∞ qu.AC sive qu.WS + ▭ OWY. Ergo qu. PS - qu.SO ∞ qu. CD - ▭ OWY ut dicebamus. Et perm. oGa naar voetnoot1) qu.DC ad qu. ZS sive qu.CL ut ▭ YPO ad ▭ SZF. sed ut qu.DC ad qu.CL ita est qu.SC ad qu.SB; ostensum enim est autem quod DC ad CL ut SC ad SB; Ergo ut q.SC ad q. SB ita ▭ YPO ad ▭ SZF. Et permutando q.SC seu q.EP ad ▭ YPO ut qu.SB ad ▭ SZF, hoc est ex hypoth. ut latus rect. hyperboles OX ad ejusdem lat. transv. Ideoque punctum E contingit hyperb. OX. quod erat dem.
|
-
voetnoot1)
- La Pièce, que nous avons divisée en quatre Parties et en paragraphes, a été empruntée aux p. 103-113 du Manuscrit A et à quelques feuilles détachées.
-
voetnoot2)
- On trouve cette Première Partie presqu'en entier (voir les notes 4 de la p. 320 et 8 de la p. 323) sur une feuille détachée de quatre pages dont la troisième contient la date du 3 février 1658. Il nous semble probable que toutes les découvertes exposées sur ces pages furent faites pendant cette journée.
-
voetnoot3)
- Ce paragraphe contient l'exposition d'une nouvelle méthode pour la quadrature des surfaces de révolution et son application au conoïde parabolique dont la surface courbe avait été déterminée auparavant par Huygens; voir la Pièce No. VI, p. 234-270 du présent Tome.
-
voetnoot4)
- Les calculs qui ont mené à cette conclusion nous sont inconnus; voir pour une démonstration en règle le ‘Theorema I’ de la Quatrième Partie, p. 338-339.
-
voetnoot5)
- C'est, dans les mêmes notations, la formule communiquée, en janvier 1658, par van Heuraet à Huygens par l'intermêdiaire de van Schooten; voir la p. 131 du T. II. Comme nous l'avons vu dans la note 6 de la p. 265, elle ne peut être déduite du résultat obtenu par Huygens en 1657 qu'à l'aide de quelques réductions relativement compliquées. Sans doute Huygens doit avoir été frappé par cette circonstance, et il en aura conclu que van Heuraet devait posséder une méthode différente de la sienne. Par conséquent il se sera mis à rechercher cette méthode.
Quant au résultat obtenu cette fois, il est évident qu'il conduit facilement à la formule de van Heuraet. Posant BC = b, on a 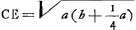 . Par suite, on trouve pour l'aire parabolique . Par suite, on trouve pour l'aire parabolique 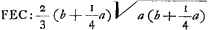 , laquelle, diminuée de l'aire BXF = 1/12 a2, donne pour le rapport indiqué: , laquelle, diminuée de l'aire BXF = 1/12 a2, donne pour le rapport indiqué:
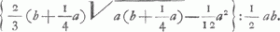
-
voetnoot6)
- Application de la nouvelle méthode à la quadrature du conoïde hyperbolique.
-
voetnoot7)
- Ce résultat est une conséquence immédiate de la méthode indiquée au § 1. Il ne s'agit donc plus que de déterminer la nature de la courbe XE.
-
voetnoot8)
- Consultez la p. 217 de l'édition de 1649 (ou la p. 245 des éditions de 1659 et de 1683) de la ‘Geometria’ de Descartes, publiée par van Schooten (voir l'ouvrage cité dans la note 1 de la p. 218 de notre T. I). Van Schooten y déduit dans ses ‘Commentarii’ l'expression x + rx/q + 1/2 r pour la longueur de la ligne BD. Ajoutons que Descartes avait donné dans le texte de sa ‘Géométrie’ la formule correspondante pour le cas de l'ellipse; comparez la note 8 de la p. 317.
-
voetnoot1)
- La courbe XE est donc une hyperbole, dont Huygens va chercher les dimensions et la situation par rapport à l'hyperbole BA.
-
voetnoot2)
- Voir les règles pour la résolution des équations quadratiques, formulées par Descartes dans sa ‘Géométrie’, p. 375 du T. VI de l'édition d'Adam et Tannery des OEuvres de Descartes.
-
voetnoot3)
- Construction pour trouver le sommet de l'hyperbole TE. On a, en effet,
 ; SB = 1/2 q; donc ; SB = 1/2 q; donc 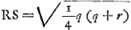 , et par suite: , et par suite: 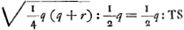 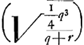 . .
-
voetnoot4)
- La signification de la lettre p nous est restée énigmatique jusqu'à l'instant où nous avons retrouvé cette notation dans la ‘Géométrie’ de Descartes (voir les p. 399-405 du T. VI de l'édition d'Adam et Tannery). Au lieu cité l'équation générale du second degré est réduite dans le cas de l'hyperbole à la forme
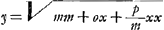 , où les x sont mesurées sur l'axe imaginaire lorsqu'on a 4mp > oo. Si l'on compare cette équation à celle de la forme , où les x sont mesurées sur l'axe imaginaire lorsqu'on a 4mp > oo. Si l'on compare cette équation à celle de la forme 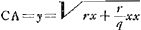 , où r représente le ‘latus rectum’ et q le ‘latus transversum’ et où les x sont mesurées sur l'axe réel, on trouve facilement p/m = q/r = latus tranversum/latus rectum. En appliquant ces considérations à l'hyperbole TXE dont le ‘latus transversum’ est égal à 2ST = 2m (où m a une signification entièrement différente de celle qu'elle a dans la fraction p/m), on aura donc, comme dans le texte: , où r représente le ‘latus rectum’ et q le ‘latus transversum’ et où les x sont mesurées sur l'axe réel, on trouve facilement p/m = q/r = latus tranversum/latus rectum. En appliquant ces considérations à l'hyperbole TXE dont le ‘latus transversum’ est égal à 2ST = 2m (où m a une signification entièrement différente de celle qu'elle a dans la fraction p/m), on aura donc, comme dans le texte:

-
voetnoot5)
- On retrouve ces résultats, avec une modification légère quant à la détermination du sommet T, dans l'‘Horologium oscillatorium, Pars Tertia’ après la Prop. IX (p. 75 de l'édition originale) sous l'en-tête: ‘Conoidis hyperbolici superficiei curvae circulum aequalem invenire’.
-
voetnoot7)
- Application de la nouvelle méthode à la quadrature du sphéroïde aplati.
-
voetnoot8)
- Comparez la note 8 de la p. 315. Le cas de l'ellipse est traité à la p. 52 de l'édition de 1649 de la ‘Geometria’ (p. 46 de celles de 1659 et 1683). Dans l'édition des ‘OEuvres de Descartes’ d'Adam et Tannery on le trouve à la p. 419 du T. VI.
-
voetnoot1)
- Par ce signe Huygens indique qu'on doit employer, selon les circonstances, le signe + ou le signe -.
-
voetnoot2)
- Comparez la note 4 de la p. 317. L'emploi de la lettre p s'explique ici d'une manière analogue.
-
voetnoot3)
- Puisque, d'après une règle alors bien connue, ce diamètre est moyen proportionnel entre les deux ‘latera’.
-
voetnoot4)
- D'après la méthode générale exposée au § 1, p. 314. La quadrature de la surface sphéroïdale est donc déjà réduite à celle de l'hyperbole. Or, Huygens entrevoit le moyen de la réduire de même d'une manière simple et élégante à la rectification de la parabole.
-
voetnoot5)
- On trouve, en effet, en posant x = 0 dans l'expression pour zz (p. 317), BV = 1/2 r, où r représente le ‘latus rectum’ de l'ellipse ABOL par rapport à l'axe BL.
-
voetnoot6)
- De cette manière la parabole AGN et l'hyperbole VEAR sont dans la relation indiquée dans l'énoncé du ‘Theorema VIII’ de la p. 249 puisqu'on a AP + PN/AN = BV/AN. On peut donc appliquer ce théorème; mais aussi le ‘Theorema IX’ (p. 253). Or, d'après ce dernier théorème, on a:
par. AGN : AN = aire RAVBL : AN × BL,
d'où il résulte, puisqu'on peut remplacer AN par une quantité quelconque pourvu qu'on le fasse à la fois dans le deuxième et dans le quatrième terme de la proportion:
par. AGN : 1/4 r = aire RAVBL : 1/4 qr = aire RAVBL : AN2 = surf. ABO : cercle AO.
-
voetnoot7)
- C'est-à-dire: aire RAVBL/BL = long. par. AGN; AN2/BL = 1/4 r.
-
voetnoot8)
- Voir la ‘Constructio’ qui suit, où cette modification est apportée.
-
voetnoot9)
- Ce résultat fut communiqué à de Sluse dans une lettre du 26 février 1658 (voir la p. 141 du T. II); on le retrouve aussi à la p. 39 du Manuscrit No. 13 (mentionné dans la note 5 de la p. 235) et de même dans l'‘Horologium oscillatorium’ (p. 75 de l'édition originale) après la ‘Prop. IX’ de la ‘Pars tertia’ sous l'en-tête: ‘Sphaeroidis lati sive compressi superficiei circulum aequalem invenire’.
-
voetnoot1)
- Application de la nouvelle méthode à la quadrature du sphéroïde allongé.
-
voetnoot2)
- BW représente la longueur de la normale au point Q, comptée de ce point jusqu'à l'intersection avec l'axe AT.
-
voetnoot3)
- Consultez la méthode exposée au § 1, p. 314.
-
voetnoot4)
- Cette équation et les trois lignes qui la suivent ont été copiées d'une autre feuille détachée; comparez la note 2 de la p. 314. La déduction de l'équation se trouve sur la même feuille, mais nous l'avons supprimée parce qu'elle est entièrement analogue à la déduction de l'équation correspondante du § 3, p. 318.
-
voetnoot6)
- Cette proportion s'explique d'une manière analogue à celle que nous avons exposée dans la note 4 de la p. 317. Comparons, à cet effet, la forme générale
 de l'équation de l'ellipse, obtenue par Descartes (p.399 du T. VI de l'édition d'Adam et Tannery), aux formes de l'équation de l'ellipse, obtenue par Descartes (p.399 du T. VI de l'édition d'Adam et Tannery), aux formes 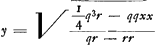 et et 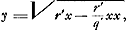 dans lesquelles l'équation de l'ellipse NOKMN peut être écrite si l'on prend NX pour axe des x et R ou N pour origine, et si l'on représente par r′ le ‘latus rectum’ par rapport à l'axe NX et par q′ la longueur de cet axe. On trouve alors: dans lesquelles l'équation de l'ellipse NOKMN peut être écrite si l'on prend NX pour axe des x et R ou N pour origine, et si l'on représente par r′ le ‘latus rectum’ par rapport à l'axe NX et par q′ la longueur de cet axe. On trouve alors:
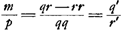 ,
où q′ = NX, le petit axe de l'ellipse NAXTN, est égal à √qr, d'après une formule bien connue. ,
où q′ = NX, le petit axe de l'ellipse NAXTN, est égal à √qr, d'après une formule bien connue.
-
voetnoot7)
- D'après la même formule, mentionnée dans la note précédente, on a
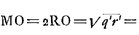
-
voetnoot8)
- Dans les trois lignes qui suivent il s'agit de trouver une construction pour RO qui, avec NR, détermine l'ellipse NOXMN dont il s'agit de carrer la partie AFNKTA, afin d'en déduire la quadrature de la surface du sphéroïde en question.
-
voetnoot9)
- Simplification de la construction de RO = RH. Il suffit donc de déterminer le foyer D de l'ellipse NAXTN et de tirer ensuite les droites RH et AH qui sont parallèles respectivement à DN et à RN.
-
voetnoot10)
- Comparez le premier alinéa du présent paragraphe.
-
voetnoot1)
- On a donc surf. NAX: cercle NX = esp. AHPVT:
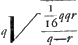 . Or, écrivant le dernier terme sous la forme . Or, écrivant le dernier terme sous la forme 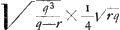 , on aperçoit que ce terme peut être représenté par un rectangle dont les côtés sont égaux à MO et 1/2 NR, c'est-à-dire par le rectangle IM. , on aperçoit que ce terme peut être représenté par un rectangle dont les côtés sont égaux à MO et 1/2 NR, c'est-à-dire par le rectangle IM.
-
voetnoot3)
- On rencontre, en effet, dans un coin de la feuille dont nous empruntons cette partie du texte le petit calcul qui suit:
‘q.mRH (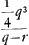 ) [ad] q. AH ( ) [ad] q. AH (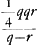 ) [ut] q. RA (1/4 qq) [ad q. AS]; AS ) [ut] q. RA (1/4 qq) [ad q. AS]; AS 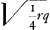 ’. ’.
-
voetnoot4)
- Cette TO remplace la ligne RH de la Fig. 5 à laquelle elle est égale; voir les lignes ponctuées de cette dernière figure.
-
voetnoot5)
- C'est sous cette dernière forme que Huygens a donné sa quadrature de la surface du sphéroïde allongé à la p. 39 du Manuscrit No. 13, sur lequel on peut consulter la note 5 de la p. 235, et de même dans l'‘Horologium oscillatorium’ sous l'en-tête ‘Sphaeroidis oblongi superficiei circulum aequalem invenire’ (p. 74 de l'édition originale).
-
voetnoot6)
- Afin de ne pas multiplier inutilement le nombre des figures nous avons adapté les notations qui suivent à celles de la Fig. 6.
-
voetnoot7)
- Dans ce cas, où q = 4/3 r, l'angle DNR égale 1/6 π. Or, si cet angle est représenté par α, on a dans le cas général (d'après le premier alinéa de cette page):
surf. sphéroïde: cercle 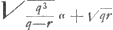 , ,
et cette proportion se réduit au cas particulier en question à celle-ci:
surf. sphéroïde: cercle 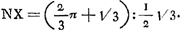 . .
-
voetnoot8)
- Les cinq alinéa's qui suivent ont été empruntés à une autre feuille détachée; comparez la note 2 de la p. 314.
-
voetnoot9)
- Ce résultat fut communiqué à de Sluse dans la lettre de Huygens du 26 février 1658 (p. 141 du T. II).
-
voetnoot2)
- Cette partie se rapporte à une nouvelle découverte, faite avant le 15 février 1658 (date de la lettre à de Sluse citée dans la note qui suit). Elle est empruntée à une feuille détachée de quatre pages. Huygens y établit une relation entre les quadratures des surfaces du sphéroïde aplati et du conoïde hyperbolique. Consultez à ce propos les p. 192-195 de l'Avertissement.
-
voetnoot3)
- Comparez la lettre à de Sluse du 15 février 1658 (p. 134 du T. II) où ce théorème est mentionné par Huygens. On le retrouve de même à la p. 76 de l'édition originale du ‘Horologium oscillatorium’.
-
voetnoot4)
- Nous avons reproduit ces considérations dans ce § 1 de la deuxième Partie.
-
voetnoot5)
- D'après la règle mentionnée dans la note 3 de la p. 318; le ‘latus rectum’ dont il est question est celui de l'ellipse TOLM par rapport à l'axe OM.
-
voetnoot6)
- Remarquons que cette hyperbole est identique avec l'hyperbole VAR de la Fig. 3 de la p. 318 de la quadrature de laquelle Huygens fait dépendre celle de la surface du sphéroïde en question. En effet, en posant x = 0 dans l'équation de cette dernière hyperbole, on trouve z = 1/2 r = VB, d'où il suit que la ligne VB de la Fig. 3 est identique avec la ligne OX de la présente figure.
-
voetnoot7)
- En représentant OM (identique avec BL de la Fig. 3 de la p. 318) par q et par r le ‘latus rectum’ de l'ellipse OLMTO par rapport à l'axe OM, on trouve pour ces données, d'après les calculs de la p. 318, les expressions
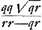 et et 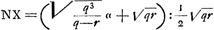 . .
-
voetnoot8)
- Comparez le § 2 de la Première Partie (p. 315-316), où l'on doit remarquer que le point R de la Fig. 2 de la p. 316, foyer de l'hyperbole BGA, est identique avec le foyer V de l'hyperbole BGH de la présente figure.
-
voetnoot9)
- Consultez le ‘Problema I’, p. 327 qui suit.
-
voetnoot10)
- Comparez la proportion au début du § 2 de la Première Partie, p. 315, et remarquez qu'on peut remplacer le deuxième et le quatrième terme respectivement par un cercle quelconque et par la moitié du carré sur son rayon.
-
voetnoot11)
- Comparez le § 3 de la Première Partie, à la p. 318.
-
voetnoot1)
- Dans ce qui suit Huygens procède au calcul des données qui déterminent le conoïde hyperbolique HB qui convient au sphéroïde LOTM. À cet effet il calcule d'abord le ‘latus rectum’ de l'hyperbole RXAT afin d'en déduire par la règle mentionnée dans la note 3 de la p. 318 le demi-diamètre conjugué de cette hyperbole qui est égal, d'après un des résultats obtenus au § 2 de la Première Partie (voir l'avant-dernier alinéa de la p. 316), au diamètre conjugué de l'hyperbole BGH.
-
voetnoot2)
- Par construction QS = OX est égal à ST2: OS; voir (p. 324) le deuxième alinéa du présent paragraphe.
-
voetnoot3)
- Voir la ‘Prop. XXI’ du ‘Libr. I’ des ‘Conicorum libri quattuor’ d'Apollonius, citée dans la note 12 de la p. 300 du T. XI, et remarquons que le rectangle sur LQ et TQ, dont il est question dans cette proposition, est égal à QS2 - ST2.
-
voetnoot4)
- Il s'agit maintenant de calculer SV, où V représente le foyer de l'hyperbole HGB. On a donc
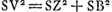 . .
-
voetnoot5)
- Comparez (p. 324-325) le troisième alinéa du présent paragraphe.
-
voetnoot7)
- Puisque la démonstration de Huygens qui va suivre n'est pas complète nous en donnons ici une autre, afin de montrer que la construction élégante qui précède est légitime.
Représentons à cet effet par a′ le demi-diamètre DK, par b′ le demi-diamètre qui lui est conjugué, par θ l'angle DKN,et soit enfin KL = ka′. On trouve alors pour l'aire du segment FKE l'expression:
2b′/a′ sin θ 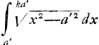 , ou bien (en substituant x = λa′), 2a′b′ sin θ , ou bien (en substituant x = λa′), 2a′b′ sin θ 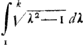 . .
Or, puisque a′b′ sin θ est invariant pour une hyperbole donnée, il est évident que l'aire du segment d'une telle hyperbole ne dépend que du rapport k = KL/KD, et, puisque ce rapport a par construction la même valeur pour les deux segments, il s'ensuit que leurs aires sont égales.
Consultez encore sur cette propriété de l'hyperbole la note 1 de la p. 194 de l'Avertissement.
-
voetnoot8)
- Voir le calcul (p. 328-329) à la fin du présent paragraphe.
-
voetnoot9)
- Puisque, en conséquence de la proportion précédente, la droite OP qui réunit les sommets de ces triangles est parallèle à leur base commune KB.
-
voetnoot10)
- Cette démonstration nous manque, mais il est évident que la conclusion est légitime. En effet, les diamètres KO et BP divisent chacun des segments BKR et KBQ en deux parties égales. Or, en ajoutant aux triangles égaux OKB et PKB le segment KB on voit que les parties OKB et PKB sont égales entre elles.
-
voetnoot12)
- Ce raisonnement manque de précision, mais probablement Huygens s'est assuré de l'exactitude de sa conclusion par des considérations plus ou moins explicites sur les parallélogrammes élémentaires qu'on peut circonscrire ou inscrire aux triangles et segments en question. En effet, après avoir divisé DL et DG dans un même nombre de parties égales, on peut remarquer que, pour des divisions correspondantes, les parallélogrammes élémentaires inscrits dans les triangles FKE et ABC sout égaux, puisque les triangles le sont eux-mêmes, de plus ces parallélogrammes ont des rapports égaux (dépendant du nombre ordinal de la division) aux parallélogrammes inscrits dans les segments hyperboliques. On en conclut à l'égalité de ces derniers parallélogrammes, et, par suite, à celle de leurs sommes qui à la limite se confondent avec les segments en question.
-
voetnoot1)
- Les trois mots qui précèdent ont été ajoutés après coup à une date inconnue.
-
voetnoot2)
- Puisque BF est parallèle au diamètre qui est conjugué à DF.
-
voetnoot3)
- Voir le calcul qui suit où Huygens démontre l'existence de la proportion DF : DA = DA : DC dans le cas où BC est la tangente à l'hyperbole au point B. La proportion avait d'ailleurs été indiquée par Apollonius; voir la note 4 de la p. 341, qui suit.
-
voetnoot4)
- Pour déterminer la tangente au point C de l'hyperbole CGA Huygens se propose d'appliquer la méthode de Fermat exposée à la p. 20 de notre T. XI.
-
voetnoot5)
- On a CM2 : GN2 = FM2 : FN2, mais d'après la ‘Prop. XXI’ du ‘Libr. I’ des ‘Conicorum libri quattuor’ d'Apollonius, citée dans la note 12, p. 300 de notre T.XI, on peut remplacer le premier de ces rapports par celui de OM × AM à ON × AN.
-
voetnoot6)
- Vérification de la proportion employée dans les démonstrations qui accompagnent les ‘Problemata’ I et II qui précèdent.
-
voetnoot7)
- Dans ce paragraphe Huygens s'occupe du cas spécial où les points A et X de la Fig. 8 (p. 326) coïncident. En effet, ces points sont remplacés dans la présente figure par le point D et de même les points Q et B par le point F. En ce cas la relation exposée au § 1 (p. 324-325) se simplifie notablement. Ajoutons que le résultat obtenu dans ce paragraphe est mentionné aux p. 76-77 de l'édition originale de l'‘Horologium oscillatorium’.
-
voetnoot8)
- On remarquera le double emploi de la lettre C dans la figure. Nous désignerons par C le point sur l'axe CBM et par C′ celui sur l'axe BA.
-
voetnoot9)
- Comparez l'avant-dernier alinéa de la p. 324. CD est donc égal à la moitié du ‘latus rectum’ de l'ellipse ACHM par rapport à l'axe CM.
-
voetnoot11)
- La ligne FD de la présente figure correspond à la ligne BX de la Fig. 2 de la p 316. Or, on trouve la longueur de BX en posaut x = 0 dans l'expression 1/2 r + rx/q pour CD (p. 315), où r représente le ‘latus rectum’ de l'hyperbole AGB qui correspond à l'hyperbole LGF de la présente figure.
-
voetnoot1)
- Voir la proportion qui précède et remarquons que le point E est donc un point de l'axe VP, qui est déterminé par cette proportion. On ne sait donc pas d'avance que la droite OE est parallèle à DF, c'est-à-dire perpendiculaire à AP; mais Huygens va démontrer qu'il en est ainsi.
-
voetnoot2)
- AQ est supposée parallèle à la tangente DC′ au point D. On a donc, d'après la proportion déduite à la fin du § 1, p. 328-329, BA : BF = BC′ : BA = BD : BO. De cette manière l'égalité des demi-segments ODRAO et FDAF est assurée (comparez la note 7 de la p. 326) et cette égalité suffit comme on le verra bientôt pour pouvoir remplacer la somme des figures QDFPQ et CDRABC par celle de deux figures rectilignes.
-
voetnoot3)
- EG qui correspond à la ligne VG de la Fig. 8 (p. 326), était primitivement la perpendiculaire élevée sur l'axe de l'hyperbole FGL au foyer E de cette courbe.
-
voetnoot6)
- À cause du parallélisme des lignes OF et DA.
-
voetnoot7)
- Comparez le début du dernier alinéa de la p. 325.
-
voetnoot8)
- Comparez le § 3 de la Première Partie à la quatrième ligne d'en bas de la p. 318.
-
voetnoot9)
- BA : BF = b: b2/x (voir la note suivante) = x. b.
-
voetnoot10)
- Puisque BF = CD est égal à la moitié du ‘latus rectum’ de l'ellipse ACHM par rapport à l'axe CM; voir la note 9 de la p. 329.
-
voetnoot12)
- Huygens va rechercher sous quelle condition se réalise le cas spécial qui l'occupe dans le présent paragraphe. Quel doit être alors le rapport des axes CB = x et AB = b de l'ellipse ACHMA?
-
voetnoot13)
- Voir la ‘Prop. XXI’ du ‘Libr. I’ des ‘Conicorum libri quattuor’ d'Apollonius, que nous venons de mentionner dans la note 3 de la p. 326. V est l'autre sommet de l'hyperbole LGF. On a donc
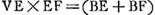 . De plus, GE, l'ordonnée de l'hyperbole FGL, qui correspond au foyer E, est la moitié du ‘latus rectum’ de cette hyperbole. On a donc GE = DF = CB = x, d'après la note 11 de la p. 329. . De plus, GE, l'ordonnée de l'hyperbole FGL, qui correspond au foyer E, est la moitié du ‘latus rectum’ de cette hyperbole. On a donc GE = DF = CB = x, d'après la note 11 de la p. 329.
-
voetnoot1)
- On a d'après la Prop. XXI d'Apollonius, citée dans la note précédente:
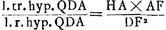
-
voetnoot4)
- Voir (p. 333) la dernière partie du présent paragraphe.
-
voetnoot5)
- Puisqu'on a BE (b3/x2): BA (b) = b2: x2 = 1: (1/2 √5 - 1/2).
-
voetnoot6)
- On trouve, lorsqu'on applique la propriété principale de la division en extrême et moyenne raison, BA : AE = BE (b3/x2): BA (b) = BA (b): x2/b, où x2/b représente la moitié du ‘latus rectum’ de ellipse ACHM par rapport à l'axe AH.
-
voetnoot7)
- Voir la p. 331, l. 7. C'est dans l'emploi de l'expression plus simple 2xx/b que consiste l'amélioration à la quelle Huygens vient de faire allusion.
-
voetnoot8)
- Comparez les proportions en bas de la page précédente.
-
voetnoot9)
- Puisque, par construction, HA = TK. √2 et CM = SI √2.
-
voetnoot10)
- On retrouve cette construction au lieu cité dans la note 7 de la p. 329. Elle n'est valable, comme Huygens le fait observer dans l'‘Horologium oscillatorium’, que dans le cas où OK et OS2: OK [Fig. 15] sont entre elles comme les segments d'une droite divisé en extrême et moyenne raison.
-
voetnoot1)
- Les points B, A, F, E, P correspondent aux points homonymes de la Fig. 13 (p. 330), tandis que BC représente la même longueur dans les deux figures. Or, on a, d'après ce qui précède, BC (x): BA (b) = BA (b): BF (b2/x) = BF (b2/x): BE (b3/x2).
-
voetnoot4)
- Puisqu'on a BC (x): BF (b2/x) = x2/b √2: TK (b√2), où x2/b √2 représente le ‘latus rectum’ de l'ellipse STIK par rapport à l'axe TK.
-
voetnoot5)
- C'est-à-dire ‘en extrême et moyenne raison’, puisqu'on a, en effet, x: b2/x = x2: b2 = (1/2 √5 - 1/2): 1; voir la note 5 de la p. 333.
-
voetnoot6)
- Dans cette Partie, empruntée à une feuille détachée, Huygens résume les résultats obtenus dans les Parties qui précèdent.
-
voetnoot7)
- Voir l'ouvrage ‘De Sphaera et cylindro’, p. 1-54 de l'édition de Bâle; Heiberg, I, p. 1-255.
-
voetnoot8)
- Voir le § 1 de la Première Partie, p. 314.
-
voetnoot11)
- Comparez les ‘Theoremata VIII et IX’, pp. 249 et 253.
-
voetnoot14)
- Comparez le troisième et le quatrième alinéa de la p. 323 et la Fig. 16 qui suit.
-
voetnoot15)
- Comparez la ‘Constructio’ de la p. 319, et la Fig. 17 qui suit.
-
voetnoot1)
- En 1659 Huygens s'est occupé de nouveau de la quadrature des surfaces des sphéroïdes et des conoïdes hyperboliques. Évidemment c'était son intention de procéder à la rédaction définitive d'un traité qui devait contenir, avec la rectification de la parabole, ses découvertes sur ces quadratures, et peut-être encore d'autres inventions géométriques, p.e. la quadrature des courbes paraboloïdes et hyperboloïdes (voir la Pièce VIII, p. 273-293). Ainsi la Quatrième et dernière Partie de la présente Pièce, qui occupe les p. 103-113 du Manuscrit A, nous donne en premier lieu un projet de préface, d'où il résulte que Huygens s'était résolu enfin à s'émanciper en partie de la méthode de démonstration archimédienne. Ensuite on y trouve dans une forme très achevée la discussion des coniques auxiliaires dont il s'était servi dans la Première Partie (p. 314-324) afin d'obtenir la réductionde la quadrature des surfaces prémentionnées à celle de l'hyperbole ou du cercle; lesquelles courbes il se proposa, d'après une annotation qu'on trouve dans le projet de préface, de désigner comme courbes adjointes (‘adjuncta’) aux courbes méridiennes des surfaces à considérer. Sans doute Huygens a voulu faire suivre après les ‘Theoremata I-III’ (que nous réproduisons aux p. 338-346) les théorèmes principaux sur les quadratures de ces surfaces, avec leurs démonstrations, mais ce dessein n'a pas été exécuté, et lors de la publication, en 1673, de son ‘Horologium oscillatorium’, il y a renoncé
définitivement en se résolvant à donner ces théorèmes sans aucune démonstration.
-
voetnoot2)
- On peut consulter quant à l'opinion de Huygens sur la méthode des indivisibles de Cavalleri les pp. 132-134 et 561 du T. I, la p. 158 du T. XI et la p. 753 du T. XIII.
-
voetnoot3)
- Voir les p. 237-270 de la Pièce No. VI.
-
voetnoot4)
- Voir pour la traduction de ce passage intéressant la note 14 de la p. 191.
-
voetnoot1)
- Dans ce qui suit Huygens donne, pour ainsi dire, une description schématique de la méthode de démonstration archimédienne. En effet, AB et DE représentent des grandeurs quelconques (longueurs, aires, volumes) auxquelles on peut circonscrire d'autres grandeurs comme AH ou DK qui ne les surpassent que d'une quantité aussi petite qu'on le veut. De plus, Huygens suppose que les rapports de ces grandeurs circonscrites aux quantités C et F soient de telle nature qu'à chaque valeur AH > AB correspond une valeur DK < DE de sorte qu'on a AH : C = DK : F. Partant de ces suppositions Huygens démontre qu'on aura AB : C = DE : F.
Voir p.e. pour une application de cette méthode la démonstration du ‘Theorema VIII’ p. 249-252.
-
voetnoot2)
- Voir la figure à côté et comparez le § 1 de la Première Partie, p. 314.
-
voetnoot6)
- Voir p.e. la p. 218 de l'édition de 1649 (p. 246 des éditions de 1659 et 1683) de la ‘Geometria’. Comparez la note 8 de la p. 315.
-
voetnoot1)
- Comparez les notes 8 des pp. 315 et 317.
-
voetnoot2)
- Comparez les formules auxquelles se rapportent les notes citées dans la note précédente. Évidemment la construction du segment KM correspond à l'emploi de ces formules. Il s'agit ensuite de donner une démonstration en règle qu'on a, en effet, KM = CD.
-
voetnoot3)
- Voir la ‘Prop. XXI’ du ‘Lib. I’ des ‘Con.’ d'Apollonius, que nous avons reproduite dans la note 12 de la p. 300 de notre T. XI. On a, d'après cette proposition, BC2: CA × CH = AG : AH; par suite
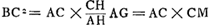 . .
-
voetnoot4)
- Voir, à la p. 26 verso de l'édition de Commandin, la première partie de la ‘Prop. XXXVII’ du ‘Lib. I’ des ‘Con.’ d'Apollonius, où l'on lit: ‘Si hyperbolen, uel ellipsim, uel circuli circonferentiam recta linea contingens cum diametro conueniat: & à tactu ad diametrum linea ordinatim applicetur: quae interiicitur inter applicatam & centrum sectionis unà cum interiecta inter contingentem, & sectionis centrum, continebit rectangulum aequale quadrato lineae, quae est ex centro sectionis’.
-
voetnoot7)
- C'est-à-dire VT2: FB2 = FB: (FB ± BQ). Soient donc q et r les ‘latera transversum et rectum’ de l'hyperbole ou ellipse BA, q′ et r′ ceux de l'hyperbole ou ellipse TE; on aura alors q′r′ = qr et q′2: q2 = q: (q ± r).
-
voetnoot1)
- Voici les considérations qui ont pu conduire à l'introduction de ces lignes auxiliaires. Les équations des courbes BA s'écrivent:
 , où y = AC, x = BC, et où l'on doit prendre le signe + dans le cas de l'hyperbole et le signe - dans celui de l'ellipse. On trouve alors, pour les équations des courbes TE, , où y = AC, x = BC, et où l'on doit prendre le signe + dans le cas de l'hyperbole et le signe - dans celui de l'ellipse. On trouve alors, pour les équations des courbes TE, 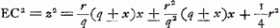 (comparez les expressions pour zz des pp. 316 et 317). Pour pouvoir traiter à la fois le cas de l'hyperbole et celui de l'ellipse, il était donc avantageux d'introduire deux lignes auxiliaires (comparez les expressions pour zz des pp. 316 et 317). Pour pouvoir traiter à la fois le cas de l'hyperbole et celui de l'ellipse, il était donc avantageux d'introduire deux lignes auxiliaires 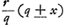 et et 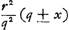 dont il faut prendre la somme dans le cas de l'hyperbole et la différence dans celui de l'ellipse. En combinant cette somme, ou cette différence, avec la ligne BC = x, on obtient le rectangle Bα qui, augmenté du carré de BN = 1/2 r, est égal au carré de z = EC. Or, on trouve
facilement que, par construction, dont il faut prendre la somme dans le cas de l'hyperbole et la différence dans celui de l'ellipse. En combinant cette somme, ou cette différence, avec la ligne BC = x, on obtient le rectangle Bα qui, augmenté du carré de BN = 1/2 r, est égal au carré de z = EC. Or, on trouve
facilement que, par construction, 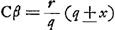 , , 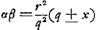 . .
-
voetnoot2)
- La lettre X manque dans la figure qui se rapporte au cas de l'ellipse; mais il s'agit alors évidemment de la courbe TEV.
-
voetnoot4)
- Voici cette proposition, qu'on trouve à la p. 174 recto de l'ouvrage cité dans la note 3 de la p. 259 du T. II: ‘Sit recta linea AB aequalis CD, & sumatur quoduis punctum E extra lineam AD. Dico rectangulum BEC rectangulo AED, & rectangulo BDC aequale esse’.

-
voetnoot5)
- Voir la p. 194 recto, où l'on lit: ‘Sit AB aequalis ipsi CD, & quoduis punctum E inter BC puncta. Dico rectangulum AED superare rectangulum BEC rectangulo ACD’.
-
voetnoot6)
- Voir la proportion de la note 7 de la p. 341, où VT = 2ST; FB = 2SB; BQ = 2BN, tandis que le rapport de ST2: SB2 peut être remplacé par celui de ST : SR, puisque, par construction, SR = SB2/ST.
-
margenoot*
-
Ga naar voetnoot8).
-
voetnoot8)
- Voir la ‘Prop. 14’ du ‘Lib. 6’ des ‘Elementa’ d'Euclide, où l'on lit: ‘AEqualium & vnum vni aequalem habentium angulum, parallelogrammorum, reciproca sunt latera, quae circum aequales angulos. Et quorum parallelogrammorum vnum angulum vni angulo aequalem habentium reciproca sunt latera, quae circum aequales angulos; illa sunt aequalia’. (Clavius, p. 566).
-
voetnoot1)
- Voir la ‘Prop. 6’ du ‘Lib. 2’ des ‘Elementa’ d'Euclide. On la trouve citée dans la note 2 de la p. 46 de notre T. XII.
-
voetnoot3)
- Il s'agit cette fois de la ‘Prop. 5’ du ‘Lib. 2’, citée à la p. 176 de notre T. XI.
-
voetnoot5)
- Comparez la dernière phrase du troisième alinéa de la p. 343.
-
voetnoot6)
- Comparez, pour ce qui suit, le § 3 de la Première Partie, p. 317-319.
-
voetnoot8)
- Écrivant q et r pour les ‘latera’ de l'ellipse OBY par rapport à l'axe BF et q′ et r′ pour ceux de l'hyperbole XO par rapport à l'axe OY, on a donc
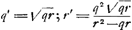 . .
-
voetnoot9)
- Puisque
 , d'après une formule bien connue. , d'après une formule bien connue.
-
voetnoot10)
- D'après la dernière partie de la ‘Prop. XXI’ du ‘Lib. I’ des Coniques d'Apollonius, que nous avons reproduite dans la note 12 de la p. 300 du T. XI.
-
voetnoot1)
- Ici Huygens reprend la proportion DC2: DC2 - ▭OWY = ZS2: ▭ SZF, démontrée quelques lignes plus haut, dans laquelle maintenant DC2 - ▭OWY peut être remplacée par ▭YPO.
|
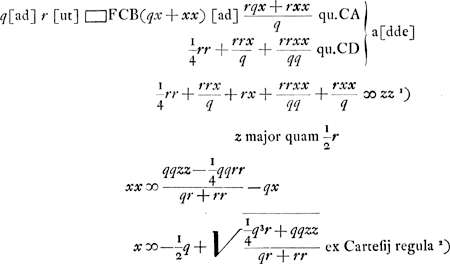

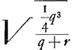 . Ergo sit BY ∞ 1/2 r et SR media prop. inter SY, SB. Et ut RS ad BS ita sit BS ad TSGa naar voetnoot3).
p [ad] mGa naar voetnoot4) [hoc est] qq [ad] qr + rr [ut] 2m [h.e.]
. Ergo sit BY ∞ 1/2 r et SR media prop. inter SY, SB. Et ut RS ad BS ita sit BS ad TSGa naar voetnoot3).
p [ad] mGa naar voetnoot4) [hoc est] qq [ad] qr + rr [ut] 2m [h.e.]  [ad]
[ad] 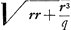 latus rect. hyperb. TE. Ergo media prop. inter hoc et l. transv. erit 2SO ∞ √rq ∞ diam. conjugatae hyperb. TE. Ergo cum hyperbolae TE, BA habeant eandem diam. conjug.m habebunt latera recta reciproce rationem laterum transversorumGa naar voetnoot5).
latus rect. hyperb. TE. Ergo media prop. inter hoc et l. transv. erit 2SO ∞ √rq ∞ diam. conjugatae hyperb. TE. Ergo cum hyperbolae TE, BA habeant eandem diam. conjug.m habebunt latera recta reciproce rationem laterum transversorumGa naar voetnoot5).
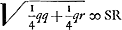 Ga naar voetnoot6); R est focus hyperb. BA, OB ∞ SR. RG ∞ 1/2 r.
Ga naar voetnoot6); R est focus hyperb. BA, OB ∞ SR. RG ∞ 1/2 r.

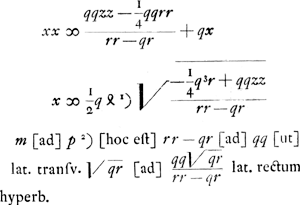
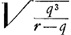 Ga naar voetnoot3).
Ga naar voetnoot3).
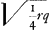 ) [ad] BN (1/2 q) [ut] XA (1/2 r) [ad] AN (
) [ad] BN (1/2 q) [ut] XA (1/2 r) [ad] AN (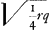 ) hinc video mutari posse constructionem ut pro ∆oAXO sumatur BKL. et pro 1/4 lat. recti sumatur 1/4 AOGa naar voetnoot8).
) hinc video mutari posse constructionem ut pro ∆oAXO sumatur BKL. et pro 1/4 lat. recti sumatur 1/4 AOGa naar voetnoot8).


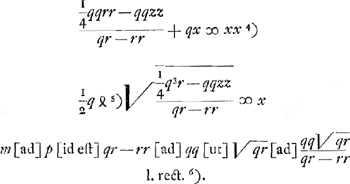
 Ga naar voetnoot7).
ALGa naar voetnoot8) ∞ 1/2 r. RG media inter RL, RA, ergo
Ga naar voetnoot7).
ALGa naar voetnoot8) ∞ 1/2 r. RG media inter RL, RA, ergo 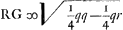 . Ut RG ad RA ita haec ad RO, ergo RO ∞
. Ut RG ad RA ita haec ad RO, ergo RO ∞ 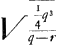 ∞ RH ∞ RP.
∞ RH ∞ RP.
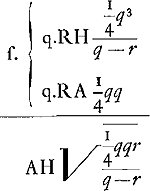
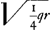 ) [ad] RP (
) [ad] RP (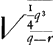 ) [ita]
) [ita]
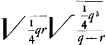 , h[oc] est
, h[oc] est 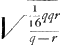 Ga naar voetnoot1).
hoc applica ad OM ∞
Ga naar voetnoot1).
hoc applica ad OM ∞ 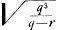 fit 1/4 √rq ∞ OI ∞ 1/2 RN.
fit 1/4 √rq ∞ OI ∞ 1/2 RN.









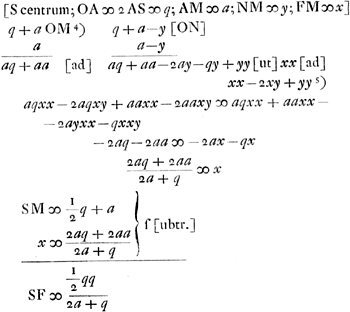

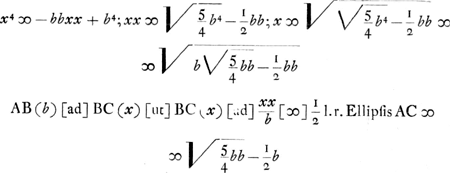


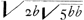 ∞ rad. circ. duabus superf.bus aequalis. Haec melius in adjuncta paginaGa naar voetnoot4).
∞ rad. circ. duabus superf.bus aequalis. Haec melius in adjuncta paginaGa naar voetnoot4).
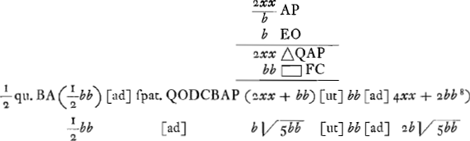
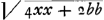 h. est
h. est  aequatur radio circuli qui aequalis est superficiebus sphaeroidis STK et conoidis hyp.i FLP.
Vel sumatur potius
aequatur radio circuli qui aequalis est superficiebus sphaeroidis STK et conoidis hyp.i FLP.
Vel sumatur potius 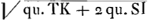 Ga naar voetnoot9).
Ga naar voetnoot9).
















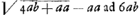
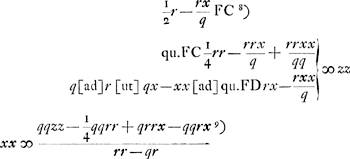
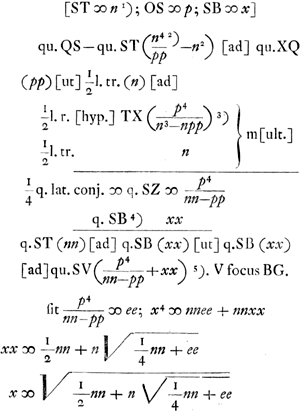
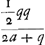 )
)