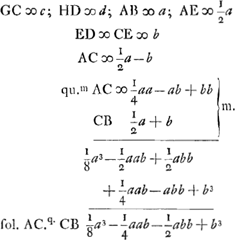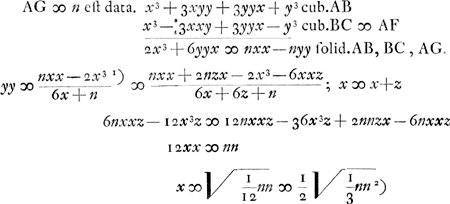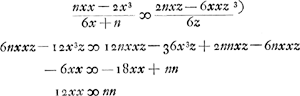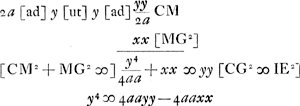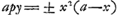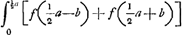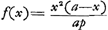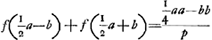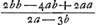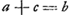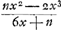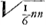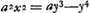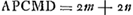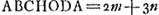Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 294]
| |
IX.
| |
[pagina 295]
| |
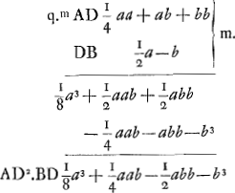 Jam si GC ductum in ▭ ap, hoc est cap, sit ∞ AC2 in CB et HD in ▭ ap, hoc est dap, ∞ AD2 in DB: Eric ut c ad d ita 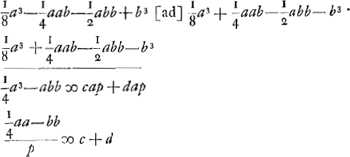 | |
[pagina 296]
| |
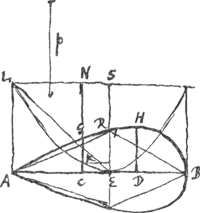 [Fig. 1.]
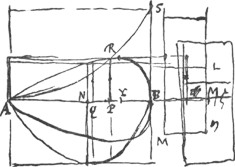
Sit ut p ad 1/2 a ita 1/2 a ad 1/4 aa/p ∞ ES. Ea erit ∞ 2RE. quoniam hic bb/p evanescit. describatur parabola vertice E axe ES, latere recto p. Ea transibit per angulum L ▭li AS. Eritque CK ∞ ∞ bb/p. Est autem CN ∞ 1/4 aa/p. Ergo 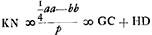 . Ergo totum spatium AGHB ∞ dimidiae parab. LES. Ergo sesquitertium ∆i LES sive ∆i ARBGa naar voetnoot1). . Ergo totum spatium AGHB ∞ dimidiae parab. LES. Ergo sesquitertium ∆i LES sive ∆i ARBGa naar voetnoot1).
AC ∞ xGa naar voetnoot2), CG ∞ y. □ AE × EB (⅛a3) [ad] □ AC × CB (axx - x3) [ut] 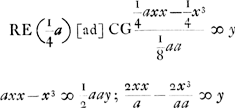 | |
[pagina 297]
| |
 [Fig. 2.]
8/15 [ad] 2/3 [id est] 4 [ad] 5 ita BY [ad] BM ∞ BN
BY [ad] BA ut 2 ad 5
Y centr. grav.Ga naar voetnoot3)
Inventio tangentis. 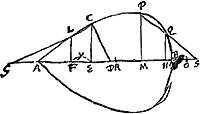 [Fig. 3.]
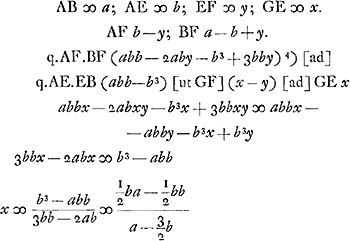 | |
[pagina 298]
| |
 [Fig. 3.]
Sit ER ∞ 1/2 AE ∞ 1/2 b et ut BR (a - 3/2 b) [ad] RE (1/2 b) ita sit BE (a - b) [ad] EG 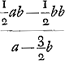 AM ∞ b; MH ∞ y; MS ∞ x; AB ∞ a; AH ∞ b + y; BH a - b - y q.mAH.BH (abb + 2aby - b3 - 3bby)Ga naar voetnoot2) [ad] q.mAM.MB (abb - b3) [ut] 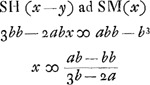 Sit MO ∞ 1/2 AM.BO (3/2 b - a) [ad] OM (1/2 b) [ut] BM (a - b) [ad] MS(x) 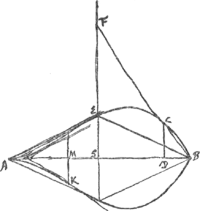 [Fig. 4.]
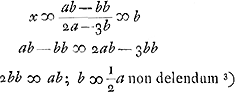 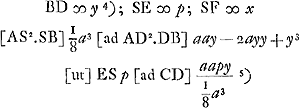 | |
[pagina 299]
| |
BS (1/2 a) [ad] SF (x) [ut] BD (y) [ad] CD (8py/a).
xy ∞ 4py; x ∞ 4p quand[o] sc. BF tangit in BGa naar voetnoot6). 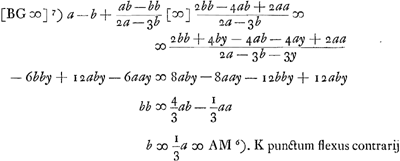 Ga naar voetnoot7)Ga naar voetnoot6) AD [Fig. 5] ∞ 3aGa naar voetnoot8), AB ∞ a, CL ∞ d, BE ∞ BF ∞ b. [BA ∞ BC]Ga naar voetnoot9) | |
[pagina 300]
| |
 [Fig. 5.]
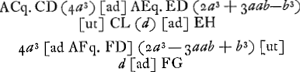 Ergo 8a3 [ad] 4a3 [ut] 2d [ad] d. Ergo FG + + EGGa naar voetnoot1) ∞ d. Ergo portio AGHLCA ∞ ∆ACL. 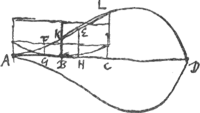 [Fig. 6.]Ga naar voetnoot2)
| |
§ 2Ga naar voetnoot3).EBD [Fig. 7] est hijperbola AEqualium laterum, axis BC, BO arbitraria. OK parallela et aequalis EC. Curva KLL ejus naturae ut qu. HL sit aequale ▭o HGF. Slusius contemplandam proposuitGa naar voetnoot4). 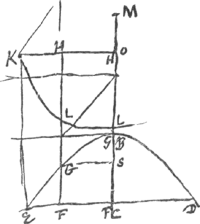 [Fig. 7.]
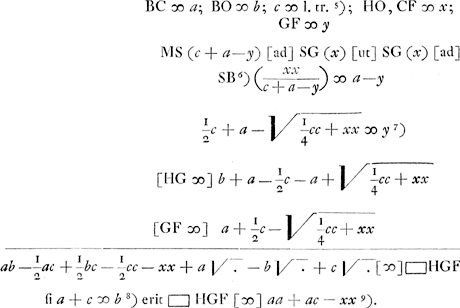 Ga naar voetnoot5)Ga naar voetnoot6)Ga naar voetnoot7)Ga naar voetnoot8)Ga naar voetnoot9) | |
[pagina 301]
| |
§ 3Ga naar voetnoot10).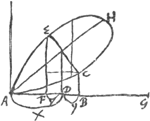 [Fig. 8.]
25 Sept. 1657.
Proprietas curvae AC, ut, sumptâ AB ad arbitrium, erectâque perpendiculari BC quae curvae occurrat in C; fiat cubus ex AB + cubo ex BC aequalis solido ex AB, BC, AG.
Ductâ AH ut ∠ HAG sit 1/2 recti, sit AH diameter lineae, ita ut omnes quae ipsam ad angulos rectos secant, bifariam ipsae secentur. Quaeritur itaque hujusmodi ordinatim applicata EC quae maxima sit omnium. Si sumatur AF ∞ BC, erit perp. FE vicissim ∞ BA. Si itaque CE est maxima, etiam BF debebit esse maxima; est autem BF ∞ AB - BC. | |
[pagina 302]
| |
[pagina 303]
| |
§ 5Ga naar voetnoot5).1658. Curva ACB ejus naturae ut posita AB ∞ a. AD ∞ y. DC ∞ x, fiat ay3 - y4 ∞ ∞ aaxx, y3/a - y4/aa ∞ xx. Hanc Slusius dicebat ad circumscriptum ▭BG sicut 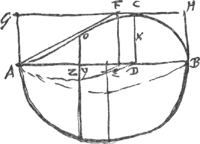 [Fig. 10.]
circulus ad quadratum circumscriptumGa naar voetnoot6). Quod falsum esse docebimus. Sit AB partium 10. AE sive GF 6 et ducatur AF. Ergo trapezium AFHB ad ▭BG ut 7 ad 10 quae multo minor est ratio quam circuli ad circumscr. quadratumGa naar voetnoot7). Atqui trapezio AFHB adhuc minus ostendemus esse spatium à curva AOCB comprehensumGa naar voetnoot8). Ergo hujus spatij ad ▭BG multo minor erit ratio quam circuli ad circumscr. quadratum. | |
[pagina 304]
| |
 [Fig. 10.]
y3/a - y4/aa 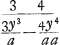 Ga naar voetnoot1) ∞ 0; 3ay3 ∞ 4y4; 3/4 a ∞ y. Ergo si AD ∞ 3/4 AB fit DC maxima altitudo Ga naar voetnoot1) ∞ 0; 3ay3 ∞ 4y4; 3/4 a ∞ y. Ergo si AD ∞ 3/4 AB fit DC maxima altitudo
27/64 aa - 81/256 aa ∞ xx; √27/256 aa ∞ 3/16; √3aa ∞ ∞ x [∞] DC. qu.AZ (yy) [ad] qu.ZO (y3/a - y4/aa [ut] aa [ad] ay - yy; non minor quam 4 ad 1Ga naar voetnoot2). qu. [AE/AB] (36/100) ad qu. [EF/AB] (27/256) [ut] 9216 [ad] 2700; minor quam 4 ad 1Ga naar voetnoot3). 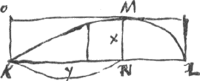 [Fig. 11.]
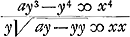 hac linea circa axem KL circumvoluta dicit solidum ab ea genitum esse ad cylindrum à ▭o LO in eadem circulatione factum, ut circulus ad circumscr. quadratumGa naar voetnoot4). | |
[pagina 305]
| |
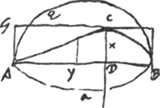 [Fig. 12.]
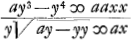 Hujus curvae spatium ad ▭BG est ut solidum praecedens ad cylindrum. (quod et Slusium puto voluisse)Ga naar voetnoot5). Ergo et spatium hoc erit ad ▭ BG ut circulus ad circumscr. quadratum quod falsum est. Sed descripto super AB semicirculo [Fig. 13]: invenio hunc duplum esse spatij ACBAGa naar voetnoot6). 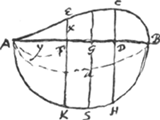 [Fig. 13.]
Est enim AFq. ad FEq. ut yy ad xx sive y3/a - y4/aa hoc est ut aa ad ay - yy, ductis omnibus in aa: hoc est ut qu.AB ad qu.FK. Ergo AF ad FE ut AB ad FK. Sit BD ∞ AF. Ergo eadem ratione AD ad DC ut AB ad DH seu FK. Quare componendo erit AF + + AD ad FE + DC ut AB ad FK. Sed est AF + + AD ∞ AB, quia AF ∞ DB. Ergo, AB ad FE + DC ut AB ad FK. Quamobrem erit FE + DC ∞ FK. Unde colligo spatium totum AECB esse ∞ quadranti GSKA. 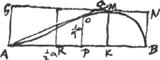 [Fig. 14.]
SiGa naar voetnoot7) AP ∞ PB fit PO ∞ 1/4 AB. Et AOQ tangens in OGa naar voetnoot8). GQ ∞ 2GA. AK ∞ 3/4 AB; KM ∞ ∞ √27/256 [AB]. Ergo qu.GR ∞ ∆GAQ. Ergo ▭BG ad trapez.AQNB sive ▭RN ut AB ad BR hoc est ut 1 ad 1 - √27/256 quam proportionem dico majorem quam quadrati ad circ. inscriptum. est enim major quam 1 ad 1 - 5/16 hoc est quam 16 ad 11, quae major quam 15 ad 11Ga naar voetnoot9). | |
[pagina 306]
| |
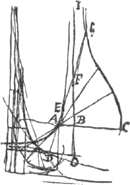 [Fig. 15.]
| |
§6Ga naar voetnoot1).Omnis conchoidis spatium infinitae est magnitudinis. Ostenditur per asymptotos hyperbolaeGa naar voetnoot2).
Sphaerae et spiraeGa naar voetnoot3). 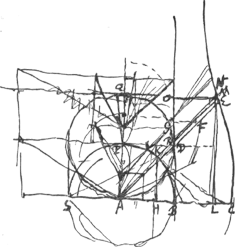 [Fig. 16.]
▱ DEGa naar voetnoot4) [ad] ∆ AK ut 2DB [ad] KHGa naar voetnoot5) h.e. ut 2BA [ad] HA vel EO. h.e. ut BA ad FGGa naar voetnoot6). ▱ DE in FG ∞ ∆ AK in AB. omnia ▱a DE in FG hoc est solida ex conversione ▱orum DE ∞ solido quod sit circa axem AB à quadrante ABP suspenso secundum centrum gravitatis suae in PGa naar voetnoot7). Unde duplo utriusque sumto, fit solidum à tota conchoide praeter sphaeram in ipso contentam quae fit à ∆isRMN aequale semispirae, quae fit conversione semicirculi ADQ circa axem AB. Ergo totum omnino solidum conchoidis infinitum aequale sphaerae BS et dimidiae spirae à semicirculo BPSGa naar voetnoot8). | |
[pagina 307]
| |
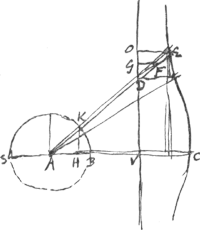 [Fig. 17.]
▱ DEGa naar voetnoot9) [ad] ∆AK ut 2VA ad AH vel ad EO. ▱DE in FG ∞ ∆AK in AV. Hinc solidum totum conchoidis aequale sphaerae BS + semispirae à semicirculo BKS, circa axem VDGa naar voetnoot10). | |
[pagina 308]
| |
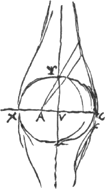 [Fig. 18.]
Si A polus conchoidis et CV ad VA ut 3/4 circumfer.ae CYX ad CVGa naar voetnoot1) fiet solidum conchoidis duplum sphaerae CX inscriptae.  [Fig. 19.]
AC est altera Conchoides in qua semper CD ∞ AB. CH ad HA ut GF ad FA, seu HB. nam FA ∞ HB quia AG ∞ CD. unde quoque HA ∞ FK. Ergo ▭ CH in HB ∞ ▭ FG in FK, fiunt enim ejusdem latitudinis haec rectangulaGa naar voetnoot2). Ergo solidum infinitum conchoidis circa BD aequale solido quod fit a quadrante ALK circa axem KE. sive BAL circa BD. Vel si Conchois ad alteram partem quoque describatur, erit totum solidum aequale ei quod fit a semicirculo LBT circa axem BDGa naar voetnoot3). Hoc autem sphaerae integrae additum aequatur annulo dimidio, qui fit a semicirculo BLK circa axem BD.
AC [Fig. 20]Ga naar voetnoot4) conchoides. D polus. EF regula. B punctum in Conchoide. BDH linea. DH ∞ ∞ EA. HK parall. DA. BG est curva ejusmodi ut semper MG ∞ ∞ DN. Eam dico esse hyperbolam per punctum B | |
[pagina 309]
| |
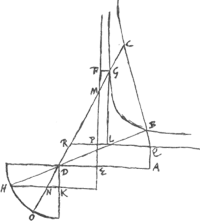 [Fig. 20.]
descriptam ad asymptotos PF, PQ. sumptâ videlicet EP ∞ DK, et ductâ PQ parall. DA. Hanc hyperbolam apparet à B versus G totam cadere intra conchoidem. Sed Hyperbolam inter et asymptoton infinitae magnitudinis spatium interjicitur. Ergo et Conchoidis spatium infinitum erit. Quod BG sit hyperb. hinc constat. Quia MG ∞ DN vel DR, erit RG ∞ MD; et GL ∞ ME. Item MF ∞ DK. Sed ut MF (h.e. DK) ad FG, ita GL (sive ME) ad ED. Ergo ▭ DK, DE ∞ ▭ FG, GL. idque semper. ergo BG est hijperb. | |
§ 7Ga naar voetnoot5).18 Mart. 1658. 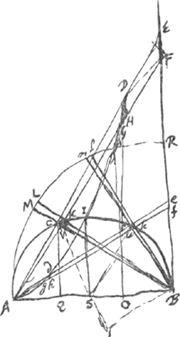 [Fig. 21.]
AIGD est Cissoides. Ergo AC ∞ DE; AK ∞ GF; Ac ∞ de. &c. trapezij DEFH eadem est altitudo ac ∆li CVAGa naar voetnoot6) unde illud trap. ad hoc ∆.m ut EF + DH ad CV. hoc est ut EB + DO ad CQ, hoc est ut BA + AO ad AQ; sive ut AB + BQ ad QA. hoc est ut qu. AB + + qu. BC ad qu. CA. hoc est ut ∆BML + ∆BCK | |
[pagina 310]
| |
 [Fig. 21.]
ad ∆ACK, sive CVA. Ergo hinc sequitur ∆BML + + ∆BCK aequari trapez.o DEFH. Et hoc semper: unde colligo spatium infinitum à curva AIH et rectis AB, BE comprehensum aequari quadranti BAMR + semicirculo AIB hoc est triplo semicirculo AIB. Item partem quamlibet abscissam recta ex A educta, velut AIDEBA aequalem esse sectori BMR + segmento BkC. hoc est triplo segmento CkB + duplo ∆oCBSGa naar voetnoot1) hoc est ∆o cujus basis ∞ 3 arcus CB-CQ, altitudo radius SB. arcus autem BkC semper duplus est MRGa naar voetnoot2). unde data arcus BkC longitudine, dabitur quadratura dictae partis AIDEBA.
Dato quadrato vel circulo aequali spatio ABCX [Fig. 22] dabitur quadratura circuli. Potest circulus inveniri qui unà cum spatio ABCX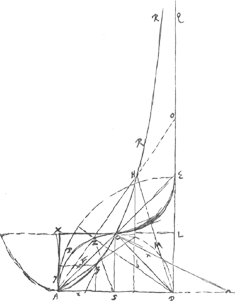 [Fig. 22.]
aequatur quadrato dato. ABCED ∞ semicirc. APCMD + + nGa naar voetnoot3) commune auferatur ABCMD CMDE ∞ ABCP + AFCP (n) CMDE + n hoc est qu. AC ∞ ∞ ABCP + 2n auferatur utrinque 2n APCB ∞ 2APCX. add. utrique APCX ABCX ∞ 3APCX semicirc. ACD + spatio ABCPA aequatur ▭ AXLDGa naar voetnoot4) circumscripto. sive quadrato circulo AD inscripto. | |
[pagina 311]
| |
Spatium infinitum ABCRRQD est triplum semicirculi ACD. Semper spatium ABCHD est triplum segmenti DZM. nam ∆DHO ∞ ∞ DZA ∞ 2DZSGa naar voetnoot5). 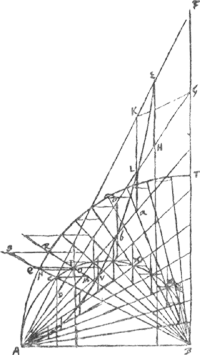 [Fig. 23.]
OstendendumGa naar voetnoot6) est spatium AVLEFBA [Fig. 23] aequari sectori BNT + segmento CXB. Primo spatium minus dicatur, sitque excess. Ω. Erit figura inscripta EHLab&c. multo minor. trapezium EFGH aequale ostenditur ∆lis BCM + BNOGa naar voetnoot7). Ejusmodi igitur figura inscribatur, ut fiant omnia simul frusta qualia CPM et NRO minora excessu Ω quo spatium AVLEFBA superari dicitur à sectore BNT + segmento CXB (hoc fieri posse ostendatur). Sed haec frusta omnia trapezijs addita, aequantur sectori BNT + segm. CXB. Ergo trapezia una cum priori excessu Ω. majora erunt sectore BNT + segm. CXB. Unde trapezia majora ipso spatio cui inscripta sunt quod absurdum. Si spatium majus esse dicatur, erit figura circumscripta FKLdb&c. multo major. Jam trapezium KG aequale ostenditur ∆lis BPQ + BRS. | |
[pagina 312]
| |
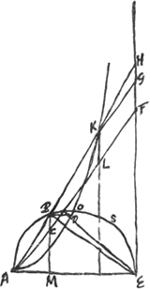 [Fig. 24.]
Alia demonstratioGa naar voetnoot1)
triangulum KHG ∞ ABC. ▱ KF ad ∆ABC ut 2KL ad BC, hoc est ut 2KA ad AB, hoc est ut 2BH ad BA, hoc est ut 2EM ad MA. hoc est ut 2 qu.EB ad [qu.] BA, hoc est ut 2∆BED ad ∆BACGa naar voetnoot2). ergo ▱ KF ∞ 2∆BED. Ergo trapezium KHFL ∞ ∆ABC + 2∆BED. Unde facile colligitur spatium AOKHE ∞ parti semicirculi ABSE + + 2 segm.o BES, hoc est 3 segmento BES + ∆lo ABEGa naar voetnoot3). | |
§ 8Ga naar voetnoot4).Sit parabola cujus diameter FA, et linea MS sectionem contingat, per M vero ipsi FA aequedistans ducatur MN, et ipsi MS in sectione ducantur aequidistantes quaelibet BLE, VRX. dico ipsas à recta MN bifariam secari; et quadrata ipsarum VR, BL esse inter se sicut RM ad LM longitudine. ducantur enim ordinatim BA, MQ, LD, EO et conveniat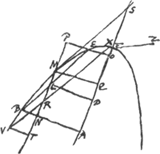 [Fig. 25.]
EO cum LM in P. et sit parabolae rectum latus FZ. Quia igitur ▭ sub FQ et lat. recto aequale est qu.o MQ, erit lat. r. ad MQ ut MQ ad QF, et sumptis consequentium duplis, lat.r. ad 2MQ seu 2AN ut MQ ad QS; (est enim QS dupla ipsius QF, quia MS parab. contingit) hoc est ut BN ad NL. Quare ▭ sub lat.r. et NL ∞ 2▭o ANB. ▭m autem sub lat.r. et NL sive AD et ▭m sub lat.r. et DF, utrumque simul aequatur qu.AB. Ergo et 2▭ ANB + ▭ [lat.]r., DF aequabitur qu.o AB; Et | |
[pagina 313]
| |
ablato utrinque 2▭ANB, erit ▭ [lat.]r, DF aequale qu.o AN + qu.o NB. Rursus quoniam ostensum est, l. r. ad 2MQ hoc est 2PO ut MQ ad QS, hoc est ut EP ad PL sive OD; erit ▭ sub l. r. et OD aequale 2▭OPE. Sed ▭ [l.] r., OD + ▭o [l.]r., OF aequatur ▭ [l.]r., DF; ergo etiam 2▭OPE + ▭ [l.]r., OF sive qu.o OE aequabitur ▭ [l.]r., DF. Sed 2▭OPE + qu.OE aequatur etiam - per 7.1. Elem.Ga naar voetnoot5) - duobus qu.is EP, et OP. Ergo patet ▭ [l.]r., DF aequari qu.is EP et OP. atqui ▭o eidem [l.]r., DF etiam aequalia ostensa sunt qu.a BN et NA. Ergo duo qu.a EP et OP aequalia duobus BN et NA. sed qu.m NA aequale qu.o OP. Ergo reliquum etiam qu. BN aequale qu.o EP. ac proinde BN ipsi EP etiam longitudine aequalis erit, Et, quoniam similia sunt ∆a BLN, ELP, et latera aequalibus angulis opposita BN, EP habent aequalia etiam reliqua latera aequalibus opposita angulis aequalia habebunt, nimirum BL ipsi LE. Eadem ratione ostend. etiam VR ipsi RX aequalis. Jam porro ducatur VT ipsi AB aequidistans. Quia ergo ostensum fuit ▭ [l.]r., DF aequale qu.is AN et NB, sed idem ▭ [l.]r., DF etiam aequale ▭is [l.]r., QF et [l.]r., QD quorum ▭ [l.]r., QF qu.o QM hic qu.AN aequale est, patet etiam reliquum ▭ [l.]r., QD seu [l.]r., LM aequari reliquo qu.o NB. Similiter ostenditur qu.VT aequale ▭ [l.]r., RM. Erit itaque qu.VT ad qu.BN ut ▭ [l.]r., RM ad ▭ [l.]r., LM, hoc est ut RM ad LM. Sed ut qu.VT ad qu.BN ita qu.VR ad qu.BL. Ergo &c. |
|