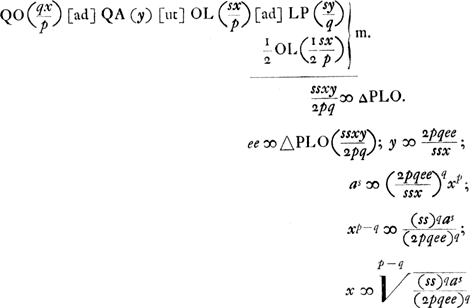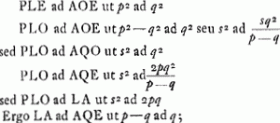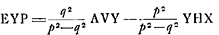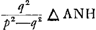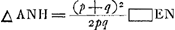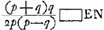Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 288]
| |
Appendice II à la pièce no. VIIIGa naar voetnoot1).
| |
[pagina 289]
| |
§ 2Ga naar voetnoot4)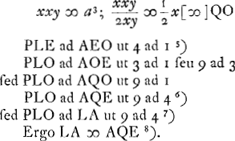 Ga naar voetnoot5)Ga naar voetnoot6)Ga naar voetnoot7)Ga naar voetnoot8) Dico PLE esse ad AOE ut 4 ad 1. hoc est PLO ad AOE ut 3 ad 1. hoc est sumta LΘ ∞ 1/3 LO, dico esse ΘPO ad ΘPL ut PLE ad AOE. | |
[pagina 290]
| |
§ 3Ga naar voetnoot1).PAHN [ad] AHEO [ut] 4 [ad] 1Ga naar voetnoot2). 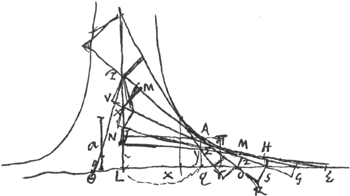 [Fig. 1.]
dem.dum posse AEQGa naar voetnoot3) eousque produci ut qualibet data quantitate minus deficiat a magnitudine ▭iLA. posse duci tangentem NHE, ut fiat triang. NEL dato quovis spatio minimoGa naar voetnoot4). Intelligatur quasi in infinitum spatia aequalia OS, SG, GE &c. progredientur et tangentes a singulis punctis.
∆PΣV majus quam 4ΣOZ. sed ∆MΣX minus quam 4ΣSR.
Omnia trilinea ut AΣTGa naar voetnoot5) possunt fieri minora dato quovis spatio. nam minora quam AoTGa naar voetnoot6). quae omnia minora quam ▭ AYGa naar voetnoot7).
supp. xxy ∞ a3. dem.dum xy aequale dato quolibet minimoGa naar voetnoot8).
xy ∞ ee minimum datum. y ∞ ee/x; eex ∞ a3; x ∞ a3/ee
x10y9 ∞ a19; xy ∞ ee; y ∞ ee/x; e18/x9 ∞ y9 duc in x10; xe18 ∞ a19 ∞ x10y9; x ∞ a19/e18. | |
[pagina 291]
| |
§ 4Ga naar voetnoot9).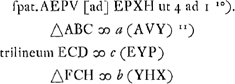 Ga naar voetnoot10)Ga naar voetnoot11) 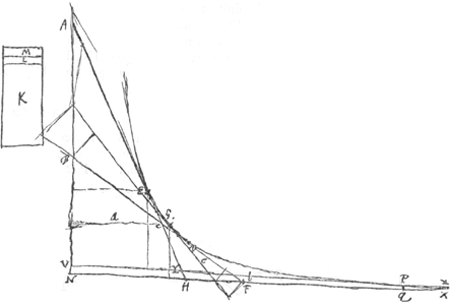 [Fig. 2.]
potest demonstrari a + c [ad] b + c [ut] 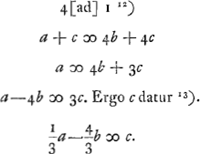 Ga naar voetnoot12)Ga naar voetnoot13) Theorema quod demonstrari potest. spatium EYP ∞ 1/3 ∆iAVY - 4/3 ∆iYHX. | |
[pagina 292]
| |
dico ubicunque sumatur P, spatium EHQP esse minus tertiâ parte trianguli AHN. Sit VPX tangens, nempe ut XQ sit subdupla ad QNGa naar voetnoot1). Jam spatium EYP aequatur 1/3 ∆ AVY - 4/3 ∆ VXNGa naar voetnoot2). Sed spat. YHQP est minus quam 4/3 VXNGa naar voetnoot2). cum sit pars hujus trianguli. Ergo EYP est minus quam 1/3 AVY - YHQP. Ergo EYP + + YHQP, hoc est EHQP minus est quam 1/3 ∆ AVY. Ergo omnino EHQP minus [Fig. 2.]
quam 1/3 ∆iANH. Ergo sp. EHQP est intra finitam magnitudinem quantumcunque PQ procul distans ab N sumatur. At si ponatur spatium quoddam minus quam tertia pars ∆iAHN, dico eousque sumi posse PQ, ut spatium EHQP sit majus spatio posito. Sit spat. KLMGa naar voetnoot3) ∞ 1/3 ∆iAHN. Etdetur spat. K minus spatio KLM. dico &c. dividatur differentia in duo spatia aequalia L et M. Et sumatur P tam procul ut fiat ∆ VNX minus quam 3/4 spatij LGa naar voetnoot4), unde | |
[pagina 293]
| |
4/3 ∆ VNX minus erit spatio L. Ergo cum EYP + 4/3 ∆iVNXGa naar voetnoot5) aequatur 1/3 ∆iAYV, Erit EYP + spatio L majus quam 1/3 ∆iAYV. Est autem spatium VYHN, omnino minus spatio L vel M, quippe pars ∆iVNX. Ergo EYP + L + M majus quam 1/3 AYV + VYHN, eoque omnino majus quam 1/3 AYV + 1/3 VYHN hoc estquam 1/3 ∆iANH. Sed spat. K + L + M aequatur 1/3 ∆iANH. Ergo EYP majus est spatio K. quod erat demonstr.mGa naar voetnoot6). |
|