Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 283]
| |
Appendice I à la pièce no. VIIIGa naar voetnoot5).
| |
[pagina 284]
| |
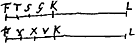 [Fig. 1.]
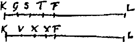 [Fig. 2.]
erunt, differentiae FY, YX, XV, VK. patetque proinde ratione FL ad LT minorem fore quam FL ad LYGa naar voetnoot1). Atqui ratio FL ad LK toties multipla est rationis FL ad LY quoties linea FK multipla est FT. Ergo eadem ratio FL ad LK rationis FL ad LT sepius multipla erit quam linea FK lineae FTGa naar voetnoot2). Similiter cum ratio FL ad LS minor sit ratione FL ad LX. ratio autem FL ad LK toties multipla sit rationis FL ad LX quoties linea FK lineae FX. Erit ratio FL ad LK rationis FL ad LS saepius multipla quam linea FK lineae FS. Similiterque ostendetur rationem FL ad LK saepius multiplicem esse rationis FL ad LG quam linea FK lineae FG. | |
Theorema [I.]Si a puncto in paraboloide recta ad axem ordinatim applicetur et accipiatur in axe, à puncto ubi applicata ei occurrit, recta verticem versus; quae ad partem axis interceptaminter applicatam et verticem sese habeat ut exponens potestatis quae in ea paraboloide consideratur in ordinatim applicatis ad exponentem potestatis quae consideratur in abscissis ad verticem, Recta quae ducitur a terminò lineae in axe acceptae ad punctum in paraboloide ab initio sumtum, paraboloidem in puncto illo continget. 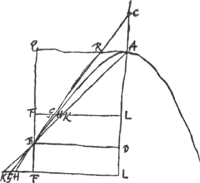 [Fig. 3.]
Sit paraboloidis AB, cujus axis AD, vertex A. Sitque ejus naturae ut quadratoquadrata ordinatim applicatarum BD, HL, sint inter se ut cubi abscissarum ad verticem DA, LAGa naar voetnoot3). Dico si sumatur in axe DC quae sit ad DA ut 4 ad 3 (quoniam nempe hi sunt exponentes qu.qu. et cubi) et ducatur recta CB, eam tangere paraboloiden in B. Sumto enim in recta CB puncto quolibet alio G, ostendemus id cadere extra paraboloiden AB. Sit GLGa naar voetnoot4) rectae BD parallela, et occurrat axi in | |
[pagina 285]
| |
L, rectae vero BF axi parallelae in F, et paraboloidi in H. Ei vero quae conjungit puncta A B, in K. Et compleatur rectang. ADBQ, cujus latus AQ secet recta CB in R. Est ergo ut CD ad DA ita CB ad BR et AQ ad QR et KF ad FG, nimirum ut 4 ad 3. Ac proinde ratio FL ad LK saepius multipla rationis FL ad LG quam FK multipla est FGGa naar voetnoot5). Id est, ratio FL ad LK major quam sesquitertia rationis FL ad LG. Atqui ratio FL sive BD ad LK sive DA ad AL est sesquitertia rationis BD seu FL ad LH. Ergo ratio FL ad LG minor quam FL ad LH. Ideoque LG major quam LH. Unde patet totam lineam CB, praeter punctum B, cadere extra paraboloidem. quod erat dem. | |
Theorema [II].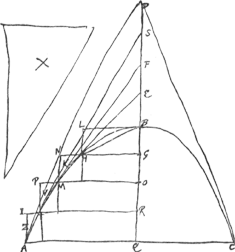 [Fig. 4.]Ga naar voetnoot6)
Paraboloidis cujusvis portio ad triangulum eandem cum ipsa basin habentem, latera vero rectas quae portionem ad terminos basis contingunt, eam habet rationem quam portionis axis ad dimidiam compositae ex eodem axe et axe dicti trianguli.
Sit Paraboloidis portio recta ABC, cujus axis vel axi perpendicularis recta BQGa naar voetnoot7); vertex B; basis AC; tangentes vero in terminis basis rectae | |
[pagina 286]
| |
 [Fig. 4.]Ga naar voetnoot6)
AD, CD, convenientes cum axe in D. Dico portionem ABQ esse ad triang. ADQ, ut BQ ad semissem lineae aequalis duabus DQ, QBGa naar voetnoot1). Hoc autem patebit si ostenderimus trilineum BHAD, curvâ BA et rectis AD, DB comprehensum, esse ad semiportionem BAQ, ut 1/2 BD ad BQGa naar voetnoot2). Erit enim, componendo, triangulum DAQ ad semiportionem ABQ ut 1/2 DB una cum BQ sive ut 1/2 DQ cum 1/2 BQ ad BQ. et convertendo. Quod si igitur trilineum BAD ad semiport. ABQ non est ut 1/2 DB ad BQ, Ergo hanc rationem habebit ad spatium quod vel majus erit vel minus semiportione ABQ. Habeat primó ad majus, quod dicitur XGa naar voetnoot3). Itaque cum spatium X sit majus quam BAQ, poterit huic figura circumscribi ordinatim ex rectangulis aeque altis ut sunt IQ, PR, &c. quae sit minor spatio X. Factum id intelligatur; itaque trilineum BAD ad omnia ista rectangula majorem rationem habebit quam ad spatium X, hoc est, quam 1/2 DB ad BQ. Ducantur tangentes paraboloidem ad puncta T, M, H, in quibus latera dictorum rectangulorum ipsam secant, nimirum rectae TS, MF, HE; Ergo hae dividunt BD in partes aequales inter se, ac totidem numero quod sunt in axe BQ latera dictorum rectangulorum. Et singulae partes ipsius BD ad singulas axis BQ eandem habent rationem quam DB ad BQ. Triangulum itaque BHE est ad rectang. LG ut 1/2 EB ad BG, hoc est, ut 1/2 DB ad BQ. Quare trilineum BHE ad idem rectang. LG minorem rationem habebit quam 1/2 DB ad BGGa naar voetnoot4). Similiter spatium EHMF, quum sit minus triangulo basin FE habenti et altitudinem MO, minorem rationem habebit ad rectang. NO quam | |
[pagina 287]
| |
1/2 FE ad GO, sive quam 1/2 DB ad BQ. Idemque verum est de ratione spatiorum caeterorum FMTS, STAD, ad rectang.a PR, IQ. Ergo omnia praedicta spatia unà cum trilineo BHE, hoc est trilineum totum BAD ad omnia simul rectang.a circumscripta minorem rationem habebit quam 1/2 DB ad BQ. Sed et majorem habere dictum fuit, quod est absurdum. Ergo trilineum BAD ad semiport. BAQ non habet majorem rationem quam 1/2 BD ad DQGa naar voetnoot4). Jam si fieri potest habeat minorem, sitque proinde spatium aliquod X minus semiportione BAQ, ad quod se habeat trilineum BAD ut 1/2 BD ad DQGa naar voetnoot5). Cum igitur spatium X sit minus semiportione BAQ, poterit ei inscribi figura ordinatim ex rectangulis aeque altis quae sit major spatio X. Sit igitur factum, ac sunto ea rectangula HO, MR, TQ. Ergo trilineum BAD ad haec rectang.a minorem rationem habebit quam ad spatium X, hoc est minorem quam 1/2 BD ad BQ. Ducantur rursus tangentes curvam ad puncta quibus anguli inscriptorum ▭orum ipsi occurrunt, quae sint HE, MF, TS, quae itaque dividunt rectam DB in partes aequales, et totidem numero quot sunt in axe BQ, et singulae partes DB ad singulas BQ eandem habent rationem quam DB ad BQ. Singulae vero tangentes productae occurrant sibi proximis in punctis K, V, Z. Itaque triang. EKF ad ▭ HO majorem habet rationem quam 1/2 FE ad GO, hoc est quam 1/2 BD ad BQ. Ac similiter majorem habebit triang. FVS ad ▭ MR, et triang. SZD ad ▭ TQ. Ergo omnia simul triang. dicta ad omnia inscripta rectang.a majorem habebunt rationem quam 1/2 BD ad BQ. Dictis autem triangulis majus est trilineum BAD, ergo hoc ad figuram ex ▭ inscriptis majorem utique rationem habebit quam 1/2 DB ad BQ. Sed et minorem habere dictum fuit, quod est absurdum. Ergo nec minorem rationem habet trilineum BAD ad semiportionem BAQ quam 1/2 BD ad BQ, nec majorem. quare eandem habeat necesse est, quod erat dem.mGa naar voetnoot5). |
|