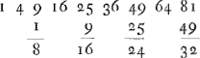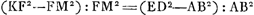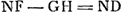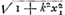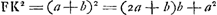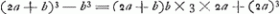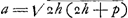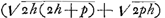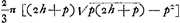Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666

[p. 234]

VI¹⁾.
1657.

[Réduction de la rectification de la parabole à la quadrature de l'hyperbole et de la quadrature de la surface du conoide parabolique à celle du cercle.]

[Première Partie²⁾.]

[Fig. 1.]

1) La Pièce que nous avons divisée en trois Parties, a été empruntée aux pp. 39 et 47-60 du livret du frère Philips que nous avons mentionné dans la note 4, p. 217 du T. XII et à quelques feuilles détachées.

2) Cette première Partie, qui occupe la p. 39 du livret, expose les découvertes faites le 27 octobre 1657. Elle ne donne aucune indication directe sur la manière dont ces découvertes ont été obtenues; mais consultez à ce propos les notes 4 de cette page et 2 de la suivante.

[p. 235]

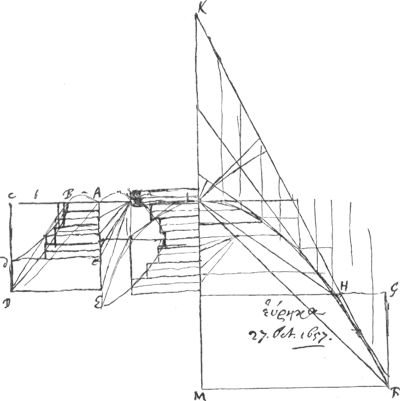
Sit LF parab. axis LM. tangens FK. Sit hijperb. BD aequalium laterum recti et transv.ⁱ et sit AB dimidium lat. transv.ⁱ sicut autem KF ad FM, sive ut HF ad HG ita sit ED ad AB. vel quod eodem redit³⁾, sicut KM ad MF ita sit AE ad AB, Et compleatur ▭ EC. Erit nisi fallor, circumferentia parabolae LF ad rectam FK, ut spatium BDEA ad ▭ ACDE⁴⁾. Potest sumi quaevis hijperbola, dummodo fiat, de sive CA ad AB ut KF ad FM⁵⁾.

3) On a, en effet, KF² : FM² = ED² : AB²; donc ; c'est-à-dire, en appliquant une propriété connue de l'hyperbole équilatère, MK² : FM² = AE² : AB², ou bien MK : FM = AE : AB.

4) La figure que nous avons reproduite en tête de cette ‘Première Partie’, contient plusieurs lignes énigmatiques qui, peut-être, se rapportent en partie à des tentatives qui n'ont pas abouti au but désiré. Toutefois il ne nous semble pas impossible de reconstruire à peu près à l'aide de la ‘Deuxième Partie’ qui constitue une démonstration en règle du résultat obtenu, et de quelques autres indications, les raisonnements qui ont guidé Huygens. Dans leur exposition nous nous servirons librement des notations modernes.
Son point de départ, indiqué par la suite de nombres qu'on trouve à côté de la figure, était sans doute la remarque que dans la parabole x² = py, où les x sont comptés dans la direction de la tangente au sommet L, les accroissements successifs des y pour des valeurs a, 3a, 5a, 7a, etc. de x sont proportionnels aux nombres 1, 2, 3, 4, etc. On peur appliquer cette remarque à la fig. 3 de la p. 239 qui suit. Dans cette figure les ordonnées à gauche du sommet B correspondent aux nombres 1, 4, 9, 16, 25, 36, 49 de la suite prémentionnée et les différences , , etc. entre la troisième et la première ordonnée, la cinquième et la troisième, etc. aux nombres 8, 16, 24, etc. Or, puisque ces derniers nombres sont proportionnels aux abscisses des points de contact des tangentes successives DG, CD, etc. menées à la parabole AEKFB, on est évidemment conduit à une relation représentée par la formule , d'où l'on peut conclure que les éléments successifs de la circonférence de la parabole sont proportionnels aux ordonnées d'une hyperbole . C'est la conclusion à laquelle Huygens arrive au Théorème V, p. 243.
Dès lors il est évident que la rectification de la parabole se réduit à la quadrature de l'hyperbole; mais si dans une telle hyperbole la première ordonnée AB [Fig. 1] prend la grandeur a, il faut que la dernière DE ou de soit égale à , où représente le rapport de ∆s à ∆x pour le point F de la parabole. On a donc, comme le texte l'indique, de (ou DE, ou CA): AB = FK : FM. Or, de même que les éléments de la parabole, qui correspondent à des accroissements égaux ∆x, sont proportionnels aux ordonnées hyperboliques , ceux de la tangente FK correspondant aux mêmes accroissements ∆x sont dans le même rapport à la dernière ordonnée de (ou DE), d'où il résulte que le rapport de la longueur de la parabole à celle de la tangente FK doit être le même que celui de l'aire hyperbolique BdeA (on BDEA) au rectangle Ad (ou AD).

5) En esset, dans la démonstration qui va suivre, et dans les énoncés donnés à diverses occasions de sa rectification de la parabole, Huygens n'emploie plus l'hyperbole équilatère BD mais une autre hyperbole, comme Bd, de forme arbitraire.
On trouve ces énoncés aux ‘Theoremata VIII et IX’, pp. 249 et 253 du présent Tome, aux pp. 344, 435, 501 et 502 du T. II et à la ‘Prop. IX’ de la ‘Pars tertia’ de l'‘Horologium oscillatorium’, p. 77 de l'édition originale. Remarquons que Huygens y remplace souvent la proportion CA : AB = KF : FM par les égalités CA = 2KF; AB = 2FM.
Ajoutons qu'on retrouve l'énoncé de l'‘Horologium oscillatorium’ sans modification essentielle a la p. 95 du Manuscrit B, qui doit dater de 1662, et de même à la p. 38 du Manuscrit N^o. 13, où Huygens à une époque inconnue (probablement vers 1667) résuma les découvertes principales qu'il avait faites jusqu'à cette époque.

[p. 236]

dato ergo centro gr. in hijperbola, inveniri poterit recta periferiae parabolicae aequalis¹⁾.

videtur conoidis parab.ⁱ superficies ad circulum redigi posse²⁾). Datâ parabolicae lineae longitudine Hyperbolam quadrare³⁾.

1) Comparez le ‘Theorema VI’ des ‘Theoremata de quadratura hyperboles, ellipsis et circuli, ex dato portionum gravitatis centro’, p. 305 du T. XI, et l'avant-dernier alinéa de la démonstration du ‘Theorema IX’, p. 253 du présent Tome.

2) Afin d'expliquer de quelle manière Huygens a pu arriver à cette conclusion, nous commençons par faire observer que, comme nous l'avons vu dans la note 4 de la p. 235, les éléments de la parabole LF (Fig. 1) sont aux éléments correspondants de la tangente KF comme les ordonnées de l'hyperbole Bd sont à la longueur constante AC, ou, si l'on veut, comme les rectangles élémentaires qui représentent approximativement les accroissements de l'aire hyperbolique ABde sont à ceux qui constituent le rectangle Ce. Or, il est évident qu'en faisant tourner ces figures élémentaires, ceux de la parabole et de la tangente autour de KM, et ceux de l'hyperbole et du rectangle autour de AC, l'égalité des rapports est conservée, c'est-à-dire que les éléments de la surface courbe du conoïde parabolique, sont aux éléments de la surface conique, décrite par KF, comme les éléments du volume engendré par l'aire hyperbolique ABde sont à ceux du cylindre décrit par le rectangle Ce. En outre, les éléments successifs de la surface conique sont entre eux dans la même proportion que les éléments correpondants du volume du cylindre Ad.
À l'aide de ces considérations Huygens a pu parvenir (comme nous l'expliquons plus loin dans la note 8 de la p. 261) au Théorème XIII, p. 259, d'après lequel le volume engendré par le rectangle Ad est au volume engendré par la figure ABde comme la surface conique KF est à la surface courbe du conoïde MLF. La quadrature de cette dernière surface dépend dès lors de la cubature du solide engendré par la révolution de la figure ABde. Or, le volume de ce dernier solide est égal à celui du cylindre engendré par le rectangle ACde, diminué du volume du conoïde hyperbolique BCd; mais la détermination de ce dernier volume avait été réduite par Archimède (voir la note 4 de la p. 263) à la cubature du cône de révolution, c'est-à-dire à la quadrature du cercle.
Quant aux résultats obtenus par ces considérations on les trouve aux ‘Theoremata XV-XVII’ (p. 264-267) et aux ‘Problemata I et II’ (p. 267-270) qui contiennent la réduction de la quadrature de la surface du conoïde à la quadrature du cercle avec les conséquences que Huygens en a tirées et les problèmes qu'il y a rattachés.
Sur la manière dont Huygens a publié ces résultats ou les a faits connaître à ses correpondants on peut consulter les notes 1 de la p. 264, 4 de la p. 266 et 10 de la p. 267.

3) Comparez le dernier alinéa de la p. 253.

[p. 237]

[Deuxième Partie⁴⁾.]

[Definitio I.]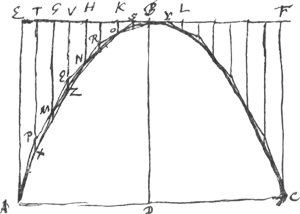

[Fig. 2.]

Si circa parabolam ab axe aequaliter sectam descriptum fuerit rectangulum AEFC eandem cum parabole basin eandemque altitudinem habens, Dividatur autem latus rectanguli EF quod parabolam in vertice contingit in partes aequales quotlibet EG, GH, HK, KB, BL, & c. numero pares. Et ducantur ab omnibus divisionum punctis rectae parabolae occurrentes, et axi parallelae GM, HN, KO, &c. atque per singula occursus puncta ducantur rectae parabolam tangentes uti et a terminis baseos A, C. hae omnes sibi invicem occurrentes, una cum parte quadam tangentis inverticem, constituent circa parabolen lineam quandam inflexam, quae vocetur ordinatè circumscripta.

Hanc autem majorem esse liquet longitudine parabolae cui circumscripta est, quum enim utriusque ijdem sint termini A, C; sintque in easdem partes cavae, necesse est comprehendentem comprehensa majorem esse. hoc enim et ab Archimede in libris de Sphaera et Cylindro⁵⁾ sumptum fuit.

4) Cette partie traite, suivant la méthode des anciens, de la réduction de la rectification de la parabole à la quadrature de l'hyperbole. Elle est empruntée aux p. 47-60 du livret de Philips, et ensuite à des feuilles détachées; voir la note 2 de la 248.
Nous avons introduit une division du texte en ‘Definitiones’, ‘Lemmata’ et ‘Theoremata’, telle que Huygens l'aurait apportée s'il avait publié la Pièce, comme c'était sans doute son intention, quoiqu'il n'y ait pas donné suite; consultez à ce propos sa lettre à Kinner à Löwenthurn, p. 503 de notre T. II.

5) Voici le postulat en question qu'on trouve au début de l'ouvrage mentionné: ‘Linearum eosdem terminos habentium rectam minimam esse. Aliarum uero quae in plano fuerint, si eosdem habuerint terminos, eas inaequales esse. Vbi autem ambae in easdem partes cauae fuerint, ut uel altera tota comprendatur ab altera, vel altera earum ab alterius superficie, & recta eosdem cum illa terminos habente contineatur: uel quidpiam ipsius contineatur, quidpiam uero habeat commune cum altera, & comprensam esse minorem’ (voir la p. 2 de l'édition de Bâle, citée dans la note 3, p. 274 du T. XI, ou les p. 9-11 du T. I de l'édition de Heiberg, citée dans la note 2, p. 50 du T. XI).

[p. 238]

[Theorema I.]

Descriptâ circa parabolen lineâ ordinatè, si ab omnibus flexionis punctis ducantur axi parallelae quae occurrant lateri circonscripti rectanguli ut sunt PT, VQ [Fig. 2.], divident hae segmenta prius facta EG, GH etc. bifariam.

[Fig. 2.]

Connectantur enim rectâ lineâ duo quaevis inter se proxima contactuum puncta, ut M, N, et occurrat rectae MN producta VQ in Z. itaque, quoniam ex puncto Q duae eductae sunt parabolam contingentes in MN, bifariam dividetur MN tactus conjungens in Z per 30.2ⁱ. Con.¹⁾ quamobrem et GH in V bifariam dividetur, cum tres hae MG, NH, ZV sint inter se parallelae. Similiter ratione liquet etiam segmentum KB axi proximum à tang. RS bifariam dividi in S.

1) Il s'agit de la ‘Prop. XXX du ‘Lib. II’ des ‘Conicorum libri quattuor’ d'Apollonius. Voir la p. 55 verso de l'édition de Commandin citée dans la note 4 de la p. 6 de notre T. I où l'on lit: ‘Si coni sectionem, uel circuli circumferentiam duae rectae lineae contingentes in unum punctum conueniant: diameter, quae ab eo puncto ducitur, lineam tactus coniungentem bifariam secabit.’

[Theorema II.]

Si circa parabolen ab axe suo aequaliter divisam linea ordinatè circumscripta fuerit, et à singulis punctis quibus

[p. 239]

inflexa est ad parabolam rectae ducantur axi parallelae eae omnes inter se aequales erunt.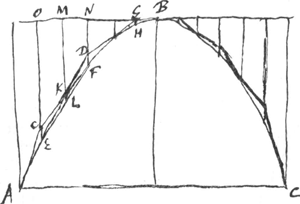

[Fig. 3.]

Sit enim parabolae ABC linea circumscripta ordinatè, et ab inflexionis angulis C, D, G, &c. ductae sint CE, DF, GH &c. axi parallelae, dico has omnes sibi aequales effici.

Producantur namque binae quaevis ipsarum sibi proximae ut EC, DF, donec occurrunt ei quae tangit parabolam in vertice, in O et N.

Producatur item MK, quae definit punctum contactus rectae CD, et occurrat rectae EF in L. Quoniam igitur per praeced. lineae DN, CO bifariam secant aequalia segmenta tangentis in vertice; Erunt quoque horum dimidia NM, MO aequalia quare et EL aequalis LF. Est autem LK diameter parabolae per cujus terminum ducta est tangens CD. Ergo per 5.2ⁱ Con.²⁾ erunt CD, EF parallelae. ac proinde parallelogrammum erit CDFE, ideoque aequalia inter se, opposita ipsius latera, CE, DF. Eodem modo demonstrabitur DF esse aequalis GH, atque ita continuè procedendo omnes tandem à punctis flexionum eductae inter se aequales esse ostendemus.

2) Voir la note 32, p. 108 du T. XI.

[Theorema III.]

Data parabola ab axe suo aequaliter divisa, potest circa eam linea ordinatè describi, quae superest parabolae excessu qui sit minor quavis proposita linea.

Sit enim data Parabola qualis dicta est ABC, lineaque proposita D [Fig. 4.]. Sumatur in axe parabolae à vertice B intervallum BE, quod sit duplum lineae D.

[p. 240]

Et ducatur ordinatim applicata EV. Descripto itaque circa parabolen rectangulo AQRC eandem basin eandemque cum ipsa altitudinem habente, potest ipsius latus QR, quod parabolam contingit in vertice, in partes dividi aequales numero

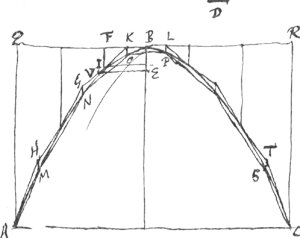[Fig. 4.]

pares ita ut singulae earum sint minores rectâ VE. Sit factum igitur, sitque partium una BF. Et ex punctis divisionum ductis lineis axi parallelis, quae parabolae occurrant, circumscribatur per occursus puncta linea inflexa ordinatè AHGKL, dico eam superare parabolam minori excessu quam sit linea D. Ducantur enim ab omnibus flexionum punctis lineae axi parallelae et parabolae occurrentes ut sunt HM, GN, KO, LP. Punctaque singula occursus cum proximis sibi jungantur rectis PO, ON, NM ab extremis vero quae basi proxima sunt M et S ducantur rectae ad terminos baseos MA, SC. Est igitur inscripta quoque hoc modo linea AMNOPSC intra parabolam, eosdem cum illa terminos habens inque eandem parte cava, quae proinde comprehendente curva minor erit. Quia autem sicut in praec. ostensum fuit¹⁾, MN est aequalis HG, et NO aequalis GK atque ita unaquae pars inscriptae aequalis parti circumscriptae sibi parallelae usque ab M ad S; Erit proinde tota pars inscriptae MNOPS aequalis parti circumscriptae HGKBLT. at verò duae HM, MA simul majores sunt HA, similiterque duae simul TS, SC majores TC; itaque apparet totam lineam inscriptam parabolae unà cum duabus MH, ST majorem esse tota circumscripta. Quare multo magis parabola una cum duabus MH, ST excedet quoque circumscriptum sibi ordinatè. Si igitur ostendatur duas MH, ST simul minores esse data D; patebit minorem esse excessum ordinatè circumscriptae supra parabolam, quam est dicta D linea. Illud autem hinc liquebit, lineae HM, ST singulae aequantur ipsi KO. Haec vero quarta pars est FI; cum sit FI ad KO ut quadratum FB ad qu. BK, sitque FB dupla ipsius BK. Igitur duae simul HM, ST aequantur dimidiae FI. Est autem FI minor quam BE, quoniam FB minor quam VE. Ergo duae simul HM, ST minores erunt dimidiâ BE hoc est datâ D. quod demonstr. supererat.

1) Voir la démonstration du théorème précédent.

[Lemma I.]

Si fuerit series quadratorum quorum latera eadem proportiene crescant qua numeri ab unitate impares, eorum exces-

[p. 241]

sus, quo unumquodque sibi proximum superat crescent secundum simplicem numerorum ab unitate seriem²⁾.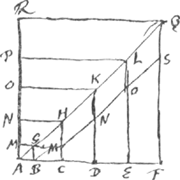

[Fig. 5.]

Sint in recta AF sumptae quotcunque AB, AC, AD, AE, AF &c. quarum inter se ratio eadem sit quam numerorum 1, 3, 5, 7, 9 &c. Sintque quadrata ab ipsis descripta BM, CN, DO, EP, FR. Sunt igitur excessus quadratorum gnomones BGMNHC, CHNOKD, DKOPLE, ELPRQF, quos ostendendum est inter sese esse sicut numeri deinceps ab unitate 1, 2, 3, 4, &c. Ducatur ex A diameter communis omnium quadratorum AQ, sumptâque CM³⁾ ∞ BG, agatur MS dictae diametro parallela. Erunt igitur omnes hae inter se aequales MH, NK, OL, SQ, et singulae ipsi BC, quia sumpta fuit MC ∞ GB hoc est AB, eratque tota CH ∞ AC. Sunt autem et BC, CD, DE, EF inter sese aequales. quare aequales quoque erunt MN, NO, OS, et singulae ipsi GH. Fit igitur trapezio BGHC simile et aequale trapez. CMND. Hoc autem trapez. duplum est ∆^li GMH, (quoniam HM dupla est MC) ac proinde aequale ▱^o MHKN. Ergo et CMND trapez. aequale erit parallelogr^o. MHKN. Itaque trapez. CHKD duplum est trapezij CMND ideoque et trapezij BGHC. Ideoque et gnomon CKN⁴⁾ duplus gnomonis BHM. Rursus trapez. DNOE quia est simile et aequale trapez.^o CHKD, erit duplum quoque trapez. BGHC. ▱ vero KO ipsi trapez. BGHC aequale est, cum sit aequale ▱^o HN. Ergo totum trapez. DKLE erit triplum trapezij BGHC. Quare et gnomon DLO triplus gnomonis BHM. Simili ratione quoniam trapez. EOSF fit simile et aequale trapezio DKLE, erit illud quoque triplum trapezij BGHC. at ▱ LS ipsi trapezio BGHC aequale est. Ergo totum trapez. ELQF quadruplum erit trapezij BGHC, et gnomon EQP quadruplus propterea gnomonis BHM. Itaque ostensum est gnomones omnes deinceps crescere secundum rationem numerorum 1, 2, 3, 4. Et patet eandem progressionem continuatum iri, quotcunque demum quadrata exponantur.

2) Comparez la suite numérique qu'on trouve à la p. 234 à côté de la Fig. 1.

3) On remarquera le double emploi dans la figure et dans le texte des lettres M, N et O.

4) Notation abrégée pour CDKONHC.

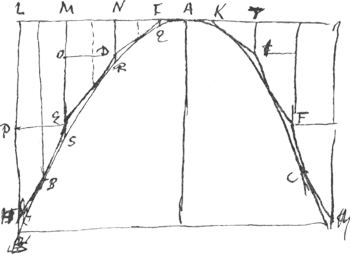
[Theorema IV.]

Circa parabolam BAC [Fig. 6], aequaliter ab axe divisam, linea ordinatè BEDIKF circumscripta sit cujus partes basi

[p. 242]

proxime EB, FC ultra basin producantur ut fiant sui ipsius duplae. Et ducantur ab omnibus flexionis punctis, item a

[Fig. 6.]

terminis duarum ultra basin productarum, rectae axi parallelae quae occurrant parabolae in vertice tangenti, sintque HL, EM, DN, FT¹⁾. Et notetur excessus quibus unaquaeque harum a sibi proxima superatur, ut sit EO excessus EM supra DN; HP excessus HL supra EM. Dico seriem linearum quarum prima sit DN reliquae vero deinceps excessus omnes dicti OE, PH, eadem ratione crescere qua numeri ab unitate crescunt. Hoc est ipsius DN duplam esse EO, triplam vero HP; atque ita deinceps si pluribus angulis fuerit ordinate circumscripta.

Productis enim ME, ND, ut parabolae occurrant in S, et R, ductaque itidem IQ axi parallela. Constat ex praec.²⁾ ipsi IQ aequales esse singulas DR, ES, HB³⁾. Constat etiam lincas AI, AN, AM, AL crescere secundum rationem numerorum imparium ab unitate 1, 3, 5, 7. Sicut autem harum inter se quadrata ita sunt longitudine IQ, NR, MS, LB. Itaque harum excessus qua unaquaeque harum à sequente superatur erunt sicuti numeri ab unitate 1, 2, 3, 4, &c.⁴⁾. Excessus autem quo superatur IQ àb NR est ND, cum sit DR aequalis IQ; Et excessus qua NR superatur àb MS est OE, quum sit NR aequalis utrisque simul MO, ES. Similiterque excessus quo MS superatur àb LB est PH, quoniam MS aequalis est duabus simul LP, HS⁵⁾. Ergo ND, OE, PH, crescent secundum rationem numerorum ab unitate 1, 2, 3, 4, &c. Quod erat dem.

1) La lettre T est mal placée dans la figure, il faut la transporter vers la droite au pied de la perpendiculaire qui part du point F.

2) Voir le théorème II, p. 238-239.

3) Ici et dans ce qui suit B indique le point le plus bas au côté gauche de la figure et non pas le point B qui se trouve entre H et E.

4) D'après le lemme qui précède.

5) Lisez: HB.

[p. 243]

[Theorema V.]

Esto parabola ab axe aequaliter divisa ABC, si circaeam linea ordinate describatur, hujusque partes quae parabolam ad terminos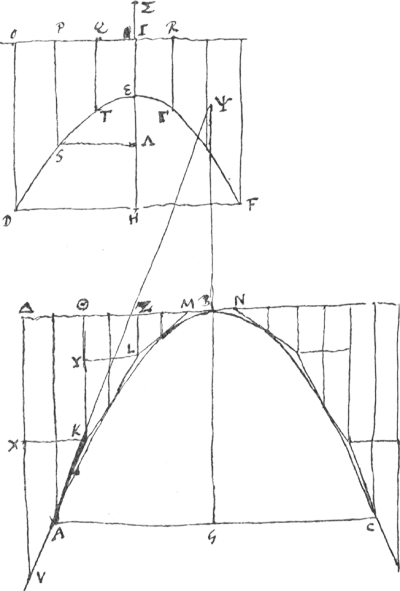

[Fig. 7.]

basis contingunt ut KA, producantur ultra basin ut fiant sui ipsius duplae.

Exponatur autem et hijperboles portio DEF ejusmodi, in qua diameter HE juncta dimidio lateris transversi EI, ad dimidium latus transversum EI eandem rationem habent quam recta Aψ parabolam in termino baseos contingens axique occurrens, ad ipsius baseos dimidium AG. Et super basi portionis hyperbolae parallelogrammum constituatur OF cujus latus basi oppositum per centrum sectionis I transeat, reliqua vero latera sint diametro portionis parallela. Et dividatur latus ▭ⁱ quod per centrum sectionis est, in partes totidem ac divisum fuit latus ▭ⁱ circa parabolen descripti cum linea ordinatè circumscriberetur. Ducanturque a punctis divisionum rectae diametro parall. PS, QT, RΓ, &c. quae hyperbolae occurrant. Dico lineam OD ad reliquas singulas PS, QT, IE, &c. eadem proportione referri qua et VK ad singulas rectas KL, LM, MN, &c. si utrobique eadem in

[p. 244]

ordine sumantur. nam quod harum multitudo eadem sit atque illarum, ex constructione manifestum est.

Ducantur omnibus circumscriptae flexionum punctis KLMN &c. rectae axi

[Fig. 7.]

parallelae itemque à terminis duarum quae ultra basin productae fuere; occurrant tangenti parabolam in vertice, in punctis Δ, Θ, Z, &c Et sint KX, LY, &c. ipsi BΔ parallelae ab ijsdem flexionum punctis eductae. Ostendemus igitur primo, quod AK¹⁾ ad KL sicut in hyperbola est DO ad SP. Sit SΛ ordinatim ad diametrum applicata, et producatur diameter usque in Σ, ut sit EΣ aequalis lateri transverso²⁾.

Quoniam igitur crescunt lineae ZL, YK, XV secundum rationem numerorum ab unitate 1, 2, 3, &c.³⁾, Eademque ratione crescunt lineae IQ, IP, IO; Erit VX ad KY sicut OI ad PI, sunt enim in ordine eaedem. Itaque et qu. VX ad qu.KY ut qu.OI ad qu.PI. hoc est ut qu.DH ad qu.SΛ, hoc est ut ▭ ΣHE⁴⁾ ad ▭ ΣΛE. per Con.⁵⁾. Est autem ▭^m ΣHE aequale qu^o. IH - qu.IE. Similiterque ▭ ΣΛE ∞ qu.IΛ - qu.IE. Itaque est qu.VX ad qu.KY sicut qu.IH - qu^o.IE ad qu.IΛ - qu^o.IE. Et permutando qu.VX ad qu.IH - q.IE ut qu.KY ad qu.

1) Lisez: VK.

2) On a donc IΣ = IE; si Huygens a pris IΣ plus courte que IE, c'est parce que la ligne OR se trouvait tout près du bord de la feuille.

3) Voir le Théorème IV, p. 241-242.

4) C'est-à-dire le rectangle dont les côtés sont égaux à ΣH et HE.

5) Il s'agit de la Prop. 21 du Livre 1 des Coniques d'Apollonius; voir la note 12, p. 300 du T. XI.

[p. 245]

IΛ - qu.IE. Porro quoniam ex datis est sicut ψA ad AG, hoc est sicut VK ad KX ita HI ad IE; erit quoque sicut qu.VK ad qu. KX ita qu.HI ad qu.IE. quare et per conversionem rationis erit qu.VK ad excessum qu.VK supra qu.KX, hoc est ad qu.VX sicut qu.HI ad qu.HI - qu.IE. Et permutando, qu.VK ad qu.HI sicut qu.VX ad qu^m.HI - qu^o.IE.

Sicut autem qu.VX ad qu.HI - qu.IE item ostendimus esse qu.KY ad qu.IΛ - qu.IE. Ergo et qu.VK ad qu.HI sicut qu.KY ad qu.IΛ - qu.IE. Verum ut qu.VK ad qu.HI ita est qu.KX ad qu.IE. (nam modo diximus esse qu.VK ad qu.KX ut qu.HI ad qu.IE). Ergo et qu.KY ad qu.IΛ - qu.IE ut qu.KX ad qu.IE. Et permutando qu.KY ad qu.KX sive ad qu.YL ut qu.IΛ - qu.IE ad qu.IE. Itaque et componendo erit sicut duo simul, qu.KY et qu.YL hoc est sicut qu.KL ad qu.YL ita qu. IΛ ad qu.IE. Sed ut qu.YL sive qu.KX ad qu.KV, ita est qu.IE ad qu.IH, ut supra patuit. Ergo ex aequali erit qu.KL ad qu.KV sicut qu.IΛ ad qu.IH, hoc est sicut qu.PS est ad qu.OD, Et convertendo. Quamobrem et linea OD erit ad SP sicut VK ad KL.

Eodem modo ostendimus quod VK ad LM sicut DO ad TQ. Sed et quod VK ad MN sicut DO ad IE manifestum fiet hac ratione. Est enim MN aequalis ipsi KX. Sicut autem VK ad KX hoc est ut ψA ad AG ita positum fuit esse HI sive DO ad IE. Quare et VK ad MN sicut DO ad IE. Itaque constat lineam OD ad singulas SP, QT, IE eadem ratione referri qua et DO ad singulas SP, TQ, EI⁶⁾.

6) Lisez: qua et VK ad singulas KL, LM, MN.

[Definitio II.]

Data hyperboles portione, si super basi ipsius ▭ describatur ita ut latus ▭ quod basi oppositum est transeat per centrum sectionis reliqua vero diametro parallela sint vocetur ejusmodi ▭ ad centrum terminatum. pars vero ejusdem quae dempta hijperboles portione remanet vocetur spatium residuum.

[p. 246]

[Fig. 8.]

Et si dividatur hujus ▭ⁱ latus quod per centr. sectionis transit in partes aequales quotlibet, numero pari, agantur que à divisionum punctis rectae diametro parall.^ae quae portioni occurrant. Circa has autem pari ipsis altitudine parallelogramma describantur, lateribus diametro portionis parallelis bases vero segmentis rectae [NM, MO, &c.]¹⁾ aequales habentia et a lineis [FM. GO, BE, &c.]¹⁾ bifariam divisas. Figura ex his ▭^is composita et ex duobus dimidiae horum latitudinis ▭^is [ut ANHK] dicatur ordinatè circa spatium residuum constituta.

1) Ici Huygens indiqua par des points qu'il y avait encore quelque chose à ajouter. Aussi, à côté de la figure avec les lettres que nous avons reproduite, il y en a une autre, presque identique, sans lettres. C'est de celle-ci sans doute qu'il s'est servi pendant la rédaction de cette définition; celle avec les lettres étant donc postérieure à cette rédaction.

1) Ici Huygens indiqua par des points qu'il y avait encore quelque chose à ajouter. Aussi, à côté de la figure avec les lettres que nous avons reproduite, il y en a une autre, presque identique, sans lettres. C'est de celle-ci sans doute qu'il s'est servi pendant la rédaction de cette définition; celle avec les lettres étant donc postérieure à cette rédaction.

[Theorema. VI.]

Data autem hyperbolae portione si ▭^m ei circumscribatur ad centrum terminatum et figura ordinatè circa spatium resid. porro describatur. Dico hanc ipso spatio residuo majorem esse.

Jungantur enim [Fig. 8] rectis lineis puncta [A, F, G, B, H, &c.]. Quoniam igitur aequales et parallelae inter se sunt AK, IF, necesse est fieri aequalia quoque ∆.^a LKA, LIF, ideoque aequale esse trapezium AFMN utrique simul ▭^o AH, HF. Eadem ratione trapezium FGOM aequale erit duobus ▭^is FP, PG. Et trapez. GBEO, ▭^is GQ, QB, atque ita de caeteris. Unde patet figuram ex omnibus trapezijs compositam AFGBHCRN aequari figurae ex ▭^is ordinatè circumscriptae. Dicta vera figura ex trapezijs composita major est spatio residuo, quoniam ipsum continet atque insuper segmenta quaedam ipsius portionis. Ergo et figura ex ▭^is ordinatè circumscripta major erit dicto residuo spatio. quod erat ostend.

[p. 247]

[Lemma II²⁾.]

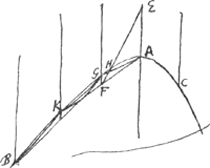[Fig. 9.]

Si hyperbolae CAB occurrant rectae quotvis parallelae, et aequalibus intervallis à se invicem distantes in punctis C, A , G, K, B fueritque earum una E A diameter sectionis. Jungantur autem rectis lineis duo quaeque sibi vicina occursuum puncta. dico, segmentorum hyperbolae hisce lineis abscissorum, maxima esse quae diametro adjacent AG, AC. Reliqua vero eo quae que minora quo ulterius ab his abfuerint.

Jungatur enim AK. eique occurrat producta IG³⁾ in F. dividet autem ipsam bifariam propter aequalem parallelarum linearum distantiam. ducatur ad centrum sectionis recta FE, secans hyperbolen in H, secabit enim ipsam quia centrum E extra sectionem est, punctum vero F intra. Et erit FH diameter portionis AHKA, ipsam proinde in duo aequalia secabit. quia autem recta FE tota inter parallelas EA, GF sita est, sequitur intersectionem H contingere inter G et A. Itaque frustum FHA pars erit frusti FGA. Unde quum recta FH dividat segmentum AGKF in duo aequalia, apparet FG ipsum dividere inaequaliter, ita ut majus sit spatium FGA quam FGK. Verum triangula hisce spatijs inscripta FGA, FGK inter se aequalia sunt. Igitur residuum segmentum GA majus esse necesse est residuo segmento GK. Eodem modo ostendetur segmentum GK majus esse segmento KB atque ita unumquodque eo quod proxime subsequitur. Quare constat propositum.

2) Comme l'état du manuscrit le prouve, le ‘Lemma II’ fut rédigé après le Théorème VII, le besoin d'un tel lemme s'étant fait sentir pendant la rédaction de la démonstration de ce théorème.

3) La lettre I manque dans la figure; on la retrouve toutefois dans une autre figure qui est moins complète sous d'autres respects. La ligne IG est la parallèle à l'axe AE, qui passe par G.

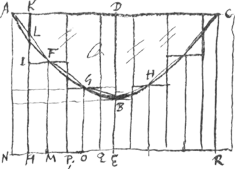
[Theorema VII.]

Data hijperbolae portione, descriptoque circa eam ▭^o ad centrum terminato, dico circa spatium residuum figuram

[p. 248]

ordinatè describi posse quae superet spatium residuum minori excessu quam sit propositum quodvis spatium.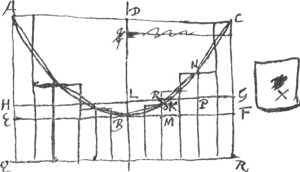

[Fig. 10.]

Detur enim portio [ABCDA] itemque spatium [X]. Et circumscripto ▭^o ad centrum terminato ducatur tangens portionem in vertice B recta EF. Eique alia agatur parallela HG, ita ut comprehensum ▭ EG sit duplum spatij X. Secet autem HG recta diametrum portionis in L, hijperbolen vero in K. Potest jam itaque figura ordinate circa spatium residuum constitui ita ut bases singulae ▭^orum ex quibus ipsa componitur sint minores rectâ LK. Sit igitur factum et jungantur bina quaeque puncta in hyperbola quibus latera dictorum ▭^orum bifariam secantur rectis lineis [CN, NO, OB] &c. Cum igitur segmentum hyperbolae vertici proximum BO sit minus triangulo BOM; triangulum BOM minus quam dimidium ▭ⁱ ML; (nam quia BM minor est ordinatim applicatâ LK, etiam MO minor erit quam BL. ideoque ∆^m BOM minus quam dimidium ▭ ML). Erit proinde et dictum segmentum BO omninò minus quam ½ ▭ ML. Reliqua vero segmenta hijperbolae quae ab eadem parte diametri sunt ON, NC, singula minora cum sint segmento BO, per [Lemma praecedens], totidem vero ▭^a MP, PF aequentur singula ▭^o ML; Erunt proinde omnia simul segmenta haec BO, ON, NC, minora ½ ▭^o BG. Eadem vero ratione, et ea quae ad alteram partem diametri sunt segmenta, minora probabuntur ½ ▭^o BH. Itaque omnia simul segmenta ab hyperbolae portione abscissa minora erunt dimidio ▭ EG, hoc est minora spatio dato X. Ideoque si spatio residuo dicta segm.^a addantur compositum minus erit quam hoc ipsum spatium + X. Atqui dicta segmenta addita spacio residuo, aequant figuram ordinatè circa spatium residuum ex ▭^is circumscriptam, sicut in praec. demonstratione¹⁾ ostensum fuit. Ergo figura ordinatè circumscripta minor erit dicto spatio una cum spatio X. Unde manifestum est excessum quo figura ordinate circumscripta superat idem spatium à rectis AQ, QR, RC et hijperbola CBA comprehensum, minorem esse ipso X spatio. Quare constat propos.²⁾.

1) Voir la démonstration du ‘Theorema VI’, p. 246.

2) Ici finit la partie que nous avons empruntée au livret de Philips. Le reste se trouve sur des feuilles détachées dont la première portele numéro 5. En effet, la démonstration du ‘Lemma II’ qui, comme nous l'avons dit dans la note 2 de la p. 247, se trouve dans le livret à la suite du ‘Theorema VII’, est suivie parles mots: ‘Reliqua in folio. Incipiunt pag. 5. signo..’, accompagnés d'un signe de renvoi qu'on retrouve sur la feuille prémentionnée.

[p. 249]

[Theorema VIII.]

Si fuerit Parabola ab axe aequaliter divisa, itemque Hijperbolae portio, ita comparatae, ut quam rationem habent duo simul latera trianguli isoscelis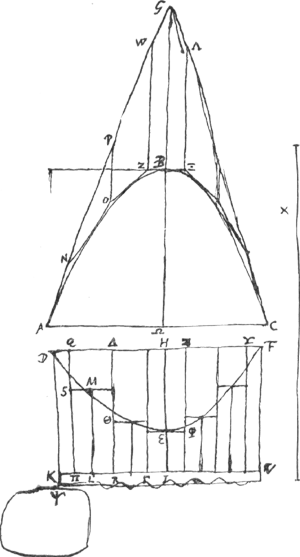

[Fig. 11.]

communem cum portione parabolica basin et duplam altitudinem habente ad ipsam basin, eandem habent hijperbolae portionis diameter [HE] juncta ½ lateris transversi ad dimidium latus transversum. Et describatur circa hyperboles portionem rectangulum ad centrum sectionis terminatum. Erit sicut dicta duo latera trianguli circa parabolam descripti ad parabolae longitudinem, ita ▭ circa hijperbolen descriptum ad partem sui quae dempta hyperboles portione relinquitur³⁾.

Esto parabola ABC qualem diximus, sitque supra basin ipsius AC descriptum ∆ AGC axem sive altitudinem parabolae duplam habens unde fiet ut latera GA, GC parabolam contingant.

Porro et hyperboles portio sit DEF cujus diameter EH, dimidium vero lateris recti⁴⁾ EI. Sitque HI ad IE sicut duo simul latera GA, GC

3) Comparez le premier alinéa de la Première Partie, p. 235.

4) Lisez: lateris transversi.

[p. 250]

ad basin AC. Describaturque circa hyperboles portionem rectangulum ad centrum sectionis terminatum FK. Dico itaque esse sicut duo latera AG, GC ad longitudinem

[Fig. 11.]

parabolae ABC, ita ▭ FK ad spatium residuum DKVFED. Si enim dictae rationes aequales esse negentur. Ergo sicut ▭ ad spatium DKVFED ita erunt dicta duo latera sive linea AGC ad lineam aliquam vel majorem vel minorem parabola ABC. Sit primo, si fieri potest, linea X major parabola ad quam AGC eandem dicatur habere rationem quam ▭ ad 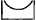. Potest itaque circa parabolam linea ordinatè describi ita ut excessus quo descripta superat parabolam minor sit excessu quo X parabola superat¹⁾. Esto descripta ejusmodi linea ordinate ANOZΞC. Ergo ipsa minor erit quam linea X. Dividatur deinde ▭ⁱ latus KV in tot partes aequales quot fuere in recta parabolam in vertice contingente ad circumscribendam lineam ordinatè. Et a punctis sectionum ducantur ad hyperbolam rectae axi parallelae, et secundum has figura ordinatè circa hyperbolen describatur, cujus extrema ▭^a quae dimidiam caeterorum latitudinem habent, altitudine vero aequant ▭ FK, sint QK, YV. Et reliqua etiam ▭^a ad hanc altitudinem producantur. A punctis vero quibus linea ordinate circum parabolem descripta inflexa

1) D'après le ‘Theorema III’, p. 239.

[p. 251]

est ducantur rectae axi parall. ut OP quae quidem in linea AGC partes aequales intercipient quarumque singulae ut NP duplae erunt ad NA, uti constat ex Prop. ...²⁾.

Quoniam igitur per [Theorema V]³⁾ dupla rectae NA ad NO, et reliquas singulas lineae circumscr.^ae partes eadem ratione refertur, qua DK ad ML et reliquarum unamquamque quae ▭^orum altitudines definiunt. Ut autem DK ad ML et singulas reliquas dictarum linearum, ita duplum ▭ QK ad ▭ SR, et reliquorum unumquodque quae secundum illas descripta sunt ▭^a Ergo sicut dupla NA hoc est sicut NP ad NO ita duplum ▭ QK, hoc est, ▭ QR ad ▭ SR. Et sicut PW ad OZ ita ▭ ΔΓ ad ▭ ΘΓ. Et sicut WGA ad ZΞ ita ▭ ΓΣ⁴⁾ ad ▭ ΓΦ. atque ita porro, sicut singulae partes lineae AGC, ad partes singulas lineae ordinatè circumscriptae, quae inter easdem secum parallelas continentur, ita ▭^a singula altitudinem DK habentia ad ea quae easdem cum ipsis bases habent. nam ipsa quoque AN prout est pars lineae AGC ad seipsam prout est pars lineae ordinate circumsciptae, ita se habet ut ▭ QK pars ▭ DV ad seipsum prout est pars fig.^ae ordinate circumscriptae. Sunt itaque quaedam magnitudines lineae AN, NP, PW, WGA, &c., partes AGC, aliaeque totidem numero ▭^a QK, QR, ΔΓ, ΓΣ &c. componentes ▭ DV quarum binae quaeque eandem inter se rationem tenent; sunt enim utrobique omnes inter se aequales praeter duas extremas quae reliquarum sunt subduplae. Referuntur autem dictae lineae singulae ad alias lineas quae constituunt lineam ordinatè circumscriptam. Itemque referuntur ▭^a dicta ijsdem proportionalibus ad alia ▭^a quae constituunt figuram ordinatè circumsriptam. Quare omnes simul lineae AN, NP, PW, WGAΛ, &c. hoc est linea AGC sese habebunt ad omnes AN, NO, OZ, ZΞ &c. hoc est ad lineam quae parabolae ordinate circumscripta est, sicut omnia ▭^a QK, QR, ΔΓ, ΓΣ &c. hoc est ▭ DV ad omnia simul QK, SR, ΘΓ, ΓΦ &c. hoc est ad figuram ordinatè descriptam circa portionem hyperboles⁺.

2) Cette Proposition n'a pas été formulée explicitement, mais elle résulte presque immédiatement du ‘Theorema I’, p. 238.

3) Voir la p. 243.

4) Voir la lettre peu lisible à droite de la lettre H.

+ Arch. 2 de Conoid.⁵⁾.

5) Il s'agit de la deuxième Proposition de l'ouvrage d'Archiméde ‘De conoidibus et sphaeroidibus’. Voici cette proposition: ‘Si fuerint quotcumque numero sumptae magnitudines, itemque totidem aliae numero ponantur magnitudines, hoc pacto, ut quamcunque unaquaque prius sumptarum ad suam proximam habuerit proportionem, eandem unaquaeque posterius sumptarum ad suam eodem ordine proximam seruet, quaecunque fuerint illae proportiones, item prius sumptae magnitudines ad quasdam alias, totidem numero magnitudines omnes, aut earum aliquas, quibuscumque proportionibus referantur: sumptae quoque posterius magnitudines ad quasdam alias totidem, eodem ordine & eisdem proportionibus sint relatae: erit tunc, ut magnitudines prius sumptae omnes, habeant ad eas magnitudines omnes ad quas dicta ratione comparantur, eandem proportionem, quam magnitudines posterius sumptae omnes habuerint, ad omnes illas magnitudines ad quas fuerint similiter comparatae’ (p. 61-62 de l'édition de Bâle; Heiberg, T. I. p. 290-291, où cette proposition porte le numéro 1).
Afin d'expliquer la portée de cette proposition, supposons qu'on ait une première suite de grandeurs a1, a2, ..., an (les parties AN, NP, etc. de la ligne brisée AGC), une deuxième b1, b2,...bn (les rectangles DΠ, QR, ΔΓ, etc.), une troisième c1, c2...cn (les côtés AN, NO, etc. de la figure circonscrite à la parabole), une quatrième d1, d2,...dn (les rectangles DΠ, SR, ΘΓ, etc.) et qu'il existe entre les termes de ces suites les relations suivantes: alors la proposition nous apprend qu'on a:

[p. 252]

Ratio autem ▭ⁱDV ad dictam figuram circumscriptam minor est quam ejusdem ▭ⁱDV ad spatium DKVFED, quoniam figura circumscripta major est spatio DKVFED¹⁾. Ergo et lineae AGC ad lineam circa parabolam ordinatè descriptam, minor erit ratio quam ▭ⁱDV ad spatium DKVFED. Quam autem rationem habet ▭DV ad spatium dictum, eam positum fuit habere linea AGC ad lineam X. Ergo ratio lineae AGC ad eam quae ordinatè circa Parabolen descripta est minor erit quam ejusdem AGC ad X. Quamobrem ordinatè circumscripta major erit quam X. Eadem vero minor antea quam X ostensa est. quod fieri non potest. Itaque non est sicut ▭DV ad spatium DKVFED ita linea AGC ad majorem aliquam quam sit parabola ABC.

Sed neque ad minorem. Nam si dicatur esse, ut ▭DV ad spatium DKVFED ita linea AGC ad minorem aliquam quam sit parabola ABC. Ergo sicut linea AGC ad parab. ipsam ABC ita erit ▭DV ad spatium quoddam majus spatio DKVFED. Esto id spatium in quo ψ. Quoniam igitur spatium in quo ψ majus est spatio DKVFED potest circa spatium DKVFED describi figura ordinatè quae sit minor spatio ψ²⁾. Descripta itaque intelligatur. Et ex quot ▭^is composita est totidem partibus constans linea ordinatè circa parabolam describatur.

Ergo similiter ut prius ostenditur lineam AGC ad ordinate circumscriptam parabolae eandem rationem habere, quam ▭DV ad figuram circa spatium DKVFED ordinate circumscriptam. Ratio autem lineae AGC ad ordinate circa par. descriptam minor est quam ejusdem AGC ad ipsam parab. ABC. Ergo et ratio ▭ⁱDV ad figuram ordinate descriptam circa spat. DKVFED minor erit quam lineae AGC ad parab. ABC. Sicut autem linea AGC ad par. ABC ita erat ▭DV ad ψ spatium. Ergo ▭ⁱDV minor erit ratio ad figuram ordinate circa spatium DKVFED descriptam, quam ad spatium ψ. Ideoque dicta figura spatio ψ major erit. Sed eadem minor quoque dicta fuit. Quod fieri nequit. Ergo neque major est ratio ▭DV ad spat. resid. DKVFED quam lineae AGC ad parab. ABC. At neque minorem esse demonstratum est. Ergo eadem erit. Quod erat demonstr.

1) D'après le ‘Theorema VI’, p. 246.

2) Voir le ‘Theorema VII’, p. 247.

[p. 253]

[Theorema IX.]

Iisdem positis³⁾ si ducatur LN quae hijperbolen in vertice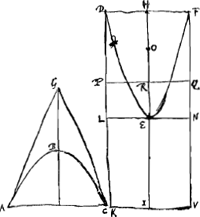

[Fig. 12.]

contingat. Dico longitudinem parab. ABC esse ad basin AC, sicut spatium residuum DKVFED ad ▭^mLV.

Quia enim ostensum fuit lineam parab. ABC esse ad lineam AGC sicut spatium DKVFED ad ▭DV. Est autem linea est, ut ▭DV ad ▭LV. Erit proinde ex aequo sicut parab. ABC ad basin AC, ita spatium DKVFED ad ▭LV quod erat dem.

Unde manifestum est, si portioni hyperboles DEF aequale abscissum fuerit ▭^mDQ, ductâ PQ parallelâ basi DF, quae secet diametrum in R; fore RI ad EI sicut parab. ABC ad basin AC.

Manifestum item, si fuerit EI, quae inter verticem hyperbolae et centrum sectionis intercipitur, ∞ basi AC, et IH ∞ duabus simul AG, GC; Et sumatur longitudini parabolae ABC aequalis recta IR. tunc ductâ PQ per R punctum parallela basi DF, effici ▭PF ∞ portioni hyperbolae DEF. Vel contra si ▭PF, portioni DEF aequale abscissum fuerit, rectam RI, aequalem fore longitudini parabolea ABC.

Quomodo autem dato gravitatis centro portionis hyperbolicae DEF, inveniatur ▭ portioni aequale, manifestum est ex ijs quae de hyperbolae quadratura antehac edidimus⁴⁾. Nempe si O fuerit dictum gravitatis centrum, et sicut IO ad tertiam partem rectae quae aequalis sit diametro HE et duplae EI, ita fiat EH ad RH. Erit ▭DQ, per R punctum abscissum, aequale portioni hyperboles DEF.

Ergo constat, si de tribus hisce unum aliquod datum fuerit nimirum longitudo lineae parabolicae; vel centrum gravitatis hyperbolae portionis; vel rectilineum hijperbolae portionis aequale; Etiam duo reliqua data esse.

3) Voir le théorème précédent, p. 249.

4) Voir la note 1 de la p. 236.

[p. 254]

[Troisième Partie¹⁾.]

[Theorema X.]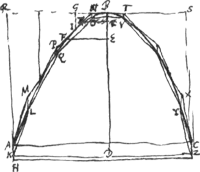

[Fig. 13.]

Data parabola ABC aequaliter ab axe BD divisa, possibile est ipsi lineam ordinatè circumscribere²⁾, ut circumductis utrisque circa manentem parabolae axem, fiat excessus quo superficies ex linea circumscripta genita superat conoidis parabolici ABC superficiem, minor spatio quovis proposito.

Fiat enim cylindrus HC eandem cum conoide ABC basin habens, cujus cylindri superficies sine basibus minor sit proposito spatio, hoc enim fieri posse perspicuum est. Sit autem dicti cylindri latus AH. Et sumatur in axe parabolae a vertice B, intervallum BE quadruplum ipsius AH. Et applicetur ordinatim EF. Porro descripto circa parabolam ▭^oARSC eandem cum ipsa basin altitudinemque habente, dividatur ipsius latus RS in partes aequales numero pares, ita ut singulae ipsarum veluti BG, minores sint recta EF. Et ex punctis divisionum ductis lineis axi parallelis quae parabolae occurrant, circumscribatur per occursus puncta linea inflexa ordinatè AMPNTXC. Dico hanc una cum parabola ABC circa BD circumductam, superficiem describere quae conoidis ABC superficiem excedat minori quam propositum est spatio.

Ducantur enim a singulis lineae circumscriptae flexionum punctis rectae axi parallelae quae parabolae occurrant, ML, PQ, NO, TV, &c. et jungantur LQ, QO, OV, &c. quae lineae aequales et parallelea erunt singulis circumscriptae partibus MP, PN, NT, &c., ut supra dem.³⁾. Sint autem et LK, YZ parallelae ipsis MA, XC; quibus proinde et aequales erunt; fientque insuper AK, CZ, aequales ipsis ML, XY. Jungantur denique AL, CY, KZ, quarum quidem KZ parallela

1) Cette Troisième Partie contient la réduction, rédigée selon la mode des anciens, de la quadrature de la surface courbe du conoïde parabolique à la quadrature du cercle. Elle est empruntée à des feuilles détachées qui font suite à celles mentionnées dans la note 2 de la p. 248.

2) Voir la ‘Definitio I’, p. 237.

3) Voir la démonstration du Theorème II, p. 239.

[p. 255]

erit AC, quoniam ML, XY inter se aequales sunt per [Theorema II⁴⁾], denique et AK, CZ.

Itaque si circa axem BD omnia circumvolvi intelligantur, apparet superficiem à circumscripta ordinatè linea AMPNTXC genitam aequalem esse ei quae fit ab inflexa KLQOVYZ, cum singulae hujus lineae partes cum singulis illius partibus et magnitudine et situ ad axem conveniant. Hac autem superficie ex KLQOVYZ major est superficies ab inflexa KALQOVYCZ, cum eosdem utraque in plano terminos habent, circumferentiam nimirum circuli quem describit in circumlationem punctum K⁵⁾. Ergo superficies ab inflexa KALQOVYCZ major quoque erit ea quae fit ab ordinate circumscr.^a AMPNTXC. Illa vero superficies composita est ex superficie quae fit ex AK latere cylindri AZ, et ex superficie genita ab inflexa ALQOVYC. Ergo hae duae superficies majores quoque erunt ea quae fit ab ordinate circumscripta. Ideoque multo magis superficies à latere AK una cum superficie conoidis ABC, major erit ea quae fit ab ordinatè circumscripta. Est enim superficies conoidis ABC major superficie genita ab inflexa ALQOVYC, quum ipsam comprehendat, eosdemque in plano habeat terminos. Minor igitur est excessus superficiei ex ordinate circumscripta genitae supra conoidis superficiem, quam est superficies à latere cylindri AK. Haec autem superficies proposito spatio adhuc minor est. Ergo fieri posse constat id quod asseruimus. Quod autem minor sit superficies à latere AK effecta spatio proposito sic ostendemus. AK aequalis est, uti jam ante dictum fuit, ipsi ML. haec vero ipsi NO per [Theorema II⁴⁾]. Est autem NO aequalis ¼ GI quum sint inter se NO, GI, sicut quadrata NB, GB. Sed GI minor est quam BE quoniam et BG minor, ex constr., quam EF. Itaque NO minor erit quam ¼ BE. Quare et AK minor erit quam ¼ BE, hoc est quam AH. Superficies autem quae fit ex conversione AH circa axem AD⁶⁾, hoc est superficies cylindri HC absque basibus, minor erit spatio proposito. Ergo omnino quoque, superficies ex AK in circumversione effecta minor erit spatio proposito.

4) Voir la p. 238.

5) Voici le postulat d'Archimède qui fait suite à celui mentionné dans la note 5 de la p. 237: ‘Similiter autem & superficierum eosdem terminos habentium, si in plano terminos habuerint, minimam esse planam. Aliarum vero superficierum, et eosdem terminos habentium, si in plano terminos habeant, eas esse inaequales: ubi autem ambae in partes easdem cauae fuerint, & uel altera tota contineatur ab altera, aut alteram earum ab altera superficie, & plana eosdem terminos cum illa habente: aut eius partem quidem comprendi constet, partem vero communem habere, & comprensam esse comprendente minorem’. (Voir la p. 2 de l'édition de Bàle, ou la p. 11 du T. I de l'édition de Heiberg).

4) Voir la p. 238.

6) Lisez: BD.

[p. 256]

[Lemma III¹⁾.]

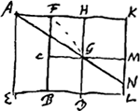[Fig. 14.]

Sunto ▭^a duo AB, CD, bases aequales et contiguas habentia EB, BD, sitque ▭ⁱ AB altitudo major quam ▭ⁱCD. Et ducatur AG recta, quae conjungat extrema utriusque ▭ⁱ latera.

Dico si circa latus GD ▭ⁱ CD, tanquam axem, vel circa aliam quamcunque, ut KL, ipsi GD aequidistantem, atque ad partes ▭ⁱ CD sumptam, circumversio fieri intelligatur majus fore solidum quod à ▭^is AF²⁾, CD efficitur quam quod à trapezio AGDE.

Sit enim primo circa GD facta conversio, conveniantque productae AF, DG in H. Igitur conversione ∆ⁱGHA conus, ▭ⁱ vero HC conversione cylindrus oritur quorum cum eadem sit altitudo HG; basis vero coni quadrupla sit baseos cylindri, (est enim circulus semid. ^oHA quadruplus circuli à semid. HF) minor proinde cono cylindrus erit. Nam si basis coni tripla duntaxat fuisset baseos cylindri fuissent conus cylindrusque inter se aequales. Itaque si uterque seorsim auferatur à cylindro qui fit conversione ▭ⁱ HE circa axem eundem HD, majus erit solidum quod relinquitur demto cylindro ab HC ▭^o effecto, hoc est solidum ex conversione ▭ AB, CD, quam quod relinquitur demto cono qui fit à ▭^o GHA, hoc est, quam solidum ex conversione trapezij AGDE.

Iam verò circa KL tanquam axem conversio facta intelligatur, cui occurrant productae AG, CG, AF, in punctis N, M, K.

Quia igitur conus efficitur conversione ∆ⁱ NKA, qui ad conum similem à ∆^o NMG productum, triplicatam habet rationem ejus quam AK ad GM, hoc est eandem quam cubus à latere AK ad cubum à latere GM. Erit per conversionem rationis, conus ab NKA ∆^o, ad solidum à trapezio MGAK, ut cubus ex AK ad differentiam cuborum ex AK et ex GM. Verum cylindrus à ▭^o KC conversione, ad conum ab NKA triangulo est sicut solidum ex qu.FK et tripla linea AH, ad cubum ex AK; quoniam cylindrus dictus ad dictum conum compositam habet rationem ex ratione qu.FK ad qu.KA, et ratione triplae KM ad KN, sive triplae AH ad AK. Igitur ex aequo erit cylindrus à ▭^o KC ad solidum ex conversione trapezij MGAK, sicut solidum ex qu^o.FK et tripla AH, ad differentiam cuborum

1) Ce ‘Lemma’ fut rédigé après le Théorème XI, pendant la démonstration duquel le besoin d'un tel ‘Lemma’ s'était fait sentir.

2) Lisez: AB.

[p. 257]

ex AK et ex GM sive HK. est autem solid. ex qu.FK in 3AH ∞ solidis à duobus quae fiunt ductis ▭^o AKH et qu.FH in 3AH; nam qu.FK ∞ ▭^oAKH una cum qu.FH³⁾. Differentia vero cuborum ex AK et HK aequalis est solido ex ▭ AKH in 3AH una cum cubo ex AH⁴⁾. Ergo cijlind. à ▭ KC ad solidum à trapezio MGAK ut solida duo quae fiunt ductis ▭^o AKH et qu.^oFH in 3AH, ad solidum ex ▭ AKH in 3AH una cum cubo ex AH. Sunt autem duo illa solida duobus hisce minora, quoniam minus est solidum ex qu.FH in 3AH, hoc est solid.^m ex 3qu^o.FH in AH, cubo ex AH⁵⁾. Igitur minor quoque erit cylindrus ex conversione ▭ⁱ K C, solido quod fit ex convers. trapezij MGAK. Communis auferatur cylindrus qui fit ex conv. ▭ⁱ KG. Ergo minus est solidum à ▭ HC quam quod à ∆^oGHA. Ideoque si utrumque horum seorsim auferatur ab eo solido quod fit conversione ▭ HE majus esse liquet solidum residuum ex convers. ▭^orum AB, CD, quam quod fit à trapezio AGDE. quod erat dem.

3) Posant AF = FH = a, HK = b, on a, en esset, .

4) Puisqu'on a .

5) C'est-à-dire 3a² × 2a < (2a)³.

[Theorema XI.]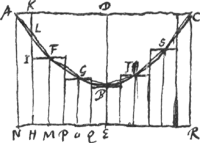

[Fig. 15,]

Data portione hyperbolae ABC cujus diam. sit basi ad rectos angulos. Si rectang. ei circum scribatur ad centrum terminatum AR, et figura ordinatè circa spatium residuum ABCRNA sicut supra praescriptum fuit⁶⁾, manente vero diam. DE omnia circumvertantur. Dico soliduum ex conversione figurae ordinatè circumscriptae, majus esse solido quod ex conversione spatij residui oritur.

Jungantur enim puncta quaeque bina quibus bases rectangulorum figurae circumscr.^ae secant hyperbolam, rectis AF, FG, GB, BT, &c. Erit igitur linea quaedam inflexa hoc modo intra hijp. portionem descripta. Jam vero si omnia circa diam. DE circumvolui intelligantur orietur solidum ex conversione spatij rectilinei à dicta inflexa et rectis AN, NR, RC comprehensi, quod solidum majus erit eo quod fit à spatio residuo ABCRNA, quum hoc illius partem esse appareat. Est autem solidum ex conversione utriusque ▭ⁱ KN, FH majus quam quod fit conversione trapezij AFMN, quoniam dicta ▭^a sibi mutuo conjuncta bases habent aequales, et latera parallela axi DE⁷⁾. Similiter et solidum ex conversione utriusque? ▭ⁱ FP, GP, majus est eo quod fit conversione trapezij FGOM. Et solidum ex conversione ▭ⁱ utriusque GQ, BQ, majus eo quod fit a trapezio GBEO. Itaque totum simul solidum quod oritur ex conversione figurae ordinatim ▭^is

6) Consultez le deuxième alinéa de la ‘Definitio II’, p. 246.

7) Voir le ‘Lemma III’, qui précède.

[p. 258]

circumscriptae majus erit solido quod fit ex conversione figurae ex omnibus dictis trapezijs compositae. Sed hoc solidum majus esse dictum est, eo quod fit ex conversione spatij residui ABCRNA. Ergo omnino quoque solidum id quod ex figura ordinatè circumscripta efficitur, majus erit eo quod fit ex dicti residui spatij circumvolutione. quod erat ostend.

[Theorema XII.]

Iisdem positis¹⁾, dico solidum ex conversione figurae ordinatè circumscriptae, excepto eo quod fit rectangulo extremo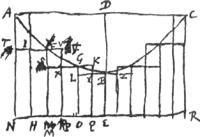

[Fig. 16.]

AH minus esse eo solido quod fit a spatio residuo ABCR.

Producantur enim reliquorum ▭^orum bases VI, KX, ZY, quae ab hyperbola bifariam dividentur, et VI quidem occurrat ipsi AN in T. KX ipsi FM in S; ZY ipsi GO in L. Itaque existit figura quaedam spatio residuo ABCRNA inscripta ex ▭^is aequalem latitudinem habentibus FN, GM, BO, &c. cujus proinde solidum ex conversione circa axem DE genitum, minus est eo quod fit à spatio residuo ABCRNA. Atqui dicto solido a ▭^is FN, GM, BO genito minus esse probatur, id quod fit à ▭^is VH, KP, BQ. hoc est solidum ex figura ordinatè circumscripta, excepto quod sit à ▭^o AH. Nam solidum quod fit a ▭ VH minus est eo quod fit à ▭^o FN, quum ▭^a quidem haec inter se sint aequalia alterum vero altero minus distet ab axe DE. Et eadem ratione solidum quod fit à ▭ KP minus est eo quod à ▭^o GM. Ac tandem illud quoque quod fit à ▭^o BQ minus apparet esse eo quod à ▭ BO. Itaque solidum effectum à figura ordinatè circumscripta citra ▭ AH, cum sit minus solido quod fit à ▭^is FN, GM, BO multo minus erit eo quod à spatio residuo ABCRN efficitur. Quod erat dem.

Itaque solidum a tota figura ordinatè circa spatium residuum ABCRNA descripta minori excessu superat solidum ab ipso spatio residuo ortum, quam sit id solidum quod fit ab extremo rectangulo AH. Unde manifestum est, posse figuram ordinatè describi circa ABCRNA spatium, ita ut solidum à dicta figura genitum exuperet illud quod à spatio ABCRNA producitur, excessu minore quam sit solidum quodvis datum. Potest enim ex tot ▭^is figura circumscripta constitui, ut extremum ▭ AH quodque ab eo efficitur solidum sit quamlibet exiguum.

1) Consultez le théorème précédent, p. 257.

[p. 259]

[Lemma IV.]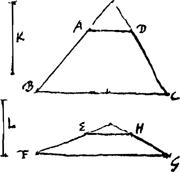

[Fig. 17.]

Si coni recti duo aequales bases habentes BC, FG secentur planis AD, EH, basi ipsorum aequidistantibus, fuerintque et qui è sectionibus fiunt circuli [AD, EH] aequales. Eam rationem inter se tenebunt superficies frustorum inter bases et secantia plana interceptae, quam earundem superficierum latera [AB, EF].

Esto enim superficiei conicae cujus latus AB, aequalis circulus radio K descriptus. Superficiei vero cujus latus EF aequalis circulus à radio L.

Itaque quadratum ex K aequatur ▭^o sub AB et dimidijs BC, AD^*, quadratum vero ex L aequatur ▭^o sub EF et dimidijs FG, EH. Est autem illud ▭ ad hoc ▭^m sicut AB ad EF, quia dimidia BC, AD aequales sunt dimidijs FG, EH, Ergo et quadratum ex K ad qu. ex EF³⁾ erit sicut AB ad EF. Sicut autem qu. ex K ad qu. ex L ita est circulus à semidiametro K ad circulum à semidiametro L. Ergo et circulus ille ad hunc erit ut AB ad EF. Circulus autem à semid. K aequalis positus fuit superficiei conicae cujus latus AB. Et circulus qui fit semid, EF⁴⁾, aequalis superficiei conicae cujus latus EF. Ergo et superficies illa ad hanc erit ut AB ad EF. Quod er. dem.

* Arch. 1. De Sphaera et Cylindro²⁾.

2) Il s'agit de la Prop. 16 du Livre 1 de l'ouvrage mentionné: ‘Si conus aequicruris secetur superficie plana, quae quidem superficies basi ipsius coni sit aequedistans: ea coni superficies, quae à sécante & à base concluditur, ei circulo aequalis esse probatur, cuius circuli semidiameter sit media secundum proportionem inter latus superficiei conicae, eius scilicet quae inter basim & secantem continetur, et inter lineam aequalem duabus semidiametris simul iunctis duorum circulorum, eorum scilicet qui in base & secante notantur’ (p. 17 de l'édition de Bâle; Heiberg, I, p. 76-79).

3) Lisez: qu. ex L.

4) Lisez: semid. L.

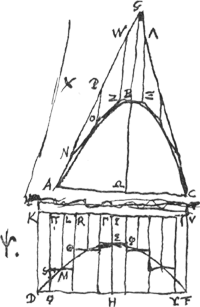
[Theorema XIII.]

Iisdem positis⁵⁾, si manente axe GBΩ [Fig. 18], parabola ABC simul cum ∆^oAGC circumvolvatur, ita ex illa conoides

5) Consultez le ‘Theorema VIII’, p. 249. En effet, à l'exception de la position inverse du rectangle KF, la présente figure et celle qui se rapporte au ‘Théorema VIII’ se correspondent ligne par ligne et lettre par lettre. Il résulte donc de l'expression ‘Iisdem positis’ que dans une rédaction antérieure et provisoire les Théorèmes VIII et XIII se suivaient immédiatement; puis les besoins de la démonstration ont nécessité l'intercalation d'autres théorèmes. Comparez encore à ce propos les notes 2 de la p. 260 et 6 de la p. 261.

[p. 260]

parabolicum ex hoc vero conus oriatur. Et manente item axe IEH, circumvolvatur hyperbolae portio DEF simul cum ▭^o

[Fig. 18.]

DV, ut ex illa conoides hyperbolicum, ex hoc fiat cylindrus. Dico quam rationem habet cylindrus DV ad partem sui residuam demto conoide DEF, eandem habere superficiem convexam coni AGC ad superficiem convexam conoidis parabolici ABC.

Nam si hoc verum esse negetur, Ergo sicut cylindrus DV ad partem sui reliquam dempto conoide DEF, ita erit superficies conica AGC ad majorem vel ad minorem quam sit superficies convexa conoidis ABC.

Esto primum ad majorem, quae sit circulus circa diametrum X. Quoniam igitur circulus circa X major ponitur superficie ABC conoidis, poterit per [Theorema X]¹⁾ circa parabolam ABC, linea inflexa ordinatè describi quae simul cum parabola circumvoluta circa axem BΩ, efficiat superficiem minorem circulo circa X diametrum. Esto descripta itaque ejusmodi linea quae sit ANOZΞC. Et circa spatium residuum ab hijperboles portione DKVFED figura item ordinate describatur, totidem ▭^is constans quot partibus linea ANOZΞC, eo modo quo in prop. praeced.²⁾. Et omnia similiter constructa sint. Manentibus autem axibus GBΩ, HEI cuncta converti intelligantur. Quoniam igitur linearum GW, WP, PN, NA³⁾ unaquaeque ad sibi proximam eadem ratione refertur qua unaquaeque harum IΓ, IR, IΠ, IK ad sibi proximam. Etiam quadrata illarum inter se eandem rationem consequenter servabunt, quam harum inter se quadrata. Sicut autem quadrata inter se linearum GW, GP, GN, GA ita se habent superficies conicae quarum hae lineae latera existunt. et sicut quadrata inter se rectarum IΓ, IR, IΠ, IK ita se habent bases cylindrorum ac proinde ipsi quoque cylindri, qui fiunt conversione ▭^orum ΓH, RH, ΠH, KH. Ergo illae superficies conicae, unaquaeque ad sibi proximam eadem ratione referentur, qua cylindrorum istorum quisque

1) Voir la p. 254.

2) Il s'agit ici sans doute du ‘Theorema VIII’. Voir la note 5 de la p. 259.

3) Lisez: GW, GP, GN, GA.

[p. 261]

ad proxime sequentem. Ideoque et minima dictarum superficierum et excessus quibus unaquae ipsarum a sequente superatur, consequenter eandem rationem inter se obtinebunt quam minimus dictorum cylindrorum et excessus quibus unusquisque ipsorum à sequente superatur. Sunt igitur magnitudines quaedam superficies genitae ex conversione linearum GW, WP, PN, NA, itemque aliae magnitudines totidem numero, nimirum solida orta ex conversione ▭^orum ΓH, ΓΔ⁴⁾, ΔΠ, ΠD, quarum binae quaeque eandem inter se rationem servant. Singulae autem dictarum superficierum ad alias quasdam superficies referuntur; videlicet superficies à latere GW ad circulum à semidiametro BZ. et superficies à latere WP ad eam quae fit a latere ZO. et quae à latere PN ad eam quae ab ON. Et quae ab NA prout est pars superficiei coni AGC ad seipsam refertur prout est pars superficiei à linea ordinatè circumscripta genitae. Et ijsdem quoque proportionibus singula dictorum solidorum ad alia quaedam solida referuntur. Est enim sicut superficies conica à latere GW ad circulum à semid. BZ, hoc est sicut linea GW ad BZ^*, hoc est sicut HI ad IE per ea quae praeced. prop.^e ostensa⁶⁾; ita cylindrus ex conversione ▭ⁱ HΓ ad cylindrum ex conversione ▭ⁱ EΓ. Et sicut superficies conica à latere WP ad superficiem conicam à latere ZO, hoc est, ut linea WP ad ZO^*, hoc est ut ΔR⁴⁾ ad ΘR ita solidum à ▭^o ΔΓ in conversione factum ad solidum à ▭ ΘΓ. nam et haec solida altitudinum suarum rationem sequi perspicuum est. Eademque ratione sicut conica superficies à latere PN in conversione effecta ad eam quae fit à latere ON, ita solidum à ▭^o ΔΠ ad solidum à rectang. SR. Et sicut superficies conica à latere NA ad seipsam ita solidum à ▭^o DΠ seipsum. Ergo sicut omnes simul superficies conicae a lateribus GW, WP, PN, NA in conversione factae, ad omnes factas à lateribus BZ, ZO, ON, NA, hoc est sicut tota superficies conica AGC ad superficiem totam a linea ordinatè circumscripta genitam, ita erunt omnia simul solida conversione ▭^orum HΓ, ΓΔ, ΔΠ, ΠD producta, ad omnia simul solida ex conversione ▭^orum EΓ, ΓΘ, RS, ΠD⁸⁾, hoc est, ita cylindrus DV ad solidum ex conversione figurae ordinate descriptae circa

4) La lettre Δ manque dans la figure 18; mais on la retrouve dans la figure 11 du théorème VIII, p. 250. Elle doit être placée à droite du point Q.

* 15 Arch. 1. de Sphaera⁵⁾.

5) Voici cette proposition d'Archimède: ‘Cuiuslibet coni aequicruris superficies ad basim suam, eandem habet proportionem, quàm latus ipsius coni habet ad lineam eductam à centro basis coni ad ejusdem circumferentiam’ (p. 17 de l'édition de Bâle, Heiberg I, p. 76-77).

6) Il s'agit toujours du ‘Theorema VIII’; voir la p. 251 où l'on lit: ‘sicut singulae partes lineae AGC, ad partes singulas lineae ordinatè circumscriptae, quae inter easdem secum parallelas continentur, ita ▭^a singula altitudinem DK habentia ad ea quae easdem cum ipsis bases habent’; c'est-à-dire les rectangles ΓE, ΓΘ, RS, ΠD.

* ... hujus⁷⁾.

7) Il s'agit du ‘Lemma IV’, p. 259.

4) La lettre Δ manque dans la figure 18; mais on la retrouve dans la figure 11 du théorème VIII, p. 250. Elle doit être placée à droite du point Q.

8) Il s'agit cette fois encore d'une application de la proposition d'Archimède mentionnée dans la note 5 de la p. 251. Ici les a sont les surfaces décrites par les lignes GW, WP, etc.; les b les solides décrits par les rectangles ΓH, ΓΔ etc.; les c les surfaces décrites par les lignes BZ, ZO, etc.; les d les solides décrits par les rectangles EΓ, ΘΓ, etc.

[p. 262]

spatium residuum DEFVKD. Ratio autem cylindri DV ad dictum solidum ex figura ordinatè circumscripta genitum minor est ratione ejusdem cylindri DV ad

[Fig. 18.]

partem sui quae relinquitur dempto conoide DEF. quoniam solidum ex figura ordinatè circumscripta majus est dicta parte residua¹⁾. Ergo et superficiei conicae AGC ad superficiem à linea ANOZB ordinatè circa parabolam descripta, minor erit ratio quam cylindri DV ad partem sui residuam dempto conoide DEF. Huic autem eadem posita fuit ratio superficiei conicae AGC ad circulum circa X diametrum. Ergo superficiei conicae AGC ad superficiem à linea ANOZB, minor erit ratio, quam ejusdem conicae superficiei AGC ad circulum circa X. Quare major erit superficies à linea ANOZB circulo circa X. Eadem vero minor hoc circulo superius dicta fuit. quod fieri non potest. Itaque non est sicut cylindrus DV ad partem sui quae remanet demto conoide DEF, ita superficies conica AGC ad majorem aliquam quam sit superficies ABC conoidis parabolici.

Sed neque ad minorem. Nam si dicatur esse ut cylindrus DV ad dictam partem residuam, ita superfic. conica AGC ad minorem aliquam superficiem quam sit conoidis ABC, Ergo quoque sicut superf. conica AGC ad ipsam superf. conoidis ABC, ita erit cylindrus DV ad solidum quoddam majus dicta parte residua. Esto id solidum in quo ψ. Ergo quia solidum ψ majus est parte cylindri DV residua post ablatum conoides DEF, sive solido quod oritur ex conversione spatij DEFVKD; constat circa spatium DEFVKD figuram ordinatè ex ▭^is describi posse, quae simul circumlata, solidum efficiat quod minus sit solido ψ²⁾. Descripta itaque intelligatur ejusmodi figura; et ex quot ▭^is ipsa composita erit, ex totidem rectis constans linea ordinatè circa parabolam ABC itidem descripta sit. Similiter itaque ut prius, ostendemus superficiem conicam AGC ad superficiem genitam à linea ordinatè parabolae circumscripta, eandem habere rationem quam cylindrus DV ad solidum ex figura ordinate circa spatium DEFVKD descripta. Est autem minor ratio superficiei conicae AGC, ad superficiem, à linea ordinatè circumscripta, ortam, quam ejusdem superficiei conicae AGC ad superficiem conoidis parabolici ABC³⁾.

1) Voir le Théorème XI, p. 257.

2) Voir le dernier alinéa du Théorème XII, p. 258.

3) Puisque, d'après le postulat d'Archimède mentionné dans la note 5 de la p. 255, la surface décrite par la figure rectiligne circonscrite à la parabole, excède celle du conoïde parabolique.

[p. 263]

Ergo et ratio cylindri DV, ad solidum quod fit ex conversione figurae ordinatè circa spatium DEFVKD descriptae, minor erit ea quam superficies conica AGC habet ad superficiem conoidis ABC. Huic autem rationi eadem posita fuit ratio cylindri DV ad solidum ψ. Ergo cylindrus DV ad solidum à dicta figura ordinatè descripta genitum minorem habebit rationem quam cylindrus idem DV ad solidum ψ. Quare solidum à figura ordinate circumscripta majus erit solido ψ. Sed et minus antea dictum fuit. Quod esse nequit.

Ergo neque erit cylindrus DV ad partem sui residuam demto conoide DEF, ita superf. conica AGC ad minorem aliquam quam sit superf. conoidis parabolici ABC. Sed neque ad majorem, ut modo ostendimus. Ergo reliquum est, ut sicut cylindrus DV ad dictam sui partem reliquam ita sit superf. conica AGC ad superf. conoidis parabolici ABC. quod erat demonstr.

[Theorema XIV.]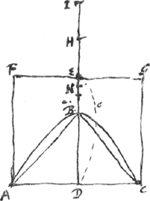

[Fig. 19.]

Esto hyperbolae portio ABC, cujus axis BD sit basi ad angulos rectos. latus autem transversum sit BH; centrum sectionis E. et describatur super eadem basi ▭^m ad centrum terminatum FC. Et manente axe ED, dictum ▭^m una cum portione ABC circumvertatur. Dico cylindrum FC ex conversione ▭ⁱ genitum, ad partem sui residuam, dempto conoide ABC, eam habere rationem quam linea tripla ED ad aequalem utrique simul et duplae ED, et ei lineae; quae sese habeat ad EB sicut BH ad HD.

Producatur enim latus transversum BH ad I ut HI sit aequalis EH vel EB et sicut HD ad DI ita sit BD ad DN. Quoniam igitur conoides hyperb. ABC ad conum eandem basin et altitudinem cum ipso habentem, eam habet rationem quam ID ad DH^*, hoc est quam ND ad DB. dictus autem conus ad cylindrum

* Archim. de Conoid.⁴⁾.

4) Il s'agit de la Prop. 27: ‘Quaelibet portio conoidalis obtusianguli’ [conoïde hyperbolique] ‘abscisa plano super axem erecto, habet ad conum, qui eandem basim & axem cum portione teneat eundem, eam proportionem, quam habet utraque simul linea quae sit aequalis axi portionis, et ea quae sit tripla lineae ad axem adiectae, ad lineam his utrisque aequalem, axi portionis & lineae duplae, ad lineam axi adiectam’ (p. 84 de l'édition de Bâle, Heiberg I, p.416-417, où elle porte le numéro 25). La ‘linea axi adjecta’ d'Archimède est représentée dans la fig. 19 par la ligne BE, c'est-à-dire par le demi-axe transverse de l'hyperbole ABC.

[p. 264]

FC, est sicut BD ad triplam DE. Erit propterea ex aequo, conoides ABC ad cylindrum FC, sicut ND ad triplam DE. Et invertendo, et per conversionem

[Fig. 19.]

rationis, cylindrus FC ad partem sui quae dempto ABC conoide remanet, sicut tripla DE ad excessum triplae DE supra DN, hoc est, ad duplam DE una cum NE. Reliquum est igitur ut ostendatur, esse NE ad EB sicut BH ad HD. quod fiet hoc modo. HD est ad DI sicut BD ad DN; quare et permutando HD ad DB ut DI ad DN, et per conversionem rationis DH ad HB ut DI ad IN. Et permutando rursus et invertendo ID ad DH ut NI ad HB, sive IE. Et dividendo IH ad HD ut NE ad EI. Et permutando et invertendo denique NE ad HI sive ad BE, ut EI sive BH ad HD. quod demonstrandum supererat.

[Theorema XV.]

Si in eadem basi consistant conoidis portio parabolici et conus rectus, sitque hujus altitudo ad illius altitudinem dupla; superficies coni ad superficiem conoidis, utrâque sine basi sumptâ, eam habebit rationem, quam latus coni triplum ad idem latus duplum junctum ei lineae quae sit ad diametrum baseos, sicut eadem diameter ad ambitum trianguli per axem coni¹⁾.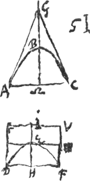

[Fig. 20.]

Esto conoides parabolicum ABC, et in eadem basi conus AGC rectus, cujus dupla sit altitudo. Et utroque per axem secto, fiat sectio conoidis parabola ABC; sectio vero coni ∆^m AGC. Et sicut hujus trianguli ambitus ad basin AC ita sit AC ad lineam s.

Ostendendum est igitur, superficiem coni AGC sine basi, esse ad superficiem ABC conoidis, itidem sine basi, sicut tripla AG ad duplam AG unà cum linea s.

Sit hyperbolae portio DEF cujus axis EH sit basi ad ang. rectos, dimidium vero latus rectum²⁾ EI sit ½AC et tota IH ∞ AG. Et descripto circa portionem ▭^lo DV ad centrum sectionis I termi-

1) C'est sous cette forme que la quadrature de la surface du conoïde parabolique fut communiquée à Gregorius à St. Vincentio le 30 octobre 1659; voir la p. 502 du T. II.

2) Lisez: lateris transversi.

[p. 265]

nato, intelligatur, manente axe HI, et portio et ▭ DV circumvolvi. Itaque cylindrus DV ex conversione ▭ⁱ ortus ad partem sui quae remanet dempto hyperbolico conoide DEF eam habebit rationem quam tripla HI ad duplam HI junctam ei lineae quae sit ad EI sicut 2EI ad utramque simul HI, IE³⁾, sive permutando, quae sit ad 2EI ut EI ad duas simul HI, IE. Est autem HI ∞ AG, et EI ∞ AΩ. Ergo dictus cylind. ad dictum residuum eam quoque habebit rationem, quam tripla AG habet ad 2AG una cum ea linea quae sit ad 2AΩ hoc est ad AC, sicut AΩ ad utramque simul AΩ, AG, sive ut AC ad ambitum ∆ⁱ AGC. Haec vero linea est s. Ergo cylindr. DV ad partem sui reliquam dempto conoide DEF, eam habet rationem quam 3AG ad 2AG una cum s linea. Sicut autem dictus cylindrus ad dictum residuum ita est superficies coni AGC sine basi ad superficiem conoidis parabolici ABC sine basi⁴⁾. Ergo et hae superficies eam inter se rationem servant quae est 3AG ad 2 AG una cum s linea. Quod erat ostend.

Hinc manifestum est superficiem coni AGC ad superficiem conoidis ABC, utrâque sine basi sumpta, minorem semper rationem habere quam sesquialteram⁵⁾.

3) Comparez le ‘Theorema XIV,’ p. 263.

4) Voir le ‘Theorema XIII,’ p. 259-260. Dans la figure de ce théorème le conoïde hyperbolique DEF a été construit de manière qu'on a 2 AG : AC = HI : IE (voir le ‘Theorema VIII’ p. 249). Il est donc évident que le conoïde hyperbolique de la figure présente constitue un cas particulier de celui du Theorème XIII.

5) C'est-à-dire plus petit que le rapport 3 : 2.

[Theorema XVI.]

Conoidis parabolici, cujus axis ad basin rectus sit, superficies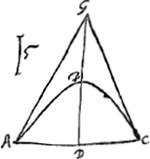

[Fig. 21.]

convexa ad basin eam habet rationem quam inter se habent lineae rectae, quarum prior composita sit ex duobus lateribus trianguli isoscelis, basin habentis diametrum circuli qui conoidis basis est, altitudinem vero conoidis duplam, et ex ea linea quae sit ad basin dicti trianguli sicut basis eadem ad totius dicti trianguli ambitum: altera vero linea dictae baseos sit sesquialtera⁶⁾.

6) Posant donc GC = a, DC = r on trouve 2r²: (a + r) pour la ligne s qu'on doit ajouter à 2a, et, par suite, pour la surface du conoïde parabolique 2(a² + ar + r²) rπ: 3(a + r). Introduisant plutôt, au lieu de a et r, la hauteur BD = h du conoïde et le paramètre p de la parabole y² = 2px on a r = √2ph; ; s = 4ph: : h, et l'on obtient pour la surface du conoïde la formule , qu'on peut vérifier aisément par les méthodes modernes et qui est conforme à celle communiquée, en janvier 1658, par van Heuraet à van Schooten (voir la p. 131 du T. II), où l'on doit remplacer, afin d'y introduire nos notations, b par h et a, le ‘latus rectum’ de la parabole, par 2p. Consultez encore à ce propos le dernier alinéa de la p. 189 de l'Avertissement.

[p. 266]

[Fig. 21.]

Quia enim superficies conoidis ABC ad superficiem coni AGC earn ostensa est habere rationem quam dupla AG juncta lineae s ad tripla AG¹⁾: Est autem superficies coni AGC ad circulum baseos AC, ut AG latus ad AD semidiametrum baseos⁺, hoc est ut tripla AG ad triplam AD, seu sesquialteram AC. Erit proinde ex aequo, superficies conoidis ABC ad circulum baseos AC ut dupla AG juncta ipsi s ad sesquialteram AC quod erat dem.

1) Voir le Théorème XV, qui précède.

+ 15 Archim. 1. de Sphaera²⁾.

2) Il s'agit de la Prop. 15 du Livre 1; voir la note 5 de la p. 261.

[Theorema XVII.]

Iisdem positis³⁾, si fuerit latus AG [Fig. 21] ad baseos semidiametrum AD sicut numerus ad numerum; dico et superficiem conoidis convexam ABC ad basin suam fore ut numerus ad numerum⁴⁾.

Quia enim GA commensurabilis AD (6. 10 Elem.)⁵⁾ erit et componendo utraque simul GA, AD commensurabilis AD (per 16. 10 Eucl.)⁶⁾; sicut autem utraque GA et AD ad AD, hoc est sicut ambitus trianguli AGC ad AC ita est AC ad s. Ergo et s ipsi AC commens. erit (11. 10)⁷⁾, ac proinde ipsis quoque AD et AG, ut et duplae AG (12. 10)⁸⁾. Quare componendo rursus erit dupla AG una cum s commensurabilis ipsi s (16. 10)⁶⁾, ac proinde ipsi AD, uti et triplae AD (12. 10)⁸⁾. Sicut autem dupla AG una cum s ad triplam AD sive sesquialteram AC, ita est superficies conoidis convexa ABC ad circulum baseos AC (per praec.). Ergo illa quoque superficies huic circulo commensurabilis est (11. 10)⁷⁾ ac proinde ad ipsum rationem habebit quam numerus ad numerum (5. 10)⁹⁾. Quod erat ostendendum.

3) Voir le Théorème XVI, qui précède.

4) C'est le Théorème que Huygens a choisi pour le communiquer, avec les deux premiers des exemples qui suivent, à de Sluse (voir la lettre du 20 déc. 1657, p. 104 du T. II) et à van Schooten (lettre du 28 déc. 1657, p. 112-113 du T. II), asin de leur montrer qu'il avait trouvé la quadrature de la surface conoïde sans leur faire connaître le résultat précis qu'il avait obtenu et qu'il voulait réserver encore. On retrouve tous les trois exemples dans la lettre à Gregorius à St. Vincentio du 30 octobre 1659 (voir la p. 502 du T. II) et dans l'‘Horologium Oscillatorium’, ‘Prop. IX’ de la ‘Pars tertia’, p. 74 de l'édition originale.

5) Il s'agit de la Prop. 6 du Livre 10 des Éléments d'Euclide, p. 215 de l'édition de 1607 de l'ouvrage de Clavius, cité dans la note 6 de la p. 477 du T. I, où l'on lit: ‘Si duae magnitudines inter se proportionem habeant quam numerus ad numerum: commensurabiles erunt magnitudines’.

6) ‘Si duae magnitudines commensurabiles componantur; & tota magnitudo vtrique ipsarum commensurabilis erit. Quod si tota magnitudo vni ipsarum commensurabilis fuerit; & quae à principio magnitudines commensurabiles erunt’ (Clavius, p. 235).

7) Il s'agit de la Proposition: ‘Si quatuor magnitudines proportionales fuerint, prima vero secundae fuerit commensurabilis; & tertia quartae commensurabilis erit. Et si prima secundae fuerit incommensurabilis: & tertia quartae incommensurabilis erit’ (Clavius, p. 225). Cette proposition porte chez Clavius le numéro 10; mais, comme Clavius le fait remarquer à la p. 230, elle fut numérotée 11 dans des éditions qui précédaient la sienne.

8) ‘Quae eidem magnitudini sunt commensurabiles, inter se sunt commensurabiles’ (Clavius, p. 230).

6) ‘Si duae magnitudines commensurabiles componantur; & tota magnitudo vtrique ipsarum commensurabilis erit. Quod si tota magnitudo vni ipsarum commensurabilis fuerit; & quae à principio magnitudines commensurabiles erunt’ (Clavius, p. 235).

8) ‘Quae eidem magnitudini sunt commensurabiles, inter se sunt commensurabiles’ (Clavius, p. 230).

7) Il s'agit de la Proposition: ‘Si quatuor magnitudines proportionales fuerint, prima vero secundae fuerit commensurabilis; & tertia quartae commensurabilis erit. Et si prima secundae fuerit incommensurabilis: & tertia quartae incommensurabilis erit’ (Clavius, p. 225). Cette proposition porte chez Clavius le numéro 10; mais, comme Clavius le fait remarquer à la p. 230, elle fut numérotée 11 dans des éditions qui précédaient la sienne.

9) ‘Commensurabiles magnitudines inter se rationem habent, quam numerus ad numerum’ (Clavius, p. 214).

[p. 267]

Si fuerit AG dupla AD, erit superficiei conoidis convexae ABC ad basin ea ratio quae quatuordecim ad novem.

Si AG tripla AD, erit dicta superficierum ratio ut 13 ad 6.

Si AG quadrupla AD, erit superficierum ratio quae 14 ad 5. quae exempli gratia attulisse sufficiat.

[Problema I.]

Dato conoide parabolico, invenire circulum conoidis superficiei aequalem¹⁰⁾.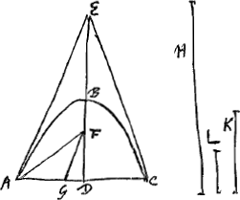

[Fig. 22].

Esto datum conoides parabolicum ABC, cujus axis BD: Et oporteat superficiei conoidis convexae ABC aequalem circulum invenire. Secetur conoides plano per axem, unde existat parabola ABC, Et producatur axis et sit ED dupla BD. Junctisque AE, EC, ducatur AF quae bifariam dividat angulum EAD, occurratque axi in F, unde ducatur FG parall. EA. Deinde esto H linea aequalis utrique simul AE et GD. Trienti vero diametri baseos AC sit aequalis recta L. Et inter utramque H et L media

10) On retrouve cette construction (avec les exemples mentionnés dans la note 4) à la p. 40 du Manuscrit N^o. 13 dont il est question dans le dernier alinéa de la note 5 de la p. 235, et de même, sous une forme légèrement modifiée, dans l'‘Horologium Oscillatorium’, après la ‘Prop. IX’ de la ‘Pars tertia’, p. 73-74 de l'édition originale.

[p. 268]

proport. sumatur K. dico circulum à semidiametro K aequalem esse superficiei conoidis convexae ABC.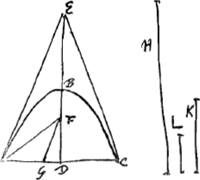

[Fig. 22.]

Quia enim bifariam dividitur angulus EAD à recta AF, Erit ut EA ad AD ita EF ad FD. Et compon.^o ut utraque simul EA, AD ad AD ita ED ad DF. Ut autem ED ad DF ita est AD ad DG. Ergo ut utraque simul EA, AD ad AD ita erit AD ad DG. Et sumptis tam antecedentium quam consequentium duplis, sicut ambitus ∆ ⁱAEC ad AC ita AC ad duplam DG¹⁾. Quamobrem sicut dupla AE una cum dupla DG ad sesquialteram ipsius AC, vel sumptis utriusque dimidijs ut AE una cum DG, hoc est ut H, ad sesquialteram ipsius AD, ita erit superficies conoidis ABC ad circulum baseos AC²⁾. Ratio autem quam habet H ad sesquialteram AD, componitur ex rationibus H ad AD, et AD ad sesquialteram AD; quarum haec eadem est quae rectae L ad AD; nam cum L sit subtripla AC erit eadem subsesquialtera AD. Igitur et ratio quam habet superficies conoidis ABC ad circulum baseos AC, eadem erit compositae ex rationibus H ad AD et L ad AD, ac proinde eadem quae ▭ⁱ ab H et L contenti hoc est quⁱ.K ad quad. AD. Sicut autem quadr. ex K ad qu.AD, ita est circulus radio K descriptus ad circulum baseos cujus semid. DA. Ergo eadem erit ratio superficiei conoidis ABC ad circulum baseos AC, quae circuli à K semid. ad eundem circulum AC. Ac proinde dicta conoidis superficies aequalis erit circulo cujus K est semidiameter. Quod erat dem.

1) La ligne DG est donc la moitié de la lignes, dont il est question dans les trois théorèmes précédents.

2) Par le ‘Theorema XVI’, p. 265.

[p. 269]

[Problema II.]

Datis circulis duobis inaequalibus, conoides parabolicum invenire cujus basis sit circulus minor, superficies vero convexa majori circulo aequetur³⁾.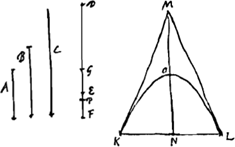

[Fig. 23.]

Sunto dati circuli à semidiametris A et B. quorum A minor B major. Et oporteat facere quod proponitur. Sit duabus A, B tertia proportionalis [C]. Et sumatur DE ∞ 3/4 C. cui adjungatur in directum EF ∞ 1/2 A. Sitque EG ∞ EF. Et excessui quo quadr. DF superat qu. A sit aequale qu. ex DP. Deinde triang. extruatur isosceles KML, basim habens KL ∞ duplae A, crura vero KM, ML singula ∞ utrique simul GD, DP. Et ductâ ad mediam basin recta MN, dividatur ea bifariam in O, et parabola describatur verticem habens O punctum; axem ON, basin vero KL. Eaque manente axe ON circumverti intelligatur. Quod igitur basis conoidis inde effecti &c manifestum⁴⁾. Dico autem convexam conoidis superficiem KOL ∞ circulo à semid.B.

Quia enim quadratum ex A aequale est differentiae qu.^orum DF, DP, ac proinde aequale duplo ▭^o DPF + qu^o PF^*, hoc est ei ▭^o quod sub PF et aequali utrisque FD, DP continetur: Erit proinde ut utraque simul FD, DP ad A ita A ad FP^*. Est autem utraque simul FD, DP aequalis utrique simul MK, KN; quia

3) On ne retrouve ce problème ni dans la correspondance de Huygens, ni dans l'‘Horologium oscillatorium’. Afin de le résoudre posons MK [Fig. 23] = x, KN = A, et soit s la ligne auxiliaire des Théorèmes XV (p. 264) et XVI (p. 265). On a alors d'après le Théorème XVI:
, où .
De la première équation on déduit: La substitution de cette valeur de s dans la seconde équation, amène l'équation quadratique: pour la racine positive de laquelle on trouve:



ou plutôt:

Or, on a percevra facilement que la construction, qui va suivre, ne fait que reproduire les opérations indiquées par cette expression algébrique.

4) Cette phrase inachevée fut intercalée après coup.

* 3.2⁵.

5 Lisez: 4.2 et consultez la p. 300 du T. XI, où la quatrième proposition du second livre des Éléments d'Euclide est appliquée d'une manière tout à fait analogue. La proposition s'y trouve citée dans la note 14.

* ...6⁶⁾.

6) Il s'agit ici de la ‘Prop.’ 17 du ‘Libr.’ 6, où l'on lit ‘Si tres rectae lineae sint proportionales: quod sub extremis comprehenditur rectangulum aequale est ei, quod à media describitur, quadrato. Et si sub extremis comprehensum rectangulum aequale sit ei, quod à media describitur, quadrato: Illae tres rectae lineae proportionales erunt’ (Clavius p. 568).

[p. 270]

FG ∞ NK, et duae simul GD, DP aequales KM. A vero ipsi KN aequalis est. Ergo, sicut utraque simul MK, KN ad KN ita est KN ad FP. ideoque ut

[Fig. 23.]

MK + FP ad 3/2 KN ita est superficies convexa conoidis KOL ad circulum baseos KL, uti ex superioridemonstratione perspicuum est¹⁾. Porro quoniam DE ∞ 3/4 C erit dupla DE ∞ 3/2 C. Sed dupla DE ∞ ∞ DG + DF, quoniam aequaliter se excedant hae tres DG, DE, DF. Itaque DG + + DF ∞ 3/2 C. Sed DG + DF ∞ MK + + PF quoniam ex constr. DG + DP ∞ MK. Itaque MK + FP ∞ 3/2 C. Unde eandem quoque rationem habebit MK + FP ad 3/2 KN quam 3/2 C ad 3/2 KN, hoc est quam C ad KN sive ad A. Quam autem habet C ad A eam habet circulus à semid. B ad circulum à semid. A, hoc est ad circulum baseos KL. Ergo ut MK + FP ad 3/2 KN ita erit circul. à semid. B ad circulum baseos KL. Atqui eandem quoque rationem habere ostendimus superficiem convexam conoidis ABC ad eundem baseos circulum KL. Ergo aequales inter se necesse est circulum à semid. B et dictam conoidis superficiem.

1) Lorsqu'on remplace les notations de la Fig. 21 (p. 266) par celles de la présente figure on trouve, en effet, que les deux surfaces sont, d'après le Théorème XVI, p. 265, dans le rapport de [2MK + KL²: 2(MK + KN)] à 3/2 KL, ou bien de 2MK + 2FP à 3NK, c'est-à-dire de MK + FP à 3/2 NK.

5) Il s'agit de la deuxième Proposition de l'ouvrage d'Archiméde ‘De conoidibus et sphaeroidibus’. Voici cette proposition: ‘Si fuerint quotcumque numero sumptae magnitudines, itemque totidem aliae numero ponantur magnitudines, hoc pacto, ut quamcunque unaquaque prius sumptarum ad suam proximam habuerit proportionem, eandem unaquaeque posterius sumptarum ad suam eodem ordine proximam seruet, quaecunque fuerint illae proportiones, item prius sumptae magnitudines ad quasdam alias, totidem numero magnitudines omnes, aut earum aliquas, quibuscumque proportionibus referantur: sumptae quoque posterius magnitudines ad quasdam alias totidem, eodem ordine & eisdem proportionibus sint relatae: erit tunc, ut magnitudines prius sumptae omnes, habeant ad eas magnitudines omnes ad quas dicta ratione comparantur, eandem proportionem, quam magnitudines posterius sumptae omnes habuerint, ad omnes illas magnitudines ad quas fuerint similiter comparatae’ (p. 61-62 de l'édition de Bâle; Heiberg, T. I. p. 290-291, où cette proposition porte le numéro 1).
Afin d'expliquer la portée de cette proposition, supposons qu'on ait une première suite de grandeurs a1, a2, ..., an (les parties AN, NP, etc. de la ligne brisée AGC), une deuxième b1, b2,...bn (les rectangles DΠ, QR, ΔΓ, etc.), une troisième c1, c2...cn (les côtés AN, NO, etc. de la figure circonscrite à la parabole), une quatrième d1, d2,...dn (les rectangles DΠ, SR, ΘΓ, etc.) et qu'il existe entre les termes de ces suites les relations suivantes: alors la proposition nous apprend qu'on a:

2) Il s'agit de la Prop. 16 du Livre 1 de l'ouvrage mentionné: ‘Si conus aequicruris secetur superficie plana, quae quidem superficies basi ipsius coni sit aequedistans: ea coni superficies, quae à sécante & à base concluditur, ei circulo aequalis esse probatur, cuius circuli semidiameter sit media secundum proportionem inter latus superficiei conicae, eius scilicet quae inter basim & secantem continetur, et inter lineam aequalem duabus semidiametris simul iunctis duorum circulorum, eorum scilicet qui in base & secante notantur’ (p. 17 de l'édition de Bâle; Heiberg, I, p. 76-79).

5) Voici cette proposition d'Archimède: ‘Cuiuslibet coni aequicruris superficies ad basim suam, eandem habet proportionem, quàm latus ipsius coni habet ad lineam eductam à centro basis coni ad ejusdem circumferentiam’ (p. 17 de l'édition de Bâle, Heiberg I, p. 76-77).

7) Il s'agit du ‘Lemma IV’, p. 259.

4) Il s'agit de la Prop. 27: ‘Quaelibet portio conoidalis obtusianguli’ [conoïde hyperbolique] ‘abscisa plano super axem erecto, habet ad conum, qui eandem basim & axem cum portione teneat eundem, eam proportionem, quam habet utraque simul linea quae sit aequalis axi portionis, et ea quae sit tripla lineae ad axem adiectae, ad lineam his utrisque aequalem, axi portionis & lineae duplae, ad lineam axi adiectam’ (p. 84 de l'édition de Bâle, Heiberg I, p.416-417, où elle porte le numéro 25). La ‘linea axi adjecta’ d'Archimède est représentée dans la fig. 19 par la ligne BE, c'est-à-dire par le demi-axe transverse de l'hyperbole ABC.

2) Il s'agit de la Prop. 15 du Livre 1; voir la note 5 de la p. 261.

5 Lisez: 4.2 et consultez la p. 300 du T. XI, où la quatrième proposition du second livre des Éléments d'Euclide est appliquée d'une manière tout à fait analogue. La proposition s'y trouve citée dans la note 14.

6) Il s'agit ici de la ‘Prop.’ 17 du ‘Libr.’ 6, où l'on lit ‘Si tres rectae lineae sint proportionales: quod sub extremis comprehenditur rectangulum aequale est ei, quod à media describitur, quadrato. Et si sub extremis comprehensum rectangulum aequale sit ei, quod à media describitur, quadrato: Illae tres rectae lineae proportionales erunt’ (Clavius p. 568).