Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666

[p. 232]

V¹⁾.
[1657].

Aug. 1657.

1) La Pièce occupe la p. 47 du Manuscrit K. Une traduction hollandaise fut publiée par J. Versluys aux p. 25-26 de l'ouvrage ‘Zes en negentig bewijzen voor het theorema van Pythagoras, verzameld en gerangschikt door J. Versluys, Amsterdam, 1914, A. Versluys.’ Comme M. Versluys le fait remarquer, il est bien curieux que parmi les démonstrations nombreuses du théorème de Pythagore, qu'on a inventées plus tôt ou plus tard, aucune n'est identique avec celle de Huygens.

Demonstratio mea Propos.^is 47 lib. 1 Euclidis.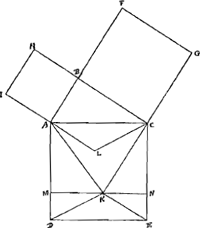

Esto triangulum rectangulum ABC rectum habens angulum ABC. Dico quadratum ex AC aequale esse quadratis ex AB, et ex BC simul sumptis.

Describatur enim super AC quadratum ADEC; super AB vero et BC quadrata AH, CF. Et producatur IA usque in L ut sit AL aequalis AI, et jungatur LC, similiter producatur CG in K, ut sit CK aequalis CG, et jungatur KA; et ducantur etiam KE, KD, et per K agatur MN parallela AC.

Quoniam itaque anguli ABC, CBF, uterque recti sunt, recta linea est FBA: estque ipsi parallela GK. Quamobrem cum inter easdem parallelas sint quadratum GB et triangulum CAK, habeantque bases GC, CK aequales, erit trianguli CAK duplum quadratum GB. Sed et rectangulum AN, duplum est ejusdem trianguli AKC,

[p. 233]

cum sint inter easdem parallelas AC, MN, habeantque basin eandem AC. Igitur rectangulum AN aequale est quadrato GB. Superest ut ostendatur rectangulum DN aequale quadrato AH. Quoniam itaque angulus uterque ACE, BCK rectus est, ablato communi angulo ACK, fiet KCE aequalis angulo BCA, verum et utrumque latus EC, CK aequale est utrique AC, CB, singula nimirum singulis. Ergo et reliquum latus KE aequale erit reliquo AB, et angulus KEC aequalis angulo BAC^*). Quare et ablato angulo KEC ab angulo recto DEC; angulo vero BAC ab angulo recto BAL, relinquentur anguli inter se aequales KED, LAC. Sed ostensa est KE aequalis AB, hoc est ipsi AL: et ED aequalis est ipsi AC. Itaque cum triangulum KED, duo latera habet aequalia duobus lateribus trianguli LAC, et angulum KED aequalem angulo LAC, erunt haec triangula inter se aequalia. Est autem trianguli KDE duplum rectangulum DN, cum eandem habeant basin DE et eandem altitudinem; trianguli vero LAC duplum est quadratum AH cum sint inter easdem parallelas HC, IL constituta, et bases aequales habeant LA, AI. Itaque necesse est rectangulum DN aequari quadrato AH. Sed et rectangulum MC aequale ostensum est quadrato CF. Ergo apparet quadratum totum DC aequari utrique simul quadrato CF, AH; quod erat demonstr.

*) 8. primi²⁾.

2) Il s'agit en vérité de la quatrième (et non pas de la huitième) Proposition du premier Livre des ‘Elementa’ d'Euclide: ‘Si duo triangula duo latera duobus lateribus aequalia habeant, vtrumque vtrique; habeant vero & angulum angulo aequalem sub aequalibus rectis lineis contentum: Et basim basi aequalem habebunt: eritque triangulum triangulo aequale; ac reliqui anguli reliquis angulis aequales erunt, vterque vtrique, sub quibus aequalia latera subtenduntur.’ (Clavius, ed. 1507, p. 41.)

2) Il s'agit en vérité de la quatrième (et non pas de la huitième) Proposition du premier Livre des ‘Elementa’ d'Euclide: ‘Si duo triangula duo latera duobus lateribus aequalia habeant, vtrumque vtrique; habeant vero & angulum angulo aequalem sub aequalibus rectis lineis contentum: Et basim basi aequalem habebunt: eritque triangulum triangulo aequale; ac reliqui anguli reliquis angulis aequales erunt, vterque vtrique, sub quibus aequalia latera subtenduntur.’ (Clavius, ed. 1507, p. 41.)