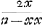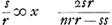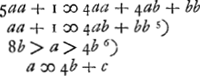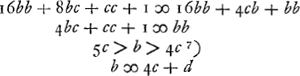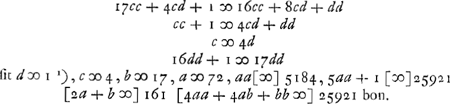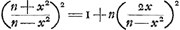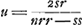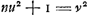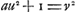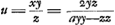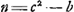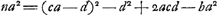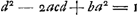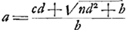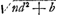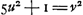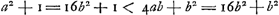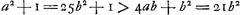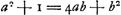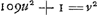|
-
voetnoot1)
- Les annotations qui suivent, empruntées aux p. 40-41 du Manuscrit A, ont été écrites à propos du ‘Commercium epistolicum’, publié par Wallis en 1658 (voir la note 3 de la p. 192 de notre T. II). Elles se rapportent aux solutions qu'on y trouve du problème de Fermat traité dans la Pièce No. III au § 3 (voir les p. 213-217 du présent Tome). Huygens se servit de ces annotations dans la composition de sa lettre à Wallis du 6 septembre 1658, p. 211-212 du T. II.
-
voetnoot2)
- Dans ce paragraphe Huygens s'occupe de la solution de Brouncker exposée à la p. 15 du ‘Commercium’ (p. 767-768 du ‘Volumen alterum’ de l'‘Algebra’ cité dans la note 10 de la p. 9).
-
voetnoot3)
- Remarquons toutefois que cela n'empêcherait pas que
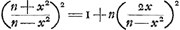 ne fût un nombre entier. ne fût un nombre entier.
-
voetnoot1)
- Il s'agit donc de choisir les nombres s et r de manière que 2sr soit divisible par nrr - ss, auquel cas
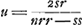 représentera une solution en nombres entiers de l'équation représentera une solution en nombres entiers de l'équation 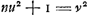 . Dès ce moment Huygens doit s'être aperçu de l'identité de la méthode de Brouncker avec la sienne telle qu'on la trouve exposée au début du § 3 à la p. 214, où une solution de l'équation . Dès ce moment Huygens doit s'être aperçu de l'identité de la méthode de Brouncker avec la sienne telle qu'on la trouve exposée au début du § 3 à la p. 214, où une solution de l'équation 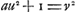 est obtenue de la forme est obtenue de la forme 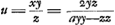 . Voir la p. 212 du T. II, où on lit: ‘Ego canonem tantum inveneram eundem fere quem pagina 57’ (p. 789 du ‘Volumen alterum’) ‘et alibi adducis’. . Voir la p. 212 du T. II, où on lit: ‘Ego canonem tantum inveneram eundem fere quem pagina 57’ (p. 789 du ‘Volumen alterum’) ‘et alibi adducis’.
-
voetnoot2)
- L'annotation qui suit se rapporte entre autres à une méthode exposée par Wallis à la p. 63 du ‘Commercium’ (p. 792 du ‘Volumen alterum’). Posant
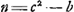 , Wallis en déduit , Wallis en déduit 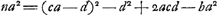 et il remarque que le nombre a sera une solution de l'équation et il remarque que le nombre a sera une solution de l'équation 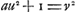 toutes les fois qu'on aura: toutes les fois qu'on aura: 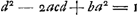 , c'est-à-dire, , c'est-à-dire, 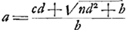 . Après quoi Wallis continue: ‘His positis. Ut cognoscatur d, quaerendum erit... quis quadratus ductus in numerum datum, assumpto numero b, faciat quadratum; (ut nempe . Après quoi Wallis continue: ‘His positis. Ut cognoscatur d, quaerendum erit... quis quadratus ductus in numerum datum, assumpto numero b, faciat quadratum; (ut nempe 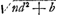 sit numerus rationalis integer). Quod quam vis videatur nihilo facilius reperiri posse quam quod primum petebatur; tamen hinc magnum futurum operae compendium, certum est, quia d ... minor semper erit quam a ... adeoque citius eo pervenietur ubi habebitur defectus b, quam ubi defectus 1.’, etc. sit numerus rationalis integer). Quod quam vis videatur nihilo facilius reperiri posse quam quod primum petebatur; tamen hinc magnum futurum operae compendium, certum est, quia d ... minor semper erit quam a ... adeoque citius eo pervenietur ubi habebitur defectus b, quam ubi defectus 1.’, etc.
-
voetnoot3)
- Dans ce paragraphe Huygens examine une méthode exposée à la p. 71 du ‘Commercium’ (p. 797 du ‘Volumen alterum’). Afin de s'assurer si elle est exacte et expéditive, il l'applique à un autre exemple que celui choisi par Wallis, c'est-à-dire à l'équation
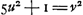 . .
-
voetnoot4)
- La méthode qui suit doit en effet être attribuée à Brouncker. Il est vrai que Huygens dans sa lettre à Wallis du 6 septembre 1658 (p. 211 du T. II) l'appelle: ‘tuane an Illustri. Brounkeri, neque enim satis certo id significas, methodus pagina 71 exposita’; mais Wallis lui répond (p. 297 du T. II) ‘... Methodum illam quae pagina 71. occurrit, quae est Illustris Brounckeri magis quam mea (quod ibidem me satis innuisse putaveram) licet eam mihi deinceps reliqueret exponendam’.
-
voetnoot5)
- En posant b = 1, a = 4, on obtient une première solution de l'équation
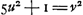 ; mais Huygens suppose b > 1 et par suite aa > 4ab, ce qui fournit la limite inférieure de l'inégalité qui suit. ; mais Huygens suppose b > 1 et par suite aa > 4ab, ce qui fournit la limite inférieure de l'inégalité qui suit.
-
voetnoot6)
- Il eût été plus conforme à la méthode de Brouncker d'écrire: 5b > a > 4b. Voici, en effet, l'artifice par lequel Brouncker obtient les limites. Pour a = 4b on a
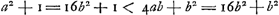 ; pour a = 5b on a au contraire ; pour a = 5b on a au contraire 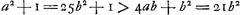 . On en peut conclure que s'il y a une valeur entière et positive de a qui satisfait à l'équation . On en peut conclure que s'il y a une valeur entière et positive de a qui satisfait à l'équation 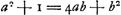 , elle doit être située entre 4b et 5b, l'autre racine de cette équation étant négative. , elle doit être située entre 4b et 5b, l'autre racine de cette équation étant négative.
-
voetnoot7)
- La limite inférieure se trouve en remarquant que nécessairement 4bc < bb.
-
voetnoot1)
- Puisque les quantités a, b, c, etc. constituent nécessairement une suite descendante quant à leurs valeurs, il est évident que la circonstance qui se présente ici, c'est-à-dire qu'une dernière équation est satisfaite en posant l'inconnue égale à l'unité, doit arriver toujours, tôt ou tard, pourvu qu'il existe une solution en nombres entiers de l'équation qu'on examine. C'est en cela que consiste la valeur de la méthode de Brouncker qui est appliquée e.a. dans le ‘Commercium’, p. 85, (voir les p. 804-805 du ‘Volumen alterum’) à l'équation
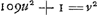 , où la solution la plus simple u = 15140424455100 est trouvée après la considération de 22 équations. Elle fut donc louée à juste titre par Huygens lorsqu'il écrivit à Wallis (voir la p. 211 du T. II): ‘Prae caeteris mihi placuit illa... methodus’; mais il ajouta à raison: ‘ex qua tamen nequaquam illud recte colligere mihi videris pagina 83’ (p. 803 du ‘Volumen alterum’) ‘dari aliquem quadratum qui in datum numerum non quadratum ductus adscita unitate faciat quadratum. Nam secundum methodum illam operatione instituta, nequaquam scis quam diu continuandae tibi sint positiones antequam quaesitum obtineas, ideoque nec omnino certus esse potes an unquam eo perventurus sis. Sunt, inquis pagina 82, differentiae b, c, d, &c. numeri integri et continuè decrescentes, ergo tandem ad unitatem deveniri necesse est. at revera ex tua tantum hypothesi sunt numeri integri eoque illud supponere videris quod erat
demonstrandum’. , où la solution la plus simple u = 15140424455100 est trouvée après la considération de 22 équations. Elle fut donc louée à juste titre par Huygens lorsqu'il écrivit à Wallis (voir la p. 211 du T. II): ‘Prae caeteris mihi placuit illa... methodus’; mais il ajouta à raison: ‘ex qua tamen nequaquam illud recte colligere mihi videris pagina 83’ (p. 803 du ‘Volumen alterum’) ‘dari aliquem quadratum qui in datum numerum non quadratum ductus adscita unitate faciat quadratum. Nam secundum methodum illam operatione instituta, nequaquam scis quam diu continuandae tibi sint positiones antequam quaesitum obtineas, ideoque nec omnino certus esse potes an unquam eo perventurus sis. Sunt, inquis pagina 82, differentiae b, c, d, &c. numeri integri et continuè decrescentes, ergo tandem ad unitatem deveniri necesse est. at revera ex tua tantum hypothesi sunt numeri integri eoque illud supponere videris quod erat
demonstrandum’.
|
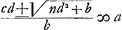 .
.


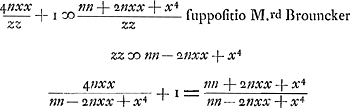
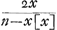 fuerit integer numerus habebitur quaesitum. utique si et x sit integer. nam alias quadr. ab x[x] + n non esset integer
fuerit integer numerus habebitur quaesitum. utique si et x sit integer. nam alias quadr. ab x[x] + n non esset integer