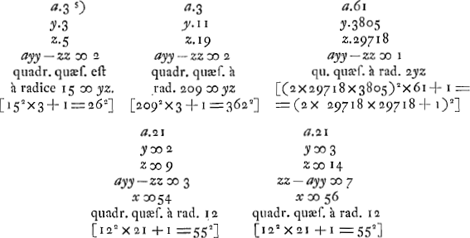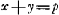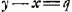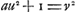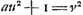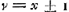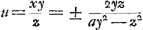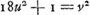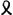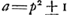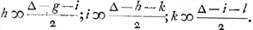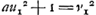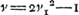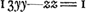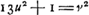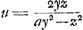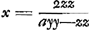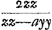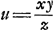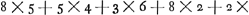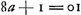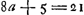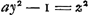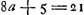Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 212]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
IIIGa naar voetnoot1).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aliter.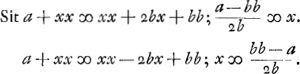 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 213]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hic oportet a - bb dividi posse per 2b quod quidem semper continget si sumatur b ∞ 1, numerusque a datus fuerit impar. at quoties par datus est, oportet experiendo quaerere. ut si datus sit 12. sit b ∞ 6, erit bb - a ∞ 24, qui dividitur per 2b ∞ 12, et fit 2. Ergo hujus quadr. 4 additum ad 12 facit 16 qui est quadratus. Multi autem numerorum parium faciunt quaestionem impossibilem, velut 6, 10;Ga naar voetnoot4) quia enim quadrata ex 3 et 4 differunt 7.rio sequitur si numeri majus sumantur quam 3 et 4, unitate differentes, eorum quadrata majoris intervallum quam 7 ac proinde quam 6 habitura et si non unitate differant sed majori numero, adhuc majus quadratorum fore intervallum. Frustra igitur b major sumetur quam 4. Quin imo necesse est 2b non sit major a. Dato enim a numero pari etiam b necessario par est assumendus ut bb - a dividi possit per 2b parem. Sed bb, quadratum à numero pari dividitur per 2b. Si igitur et bb - a dividetur per 2b, etiam reliquum a dividi poterit per 2b; ideoque 2b non debet major esse quam a. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 2.Cur omnis numerus primus addita vel dempta unitate dividitur per 6, item per 4? exceptis 2 et 3.Quoniam omnis primus numerus est impar sequitur sive addita sive ablata unitate fieri parem, ideoque dividi per 2. Sed et impar numerus primus existens per 3 divisus relinquit 1 vel 2 necessario. itaque si relinquat 1, demptâ 1 metietur eum 3, sin relinquat 2, addita unitate rursus 3 ipsum metietur. fit igitur addendo vel auferendo unitatem ut 2 et 3 ipsum metiatur. Quare et 6 qui fit ex 2 et 3 ipsum metietur. Porro omnis impar numerus per 4 divisus relinquit 1 vel 3. Ideoque si relinquat 1, demptâ 1 metietur ipsum 4. si vero relinquat 3, additâ 1 rursus ipsum metietur 4. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 3.Si numerus non quadratus in quadratum ducatur productus quadratus non erit. Addita autem unitate fieri potest quadratus. Itaque Fermattius hoc problema proposuitGa naar voetnoot5): dato numero non quadrato invenire quadratum per quem multiplicatus, additâ ad productum unitate, fiat denuo quadratus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 214]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sit datus non quadratus a. sit axxyy/zz + 1 ∞ xx + 2x + 1, qu. ab x + 1. 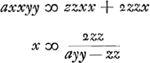 hunc oportet esse numerum integrum quod fiet si ayy - zz ∞ 1, hoc est, si ayy - 1 ∞ zz. Idem etiam continget si ayy - zz fuerit ∞ 2, hoc est ayy - 2 ∞ zz. Experiendo igitur inveniendum est quadratum yy quod in a ductum demptâ 1 vel 2 relinquat quadratum. Quod si superius quadratum formatum fuisset ab x - 1 inventa fuisset aequatio 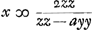 . .
Ubi si zz - ayy ∞ 1, hoc est ayy + 1 ∞ zz rursus quaestio resoluta est. Sed hic ad ipsum primum quaesitum devenimus ut sit nempe ayy + 1 aequale quadrato. Si vero zz - ayy ∞ 2, rursus integrum numerum x inveniemus. Hoc est si ayy + 2 ∞ zz. Quod si 2zz per zz - ayy vel per ayy - zz tantummodo dividi possit erit rursus x numerus integerGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Aliter.Si axx Ga naar voetnoot2) 2x esset quadratus is propositum efficeret, nam ductus in a, fit aaxx Ga naar voetnoot2) 2x esset quadratus is propositum efficeret, nam ductus in a, fit aaxx  2ax qui additâ 1 facit aaxx 2ax qui additâ 1 facit aaxx  2ax + 1 qui est quadr. Sit ergo 2ax + 1 qui est quadr. Sit ergo
axx  2x ∞ zzxx/yy 2x ∞ zzxx/yy
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 215]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
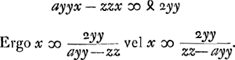 Consideratis itaque simul hac et antecedenti aequatione huc deventum esse liquet, ut quaerendus sit numerus quadratus qui si in datum numerum ducatur productumque ab aliquo quadrato auferatur, vel hoc ab illo, residuum metiatur alterutrius dictorum quadratorum duplum. Quotiens enim erit x. Quoties autem datus numerus aliquem quadratum unitate superat vel ab eodem unitate deficit sumendus est y ∞ 1, et zz quadratum isti quadrato aequale, ut ita fiat ayy - zz vel zz - ayy ∞ 1, unde secundum priorem modumGa naar voetnoot3) fit x ∞ 2zz, ideoque xxyy/zz ∞ 4zzGa naar voetnoot4). Ex. gr. numerus 5 superat unitate quadratum 4. ergo sumatur zz ∞ 4. Ergo xxyy/zz ∞ 4zz ∞ 16. 16 est quadratus qui ductus in 5 facit 80 cui addita 1, efficit 81 quadratum. Sic numerus 3 unitate minor est quadrato 4 quare rursus sit zz ∞ 4, Eritque xxyy/zz ∞ 16. 16 quadratus ductus in 3 facit 48 cui si addatur 1 fiunt 49 quadratus. Quoties vero datus numerus, quadratum aliquem binario superat, vel binario minor est eodem quadrato: sumendum rursus est quadr. zz isti quadrato aequale, et y ∞ 1, ut fiat ayy - zz vel zz - ayy ∞ 2. Unde secundum priorem rursus modumGa naar voetnoot3) fit x ∞ zz, ideoque xxyy/zz ∞ zzGa naar voetnoot5). Ex. gr. 11 binario superat quadr. 9. Ergo 9 est zz, qui ductus in 11 facit 99, cui additâ 1 fiunt 100 quadratus. Item 7 binario minor quam 9, ductus in 9 facit 63, cui si apponatur 1, fiunt 64 quadr. numerus. Quoties itaque numerus datus quadratum numerum unitate vel binario excedit vel alterutro horum à quadrato deficit facile problema solvitur per ea quae jam dicta sunt. Sciendumque quod uno reperto quadrato qui propositum efficiat infiniti alij idem facientes inveniri possint. Si enim inventus quadratus vocetur yy. Ergo | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 216]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
quia ayy + 1 aequatur quadrato quod vocetur zz, erit zz - ayy ∞ 1. Et secundum priorem methodum 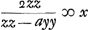 numerus integer quia scil. divisor est unitas, itaque numerus integer quia scil. divisor est unitas, itaque 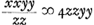 . Sed zz est ∞ ayy + 1. Ergo 4zzyy ∞ ∞ 4ay4 + 4yy, quod quadratum ductum in a, addita ad productum unitate rursus quadratum efficiet. Quoniam autem fit 4ay4 + 4yy ex ductu ayy + 1 in 4yy, hinc talis existit regula. . Sed zz est ∞ ayy + 1. Ergo 4zzyy ∞ ∞ 4ay4 + 4yy, quod quadratum ductum in a, addita ad productum unitate rursus quadratum efficiet. Quoniam autem fit 4ay4 + 4yy ex ductu ayy + 1 in 4yy, hinc talis existit regula.
Quadratum inventum (qui nimirum propositum efficit) duc in datum numerum, producto adde unitatem, summam duc in quadruplum ejusdem quadrati inventi, prodibitque aliud quadratum quaestioni satisfaciens. Et simili ratione ex hoc rursus aliud invenitur, atque ita alia quot libueritGa naar voetnoot1). Exempl. gr. Quoniam inventum est quadratum 16 quod ductum in 3, assumpta ad productum unitate facit quadratum 49. ducatur ergo 49 in 64 quadruplum scilicet 16, fit 3136 quadratus necessario quem dico proposito convenire. Nam ductus in 3 facit 9408, cui additâ 1 fit 9409 quadratus à radice 97.
Datus sit numerus 13, qui vocetur a. Ergo secundum primam regulamGa naar voetnoot2), quia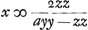 ; sit y ∞ 5. z ∞ 18Ga naar voetnoot3). yy ∞ 25; ayy ∞ 325; zz ∞ 324; ayy - zz ∞ 1; ; sit y ∞ 5. z ∞ 18Ga naar voetnoot3). yy ∞ 25; ayy ∞ 325; zz ∞ 324; ayy - zz ∞ 1;
2zz ∞ x. ergo 4zzyy ∞ xxyy/zz. 4zzyy ∞ 32400  quadr. quaes. 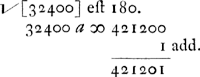 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 217]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
§ 4.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 218]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Numerus qui rejectis novenarijs, (ut fieri solet in examine additionis) non relinquit 1, 4, 7 aut 0 non erit quadratus. Quia enim ut fiat quadratus idem est multiplicatus numerus ac multiplicandus; necesse autem est ut uterque simul horum rejectis novenarijs relinquat 1, 2, 3, 4, 5, 6, 7, 8, vel 0; sequitur productum quoque multiplicationis, hoc est ipsum quadratum numerum, abjectis novenarijs tantum relinquere debere quantum quadratum alicujus harum simplicium notarum, rejectis itidem si opus sit novenarijs, nam alias constat multiplicationem non recte se habere. atqui quadratum alicujus simplicium notarum rejecto quoties potest novenario relinquit 1, 4, 0 aut 7. Ergo omnis quoque quadratus numerus abjectis novenarijs relinquit 1, 4, 7 aut 0, quod erat demonstr.
Numerus qui rejectis novenarijs non relinquit 1, 8 vel 0 non erit cubus.
Proprietas illa insignis novenarij in examinandis omnium specierum supputationibus (nam etsi nonnulli examina istiusmodi rejiciant, magnam tamen utilitatem habent, quod certos faciant, vitiosum esse calculum, quoties numeri non respondent) non aliunde est quam quod 9 proximus est 10, cum denariâ progressione numeri scribantur; quod facile esset ostendere. Si itaque alia progressione numeri scriberentur, alterius numeri nec amplius novenarij illa esset proprietas. Veluti si non ultra septem simplices characteres adhibere placuerit, adeo ut secundi loci numerus octuplum faciat primi, et tertij loci numerus octuplum secundi, &c. jam septenarij eadem praerogativa erit ut examen per ipsum possit institui, sicut alias per 9 solet. Foret autem secundum hanc octonariam progressionem pro 8 scribendum 10, pro 9, 11, pro 20, 24, &c. quod facile est intelligere. Quod si vero dati quivis numeri secundum denarium progressum scripti, continuo ad octonarium reduci possent, prodesset hoc ad alterum instituendum examen cujusvis arithmeticae operationis, posteaquam jam per 9 experti essemus: juvaretque praeterea in quadratis numeris discernendis, de qua re modo egimus. Verum reductio illa expeditè fieri non potest; sed tabulam primo construere necesse esset; tum deinde molesta atque insolita additio peragenda. Hoc incommodo evitando aliud compendium inveni, tabellâ nimirum conditâ quae ostendat | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 219]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
de singulis denarijs, centenarijs, millenarijs, &c., quantum quisque relinquat septenarijs abjectis, sive per 7 divisus, cujus tabellae construendam rationem primò, deinde usum exponam.
Characteres supernè inscripti denotant ordines numerorum secundum denarium progressum scriptorum. Scilicet qui sub 2 in columna habentur ad denarium pertinent, qui sub 3, ad centenarium, &c. Qui autem ad latus adscripti sunt characteres indicant ad quotum denarium, centenarium, millenariumve &c. pertineant, qui in eo tranverso ordine continentur. Itaque in columna sub 1, continentur ij numeri quibus numeri simplices seu primi ordinis excedunt septenarium nec in his nisi duo maximi 8, 9 septenarium excedunt. In columna sub 2, continentur ij quibus denarij sive 2di ordinis numeri septenarium vel septenarios excedunt. Primi nempe denarij excessus est 3, secundi sive numeri 20 excessus supra septenarios est 6, atque ita de caeteris. qui quidem facile inveniuntur. Nam cum compertum sit primum denarium excedere per 3, ut hinc sciam quid excessus secundi denarij, multiplico ipsum 3 per 2 in columna laterali fitque 6, quod in concursu utriusque ordinis colloco. Rursus ut tertij denarij excessum supra septenarios invenio multiplico 3 laterale in idem 3 excessum sc. primi denarij fiuntque 9 quae rejecto septenario relinquunt 2, quod similiter in concursu ordinum colloco. Et sic tota columna sub 2 consequenter perficitur. Rursus ut primi centenarij excessus habeatur sive primus numerus in columna sub 3, duco eundem rursus excessum denarij 3, in seipsum, fiunt 9, et rejecto septenario, 2, qui est excessus primi centenarij quaesitus. Nam cum denarij excessus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 220]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
sit 3, necesse est eum qui fit ex ductu denarij in se ipsum, hoc est primum centenarium excedere (collectis in unum omnibus characteribus cum per octonarium progressum scriptus erit) quantum 3 in 3 ductum, septenarium excedit; quoniam videlicet eadem tunc septenarij proprietas est quae solet alias esse novenarij in multiplicatione. Cognito autem excessu primi centenarij 2, ut habeatur exc. secundi centenarij ducendum est rursus 2 laterale in ipsum excessum 2 fit 4 pro quaesito excessu. atque ita porro columna haec ac deinceps tota tabella repletur, estque animadvertendum postquam supremus columnae numerus idem contigerit cum aliquo supremorum columnae alicujus praecedentis, quod ex inde eaedem columnae in ijsdem numeris revertantur, adeo ut describere tantum sit opus. ut hic in 7a columna fieri coepit. Dato itaque numero aliquo secundum vulgarem denariam progressionem scripto velut 853824, si scire velim quid relicturus sit abjectis septenarijs si ad octonariam progressionem reducatur, scribo, sub 8 quod sextum locum occupat, 5, quia hoc invenio in concursu columnae sub 6 et transversi ordinis cui ad scriptum est 8. Et constat sane, si numerum 800000 totum per octonarium progressum exprimerem, rejectis postea septenarijs superfuturum 5: ex constructione nimirum tabellae. Rursus simili ratione invenio pro charactere secundo numeri dati qui est 5, scribendum esse 6, quod sub dicto charactere 5 repono: atque ita de caeteris omnibus, ut datus numerus cum subscripto sit.
853824/564264
Hic jam subscriptus rejectis septenarijs tantundem relicturus est, atque integer numerus datus si ad octonarium progressum reductus esset; relinquit autem 6, idque patet ea simplici notarum additione rejecto quoties opus est 7narioGa naar voetnoot1). Possunt itaque numeri ex multiplicatione vel alia operatione arithmetica orti hac ratione immutari ut inde, per septenarium, examen eodem modo instituatur sicut solet per 9. Quanquam etiam absque ulla immutatione idem examen institui potest, sed tunc per 7 dividendum est: veluti in multiplicatione, primum uterque numerus qui sese invicem multiplicant per 7 dividendus est, et reliquum ab utroque in se invicem ducendum et videndum quis sit excessus producti hujus supra 7.os cum quo idem esse debet excessus producti multiplicationis per 7 divisi. Unde constat omnem numerum quadratum sive hoc modo sive praecedenti per 7 examinatum relinquere debere 1, 2, 4 aut 0Ga naar voetnoot2). Quod eodem modo demonstratur sicuti | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 221]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
supra de examine per 9 ostensum est, nempe quod illic quadrati numeri relinquant semper 1, 4, 7 aut 0. Facto itaque examine per 9, si non deprehendatur non quadratus, neque ex finalibus notis agnoscatur, deinceps per 7 explorandus est. Sed antea potius per 11, quoniam expedita est magis operatio, ut jam ostendemus. Tabella sequens indicat quo excessu quilibet denarius, centenarius, millenarius &c. superet undenarios, estque eâdem methodo descripta, qua praecedens ad septenarios pertinens. Hujus autem usu non indigebimus, sed eo tantum proponitur ut demonstrentur proprietates quaedam numeri 11. Nota τ significat 10.
Apparet autem numeros in columnis alternatim reverti eosdem, quod necessario contingere ex constructionis ratione manifestum est. Dato itaque numero aliquo secundum consuetum denarij progressum scripto si velim ipsum reducere ad alios characteres, ita ut examen per 11 ex collectione simplici notarum peragi queat, (sit verbi gr. numerus datus 255481) liquet omnibus locis imparibus, à dextra incipiendo, nempe primo, tertio, quinto &c., eosdem characteres haberi quos ex tabella substituere oporteret; locis autem paribus illos fore substituendos quibus quisque datorum characterum ab 11 deficit. Veluti quia secundo loco habetur 8, substituetur 3, et sic de ceteris. Hoc cum constet, nihil opus esse | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 222]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
video ut datus numerus in alios characteres transcribatur, sed tantum ut primò ex notis locorum imparium undenarius rejiciatur quoties potest (hic ne semel quidem potest sed fiunt 10 ex simplici additione notarum 1, 4, 5,) deinde ex notis locorum parium undenarius similiter quoties potest rejiciatur, (fit hic excessus 4), atque posterior hic excessus a priore auferatur, qui quidem si minor est augendus est undenario; reliquum enim fore quo totus numerus datus undenarios superat sive id quod supererit cum per 11 dividetur. fit autem hic 6. Et hic quidem examandi modus expeditus est fere aeque ac qui per 9 solet usurpari. Utique si hoc quoque observetur in additione simplici notarum et quoties supra 10 ascenderis, veluti ad 17, &ct, auferas tantum sinistram notam à dextra nota velut hic 1 à 7 fit 6; unde scias excessum ipsius 17 supra 11 esse 6. nam hoc facilius cogitatione fit quam si ex 17 demas 11. Porro ut quadratos numeros hoc examine exploremus sciendum est omnem quadratum per 11 divisum relinquere necessario, 0, 1, 3, 4, 5 aut 9 adeoque si per examen inveniatur excessus, 2, 6, 7, 8 aut 10, non erit quadratus numerus. Cujus ratio eadem est quam supra de quadratis per 9 explorandis dedimus, vel in universum haec erit, quod quoties numeri duo sigillatim per aliquem numerum dividuntur, atque utriusque residua, in se invicem ducuntur, ejus producti excessus supra eundem illum divisorem idem erit cum excessu qui habetur si productum duorum ab initio dictorum numerorum per eundem quoque divisorem dividatur.
Sint propositi numeri a et b, et sumatur divisor c. Et diviso a per c fiat quotiens d et residuum e. Rursus diviso b per c fiat f quotiens et residuum g. Est igitur dc + e ∞ a et fc + g ∞ b. Quare ab productum numerorum erit ∞ dfcc + dcg + + fce + eg. Quo diviso per c apparet residuum fieri eg, (omnibus reliquis partibus per c divisionem recipientibus), quod idem est cum residuo producti duorum residuorum e et g per c divisi. quod erat demonstr.Ga naar voetnoot1)
Ex hoc theoremate proprietas undenarij quae ex praec. tabella colligitur demonstrari potest quod nimirum quilibet numerus unum characterem habens, cum sequente pari numero cifrarum, per 11 divisus tantundem relinquat, atque ipse characterinitialis unitates denotat. Ut si 700 per 11 dividatur relinquetur 7, si 40000, relinquetur 4, &c. Numerus autem unum characterem habens cum adjectis cifris imparibus, si per 11 dividatur, tantum relinquet quantum character initialis ab 11 deficit. Ut si 3000 vel 30 per 11 dividas supererit 11-3 hoc est 8.
Tentato examine per 8, inveni id ad tres extremos characteres tantum pertinere quia 1000 per 8 divisum nihil relinquit, ideoque etiam omnes numeri qui tres | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 223]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pluresve cifras adjectas habent. Tres ergo postremi characteres omnis quadrati numeri si per 8 dividantur debent relinquere 1, 4 aut 0Ga naar voetnoot2). Ex tabella autem ad octonarium comparata inveniGa naar voetnoot3), quadratos numeros quorum extrema est 9 sic
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 224]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
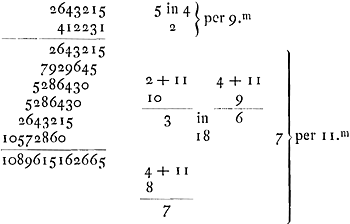 Facto examine per 9rium si convenire numeri inveniantur, erunt 9 partes pro recto calculo, 1 pars pro vitioso. Facto examine per 11rium erunt 11 partes pro recto, una pro vitioso. Peracto vero tum per 9m tum per 11m examine, si convenire numeri inveniantur, erunt 99 partes pro recto calculo, una pro vitioso. |
|