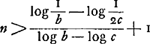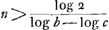Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 156]
| |
Appendice VIIGa naar voetnoot1)
Elck heeft 1/2 a ingeset. die ten eersten een 6 met eene steen neemt te werpen
| |
[pagina 157]
| |
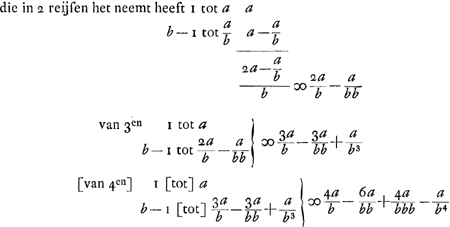 b - 1 ∞ cGa naar voetnoot3), a ∞ 1 hebbende elck 1/2 ingeset 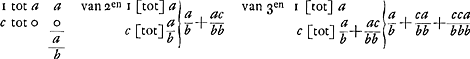 Traduction: | |
[pagina 158]
| |
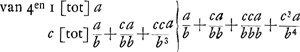 maer a is ∞ 1, ergo 1/b + c/bb + cc/b3 + c3/b4 [... ∞] 1/2, dat is men moet sien wanneer de somme van de progressie gelijck werdt aen 1/2, want dan is de kans gelijck van die het in soo veel reijsen genomen heeft.  prop. u ut summa prop.um sit ∞ 1/2 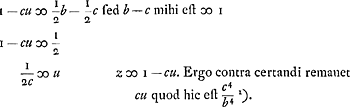 Traduction: | |
[pagina 159]
| |
Quoto jactu duarum tesserarum duos senarios me daturum certare possum cum lucro? Sunt jactus 36. Ergo hic b est 36. et c ∞ 35. prima proportionalium 1/b ∞ 1/36. Quaerendum ergo quot proportionales statuendae sint in ratione 36 ad 35 ut ultima u sit minor quam 1/2c hoc est hic quam 1/70. tunc enim summa proportionalium (quae significat partem quam ex unitate seu (a) mihi arrogare possum) excedet 1/2. adeo ut illo jactuum numero potior esse incipiat conditio mea. Quod si fiat ut 36 ad 35 ita 1/36 ad aliam ea erit secunda proportionalis et sic deinceps faciendum donec proportionalis inveniatur quae sit minor quam 1/70. Hoc autem per logarithmos facile estGa naar voetnoot2), nam si ab log. 1/36 qui est - 1.5563025 auferatur differentia log. 35 et 36, quae est 0.0122345, habebitur log. dictae secundae proportionalis. Invenio autem 24ter dictam differentiam auferendam a logarithmo 1/36 priusquam habeatur logarithm. minoris fractionis quam 1/70, quia dividendo differentiam logg. 1/70 et 1/36 quae est - 0.2887955 per dictam differ. logg. 36 et 35 quae est 0.0122345, fiunt plus quam 23, ideoque 24 sumendum ut perveniatur ad fractionem minorem quam 1/70. Itaque 24 proportionales statuendae praeter primam 1/36. adeo ut omnino sint 25. ac proinde 25o jactu certare possum eventuros duos senarios, idque conditione potiori quam sit contra certantis. | |
[pagina 160]
| |
Quoto jactu 3um tesserarum tres senarios jacturum me certare possum. Resp. 150.  Quoto jactu 4or tesserarum quatuor senarios? Resp. 899Ga naar voetnoot2). 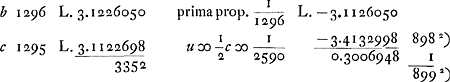 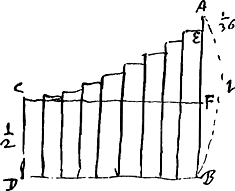 Brevius haec omnia peragi possuntGa naar voetnoot3). Exempli gratia cum queritur quoto jactu duarum tesserarum possint duo senarij haberi, ita ut certetur cum lucro. Tantummodo quaerendum quoties ratio 36 ad 35 continentur in ratione 2 ad 1Ga naar voetnoot4). dividendo nempe logarithmum binarij 0,30103 per differ. logarithmorum 36 et 35, qui est 0,01223. fit 24 et aliquid superest. Tum addenda 1. et fit 25 numerus proportionalium quarum summa superabit 1/2. Ideoque 25 jactibus cum lucro certatur obventuros duos senarios. | |
[pagina 161]
| |
Simili ratione si quaeratur quot jactibus quatuor senarij quatuor tesseris possint obtineri ut certetur cum lucro: quia sunt jactus diversi quatuor tesserarum 1296; oportet dividere logarithmum binarij, (qui est logar. rationis 2 ad 1) per differentiam logarithmorum 1296 et 1295, quae differentia est 3352. Quotienti addenda unitas. 898 + 1 ∞ 899 vicibus cum lucro certatur.
Ut sciatur quantum valeat spes utriusque, sive quae pars ejus quod depositum est utrique debeatur, cum certo numero jactuum omnibus tesseris senarius eventurus certatur. tantummodo fractio constituenda est cujus denominator sit numerus diversorum jactuum qui dato tesserarum numero conveniunt, nominator vero numerus unitate minor illo jam dicto. Hujus fractionis potestas ea quae convenit numero jactuum, (veluti quadratoquadratum si quatuor jactibus senarij eventuri certantur) designabit partem quae contra certanti debetur ex eo quod depositum est. Ex. gr. si duabus tesseris quarto jactu duos senarios mihi venturos certem, quia duarum tesserarum jactus diversi sunt 36 erit fractio constituenda 35/36. Porro quia numerus jactuum datorum est 4 hinc quarta potestas positae nempe 35.35.35.35/36.36.36.36 sive 1500625/1679616 a (si a vocetur quod depositum est) est pars debita contra certanti; ut proinde mihi restent 178991/1679616 a. Et valor meae spei ad illius ut 178991 ad 1500625. Ratio horum haec est quod fol. praec. inventa fuit z summa proportionalium, (quae etiam est fractio designans partem certantis) aequalis 1 - cu. unde contra certanti relinqui apparet cu, Est autem cu productum ultimae proportionalium in c, unde si ultima proportionalis sit c3/b4, ut in hoc exemplo fit productum illud c4/b4Ga naar voetnoot5). | |
[pagina 162]
| |
Est autem logarithmorum etiam hic usus, cum absque his longum futurum sit potestates istas fractionis formare, cum magnus numerus jactuum certanti conceditur. Sic in exemplo superiori, si datis jactibus 899 quatuor tesserarum, quibus quatuor senarios evenire oporteat, scire velim quantum valeant spes utriusque; fractio hic erit 1295/1296; cujus ut sciatur potestas 899.ma  Qui vicibus continuis, quarum numerus sit a, eventurum certat ad quod ut eveniat sunt casus b, ut autem non eveniat sunt casus c; ejus sors (posito d ∞ b + c) ad sortem contra certantis ut ba ad da - ba. hoc est ut b toties in se ductum quot sunt unitates in a, ad summam b + c toties in se ductam minus b toties in se ducto. Ex. gr.Ga naar voetnoot1) si quis, duabus tesseris, sese supra 5 puncta jacturum certet, idque | |
[pagina 163]
| |
3 continuis vicibus. Hic 26 casus sunt punctorum supra quinque; 10 vero casus quinorum vel infra. Ergo hic a ∞ 3; b ∞ 26; c ∞ 10. b + c ∞ d ∞ 36. unde sors certantis erit ad sortem contra certantis ut cubus à 26, ad cubum a 36 - cubo a 26: hoc est ut 17576 ad 29180. Hujus facilis est demonstratio. Nam qui semel supra 5 se jacturum certat habet cas. 26 ad n, 10 ad 0. Ergo 26n/36. Qui bis habet cas. 26 ad 26/36n, 10 ad 0. Ergo 26.26.n/36.36. qui ter habet casus 26 ad 26.26.n/36.36 et 10 ad 0. Ergo 26.26.26n/36.36.36. atque ita porro. |
|


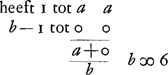
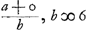 . Qui accepte de le faire en
. Qui accepte de le faire en