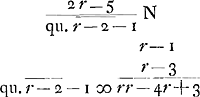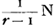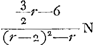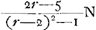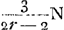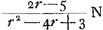- 49/231; 19/99; - 25/143; 23/143; [-] 29/195; 9/65; [-] 11/85; 31/255; [-] 37/323; 35/323; [-] 41/399; 39/399; [-] 45/483; 43/483; [-] 49/575; 47/575; [-] 53/675; 51/675
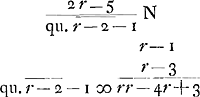
Soit r le nombre pair des cartes qui restent, et que la carte en jeu y soit 4 fois. alors l'avantage du Banquier est cette fraction de N, c'est a dire de ce qui a estè mis sur la carte en jeuGa naar voetnoot1).
|
-
voetnoot1)
- La Pièce occupe les p. 169-171 du Manuscrit E. Ajoutons qu'à la p. 168 on trouve encore les annotations suivantes qui se rapportent au jeu de la Bassette: ‘Si les 2 premieres estant semblables à la carte en jeu, le banquier gagne l'entier ou les 2/3 seulement? R. les 2 tiers. Et la deuxième alors n'est point considerée, si l'on ne reva [sic!].
Si ce desavantage du Banquier des 2/3 au lieu du tout, a lieu autrement qu'à la première carte de tout le jeu? R. à toutes.’
Il nous semble qu'il résulte de ces annotations que Huygens s'est informé sur les particularités du jeu chez quelque personne compétente. Or, on lit en effet à la p. 169 du Manuscrit l'annotation suivante: ‘demand. à m.e le Cocq. de la Bassette’. Voir encore les deux derniers alinéas de la note 1 de la p. 168.
-
voetnoot2)
- D'après le lieu d'où nous avons emprunté la Pièce.
-
voetnoot3)
- Les règles de ce jeu, telles qu'on les trouve exposées par M. Sauveur dans le ‘Journal des Sçavans’ du lundi 13 février 1679 aux p. 45-46 de l'édition d'Amsterdam, sont assez compliquées; mais puisque Huygens ne les applique pas toutes dans les calculs qui suivent, nous nous bornerons ici à celles qu'on doit connaître pour comprendre ces calculs. À cet effet nous citons de l'article de Sauveur les passages suivants: ‘Celuy qui taille qu'on nomme Banquier ou Tailleur a un Jeu entier de cinquante deux cartes & ceux qui joüent contre luy ont chacun en main treize Cartes d'une couleur, qu'on appelle le livre. Apres que le Tailleur a battu ses Cartes, les Joüeurs découvrent devant eux telles cartes de leur livre qu'ils veulent, sur lesquelles ils couchent de l'argent à discretion; ensuite le Tailleur tourne son jeu de Cartes, ensorte qu'il voit la premiere qui estoit dessous. Apres cela il tire ses cartes deux à deux jusqu'à la fin du Jeu en commençant par celle qu'il voit; & par la nature de ce jeu, la premiere de chaque couple ou main, est toûjours pour luy, & la seconde ordinairement pour le Joüeur, de sorte que si la premiere est par exemple un Roy, le banquier gaigne tout ce qui a esté coûché sur les Rois, mais si la seconde est un Roy, le Banquier donne aux joüeurs autant qu'ils ont couché sur les Rois, & en cela precisement l'avantage du Banquier n'est pas plus grand que celuy du joüeur. Mais il faut remarquer.
1. Que si la premiere & la seconde carte sont, par exemple des Rois (ce qu'on appelle doublets) le coup devroit estre nul, cependant le Banquier gaigne ce qui a esté couché sur les Rois.
2. Chaque joüeur a la liberté de coucher de l'argent sur telle carte qu'il veut lors que le jeu est commencé, de sorte que s'il couchoit de l'argent, par exemple sur une Dame lorsque le jeu est commencé, il pourroit arriver que dans le reste des cartes, il y auroit 4, ou 3, ou 2, ou enfin 1 Dame: ce qui diversifie les avantages du Banquier .....
3 ..... la derniere carte est nulle, laquelle devroit estre pour le Joüeur .....’
-
voetnoot4)
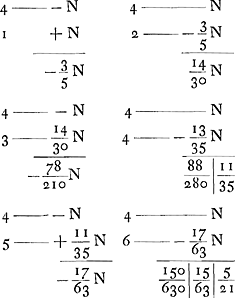
- Ce chiffre représente le nombre des cartes qui sont encore dans le jeu tenu par le banquier. Il va les tirer deux à deux, les mises N étant faites auparavant par les joueurs. Or, il est évident que dans le cas présent de deux cartes qui restent le banquier a une chance à gagner, c'est-à-dire si la première carte est la carte en question, et une à être quitte, quand cette carte vient comme deuxième, c'est-à-dire comme la dernière du jeu.
-
voetnoot5)
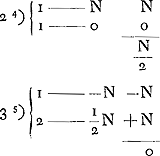
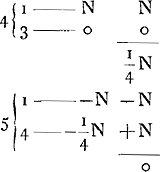
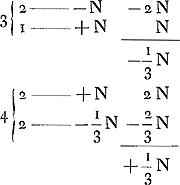
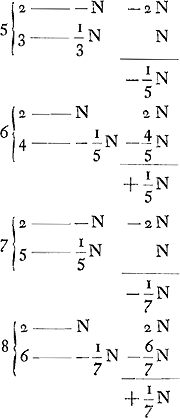
- À propos des calculs qui se rapportent aux cas où le nombre des cartes restantes est impair on doit remarquer que le compte entre le banquier et le joueur n'est réglé qu'après que les deux cartes ont été tirées. Par suite les désavantages du banquier, qui se présentent à commencer par la deuxième colonne de la p. 165 toutes les fois que le nombre des cartes est impair, n'existent pas en réalité; ce qui n'empêche pas que Huygens ne puisse se servir dans ses calculs de ces cas. Considérons, pour le montrer, le deuxième cas de la deuxième colonne de la p. 165, où il y a 4 cartes restantes, a1, a2, b, c, dont deux, a1, et a2, soient conformes à celle sur laquelle la mise est faite. Il y a alors deux chances que la première carte est a1 ou a2, auquel cas le banquier gagne la mise, et deux autres où elle est b ou c. Dans ces derniers cas le jeu continue avec trois cartes restantes et il
s'agit de calculer les avantages et désavantages qui peuvent se présenter encore. C'est ce que Huygens a fait par le premier calcul de cette deuxième colonne et il est évident qu'il doit supposer dans ce calcul, et dans tous ceux qui se rapportent aux cas d'un nombre impair de cartes, que la carte qui a précédé n'était pas conforme à celle sur laquelle la mise a été faite, de sorte que si la première du nombre impair des cartes restantes est conforme à cette carte il n'y a jamais de ‘doublet’, mais c'est le joueur qui gagne.
-
voetnoot1)
- En résumé Huygens a donc trouvé dans les quatre cas différents pour les avantages du banquier, respectivement: 1/r N,
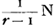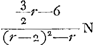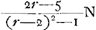 ,  ,  . Or, dans l'article cité de Sauveur (voir la note 3 de la p. 165) celui-ci-donne (sans démonstration) pour ces mêmes avantages, si on les exprime dans la notation de Huygens: 1/rN, ,  ,  .
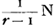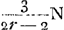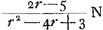On voit donc facilement que les résultats de Huygens et de Sauveur sont identiques; mais la forme sous laquelle Huygens présente le troisième résultat nous semble indiquer que l'article de Sauveur lui était inconnu lorsqu'il composa la présente Pièce.
D'ailleurs Sauveur donne encore d'autres résultats qui se rapportent aux règles plus compliquées qu'il expose dans son article. Parmi ces règles il y a celle de la face, qu'il explique comme il suit: ‘Cependant parce que l'avantage du Banquier seroit trop grand, on l'a diminué en faisant que lorsqu'il gagne à la première main dans laquelle il peut gagner une carte découverte, il face pour lors, c'est à dire qu'il ne prend que les deux tiers de ce qui a esté couché sur cette carte, de sorte qu'il y perd un tiers’.
C'est évidemment à propos de cette règle que Huygens a pris les informations que nous avons reproduites dans la note 1 de la p. 164. Nous y trouvons une preuve de plus que Huygens ne connaissait pas encore l'article de Sauveur, où les questions qu'il pose sont résolues assez clairement.
|
Auteursrecht onbekend
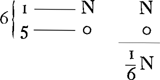
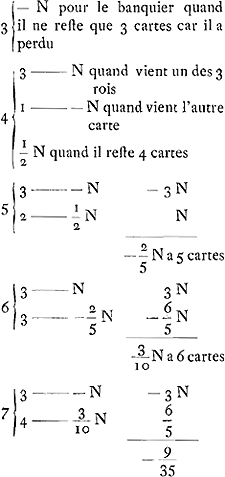
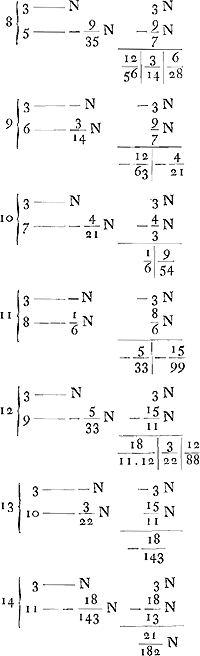
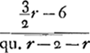
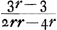desavantage du Banq.
