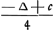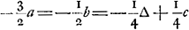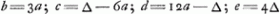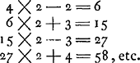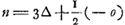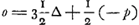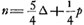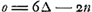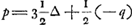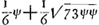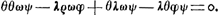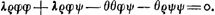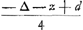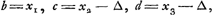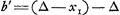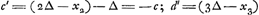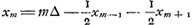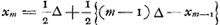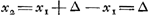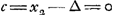|
| |
| |
| |
Appendice VGa naar voetnoot1)
Au traité ‘Van rekeningh in spelen van geluck’.
1665.
Jul. 1665
A speelt tegen B werpende met beurten kruys of munt, op conditie dat die munt werpt ieder reys een ducaet sal in setten, maer die kruys werpt sal alles strijcken dat in geset is, en A sal eerst werpen als noch niets in geset is. En werdt oock verstaen dat het spel niet eer eyndight dan als er iets in geset geweest is, en weder uyt getrockenGa naar voetnoot3).
Traduction:
A joue croix ou pile contre B; les deux joueurs jettent tour à tour à condition que celui qui amène pile mettra chaque fois un ducat, mais qui jette croix prendra tout ce qui est mis; et A jettera le premier, alors qu'on n'a encore rien mis. Et il est entendu que le jeu ne finira pas avant que quelque chose ait été mise, et enlevée.
| |
| |
Zij gestelt dat de geene die moet werpen als van weder sijden noch niets in geset is verliest a, dat is
| laet hij hebben - a die 0 tegen 0 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + b die 0 tegen 1 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + c die 1 tegen 1 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + d die 1 tegen 2 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + e die 2 tegen 2 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + f die 2 tegen 3 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + g die 3 tegen 3 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + h die 3 tegen 4 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + i die 4 tegen 4 heef ingeset en hij selfs moet werpen. |
| laet hij hebben + k die 4 tegen 5 heef ingeset en hij selfs moet werpen. |
(Men soude beter de quaestie voorstellen dat A en B ieder een ducaet souden ingeset hebben. Wanneer de avantagie van A waerd wordt bevonden 1/9 ducaets. als pag. sequ. werd gerekentGa naar voetnoot4).)
dewijl nu den eenen effen soo veel wint als den anderen verliest, soo heeft dan B, die 0 tegen 0 heeft in geset, den andere moetende werpen, soo veel als + a.
Traduction:
Soit supposé que celui qui doit jeter quand rien n'a encore été mis, ni par l'un, ni par l'autre, perd a, c'est à dire:
| soit l'avantage - a |
de celui qui a mis |
0 |
contre |
0 et qui doit jeter. |
| soit l'avantage + b |
- |
0 |
- |
1 et qui doit jeter. |
| soit l'avantage + c |
- |
1 |
- |
1 et qui doit jeter. |
| soit l'avantage + d |
- |
1 |
- |
2 et qui doit jeter. |
| soit l'avantage + e |
- |
2 |
- |
2 et qui doit jeter. |
| soit l'avantage + f |
- |
2 |
- |
3 et qui doit jeter. |
| soit l'avantage + g |
- |
3 |
- |
3 et qui doit jeter. |
| soit l'avantage + h |
- |
3 |
- |
4 et qui doit jeter. |
| soit l'avantage + i |
- |
4 |
- |
4 et qui doit jeter. |
| soit l'avantage + k |
- |
4 |
- |
5 et qui doit jeter. |
(Il vaudrait mieux proposer la question en ajoutant la condition que A et B auraient mis chacun un ducat. Alors on trouvera que l'avantage de A vant 1/9 ducat, comme nous l'avons calculé à la page suivanteGa naar voetnoot4).)
Or, puisque l'un gagne précisément autant que l'autre perd, il s'ensuit que l'avantage de B, qui a mis 0 contre 0, l'autre devant jeter, est égal à + a. Et de même celui
| |
| |
En van gelijcken die 1 tegen 0 heeft in geset en den andere moet werpen, sal hebben - b, om dat die werpt heeft + b, en soo voorts.
die nu eerst werpt als 0 tegen 0 is ingeset, wiens kans werd gesteld - a, indien hij kruijs werpt, soo heeft hij de selve kans die den anderen tegenwoordigh heeft dat is + a; maer indien hij munt werpt soo moet hij 1 tegen 0 in setten, en den anderen sal werpen, dat is, soo heeft hij - b. Soo is dan - a ∞ 1 kans tot + a en 1 kans tot - b. Ergo 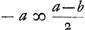 , door het 2. voorstel van onse Rekening in spelen van geluck Ga naar voetnoot1). Van gelijcken kan men licht verstaan dat + b, dat is de kans van die 0 tegen 1 heeft ingeset, en selfs moet werpen, is ∞ 1 kans tot een ducaet te hebben, welck zij genoemt ∆, en 1 kans tot - c, soodat hierom is 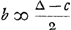 .
Item is c ∞ 1 tot ∆ en 1 tot - d. daerom 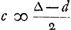
Item is d ∞ 1 tot 2∆ en 1 tot - e. daerom 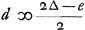
Item is e ∞ 1 tot 2∆ en 1 tot - f. daerom 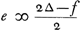
Item f ∞ 1 tot 3∆ en 1 tot - 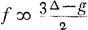
Item g ∞ 1 tot 3∆ en 1 tot - h. daerom 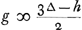
En soo voorts 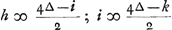
Traduction:
qui a mis 1 contre 0, l'autre devant jeter, aura - b, parce que celui qui jette a + b et ainsi de suite.
Or, quant à celui qui jette le premier lorsqu'il est mis 0 contre 0, dont l'avantage fut posé - a, s'il jette croix il a le même avantage que l'autre a maintenant, c'est-à-dire + a; mais s'il jette pile il doit mettre 1 contre 0, et l'autre jettera, c'est-à-dire il aura - b. Ainsi donc - a est équivalent à une chance d'avoir + a et 1 d'avoir - b. Par conséquent 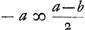 , par la deuxième proposition de notre Calcul dans les jeux de hasardGa naar voetnoot1). De même on peut concevoir aisément que + b, c'est-à-dire l'avantage de celui, qui a mis 0 contre 1 et qui doit jeter lui-même, est égal à 1 chance de recevoir un ducat, que nous répresenterons par ∆, et 1 chance d'avoir - c. On a donc , par la deuxième proposition de notre Calcul dans les jeux de hasardGa naar voetnoot1). De même on peut concevoir aisément que + b, c'est-à-dire l'avantage de celui, qui a mis 0 contre 1 et qui doit jeter lui-même, est égal à 1 chance de recevoir un ducat, que nous répresenterons par ∆, et 1 chance d'avoir - c. On a donc 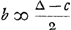 . .
On a de même c ∞ 1 à ∆ et 1 à - d. donc 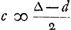
...............................
...............................
Et ainsi de suite 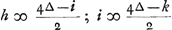
| |
| |
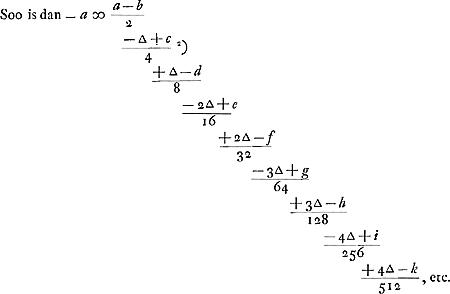
Ga naar voetnoot2)
waeruyt blijckt dat
- a∞ 1/2 a - 1/4 ∆ + 1/8 ∆ - 2/16 ∆ + 2/32 ∆ - 3/64 ∆ + 3/128 ∆ - 4/256 ∆ + 4/512 ∆ - 1/512 k.
Traduction:
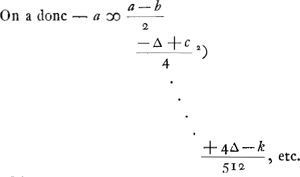
Ga naar voetnoot2) d'où il s'ensuit:
- a∞ 1/2 a - 1/4 ∆ + 1/8 ∆ - 2/16 ∆ + 2/32 ∆ - 3/64 ∆ + 3/128 ∆ - 4/256 ∆ + 4/512 ∆ - 1/512 k.
| |
| |
maer dese laetste quantiteit welcke hier is 1/512 k, werd oneijndelijk kleijn indien in infinitum de rye continueert want dewyl men noch soo veel ducaten niet en verliest als men ingeset heeft soo is b minder als een ducaet of ∆ en d minder als 2∆ en f minder als 3∆ en h minder als 4∆ en k minder als 5∆ maer den denominator van 't gebroken gaet voort in de dobbele proportie 2, 4, 8, 16, etc. Ergo moet noodsaekelijk, als geseght is, de laetste quantiteyt, sijnde hier 1/512 k, eijndelijck soo kleijn werden als men wil, en daerom gerekent werden als 0.
Ergo - a ∞ 1/2 a - 1/4 ∆ + 1/8 ∆ - 2/16 ∆ + 2/32 ∆ - 3/64 ∆ + 3/128 ∆ - 4/256 ∆ + + 4/512 ∆ - 5/1024 ∆ etc. in infin.
Voorts siet men hier dat de quantiteyten daer ∆ in is en + voorstaet tot die daer - voorstaet sijn als 1 tot 2.
Maer de geene daer - voorstaet kan haar somme doch aldus geschreven werden
Traduction:
mais cette dernière quantité, représentée ici par 1/512 k, devient infiniment petite si la suite continue indéfiniment, car, puisqu'on ne perd pas encore autant de ducats qu'on a mis, il suit que b est moins qu'un ducat ou ∆, et d moins que 2∆, et f moins que 3∆, et h moins que 4∆, et k moins que 5∆, mais le dénominateur de la fraction monte dans la proportion double 2, 4, 8, 16, etc. Par suite il est nécessaire, comme il a été dit, que la dernière quantité, étant ici 1/512 k, devienne finalement aussi petite qu'on le veut: elle doit donc être comptée pour zéro.
On a donc - a ∞ 1/2 a - 1/4 ∆ + 1/8 ∆ - 2/16 ∆ + 2/32 ∆ - 3/64 ∆ + 3/128 ∆ - 4/256 ∆ + + 4/512 ∆ - 5/1024 ∆ etc. jusqu'à l'infini.
Ensuite on voit ici que les quantités où ∆ entre et qui sont précédées de + sont à celles précédées de - comme 1 est à 2.
Mais, quant à celles qui sont précédées de -, leur somme peut aussi être écrite comme il suit:
| |
| |
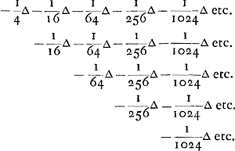
want dit alles te samen is ∞ - 1/4 ∆ - 2/16 ∆ - 3/64 ∆ - 4/256 ∆ - 5/1024 ∆ etc.
In de bovenste rije nu; dewijl ieder volgende quantiteyt is 1/4 van de voor gaende, soo sijn se alle te samen 4/3 van de voorste, dat is van - 1/4 ∆ soo dat se maecken - 1/3 ∆.
Van gelijcken is de tweede rye ∞ 4/3 van haer voorste quantiteyt - 1/16 ∆. En soo voorts ieder rye ∞ 4/3 van sijn voorste quantiteyt soo sijn dan alle de ryen te
Traduction:
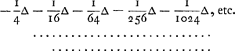
car tout cela ensemble est égal à - 1/4 ∆ - 2/16 ∆ - 3/64 ∆ - 4/256 ∆ - 5/1024 ∆, etc.
Or, dans la suite supérieure, puisque toute quantité qui suit est 1/4 de celle qui la précède, ces quantités seront toutes ensemble ∞ 4/3 de la première, c'est-à-dire de - 1/4 ∆. Leur somme sera donc - 1/3 ∆.
De même la deuxième suite est ∞ 4/3 de sa première quantité - 1/16 ∆. Et ainsi partout, chaque suite étant ∞ 4/3 de sa première quantité. Il en résulte que toutes les suites
| |
| |
samen ∞ 4/3 van de schuijnse rije die bestaet uyt alle de voorste quantiteyten, en welcke deselve is met de bovenste rije. Maer dese was ∞ - 1/3 ∆. Ergo al de ryen te samen ∞ 4/3 van - 1/3 ∆, dat is, gelijck - 4/9 ∆. Soo sijn dan de quantiteyten van de voorgaende aequatie daer ∆ in komt en - voor staet ∞ - 4/9 ∆. maer dese waren tot die daer + voor staet als 2 tot 1. Ergo die met + geteykent sijn doen te samen + 2/9 ∆. Welcke van die met - afgetrocken resteert - 2/9 ∆. Soo dat de aequatie is
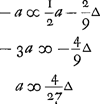
soo verliest dan A die eerst uitwerpt 4/27 van een ducaet Ga naar voetnoot1).
Traduction:
ensemble sont égales à 4/3 de la suite oblique qui est formée par toutes les premières quantités et qui est identique à la suite supérieure. Mais cette dernière est égale à - 1/3 ∆; par conséquent toutes les suites ensemble sont égales à 4/3 de - 1/3 ∆, ce qui fait - 4/9 ∆. Ainsi donc les quantités de l'équation précédente, où ∆ entre et qui sont précédées de -, ont pour somme - 4/9 ∆; mais celles-ci étaient à celles qui sont précédées de + comme 2 est à 1. Il s'ensuit que celles précédées par + sont ensemble + 2/9 ∆. Si on les soustrait de celles affectées du signe -, on obtient - 2/9 ∆.
On a donc l'équation 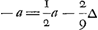 , ou bien - 3a = - 4/9 ∆, ou enfin a = 4/27 ∆, et il s'ensuit que A, qui jette le premier, perd 4/27 d'un ducatGa naar voetnoot1). , ou bien - 3a = - 4/9 ∆, ou enfin a = 4/27 ∆, et il s'ensuit que A, qui jette le premier, perd 4/27 d'un ducatGa naar voetnoot1).
| |
| |
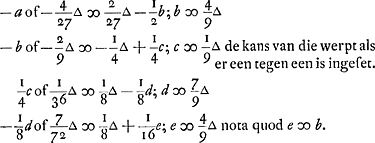
Traduction:
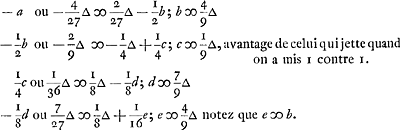
| |
| |
| |
Naer dese Rekening is oock licht te verstaen die van de questie pag. 1 voorgesteltGa naar voetnoot2) doch tot meerder verklaring sal dienen het volgende: als er staet 1. - b en 2. + kGa naar voetnoot3), dat is kortelijck geseght 1 kans tot -b en 2 kanssen tot + k. En soo in al d'andere. δ in dese rekening beteykent een ducaet of 't geen ieder reijse werdt ingeset.
Traduction:
À l'aide du calcul qui précède on comprendra aisément aussi le calcul de la question posée à la p. 1Ga naar voetnoot2). Mais ce qui suit servira à expliquer plus en détail ce dernier calcul: lorsque nous écrivons ‘1. - b et 2. + k’Ga naar voetnoot3), cela exprime brièvement qu'on a ‘une chance d'avoir - b et deux chances d'avoir + k’. Et ainsi partout. Dans ce calcul δ représente un ducat, ou bien ce qui se met chaque fois.
| |
| |
De rekening vervolght pag. 2 en 3Ga naar voetnoot4). In 't begin van pag. 2 blijckt dat a is ∞ 2/9 a en daerenboven al de quantiteijten der 2 neergaende ryen daar δ in komtGa naar voetnoot5). Pag. 3 komt eerst het vervolg van de eerste suppositien pag. 1 begost en daer aldaar geen plaats toe en wasGa naar voetnoot6). Voorts werden pag. 3 de quantiteijten der rije B pag. 2 daer δ in komt met + daer voor, opgesomt, volgens het theorema boven aen op deze pag. 3 gesteltGa naar voetnoot7). Ende uijt de aengemerckte proportie deser quantiteijten tot die met - geteijckent sijn in de selve rije B, en tot die met - en + staen in d'andere rije A, werden dese haere sommen oock gevonden. Waeruijt dan in plaats van de aequatie pag. 2 komt dese 2/9 a - 23/49 δ ∞ a en eyndelijck - a ∞ 207/343 δ. dat is te seggen dat - a, 't welck was 't geen hadde J. die eerst werpt als noch niets was in geset, is 207/343 δ. soo dat al hoewel dit met - gestelt wierdt als of J. verloor, soo vind men nochtans dat hij wint 207/343 van een ducaet.
Traduction:
Le calcul est continué p. 2 et 3Ga naar voetnoot4). Au commencement de la p. 2 on trouve a ∞ 2/9 a augmenté de toutes les quantités des deux suites descendantes où entre δGa naar voetnoot5). La p. 3 contient en premier lieu la continuation des suppositions préalables qui commencent à la p. 1 et pour lesquelles il n'y avait pas assez de place à cette pageGa naar voetnoot6). Ensuite les quantités de la suite B de la p. 2, où entre δ et qui sont affectées du signe +, sont additionnées à la p. 3 à l'aide du théorème qu'on trouve en haut de cette pageGa naar voetnoot7). Or, en remarquant la proportion de ces quantités à celles marqués - de la même suite B et à celles affectées du signe - et du signe + de l'autre suite A, on détermine aussi les sommes de ces dernières quantités. Il en résulte qu'on peut remplacer l'équation de la p. 2 par: 2/9 a - 23/49 δ ∞ a et enfin par - a ∞ 207/343 δ. Ce qui veut dire que - a, c'est-à-dire l'avantage de J. qui jette le premier quand il n'y a encore rien à l'enjeu, est égal à 207/343 δ. Ainsi, quoique cet avantage fût supposé être négatif, c'est-à-dire que ce serait J. qui perdrait, on trouve
néanmoins qu'il gagne 207/343 d'un ducat.
| |
| |
| |
Pag. 10 Ga naar voetnoot2) werdt het getal der schijven van B gestelt ∞ ω en daer van φ witte en ψ swarte; zoo dat φ + ψ ∞ ω. Dese questie is eerst volgens het voorgestelde Ga naar voetnoot3) berekent op pag. 10. 11. 12. Ga naar voetnoot4) alwaer de proportie van φ tot ψ gedetermineert werdt door dese aequatie 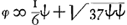 Ga naar voetnoot5) Ga naar voetnoot5) soo dat se in geen getalen kan gegeven werden Ga naar voetnoot6). In de aequatie die begint boven aen pag. 11 is a gelijck aan al de quantiteijten der neergaende 2 rijen daer ∆ in komt en daerenboven aan 2 φa/3 ω
staende boven aen de rije geteykent met B Ga naar voetnoot7). Maer om dat men
Traduction:
À la p. 10Ga naar voetnoot2) le nombre des jetons de B fut posé ∞ ω, dont ϕ blancs et ψ noirs; de sorte que ϕ + ψ ∞ ω. Cette question est résolue d'abord aux p. 10. 11. 12Ga naar voetnoot4) suivant ce qui fut proposéGa naar voetnoot4). La proportion de ϕ à ψ y est déterminée par l'équation 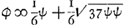 Ga naar voetnoot5), de sorte qu'elle ne peut pas être définie par des nombresGa naar voetnoot6). Dans l'équation qui commence en haut de la p. 11, a est égal à
toutes les quantités des deux suites descendantes, où entre ∆, augmentées de l'expression 2ϕa/3ω qu'on trouve en haut de la suite marquée BGa naar voetnoot7). Mais parce qu'on désire que les chances des deux joueurs Ga naar voetnoot5), de sorte qu'elle ne peut pas être définie par des nombresGa naar voetnoot6). Dans l'équation qui commence en haut de la p. 11, a est égal à
toutes les quantités des deux suites descendantes, où entre ∆, augmentées de l'expression 2ϕa/3ω qu'on trouve en haut de la suite marquée BGa naar voetnoot7). Mais parce qu'on désire que les chances des deux joueurs
| |
| |
de kanssen der 2 speelders gelijckwaerdigh begeert, soo is dan a ∞ 0. En daerom oock dese voornoemde quantiteijt 2φa/3ω ∞ 0; daerom dan deze in de aequatie in fine pag. 11Ga naar voetnoot8) voor 0 gehouden wordt. Ende is te weten dat in dese aequatie alleen gestelt werden de sommen der quantiteijten daer ∆ in komt van beijde de neergaende rijen A en B. Ende dewijl was a ∞ - 1/3 b + 2/3 kGa naar voetnoot9), en a moet sijn ∞ 0, soo moet dan oock - 1/3 b + 2/3 k sijn ∞ 0, of 1/3 b ∞ 2/3 k. daerom dan de plussen en minussen der quantiteijten met ∆ der rije A, nae dat haere teijckens in contrarie verandert sijn, moeten gelijck sijn aen de plussen en minussen der quantiteijten ∆ der rije B. gelijck gestelt werd in de aequatie in fine pag. 11. welcke aequatie vervolght pag. 12Ga naar voetnoot10).
Op de selfde pag. 10 en 11 werd begonnen de Rekening van de voorgaende questie in 't generael. soo dat in plaets van het getal der schijven daer A uijt treckt te weten 3 werdt gestelt ρ, en het getal der witte schijven 2 ∞ θ, en der swarte 1 ∞ λ. Soo dat θ + λ ∞ ρ. En tot dese rekening behooren de quantiteijten die
Traduction:
soient égales, on a donc a ∞ 0. Et, par suite, on a aussi 2ϕa/3ω ∞ 0. C'est pourquoi cette expression est supposée égale à zéro dans l'équation qu'on trouve au bas de la p. 11Ga naar voetnoot8). Et l'on remarquera que cette équation contient seulement les sommes des quantités, où entre ∆, des suites descendantes A et B. Et parce qu'on avait a ∞ - 1/3 b + 2/3 kGa naar voetnoot9) et que a doit être ∞ 0, il s'ensuit qu'on doit avoir aussi - 1/3 b + 2/3 k ∞ 0, ou bien 1/3 b ∞ 2/3 k. Par conséquent, tous les + et les - des quantités, contenant ∆, de la suite A doivent être égaux après changement de signe aux + et aux - des quantités, contenant ∆, de la suite B, comme nous l'avons posé dans l'équation au bas de la p. 11, laquelle équation est reprise à la p. 12Ga naar voetnoot10).
Aux mêmes pag. 10 et 11 on a commencé le Calcul de la question générale, d'après laquelle le nombre des jetons, à savoir 3, dont A tire le sien, fut posé ∞ ρ, et le nombre des jetons blancs (étant 2) ∞ θ, et des noirs (étant 1) ∞ λ; de sorte que θ + λ ∞ ρ. Et à ce calcul se rapportent les quantités que nous avons entourées de
| |
| |
pag. 10 en 11 met ringen omgetrocken sijn Ga naar voetnoot1). En werd vervolght pag. 14 en 15. alwaer den Regel totte generale solutie van dese questie, te weten om de kansen gelijckwaerdigh te maecken gevonden werdt, namentlijck 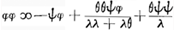 Ga naar voetnoot2) Ga naar voetnoot2),
Voorts heb ick oock in 't generael willen rekenenGa naar voetnoot3), gegeven sijnde het getal der witte en swarte schijven van ieder der 2 speelders, ceteris positis ut prius, hoe haere kanssen staen dat is hoeveel A die eerst werpt verliest of wint. Welcke rekening uyt de voorgaende aequatie pag. 14Ga naar voetnoot4), oock licht gededuceert werdt, moetende nochtans hier soo gevonden werden de sommen der quantiteijten daer ∆ in komt met + of - van een der neergaende rijen A of B. Gelijck in dese casus ick gerekent hebbe de plussen der rije B, welcke rekeningh begint pag. 15 in fin.Ga naar voetnoot5) en vervolght pag. 16. alwaer dese somme gevonden sijnde door het theorema boven aen pag. 3Ga naar voetnoot6); soo werden voorts daerdoor oock de plussen en minussen der andere quantiteijten met ∆ der rijen A en B gevonden, dewijl haere
Traduction:
de cercles aux p. 10 et 11Ga naar voetnoot1). Et le calcul est continué aux p. 14 et 15, où la Règle est déduite qui donne la solution générale de cette question, à savoir: de faire en sorte que les chances deviennent égales, c'est-à-dire 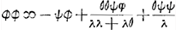 Ga naar voetnoot2). Ga naar voetnoot2).
Ensuite j'ai voulu calculer aussiGa naar voetnoot3), pour le cas général, quelles sont les chances des deux joueurs quand le nombre des jetons blancs et noirs de chacun des 2 joueurs est donné, ceteris positis ut prius, c'est-à-dire: quel est l'avantage ou le désavantage de A qui jette le premier. Ce calcul peut facilement être déduit de l'équation précédente de la p. 14Ga naar voetnoot4), mais on doit néanmoins chercher alors, pour une des suites descendantes A ou B, la somme des quantités où entre ∆ qui sont affectées du signe + ou du signe -. Ainsi j'ai déterminé dans le cas présent les + de la suite B. Ce calcul commence vers la fin de la p. 15Ga naar voetnoot5) et continue à la p. 16, où cette somme est trouvée par le théorème qu'on rencontre en haut de la p. 3Ga naar voetnoot6); on connaît alors aussi les sommes des + et des - des autres quantités des suites A et B, puisque les proportions qu'elles ont les unes aux autres sont connues et indiquées au côté droit
| |
| |
proportiën onder malkander bekent sijn pag. 14. aen de rechter handenGa naar voetnoot7). Waer uijt dan voortkomt den regel pag. 16 in fineGa naar voetnoot8). alwaer de quantiteijt - θφa/ρω gehaelt is uyt de aequatie pag. 14 init.Ga naar voetnoot9) want dese quantiteijt hier nu niet en is ℞ 0 dewijl a geen 0 en is. De aequatie die desen Regel in fin. pag. 16 begrijptGa naar voetnoot8) soude misschien konnen gedivideert werden als men overal voor ρ stelde θ + λ en voor ω, φ + ψ, welcke volgens 't bovengestelde haer gelijck sijnGa naar voetnoot10).
Traduction:
de la p. 14Ga naar voetnoot7). D'où l'on déduit la règle de la p. 16 vers la finGa naar voetnoot8), où la quantité - θϕa/ρω provient de l'équation en haut de la p. 14Ga naar voetnoot9). En effet, ici cette quantité n'est plus égale à zéro, puisqu'il n'en est pas ainsi pour a. Peut-être l'équation qui résume cette règle vers la fin de la p. 16Ga naar voetnoot8), pourrait-elle être divisée, si l'on y remplaçait partout ρ par θ + λ et ω par ϕ + y; quantités qui leur sont égales d'après ce que nous avons posé plus hautGa naar voetnoot10).
| |
| |
| |
In de questie van kruijs of munt pag. 21.Ga naar voetnoot2) wil men weten hoe veel dat ieder speelder van eersten aen soude moeten in setten, (ieder even veel) om te maecken dat A die voorwerpt soo goede kans soude hebben als B. komt ieder 2/3 van een ducaetGa naar voetnoot3).
Sit z quod unusquisque deponit ab initio.
A die eerst werpt heeft 1 kans tot z, en 1 kans om in te zetten ∆Ga naar voetnoot4) behalven z, en den anderen te laeten werpen 't welck hem waert zij - c. Ergo aen B is het waert + c. En sal wesen c ∞ 1 kans tot ∆ + z en 1 kans tot in te setten ∆ + z tegen ∆ + z en laten den andere werpen 't welck aen B waert sij - d. En soo voort.
Traduction:
Dans la question de croix ou pile p. 21Ga naar voetnoot2) on veut savoir combien chaque joueur devrait mettre au début (chacun la même somme), afin que A, qui jette le premier, eût une chance aussi bonne que B. Il vient: chacun 2/3 d'un ducatGa naar voetnoot3).
Soit z ce que chacun met dès le commencement.
A, qui jette le premier, a 1 chance d'obtenir z, et 1 chance de mettre ∆Ga naar voetnoot4) en plus de sa mise z et de laisser jeter l'autre; ce qui lui vaille - c. Par conséquent, cela vaut c à B. Et on aura c ∞ 1 chance d'obtenir ∆ + z et 1 chance de mettre ∆ + z contre ∆ + z et de laisser jeter l'autre; ce qui vaille - d à B. Et ainsi de suite:
| |
| |
| |
| |
- a ∞ 1/2 z - 1/6 z - 2/9 ∆ ∞ 0Ga naar voetnoot1) nam - a volumus esse ∞ 0 ut sors utriusqu aequalis sit.
z ∞ 2/3 ∆
| |
15 Jul. 1665.
Pag. 19 en 20Ga naar voetnoot3) was getenteert de solutie van dese questie die alhier sal berekent werden, sijnde als volght.
A en B werpen met beurten kruys of munt, op conditie dat die munt werpt een ducaet daer voor ieder reijse sal in setten, maer die kruijs werpt sal ieder reijse daer voor een ducaet trecken als er iets in geset is. En A sal eerst werpen als noch niets is in geset en het spel niet uijt sijn eer er iets in geset is, en men sal soo lang spelen tot alles weder uijtgetrocken is. De vrage is hoe veel A hierdoor verliest. facit 1/6 van een ducaet.
Traduction:
- a ∞ 1/2 z - 1/6 z - 2/9 ∆ ∞ 0Ga naar voetnoot1) car nous supposons que - a soit zéro, afin que la chance soit égale pour les deux joueurs.
z ∞ 2/3 ∆
| |
15 juillet 1665.
Aux p. 19 et 20Ga naar voetnoot3) nous avons tenté la solution de la question suivante, qui sera résolue ici:
A et B jettent à tour de rôle croix ou pile, à condition que celui qui jette pile mettra chaque fois un ducat à l'enjeu, mais celui qui jette croix recevra chaque fois un ducat si quelque chose a été mis. Et A jettera le premier quand il n'y a encore rien à l'enjeu, et le jeu ne finira pas avant que quelque chose ait été mis, et l'on jouera jusqu'à ce que tout a été enlevé. On demande quel est le désavantage de A. facit 1/6 d'un ducat.
| |
| |
Ergo die niet en werpt heeft dan + a, want dat d'een verliest wint den anderen.
zij ∆ ∞ een ducaet.
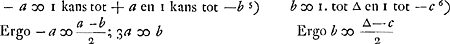
Ga naar voetnoot5)Ga naar voetnoot6)
Traduction:
Parsuite, celui qui ne jette pas a l'avantage + a car ce que l'un gagne, l'autre le perd.
Soit ∆ ∞ un ducat.
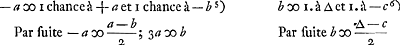
Ga naar voetnoot5)Ga naar voetnoot6)
| |
| |
Voorts is c ∞ een kans om te hebben ∆ - b en 1 tot - d, waer van de reden is dese, dat die kruijs werpt als er 1 tegen 1 staet, kan bedacht werden te trekken de ∆ ofte ducaet die den anderen heeft ingeset, en sijne eijghene te laten staen, te weten 1 tegen 0, en den anderen moet werpen, 't welck hem die niet en werpt - b weerdt is. soo heeft hij dan 1 kans tot ∆ - b, en 1 tot - d dat is om 2 tegen 1 in te setten en den anderen te laten werpen daerom dan is 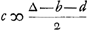 .
Van gelijcken is d ∞ 1 tot ∆ - c en 1 tot - e; daerom 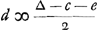

Ga naar voetnoot1)
Traduction:
Ensuite c est égale à une chance d'avoir ∆ - b et 1 d'avoir - d, pour la raison que celui qui jette croix quand il y 1 contre 1 à l'enjeu peut être estimé avoir gagné le ducat que l'autre a mis et laisser son propre ducat à l'enjeu: ce qui est 1 contre 0, l'autre devant jeter, et cela vaut - b à celui qui ne doit pas jeter; de sorte qu'il a donc 1 chance d'avoir ∆ - b, et 1 d'avoir - d, c'est-à-dire: de mettre 2 contre 1 et de laisser jeter l'autre. C'est pourquoi 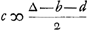 . .
De même, d ∞ 1 à ∆ - c et 1 à - e; ainsi 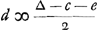 et de la même façon on trouve ensuiteGa naar voetnoot1) et de la même façon on trouve ensuiteGa naar voetnoot1)
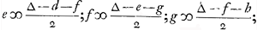
| |
| |
| |
| |
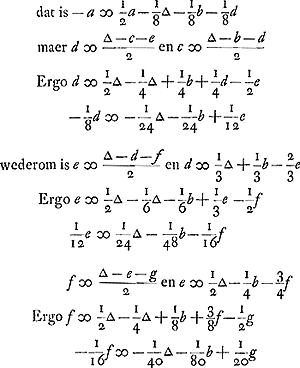
Traduction:
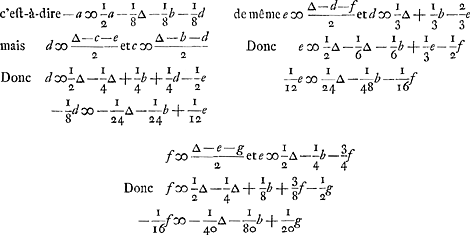
| |
| |
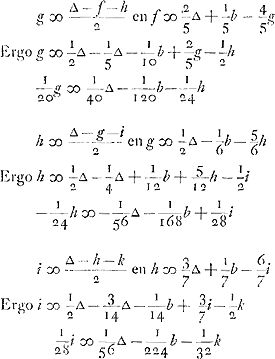
Traduction.
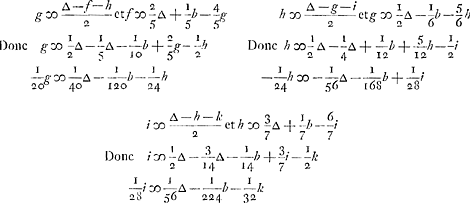
| |
| |
| |
| |
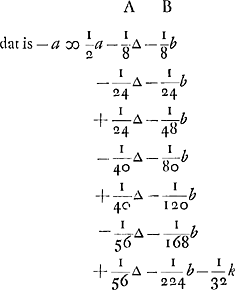
De laetste quantiteijt, als hier 1/32 k, wordt infinitè kleijn, dewijl kGa naar voetnoot2) niet oneijndigh groot en werdt, om dat als den eenen maer een meer als den anderen
Traduction:
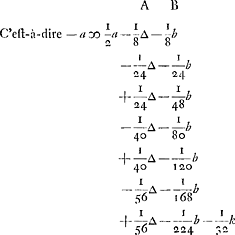
La dernière quantité, ici 1/32 k, devient infiniment petite, puisque kGa naar voetnoot2) ne devient pas infiniment grand, parce que si l'un n'a mis qu'un seul ducat de plus que
| |
| |
ingeset heeft, soo siet men wel dat hij in dit spel niet boven 1 of 2 en verliest, maer den divisor, (sijnde hier 32) werd oneindigh groot wassende met 4. Soo dat dan de laetste quantiteijt, (hier 1/32 k,) voor 0 moet gerekent werden, als men verstaet in infinitum voort gegaen te sijn, ende dienvolgens dat - a is ∞ 1/2 a - de rije onder A - de rije onder B.
maer in de rije onder A, sijn al de + gelijck al de -, behalve de bovenste - 1/8 ∆. Soo is dan - a ∞ 1/2 a - 1/8 ∆ - de rije onder B in infinitum vervolght.
maer de rije onder B is 1/8 van dese rije - 1/1 b - 1/3 b - 1/6 b - 1/10 b - 1/15 b - 1/21 b - 1/28 b &c. En dese rije is ∞ - 2b gelijck hier nae gethoont sal werden (pag. 28, 29, 30Ga naar voetnoot1)), sijnde de divisores van dese gebrokens de triangulare getallen van
Traduction:
l'autre, il est assez évident que dans ce jeu il ne perd pas plus que 1 ou 2 ducats, mais le diviseur (étant ici 32) devient infiniment grand, augmentant chaque fois de 4. Par conséquent la dernière quantité (ici 1/32 k) doit être comptée pour 0, si l'on suppose qu'on a continué le calcul jusqu'à l'infini. On trouve donc - a ∞ 1/2 a - la suite sous A - la suite sous B.
Mais dans la suite sous A tous les + sont égaux à tous les -, à l'exception du premier terme - 1/8 ∆. On a donc - a ∞ 1/2 a - 1/8 ∆ - la suite sous B qu'on doit continuer jusqu'à l'infini.
Mais la suite sous B est 1/8 de la suite: - 1/1 b - 1/3 b - 1/6 b - 1/10 b - 1/15 b - 1/21 b - 1/28 b &c. Et cette suite est égale à - 2b comme nous le montrerons plus bas (pag. 28, 29, 30Ga naar voetnoot1)), les diviseurs de ces fractions étant les nombres triangulaires à com-
| |
| |
vooren af. En 1/8 van - 2 b is ∞ - 1/4 b. Soo is dan
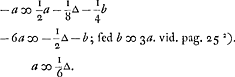
Ga naar voetnoot2)
Soo verliest dan A die eerst werpt 1/6 van een ducaet.
Sijnde dan a ∞ 1/6 ∆ en b ∞ 3 a; b ∞ 1/2 ∆ sed 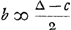 . vid. pag. 25 Ga naar voetnoot2).
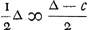 ; ∆ ∞ ∆ - c, c ∞ 0, soo dat als er 1 tegen 1 instaet de kansen gelijck sijn. sed 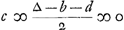 ; ∆ ∞ b + d, en b ∞ 1/2 ∆; 1/2 ∆ ∞ d, soo is d ∞ b dat is dese kanssen even goedt, te weten die van 0 tegen 1 of van 1 tegen 2 ingeset te hebben en te moeten werpen.
Traduction:
mencer par le premier. Et 1/8 de - 2b est - 1/4 b. On a donc - a ∞ 1/2 a - 1/8 ∆ - 1/4 b; - 6a ∞ - 1/2 ∆ - b; mais b ∞ 3a. vid. pag. 25Ga naar voetnoot2); a ∞ 1/6 ∆.
A, qui jette le premier, perd donc 1/6 d'un ducat.
On a donc a ∞ 1/6 ∆ et b ∞ 3a; b ∞ 1/2 ∆, mais 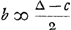 . vid. pag. 25Ga naar voetnoot2). . vid. pag. 25Ga naar voetnoot2).
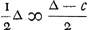 ; ∆ ∞ ∆ c, c ∞ 0; ainsi, si l'on a mis 1 contre 1 les chances sont égales. Mais ; ∆ ∞ ∆ c, c ∞ 0; ainsi, si l'on a mis 1 contre 1 les chances sont égales. Mais 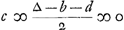 ; ∆ ∞ b + d, et b ∞ 1/2 ∆; 1/2 ∆ ∞d, par suite d ∞ b, c'est-à-dire: ces chances sont égales; savoir: celle qu'on a lorsqu' on a mis 0 contre 1 ou 1 contre 2 et qu'on doit jeter. ; ∆ ∞ b + d, et b ∞ 1/2 ∆; 1/2 ∆ ∞d, par suite d ∞ b, c'est-à-dire: ces chances sont égales; savoir: celle qu'on a lorsqu' on a mis 0 contre 1 ou 1 contre 2 et qu'on doit jeter.
| |
| |
sed 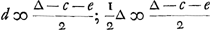 , sed c ∞ 0; 1/2 ∆ ∞ 1/2 ∆ - 1/2 e, e ∞ 0; soo dat als er 2 tegen 2 in staet de kanssen wederom gelijck sijn.
sed 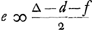 ; Ergo 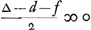 ; Ergo ∆ ∞ d + f sed d ∞ 1/2 ∆; 1/2 ∆ ∞ f. Ergo f ∞ d ∞ b.
En soo konnen voorts oock d'andere kanssen gevonden werden sijnde overhands ∞ 0 en gelijck 1/2 ∆Ga naar voetnoot1).
Men moest sien of men in dese questie door korter wegh tot seecker besluit zoude konnen geraecken, 't welck soude sijn indien men besluiten konde dat als er 1 tegen 1 ingeset is de kansen gelijck sijnGa naar voetnoot2). Siet pag. praecedGa naar voetnoot3).
Traduction:
Mais 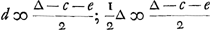 ; mais c ∞ 0; 1/2 ∆ ∞ 1/2 ∆ - 1/2 e, e ∞ 0; de sorte que s'il y a 2 contre 2 à l'enjeu les chances sont de nouveau égales. ; mais c ∞ 0; 1/2 ∆ ∞ 1/2 ∆ - 1/2 e, e ∞ 0; de sorte que s'il y a 2 contre 2 à l'enjeu les chances sont de nouveau égales.
Mais 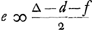 ; par suite ; par suite 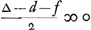 ; donc ∆ ∞ d + f, mais d ∞ 1/2 ∆ 1/2 ∆ ∞ f. Donc f ∞ d ∞ b. ; donc ∆ ∞ d + f, mais d ∞ 1/2 ∆ 1/2 ∆ ∞ f. Donc f ∞ d ∞ b.
Et l'on peut trouver ensuite les autres chances de la même manière. Elles sont alternativement ∞ 0 et égales à 1/2∆Ga naar voetnoot1).
Il faudrait examiner si dans cette question on ne pourrait pas arriver à un résultat certain par une voie plus courte. Cela serait ainsi si l'on pouvait conclure que les chances sont égales quand on a mis 1 contre 1Ga naar voetnoot2). Voir la page précédenteGa naar voetnoot3).
| |
| |
De kanssen van 2 of meer speelders sijn gelijck ofte evenwaerdich, als het spel soodanigh is dat, even geluckigh spelende tot het eijnde van 't spel, niemandt winnen kan noch verliesen: Ende dat een selfde exces van geluck aen d'een of d'ander evenveel gewin of avantage toebrengen soude.
Hier uijt volght dat als in 't spel daer van hier gehandelt werdt, 1 tegen 1 ingeset is, (want als A kruijs werpt en B mede, soo treckt elk een en het spel is uijt Ga naar voetnoot4)) of 2 tegen 2, of 3 tegen 3, &c. dat dan de kanssen van de speelders A en B gelijck sijn Ga naar voetnoot5). Nu als 0 tegen 0 ingeset is, en A moet eerst spelen, soo is sijn verlies gestelt te zijn 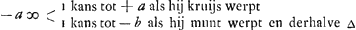 moet insetten
maar 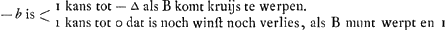 tegen 1 moet insetten.
Traduction:
Les chances de 2 ou de plusieurs joueurs sont égales ou équivalentes si le jeu est tel que lorsqu'on joue jusqu'à la fin avec un succès égal personne ne gagne ni ne perd: Et qu'un même excès de bonne chance apporte autant de gain ou d'avantage à l'un qu'il en apporte à l'autre.
Il en résulte que si, dans le jeu dont nous traitons ici, on a mis 1 contre 1 (car si A jette croix et B de même, chacun prend un ducat et le jeu est finiGa naar voetnoot4)) ou 2 contre 2, ou 3 contre 3, etc., qu'alors les chances des joueurs A et B sont égalesGa naar voetnoot5). Or, si l'on a mis 0 contre 0 et que A doit jouer le premier, nous avons posé pour sa perte: 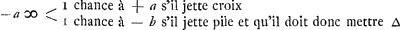 ; ;
mais 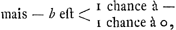 1 contre 1. 1 contre 1.
| |
| |
Soo is - b ∞ - 1/2 ∆. Ergo 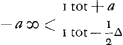 . Ergo 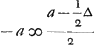 . Ergo 3 a ∞ ∞ 1/2 ∆. En a ∞ 1/6 ∆. Even als in d'andere solutie.
| |
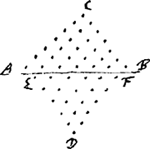
1. Om den triangel van een gegeven getal te vinden soo addeert men het getal tot sijn quadraet, en de helft der somme is den gesochten triangel twelck uijt dese figuur blijckt, want als men tot het getal ACBD, sijnde het quadraet des getals AB, noch eens bij doet het getal der rije AB, soo heeft men 2 mael het getal des triangels ACB, daerom de helft der voorzegde somme moet wesen gelijck den triangel ACB, welck is den triangel des getals AB. Sijnde dan x de sijde soo is den triangel 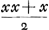 .
Traduction:
Donc - b ∞ - 1/2 ∆. Par suite 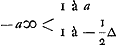 . Donc . Donc 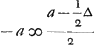 . Donc 3a 1/2 ∆. Et a ∞ 1/6 ∆. Comme dans l'autre solution. . Donc 3a 1/2 ∆. Et a ∞ 1/6 ∆. Comme dans l'autre solution.
| |
1. Pour trouver le triangle d'un nombre donné on ajoute ce nombre à son carré; la moitié de cette somme est le triangle cherché ainsi qu'il résulte de la figure à côté, car si l'on ajoute au nombre ACBD, c'est-à-dire au carré du nombre AB, encore une fois le nombre de la ligne AB, on a deux fois le nombre du triangle ACB. Par suite, la moitié de la somme prémentionnée doit être égale au triangle ACB qui est le triangle du nombre AB. Soit donc x le côté, alors le triangle est 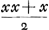 . .
| |
| |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 1/1 |
1/3 |
1/6 |
1/10 |
1/15 |
1/21 |
1/28 |
1/36 |
1/45 |
1/55 |
1/66 |
1/78 |
1/91 |
1/105 |
1/120 |
2. dese rije van gebroocken getallen sijnde soo danigh dat al de tellers sijn 1, en de noemers de achtereenvolgende triangulen van de getallen daer boven geschreven beginnende van 1 en met 1 opgaende: indien men eenighe 2 achtereenvolgende deser gebroockens te samen addeert, nemende tot voorste soo een wiens noemer is den triangel van een even getal; soo sal de somme gelijck sijn aen de helft van het gebroocken deser rije wiens noemer den triangel is van de helft der sijde welckers triangel was den noemer van het voorste der 2 geaddeerde gebroockens. bij exempel adderende de gebroockens deser rije 1/55 en 1/66, soo sal haer somme sijn 1/30, dat is de helft des gebroockens 1/15, wiens noemer 15 den triangel is van 5, sijnde de helft van 10, wiens triangel 55 is den noemer des eersten der 2 gebroockens. want laet de sijde des noemers van 't eerste gebroken sijn ∞ x, soo is sijn triangel, dat is, den noemer des eersten gebroockens,
Traduction:
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| 1/1 |
1/3 |
1/6 |
1/10 |
1/15 |
1/21 |
1/28 |
1/36 |
1/45 |
1/55 |
1/66 |
1/78 |
1/91 |
1/105 |
1/120 |
2. Cette suite de nombres fractionnaires est telle que tous les numérateurs sont égaux à l'unité, et que les dénominateurs sont les nombres trangulaires successifs des nombres qu'on a écrit au-dessus, en commençant par 1 et augmentant chaque fois de 1: si de ces fractions on en additionne deux successives, dont la première est telle que le dénominateur est le triangle d'un nombre pair, alors la somme sera égale à la moitié d'une fraction de la même suite, dont le dénominateur est le triangle de la moitié du nombre duquel le triangle constitue le dénominateur de la première des deux fractions qu'on a additionnées. Par exemple, en additionnant les fractions 1/55 et 1/66, appartenant à cette suite, leur somme sera 1/30, c'est-à-dire la moitié de la fraction 1/15, dont le dénominateur est le triangle de 5, c'est-à-dire de la moitié de 10 dont le triangle 55 est le dénominateur de la première des 2 fractions; car: soit le côté du triangle qui constitue le dénominateur de la première fraction ∞ x, alors son triangle, c'est-à-dire le
| |
| |
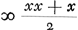 en het eerste gebroken dan 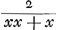 . Voorts sal de sijde des noemers van 't volgende gebroken sijn x + 1, en daerom sijn triangel, dat is den noemer des 2 den gebrokens 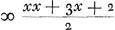 . En dienvolgens het volgende gebroken 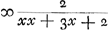 . om tot het welck te adderen het eerste gebroken 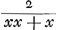 , soo is den gemeenen noemer x3 + 3 xx + 2 x ende haer somme 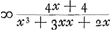 , dat is 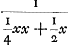 . Nemende nu 1/2 x voor sijde, welck een heel getal sal sijn, dewijl x een even getal gestelt werdt, soo is sijn triangel 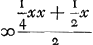 ofte 1/8 xx + 1/4 x. Ende diensvolgens 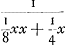 sal sijn het gebroken, wiens noemer den triangel is
Traduction
dénominateur de la première fraction, est égal à 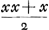 et la première fraction à et la première fraction à 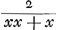 . Puis le côté du dénominateur de la fraction qui suit sera x + 1. Donc son triangle, qui est le dénominateur de la seconde fraction, sera . Puis le côté du dénominateur de la fraction qui suit sera x + 1. Donc son triangle, qui est le dénominateur de la seconde fraction, sera 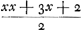 . Par conséquent la fraction qui suit sera . Par conséquent la fraction qui suit sera 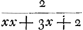 . Afin de faire l'addition de cette fraction à la première . Afin de faire l'addition de cette fraction à la première 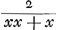 , on remarquera que leur dénominateur commun est x3 + 3xx + 2x et leur somme , on remarquera que leur dénominateur commun est x3 + 3xx + 2x et leur somme 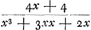 , c'est-à-dire , c'est-à-dire 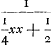 . Or, en prenant le côté égal à 1/2 x, ce qui représentera un nombre entier puisque x a été supposé pair, son triangle est . Or, en prenant le côté égal à 1/2 x, ce qui représentera un nombre entier puisque x a été supposé pair, son triangle est 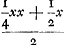 ou 1/8xx + 1/4x. Par suite ou 1/8xx + 1/4x. Par suite 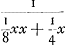 constituera la fraction dont le dénominateur est le constituera la fraction dont le dénominateur est le
| |
| |
van de helft der sijde x, welckers triangel was den noemer des eerste gebrokens 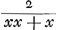 . nu is oock 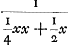 , de gevonden somme der 2 gebrokens gelijck de helft van 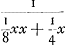 , quod erat demonst.
3. Indien men nu oock een rije van gebroockens stelt die proportionael sijn tot die van de voorgaende triangulare rije, het is seecker, dat gelijck de somme van 2 aan een volgende der triangulare rije gelijck is aan de helft van het gebroken in 't voorgaende voorstel geseght, alsoo oock de somme der 2 proportionale der selve 2 gebrokens, gelijck sal sijn aan de helft van het proportionale des geseijden gebrokens.
| 1 |
2 |
3 |
4 |
5 |
| 1/1 |
1/3 |
1/6 |
1/10 |
1/15 |
| 1/4 |
1/12 |
1/24 |
1/40 |
1/60 |
Bij exempel dewijl 1/10 + 1/15 sijn ∞ de helft van 1/3, dat is gelijck 1/6, so sal oock in de onderste proportionale rije wesen 1/40 + 1/60 ∞ de helft van 1/12 dat is gelijck 1/24.
Traduction:
triangle de la moitié du côté x dont le triangle était le dénominateur de la première fraction 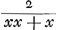 . Or, en effet, . Or, en effet, 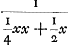 , c'est-à-dire la somme des deux fractions, est égale à la moitié de , c'est-à-dire la somme des deux fractions, est égale à la moitié de 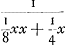 , ce qu'il fallait démontrer. , ce qu'il fallait démontrer.
3. Si maintenant on forme de même une suite de fractions qui sont proportionnelles à celles de la suite triangulaire précédente, il est certain que, puisque la somme de deux fractions successives de la suite triangulaire est égale à la moitié de la fraction indiquée plus haut, la somme des 2 fractions proportionnelles aux 2 dites fractions sera égale à la moitié de la fraction proportionnelle à la fraction susdite.
| 1 |
2 |
3 |
4 |
5 |
| 1/1 |
1/3 |
1/6 |
1/10 |
1/15 |
| 1/4 |
1/12 |
1/24 |
1/40 |
1/60 |
Par exemple, puisque 1/10 + 1/15 ∞ la moitié de 1/3, c'est-à-dire, égal à 1/6, on aura aussi dans la suite proportionnelle inférieure 1/40 + 1/60 ∞ la moitié de 1/12, c'est-à-dire égal à 1/24.
| |
| |
4. In de rije der gebroockens welckers noemers sijn de achter een volgende triangulare getallen en de tellers alle 1, is de somme der gansche rije in infinitum gelijck 2.
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| Eerste rije |
1/1 |
1/3 |
1/6 |
1/10 |
1/15 |
1/21 |
1/28 |
1/36 |
1/45 |
1/55 |
1/66 |
1/78 |
1/91 |
1/105 |
1/120 |
| tweede rije |
|
1/2 |
1/6 |
1/12 |
1/20 |
1/30 |
1/42 |
1/56 |
| derde rije |
|
1/4 |
|
1/12 |
|
1/24 |
|
| 4de rije |
|
1/8 |
|
Zij genomen de eerste deser rijen in infinitum te gaen. En laet de 2e rije bestaen uijt de sommen der gebrookens der eerste rije, genomen 2 aan 2, van welcke twee ieder minste sijn noemer sij den triangel van een even getal. Soo sijn dan de getalen der 2e rije, door het 2e voorstelGa naar voetnoot1), ieder de helft der getalen van de eerste
Traduction:
4. Dans la suite des fractions dont les dénominateurs sont les nombres triangulaires successifs et les numérateurs tous 1, la somme de la suite totale prolongée jusqu'à l'infini est égale à 2.
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
| première suite |
1/1 |
1/3 |
1/6 |
1/10 |
1/15 |
1/21 |
1/28 |
1/36 |
1/45 |
1/55 |
1/66 |
1/78 |
1/91 |
1/105 |
1/120 |
| deuxième suite |
|
1/2 |
1/6 |
1/12 |
1/20 |
1/30 |
1/42 |
1/56 |
| troisième suite |
|
1/4 |
|
1/12 |
|
1/24 |
|
| 4e suite |
|
1/8 |
|
Supposons que la première suite continue jusqu'à l'infini et que la deuxième suite se compose des sommes des fractions de la première suite, prises 2 à 2, de manière que le plus petit dénominateur de chaque couple soit le triangle d'un nombre pair. Alors les nombres de la deuxième suite sont, d'après la seconde propositionGa naar voetnoot1), les moitiés
| |
| |
rije, als men de evenveelste in de order neemt. laet men wederom de 3de rije bestaen uijt de sommen der getallen van de 2de rije, genomen 2 aen 2, en weder het eerste overslaende, soo sijn dan, door het derde voorstelGa naar voetnoot2), de getallen der 3e rije ieder de helft van de getallen der 2de rije.
En van gelijcken soo de 4de rije bestaet uijt de sommen van ieder 2 getallen der 3de rije, overslaende het eerste. soo sullen de getallen deser 4de rije ieder de helft sijn van die van de 3e rije.
En soo voorts met al de andere leegher rijen in infinitum te bedencken.
Nu soo blijckt dat het eerste getal der tweede rije, te weten 1/2, is de somme van de 2 getallen der eerste rije die nae het eerste getal volgen.
En dat het eerste getal der 3de rije is de somme van de 4 volgende getallen der eerste rije.
En dat het eerste getal der 4de rije is de somme van de 8 volgende getallen der eerste rije.
En van gelijcken dat het eerste getal der 5e rije soude sijn de somme van de 16 volgende getallen der eerste rije en soo voort.
Traduction:
des nombres de la première suite, pris dans le même ordre. Si maintenant la 3me suite se compose de nouveau des sommes des nombres de la 2me suite, pris 2 à 2, en laissant derechef de côté le premier de ces nombres, les nombres de la 3me suite seront, d'après la troisième propositionGa naar voetnoot2), chacun la moitié des nombres de la 2me suite.
Et de même, si la 4me suite se compose des sommes de chaque couple de 2 nombres de la 3me suite, laissant de côté le premier, les nombres de cette 4me suite seront chacun la moitié de ceux de la 3me suite. Et de la même manière on traitera toutes les suites inférieures jusqu'à l'infini.
Or, il s'ensuit que le premier nombre de la deuxième suite, c'est-à-dire 1/2, est la somme des 2 nombres de la première suite qui suivent après le premier nombre.
Et que le premier nombre de la 3me suite est la somme des 4 nombres suivants de la première suite.
Et que le premier nombre de la 4me suite est la somme des 8 nombres suivants de la première suite.
Et de même que le premier nombre de la 5me suite serait la somme des 16 nombres suivants de la première suite, etc.
| |
| |
Dewijl dan aldus de eerste getallen der rijen maecken de somme van al de getallen der eerste rije; en dat de selve eerste getallen der rijen ieder de helft bewesen sijn te sijn van het voorgaende, en dienvolgens al te samen in infinitum gelijck aen 2 mael het eerste 1/1; soo sijn dan oock al de getallen der eerste rije te samen ∞ 2 mael 1/1 dat is ∞ 2 quod erat dem.
Traduction
Puisque donc les premiers nombres des suites constituent la somme de tous les nombres de la première suite, et qu'on a démontré que ces premiers nombres des suites sont chacun la moitié de celui qui précède, et que, par conséquent, tous ensemble jusqu'à l'infini sont égaux à 2 fois le premier nombre 1/1, il en résulte que tous les nombres de la première suite ensemble sont aussi ∞ 2 fois 1/1, c'est-à-dire ∞ 2. Ce qu'il fallait démontrer.
|
-
voetnoot1)
- Cet Appendice, que nous avons divisé en paragraphes, est emprunté aux p. 63-74 du Manuscrit C. Ces pages étaient numérotées de 19 à 30 par Huygens.
-
voetnoot2)
- Ce paragraphe contient la solution du problème sur le jeu de croix et pile, proposé par Huygens à Hudde dans une lettre du 4 avril 1665; voir les pp. 304 et 308 du T. V. On peut encore consulter sur ce problème les p. 33-34 de l'Avertissement.
-
voetnoot3)
- On peut consulter sur l'adjonction de la dernière phrase qui manquait dans l'énoncé du problème envoyé à Hudde, la p. 422 du T. V, ou bien la p. 34 de l'Avertissement.
-
voetnoot1)
- Voir la p. 65 du présent Tome; mais il s'agit plutôt de la première Proposition, p. 63.
-
voetnoot1)
- Voir la p. 65 du présent Tome; mais il s'agit plutôt de la première Proposition, p. 63.
-
voetnoot2)
- Cette notation indique que l'on peut remplacer - b/2 par
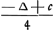 . .
-
voetnoot2)
- Cette notation indique que l'on peut remplacer - b/2 par
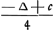 . .
-
voetnoot1)
- Le problème est donc résolu. Ajoutons que quelques pages plus haut dans le même Manuscrit (p. 38-42) on rencontre des calculs, datés du 16 mars 1665, par lesquels Huygens, sans réussir à résoudre le problème, qu'il y appelle ‘quaestio difficillima’, enferme la valeur a de l'avantage du second joueur B dans des limites de plus en plus rapprochées.
Or, à cause de leur rédaction confuse et incomplète, il aurait été très difficile de reproduire ces calculs. Nous nous bornons donc à en donner un résumé.
Remarquons, à cet effet, que les équations qu'on peut déduire des expressions successives pour - a (p. 119) peuvent s'écrire:
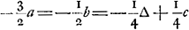
Il en résulte:
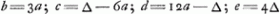 Dans ces équations les coefficients de a constituent une suite géométrique et la formation des coefficients de ∆ est facilement expliquée par l'algorithme suivant:
Dans ces équations les coefficients de a constituent une suite géométrique et la formation des coefficients de ∆ est facilement expliquée par l'algorithme suivant:
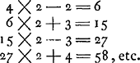
Voyons maintenant de quelle manière, entre autres, les deux limites les plus rapprochées ont été obtenues par Huygens. Nous considérons à cet effet d'abord l'avantage n de celui qui jette le premier quand il a mis à l'enjeu 6 ducats contre 6 qui ont été mis par l'autre joueur. Il est clair qu'on aura 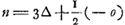 , et de même , et de même 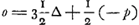 ; par suite ; par suite 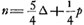 . Or, on a évidemment p > n, puisque l'enjeu est le plus grand dans le cas auquel l'avantage p se rapporte. Il en résulte n > 5/4 ∆ + 1/4 n et par conséquent n > 5/3 ∆; mais . Or, on a évidemment p > n, puisque l'enjeu est le plus grand dans le cas auquel l'avantage p se rapporte. Il en résulte n > 5/4 ∆ + 1/4 n et par conséquent n > 5/3 ∆; mais 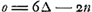 , donc o < 8/3 ∆. On en déduit 12288a - 1818 ∆ < 8/3 ∆, ou bien a < 5462/36864 ∆. , donc o < 8/3 ∆. On en déduit 12288a - 1818 ∆ < 8/3 ∆, ou bien a < 5462/36864 ∆.
En partant de la supposition q > o, on peut déduire de la même manière des équations 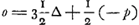 et et 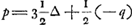 la relation p > 7/3 ∆, d'où il s'ensuit 3643∆ - 24576a < 7/3 ∆, ou bien, a > 5461/36864 ∆. la relation p > 7/3 ∆, d'où il s'ensuit 3643∆ - 24576a < 7/3 ∆, ou bien, a > 5461/36864 ∆.
On trouve donc enfin:
5462/36864 ∆ > a > 5461/36864 ∆.
Il est vrai, qu'à la dernière des pages citées du Manuscrit, Huygens vérifie si, en effet:
5462/36864 > 4/27 > 5461/36864;
mais ce petit calcul a probablement été ajouté après que la valeur 4/27 avait été trouvée par une autre méthode.
D'ailleurs Huygens a calculé la limite supérieure 5462/36864 ∆ > a encore d'une autre manière, c'est-à-dire en employant directement la relation p > n, qui peut s'écrire 3643∆ - 24576a > > 912∆ - 6144a.
-
voetnoot1)
- Le problème est donc résolu. Ajoutons que quelques pages plus haut dans le même Manuscrit (p. 38-42) on rencontre des calculs, datés du 16 mars 1665, par lesquels Huygens, sans réussir à résoudre le problème, qu'il y appelle ‘quaestio difficillima’, enferme la valeur a de l'avantage du second joueur B dans des limites de plus en plus rapprochées.
Or, à cause de leur rédaction confuse et incomplète, il aurait été très difficile de reproduire ces calculs. Nous nous bornons donc à en donner un résumé.
Remarquons, à cet effet, que les équations qu'on peut déduire des expressions successives pour - a (p. 119) peuvent s'écrire:
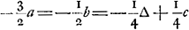
Il en résulte:
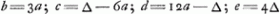 Dans ces équations les coefficients de a constituent une suite géométrique et la formation des coefficients de ∆ est facilement expliquée par l'algorithme suivant:
Dans ces équations les coefficients de a constituent une suite géométrique et la formation des coefficients de ∆ est facilement expliquée par l'algorithme suivant:
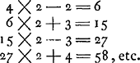
Voyons maintenant de quelle manière, entre autres, les deux limites les plus rapprochées ont été obtenues par Huygens. Nous considérons à cet effet d'abord l'avantage n de celui qui jette le premier quand il a mis à l'enjeu 6 ducats contre 6 qui ont été mis par l'autre joueur. Il est clair qu'on aura 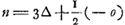 , et de même , et de même 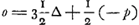 ; par suite ; par suite 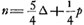 . Or, on a évidemment p > n, puisque l'enjeu est le plus grand dans le cas auquel l'avantage p se rapporte. Il en résulte n > 5/4 ∆ + 1/4 n et par conséquent n > 5/3 ∆; mais . Or, on a évidemment p > n, puisque l'enjeu est le plus grand dans le cas auquel l'avantage p se rapporte. Il en résulte n > 5/4 ∆ + 1/4 n et par conséquent n > 5/3 ∆; mais 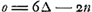 , donc o < 8/3 ∆. On en déduit 12288a - 1818∆ < 8/3 ∆, ou bien a < 5462/36864 ∆. , donc o < 8/3 ∆. On en déduit 12288a - 1818∆ < 8/3 ∆, ou bien a < 5462/36864 ∆.
En partant de la supposition q > o, on peut déduire de la même manière des équations 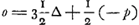 et et 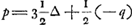 la relation p > 7/3 ∆, d'où il s'ensuit 3643∆ - 24576a < 7/3 ∆, ou bien, a > 5461/36864 ∆. la relation p > 7/3 ∆, d'où il s'ensuit 3643∆ - 24576a < 7/3 ∆, ou bien, a > 5461/36864 ∆.
On trouve donc enfin:
5462/36864 ∆ > a > 5461/36864 ∆.
Il est vrai, qu'à la dernière des pages citées du Manuscrit, Huygens vérifie si, en effet:
5462/36864 > 4/27 > 5461/36864;
mais ce petit calcul a probablement été ajouté après que la valeur 4/27 avait été trouvée par une autre méthode.
D'ailleurs Huygens a calculé la limite supérieure 5462/36864 ∆ > a encore d'une autre manière, c'est-à-dire en employant directement la relation p > n, qui peut s'écrire 3643∆ - 24576a > > 912∆ - 6144a.
-
voetnoot1)
- Ce paragraphe contient l'explication des calculs que nous avons reproduits dans l'Appendice III (p. 102 - 107).
-
voetnoot5)
- Voir à la p. 104 l'équation a ∞ 1/3 b - 2/3 k et à la p. 105 les expressions pour 1/3 b et - 2/3 k.
-
voetnoot5)
- Voir à la p. 104 l'équation a ∞ 1/3 b - 2/3 k et à la p. 105 les expressions pour 1/3 b et - 2/3 k.
-
voetnoot1)
- Explication des calculs qu'on trouve dans l'Appendice IV, p. 108-115 du présent Tome.
-
voetnoot3)
- C'est-à-dire suivant la manière dont le problème fut posé par Hudde qui suppose que le joueur A doit choisir entre 2 jetons blancs et 1 noir; comparez les notes 1 et 2 de la p. 108.
-
voetnoot4)
- Voir le § 1 (p. 108-113) de l'Appendice IV, où l'on doit substituer partout θ = 2, λ = 1 pour retrouver les expressions qui se rapportent au problème tel qu'il fut posé par Hudde.
-
voetnoot5)
- Lisez:
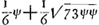 et comparez la p. 113 du présent Tome. et comparez la p. 113 du présent Tome.
-
voetnoot6)
- On retrouve cette manière d'indiquer l'incommensurabilité d'un rapport chez Euclide, voir p.e. la ‘Prop. 7’ du ‘Lib. X’, où on lit: ‘Incommensurabiles magnitudines inter se proportionem non habent, quam numerus ad numerum’ (p. 217 de l'édition de 1607 des ‘Elementa’ par Clavius).
-
voetnoot7)
- Voir à la p. 111 le premier terme du second membre de la suite pour θk/ϱ, où il faut toujours substituer θ = 2, λ = 1, ϱ = 3.
-
voetnoot4)
- Voir le § 1 (p. 108-113) de l'Appendice IV, où l'on doit substituer partout θ = 2, λ = 1 pour retrouver les expressions qui se rapportent au problème tel qu'il fut posé par Hudde.
-
voetnoot4)
- Voir le § 1 (p. 108-113) de l'Appendice IV, où l'on doit substituer partout θ = 2, λ = 1 pour retrouver les expressions qui se rapportent au problème tel qu'il fut posé par Hudde.
-
voetnoot5)
- Lisez:
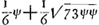 et comparez la p. 113 du présent Tome. et comparez la p. 113 du présent Tome.
-
voetnoot6)
- On retrouve cette manière d'indiquer l'incommensurabilité d'un rapport chez Euclide, voir p.e. la ‘Prop. 7’ du ‘Lib. X’, où on lit: ‘Incommensurabiles magnitudines inter se proportionem non habent, quam numerus ad numerum’ (p. 217 de l'édition de 1607 des ‘Elementa’ par Clavius).
-
voetnoot7)
- Voir à la p. 111 le premier terme du second membre de la suite pour θk/ϱ, où il faut toujours substituer θ = 2, λ = 1, ϱ = 3.
-
voetnoot8)
- Il s'agit de l'équation - λ + λφϱ/θψ ∞ θ - λφ/ω (p. 112), ou plutôt de celle qu'on en déduit en posant θ = 2, λ = 1.
-
voetnoot10)
- Voir aux p. 112-113 les réductions successives de l'équation en question.
-
voetnoot8)
- Il s'agit de l'équation - λ + λφϱ/θψ ∞ θ - λφ/ω (p. 112), ou plutôt de celle qu'on en déduit en posant θ = 2, λ = 1.
-
voetnoot10)
- Voir aux p. 112-113 les réductions successives de l'équation en question.
-
voetnoot1)
- Ce sont ces quantités que nous avons reproduites aux p. 109-114 à l'exclusion de celles qui se rapportent à la solution particulière; voir la note 2 de la p. 108.
-
voetnoot3)
- Il s'agit du § 2 de l'Appendice IV, p. 113-115.
-
voetnoot1)
- Ce sont ces quantités que nous avons reproduites aux p. 109-114 à l'exclusion de celles qui se rapportent à la solution particulière; voir la note 2 de la p. 108.
-
voetnoot3)
- Il s'agit du § 2 de l'Appendice IV, p. 113-115.
-
voetnoot7)
- Voir la p. 112 après le premier alinéa.
-
voetnoot8)
- Voir la première ‘Regula’ de la p. 114.
-
voetnoot9)
- L'équation a ∞ - λb/ϱ + θk/ϱ, où θk/ϱ ℞ θφa/ϱω + θψl/ϱω; voir les p. 110-111.
-
voetnoot8)
- Voir la première ‘Regula’ de la p. 114.
-
voetnoot10)
- Voir la p. 109. Remarquons que dans le cas qu'une telle division serait possible le numérateur de la fraction qui est égal à a - θφa/δω d'après la première ‘Regula’ de la p. 114 devrait contenir un facteur rationnel, mais qu'il est facile de constater qu'il n'en est pas ainsi.
En effet, si l'on suppose a = 0, il faut que ce numérateur soit égal à zéro, c'est-à-dire qu'on ait:
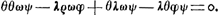
Cette équation doit donc amener, outre les solutions éventuelles qui dépendraient du facteur soupçonné, la solution irrationnelle du problème traité dans le § 1 de l'Appendice IV (p. 108-113). Or, cette dernière solution est exprimée par l'équation qui résume la ‘Regula’ de la p. 112 et qui peut s'écrire:
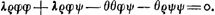
L'égalité du degré des premiers membres de ces équations par rapport aux quantités θ, λ, ϱ, φ, ψ, ω prouve déjà que'le numérateur en question ne contient pas de facteur supplémentaire. D'ailleurs l'identité complète des deux équations est aisément vérifiée en substituant dans la première φ + ψ à ω.
-
voetnoot7)
- Voir la p. 112 après le premier alinéa.
-
voetnoot8)
- Voir la première ‘Regula’ de la p. 114.
-
voetnoot9)
- L'équation a ∞ - λb/ϱ + θk/ϱ, où θk/ϱ ℞ θφa/ϱω + θψl/ϱω; voir les p. 110-111.
-
voetnoot8)
- Voir la première ‘Regula’ de la p. 114.
-
voetnoot10)
- Voir la p. 109. Remarquons que dans le cas qu'une telle division serait possible le numérateur de la fraction qui est égal à a - θφa/δω d'après la première ‘Regula’ de la p. 114 devrait contenir un facteur rationnel, mais qu'il est facile de constater qu'il n'en est pas ainsi.
En effet, si l'on suppose a = 0, il faut que ce numérateur soit égal à zéro, c'est-à-dire qu'on ait:
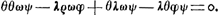 Cette équation doit donc amener, outre les solutions éventuelles qui dépendraient du facteur soupçonné, la solution irrationnelle du problème traité dans le § 1 de l'Appendice IV (p. 108-113). Or, cette dernière solution est exprimée par l'équation qui résume la ‘Regula’ de la p. 112 et qui peut s'écrire:
Cette équation doit donc amener, outre les solutions éventuelles qui dépendraient du facteur soupçonné, la solution irrationnelle du problème traité dans le § 1 de l'Appendice IV (p. 108-113). Or, cette dernière solution est exprimée par l'équation qui résume la ‘Regula’ de la p. 112 et qui peut s'écrire:
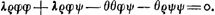 L'égalité du degré des premiers membres de ces équations par rapport aux quantités θ, λ, ϱ, φ, ψ, ω prouve déjà que'le numérateur en question ne contient pas de facteur supplémentaire. D'ailleurs l'identité complète des deux équations est aisément vérifiée en substituant dans la première φ + ψ à ω.
L'égalité du degré des premiers membres de ces équations par rapport aux quantités θ, λ, ϱ, φ, ψ, ω prouve déjà que'le numérateur en question ne contient pas de facteur supplémentaire. D'ailleurs l'identité complète des deux équations est aisément vérifiée en substituant dans la première φ + ψ à ω.
-
voetnoot1)
- Ce paragraphe, emprunté à la p. 63 du Manuscrit C (numérotée 19 par Huygens), contient la solution d'un problème posé par Huygens dans sa lettre à Hudde du 10 mai 1665; voir la p. 353 du T. V. On peut encore consulter sur ce problème la p. 38 de l'Avertissement.
-
voetnoot5)
- Par cette notation Huygens indique qu'on peut emplacer - c/2 par - ∆
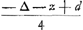 . .
-
voetnoot6)
- La somme de ces quantités représente la suite ‘des - ∆’, c'est-à-dire des termes négatifs de l'expression pour - a.
-
voetnoot5)
- Par cette notation Huygens indique qu'on peut emplacer - c/2 par
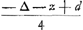 . .
-
voetnoot6)
- La somme de ces quantités représente la suite ‘des - ∆’, c'est-à-dire des termes négatifs de l'expression pour - a.
-
voetnoot1)
- C'est-à-dire en supposant que le dernier terme, comme ici i/128, s'approche indéfiniment de zéro; comparez la p. 120.
-
voetnoot2)
- Ce paragraphe contient la solution d'un problème dont Huygens et Hudde se sont occupés dans les mois de juillet et d'août 1665; voir la p. 463 du T. V et surtout la note 2 de la même page. On peut encore consulter sur ce problème les p. 38-48 de l'Avertissement.
-
voetnoot3)
- Ces pages contiennent des calculs qui correspondent en partie avec ceux qui vont suivre, mais qui n'ont pas été terminés.
-
voetnoot1)
- C'est-à-dire en supposant que le dernier terme, comme ici i/128, s'approche indéfiniment de zéro; comparez la p. 120.
-
voetnoot2)
- Ce paragraphe contient la solution d'un problême dont Huygens et Hudde se sont occupés dans les mois de juillet et d'août 1665; voir la p. 463 du T. V et surtout la note 2 de la même page. On peut encore consulter sur ce problème les p. 38-48 de l'Avertissement.
-
voetnoot3)
- Ces pages contiennent des calculs qui correspondent en partie avec ceux qui vont suivre, mais qui n'ont pas été terminés.
-
voetnoot4)
- Pour préciser dès l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
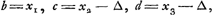 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 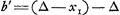 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 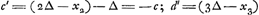 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans
que la mise soit épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans
que la mise soit épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dès l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
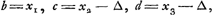 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 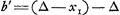 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 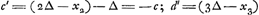 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans
que la mise soit épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans
que la mise soit épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
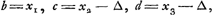 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 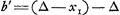 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 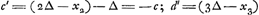 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
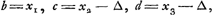 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 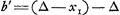 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 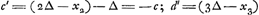 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
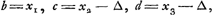 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 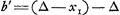 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 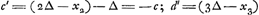 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
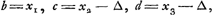 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 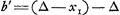 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 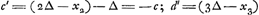 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
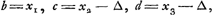 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 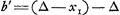 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 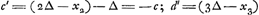 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
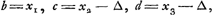 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 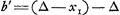 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 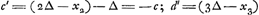 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
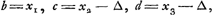 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 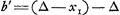 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 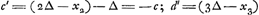 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
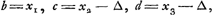 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 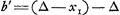 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 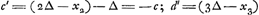 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dès l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
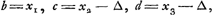 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 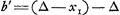 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 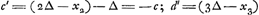 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit
épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dès l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
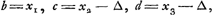 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 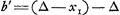 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 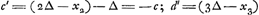 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit épuisée.
Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit épuisée.
Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
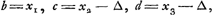 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 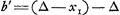 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 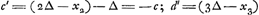 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment
sans que la mise soit épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment
sans que la mise soit épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
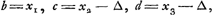 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 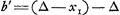 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 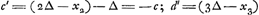 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment
sans que la mise soit épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment
sans que la mise soit épuisée. Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot4)
- Pour préciser dés l'abord le sens attaché par Huygens aux quantités b, c, d, etc., appelons xm la part due à celui qui doit jeter le premier, lorsqu'il s'agit de partager, sans terminer la partie, un enjeu m∆ (∆ = un ducat), qui s'est formé durant le jeu. On aura alors:
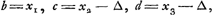 . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement . Au contraire les avantages (pris dans le sens de Huygens) de l'autre joueur seront respectivement 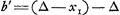 (puisqu'on doit retrancher le ducat mis par lui même) = - b; (puisqu'on doit retrancher le ducat mis par lui même) = - b; 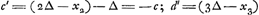 , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit épuisée.
Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité. , etc; voir toutefois les p. 43-47 de l'Avertissement, où il est montré que l'hypothèse que la somme des espérances des deux joueurs est égale à la mise totale est sujette à caution à cause de la possibilité que le jeu se continue indésiniment sans que la mise soit épuisée.
Mais ici et dans les notes qui suivent nous accepterons cette hypothèse sans laquelle les raisonnements de Huygens perdent leur validité.
-
voetnoot1)
- Sous la réserve que nous avons formulée dans la note 4 de la p. 133, le raisonnement qui conduit aux équations mentionnées est exact. Pour l'appliquer il suffit de supposer que le joueur qui jette croix prend toujours un des ducats qui appartiennent à la mise de l'autre joueur. Toutefois cette supposition peut sembler un peu artificielle. Il n'est donc peut-être pas inutile de faire remarquer que toutes ces équations, quand on y substitue les valeurs de b, c, d, etc. indiquées dans la même note 4 de la p. 133, se réduisent à des cas particuliers de l'équation
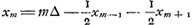 ; équation qui découle de la définition de xm telle que nous l'avons donnée dans la note citée, puisqu'on a évidemment par suite de cette definition ; équation qui découle de la définition de xm telle que nous l'avons donnée dans la note citée, puisqu'on a évidemment par suite de cette definition 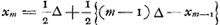 . .
-
voetnoot1)
- Sous la réserve que nous avons formulée dans la note 4 de la p. 133, le raisonnement qui conduit aux équations mentionnées est exact. Pour l'appliquer il suffit de supposer que le joueur qui jette croix prend toujours un des ducats qui appartiennent à la mise de l'autre joueur. Toutefois cette supposition peut sembler un peu artificielle. Il n'est donc peut-être pas inutile de faire remarquer que toutes ces équations, quand on y substitue les valeurs de b, c, d, etc. indiquées dans la même note 4 de la p. 133, se réduisent à des cas particuliers de l'équation
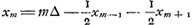 ; équation qui découle de la définition de xm telle que nous l'avons donnée dans la note citée, puisqu'on a évidemment par suite de cette definition ; équation qui découle de la définition de xm telle que nous l'avons donnée dans la note citée, puisqu'on a évidemment par suite de cette definition 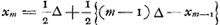 . .
-
voetnoot1)
- Cette notation indique qu'on peut remplacer - 1/8 d par sa valeur, trouvée plus haut à la p. 136.
-
voetnoot1)
- Cette notation indique qu'on peut remplacer - 1/8 d par sa valeur, trouvée plus haut à la p. 136.
-
voetnoot2)
- Consultez sur la signification précise de k la note 4 de la p. 133. On peut encore définir 2k - ∆ comme la différence des espérances mathématiques des deux joueurs dans le cas où ils auraient à partager entre eux un enjeu de neuf ducats suivant les règles du jeu en question. D'autre part 2i est égal à la différence des espérances dans le cas où il y a huit ducats à l'enjeu.
-
voetnoot2)
- Consultez sur la signification précise de k la note 4 de la p. 133. On peut encore définir 2k - ∆ comme la différence des espérances mathématiques des deux joueurs dans le cas où ils auraient à partager entre eux un enjeu de neuf ducats suivant les règles du jeu en question. D'autre part 2i est égal à la différence des espérances dans le cas où il y a huit ducats à l'enjeu.
-
voetnoot1)
- Voir le § 6 qui suit (p. 144-150) et surtout la note 1 de la p. 144.
-
voetnoot1)
- Voir le § 6 qui suit (p. 144-150) et surtout la note 1 de la p. 144.
-
voetnoot1)
- Comparez la note 4 de la p. 41 de l'Avertissement.
-
voetnoot2)
- On peut, en effet, arriver à cette conclusion par une voie très courte. Reprenons à cet effet les notations de la note 4 de la p. 133. Soit donc x2 l'espérance mathématique du joueur qui doit jeter (c'est à-dire la part qui lui est due des deux ducats qui se trouvent à l'enjeu) et soit A ce joueur. On peut partager le jeu en deux périodes dont la première s'étend jusqu'au moment où pour la première fois l'enjeu est réduit à un seul ducat. La deuxième période s'étend depuis cet instant jusqu'à la fin du jeu, et il est évident que l'espérance mathématique totale x2 est égale à la somme des espérances mathématiques partielles concernant les deux périodes. Or, l'espérance concernant la première période est la même que s'il n'y avait qu'un seul ducat à l'enjeu et que l'on jouât jusqu'à l'épuisement de l'enjeu; elle est donc égale à x1. Quant à la deuxième période, il est sûr que lorsqu'elle commence ce sera B qui doit jeter (puisque c'est toujours son tour de jeter quand le nombre des ducats à l'enjeu est impair). L'espérance de B sera donc x1, et ∆ - x1 celle de A. Par suite,
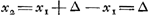 . L'avantage de A, dans le sens que
Huygens y attache, est donc . L'avantage de A, dans le sens que
Huygens y attache, est donc 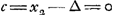 ; ce qu'il fallait prouver. ; ce qu'il fallait prouver.
-
voetnoot3)
- Le raisonnement qui va suivre fut écrit par Huygens sur la page précédente du Manuscrit dans un espace qui jusque là était resté vide.
-
voetnoot1)
- Comparez la note 4 de la p. 41 de l'Avertissement.
-
voetnoot2)
- On peut, en effet, arriver à cette conclusion par une voie très courte. Reprenons à cet effet les notations de la note 4 de la p. 133. Soit donc x2 l'espérance mathématique du joueur qui doit jeter (c'est à-dire la part qui lui est due des deux ducats qui se trouvent à l'enjeu) et soit A ce joueur. On peut partager le jeu en deux périodes dont la première s'étend jusqu'au moment où pour la première fois l'enjeu est réduit à un seul ducat. La deuxième période s'étend depuis cet instant jusqu'à la fin du jeu, et il est évident que l'espérance mathématique totale x2 est égale à la somme des espérances mathématiques partielles concernant les deux périodes. Or, l'espérance concernant la première période est la même que s'il n'y avait qu'un seul ducat à l'enjeu et que l'on jouât jusqu'à l'épuisement de l'enjeu; elle est donc égale à x1. Quant à la deuxième période, il est sûr que lorsqu'elle commence ce sera B qui doit jeter (puisque c'est toujours son tour de jeter quand le nombre des ducats à l'enjeu est impair). L'espérance de B sera donc x1, et ∆ - x1 celle de A. Par suite,
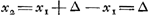 .
L'avantage de A, dans le sens que Huygens y attache, est donc .
L'avantage de A, dans le sens que Huygens y attache, est donc 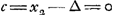 ; ce qu'il fallait prouver. ; ce qu'il fallait prouver.
-
voetnoot3)
- Le raisonnement qui va suivre fut écrit par Huygens sur la page précédente du Manuscrit dans un espace qui jusque là était resté vide.
-
voetnoot4)
- Cette phrase se trouve en marge du Manuscrit.
-
voetnoot5)
- Ce raisonnement n'a pu entièrement satisfaire Huygens. Il nous semble qu'on doit plutôt considérer cette partie de la présente Pièce comme une annotation provisoire sur laquelle il y aurait lieu peut-être de revenir. Comparez d'ailleurs les p. 43-48 de l'Avertissement, et surtout la note 1 de la p. 46, où nous avons voulu montrer qu'en effet les chances des deux joueurs sont égales dans les cas mentionnés, mais que l'enjeu doit être considéré comme perdu pour eux s'ils appliquent, sans en déroger en aucun cas, les règles du jeu, telles qu'elles sont formulées â la p. 132.
-
voetnoot4)
- Cette phrase se trouve en marge du Manuscrit.
-
voetnoot5)
- Ce raisonnement n'a pu entièrement satisfaire Huygens. Il nous semble qu'on doit plutôt considérer cette partie de la présente Pièce comme une annotation provisoire sur laquelle il y aurait lieu peut-être de revenir. Comparez d'ailleurs les p. 43-48 de l'Avertissement, et surtout la note 1 de la p. 46, où nous avons voulu montrer qu'en effet les chances des deux joueurs sont égales dans les cas mentionnés, mais que l'enjeu doit être considéré comme perdu pour eux s'ils appliquent, sans en déroger en aucun cas, les règles du jeu, telles qu'elles sont formulées â la p. 132.
-
voetnoot1)
- Ce paragraphe apprend à sommer la suite des valeurs réciproques des nombres triangulaires. Nous n'avons par voulu le supprimer puisqu'il fait connaître la manière dont cette somme a été obtenue par Huygens; mais on sait qu'on l'obtient bien plus facilement en remarquant que
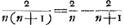 et que, par conséquent, la suite se réduit à 1 + 1 - 2/3 + 2/3 - 2/4 + + 2/4 - 2/5 etc. et que, par conséquent, la suite se réduit à 1 + 1 - 2/3 + 2/3 - 2/4 + + 2/4 - 2/5 etc.
-
voetnoot1)
- Ce paragraphe apprend à sommer la suite des valeurs réciproques des nombres triangulaires. Nous n'avons par voulu le supprimer puisqu'il fait connaître la manière dont cette somme a été obtenue par Huygens; mais on sait qu'on l'obtient bien plus facilement en remarquant que
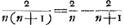 et que, par conséquent, la suite se réduit à 1 + 1 - 2/3 + 2/3 - 2/4 + + 2/4 - 2/5 etc. et que, par conséquent, la suite se réduit à 1 + 1 - 2/3 + 2/3 - 2/4 + + 2/4 - 2/5 etc.
-
voetnoot1)
- Voir, à la p. 145, l'alinéa numéroté 2.
-
voetnoot1)
- Voir, à la p. 145, l'alinéa numéroté 2.
|
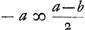 , door het 2. voorstel van onse Rekening in spelen van geluckGa naar voetnoot1). Van gelijcken kan men licht verstaan dat + b, dat is de kans van die 0 tegen 1 heeft ingeset, en selfs moet werpen, is ∞ 1 kans tot een ducaet te hebben, welck zij genoemt ∆, en 1 kans tot - c, soodat hierom is
, door het 2. voorstel van onse Rekening in spelen van geluckGa naar voetnoot1). Van gelijcken kan men licht verstaan dat + b, dat is de kans van die 0 tegen 1 heeft ingeset, en selfs moet werpen, is ∞ 1 kans tot een ducaet te hebben, welck zij genoemt ∆, en 1 kans tot - c, soodat hierom is 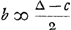 .
Item is c ∞ 1 tot ∆ en 1 tot - d. daerom
.
Item is c ∞ 1 tot ∆ en 1 tot - d. daerom 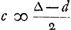 Item is d ∞ 1 tot 2∆ en 1 tot - e. daerom
Item is d ∞ 1 tot 2∆ en 1 tot - e. daerom 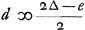 Item is e ∞ 1 tot 2∆ en 1 tot - f. daerom
Item is e ∞ 1 tot 2∆ en 1 tot - f. daerom 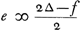 Item f ∞ 1 tot 3∆ en 1 tot -
Item f ∞ 1 tot 3∆ en 1 tot - 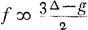 Item g ∞ 1 tot 3∆ en 1 tot - h. daerom
Item g ∞ 1 tot 3∆ en 1 tot - h. daerom 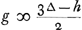 En soo voorts
En soo voorts 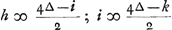
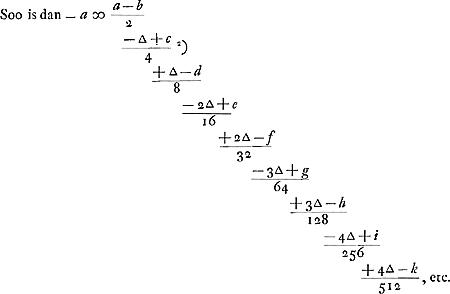
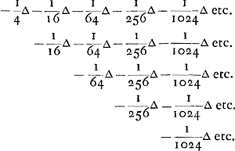
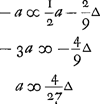
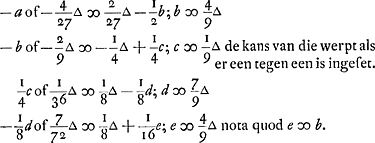
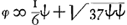 Ga naar voetnoot5) soo dat se in geen getalen kan gegeven werdenGa naar voetnoot6). In de aequatie die begint boven aen pag. 11 is a gelijck aan al de quantiteijten der neergaende 2 rijen daer ∆ in komt en daerenboven aan 2φa/3ω
staende boven aen de rije geteykent met BGa naar voetnoot7). Maer om dat men
Ga naar voetnoot5) soo dat se in geen getalen kan gegeven werdenGa naar voetnoot6). In de aequatie die begint boven aen pag. 11 is a gelijck aan al de quantiteijten der neergaende 2 rijen daer ∆ in komt en daerenboven aan 2φa/3ω
staende boven aen de rije geteykent met BGa naar voetnoot7). Maer om dat men
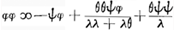 Ga naar voetnoot2),
Ga naar voetnoot2),
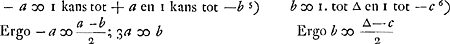
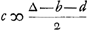 .
Van gelijcken is d ∞ 1 tot ∆ - c en 1 tot - e; daerom
.
Van gelijcken is d ∞ 1 tot ∆ - c en 1 tot - e; daerom 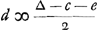

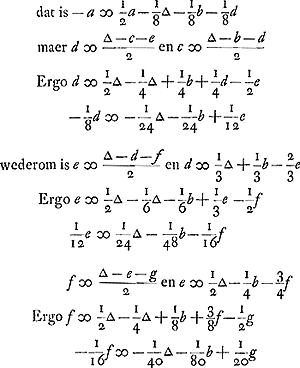
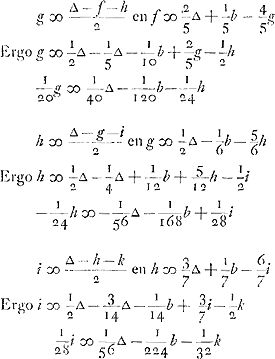
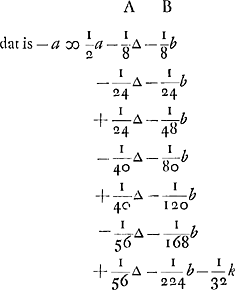
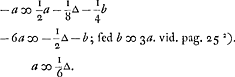
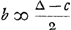 . vid. pag. 25Ga naar voetnoot2).
. vid. pag. 25Ga naar voetnoot2).
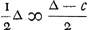 ; ∆ ∞ ∆ - c, c ∞ 0, soo dat als er 1 tegen 1 instaet de kansen gelijck sijn. sed
; ∆ ∞ ∆ - c, c ∞ 0, soo dat als er 1 tegen 1 instaet de kansen gelijck sijn. sed 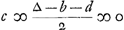 ; ∆ ∞ b + d, en b ∞ 1/2 ∆; 1/2 ∆ ∞ d, soo is d ∞ b dat is dese kanssen even goedt, te weten die van 0 tegen 1 of van 1 tegen 2 ingeset te hebben en te moeten werpen.
; ∆ ∞ b + d, en b ∞ 1/2 ∆; 1/2 ∆ ∞ d, soo is d ∞ b dat is dese kanssen even goedt, te weten die van 0 tegen 1 of van 1 tegen 2 ingeset te hebben en te moeten werpen.
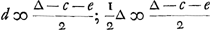 , sed c ∞ 0; 1/2 ∆ ∞ 1/2 ∆ - 1/2 e, e ∞ 0; soo dat als er 2 tegen 2 in staet de kanssen wederom gelijck sijn.
sed
, sed c ∞ 0; 1/2 ∆ ∞ 1/2 ∆ - 1/2 e, e ∞ 0; soo dat als er 2 tegen 2 in staet de kanssen wederom gelijck sijn.
sed 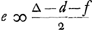 ; Ergo
; Ergo 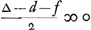 ; Ergo ∆ ∞ d + f sed d ∞ 1/2 ∆; 1/2 ∆ ∞ f. Ergo f ∞ d ∞ b.
; Ergo ∆ ∞ d + f sed d ∞ 1/2 ∆; 1/2 ∆ ∞ f. Ergo f ∞ d ∞ b.
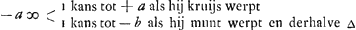 moet insetten
maar
moet insetten
maar 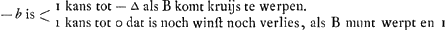 tegen 1 moet insetten.
tegen 1 moet insetten.
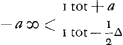 . Ergo
. Ergo 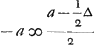 . Ergo 3a ∞ ∞ 1/2 ∆. En a ∞ 1/6 ∆. Even als in d'andere solutie.
. Ergo 3a ∞ ∞ 1/2 ∆. En a ∞ 1/6 ∆. Even als in d'andere solutie.

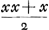 .
.
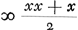 en het eerste gebroken dan
en het eerste gebroken dan 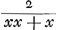 . Voorts sal de sijde des noemers van 't volgende gebroken sijn x + 1, en daerom sijn triangel, dat is den noemer des 2den gebrokens
. Voorts sal de sijde des noemers van 't volgende gebroken sijn x + 1, en daerom sijn triangel, dat is den noemer des 2den gebrokens 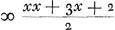 . En dienvolgens het volgende gebroken
. En dienvolgens het volgende gebroken 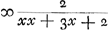 . om tot het welck te adderen het eerste gebroken
. om tot het welck te adderen het eerste gebroken 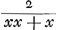 , soo is den gemeenen noemer x3 + 3xx + 2x ende haer somme
, soo is den gemeenen noemer x3 + 3xx + 2x ende haer somme 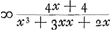 , dat is
, dat is 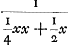 . Nemende nu 1/2 x voor sijde, welck een heel getal sal sijn, dewijl x een even getal gestelt werdt, soo is sijn triangel
. Nemende nu 1/2 x voor sijde, welck een heel getal sal sijn, dewijl x een even getal gestelt werdt, soo is sijn triangel 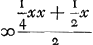 ofte 1/8 xx + 1/4 x. Ende diensvolgens
ofte 1/8 xx + 1/4 x. Ende diensvolgens 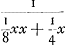 sal sijn het gebroken, wiens noemer den triangel is
sal sijn het gebroken, wiens noemer den triangel is
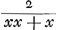 . nu is oock
. nu is oock 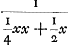 , de gevonden somme der 2 gebrokens gelijck de helft van
, de gevonden somme der 2 gebrokens gelijck de helft van 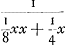 , quod erat demonst.
, quod erat demonst.


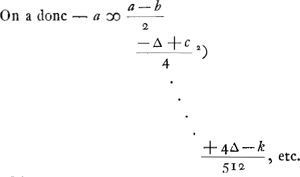
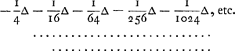
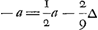 , ou bien - 3a = - 4/9 ∆, ou enfin a = 4/27 ∆, et il s'ensuit que A, qui jette le premier, perd 4/27 d'un ducat
, ou bien - 3a = - 4/9 ∆, ou enfin a = 4/27 ∆, et il s'ensuit que A, qui jette le premier, perd 4/27 d'un ducat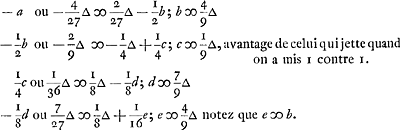
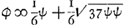
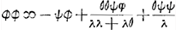
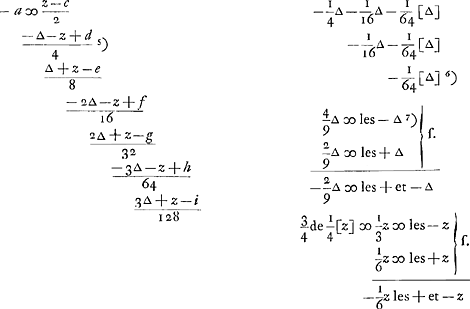
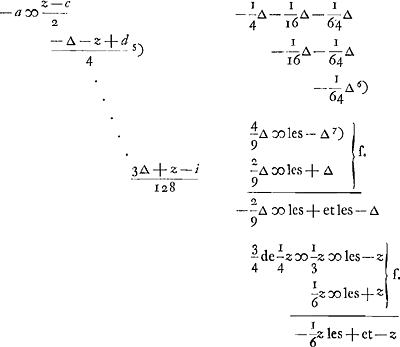
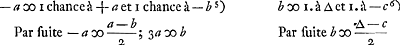
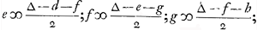

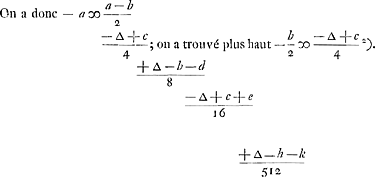
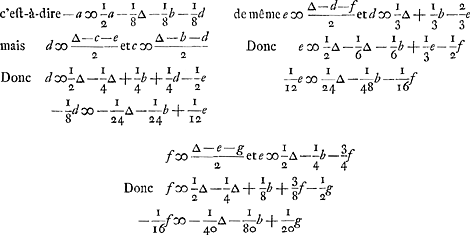
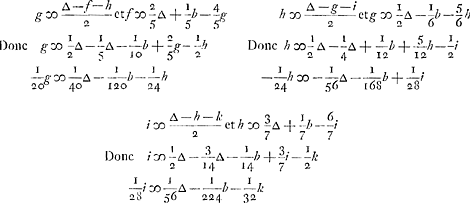
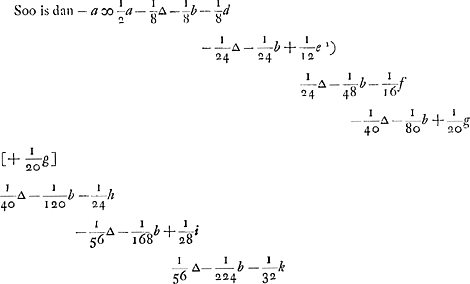
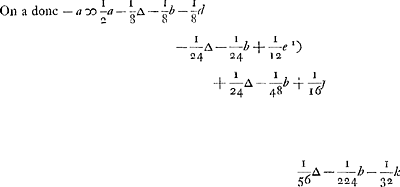
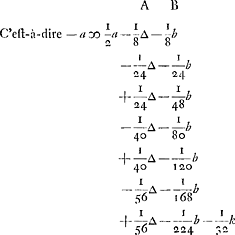
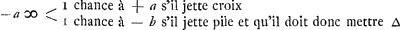 ;
;
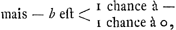 1 contre 1.
1 contre 1.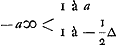 . Donc
. Donc 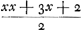 . Par conséquent la fraction qui suit sera
. Par conséquent la fraction qui suit sera 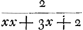 . Afin de faire l'addition de cette fraction à la première
. Afin de faire l'addition de cette fraction à la première 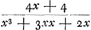 , c'est-à-dire
, c'est-à-dire 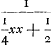 . Or, en prenant le côté égal à 1/2 x, ce qui représentera un nombre entier puisque x a été supposé pair, son triangle est
. Or, en prenant le côté égal à 1/2 x, ce qui représentera un nombre entier puisque x a été supposé pair, son triangle est 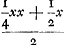 ou 1/8xx + 1/4x. Par suite
ou 1/8xx + 1/4x. Par suite