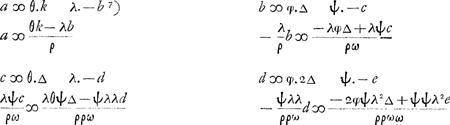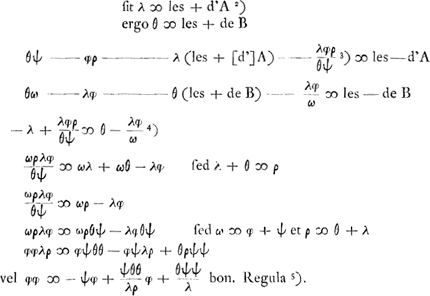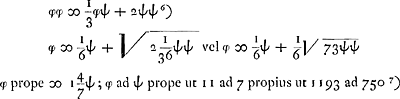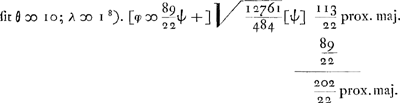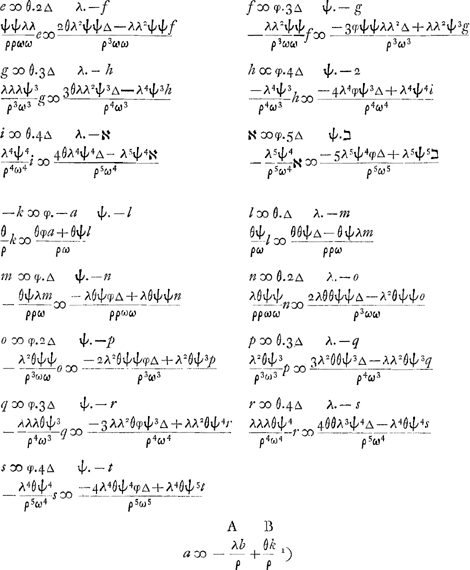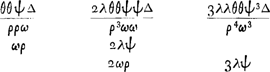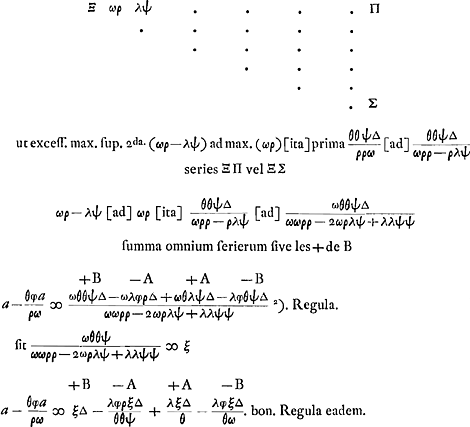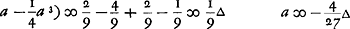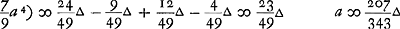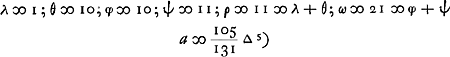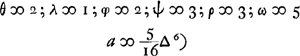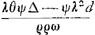A kiest uyt 3 [of uit ρ ∞ θ + λ] schijven waer van 2 [θ] wit, 1 [λ] swartGa naar voetnoot4).
B kiest uyt ω schijven waervan φ wit, ψ swart. ω ∞ φ + ψ.
| a |
is 't geen heeft |
A |
als hij |
0 |
tegen |
0 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| b |
is 't geen heeft |
B |
als hij |
0 |
tegen |
1 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| c |
is 't geen heeft |
A |
als hij |
1 |
tegen |
1 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| d |
is 't geen heeft |
B |
als hij |
1 |
tegen |
2 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| e |
is 't geen heeft |
A |
als hij |
2 |
tegen |
2 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| f |
is 't geen heeft |
B |
als hij |
2 |
tegen |
3 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| g |
is 't geen heeft |
A |
als hij |
3 |
tegen |
3 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| h |
is 't geen heeft |
B |
als hij |
3 |
tegen- |
4 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| i |
is 't geen heeft |
A |
als hij |
4 |
tegen |
4 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| א |
is 't geen heeft |
B |
als hij |
4 |
tegen |
5 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| ב |
is 't geen heeft |
A |
als hij |
5 |
tegen |
5 heeft ingeset en hij moet kiesenGa naar voetnoot5). |
| - k 't geen heeft B |
als hij |
0 |
tegen |
0 heeft ingeset, en hij moet kiesen. |
| + l 't geen heeft A |
als hij |
0 |
tegen |
1 heeft ingeset, en hij moet kiesen. |
| m 't geen heeft B |
als hij |
1 |
tegen |
1 heeft ingeset, en hij moet kiesen. |
| n 't geen heeft A |
als hij |
1 |
tegen |
2 heeft ingeset, en hij moet kiesen. |
| o 't geen heeft B |
als hij |
2 |
tegen |
2 heeft ingeset, en hij moet kiesen. |
| p 't geen heeft A |
als hij |
2 |
tegen |
3 heeft ingeset, en hij moet kiesen. |
| q 't geen heeft B |
als hij |
3 |
tegen |
3 heeft ingeset, en hij moet kiesen. |
| r 't geen heeft A |
als hij |
3 |
tegen |
4 heeft ingeset, en hij moet kiesen. |
| s 't geen heeft B |
als hij |
4 |
tegen |
4 heeft ingeset, en hij moet kiesen. |
| t 't geen heeft A |
als hij |
4 |
tegen |
5 heeft ingeset, en hij moet kiesen. |
Δ is een ducaet die ingeset werdtGa naar voetnoot6).
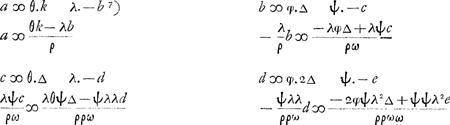
Ga naar voetnoot7)
| |
|
-
voetnoot1)
- La Pièce est empruntée aux p. 54-61 (numérotées 10-17 par Huygens) du Manuscrit C. Elle contient la solution du problème posé par Hudde dans sa lettre du 5 mai 1665 (voir la p. 350 du T. V) et de quelques autres problèmes qui s'y rattachent.
-
voetnoot2)
- Ce paragraphe s'occupe du problème de Hudde, où A doit choisir entre 2 jetons blancs et 1 noir, et de la généralisation que Huygens y a donnée en représentant le nombre des blancs par θ et celui des noirs par λ. Huygens traite conjointement ces deux problèmes, mais, pour éviter la confusion qui en résulterait ici, il nous a semblé préférable d'omettre tout ce qui se rapporte à la solution particulière sauf l'endroit où il s'agit de l'application de la solution générale à ce cas spécial. On peut encore consulter sur ces problèmes les p. 35-37 de l'Avertissement.
-
voetnoot3)
- Traduction: ‘A et B choisissent à l'aveuglette à tour de rôle, A toujours un de 3 [ou de θ + λ] jetons dout 2 [θ] blancs et 1 [λ] noir, mais B un d'un nombre inconnu de jetons blancs et noirs, à condition que celui qui tirera un jeton blanc aura tout ce qui est mis; mais celui qui tire un jeton noir ajoutera chaque fois un ducat à l'enjeu, et A tirera le premier. On demande lorsqu'on veut que les chances de A et de B soient équivalentes, quelle proportion devra exister entre les nombres des jetons blancs et noirs de B’.
-
voetnoot4)
- Traduction: ‘A choisit un de 3 [ou de θ + λ] jetons dont 2 [θ] blancs, 1 [λ] noir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot5)
- Traduction: ‘a est l'avantage de A quand il a mis 0 contre 0 et qu'il doit choisir’.
-
voetnoot6)
- Traduction: ‘Δ est un ducat qui est mis à l'enjeu’.
-
voetnoot7)
- Voir à propos de cette notation la note 6 de la p. 103.
-
voetnoot1)
- Voir plus haut à la p. 109. Dans ce qui suit, Huygens désigne par A le premier terme - λb/ϱ, par B le deuxième terme θk/ϱ du second membre de cette équation.
-
voetnoot2)
- Cette notation indique qu'on peut remplacer λψc/ϱω par
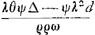 . .
-
voetnoot3)
- Il s'agit des pages dont nous avons emprunté ce qui précède la dernière équation de la p. 110.
-
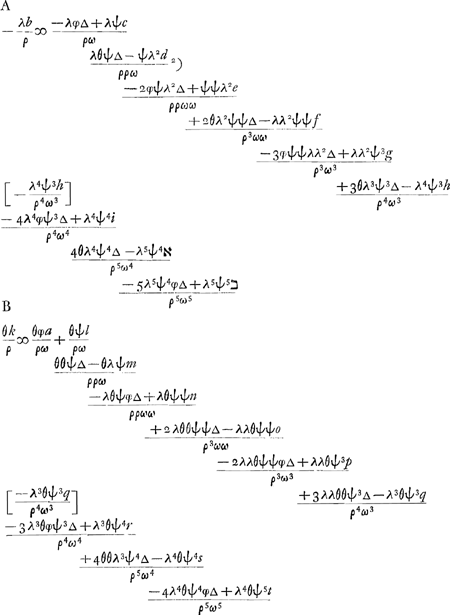
voetnoot1)
- Par ‘l'hypothese’ Huygens entend les définitions des quantités a, - b, etc. données au début de cette Pièce à la p. 109. Or, chacune des quantités, qui entrent dans une même suite, peut être considérée comme la somme de trois parties dont la première et la deuxième sont proportionnelles, respectivement, aux mises des joueurs A et B, lesquelles croissent chaque fois de l'unité, et dont la troisième ne varie pas. À la première et à la deuxième partie le raisonnement de Huygens s'applique; quant à la troisième, son produit avec les coefficients indiqués, s'approche a fortiori de
zéro.
-
voetnoot2)
- Puisque la solution cherchée dépend exclusivement des rapports qui existent entre les sommes des + et - de A et de B, on peut remplacer ces sommes par des quantités qui leur sont proportionnelles, et choisir pour l'une d'elles une valeur arbitraire. De cette manière il n'est pas nécessaire de déterminer la somme de l'une des suites formées par les quantités + ou - de A ou de B, comme Huygens l'avait fait pour les + de B à l'occasion du problème qui précède, où, évidemment, cette sommation ne pouvait être évitée; voir la p. 106.
-
voetnoot3)
- Cette notation indique que θψ est à φϱ comme λ est à λφϱ/θψ.
-
voetnoot4)
- Puisque les chances des deux joueurs doivent être équivalentes au commencement du jeu, on doit avoir a = 0 et, par suite, - A = B; voir la dernière équation de la p. 110 et la note 1 de cette même p. 110.
-
voetnoot5)
- Par cette règle le problème peut être considéré comme résolu. En effet, pour déterminer la proportion désirée entre les nombres φ et ψ des jetons blancs et noirs, il ne s'agit plus que de résoudre une équation quadratique à racines toujours réelles et de signes contraires, dont la racine positive est la seule qui satisfait aux conditions du problème.
-
voetnoot6)
- Application de la ‘Regula’ au problème posé par Hudde où θ = 2, λ = 1, ϱ = 3.
-
voetnoot7)
- On ne voit pas comment la première approximation a été obtenue, mais de petits calculs en marge du Manuscrit permettent de constater que la seconde a été trouvée en calculant la racine quadratique de 73000000 qui est égale à 8544, d'où il suit φ = 9544/6000 ψ = 1193/750 ψ.
-
voetnoot8)
- Voir à propos de cette proportion de 10 à 1, qu'on retrouve plusieurs fois dans la correspondance entre Huygens et Hudde, les pp. 386 et 393 du T. V.
-
voetnoot9)
- Dans ce paragraphe Huygens détermine l'avantage du joueurs A pour des valeurs données de θ, λ, φ et ψ; problème dont il a résolu un cas particulier dans l'Àppendice III (p. 102-107). À cet effet il doit chercher la somme de l'une des quatre suites dont il est question dans la note 2 de la page précédente, desquelles il choisit celle des ‘+ de B’.
-
voetnoot10)
- Voir les trois premiers termes positifs de la suite B de la p. III.
-
voetnoot1)
- Pour comprendre les calculs qui suivent, il suffira de considérer le ‘Theorema’ de la p. 106 et l'algorithme dont Huygens s'est servi à cette page pour la sommation de la suite des ‘+ de B’.
-
voetnoot2)
- Comparez l'équation ‘a ∞ - λb/ϱ + θk/ϱ’ de la p. 110.
-
voetnoot3)
- Application au problème de croix ou pile qu'on trou vera formulé au début de l'Appendice V, p. 116. Il est clair que la solution de ce problème peut être obtenue au moyen de la règle générale précédente en posant θ = λ = φ = ψ = 1, et par suite ϱ = ω = 2.
-
voetnoot4)
- Application au problème traité dans l'Appendice III, p. 102, où θ = 2, λ = 1, φ = 1, ψ = 2, donc ϱ = ω = 3.
-
voetnoot5)
- Voir sur ce problème une lettre de Huygens à Hudde du 7 juillet 1665, p. 393 du T. V.
-
voetnoot6)
- Lisez 5/11 Δ. On ne rencontre ce problème nulle part dans les lettres échangées entre Huygens et Hudde, ni ailleurs dans la correspondance de Huygens.
|