Oeuvres complètes. Tome XIV. Probabilités. Travaux de mathématiques pures 1655-1666
(1920)–Christiaan Huygens–
[pagina 60]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Du calcul dans les jeux de hasard.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 61]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Van rekeningh in spelen van geluck.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 62]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
écusGa naar voetnoot1) dans une main et sept dans l'autre, et me donne à choisir entre les deux mains, je dis que cet offre a pour moi la même valeur que si j'étais certain d'obtenir cinq écus; en effet, lorsque je possède cinq écus, je puis de nouveau me mettre dans le cas d'avoir des chances égales d'obtenir trois ou sept écus, et cela dans un jeu équitable, comme cela sera démontré plus basGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition I.Avoir des chances égales d'obtenir a ou b me vaut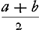 . .
Afin de non seulement démontrer cette règle mais aussi de la découvrir, appelons x la valeur de ma chance. Il faut donc que, possédant x, je puisse me procurer de nouveau la même chance par un jeu équitable. Supposons que ce jeu soit le suivant. Je joue x contre une autre personne, dont l'enjeu est également x; il est convenu que celui qui gagne donnera a à celui qui perd. Ce jeu est équitable, et il appert que j'ai ainsi une chance égale d'avoir a en perdant, ou 2x - a en gagnant le jeu; car dans ce dernier cas j'obtiens l'enjeu 2x, duquel je dois donner a à l'autre joueur. Si 2x - a était égal à b, j'aurais donc une chance égale d'àvoir a ou d'avoir b. Je pose donc 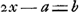 , d'où je tire la valeur de ma chance , d'où je tire la valeur de ma chance 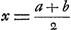 . La preuve en est aisée. En effet, possédant . La preuve en est aisée. En effet, possédant 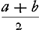 , je puis hasarder cette somme contre un autre joueur qui mettra également , je puis hasarder cette somme contre un autre joueur qui mettra également 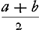 , et convenir avec lui que le gagnant donnera a à l'autre. J'aurai de sorte une chance égale d'avoir a si je perds, ou b si je gagne; car dans ce dernier cas j'obtiens l'enjeu a + b et je lui en donne a. , et convenir avec lui que le gagnant donnera a à l'autre. J'aurai de sorte une chance égale d'avoir a si je perds, ou b si je gagne; car dans ce dernier cas j'obtiens l'enjeu a + b et je lui en donne a.
En chiffres. Lorsque j'ai une chance égale d'avoir 3 ou d'avoir 7, la valeur de ma chance est 5 d'après cette Proposition; et il est certain qu'ayant 5 je puis me procurer de nouveau la même chance. En effet, si je joue 5 contre une autre personne dont la mise est également 5, à condition que le gagnant donnera 3 à l'autre, c'est là un jeu équitable, et il est évident que j'ai la même chance d'avoir 3 en perdant, ou d'avoir 7 en gagnant; car en ce cas j'obtiens 10, dont je lui en donne 3. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 63]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d'eene handt 3 schellingenGa naar voetnoot1) verbergt, en in d'ander 7 schellingen, ende my te kiesen geeft welck van beyde ick begeere te hebben, ick segge dit my even soo veel weerdt te zijn, als of ick 5 schellingen seecker hadde. Om dat, als ick 5 schellingen hebbe, ick wederom daer toe kan geraecken, dat ick gelijcke kans sal hebben, om 3 of 7 schellingen te krijgen, en dat met rechtmatigh spel: gelijck hier naer sal betoont werdenGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
I. Voorstel.Als ick gelijcke kans hebbe om a of b te hebben, dit is my so veel weerdt als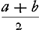 . .
Om desen regel niet alleen te bewijsen maer oock eerst uyt te vinden, soo zy gestelt x voor het geene dat mijn kansse weerdt is. Soo moet ick dan x hebbende weder tot deselfde kans konnen geraecken met rechtmatig spel. Laet dit het spel zijn: dat ick tegen een ander speele om x, en dat den anderen daer tegen mede x in-sette: ende dat bedongen zij, dat de geene die wint aen die verliest sal geven a. Dit spel is rechtmaetigh, ende het blijckt dat ick hier door gelijcke kans heb om a te hebben, te weeten, als ick 't spel verlies; of 2x - a, als ick 't win: want alsdan soo treck ick 2x die in-geset zijn, daer van ick den anderen moet geven a. Indien nu 2x - a soo veel ware als b, soo soude ick ghelijcke kans hebben tot a of b. Ick stelle dan 2x - a ∞ b, so komt x ∞ 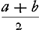 , voor de waerde van mijn kans. En het bewijs hier van is licht. Want , voor de waerde van mijn kans. En het bewijs hier van is licht. Want 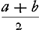 hebbende, soo kan ick dat tegen een ander waegen die mede hebbende, soo kan ick dat tegen een ander waegen die mede 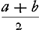 sal in-setten, ende bedingen dat die het spel wint, den anderen sal a geven. Waer door ick gelijcke kans sal bekomen om a te hebben, te weeten, als ick verlies, of b als ick win; want alsdan soo treck ick a + b dat ingeset is, ende geef hem daer van a. sal in-setten, ende bedingen dat die het spel wint, den anderen sal a geven. Waer door ick gelijcke kans sal bekomen om a te hebben, te weeten, als ick verlies, of b als ick win; want alsdan soo treck ick a + b dat ingeset is, ende geef hem daer van a.
In getaelen. Indien ick gelijcke kans heb om 3 te hebben of 7, soo is door dit Voorstel mijn kansse 5 weerdt; ende het is seecker dat ick 5 hebbende weder tot de selfde kansse kan geraecken. Want speelende om de selve tegen een ander die daer 5 tegen set, met beding dat de geene die wint den anderen 3 sal geven; soo is dit rechtmaetig spel, ende het blijckt dat ick gelijcke kans hebbe om 3 te hebben, te weeten, als ick verlies, of 7 indien ick win; want alsdan treck ick 10, daer van ick hem 3 geef. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 64]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition II.Avoir des chances égales d'obtenir a, b ou c me vaut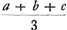 . .
Pour trouver ceci, appelons derechef x la valeur de ma chance. Il faut donc que, possédant x, je puisse me procurer de nouveau les mêmes chances par un jeu équitable. Que ce jeu soit le suivant: Je joue contre deux autres personnes; chacun de nous trois met x; je conditionne avec la première qu'elle me donnera b si elle gagne le jeu et réciproquement, avec la seconde qu'elle me donnera c si elle gagne et réciproquement. Il appert que ce jeu est équitable. J'aurai ainsi une change égale d'avoir b, savoir si le premier joueur gagne, ou c, si le deuxième gagne, ou enfin 3x - b - c si je gagne moi-même; car dans ce dernier cas j'obtiens l'enjeu 3x, dont je donne b à l'un et c à l'autre. Or, si 3x - b - c était égal à a, j'aurais des chances égales d'avoir a, b ou c. Je pose donc 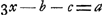 , d'où je tire , d'où je tire 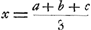 , valeur de ma chance. On trouve de même qu'avoir des chances égales d'obtenir a, b, c ou a me vaut , valeur de ma chance. On trouve de même qu'avoir des chances égales d'obtenir a, b, c ou a me vaut 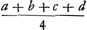 , et ainsi de suite. , et ainsi de suite.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition IIIGa naar voetnoot1).Avoir p chances d'obtenir a et q d'obtenir b, les chances étant équivalentes, me vaut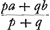 . .
Pour découvrir cette règle, appelons de nouveau x la valeur de ma chance. Il faut donc que, possédant x, je puisse rentrer dans mon premier état par un jeu équitable. À cet effet je prends un nombre de joueurs tel qu'avec moi il y en a p + q en tout, dont chacun met x, de sorte que l'enjeu total sera px + qx; chacun | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 65]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
II. Voorstel.Als ick gelijcke kans hebbe tot a of b of c, het is my soo veel weerdt als of ick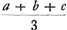 hadde. hadde.
Om dit wederom te vinden, soo zy als vooren gestelt x voor de waerde van mijn kans. Soo moet ick dan x hebbende weder tot de selfde kansse konnen geraecken door rechtmaetig spel. Laet dit het spel zijn, dat ick tegen 2 andere speele, insettende ieder van ons drien x, ende laet ick met den eenen dese voorwaerde maecken, dat soo hy het spel wint hy my sal geven b, ende ick b aen hem, soo ick het kome te winnen. Met den anderen laet ick dese voorwaerde maecken, dat hy het spel winnende my sal geven c, of ick aen hem c als ick het win. Het blijckt dat dit spel rechtmaetig is. Ende ick sal daer door gelijcke kans hebben, om b te hebben, te weeten, als het den eersten wint, of c, als het den tweeden wint, of 3x - b - c als ick het win; want dan treck ick 3x die ingeset zijn, en geve daer van aen den eenen b, aen den anderen c. Indien nu 3x - b - c gelijck waer aen a, so soude ick gelijcke kans hebben tot a of b of c. So stel ick dan 3x - b - c ∞ a, en komt x ∞ 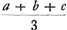 , voor de waerde van mijn kans. Op gelijcke manier werdt gevonden, dat als ick gelijcke kans hebbe tot a of b of c of d, dit soo veel weerdt is als , voor de waerde van mijn kans. Op gelijcke manier werdt gevonden, dat als ick gelijcke kans hebbe tot a of b of c of d, dit soo veel weerdt is als 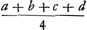 , ende soo voorts. , ende soo voorts.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
III. VoorstelGa naar voetnoot1).Als het getal der kanssen die ick hebbe tot a is p, ende het getal der kanssen die ick tot b heb is q; nemende altijdt dat ieder kans even licht kan gebeuren: Het is my weerdt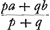 . .
Om desen regel uyt te vinden, so zy wederom x gestelt voor het geene mijn kans weerdt is. So moet ick x hebbende wederom in staet als vooren konnen geraecken door rechtmaetig spel. Laet ick hier toe soo veel speelders nemen, datse met my te saemen het getal van p + q uytmaecken, insettende elck x, soo datter | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 66]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
joue pour son propre compte avec une même chance de gagner. Supposons en outre qu'avec q joueurs, c'est-à-dire avec chacun d'eux en particulier, je fasse cette convention que si l'un d'eux gagne la partie, il me donnera la somme b, et que si moi je gagne, je lui donnerai la même somme. Supposons enfin qu'avec les p - 1 joueurs qui restent, ou plutôt avec chacun d'eux en particulier, je fasse la convention que si l'un d'eux gagne la partie, il me donnera la somme a, et que je lui donnerai également la somme a si c'est moi qui gagne la partie. Il est évident qu'à ces conditions le jeu est équitable, attendu que les intérêts d'aucun joueur ne se trouvent lésés. On voit de plus que j'ai maintenant q chances d'obtenir b, p - 1 chances d'obtenir a et une chance (au cas où c'est moi qui gagne) d'avoir px + qx - bq - ap + a; en effet, dans ce dernier cas je reçois l'enjeu px + qx dont je dois céder b à chacun des q joueurs et a à chacun des p - 1 joueurs, ce qui fait en tout qb + pa - a. Or, si px + qx - bq - ap + a était égal à a, j'aurais p chances d'avoir a (car j'avais déjà p - 1 chances d'obtenir cette somme) et q chances d'avoir b; je serais donc revenu à mes chances premiàres. Je pose donc 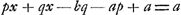 , et je trouve , et je trouve
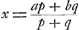 pour la valeur de ma chance, conformément à l'énoncé. pour la valeur de ma chance, conformément à l'énoncé.
En chiffres. Si j'ai 3 chances de gagner 13, et 2 chances de gagner 8, je possède pour ainsi dire 11, d'après cette règle. Et il est aisé de faire voir qu'étant en possession de 11, je puis me procurer de nouveau ces mêmes chances. En effet, je puis jouer avec 4 autres personnes et chacun de nous cinq peut mettre 11; je conviendrai alors avec deux de ces personnes que si l'une d'elles gagne la partie elle me donnera 8 et que, si c'est moi qui gagne, je leur donnerai à chacune la même somme. De même je conviens avec les deux autres que celle des deux qui gagne la partie me donnera 13 et que, si moi je gagne, je leur donnerai à chacune 13 également. Ce jeu sera équitable. Et l'on voit que j'ai ainsi 2 chances d'avoir 8, savoir au cas où l'un des deux joueurs qui m'ont promis cette somme emporte l'enjeu, et 3 chances d'avoir 13, savoir si l'un des deux autres qui doivent me donner cette somme gagne la partie, ou si je la gagne moi-même. En effet, dans ce dernier cas je reçois l'enjeu qui est de 55, dont je dois donner 13 à chacun de deux joueurs et 8 à chacun de deux autres joueurs, de sorte qu'il m'en reste également 13. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition IV.Supposons que je joue contre une autre personne à qui aura gagné le premier trois parties, et que j'aie déjà gagné deux parties et lui une. Je veux savoir quelle partie de l'enjeu m'est due au cas où nous voulons interrompre le jeu et partager équitablement les mises. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 67]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
in sal staen px + qx, ende elck voor sijn hooft speelende met even goede kans om te winnen. Voorts laet ick met soo veel deser speelders, als het getal q is, ieder in 't byzonder dit verding maecken, dat als hy het spel komt te winnen hy my sal b geven, of ick daer entegens het selfde aen hem als ick het win. Laet ick oock met de rest van de speelders, zijnde p - 1, dit verding maecken met elck in 't bysonder, dat hy het spel winnende my sal a geven, ende ick hem van gelijcken a indien ick het kome te winnen. Het blijckt dat dit spel met dese voorwaerden rechtmaetig is, niemandt hier door verongelijckt wesende. Het blijckt mede dat ick alsnu q kanssen hebbe tot b, ende p - 1 kanssen tot a, en 1 kansse, (te weeten, als ick het win,) tot px + qx - bq - ap + a, want alsdan soo treck ick px + qx dat ingeset is, waer van ick aen yder van q speelders moet geven b, en aen yder van p - 1 speelders a, maeckende te saemen qb + pa - a. Indien nu px + qx - bq - ap + a gelijck waer aen a, soo soude ick p kanssen hebben tot a, (want ick alreede p - 1 kanssen daer toe hadde) ende q kanssen tot b, ende soude also tot mijn voorige kansse wederom geraeckt zijn. Soo stel ick dan te zijn px + qx - bq - ap + a ∞ a; en komt 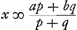 voor het geene dat mijn kansse
weerde was, gelijck in 't begin is gestelt. voor het geene dat mijn kansse
weerde was, gelijck in 't begin is gestelt.
In getaelen. Indien ick 3 kanssen hebbe tot 13, en 2 kanssen tot 8, soo heb ick door desen regel soo veel als 11. En is licht te thoonen, dat ick 11 hebbende wederom tot de selfde kansse kan geraecken. Want speelende tegen 4 andere, en settende elck van ons vyven 11 in, soo sal ick met 2 van haer verdraegen elck in 't bysonder, dat soo hy het spel wint hy my 8 sal geven, of ick aen hem 8, indien ick het winne. Met de ander 2 van gelijcken, dat die van haer het spel wint my sal 13 geven, of ick aen hem 13 als ick het kom te winnen. Welck speelen rechtmaetig is. Ende het blijckt, dat ick daer door 2 kanssen hebbe tot 8, naementlijck als een van de twee die my 8 belooft hebben wint, en 3 kanssen tot 13, te weeten als een van de twee andere die my 13 gheven moeten wint, of als ick selver het spel win. Want ick het winnende soo treck ick 't geen ingeset is dat's 55, daer van ick aen elck van 2 moet geven 13, en aen elck van de 2 andere 8, soo dat voor my dan oock 13 overblijft. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
IV. Voorstel.Genomen dan dat ick tegens een ander speele ten dryen uyt en dat ick alreede 2 spelen hebbe en hy maer een. Ick wil weeten, ingevalle wy het spel niet en wilden voortspeelen, maer het geen ingeset is gerechtelijck wilden deelen, hoeveel my daer van komen soude. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 68]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Il est nécessaire de commencer par les cas les plus simples pour arriver à la solution des questions proposées en premier lieuGa naar voetnoot1) au sujet du partage de l'enjeu entre plusieurs joueurs dont les chances sont inégales. Il faut remarquer d'abord qu'il suffit de tenir compte des parties qui manquent de part et d'autreGa naar voetnoot2). Car il est certain que si nous jouions à qui aura gagné le premier 20 parties, et que j'eusse gagné 19 parties et mon adversaire 18, j'aurais le même avantage que dans le cas énoncé, où sur trois parties j'en ai gagné deux et lui une seule, et cela parce que dans les deux cas il ne me manque qu'une partie tandis qu'il lui en manque deux. Ensuite, pour calculer la part qui revient à chacun de nous, il faut faire attention à ce qui arriverait si nous continuions le jeu. Il est certain que si je gagnais la première partie, j'aurais terminé le jeu, et qu'ainsi j'obtiendrais l'enjeu tout entier que j'appellerai a. Mais si l'autre joueur gagnait la première partie nos chances seraient désormais égales, attendu qu'il nous manquerait une partie à chacun; nous aurions donc chacun droit à 1/2 a. Or, il est évident que j'ai autant de chance de gagner la première partie que de la perdre. J'ai donc des chances égales d'avoir a ou 1/2 a, ce qui, d'après la première PropositionGa naar voetnoot3), équivaut à la somme des moitiés, c'est-à-dire à 3/4 a, de sorte qu'il reste 1/4 a pour mon adversaire. J'aurais d'ailleurs pu faire pour lui aussi un calcul direct, en suivant la même méthode. Il en ressort que celui qui voudrait continuer le jeu en mon lieu, pourrait m'offrir 3/4 a, et qu'on peut donc toujours hasarder 3 contre 1 en acceptant de gagner un jeu avant qu'un autre joueur en gagne deux. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition V.Supposons qu'il me manque une partie à moi et trois à mon adversaire. Il s'agit de partager l' enjeu dans cette hypothèse.
Considérons de nouveau l'état où nous serions si moi je gagnais la première partie ou bien si mon adversaire la gagnait. Si je la gagnais, j'aurais l'enjeu a, mais si c'était lui qui la gagnait, il lui en manquerait encore 2 contre une qui me manquerait à moi; nous nous trouverions donc dans l'état considéré dans la proposition précédente, et il me reviendrait 3/4 a, comme nous l'avons vu à cet endroit. J'ai | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 69]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Om nu tot de eerst voor-gestelde questienGa naar voetnoot1) te komen, aengaende de verdeelingh onder verscheyde speelders te maecken, als haere kanssen ongelijck zijn, soo is 't noodigh van de lichtste te beginnen. Voor eerst moet acht genomen werden alleen op de spelen, die weder-zijds noch ontbreecken. Want het is seecker, dat, of wy een 20gen uyt speelden, en dat ick 19 hadde, en die tegens my speelt 18, dat ick even het selfde voordeel soude hebben als nu, hebbende van drie spelen 2 gewonnen en hy een: door dien in beyde gevallen my noch maer een spel ontbreeckt en hem twee spelen. Voorts om te vinden, wat deel ons elck toekomt, soo moet aengemerckt werden watter soude gebeuren indien wy voort speelden. Het is seecker indien ick het eerste spel quam te winnen, dan soude ick uyt wesen en hebben al dat ingeset is, het welck zy genoemt a. Maer indien den anderen het eerste spel won, dan zouden wy gelijcke kans hebben, elck noch een spel ontbreeckende, en daerom elck gerechtige zijn tot 1/2 a. Het is nu seecker dat ick gelijcke kans heb om dat eerste spel te winnen of te verliesen. Soo heb ick dan gelijcke kans om a te hebben of 1/2 a, het welck door het 1ste VoorstelGa naar voetnoot2) soo veel is als of ick van beyde de helft hadde dat is 3/4 a, en blijft voor die tegens my speelt 1/4 a. Wiens rekening oock van eersten aen op de selve manier hadde konnen gemaeckt werden. Hier uyt blijckt, dat die mijn spel soude willen overnemen my 3/4 a daer voor kan geven; en dat men dienvolgens altijdt kan 3 tegen 1 setten, als men neemt 1 spel te winnen, eer dat een ander 2 spelen wint. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
V. Voorstel.Zij gestelt dat my 1 spel ontbreeckt, en die tegens my speelt 3 spelen. Nu moet men de verdeeling maecken.
Laet ons wederom acht nemen, in wat staet wy souden zijn, indien ick of hy het eerste spel quam te winnen. Als ick het won soo had ick het geen in-geset is dat is a, maer als hy het eerste spel won, dan souden hem noch 2 spelen ontbreecken tegen mijn 1, en wy souden daerom in staet zijn gelijck in 't voorgaende voorstel gestelt wierdt, en my toekomen 3/4 a, gelijck aldaer bethoont is. Soo heb | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 70]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
donc des chances égales d'obtenir a ou 3/4 a, ce qui, d'après la première PropositionGa naar voetnoot1), me vaut 7/8 a. Reste 1/8 a pour l'autre joueur. Ma chance est donc à la sienne comme 7 est à 1. De même que ce calcul-ci dépend du calcul précédent, de même le résultat obtenu ici est nécessaire au calcul qui se rapporte au cas suivant, où il me manque une partie, tandis qu'il en manque quatre à mon adversaire. On trouve de la même façon qu'il me revient dans ce cas 15/16 de l'enjeu, et 1/16 à lui. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VI.Supposons qu'il me manque deux parties et qu'il en manque trois à mon adversaire.
La première partie aura maintenant pour effet, ou bien qu'il me manquera encore une partie à moi et trois à l'autre joueur (auquel cas il me reviendra 7/8 a d'après ce qui précède), ou bien qu'il nous manquera deux parties à chacun de nous, auquel cas il me revient 1/2 a, attendu que nos chances seront devenues égales. Mais j'ai une chance contre une de gagner la première partie ou de la perdre; j'ai donc des chances égales d'obtenir 7/8 a ou 1/2 a, ce qui me vaut 11/16 a d'après la première PropositionGa naar voetnoot1). Onze parties de l'enjeu me sont donc dues contre cinq à mon adversaire. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VII.Supposons qu'il me manque encore deux parties et lui quatre.
Ayant gagné la première partie, j'aurai donc encore 1 partie à gagner contre 4; l'ayant perdue, encore 2 contre 3. J'ai donc des chances égales d'avoir 15/16 a ou 11/16 a, ce qui me vaut 13/16 a d'après le première PropositionGa naar voetnoot1). Il en résulte | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 71]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ick dan een kans tegen een om a te hebben of 3/4 a, het welck so veel is door het 1ste VoorstelGa naar voetnoot1) als 7/8 a. En blijft 1/8 a voor den anderen. Soo dat mijn kans is tot de syne als 7 tot 1. Gelijck nu tot dese reeckeningh vereyscht is geweest de voorgaende, so is wederom dese nodigh tot de volgende, te weeten, als men stelt dat my 1 spel ontbreeckt, ende mijn party 4 spelen. En werdt op gelijcke manier bevonden, dat my komt 15/16 van 't geen ingeset is, en hem 1/16. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VI. Voorstel.Zij gestelt dat my twee spelen ontbreecken, en hem die tegen my speelt drie spelen.
Nu sal gebeuren door het eerste spel, of dat my noch 1 spel sal ontbreecken en hem 3 (toekomende my daerom door het voorgaende 7/8 a), of dat ons elck noch twee spelen sullen ontbreecken, waer door my komt 1/2 a, om dat dan elck even goede kans heeft. Maer ick heb een kans tegen een, om het eerste spel te winnen of te verliesen; soo heb ick dan ghelijcke kans tot 7/8 a of 1/2 a, het welck my weerdt is 11/16 a door het eerste VoorstelGa naar voetnoot1). Soo dat my komen elfdeelen van 't geen ingestelt is, en die tegens my speelt vijf deelen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VII. Voorstel.Zy gestelt dat aen my noch twee spelen ontbreecken en hem 4 spelen.
Soo sal ick het eerste spel winnende noch 1 spel tegen 4 te winnen hebben; of, het selve verliesende, noch 2 tegen 3. Soo dat ick gelijcke kans heb tot 15/16 a of 11/16 a, dat soo veel is als 13/16 a, door het 1ste VoorstelGa naar voetnoot1). Waer uyt blijckt dat het | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 72]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
qu'il est plus avantageux d'avoir deux parties à gagner contre quatre, qu'une contre deux. Car dans ce dernier cas: à savoir le cas d'une partie contre deux, ma part est 3/4 a d'après la 4ième PropositionGa naar voetnoot1), ce qui est moins que 13/16 a. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VIII.Supposons maintenant que trois personnes jouent ensemble et qu'il manque une partie à la première ainsi qu'à la deuxième, mais qu'il en manque deux à la troisième.
Pour calculer la part du premier joueur, il faut derechef tenir compte de ce qui lui reviendrait si lui-même ou si l'un des deux autres gagnait la première partie. S'il la gagnait, il obtiendrait l'enjeu que j'appelle a. Si le deuxième gagnait cette partie, le premier n'aurait rien, car le deuxième aurait terminé le jeu. Si le troisième gagnait, il manquerait encore une partie à chacun des trois: par suite le premier, ainsi que chacun des deux autres, aurait droit à 1/3 a. Le premier a donc 1 chance d'obtenir a, 1 chance d'obtenir 0, et 1 chance d'obtenir 1/3 a (car chacun des trois a la même chance de gagner la première partie), ce qui lui vaut 4/9 a d'aprés la deuxième PropositionGa naar voetnoot2). Au deuxième joueur revient donc la même part, c'est-à-dire, 4/9 a, de sorte qu'il reste 1/9 a pour le troisième. On aurait pu trouver directement la part de ce dernier et calculer en partant de là la part des autresGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition IXGa naar voetnoot4).Pour calculer la part de chacun d'un nombre donné de joueurs, auxquels manquent des parties en nombres donnés pour chacun d'eux séparémentGa naar voetnoot5), il faut d'abord se rendre | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 73]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
beter kans is 2 spelen te moeten winnen tegen 4, als een spel tegen twee. Want in dit laetste geval, te weeten, van 1 tegen 2, so is mijn deel 3/4 a, door het 4de VoorstelGa naar voetnoot1), zijnde minder als 13/16 a. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
VIII. Voorstel.Laet ons nu stellen dat drie persoonen t' samen speelen, daer van den eersten 1 spel ontbreeckt, den tweeden mede 1 spel, maer den derden 2 spelen.
Om het deel van den eersten te vinden, so moet weder aengemerckt werden wat hem soude komen, indien hy of een van de twee anderen het eerste spel quam te winnen. Als hy het won soo had hy het geen dat ingeset is, 't welck zy a. Als het den tweeden won soo hadde den eersten niets, want den tweeden soude daar mede uyt zijn. Als het den derden won soo soude aen elck van drien noch 1 spel ontbreecken, en daerom den eersten so wel als elck van d'andere 1/3 a toekomen. Soo isser dan voor den eersten 1 kans tot a, 1 kans tot 0, en een kans tot 1/3 a, (want het even licht kan gebeuren aen yeder van drien het eerste spel te winnen,) het welck hem weerdt is 4/9 a door het 2de VoorstelGa naar voetnoot2). Soo komt dan oock voor den tweeden 4/9 a, en voor den derden blijft over 1/9 a. Wiens deel in 't bysonder oock hadde konnen gevonden worden, en daer door de andere haer deelen bepaeltGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
IX. VoorstelGa naar voetnoot4).Om tusschen soo veel speelders als voor-gestelt zijn, waer van d' eene meer en d'ander minder speelen ontbreecken een ieder haer deel te vindenGa naar voetnoot5), soo moet ingesien worden, wat | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 74]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
compte de ce qui reviendrait à celui dont on veut savoir la part dans le cas où lui et dans ceux où chacun des autres à son tour aurait gagné la première partie suivante. En ajoutant toutes ces parts et en divisant la somme par le nombre des joueurs ou trouve la part cherchée du joueur considéré.
Supposons que 3 personnes A, B et C jouent ensemble et qu'il manque 1 partie à A, 2 à B et également 2 à C. On veut savoir quelle part de l'enjeu que j'appelle q revient au joueur B. Nous devons examiner d'abord à quelles parts B aurait droit, si lui-même ou A ou C aurait gagné la première partie suivante. Si A la gagnait, il aurait terminé le jeu. B recevrait par conséquent 0. Si B était lui-même le gagnant, 1 partie lui manquerait encore, ainsi qu'à A, tandis qu'il en manquerait 2 à C. B aurait donc droit à 4/9 q d'après la huitième Proposition. Enfin, si C gagnait la première partie suivante, il manquerait 1 partie à A et à C, tandis qu'il en manquerait 2 à B; B, par conséquent, aurait droit à 1/9 q d'après la même Proposition VIII. Il faut maintenant ajouter les parts qui reviendraient à B dans ces trois hypothèses, savoir 0, 4/9 q et 1/9 q. Il vient 5/9 q. En divisant ce nombre par 3, le nombre des joueurs, on trouve 5/27 q. C'est là la part juste du joueur B. On le démontre par la deuxième PropositionGa naar voetnoot1). En effet, comme B a des chances égales d'obtenir 0, 4/9 q ou 1/9 q, il possède, d'après cette Proposition, pour ainsi dire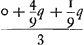 ou 5/27 qGa naar voetnoot2). Et il est certain que le diviseur 3 est égal au nombre des joueurs. ou 5/27 qGa naar voetnoot2). Et il est certain que le diviseur 3 est égal au nombre des joueurs.
Mais pour savoir ce qui reviendra dans chaque cas à chaque joueur lorsque luimême ou l'un quelconque des autres aura gagné la première partie suivante, il faut d'abord faire le calcul pour les cas les plus simples et ensuite, en partant de là, pour les cas suivants. Car de même que le dernier cas que nous avons considéré ne pouvait être soumis au calcul sans que d'abord la huitième Proposition eût été résolue, dans laquelle les parties manquantes étaient aux nombres de 1, de 1 et de 2, de même aussi la part de chaque joueur au cas où les nombres des parties manquantes sont 1, 2, 3Ga naar voetnoot3) ne peut être calculée sans qu'on cherche d'abord cette | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 75]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
hem, wiens deel men begeert te weeten, soude toekomen, indien of hy, of elck van d'andere in 't besonder het eerste volgende spel quam te winnen. Dit dan alles te saemen geaddeert en door het getal der speelders gedeelt, soo komt het gesochte gedeelte van den eenen.
Zy genomen dat 3 persoonen A, B, en C te saemen speelen, en dat aen A een spel ontbreeckt, aen B 2 spelen, en aen C van gelijcken 2 spelen. Men begeert te weeten wat deel aen B toekomt van het geene ingeset is, het welck zy genoemt q. Voor eerst moeten wy ondersoecken wat B soude komen, als hy selfs, of A, of C het eerste volgende spel quam te winnen. Als het A won, so soude hy uyt zijn, en dienvolgens soude B toekomen 0. Als B selfs het won, so ontbrack hem noch 1 spel, en aen A mede 1 spel, maer aen C 2 spelen. Daerom soude B in dit geval toekomen 4/9 q door het 8ste Voorstel. Eyndelijck als C het eerste volgende spel quam te winnen, soo soude A en C elck 1 spel ontbreecken, maer aen B 2 spelen; en dienvolgens soude B komen 1/9 q, door het selfde 8ste Voorstel. Nu moet geaddeert werden het geen in deze 3 voorvallen aen B soude toekomen, te weeten, 0, 4/9 q, 1/9 q en komt 5/9 q. Dit door 3, het getal der speelders, gedeelt, komt 5/27 q. 'Twelck B zijn gerechte deel is. Het bewijs nu hier van blijckt door het 2de VoorstelGa naar voetnoot1). Want naer dien B gelijcke kans heeft tot 0, 4/9 q, of 1/9 q, soo heeft hy door het 2de Voorstel soo veel als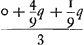 dat is 5/27 qGa naar voetnoot2). Ende het is seecker dat desen divisor 3 het getal van de speelders is. dat is 5/27 qGa naar voetnoot2). Ende het is seecker dat desen divisor 3 het getal van de speelders is.
Doch om te weeten, wat iemandt komt in elck geval, te weeten, als hy selfs of een van d'andere het eerste volgende spel wint: soo moeten de simpelste voorvallen eerst uytgevonden werden, en door haer behulp de volgende. Want gelijck dit laetste voorval niet konde afgedaen werden sonder dat eerst dat van het 8ste Voorstel uytgereeckent was, in 't welck de resterende spelen waeren 1, 1, 2, soo kan insgelijcks ieders deel niet gevonden werden in so een geval, als de resterende spelen zijn 1, 2, 3Ga naar voetnoot3), of men moet eerst uytgereeckent hebben het voorval van 1, 2, 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 76]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
part dans le cas des nombres 1, 2, 2, comme nous venons de le faire, ainsi que dans celui des nombres 1, 1, 3, ce qui peut être fait d'après la huitième Proposition. C'est en suivant cette méthode qu'on trouve les parts correspondant aux nombres du tableau suivant, ainsi qu'à une infinité d'autres. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tableau pour trois joueurs.
À l'égard des dés, on peut poser ces questions: à savoir en combien de fois l'on peut accepter de jeter avec un dé un 6 ou bien un des autres nombres; de même en combien de fois 2 six avec 2 dés ou 3 six avec 3 dés. Et bien d'autres questions encore. Pour les résoudre, il faut remarquer ce qui suit. D'abord qu'on peut faire avec un dé six coups différents également vraisemblables. Car je suppose que le dé a la forme d'un Cube parfait. Ensuite qu'on peut faire 36 coups différents avec 2 dés, lesquels ont aussi des vraisemblances égales. En effet, avec chaque coup du premier dé chacun des 6 coups du deuxième dé peut se combiner. Et 6 fois 6 font 36. De même qu'il y a 216 coups de 3 dés. Car avec chacun des 36 coups | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 77]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
gelijck wy terstond gedaen hebben, ende noch dat van 1, 1, 3, het welck door behulp van het 8ste Voorstel mede konde bereeckent werden. Op dese manier dan werden vervolgens al de voorvallen uytgevonden, die in de volgende tafel zijn vervat, en oneyndelijcke andere. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Tafel voor drie Speelders.
De dobbel-steenen aengaende konnen dese questien werden voorgestelt, te weeten, van hoeveel reysen men kan nemen met eene steen een 6 te werpen of een van d'ander ooghen. Oock van hoeveel reysen 2 sessen met 2 steenen, of 3 sessen met 3 steenen. Ende noch veel andere. Om welcke te solveeren, so moet hier op werden acht genomen. Eerstelijck dat op 1 steen zijn 6 verscheyde werpen, die even licht konnen gebeuren. Want ick neeme dat een dobbel-steen de perfecte figure van een Cubus heeft. Voorts, dat op 2 steenen sijn 36 verscheyde werpen, die insgelijcx even licht konnen voorkomen. Want tegen elcke werp van de eene steen kan een van de 6 werpen van d'andere steen te gelijck boven leggen. En 6 mael 6 maeckt 36. Oock dat op 3 steenen zijn 216 werpen. Want tegen elck van de 36 werpen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 78]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
des 2 dés peut se combiner l'un quelconque des 6 coups du troisième. Et 6 fois 36 font 216. On trouve de la même façon qu'il y a 6 × 216 ou 1296 coups de quatre dés; et qu'on peut en continuant ainsi calculer le nombre de coups pour un nombre quelconque de dés: on multiplie par 6 le nombre précédent de coups, chaque fois qu'on ajoute un nouveau dé. Ensuite, il faut savoir qu'avec deux dés on ne peut faire qu'un coup de 2 ou de 12 points, et 2 coups de 3 ou de 11 points. En effet, si nous appelons les dés A et B respectivement, il est évident que pour jeter 3 points A peut donner un as et B un 2, ou bien B un as et A un 2. De même pour obtenir 11 points, A peut donner 5 et B 6, ou bien A 6 et B 5. Le coup de 4 points est triple, savoir A 1, B 3, ou A 3, B 1, ou A 2, B 2. Le coup de 10 points est également triple. Celui de 5 ou de 9 points, quadruple. Celui de 6 ou de 8 points, quintuple. Celui de 7 points, sextuple.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition X.Trouver en combien de fois l'on peut accepter de jeter un six avec un dé.
Il est certain que le joueur qui accepte de jeter un 6 en un seul coup à 1 chance de gagner l'enjeu et 5 de perdre. Car il y a 5 coups contre lui et pas plus qu'un seul pour lui. Appelons l'enjeu a. Il a donc 1 chance d'obtenir a et 5 chances de n'obtenir rien, ce qui d'après la deuxième PropositionGa naar voetnoot1) lui vaut 1/6 a. Il reste 5/6 a pour celui qui l'engage à jeter le dé. Celui qui joue une partie d'un seul coup, ne peut donc mettre que 1 contre 5. La part de celui qui parie de jeter un 6 en deux coups, est calculée de la façon suivante. S'il jette un 6 la première fois, il gagne a. S'il manque son coup, il en a encore un, ce qui lui vaut 1/6 a d'après le calcul précédent. Mais il n'a qu'une chance de jeter un 6 du premier coup et il en a 5 de manquer ce coup. Il a donc | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 79]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
der 2 steenen kan een van de 6 werpen komen, die op de derde zijn. En 6 mael 36 maeckt 216. Van gelijcken blijckt, dat op 4 steenen zijn 6 mael 216 werpen, dat is, 1296; en dat men soo voort de werpen van soo veel steenen als men wil kan bereeckenen, altijdt door het toe-doen van eene steen 6 mael de werpen der voorgaende nemende. Vorders moet men weeten, dat op twee steenen maer eene werp en is van 2 of 12 oogen, en 2 werpen van 3 of 11 oogen. Want gevende aen de steenen de naemen van A en B, soo blijckt dat om 3 oogen te werpen op A een aes kan zijn, en op B een 2; of op B een aes, en op A een 2. Van gelijcken om 11 oogen te hebben, so kan op A 5 zijn, en op B 6; of op A 6 en op B 5. Van 4 oogen zijnder 3 werpen, te weeten, A 1, B 3; of A 3, B 1; of A 2, B 2. Van 10 oogen insgelijcks 3 werpen. Van 5 of 9 oogen 4 werpen. Van 6 of 8 oogen 5 werpen. Van 7 oogen 6 werpen.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
X. Voorstel.Te vinden van hoeveel reysen men kan neemen een 6 te werpen met eene steen.
Die het ten eersten neemt, het is seecker dat hy 1 kans heeft om te winnen, ende te hebben het geen ingeset is, tegen 5 kanssen om te verliesen. Want daer sijn 5 werpen tegen hem, en maer een voor hem. Het geen ingeset is zy genoemt a. Soo heeft hy dan 1 kans om te hebben a, en 5 kanssen om 0 te hebben, het welck door het 2de VoorstelGa naar voetnoot1) so veel is als 1/6 a. En blijft voor die het hem geeft te werpen 5/6 a. Soo dat hy maer 1 tegen 5 kan setten, die het ten eersten neemt. Die van tween eens een 6 neemt te werpen, werdt sijn deel aldus bereeckent. Indien hy de eerste reys een 6 raeckt, soo heeft hy a. Indien hy mist, soo heeft hy noch eene werp, dewelcke door het voorgaende soo veel is als 1/6 a. Maer hy heeft maer een kans om in de eerste reys een 6 te werpen, en 5 kanssen om die te missen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 80]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
au commencement 1 chance d'obtenir a et 5 chances d'obtenir 1/6 a, ce qui lui vaut 11/36 a d'après la deuxième Proposition. Il reste 25/36 a pour celui qui gage contre lui. Celui qui joue en 2 coups peut donc mettre 11 contre 25, ce qui est moins que 1 contre 2. En partant de ce résultat, on calcule de la même manière que la part de celui qui parie de jeter un 6 en trois coups est 91/216 a. Il peut donc mettre 91 contre 125, c'est-à-dire à peu près 3 contre 4. La part de celui qui joue en 4 coups est 671/1296 a. Il peut donc mettre 671 contre 625, c'est-à-dire plus que 1 contre 1. La part de celui qui joue en 5 coups est 4651/7776 a; il peut mettre 4651 contre 3125, c'est-à-dire à peu près 3 contre 2. La part de celui qui joue en 6 coups est 31031/46656 a, et il peut mettre 31031 contre 15625, c'est-à-dire à peu près 2 contre 1. On peut poursuivre ce calcul successivement pour chaque nombre de coups. Mais on peut aussi avancer par de plus grands bonds, comme nous l'indiquerons à la Proposition suivante; sans quoi le Calcul deviendrait fort long. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XI.Trouver en combien de fois l'on peut accepter de jeter 2 six avec 2 dés.
Celui qui joue en un seul coup, a 1 chance de gagner, c'est-à-dire d'avoir a, contre 35 chances de perdre, c'est-à-dire d'avoir 0, attendu qu'il y a 36 coups. De sorte qu'il a 1/36 a d'après la deuxième PropositionGa naar voetnoot1). Quant à celui qui joue en 2 coups, il gagne a s'il jette 2 six la première fois. S'il manque son coup la première fois, il lui en reste encore un, ce qui lui vaut 1/36 a d'après ce que nous venons de dire. Mais il n'a qu'une chance de jeter 2 six la première fois contre 35 chances de manquer son coup. Il a donc au commence- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 81]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
So heeft hy dan van eersten aen 1 kans om a te hebben, en 5 kanssen tot 1/6 a, het welck door het 2de Voorstel soo veel is als 11/36 a. Ende blijft voor die het hem geeft 25/36 a. Soo dat die het van tween neemt 11 tegen 25 kan stellen, dat is, min als 1 tegen 2. Hier uyt nu werdt op deselve manier bereeckent, dat die van dryen eens neemt een 6 te werpen, zijn deel is 91/216 a. Soo dat hy kan 91 tegen 125 setten, dat is, weynigh min als 3 tegen 4. Die het van vieren neemt, sijn deel is 671/1296 a. Soo dat hy 671 tegen 625 kan setten, dat is, meer als 1 tegen 1. Die het van vyven neemt, syn deel is 4651/7776 a, ende kan 4651 tegen 3125 setten, dat is, weynig min als 3 tegen 2. Die het van sessen neemt, sijn deel is 31031/46656 a, ende kan 31031 tegen 15625 setten, dat is, weynigh min als 2 tegen 1. Aldus kan men vervolgens yder getal van werpen vinden. Maer men kan oock met grooter sprongen voort gaen, gelijck wy in't volgende Voorstel aenwysen sullen, sonder 't welck de Reeckening anders seer lang soude vallen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
XI. Voorstel.Te vinden van hoe veel reysen men kan neemen 2 sessen te werpen met 2 steenen.
Die het ten eersten neemt, heeft 1 kans om te winnen, dat is, om a te hebben, tegen 35 kanssen om te verliesen ofte 0 te hebben; om datter 36 werpen zijn. Sulcx dat hy door het 2de VoorstelGa naar voetnoot1) heeft 1/36 a. Die het van tween neemt, indien hy de eerste reys 2 sessen werpt, soo heeft hy a. Indien hy d'eerste reys mist, soo heeft hy noch eene werp overig, dat is, door 't geen geseyt is, soo veel als 1/36 a. Maer hy heeft maer 1 kans om in de eerste reys 2 sessen te werpen, tegen 35 kanssen om die te missen. Soo heeft hy dan van eersten aen 1 kansse tot a, en 35 kanssen tot 1/36 a, het welck door het 2de Voor- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 82]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ment 1 chance d'obtenir a et 35 chances d'obtenir 1/36 a, ce qui lui vaut 71/1296 a d'après la deuxième Proposition. Il reste 1225/1296 a pour celui qui l'engage à jeter. On peut trouver en partant de là la chance ou la part de celui qui joue en 4 coups; on peut sauter le cas du jeu en 3 coups. En effet, celui qui joue en 4 coups, obtient a, s'il jette 2 six l'une des deux premières fois; sinon, il lui reste encore 2 coups, ce qui lui vaut 71/1296 a d'après le calcul précédent. Mais d'après le même calcul il a 71 chances de jeter 2 six l'une des deux premières fois, contre 1225 chances de les manquer. Il a donc an commencement 71 chances d'obtenir a et 1225 chances d'obtenir 71/1296 a; ce qui, d'après la deuxième Proposition, lui vaut 178991/1679616 a. Il reste 1500625/1679616 a pour celui qui gage contre lui. Leurs chances sont donc l'une à l'autre comme 178991 est à 1500625. Partant de là, on trouve de la même manière la chance de celui qui parie de jeter une fois 2 six en 8 coups. Ensuite, en partant de là, la chance de celui qui joue en 16 coups. Et en partant de la chance de ce dernier, jointe à celle de celui qui joue en 8 coups, on trouve la chance de celui qui joue en 24 coups. Dans ce calcul, comme il s'agit surtout de chercher pour quel nombre de coups les chances des deux joueurs commencent à devenir égales, on peut omettre une partie des derniers Chiffres des nombres qui sans cela deviendraient très grands. Je trouve que celui qui joue en 24 coups a encore un léger désavantage, et qu'on ne peut accepter la partie avec avantage qu'en jouant en 25 coups au moinsGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XII.Trouver le nombre de dés avec lequel on peut accepter de jeter 2 six du premier coup.
Cela équivaut à vouloir savoir en combien de coups d'un seul dé l'on peut compter jeter deux fois un 6. D'après ce que nous avons démontré plus hautGa naar voetnoot2), celui qui accepterait de jeter 2 six en 2 coups, aurait droit à 1/36 a. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 83]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
stel soo veel is als 71/1296 a. En blijft voor die het hem geeft te werpen 1225/1296 a. Hier uyt nu kan gevonden worden, wat kans ofte deel hy heeft die het neemt van 4 werpen, overslaende de kansse van die het neemt van dryen. Want die het van vieren neemt, indien hy het doet in een van de 2 eerste reysen, soo heeft hy a; indien niet, soo heeft hy noch 2 werpen overig, dat is, door 't geen te vooren geseyt is, soo veel als 71/1296 a. Maer hy heeft oock door het selve 71 kanssen om van de 2 eerste werpen eens 2 sessen te werpen, tegen 1225 kanssen om die te missen. Soo heeft hy dan van eersten aen 71 kanssen tot a, en 1225 kanssen tot 71/1296 a; het welck door het 2de Voorstel so veel weerdt is als 178991/1679616 a. Ende blijft voor die het hem geeft 1500625/1679616 a. Staende haere kanssen tegen een, als 178991 tegen 1500625. Hier uyt werdt vorders op deselve manier gevonden de kans, van die van 8 reysen eens 2 sessen neemt te werpen. En daer uyt dan wederom de kans, van die het neemt van 16 reysen. En uyt dese sijn kans, ende uyt de kans van die het neemt van 8 werpen, werdt gevonden de kans van die het neemt van 24gen. In welcke werckingh, alsoo voornamentlijck maer gesocht werdt in wat getal van werpen de gelijcke kansse begint tusschen die het neemt en geeft, soo magh men van de getalen, die anders seer groot souden werden, een deel van de achterste Cijfers af-snijden. Ick vinde dat die het neemt van 24gen, noch yets te kort komt; en dat het eerst van 25gen genomen kan werden met voordeelGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
XII. Voorstel.Te vinden met hoe veel steenen men kan nemen ten eersten 2 sessen te werpen.
Dit is soo veel dan of men wilde weeten, in hoe menige werp met eene steen men kan nemen tweemael een 6 te raecken. Het welck die het in 2 werpen nam, soude, door het geen hier te vooren is bewesenGa naar voetnoot2), 1/36 a toekomen. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 84]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Quant à celui qui jouerait en 3 coups, si son premier coup n'était pas un 6, il lui resterait encore 2 coups lesquels devraient être des 6 l'un et l'autre; ce que nous avons dit valoir 1/36 a. Mais si son premier coup est un 6, il ne lui faut plus jeter qu'un seul 6 dans les deux coups suivants, ce qui d'après la dixième PropositionGa naar voetnoot1) lui vaut 11/36 a. Or, il est certain qu'il a 1 chance de jeter un 6 du premier coup contre 5 chances de le manquer. Il a donc au commencement 1 chance d'obtenir 11/36 a et 5 chances d'obtenir 1/36 a, ce qui d'après la deuxième PropositionGa naar voetnoot2) lui vaut 16/216 a ou 2/27 a. Prenant ainsi chaque fois un coup de plus, on trouve qu'on peut accepter avec avantage de jeter 2 six avec un dé en 10 coups ou avec 10 dés en un coupGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XIII.Dans l'hypothèse que je joue un coup de deux dés contre une autre personne à condition que s'il vient 7 points, j'aurai gagné, mais qu'elle aura gagné s'il en vient 10, et que nous partagerons l'enjeu en parties égales s'il vient autre chose, trouver la part qui revient à chacun de nous.
Comme parmi les 36 coups qu'on peut faire avec 2 dés, il y en a 6 de 7 points et 3 de 10 points, il en reste 27 qui ne font gagner ni l'un ni l'autre. Dans ce dernier cas, nous avons chacun droit à 1/2 a. Mais sinon, j'ai 6 chances de gagner, c'est-à-dire d'avoir a, et 3 chances de perdre, c'est-à-dire d'avoir 0; ce qui d'après la deuxième PropositionGa naar voetnoot2) me vaut 2/3 a pour ce cas. J'ai donc au commencement 27 chances d'avoir 1/2 a et 9 chances d'avoir 2/3 a; ce qui d'après la deuxième Proposition me vaut 13/24 a. Et il reste 11/24 a pour l'autre joueur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 85]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Die het in dryen nam, indien zijn eerste werp geen 6 en waer, soo had hy noch 2 werpen, die beyde een 6 souden moeten zijn; het welck geseyt is soo veel weerdt te zijn als 1/36 a. Maer zijn eerste werp een 6 wesende, soo behoeft hy van tween noch maer eens een 6 te werpen, het welck soo veel is door het 10de VoorstelGa naar voetnoot1) als of hy 11/36 a hadde. Nu is seecker dat hy 1 kans heeft om ten eersten een 6 te werpen, tegen 5 kanssen om die te missen. Soo heeft hy dan van eersten aen 1 kans tot 11/36 a, en 5 kanssen tot 1/36 a, het welck door het 2de VoorstelGa naar voetnoot2) soo veel is als 16/216 a of 2/27 a. Op dese manier t'elckens een werp meer nemende soo werdt bevonden, dat in 10 werpen met eene steen, of met 10 steenen ten eersten, kan genomen werden 2 sessen te werpen, en dat met voordeelGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
XIII. Voorstel.Als ick tegen een ander speel met 2 steenen alleen eene werp, op conditie, dat, indien der 7 oogen komen, ick winnen sal; maer hy, indiender 10 oogen komen; en ingevalle iets anders, dat wy dan gelijckelijck deelen sullen het geen ingeset is: Te vinden wat deel daer van ons elck toekomt.
Dewijl van de 36 werpen, die op 2 steenen zijn, 6 werpen zijn van 7 oogen, en 3 werpen van 10 oogen, soo resteren noch 27 werpen, die het spel konnen kamp maecken. Het welck gebeurende so komt ons ieder 1/2 a. Maer als het geen kamp is, soo heb ick 6 kanssen om te winnen dat is om a te hebben, en 3 kanssen om te verliesen ofte 0 te hebben; het welck door het 2deGa naar voetnoot2) soo veel is, als of ick in sulcken geval 2/3 a hadde. Soo heb ick dan van eersten aen 27 kanssen tot 1/2 a, en 9 kanssen tot 2/3 a; het welck door het 2de soo veel is als 13/24 a. En blijft voor den anderen 11/24 a. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 86]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XIV.Si un autre joueur et moi jettent tour à tour 2 dés à condition que j'aurai gagné dès que j'aurai jeté 7 points et lui dès qu'il en aura jeté 6, tandis que je lui laisse le premier coup, trouver le rapport de ma chance à la sienne. Soit x la valeur de ma chance, et a l'enjeu. La chance de l'autre joueur a donc la valeur a - x. Il est évident aussi que chaque fois que c'est son tour de jeter, ma chance aura de nouveau la valeur x. Mais chaque fois que c'est mon tour de jeter, ma chance doit avoir une valeur supérieure, mettons y. Or, attendu que parmi les 36 coups qu'on peut faire avec 2 dés, il y en a 5 qui peuvent donner 6 points à mon adversaire et lui faire gagner la partie, et 31 coups à son désavantage, c'est-à-dire qui amènent mon tour de jeter, j'ai 5 chances d'avoir 0 lorsqu'il jette la première fois, et 31 chances d'avoir y; ce qui d'après la troisième PropositionGa naar voetnoot1), me vaut 31y/36. Mais nous avons posé que ma chance valait x au commencement du jeu. De sorte que 31y/36 = x, partant y = 36x/31. Nous avons posé en outre que ma chance vaut y, lorsque c'est mon tour de jeter. Mais lorsque je jette, j'ai 6 chances d'avoir a, attendu qu'il y a 6 coups de 7 points qui me font gagner; et j'ai 30 chances de faire revenir le tour de mon adversaire, c'est-à-dire d'avoir pour ma part x. La valeur y est donc équivalente à 6 chances d'avoir a et 30 chances d'avoir x; ce qui, d'après la troisième Proposition, me vaut 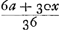 . Cette expression étant donc égale à y, et
y d'après ce qui
précède à 36x/31, il faut que . Cette expression étant donc égale à y, et
y d'après ce qui
précède à 36x/31, il faut que 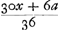 soit égal à 36x/31, d'où l'on tire x = 31a/61; valeur de ma chance. Par conséquent, la chance de mon adversaire vaudra 30a/61. Le rapport de nos chances est donc de 31 à 30Ga naar voetnoot2). soit égal à 36x/31, d'où l'on tire x = 31a/61; valeur de ma chance. Par conséquent, la chance de mon adversaire vaudra 30a/61. Le rapport de nos chances est donc de 31 à 30Ga naar voetnoot2).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 87]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
XIV. Voorstel.Als ick en noch een ander met beurten werpen met 2 steenen, ende bespreecken dat ick sal winnen, soo haest ick 7 ooghen werp, ende hy, soo haest als hy 6 ooghen werpt, mits dat ick hem de voorwerp geve. Te vinden in wat reden mijn kans tegen de sijne staet. Laet mijn kans weert sijn x, ende het geen ingeset is sy genoemt a; soo is dan de kans van den anderen weerdt a - x. Het blijckt oock dat elcke mael, als sijn beurt van werpen weder komt, mijn kans dan weder moet x weerdt zijn. Maer soo dickmaels als het mijn beurt is te werpen, soo moet mijn kans meerder weerdt zijn. Laet ons y stellen voor het geene datse dan weerdt is. Overmits nu datter 5 werpen zijn van de 36 werpen op 2 steenen, die mijn tegen speelder 6 ooghen konnen geven, ende het spel doen winnen, en 31 werpen die hem doen missen, dat is, die mijn beurt van werpen doen komen: soo heb ick dan, als hy begint te werpen, 5 kanssen om 0 te hebben, en 31 kanssen om te hebben y; het welck door het 3de VoorstelGa naar voetnoot1) weerdt is 31y/36. Maer daer is gestelt, dat mijn kans van eersten aan x weerdt is. Soo is dan 31y/36 ∞ x, en daerom y ∞ 36x/31. Voorts soo is gestelt, dat, mijn beurt van werpen gekomen zijnde, mijn kans dan y weerdt is. Maer ick sullende werpen, soo heb ick 6 kanssen tot a; om datter 6 werpen zijn van 7 ooghen, dewelcke my doen winnen; en ick heb 30 kanssen om de beurt van mijn tegen-speelder te doen wederkeeren, dat is, om voor my x te hebben. Soo is dan y soo veel weerdt als 6 kanssen tot a en 30 kanssen tot x; 't welck door het 3de Voorstel soo veel is als 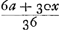 . Dit dan zijnde gelijck aen y, ende te voren gevonden zijnde
36x/31 ∞ y, soo moet . Dit dan zijnde gelijck aen y, ende te voren gevonden zijnde
36x/31 ∞ y, soo moet 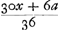 gelijck zijn aen 36x/31; waer uyt
gevonden werdt x ∞ 31a/61, het welck de weerde is van mijn kans. En diensvolgens sal de kans van die tegens my speelt weerdt zijn 30a/61. Soo dat onse kanssen tegen malkanderen staen, als 31 tot 30Ga naar voetnoot2). gelijck zijn aen 36x/31; waer uyt
gevonden werdt x ∞ 31a/61, het welck de weerde is van mijn kans. En diensvolgens sal de kans van die tegens my speelt weerdt zijn 30a/61. Soo dat onse kanssen tegen malkanderen staen, als 31 tot 30Ga naar voetnoot2).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 88]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Je termine en faisant suivre encore quelques PropositionsGa naar voetnoot1).IGa naar voetnoot2). A et B jouent ensemble avec 2 dés à la condition suivante: A aura gagné s'il jette 6 points, B s'il en jette 7. A fera le premier un seul coup; ensuite B 2 coups successifs; puis de nouveau A 2 coups, et ainsi de suite, jusqu'à ce que l'un ou l'autre aura gagné. On demande le rapport de la chance de A à celle de B? Réponse: comme 10355 est à 12276. IIGa naar voetnoot3). Trois joueurs A, B et C prennent 12 jetons dont 4 blancs et 8 noirs; ils jouent à cette condition que celui gagnera qui aura le premier, en choisissant à l'aveuglette, tiré un jeton blanc, et que A choisira le premier, B ensuite, puis C, puis de nouveau A et, ainsi de suite, à tour de rôle. On demande le rapport de leurs chances? IIIGa naar voetnoot4). A parie contre B, que de 40 cartes, dont dix de chaque couleur, il en tirera 4 de manière à en avoir une de chaque couleur. On trouve dans ce cas que la chance de A est à celle de B comme 1000 est à 8139. IVGa naar voetnoot5). On prend comme plus haut 12 jetons dont 4 blancs et 8 noirs. A parie | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 89]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Volgen tot een bessluyt noch eenige VoorstellenGa naar voetnoot1).IGa naar voetnoot2). A en B speelen teghen malkander met 2 steenen, op dese conditie: dat A sal winnen als hy 6 oogen werpt, maer B sal winnen als hy 7 oogen werpt. A sal eerst eene werp doen; daernae B twee werpen achtervolgens; dan weder A 2 werpen; en soo voorts, tot dat d'een of d'ander sal winnen. De vrage is in wat reden de kans van A staet tegen die van B? antw. als 10355 tot 12276. IIGa naar voetnoot3). Drie speelders A, B en C nemende 12 schijven, van de welcke 4 wit zijn en 8 swart, speelen op conditie, dat die van haer blindeling eerst een witte schyve sal gekosen hebben winnen sal, en dat A de eerste sal nemen, B de tweede, en dan C, en dan wederom A, en soo vervolgens met beurten. De vraghe is in wat reden haere kanssen staen tegens malkander? IIIGa naar voetnoot4). A wed tegens B, dat hy uyt 40 kaerten, dat is, 10 van ieder soort, 4 kaerten uyttrecken sal, soo dat hy van elcke soorte een sal hebben. Hier wordt de kans van A tegen die van B gevonden, als 1000 tegen 8139. IVGa naar voetnoot5). Genomen hebbende ghelijck hier te vooren 12 schyven, 4′ witte en 8 swarte; soo wed A tegen B dat hy blindeling 7 schyven sal daer uyt nemen, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 90]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
contre B que parmi 7 jetons qu'il en tirera à l'aveuglette, il se trouvera 3 blancs. On demande le rapport de la chance de A à celle de B. VGa naar voetnoot1). Ayant pris chacun 12 jetons, A et B jouent avec 3 dés à cette condition qu'à chaque coup de 11 points, A doit donner un jeton à B, mais que B en doit donner 1 à A à chaque coup de 14 points, et qui celui là gagnera qui sera le premier en possession de tous les jetons. On trouve dans ce cas que la chance de A est à celle de B comme 244140625 est à 282429536481.
FIN. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 91]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
onder welcke 3 witte sullen zijn. Men vraegt in wat reden de kans van A staet tegen die van B. VGa naar voetnoot1). A en B genomen hebbende elck 12 penningen spelen met 3 dobbelsteenen op dese conditie: dat, als'er 11 oogen geworpen worden, A een penning aen B moet geven; maer als'er 14 geworpen werden, dat dan B een penning aen A moet geven; en dat hy het spel winnen sal, die eerst al de penningen sal hebben. Hier werdt ghevonden de kans van A tegen die van B te zijn, als 244140625 tot 282429536481.
EYNDE. |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

