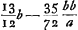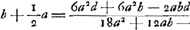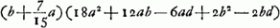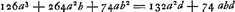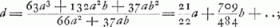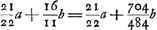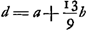Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 803]
| |
Troisième Complément à la ‘Dioptrique’Ga naar voetnoot1). [Recherches sur les lunettes catoptriques.]
| |
[pagina 804]
| |
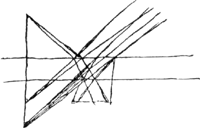
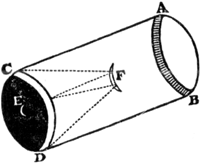 [Fig. 1.]
et pour ce qui est de la derniere on y a apportè du changement mal a propos en placant la lentille dans l'ouverture E du grand miroirGa naar voetnoot1). L'on auroit vu le mauuais effect que cela doit faire si on avoit jamais fait l'essay de cette lunette, car le grand jour qui entre par l'ouverture AB eblouiroit si fort la vue du spectateur qui auroit l'oeil pres de l'ouverture E qu'il ne verroit rien du tout des objets, bien loin de jouir d'une vision agréable que l'on promet parmi d'autres avantages de cette invention par dessus celle de m.r NewtonGa naar voetnoot2). L'on y compte aussi sans raison, que l'ouverture AB pourra estre aussi grande que l'on voudra. car elle ne le sera pas d'avantage que celle de la lunette de m.r Newton, a moins que le miroir CD ne soit parabolique, dont il n'est point parlè dans la description. de mesme ce qui est dit de la reflexion des rayons qu'elle sera tres naturelle a cause qu'elle se fait dans l'axe, est sans fondement, et le petit miroir plat dont se sert m.r Newton doit reussir incomparablement mieux que le petit convexe F, tant a cause de la grande difficultè de bien placer cettuicy que parce qu'il doit avoir la figure parabolique. L'on pourroit faire plat le miroir F, mais alors il devroit avoir le diametre la moitiè aussi grand que le miroir CD, et par consequent il empescheroit la 4e partie des rayons qui vienent des objects vers ce miroir. Enfin si m.r Gregori n'avoit pas jugè sa lunette impossible a executer, il y a apparence qu'il l'auroit pratiquè il y a longtemps. Et commeje vous ay dit c'est la mesme qui est rapportee dans ces memoires, sinon, qu'elle a encore d'autre defauts trop visibles. LaGa naar voetnoot3) construction de la trompetteGa naar voetnoot4) est sans aucun fondement puis qu'il ne paroit point de raison pourquoy les proportions que l'on y voit observées devroient produire quelque effet en ce qui regarde la multiplication ou renforcement du son dont il s'agit, ni mesme en ce qui est de l'harmonie, supposè que l'on en cherchast dans cet instrument. Et la regle des fondeurs, qui doublent le diametre des cloches qu'ils veulent avoir a l'octave l'une de l'autre, est a mon avis tres mal prise pour principe en cette Theorie. Au reste la ligne courbe de sa trompette est | |
[pagina 805]
| |
precisement l'Hyperbole, comme il seroit facile a demonstrer, et si l'experience faisoit voir peut estre que cette figure fait un meilleur effect qu'aucune autre pour le grossissement du son, il en faudroit chercher la raison dans les proprietez de cette ligne, apres avoir trouvè premierement des principes en ce qui regarde la nature du son et les manieres de le produire. | |
§ 2Ga naar voetnoot5). 1691.[Première Partie.]In speculo vitreo cavo aequalium sphaerarum, invenire quantum distet focus reflexionis principalis a foco reflexionis superficiei vitreae in quam primum radij incidunt. fit fere 13/12 crassitudinis ED. | |
[pagina 806]
| |
 [Fig. 2.]
SE, AD ∞ aGa naar voetnoot1); AQ ∞ 2aGa naar voetnoot2); SA, ED ∞ b; EBGa naar voetnoot3) ∞ x. QS (2a+b) ad SB (a-x) ut QE (3a+b) ad EB (x)Ga naar voetnoot4). 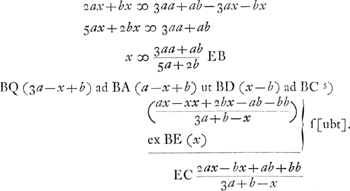 Ga naar voetnoot5) | |
[pagina 807]
| |
[Deuxième Partie.]In speculo sphaerico superficierum concentricarum distabit focus principalis a foco superficiei vitreae fere ⅓ crassitudinis speculi. 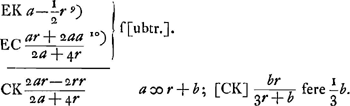 Ga naar voetnoot9)Ga naar voetnoot10) hic calculus est in libello SGa naar voetnoot11). | |
[pagina 808]
| |
[Troisième Partie.]In speculo vitreo aequalium sphaerarum, invenire quantum distent inter se foci reflexionis principalis qui ad extremos colores pertinent. Posita secundum Newtonum refractionis proportione in rubro esse ut 140 ad 91: in violaceo extremo ut 142 ad 91Ga naar voetnoot1). Fit ea distantia proxime 1/156 crassitudinis ED. Ergo multum abest ut nocere possit haec aberratio.  [Fig. 2.]
ES ∞ DA ∞ a; ED ∞ SA ∞ b; AQ ∞ d; DQ ad QA proportio refract.Ga naar voetnoot2) QS (d+b) ad SB (a-x) ut QE (d+a+b) ad EB (x); quia ang. QGB bifariam secatur recta GS. 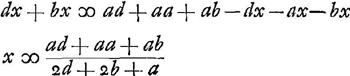 BQ (d+a+b-x) ad BA (a+b-x) ut BD (x-b) 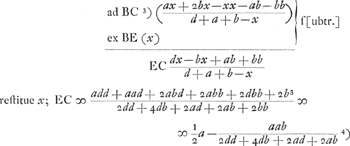 Ga naar voetnoot3)Ga naar voetnoot4) sive 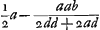 , hujus quantitas jam bis supputatur, ex binis refractionis proportionibus. , hujus quantitas jam bis supputatur, ex binis refractionis proportionibus.
| |
[pagina 809]
| |
a ∞ 51; d ∞ 91Ga naar voetnoot5); EC prima 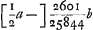 a ∞ 49; d ∞ 91; EC altera
a ∞ 49; d ∞ 91; EC altera 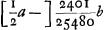
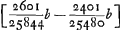 proxime 1/156b. distantia focorum à coloribus extremis. proxime 1/156b. distantia focorum à coloribus extremis.
| |
[Quatrième Partie].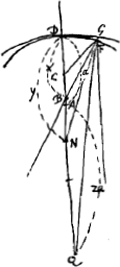 [Fig. 3.]
Ponitur in medio D nulla esse crassitudo speculi vitrei. DA ∞ a radius superficiei DF; AQ ∞ 2aGa naar voetnoot2); DN ∞ y radius superf. DG; DB ∞ x. B concursus post refractionem in F et reflexionem in G.C concursus post duas refractiones et reflexionem. Oportet DC esse ∞ ½ DAGa naar voetnoot6). QN (3a-y) ad NB (y-x) ut QD (3a) ad DB (x). quia angulus QFB bifariam secatur ab FN, ex lege repercussus. arcus DG minimus quia tantum distantia focorum quaeritur. 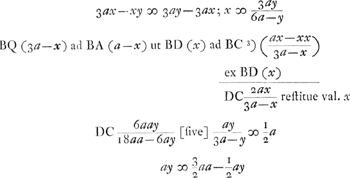 Ga naar voetnoot3) | |
[pagina 810]
| |
[Cinquième Partie]. 1691. Maj. [Fig. 4.]
Data speculi superficie sphaerica cava DF, et crassitudine DE, invenire superficiem EG, ut concursus parallelorum principalis incidat in concursum reflexorum a superficie DF. fit NE rad. superf. EG prox. rad. superf. DF, AD ∞ a; rad. superf. EG, NE ∞ d; ex proport. ref. 3/2, AQ ∞ 2aGa naar voetnoot2); crassitudo ED ∞ b; EB ∞ x, B concursus ante secundam refract.; QD ∞ 3a. 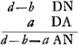 QN (3a-d+b) ad NB (d-x) ut QE (3a+b) ad EB(x) nam QE ad EB ut QG ad GB quia arcus EG hic ponitur minimus, ad quaerendos focos. 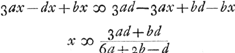 BQ (3a+b-x) ad BA (a+b-x) ut BD (x-b) ad BCGa naar voetnoot3); C concursus ultimus seu focus speculi vitrei.  | |
[pagina 811]
| |
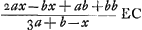 restitue val. x.
Ponitur C punctum concursus a superficie DF reflexorum, unde EC ∞ restitue val. x.
Ponitur C punctum concursus a superficie DF reflexorum, unde EC ∞ 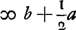
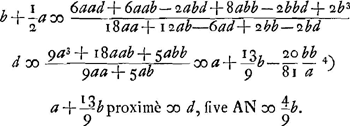 Ga naar voetnoot4) Conservatur in hujusmodi speculis vitreis id quo speculi metallici reflexio praestabat in congregandis radijs parallelis comparatione lentis vitreaeGa naar voetnoot5); sed et praeterea corrigitur defectus à diversitate refractionum quae a coloribus, unde aberratio multo major oriebaturGa naar voetnoot6). Radij lucis bis transire debent speculi crassitudinem, cum lentem semel tantum. Unde in speculis hujusmodi plus de luce amittitur. sed rursus acquiritur lux quae ex utraque superficie lentis deperibat ob radios repercussos. ut fiat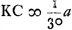 , sed ita ut C cadat inter K et D, erit d sive NE rad. proximè , sed ita ut C cadat inter K et D, erit d sive NE rad. proximè 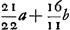 Ga naar voetnoot7). Ga naar voetnoot7).
| |
[pagina 812]
| |
 [Fig. 5.]
1691. Maj.
quia A et N proxima, (nam tantum distant 4/9 ED) fit NQ fere dupla NG. unde ang. NGQ fere duplus NQG. Sed HGF est duplus NGQ. Ergo HGF fere quadruplum NQG. QD (3a) ad DH (p) ut DE sive HG (b) ad ¼ HF(bp/3a)Ga naar voetnoot1) DH ad DFGa naar voetnoot2) ut p ad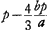
DH ad FH ut p ad 4/3 bp/a ut 3a ad 4b [a ∞ 300; b ∞ 1] [DH ad FH ut] 900 ad 4 ut 140 ad 560/900 ∞ 28/45 pr[ox.] ⅗ [DH ad DF ut] 140 ad 140 ⅗ | |
[pagina 813]
| |
P.S. 1692 maj. 5.
Putabam duas diversas amplificationes hic futuras, propter angulum HKF, sed fallebar; non enim putandus oculus poni in K. Sed radij HK, FK producti et lente oculari ad parallelismum reducti, convenient in oculi fundo ad punctum unum, ac proinde non erunt rei visae imagines binae. Ergo optime succedet constructio hujusmodi Neutoniani telescopij. Praecipua erit difficultas ut radius NE convexi exterioris sit precise ∞ radio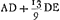 crassitudinis. Crassitudo ponenda est quanta requiritur ne invisibili flexu vitri figura falsa oriatur. alias crassitudo temperari posset ad cognitos exacte convexi et cavi radios.
Videndum an tenuiores laminae vitreae expoliri possint, in quibus parum noceret diversitas focorum; quae ∞ ⅓b, si superficies sint concentricaeGa naar voetnoot3). Deberent firmiores reddi, affixis orbibus marmoreis, dura mastiche. gypsum expertus sum, sed frustratus expectatione. comparanda repercussio speculi vitrei vel argenti vivi cum speculo metallico, an multo fortior sit? videtur mihi hydrargyrus totam lucem remittere. crassitudinis. Crassitudo ponenda est quanta requiritur ne invisibili flexu vitri figura falsa oriatur. alias crassitudo temperari posset ad cognitos exacte convexi et cavi radios.
Videndum an tenuiores laminae vitreae expoliri possint, in quibus parum noceret diversitas focorum; quae ∞ ⅓b, si superficies sint concentricaeGa naar voetnoot3). Deberent firmiores reddi, affixis orbibus marmoreis, dura mastiche. gypsum expertus sum, sed frustratus expectatione. comparanda repercussio speculi vitrei vel argenti vivi cum speculo metallico, an multo fortior sit? videtur mihi hydrargyrus totam lucem remittere.
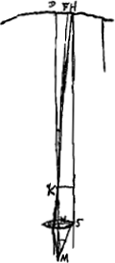 [Fig. 6.]
debent radij cavitatis et convexi non multum differre magnitudine, quia alias colorum aberratio revertitur. | |
[Sixième Partie.]Ga naar voetnoot4)Augmentum ut ang. SMN ad NKO seu DKH. hoc est ut DK ad NM seu KNGa naar voetnoot5). Ex Newtoni figura telescopij suiGa naar voetnoot6) videtur ad foci distantiam 6 ⅓ digitorumGa naar voetnoot7) (mihi 5 poll.) ponere diametrum aperturae speculi 1 11/12 pollicisGa naar voetnoot8) seu fere 2 poll. | |
[pagina 814]
| |
Aperturae speculi rationem sequentur quam inveneram in lentibus telescopij posita aberratione sola quae figura sphaericaGa naar voetnoot1) superficierum. aberratio est ½ profunditatis seu sinus versi. vid lib. H. pag....Ga naar voetnoot2) | |
§ 3Ga naar voetnoot3). [1692]Ga naar voetnoot4).[Première Partie.]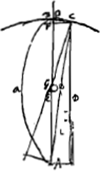 [Fig. 7.]
rad, AB ∞ a; CF perp. AB. EB ∞ ½ aGa naar voetnoot5). GE ∞ e aberrat.; BF ∞ q. GO ∞ GC. OF ∞ 2BF ∞ 2q prox.Ga naar voetnoot6); OE ∞ ½a+q; GC ∞ OG ∞ ½a+q-e. 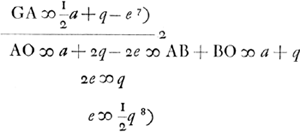 Ga naar voetnoot7)Ga naar voetnoot8) In his telescopijs ergo erit ratio aperturarum eadem quam in aliis inveneram, ex tota aberratione propter figuram lentium sphaericamGa naar voetnoot9). | |
[pagina 815]
| |
[Deuxième Partie.]Quia difficillimum esset observare accurate mensuras radiorum a et d quae inventae sunt pag. 74 lib. GGa naar voetnoot10), quibusque conveniunt in unum duo foci, volui hic quaerere qua proportione rad. a et d fiat ut procul a se recedant focus uterque. qua ratione forsan non multum nocebunt. non duplicabunt sed nonnihil nebulae inducent. vide lib. G, pag. 74. et quae illic figuramGa naar voetnoot11). 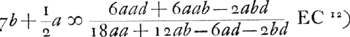 [Fig. 4.]
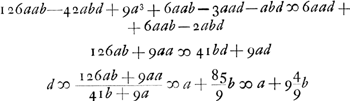 Ga naar voetnoot12) neglectis in quibus bb. 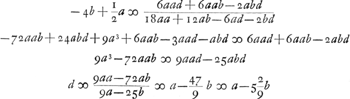 Sit a ∞ 12 ped. ut foci distantia sit circiter 6 ped.; b ∞ ⅓ poll. d ∞ 4/3 poll.+12 ped.Ga naar voetnoot13), a ad d ut 144 ad 144 4/3 ut 432 ad 436 ut 108 ad 109. | |
[pagina 816]
| |
 ut positis a et b sicut prius, focus superficiei summae seu vitri distet 3bGa naar voetnoot1) seu 3 crassitudinibus longius a speculo quam focus principalis. Jam radius d superficiei convexae fit minor quam radius superfic. cavae. 3b aequatur pollici, quia b ∞ ⅓ poll. posita fuit 5 2/9b ∞ 1 5/7 circiter poll. | |
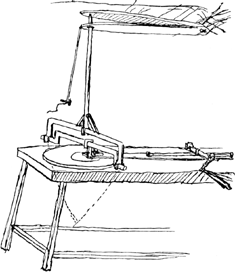
[Troisième Partie.]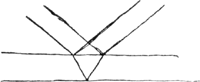 [Fig. 8.]
Posset politoriae mensaeGa naar voetnoot2) elater superne lignis affigi, ut longiores fiant baculi prementes quam nunc sunt funes trahentes, qui nimis oblique trahunt circa extremas formae margines. hoc praecipue conduceret, imo necessario esset faciendum, si specula vitrea cava polire vellemus, sic primum superficies eorum convexa perficeretur. deinde et cava, movendo patinam metallicam super vitro immobili. Vel hanc partem funiculorum tractione, ut hactenus elaborare possumus. Vel posset mensa ipsa altior fieri pede uno aut altero, et simul sedes quoque, ne difficilius circumagatur ancon. | |
[pagina 817]
| |
 [Fig. 9.]
Si speculi vitrei duae superficies inter se parallelae fuerint non duplicabit rei visae procul dissitae imaginem, etiamsi oblique inspectam. Quia radij ex utriusque superficiei repercussu ad oculum paralleli ferentur, si paralleli in supremam superficiem incidant, unde ad punctum 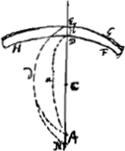 [Fig. 10.]
unum in oculi fundo convenientGa naar voetnoot3). Sed propinqui visibilis duplex fiet imago.
Il seroit aisè a ceux qui soufflent les glaces des miroirs dans les verreries, de les etendre sur une forme concave et les mettre ainsi a recuire, aussi bien qu'ils les etendent sur une plaque plane. ainsi on auroit la glace formee pour faire un miroir concave aussi grand qu'on en fait de plans, pourvu qu'on leur donnast un creux de fer battu de la grandeur qu'il faut. Pour user et doucir ces verres planoconcaves on pourroit les attacher avec un ciment doux de cire jaune et ⅓ de terbentine à une pierre creuse de marbre ou pierre Suedoise. Si on trouve qu'alors ils pesent trop sur la forme, on peut les alleger avec un contrepoids sur une poulie. Pour appliquer la feuille avec le vif argent, il faudroit battre doucement ces feuilles d'etain dans la forme pour leur faire prendre la figure. le marteau seroit de bois arrondi et bien uni. Il faudroit commencer a battre par les bords de la forme, qui devroient estre arrondis et point tranchants.
On peut battre la forme spherique pour la verrerie assez exactement, selon une plaque couppée; En appliquant les endroits defectueux sur un creux de bois, et battant alors pour les relever ou abaisser selon qu'il est requis. La mesme forme pourroit servir à user ensuite le verre des deux costez. Estant de leton on la perfectionneroit plus aisement. | |
[pagina 818]
| |
des grands verres de 3 pieds devroient bien avoir l'epaisseur d'un demi pouce.
Il faudroit rendre la glace creuse d'egale epaisseur par les bords, ce qui manque a tous les miroirs plats. | |
[Quatrième Partie.]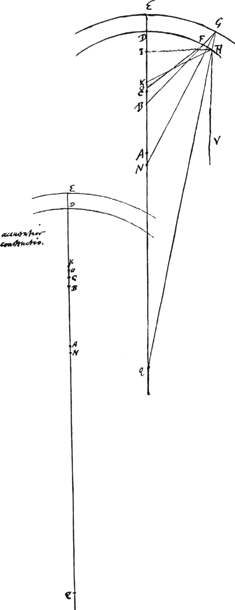 [Fig. 11.]
AD [a] radius cavi DF; NE rad. convexi EG. DE crassitudo media ∞ b. Si NE sit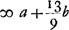 , fit speculum perfectum, convenientibus utrisque focis rad. parallelorum in C, medio puncto rectae AD ut ostensum lib. G pag. 74Ga naar voetnoot1). , fit speculum perfectum, convenientibus utrisque focis rad. parallelorum in C, medio puncto rectae AD ut ostensum lib. G pag. 74Ga naar voetnoot1).
Sit DE ⅖ pollicis. DA ∞ 2 pedum. fit NE 2 ped. +26/45 poll. sive NE prox. 2 ped. +5/9 poll. Sit latitudo speculi FH 7 poll. ad Telescopium pedalis longitudinis. Ut proportiones istae facilius obtineantur, modulus ex ferro vel aere cudatur cujus cavitatis radius sit bipedalis, radius convexitatis vero dimidio circiter pollice major; quae differentia exactissime capiatur postquam utraque superficies perfecta suerit. Ejus 9/13 debent speculi vitrei crassitudinem mediam efficere, in isto modulo formandi et expoliendi. | |
[pagina 819]
| |
[Cinquième Partie.]Ga naar voetnoot2)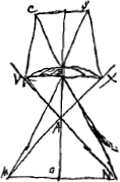 [Fig. 12.]
AD radius superficiei DH; AC ∞ CD. C erit focus communis duarum superficierum in speculo ordinato sicut pag. 59Ga naar voetnoot3). Radius VHK, faciet CK ∞ ½ DI prox.Ga naar voetnoot4). Sed radius VHGFO faciet OC minorem quam CK, quantum video ex constructione hac. Ergo hic radius minus aberrabit priore. adeo ut si aberratio KC non fuerit nimia nocensque, non verendum sit ne aberratio OC noceat. Puncta autem C, O, K tam propinqua esse debent ut pro uno sint, quod moderanda apertura DH est efficiendum. |
|


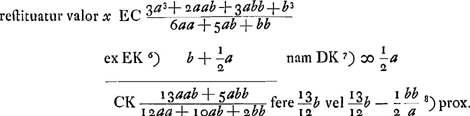
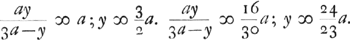
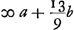 .
.