Oeuvres complètes. Tome XIII. Dioptrique

[p. 820]

Quatrième Complément à la ‘Dioptrique’¹⁾.
[Remarques critiques sur des ouvrages ou des travaux de dioptrique.]
[1668-1692].

§ 1²⁾. [1668]³⁾.

Perspicilla quae author⁴⁾ in gratiam myopum aptanda proponit⁵⁾ sunt telescopia brevissima ex convexa et cava lente composita, puta pollicum duorum vel unius vel etiam minus res visas in prop. duplo circiter augentia⁶⁾. Qualia jam ante annos decem constructa novimus, multisque utiliter usurpata. In his illud eximium est quod lentem objectivam maximae aperturae pati possunt, eoque mag-

1) Dans ce Complément nous réunissons les critiques et remarques de Huygens sur les ouvrages de dioptrique d'autres savants, pour autant qu'ils n'ont pas encore trouvé leur place dans la ‘Correspondance’ contenue dans les Tomes I-X de notre publication.

2) Ce paragraphe est emprunté à une feuille séparée de quatre pages.

3) Voir les notes 1 et 2 des pp. 323 et 324 du T. VI et consultez la note qui suit.

4) Cet auteur est sans doute Francesco Eschinardo (voir sur lui la note 3, p. 323 du T. VI); pour s'en convaincre il suffira de prendre connaissance de la Pièce N^o. 1687, p. 324-326 du T. VI. Dans cette pièce Eschinardo répond aux objections qui suivent et qui, d'après la suscription de la pièce citée, lui ont été transmises; probablement par l'intermédiaire de quelque ami commun.

5) Il s'agit de la ‘Centuria Problematum Opticorum’, le deuxième des ouvrages cités dans la note 2 de la p. 323 du Tome VI. Cet ouvrage traite la première moitié des cent problèmes mentionnés dans le titre, mais il contient en outre un ‘addendum’, ajouté évidemment après l'impression des cinquante problèmes et solutions qui le précèdent. C'est à cet ‘addendum’ que se rapportent les remarques de Huygens qui suivent. Il porte la suscription: ‘Ad doctissimum Geometram Lemnium de Rubeis in Perusino Archigymnasio Philos. et Mathemat. Professorem emeritum Epistola Francisci Eschinardi è Soc. Jesu. 15. Sept. 1667’, et il débute ainsi: ‘Indicavcram tibi ex mea Centuria Optica methodum conficiendi Perspicilia pro Myope, in quibus, vel nulla, vel minima fieret iactura magnitudinis apparentiae; vel etiam aliquid augmenti lucraremur pro vario oculorum vitio (neque enim ampullas, & iactantium amo; exagerando absolutè artem, quae non possit in praxim reduci): Nunc quandoquidem ita iubes; rem prolixius expono’.
Ajoutons que l'ouvrage d'Eschinardo ne se trouve dans aucune des bibliothèques des Pays-Bas et que les tristes évènements de l'année 1914 ne permettaient pas d'encourir le risque de le faire venir d'ailleurs. Nous apprécions d'autant plus la bienveillance de M. le professeur Silvanus P. Thompson qui a bien voulu examiner et copier pour nous de l'exemplaire du British Museum les passages qui sont nécessaires pour bien saisir la portée des remarques de Huygens.

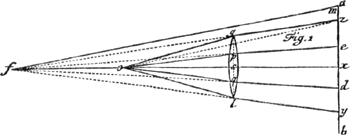
6) Voici comment on doit se figurer ces télescopes très courts. On doit placer au point A de la Fig. 1 une lentille concave contre laquelle on applique l'oeil. On verra alors l'objet CS, qu'on suppose situé à une certaine distance, sous l'angle visuel VAX et l'on pourra choisir la concavité de cette lentille de manière à assurer la netteté de l'image vu par un myope dont la distance de la vision distincte est connue. Voir d'ailleurs la Fig. 2.

[p. 821]

nam objectorum latitudinem exhibere uno intuitu. Oportet autem lentem eam plano convexam esse et superficiem convexam extrorsum collocari, nam si contrario modo disponatur, flexa et intorta omnia videri faciet.

Quanquam vero in dioptricis vel mediocriter versato sola

[Fig. 1.]

experientia duce facile sit telescopia hujusmodi construere quae eadem ad res longinquas et propinquas videndas accommodantur, prout lentium distantia pauxillum contrahitur vel augetur, non ineleganter tamen determinationem rei ex dioptrica doctrina autor tentat, proponens sibi problema hujusmodi, data distantia rei videndae a lente objectiva et ea qua lentes telescopij inter se disjungi volumus, item proportione qua rei visae speciem cupimus augeri, et praeter haec distantia ea qua myops primum nudis oculis distincte videre solitus est. Invenire convexitatem lentis objectivae et cavitatem ocularis, ponendo utramque planoconvexam quae deinde in alias mutari possunt⁷⁾. quae autem ad solutionem problematis hujus praemittit⁸⁾, obscure explicata sunt et in figuris pluscula videntur vel peccata vel

7) Voici comment à la p. 256 de son livre Eschinardo formule les données du problème: ‘fingamus proponi nobis, vt fiat perspicilium, quo Miops legat caracteres in distantia circiter 20 vnciarum (contempta scilicet crassitie vitrorum) et sub angulo visorio artificiali, qui sit duplo maior naturali; ita vt cauum post conuexum distet à conuexo per vnam vnciam, & vnam nonam, verbi gratia; oculus autem immediatè post cauum positus excipiat visuales à singulis punctis objectiuis ita diuergentes, ac si naturaliter, & sine artificio vitrorum legeret caracteres in distantia ab oculo per 6 vncias’. Ensuite il ajoute ‘Sic operaberis. Accipe lentem planoconvexam (quod de planoconvexa dico, applicetur proportionaliter vtrimque convexae) diametri duarum vnciarum; Huic adde lentem planoconcavam semidiametri 8/18 vnius vnciae, & pone illam in distantia à convexo, per vnam vnciam, & vnam nonam vnciae; & habebis intentum’.

8) Aux p. 253-256.

[p. 822]

[Fig. 1.]

omissa. ut in problemate primo¹⁾ ubi rectae MAX, NAV ut hic, debebant occurrere lenti B, et ab S radius duci ad X, et a C ad V, ut pateat oculum in A percipere puncta C, S per rectas XA, VA. quemadmodum haec cernere est in prop. 45 Opt. Promotae Jacobi Gregorij²⁾. cujus demonstratio vel repetenda fuerat authori vel lector ad eam remittendus³⁾.

Porro calculus quo diametrum lentis convexae in telescopio suo inquirit veros numeros exhibet. Quo cavae non item, nam diameter hujus quam facit⁴⁾ 16/18 sive 8/9 unciae debebat esse 15/16 unciae.

AB [Fig. 2] ∞ BC⁵⁾. AC foci distantiam parallelorum 2 unc.⁶⁾ FA distantia objecti ab lente objectiva 20 unc. Erit AE distantia puncti ubi imago objecti distinctè pingitur 2 2/9 unc.⁷⁾.

1) Lisez: ‘Propositione prima’, puisqu'il s'agit de la première Proposition, p. 253-254, que nous reproduisons ici avec la figure qui l'accompagne: ‘In praesenti figura, in qua sit obiectum CS: & MN Basis distincta producta per Vitrum obiectum



VBX: Angulus visorius artificialis post lentem conuexam habitus per lineas refractas, verbi gratia in A eam habet proportionem ad angulum visorium naturalem in loco lentis B; quam habet altitudo Trianguli MBN post lentem conuexam, (cuius Trianguli Basis est ipsa imago MN producta per dictam lentem), ad altitudinem Trianguli MAN super eadem dicta Basi MN, cuius vertex sit Angulus A’.
La proposition est évidente (pour des angles assez petits pour que l'on puisse les remplacer par leurs tangentes) si l'on considère que les rayons CBN et SBM peuvent être censés passer par le centre optique de la lentille B, de manière que l'angle MBN est égal à l'angle CBS, et que l'on suppose que l'oeil soit placé avec la lentille concave au point A.

2) Voir la p. 62 de l'ouvrage cité dans la note 6, p. 330 du T. IV. On y trouve, en effet, une figure où les lignes indiquées par Huygens comme manquant dans la figure d'Eschinardo ont été tracées.
Voici la ‘Prop. 45’ mentionnée: ‘Si cujuscunque visibilis, singulorum punctorum radii, ad alia puncta convergantur; oculo inter lentem, vel speculum, & puncta concursuum posito, semper apparebit imago visibilis confusa, & eo angulo visorio, quo apices penicillorum, extremorum visibilis punctorum, ex oculi centro. Apices autem penicillorum, extremorum visibilis punctorum, eodem angulo apparent ex vertice emersionis, quo visibile ex vertice incidentiae.’

3) Toutefois Eschinardo a donné une démonstration de sa proposition qui, quoique un peu prolixe, est juste au fond. Elle correspond à ce que nous avons remarqué dans le deuxième alinéa de la note 1.

4) Voir les dernières phrases de la note 7, p. 821.

5) B est le centre de la surface convexe de la lentille A, AC sa distance focale, qui (d'après la Prop. XIV, Part. I, Liv. I, p. 81) égale le diamètre de cette surface.

6) Cette distance focale ne figure pas parmi les données du problème; mais, puisque le problème n'est pas suffisamment déterminé par ces données, on peut encore choisir à volonté la distance focale de l'une des deux lentilles.

7) Voir la Prop. XX, Part I, Liv. I, p. 99.

[p. 823]

[Fig. 2.]

Jam posita AD distantia cavi a convexo 1 1/9 unc. et posito oculo in D fit augmentum duplum ejus quod percipitur ex A⁸⁾. huc usque verum est quod dicit⁹⁾.

fit ergo CE 2/9 unc. qua ablata ab ED seu DA quae erat 10/9 unc. fit CD 8/9 unc. quantam ille vult esse diametrum cavae lentis D¹⁰⁾. atqui haec per regulam nostram⁷⁾ disperget radios ad punctum E tendentes ac si venirent a distantia unc. 4 4/9¹¹⁾ non autem unc. 6 ut ille vult. ergo male rationem inijt¹²⁾.

dico autem diametrum cavi debere esse 15/16 unciae¹³⁾.

8) Voir la note 1.

9) Voici le passage en question du texte d'Eschinardo (p. 257), qui fait suite à celui que nous avons cité dans la note 7 de la p. 821: ‘Nam ex supra ostensis; posito obiecto in distantia 20. vnciarum à lente convexa, cuius diameter. 2. vnciarum, habetur socus, seu imago in distantia à dicta lente per duas vncias, & 2/9; quod si in hoc triangulo, cuius Basis est imago, vertex verò ipse vertex emersionis lentis convexae, ponatur oculus in ipsa media altitudine in A prout in prima figura huius problem.;’ [Fig. 1] ‘scilicet distantia à lente conuexa per vnciam 1. 1/9, habebis angulum visorium artificialem duplum anguli naturalis;’ après ce passage on lit encore à propos du même problème: ‘hic si applicetur lens caua diametri 16/18 unius vnciae, & retinebitur pro oculo immediatè applicato ad lentem cauam angulus visorius supradictus duplus naturalis; & fiet nouus focus, vnde diuergent radij à singulis punctis in distantia 6. vnciarum; hoc est ita se habebit oculns, ac si in distantia 6. vnciarum legeret caracteres naturaliter: quae omnia patent tum ex supradictis; tum ex doctrina praecedentis nostrae Centuriae Opticae impressae’.

10) Voir le deuxième passage cité dans la note précédente.

7) Voir la Prop. XX, Part I, Liv. I, p. 99.

11) Voir la note 1 de la p. 824.

12) Consultez sur l'origine de l'erreur d'Eschinardo la note 5 de la p. 825.

13) Voir le calcul qui suit, à commencer par la deuxième proportion.

[p. 824]

[Fig. 2.]

^1)2)3)4)5)

1) Il s'agit ici de calculer, d'après la règle de la Proposition citée dans la note 7 de la page précédente, le lieu du point qui, par rapport à la lentille D, correspond au point E verslequel se dirigent, après leur réfraction par la lentille A, les rayons venant de l'objet placé en F. Or, on trouve 50/9 pour la distance de ce point jusqu'au point E, c'est-à-dire 50/9 - 10/9 = 4 4/9 pour celle à la lentille A.

2) Ici x représente la distance focale à calculer d'après la règle mentionnée dans la note 7 de la page précédente; mais lisez dans le numérateur 100/81 au lieu de 10/81, et consultez plutôt le calcul qui commence à la ligne qui suit.

3) Dans cette proportion p désigne la distance DE, c'est-à-dire la distance à la lentille D de l'image formée par la lentille A. De cette manière on trouve par la règle de la Prop. XX (p. 99) l'expression pour la distance de l'image définitive au point E et, par conséquent, pour sa distance à la lentille D où l'oeil du myope est placé pour lequel la distance de la vision distincte est supposée égale à 6 pouces.

4) C'est donc la grandeur cherchée du diamètre de la surface concave de la lentille D. Elle est obtenue en substituant p = 10/9 dans l'expression pour x.

5) Vérification du résultat obtenu. Ajoutons que la cause de l'erreur d'Eschinardo, qui avait trouvé 16/18 au lieu de 15/16 pour le diamètre en question, ne peut être qu'une erreur de calcul. En effet, à la p. 255 de son ouvrage Eschinardo avait donné pour le calcul du diamètre de la surface courbe d'une lentille planconcave, quand les lieux de l'image et de l'objet sont connus, la règle suivante, dans laquelle nous avons changé les notations pour les adapter à celles de la Fig. 2: ‘Quod idem valet’ (il s'agit de la règle pour calculer d'après les mêmes données le diamètre d'une lentille convexe) ‘pro inuenienda diametro lentis Cauae... in quo solum advertendum est, vt paritur ibi aduertimus; quod quando lens caua, vt in casu praesenti, ponitur inter vitrum conuexum obiectiuum; & imaginem, seù Basim distinctam ab illo producendam: tunc dicta Imago censenda est loco obiecti, focus autem imaginarius, qui de nouo sit per lentem Cauam, censendus est loco soci, de quo hic agimus: quare hic etiam valet, quod eadem proportio est inter totam distantiam Imaginis, seù Basis distinctae E producendae à vitro conuexo; distantiam in quam à lente planoconcaua D (quod deinde proportionaliter applicetur vtrimque concauae, quae videtur esse aptior), & sesquialteram distantiae noui foci N,’ (pas marqué dans la figure) ‘qui producitur per lentem cauam D; quae proportio est inter tertiam partem lineae DE (dempta hinc prius diametro); & semidiametrum lentis cauae’.
Or, posant a pour la distance de la vision distincte du myope, p pour la distance DE, et x pour le diamètre de la surface concave, cette règle conduit à la proportion , ce qui donne , conforme au résultat trouvé par Huygens.

[p. 825]

§ 2⁶⁾. 2. Maj. 1684.

Ex Manusc.^o P. Gottignies⁷⁾ S.J. quod Roma attulerat D. Guldestolp⁸⁾ Sueciae Legatus, mihique legendum dederat.

Hujus generis telescopia⁹⁾, longe post Galilei tempora inventa illa sunt quae nunc adhibentur et habentur in praetio. Hujusmodi telescopij constructio prae caeteris specialem habet difficultatem a paucis admodum in haec usque tempora omni ex parte superatam, et ego quidem nullum unquam offendere potui ante

6) La pièce est empruntée à la p. 193 du Manuscrit F.

7) Voir sur le père G.F. de Gottigniez la note 1, p. 472 du T. II et sur ses ouvrages les notes 5, p. 194, 1, p. 239 et 1, p. 252 du T. V.

8) Nils Gyldenstolpe, comte de Noor, baron de Segerstad, seigneur de Jackula, Lidingenäs et Atta, fils de Michaël Wexonius Gyldenstorpe, naquit à Abo le 5 novembre 1648. En 1669 il entra dans le corps diplomatique et joua un rôle important dans les relations entre la Suède et la Hollande en préparant les traités conclus en 1674 et en 1686. Plus tard il fut nommé Chancelier de la Cour de Suède et Plénipotentiaire du Roi. Il mourut le 4 mai 1709.

9) C'est-à-dire les télescopes à deux verres convexes.

[p. 826]

annum hujus saeculi sexagesimum fabricatum in quo nihil eorum deesset quae in telescopijs aestimantur.

N.B. me anno 1659 in Systemate Saturnio meo docuisse usum diaphragmatis quod vocant, in foco ocularis lentis ponendi, absque quo colorum vitio haec telescopia carere non poterant¹⁾.

scribit Thelescopia. et tamen a τέλος finis et σκοπέω compositam vocem putat. cum sit a τῆλε, procul.

de apertura lentis objectivae nihil certi definit sed experiendo vult eam investigari, et mutari pro luce et splendore rei visae.

1) Voir les p. 82-84 de l'édition originale de l'ouvrage cité dans la note 2, p. 441 du T. II. Consultez d'ailleurs sur ce diaphragme les pp. 259 (note 2) et 473.

§ 3²⁾. [1692.]

Ex Dioptrica nova Guilielmi Molyneux. Edita 1692³⁾.

Concessio approbatoris est a.ⁱ 1690⁴⁾. item dedicatio 1690. 17 apr.⁵⁾ item monitum ad Lectorem⁶⁾.

Egregia est dedicatio ubi scolastica ac barbara philosophia exagitatur. nova experimentalis laudatur⁷⁾.

2) La pièce se trouve écrite sur une feuille séparée de quatre pages. Elle date probablement de mars ou d'avril 1692 quand Huygens venait d'emprunter la ‘Dioptrica nova’ à Steigerthal; voir les pp. 279 et 281 du T. X.

3) Voir sur cet ouvrage la note 11, p. 260 du T. X, et sur l'auteur la note 2, p. 528 du T. VIII.

4) On la trouve sur la page vis-à-vis du titre. Elle est rédigée ainsi: ‘I think this Book fit to be Printed. John Hoskyns. V.P.R.S. June the 4th. 1690’.

5) C'est-à-dire la dédicace ‘To the Illustrious The Royal Society’. Elle occupe 8 pages sans pagination.

6) L'‘Admonition to the Reader’ de trois pages sans pagination.

7) En effet, dans cette dédicace Molyneux attaque dans un style très vif ‘[the] sensless kind or Jargon, which they call'd Philosophy; and ... studied with the greatest Labour and Assiduity, that they might attain the name of Wise and Learned...the greatest Cheat [that] was ever imposed on the mind of Man’ pour le mettre en contraste ‘[to] that excellent Method of Experimental Philosophy, which now, by your [the Royal Society's] Example and Incouragement, does so universally prevail, and is so highly advanced all over Europe, and other Parts of the World’.

[p. 827]

Il demontre tout par l'hypothese que l'angle de refraction est ⅓ de l'angle d'inclination a la perpendiculaire⁸⁾.

Il n'a point mon theoreme du point correspondant pour une surface seule. scavoir qu'il y a 4 proportionelles⁹⁾.

Il a le theoreme aequivalent au mien pour le point correspondant dans un verre convexe¹⁰⁾, mais ne le demontre que dans un planoconvexe¹¹⁾, et cela par les angles. pag. 42. il met 4 proportionelles.

Pour estimer la multiplication il se sert de basis distincta selon Gregorius¹²⁾.

8) Molyneux reconnaît pleinement la loi des sinus; mais déjà dans l' ‘Admonition to the Reader’ il avertit ainsi le lecteur: ‘Thus we shall find in what follows, that many Lines are supposed equal, which strictly taken are really not so; but yet are so very little different, that for all use, and ease of Demonstration, they may be taken as equal. Thus also we suppose very small Angles and their Sines to be proportional; which precisely is not so, but is to the smallest and most insensible Difference’. Ensuite, à la p. 3 de son ouvrage, il adopte la proportion en question ‘as confirmed by Kepler's Experiments, and usually retain'd by most Optick Writers’; mais il ajoute: ‘These [Proportions]... we shall retain in the following Demonstrations, for the Ease and Plainness thereof. But in Calculation we shall observe the Proportion that follows in the 6^th Experiment’. Or, cette Sixième Expérience, qu'il fait suivre, repose sur une communication de Newton d'après laquelle: ‘from Air to Glass the Sine... of the Angle of Incidence... is to the Sine of the refracted Angle as 300 to 193 (or near, as 14 to 9)’.

9) Il s'agit de la Prop. XII, Part. I, Liv. I, p. 41.

10) En vérité Molyneux distingue plusieurs cas différents d'après la situation du point donné, c'est-à-dire plus près ou plus éloigné de la lentille, ou de l'autre côté, que le foyer des rayons parallèles, et d'après la convexité ou la concavité de la lentille. Toutefois les règles qu'il donne dans les Prop. V (p. 42), VIII (p. 48), XIV (p. 63), XV (p. 66) et dans les Corollaires des pp. 50 et 68 sont si peu différentes qu'on peut les considérer comme une règle unique et générale, équivalente à celle de Huygens. En effet, dans la Prop. V, qui correspond au cas de la Fig. 57, p. 98 du Tome présent, cette règle est formulée ainsi: ‘As the Difference, between the Distance of the Object, and Focus: Is to the Focus, or Focal Length::So the Distance of the Object from the Glass: To the Distance of the Respective Focus or Distinct Base from the Glass’; c'est-à-dire dans les notations de la figure mentionnée DO::OC = DC:CP. Or, par la règle de Huygens, formulée dans la Prop. XX, Part. I, Liv. I, p. 99, on obtient la proportion équivalente DO:DC = DC:DP.

11) Voir la p. 55 de l'ouvrage de Molyneux, où l'on lit: ‘I have chosen a Plano-Convex Glass to demonstrate this Rule, which holds as true in double Convexes, but would in them be more difficult and intricate to demonstrate’.

12) Il s'agit en premier lieu des Prop. XXXVII (p. 128), XL (p. 134), XLII (p. 137), XLVI (p. 148), XLVII (p. 150) et XLIX (p. 152) qui traitent le même sujet que les Prop. II, III, et IV, Part. I, Liv. II, p. 175-187 du Tome présent; c'est-à-dire le grossissement d'un objet vu distinctement ou confusément à travers une seule lentille. Ensuite dans la Prop. LIII (p. 161) (‘the great Proposition asserted by most Dioptrick Writers, but hitherto proved by none’) Molyneux apprend à calculer le grossissement d'une lunette à deux verres convexes comme il suit: ‘The apparent Diametral Magnitude of an Object viewed through the Telescope of Prop. L. Is to the apparent Diametral Magnitude of the Object viewed by the naked Eye at the Station of the Object-Glass::As the Focal length of the Object-Glass: to the Focal length of the Eye-Glass.’ A cette occasion encore il se sert dans la démonstration de la ‘basis distincta’ c'est-à-dire de l'image de l'objet dans le plan focal commun aux deux lentilles. En effet, il applique à cette image, considérée comme un objet que l'on voit à travers l'oculaire, un théorème pour l'exposition duquel il renvoie à la ‘Prop. L, Sec. 3 & 5’ ou à la ‘Prop. XXXIV’. En suivant la première de ces indications on arrive à un autre renvoi (à la Prop. XXXIII) qui renvoie à son tour à la Prop. 44 de l'Optica Promota de Gregory (voir la p. 58 de l'ouvrage de 1663 cité dans la note 6 de la p. 330 du T. IV). Cette proposition, qui ressemble à la Prop. XIII, Part. I, Liv. II, p. 233 du Tome présent, se lit comme il suit: ‘Si cujuscunque visibilis, singulorum punctorum radii, ad parallelismum reducantur: oculo radios parallelos recipienti, semper videbitur visibilis imago, eodem angulo visorio, quo videtur visibile ex vertice incidentiae lentis, vel speculi’.
Ajoutons encore 1^o. que la seconde indication, celle qui renvoie à la Prop. XXXIV de Molyneux, nous conduit à la démonstration d'un théorème semblable à celui de Gregory que nous venons de citer, 2^o. qu'on ne rencontre nulle part dans l'ouvrage de Gregory l'expression ‘basis distincta’.

[p. 828]

p. 155. Que la plus grande augmentation est quand un convexe est au milieu entre l'oeil et l'objet, il le prouve par un calcul. Et de mesme de la diminution du concave¹⁾.

de meniscorum focis plures habet propositiones²⁾. tandem etiam regulam universalem³⁾, cujus ipsi longa et triplex demonstratio⁴⁾. Ponit ut ego crassitudinem lentis velut nullam.

1) Voir les p. 153-155 de l'ouvrage de Molyneux et comparez les Prop. VII et VIII, Part. I, Liv. II, pp. 207 et 219 du Tome présent.

2) Il s'agit des Prop. XIX (p. 83). ‘In a Meniscus, if both spherical Superficies have the same Diameter, the Ray that falls thereon Parallel to the Axis, after its second Refraction proceeds again Parallel’; XX (p. 84) ‘In a Meniscus, if the Semidiameter of the Concavity be triple the Semidiameter of the Convexity, the Focal Length is equal to the Semidiameter of the Concavity’ et XXI (p. 86) ‘In a Meniscus, the Semidiameter of whose Convexity is triple the Semidiameter of the Concavity, the Virtual Focus is distant the Semidiameter of the Convexity’.

3) Cette règle énoncée par Molyneux à la p. 83 est démontrée dans la Prop. XXII (p. 86-91). Elle est formulée ainsi: ‘As the difference of the Semidiameters: To either of the Semidiameters whether of the Convexity or Concavity::So is the Diameter of the other Surface: To the Focus Real or Virtual’; comparez la règle identique formulée par Huygens dans le quatrième alinéa de la p. 89 du Tome présent.

4) C'est-à-dire pour les trois cas différents que Molyneux a cru nécessaire de distinguer.

[p. 829]

Focum sphaerae vitrae, ut et hemispherae docet theorematibus⁵⁾. in hoc distare air semidiametro et ⅓ semidiametri⁶⁾. quidni ⅔ diametri? omnia per angulum refractionis ∞ ⅓ anguli inclinationis, (nempe cum perpendiculari).

Proportionem Newtoni. refractionis vitri ait esse ut 300 ad 193⁷⁾. Ego pono 3 ad 2⁸⁾. sed sciendum est in varijs vitri generibus aliam atque aliam esse⁹⁾, unde telescopiae lentis majoris foci distantias majores multo inveni ex vitro albo quam in magis excocto et obscuriori licet in eodem cavo formatis.

Per binas lentes locum distinctae basis (ut vocat) invenit¹⁰⁾. Point solutionem Flamstedij¹¹⁾. Oculum et videndi rationem exponit p. 103¹²⁾. Utrum immutatione convexi chrystallini, an mutata distantia an utroque aptentur oculi ad diversas rei visae distantias dubitat et non definit¹³⁾. Cur inversâ in oculum picturâ tamen recta videamus bene declarat¹⁴⁾. Mariottum pro choroide allegat, sed nihil referre ait¹⁵⁾; rectè.

5) Il s'agit des Prop. XXIV (p. 93) ‘An intire Glass-Sphere Unites the Parallel Rays at the Distance almost of half its Semidiameter behind it’ and XXV (p. 94) ‘A Glass IIemisphere Unites the Parallel Rays at the Distance of a Diameter and one third of a Semidiameter from the Pole of the Glass’; comparez, quant à la première de ces propositions, la Prop. XIII, Part. I, Liv. I, p. 79 du Tome présent.

6) Il s'agit ici de la distance du foyer de l'hémisphère de verre à sa surface plane, laquelle distance (qu'on doit distinguer de celle du foyer au pôle, mentionnée dans la Prop. XXV citée dans la note précédente) est, en effet, trouvée par Molyneux (p. 94) comme étant égale à ‘a Semidiameter and one third of a Semidiameter’.

7) Voir les dernières phrases de la note 8 de la p. 827.

8) Voir la p. 13 du Tome présent.

9) Comparez l'Appendice III au Liv. I, Part. I, p. 154.

10) Voir les Prop. XVI, p. 69, XVII, p. 74, et XVIII, p. 75, où Molyneux apprend à calculer, en distinguant plusieurs cas différents, le lieu de l'image (‘Distinct Base’) d'un objet, situé quasi à l'infini, qui se forme après la réfraction par deux verres convexes, ou par un verre convexe et un concave. Le premier cas qu'il considère est celui de deux convexes où l'oculaire est placé à une distance de l'objectif inférieure à la distance focale du dernier, à propos dnquel cas il ajoute: ‘This Problem is of considerable Use in Dioptricks, being the Foundation of an excellent sort of Telescope much used in England for the Night’.

11) On trouve des solutions de Flamsteed des mêmes problêmes aux pp. 71-73 et 77-81 de l'ouvrage de Molyneux. Les règles auxquels il arrive sont identiques avec celles de Molyneux. Voici p.e. celle formulée pour le cas mentionné spécialement dans la note précédente: ‘As the longer Focus - the Glasses Distance+the shorter Focus: To the longer Focus - the Glasses Distance::So the shorter Focus: To the Distance of the Distinct Base from the inward Glass.

12) Voir la ‘Prop. XXVIII. The manner of Plain Vision with the naked Eye is expounded’.

13) Voir la p. 104 où l'on lit: ‘But whether this variety of Conformation consist in the Crystallines approaching nigher to, or removing farther from the Retina; Or in the Crystallines assuming a different Convexity, sometimes greater, sometimes less, according as is requisite, I leave to the scrutiny of others, and particularly of the curious Anatomist. This only I can say, that either of these Methods will serve to explain the various Phaenomena of the Eye; And I am apt to believe, that both these may attend each other, viz. a Less Convex Crystalline requires an Elongation of the Eye, and a more Convex Crystalline requires a shortning thereof.; As a more Flat Convex Object-Glass or of a Larger Sphere requires a Longer Tube, and one more Protuberant, bulging or of a Smaller Sphere requires a shorter Tube’. Comparez les pp. 133, 789 et 794 du Tome présent où Huygens a exposé ses idées sur l'accommodation.

14) Voir les p. 105-106 de l'ouvrage de Molyneux et la p. 745 du Tome présent.

15) ‘I know likewise, that by a curious Experiment in Opticks discover'd by an Ingenious French-Man Monsieur Mariotte, 'tis controverted, whether the Retina or Choroide be the Seat of Vision, or the Place on which the Pictures of outward Objects are expressed (vid. Philosoph. Transact. Num. 35 and 59). But to our business it matters not which of them we pitch on; and therefore I chuse to speak as commonly 'tis presumed; and mention the Retina, or rather the Fund of the Eye, as the Place that receives this Picture’ (p. 107). Comparez la p. 795 du Tome présent. Dans le premier des numéro's cités des Phil. Trans. (p. 668-671 de celui du 18 mai 1668) on trouve le résumé de deux lettres (mentionnées dans la note 8, p. 8 du T. VII), qui furent échangées entre Mariotte et Pecquet, dans la première desquelles Mariotte expose sa découverte du punctum caecum et la conclusion qu'il en tire que probablement ce n'est pas la rétine, mais plutòt la choroïde, qui est le siège de la vision. De même le second numéro cité, qui est du 23 mai 1670, contient aux p. 1023-1042 la traduction anglaise d'une nouvelle lettre de Mariotte à Pecquet (celle mentionnée en troisième lieu dans la note citée), dans laquelle il persiste dans son opinion sur le rôle de la choroïde dans la vision.

[p. 830]

In oculis myopum et πρεσβυτων refractionis vitium singulis figuris explicat¹⁾.

De loco imaginis multis inquirit²⁾ et haerere se fatetur itidem ut Barrovius in difficultate eadem. p. 119³⁾. quia nempe etiam uno oculo distantiam estimari vult. Visibilem aream rei visae ubique inquirit⁴⁾, quod vix operae pretium.

1) Voir la p. 108 et les Fig. 2 et 3 de la Table 25 de l'ouvrage de Molyneux.

2) Il s'en occupe aux p. 113-121 à propos de la ‘Prop. XXXI. Concerning the Apparent Place of Objects seen through Convex-glasses’. Dans ces pages, après avoir remarqué qu' ordinairement l'évaluation de la distance des objets proches se fait avec les deux yeux, il se rallie entièrement à l'opinion de Barrow que l'évaluation avec un seul oeil devient possible dès que le diamètre de la pupille a une grandeur sensible par rapport à la distance de l'objet. Ensuite il revient an même sujet dans la ‘Prop. XLV. Concerning the Apparent Place of Objects seen through Concave Glasses’ (p. 147).

3) Consultez sur cette difficulté les pp. 775 et 779 et surtout les notes 25 et 10 de ces pages. En suivant la théorie de Barrow, Molyneux identifie le lieu où l'observateur place un objet vu à travers une lentille convexe avec le lieu de la ‘Distinct base’, c'est-à-dire de l'image virtuelle ou réelle de l'objet, mais alors, dans le cas où l'oeil se trouve entre la lentille et cette ‘Distinct base’, il se heurte à la difficulté en question et il poursuit: ‘In this.... lies the great Difficulty, which the Incomparable and most profoundly Learned Barrow...confessedly passes over as insuperable, and not to be explained by whatever Theories we have yet of vision’. Ensuite, après avoir décrit, à l'exemple de Barrow, ce que l'oeil observe dans ce cas, il fait suivre à la p. 119, citée dans le texte: ‘All which (continues the candid Barrow) seems repugnant, or at least not so well to agree to what we have laid down. And so he leaves this Difficulty to the solution of others, which I (after so great an Example) shall do likewise; but with the resolution of the same admirable Author, of not quitting the evident Doctrine, which we have before laid down, for determining the Locus Objecti, on the account of being pressed by one Difficulty, which seems inexplicable, till a more intimate Knowledg of the Visive Faculty be obtained by Mortals. In the mean time, I propose it to the consideration of the ingenious, whether the Locus apparens of an Object placed as in this 9^th Section, be not as much before the Eye, as the Distinct Base is behind the Eye’.

4) Molyneux s'occupe de ce sujet dans les Prop. XXXIV (p. 125), XXXV (p. 126), XXXVII (p. 128), XL (p. 134), XLII (p. 137). XLVI (p. 148) et XLVIII (p. 151). Dans toutes ces propositions il ne s'agit que de la détermination de la partie visible d'un objet vu à travers une seule lentille convexe ou concave, le lieu de l'oeil et de l'objet étant donné. Ensuite, à la Prop. LIV (p. 168), il traite la lunette à deux verres convexes et arrive à la règle suivante: ‘as the Distance between the Object-Glass and Eye-Glass: To half the Breadth of the Eye-Glass::So Radius: To the Tangent of half the Angle received’. De même, dans la Prop. LVI, il traite (p. 174) le champ de vision de la lunette à quatre verres convexes (celle décrite par Huygens dans la Prop. V, Part. III, p. 469). Enfin, dans la Prop. LVII, il explique à la p. 178 comment le champ de vision de la lunette à lentille oculaire concave peut dépendre de la largeur de la pupille; comparez la Prop. II, Part. III, p. 451-453 du Tome présent.

[p. 831]

augmentum unius convexi non exhibet Theoremate, sed ex Gregorio⁵⁾, et tantum invenire docet.

aliquid de inflexis rectis per lentem convexam visis p. 137⁶⁾.

Locum apparentem dicit esse in foco objectivae in telescopio ex 2 convexis⁷⁾. probat male quia filum ibi positum apparet inherere rei visae. Respondeo, utrumque distincte ibi cerni, sed non ideo ibi apparet objectum. Tamen rectè secundum illos, quia uno oculo estimaret distantiam.

5) Il s'agit des Prop. XXXIII (p. 122), XXXIV (p. 125), XXXVII (p. 128), XL (p. 134) et XLII (p. 137), qui traitent les mêmes questions résolues par Huygens dans les Prop. II et III, Part. I, Liv. II (p. 175-183). Il est vrai que les Prop. XXXIII, XXXVII, XL et XLII contienuent aux pp. 123, 129, 135 et 139 des renvois à l'Optica Promota de Gregory; toutefois il paraît que le but de ces renvois est plutôt d'indiquer les théorèmes correspondants de Gregory que de servir dans les démonstrations; puisque les raisonnements de Molyneux nous semblent donner des indications qui suffisent pour ses démonstrations.

6) Voici le passage en question: ‘And we shall find by Calculation (as indeed 'tis evident by the very Inspection of the Schemes) that the Collateral parts ze, dy, of the Object zy, are



much more magnified (in respect of their Natural Appearances) by Broad Glasses formed on small Spheres, than the Middle Parts ex, dx, for the Angle gop is the Optick-Angle, through the Glass, of the Part ze; and the Angle pos is the Optick-Angle, through the Glass, of the part ex; but the former exceeds the Natural Optick-Angle much more than the latter...From hence it is, that by Broad Glasses formed on small Spheres, the extreme Parts of strait Objects, seem to be incurved and bent; as is manifest in the Case of the Micrometer, or lattice of fine Hairs, strained before the Eye Glass in a Telescope, for Measuring the Diameter of Objects. As Pere Cherubin complains in his Dioptrique Oculair’ [l'ouvrage cité dans la note 1, p. 456 du T. VII] ‘Part. III. Sec. 7. Chap. I. pag. 239. but understood not the reason. Of this we may make Experiment, by looking with a very Convex Glass at two Parallel Lines drawn pretty close on a Paper’.
On remarquera que l'explication de Molyneux, où l'aberration sphérique n'entre pas, n'est nullement satisfaisante, puisqu'elle aurait dû le conduire à la conclusion contraire à celle qu'il énonce, c'est-à-dire, que les parties les plus éloignées de l'axe seraient moins agrandies que les autres.
Consultez à propos des idées de Huygens sur la déformation des images la note 20 de la p. 771.

7) Voici le ‘Scholium’ en question (p. 159-160): ‘The Locus Apparens of an Object through this Glass’ [l'oculaire d'une lunette à deux verres convexes] ‘is the Distinct Base’ [l'image formée par l'objectif] ‘as is manifest from this Experiment. Stretch an Hair exactly in this Distinct Base, it shall appear as it were fixt to the very Object’.

[p. 832]

Prop. 53. p. 161. amplificationem telescopij ex duobus convexis, theorematice ponit ut ego¹⁾, et me allegat ex Systemate Saturnio²⁾. The learned and ingenious monsieur Hugens &c. But hitherto we are so unhappy as to want that excellent Persons dioptrics.

dicit hanc a plerisque dioptr. authoribusque affirmari, non probari. allegat Cherubin. part. 2. prop. 21. 59. 60. 62³⁾. Cepleri diopt. prop. 124⁴⁾. Galil. nunt. Syder⁵⁾. quos vide. puto neminem ante me hoc vidisse.

Hon. Fabri in Synopsi dioptr.⁶⁾ demonstrationem improbat quae prop. 44 et 45⁷⁾.

1) Voir la note 12, p. 827, et quant au traitement de la même question par Huygens la Prop. III, Part. III, p. 455.

2) Voici, enentier, le passage en question tel que Molyneux l'a publié à la p. 168 de son ouvrage dans un ‘Scholium’ ajouté à la Prop. LIII qui traite le grossissement de la lunette à deux verres convexes: ‘From hence it is manifest, how requisite it is in relating any Phaenomena observed by the Telescope (or even by the Microscope) to mention not only the length or the Tube in general; But to specifie the particular Focus of the Eye-Glass, as well as of the Object-Glass; as also the Aperture of the Object-Glass. For by this means, they that intend to observe the same Phaenomena, may understand how to adapt their Telescopes proper for the Observation. This the Learned and Ingenious Monsieur Huygens in his Systema Saturnium puts down exactly, pag. 4. Where also we find this passage. Illud in Dioptricis Nostris demonstratum invenietur, Speciei per Tubum visae ad eam quae Nudo Oculo percipitur, hanc secundum Diametrum esse rationem, quae Distantiae Foci in Exteriori vitro (Objectivo Scilicet) ad illam quae in Interiori sive Oculari vitro est Foci Distantiam. But hitherto we are so unhappy as to want that excellent Persons Dioptricks. In the mean time, let that which I have given in the foregoing Prop. LIII. serve till a better be offered.

3) Il s'agit de l'ouvrage de 1671, cité dans la note 1 de la p. 456 du T. VII. Voici les Prop. mentionnées: 21. Plusieurs verres convexes, estants successivement assemblez avec un mesme verre concave; celuy de plus grande sphere, représentera les objets plus grands, avec ce mesme verre concave. 59. Connoistre la proportion, qui se trouve entre deux verres; de l'Oculaire Dioptrique. 60. Connoistre, par l'habitude reciproque, des verres; de deux, ou de plusieurs Oculaires Dioptriques; la proportion de leurs effets; et l'augmentation, de l'espece de l'obiet. 62. Connoistre de combien, l'oculaire dioptrique de quelconque espece; augmente la representation de l'effet’.
Ajoutons que la règle exacte est donnée sans démonstration proprement dite dans un Corollaire qui appartient à la Prop. 60. La Prop. 62 traite seulement la manière de déterminer expérimentalement le grossissement à l'aide d'une règle de bois divisée qu'on regarde à la fois par la lunette et par l'oeil nu.

4) Cette Prop. 124 ‘Magnitudinem ampliatae speciei artificiosè aestimare’ se trouve à la p. 66 de l'ouvrage de 1611, cité dans la note 5, p. 6 du T. I. Elle a la même portée que la Prop. 62 de Cherubin, mentionnée dans la note précédente.

5) Il s'agit du passage suivant: ‘Vt autem de multiplicatione instrumenti quilibet paruo negotio certior reddatur, circulos binos, aut quadrata bina chartacea contornabit, quorum alterum quatercenties altero mains existat, id autem erit tunc, cum maioris diameter, ad diametrum alterius longitudine fuerit vigecupla; deinde superficies ambas in eodem pariete infixas simul à longe spectabit, minorem quidem altero oculo ad Perspicillum admoto, maiorem verò altero oculo libero; commodè enim id fieri licet uno eodemque tempore oculis ambobus adapertis; tunc enim sigurae ambae eiusdem apparebunt magnitudinis, si Organum secundum optatam proportionem obiecta multiplicauerit’.

6) Voir sur cet ouvrage la note 5 de la p. 445 du T. VIII.

7) Sur ces propositions Molyneux s'exprime comme il suit: ‘Honoratus Faber in his Synopsis Optica Prop. XLIV, for the Telescope consisting of a Convex Object Glass and Concave Eye-Glass; and in Prop. XLV. for the Telescope consisting of a Convex Object-Glas and Convex Eye-Glass, indeavours at something, which he calls a Demonstration of this Property. But whether that which he there offers will amount to clear Satisfaction, I leave to their Judgments, who shall Read him’.

[p. 833]

p. 171. Tabulam aperturarum dat ex mente Auzotij, qui subduplicatam rationem esse ponit diametrorum aperturae, ad rationem longitudinum seu foci distantiarum; experimento ut puto doctus, quum nos id demonstremus posita radij diffusione Newtoniana⁸⁾.

Imo Auzotium promittere ait⁹⁾ demonstrationem, in dioptricis suis. et citat Philos. Trans N. 4, P. 55¹⁰⁾. ubi ipsius Tabella aperturarum. Sed illo tempore nondum cognita erat diffusio radij Newtoniana. ex qua pendet haec demonstratio. Ergo eam non habuit Auzotius. Dicit debuisse docere Auzotium an Lunae an Jovi, Veneri, &c. spectandae tales aperturae convenirent¹¹⁾. quod tamen subduplicatam istam rationem non evertit.

distinguit optimas, bonas, ordinarias lentes¹²⁾. In longitudine 6 pedum ponit in his diametros aperturae 1 poll. 7 lin.: 1 poll. 5 lin.: 1 poll. 2 lin. In long. 100 ped. 6 poll. 8 lin.: 5 poll. 9 lin.: 4 pol. 10 lin. in longitudine 300 pedum. 11.6::10.0:8.5. In longit. 200 ped. 9.6:8.0:6.9¹³⁾. nihil habet de diaphragmate¹⁴⁾.

Prop. 56. p. 172. Explicat telescopium cum 3 convexis ocularibus aequalibus¹⁵⁾ satis bene in magno schemate, quia in unum confert quae nos duobus dividimus.

8) Voir les p. 487-495 du Tome présent.

9) Voir la p. 170 de l'ouvrage de Molyneux.

10) Voir dans les Phil. Trans. du 5 juin 1665 l'article: ‘Monsieur Auzout's Judgment touching the Apertures of Object-Glasses, and their Proportions, in respect of the several Lengths of Telescopes’. D'après cet article Auzout promit d'exposer la raison de cette proportion dans sa Dioptrique, qu'il était occupé à écrire et qu'il finirait aussitôt que sa santé le lui permettrait. Cette Dioptrique n'a jamais paru.

11) En effet, Molyneux fait suivre (p. 170): ‘But this Ingenious Person’ [Auzout] ‘should have told us, when he speaks of the Apertures of Glasses, whether he designs them for Objects on the Earth or in the Heavens. And if in this latter, whether for the Moon, Mars, Jupiter, or Venus. For each of these Objects will require a different Aperture of the same Glass. Because the strength of their Light is different. For to view Venus there is requisite a much smaller Aperture than to view the Moon, Saturn or Jupiter’. Comparez sur cette question les p. 505-511 du Tome présent.

12) C'est-à-dire à l'exemple d'Auzout dont la table des ouvertures est reproduite par Molyneux sans changement.

13) Comparez la table de la p. 499 où Huygens recommande p.e. une ouverture de 7,75 pouces pour une longueur de 200 pieds.

14) Comparez les pp. 473, 774 et 826.

15) Il s'agit du télescope décrit dans la Prop. V, Part. III, p. 469 du Tome présent.

[p. 834]

Prop. 57. p. 176. Explicat telescopium ex convexo et cavo, per bazin distinctam¹⁾ Gregorij (quem vide) quae hic non tam bene adhibetur quam in 2^bus convexis. Etiam aream visam ex pupillae amplitudine pendere notat²⁾.

Unico folio explicat microscopia³⁾; dein Laternam magicam⁴⁾.

Parte 2^da. Leibnitij principium in Opticis, quo vult probare leges reflexionis et refractionis⁵⁾, post Fermatium tamen⁶⁾. Nempe naturam agere via brevissima quod non admodum apposite hic adhibetur, cum nos multo meliores rationes adduxerimus in Libro de Luce. et phenomenon Fermatij demonstremus⁷⁾. quid dicerent de refracto perpendiculari radio in Crystallo Islandico⁸⁾. Author non vidit puto nostrum de luce.

Cur in convexis speculis non item brevissimam viam affectat natura?⁹⁾

p. 196. Causas refractionis investigat secundum Barrovium¹⁰⁾, fingendo radium lucis velut parallelogrammum. sed frustra. sic et Magnanus¹¹⁾ fere.

p. 198. Lucem vult probare esse corpus¹²⁾. potius dixisset esse motum corporis

1) Voir sur cette expression la note 12 de la p. 827.

2) Comparez la Prop. II, Part. III, p. 451 du Tome présent.

3) C'est-à-dire dans une feuille de deux pages. Voir la ‘Prop. LVIII. The double Microscope composed of a Convex Object Glass, and Convex Eye-Glass is Explained’, p. 181-182 de l'ouvrage de Molyneux.

4) Voir la ‘Prop. LIX. The Explication of the Magick Lantern, sometimes called Lanterna Megalographica’, p. 183-184 de son ouvrage.

5) Dès le début de cette seconde Partie le principe en question, que la lumière suit la voie la plus facile, est introduit en traduisant une partie de l'article de Leibniz, que nous avons cité dans la note 12, p. 602 du T. X.

6) Voir les p. 75-82 du T. IV. D'ailleurs Molyneux lui-même mentionne Fermat à la p. 196 de son ouvrage comme l'auteur ‘d'une longue démonstration’ du même principe.

7) Voir les p. 32-41 de l'édition originale du ‘Traité de la lumiere’.

8) Voir le Chap. V. ‘De l'estrange refraction du cristal d'Islande’, p. 48-101 de l'ouvrage cité dans la note précédente.

9) Lisez concaves, puisque le cas où le chemin suivi est un maximum au lieu d'un minimum ne peut se présenter que chez un miroir concave. Molyneux s'était borné au cas du miroir plan.

10) En effet, le passage en question constitue une traduction presque littérale des considérations peu précises exposées par Barrow dans la ‘Lectio II’, p. 14-15 des ‘Lectiones opticae’, où il considère les différentes parties d'un rayon de lumière comme excerçant les unes sur les autres des forces élastiques par lesquelles celles qui sont déjà entrées dans le milieu le plus dense forceraient les autres à changer la direction de leur route.

11) Il s'agit probablement de l'ouvrage de 1673 cité dans la note 8 de la p. 195 du T. II.

12) ‘And thus much concerning Refraction. The consideration whereof does naturally suggest unto us, that Light is a Body. For however the Antient Aristotelians desined it, Actus perspicui quatenus perspicuum, which is perfectly unintelligible; yet so much we may perceive hereby, that they designed to exclude it from all Corporeal Notion. But the various Properties of Light, that do necessarily belong to a Body, are so many and evident, that they leave no room for any farther doubt in this matter. I shall mention but a few. And first, by this Affection of being refracted, 'tis manifest that Light in its passage through this and t'other Diphanous Body does find a different Resistance.... The second Property, that confirms Light to be a Body.... moved or thrust forward, is, That it requires time to pass from one place to another.... A third proof.... is, That it cannot by any Art or Contrivance whatever be increased or diminished; that is to say, we cannot magnifie (for instance) the Light of the Sun or a Candle, no more than we can magnifie a Cubick Inch of Gold, or make it more than a Cubick Inch...’.

[p. 835]

choroidem afficientem. sicut sonus non est corpus sed motus aeris seu succussionem, in aures agentem.

Romeri observationem de lucis celeritate refert, et a Flamstedio et Halleio probari dicit¹³⁾.

Ut bene centrentur lentes objectivae aliqua adfert¹⁴⁾, sed meam rationem non attingit.

p. 232¹⁵⁾. de dirigendis telescopijs in caelum, nostram quoque Astroscopiam compendiariam allegat, et a.^o 1685 vidisse ait Hagae in horto nostro, quae esset ratio inventi. The deservedly celebrated mons.^r Hugens, one of the chief mathematick Luminairies of the present age &c.¹⁶⁾ Addit se eodem tempore vidisse Machinam meam Planetariam, or moving Ephemeris¹⁷⁾ a machine that cannot be sufficiently admired.

p. 226. Hookij inventum refert parandis longis lentibus ex datis brevioribusque inter binos orbes vitreos alterum utrinque planum alterum planoconvexum interposita aqua vel alio liquore pellucido, conjungit, ut convexa superficies sit

13) Après avoir mentionné la démonstration de Römer sur la vitesse finie de la lumière et la remarque à ce sujet de Newton dans ses ‘Principia, Lib. I, Schol. Prop. 96’, Molyneux fait suivre (p. 199); ‘For a conformation of all which I appeal to the Labours of the Ingenious Mr. Flamsteed and Mr. Halley, to whom the Learned World is for ever obliged by their Advancements of Astronomy’.

14) Molyneux consacre à ce sujet les p. 218-222 du ‘Chap. IV. Of Mechanick-Dioptricks’.

15) Lisez: ‘223’.

16) Voici le passage en entier: ‘The deservedly Celebrated Mons. Hugens, one of the chief Mathematick Luminaries of the present Age, has publish'd a small Tract, Astroscopia Compendiaria, designed only for Describing his way of Managing great Glasses with very little trouble, and without a Tube. This I am sure is no barren Speculation of the Ingenious Author's, but successfully practised by him; as I can gratefully testifie, having had the favour of being shewn the whole Contrivance by the Excellent Author himself in his Garden at the Hague, Ànn. 1685. at which time I had the happiness also of seeing his Planetary Clock, or Moving Ephemeris, a Machine that cannot be sufficiently admired’. On peut comparer la relation (p. 528-531 du T. VIII) d'une visite rendue en 1684 à Huygens par Thomas Molyneux, frère de l'auteur de la ‘Dioptrica nova’. En juin 1685 ce dernier visita lui-même son frère Thomas qui alors étudiait la médecine à Leiden et c'est sans doute à cette occasion qu'eut lieu l'entrevue entre William Molyneux et Huygens dont il est question ici.

17) Voir la description de cet instrument dans l'ouvrage de Huygens cité dans la note 5, p. 343 du T. VIII.

[p. 836]

interior. Il doute s'il pourroit succeder, parce qu'on ne l'a pas encore pratiquè¹⁾. Sed alia ratio reddi posset, uti et de menisco.

Si hoc modo producere vellet foci distantiam, etiam tanto perfectior lens esse deberet, imo et superficies istae utrinque planae lentis. Ergo multo facilius unam lentem convexam longioris foci distantiae fabricare, ut omittam tot supervacuas reflexiones.

De micrometri inventore agit²⁾. cujus non advertit me fundamentum jecisse in Systemate saturnio³⁾. la Hire praestare ait lamellam in foco objectam ad metiendas distantias⁴⁾.

1) Molyneux, après avoir cité l'article de Hooke ‘A method by which a Glass of small Plano-convex Sphere may be made to refract the Rayes of light to a Focus of a far greater distance than is usual’ (Phil. Trans. du 7 mai 1666, p. 202-203), continue comme il suit: ‘This, I must confess is an ingenious Hint: But I doubt the desired Effect will not be so successfully attained thereby, so as so constitute an Object-Glass for a Telescope. For certainly, were it effectual; 'tis so easie and withal so useful, that before this time it would have obtained, and been practised universally. And this makes me question, whether it would be of any better effect, than a Meniscus-Glass, or a Combined Glass of Prop. XVII. Part. I’ (c'est-à-dire la combinaison d'un verre convexe avec un planconcave de plus grande distance focale, placé à quelque distance de l'autre).

2) Voir les p. 246-247, où l'on lit: ‘The next Telescopick Instrument which I shall explain, is the Micrometer. Concerning the Invention of the Ingenious Instrument, I have only this to say, That for the Honour thereof, there are several Competitors: Mons. Petit, Surveyor of the Fortifications in France, was the first that published to the World the rough Draught hereof, 12 Mar. 1667. Vid. Journal des Scavans, 16. May 1667. After him Mons. Auzout, another Ingenious Frenchman, publish'd a Tract concerning the exact Mensuration of the Planets Diameters, wherein he seems to challenge the Invention of this Instrument to himself and Mons Picard, Journ. des Scavans, 28 Juin. 1667. and Philosoph. Transact. Num.] 21. pag. 373. But last of all a Candid Englishman of our own, Mr. Rich. Townley, does vindicate the first Contrivance hereof to its true and original Author, Mr. Gascoigne an English Gentleman who was kill'd in King Charles I. Service, Vid. Philosoph. Transact. Num. 25. pag. 457. wherin Mr. Townley (who is of Undoubted Credit) asserts, that Mr. Gascoigne made and used this Instrument before the Civil Wars in England: And that Mr. Townley had then in his Custody two or three of these Instruments first devised by Mr. Gascoigne; to which Mr. Townley himself had added some considerable Improvements. All which, with the exact Fabrick, and fitting of the Body of the Instrument to a Telescope, we shall find accurately discribed in Num. 29. p. 541. Philosoph. Transact. to which I shall therefore refer the Reader....’.

3) Voir la note 11, p. 63 du T. VI.

4) Consultez sur ce procédé la p. 843 qui suit. Mais ajoutons que, ni dans le résumé de l'invention du micromètre que nous venons de citer dans la note 2 qui précède, ni ailleurs dans l'ouvrage de Molyneux, le nom de la Hire est mentionné à ce propos. Probablement il s'agit d'une inadvertance de Huygens écrivant ‘la Hire’ au lieu d'‘Auzout’.

[p. 837]

Cap. 6. p. 251, multa memorabilia adfert de inventore ocularium primo qui ignoratur sed extitisse videtur paulo post annum 1285. allegat Dictionarium della Crusca in voce Occhiale⁵⁾. Ubi de concione fr. Jordani de rivalto &c. item alios 2 vel 3⁶⁾. Putat inter monachos primum innotuisse⁷⁾.

Telescopij inventum primum ad Baconum anglum⁸⁾ qui anno 1292 obijt pro-

5) Voir la p. 255 de l'ouvrage de Molyneux, où l'on lit: ‘The Italian Dictionary, de la Crusca, on the Word Occhiale, makes this remark, That Frier Jordan de Rivalto, who dyed at Pisa, An. 1311. in a Book of Sermons which he writ An. 1305. tells his Auditory in one of them, that it is not Twenty years since the Art of making Spectacles was found out, and is indeed one of the best and most necessary Inventions in the World’.

6) On lit encore à la p. 254 ‘But however we may doubt of Spectacles being so ancient as 1150. We may be certain that about the Thirteenth Century, they were commonly known and used. For (beside what we shall say hereafter of our Country-man Frier Bacon) the most learned Mon. Spon in his Recherches Curieuses D'Antiquitè, Dissert. 16. inserts a Letter of Signior Redi to Paulus Falconerius, concerning the Time when Spectacles were invented; and this he fixes between 1280 and 1311. from the Testimony of a Manuscript Chronicle in Latin, in the Library of the Friers Preachers of St. Katherine at Pisa, Fol. 16. Wherein it is said, that Frater Alexander de Spina, Vir Modestus & bonus, quaecunque vidit aut audivit facta, scivit & facere. Ocularia ab aliquo primo facta, & communicare nolente, ipse fecit & communicavit corde hilari & volente. And this Alexander de Spina was a Native of Pisa, and dyed there, An. 1313’.
Après cela Molyneux fait suivre: ‘Signior Redi has in his Library a Manuscript written An. 1299. Di Governo della Famiglia de Scandro di Pipozzo. In which there is this Passage; Mi truovo cosi Gravoso di Anni che non arei Valenza Di Leggere e Scrivere senza Vetri appellati Okiali, Truovati novellamente per Commodità delli Pouveri Veki, quando affiebolano del Vedere’.
Enfin on lit à la p. 255: ‘About the same time viz. 1305. Bernard Gordon a famous Physician of Montpelier, in his Lilium Medicinae, thus commends a certain Eye-Salve: Et est tantae Virtutis, quod decrepitum faceret legere Literas minutas absque Ocularibus. And An. 1363. Guido de Chauliac, in his Book entituled Grand Chirurgery, after proposing several Collyria, saith; If these or the like will not do, you must make use of Spectacles’.

7) ‘'Tis true indeed, if we credit the forementioned Chronicle’ [voir la note 6] ‘of the Convent at Pisa, Frier Spina makes as fair a Challenge to the Invention, as the first Author, who refused to communicate it. But I am apt to believe, That, whoever this close Man was that would not impart to Spina, He was a Frier; and that these Monkish Men, and Jordan amongst the rest, had this Invention whispered amongst themselves, before it was publick; and that they all had the First Hint thereof from our Country-Man Frier Roger Bacon’. Après quoi Molyneux expose les raisons qui lui font croire que le frère Bacon connaissait non seulement l'effet des verres convexes et concaves mais aussi de leurs combinaisons dans la composition des télescopes.

8) Roger Bacon, le moine franciscain à qui l'on avait donné le surnom de ‘doctor admirabilis’, naquit vers 1214 à Ilchester ou près de cette ville. Après avoir étudié à Oxford et ensuite á Paris, il retourna vers 1250 en Angleterre où il demeura à Oxford jusqu'en 1257. Tombé en disgrâce auprès de ses supérieurs qui, à cause de ses expériences de physique et de chimie, l'accusaient de sorcellerie, on l'envoya à Paris où il fut tenu dans un isolement complet pendant plusieurs années. Toutefois le pape Clément IV l'enjoignit de mettre ses idées en écrit et de lui envoyer secrètement ses ouvrages. Après qu'il eut recouvré en partie sa liberté ses écrits furent condamnés en 1278 comme renfermant des nouveautés suspectes et dangereuses; ce qui valut à l'auteur de nouveau une longue détention. Il mourut à Oxford, probablement en 1294.
Plusieurs de ses manuscrits furent publiés après sa mort, parmi lesquels se trouve l'‘Opus Majus ad Clementem Papam, ed. S. Jebb, London, 1733’, f.^o. Il est vrai que dans ces écits il se fait connaître comme un homme qui avait devancé son siècle sous plusieurs rapports; toutefois plusieurs de ses descriptions semblent plutôt dues au libre cours de sa fantaisie qu'à des observations et des expériences exactes. C'est pourquoi, afin qu'on puisse mieux juger de la portée des citations qui suivent, nous leur avons donné quelquefois dans les notes un peu plus d'extension que ne l'avait fait Molyneux.

[p. 838]

babiliter referri contendit. Is in libro perspectivae¹⁾ part. 3. dis. 2. C. 3²⁾. haec habet. Si vero corpora non sunt plana per quae visus videt, sed sphaerica, tunc est magna diversitas, nam vel concavitas corporis est versus oculum, vel convexitas. Item eodem loco Dis. Ult. sic.³⁾ de visione fracta majora sunt, nam de facile patet, maximà posse apparere minima et è contra: et longe distantia videbuntur propinquissimae et è converso. Sic etiam faceremus solem et lunam et stellas descendere secundum apparentiam hic inferius &c. Hinc apparet, inquit, eximum quoddam circa optica vitra secretum ei cognitum fuisse. addit ex ejusdem Baconi Epistola ad Parisiensem⁴⁾ (an Jo. Paris?⁵⁾) de secretis artis et naturae. Cap. 5⁶⁾. Possunt etiam sic formari perspicua, ut longissime posita appareant propinquissima, et è contra: Ita quod ex incredibili distantia legeremus literas minutissimas, et numeraremus res quantumcunque parvas, et stellas faceremus apparere quo vellemus. Sed si quid praeter haec verba aut vota habuisset an saltem de lunae phaenomenis nil percepisset? Plura scire cupienti consulere suadet authores Ant. a Wood, Historie et antique universitatis Oxon.

1) Le livre ‘De Scientia Perspectiva’ constitue la Partie Cinquième de l'‘Opus Majus’, mais il fut aussi publié séparément sous le titre: ‘Rogeri Baconis Angli viri eminentissimi Perspectiva, opera et studio Johannis Combachii, Phil. Prof. in acad. Marpurgensi, Frankfurt, 1614, in 4.^to’.

2) Il s'agit du Capitulum III ‘De diversitate loci imaginis in sphaericis’, appartenant à la ‘Distinctio Secunda Tertiae partis, quae est de visu fracto’, laquelle troisième partie appartient à son tour à la ‘Pars Quinta Hujus Persuasionis De Scientia Perspectiva; habens tres partes’. On retrouve, en effet, le passage en question à la p. 150 du Vol. II de l'édition de J.H. Bridges, Oxford, 1897, de l'‘Opus Majus’, où l'on lit: ‘Si vero non sint corpora plana per quae visus videt sed sphaerica, tunc est magna diversitas. Nam vel concavitas corporis est versus oculum vel convexitas’.

3) Voici le passage de l'‘Ultima Distinctio. De comparatione perspectivae ad sacram sapientiam et mundi utilitates, habens capitula quatuor. Capitulum IV’ (p. 165 de l'édition de Bridges) ‘De visione fracta majora sunt; nam de facili patet per canones supradictos, quod maxima possunt apparere minima, et e contra, et longe distantia videbuntur propinquissima et e converso. Nam possumus sic figurare perspicua, et taliter ea ordinare respectu nostri visus et rerum, quod frangentur radii et flectentur quorsumcunque voluerimus, ut sub quocunque angulo voluerimus videbimus rem prope vel longe. Et sic ex incredibili distantia legeremus literas minutissimas et pulveres et arenas numeraremus propter magnitudinem anguli sub quo videremus, et maxima corpora de prope vix videremus propter parvitatem anguli sub quo videremus, nam distantia non facit ad hujusmodi visiones nisi per accidens, sed quantitas anguli. Et sic posset puer apparere gigas, et unus homo videri mons, et in quacunque quantitate, secundum quod possemus hominem videre sub angulo tanto sicut montem, et prope ut volumus. Et sic parvus exercitus videretur maximus, et longe positus apparet prope, et e contra: sic etiam faceremus solem et lunam et stellas descendere secundum apparentiam hic inferius, et similiter super capita inimicorum apparere et multa consimilia, ut animus mortalis ignorans veritatem non posset sustinere’.

4) Il s'agit de l'‘Epistola Fratris Rogerii Baconis de Secretis operibus Artis & Naturae et de Nullitate Magiae’. Cette lettre fut publiée entre autres par Orontius Finaeus en 1542 à Paris. Nous la citerons d'après l'ouvrage: ‘Jo. Jacobi Mangeti Medicinae Doctoris et Sereniss. ac Potentiss. Regis Prussiae Archiatri Bibliotheca Chemica Curiosa seu Rerum ad Alchemiam pertinentium Tomus Primus, Genevae, MDCCII’, où elle occupe les p. 616-624.

5) Ici Huygens a en vue Jean de Paris le disciple de Bacon par lequel celui-ci fit parvenir son ‘Opus Magnus’ à Clément IV; mais la lettre en question n'était pas adressée à lui puisqu'elle est souscrite: ‘Ad Guilielmum Parisiensem conscripta’.

6) Voici, plus au complet, le passage qui suit tel qu'on le trouve au ‘Cap. V. De Experientiis perspectivis artificialibus’ à la p. 620 de l'ouvrage cité dans la note 4: ‘Et sic omni civitati, & exercitui contrario, possunt sieri terrores maximi: ut vel propter multitudinem apparitionum stellarum vel hominum super ipsos congregatorum dispereant, praecipue si sequens documentum cum illo primo habeatur, possunt enim sic figurari perspicua ut longissime posita appareant propinquissima, & è contrario: ita quod ex incredibili distantia legeremus literas minutissimas, & numeraremus res quantumcunque parvas, & stellas faceremus apparere quò vellemus’.

[p. 839]

l. 1. pag. 136. D.^rem Plott. Nat. Hist. of Oxfordshire Cap. 9, Sect. 2 et 3 &c. and Sect. 39, 40, 41. ubi de monachis Baconum male vexantibus et in carcerem compingentibus velut magum et praestigiatorem. Ubi et de initio pulveris pyrici ab eodem Bacono profecto. ex literis ad Parisiensem Cap. 6.⁷⁾ annis 100 ante Barthold Swartz. In omnem distantiam quam volumus, possumus artificialiter componere ignem comburentem ex sale petrae et alijs. (haec vero alia in alio manuscripto codice sunt sulphur et carbonum pulvis). Et paulo post addit, Praeter haec (id est combustionem) sunt alia stupenda Naturae. Nam soni velut tonitrus, et coruscationes possunt fieri in aere, imo majore horrore quam illa quae fiunt per naturam. Nam modica materia adapta, sc. ad quantitatem unius pollicis, sonum facit horribilem, et coruscationem ostendit violentam, et hoc fit in multis modis, quibus civitas aut exercitus destruatur: igne exsiliente cum fragore inestimabili, mira haec sunt, si quis sciret uti, in debita quantitate et materia. monet author

7) Voici encore le passage du ‘Cap. VI. De experimentis mirabilibus’, auquel Molyneux fait allusion, tel qu'on le trouve à la p. 620 de l'ouvrage cité: ‘His verò sunt quaedam annexa sive figurationibus: nam in omnem distantiam quam volumus possumus artificialiter componere ignem comburentem ex sale petrae & aliis. Item ex oleo petroleo & aliis. Item ex maltha et naphta & similibus secundum quod Plinius dicit in libro secundo capit. 104. civitatem quandam se defendisse contra exercitum Romanum: Nam maltha projecta combussit militem armatum. His vicinus est ignis Graecus & multa comburentia.... Praeter verò haec sunt alio stupenda naturae. Nam soni velut tonitrus, & corruscationes possunt fieri in aere; immò majore horrore quam illa quae fiunt per naturam. Nam modica materia adaptata, scilicet ad quantitatem unius pollicis, sonum facit horribilem & corruscationem ostendit vehementem, & hoc fit multis modis, quibus civitas, aut exercitus destruatur ad modum artificii Gedeonis, qui lagunculis fractis, & lampadibus, igne exsiliente cum fragore inaestimabili, infinitum Midianitarum destruxit exercitum cum trecentis hominbus. Mira sunt haec, si quis sciret uti ad plenum in debitâ quantitate & materia’.

[p. 840]

non esse ad manum libros unde haec citat, sed aliorum fidem se secutum¹⁾.

Sirturum sequitur in disquisitione recentium auctorum telescopij²⁾. Metio fratrem ejus adserere ait; quod ego refutabo³⁾. Bapt. Portae nihil concedit⁴⁾, sed injuria⁵⁾. nam si magia natur. ubi rudimenta habet hujus inventi, edita est a^o. 1589⁶⁾, quomodo vult eum a Batavis ejus notitiam hausisse ubi demum a^o. 168⁷⁾ vel 1610 exortum fuit?

Fr. Fontanae Neapol.^o microscopij duplicis inventum vindicari ait. ut ab anno 1618 reperto⁸⁾. potest fieri⁹⁾.

1) Voici comment Molyneux s'exprime à cet effet (p. 258): ‘I Confess, I have not by me at this time the Originals, from whence these Passages are quoted; the present Distractions of our miserable Country’ [l'Irlande] ‘Having separated me and my Books; and the Place where I am, affords not the Copies: Therefore, if in the Quotations I am any wise mistaken, I must not be blamed, acknowleging that I have them at second hand from the forenamed Authors’ (il s'agit de Wood et de Plott; voir plus haut dans le texte).
Or, on sait que Molyneux, gentilhomme protestant Irlandais, pour échapper aux poursuites de Tyrconnel, se réfugia en janvier 1689 à Chester en Angleterre, où il habita une petite maison hors des portes. Il ne retourna à Dublin qu'après la bataille de la Boyne, en décembre 1690, et c'est pendant son séjour à Chester qu'il composa la plus grande partie de la ‘Dioptrica nova’.

2) Comparez la p. 437 du Tome présent. Ajoutons que Molyneux au passage en question (p. 259) mentionne Borellus et Sirturus comme promoteurs des droits à l'invention des lunettes respectivement de ‘Zacharias Joannides’ et de ‘Johannes Lipperhoy, or la Prey’.

3) Voir la p. 437 et l'Appendice III à la Troisième Partie de la Dioptrique présente, p. 591.

4) Voici le passage mentionné, qu'on trouve à la p. 260 de l'ouvrage de Molyneux: ‘However I must not here conceal the Pretense of Baptista Porta, who in his Magia Naturalis, Lib. 17. Cap. 10. Printed An. 1589. has these words, Si utramque (Lentem sc. Concavam & Convexam) rectè componere noveris, & longinqua & proxima, major & clara videbis. But Porta's Character is so well known, that we may easily imagine, he had got this Hint from Holland’.

5) Comparez les pp. 437, 586, 588 et 748.

6) Voir la note 2 de la p. 586. Les passages cités dans la note 7 de la p. 436 ne se rencontrent que dans les éditions postérieures, y compris celle de 1589.

7) Lisez 1608. Il est vrai que, d'après Boreel, si l'on en croyait le témoignage du fils de Zacharias Jansen, l'invention aurait eu lieu en 1590; mais Huygens se tient à la date où l'invention fut connue, la seule dont on ait quelque sûreté.

8) Voici le passage dont il s'agit (p. 280 de la ‘Dioptrica nova’): ‘Franciscus Fontana in his Observationes Coelestium Terrestriumque Rerum (wherein he challenges to himself the Invention of the double Microscope, An. 1618) is the first (that I can learn) who published Microscopical Observations of some few Bodies’.

9) Comparez la p. 513 du Tome présent.

[p. 841]

Pag. 261. de Galilei observatis. Pag. 264, de meis circa Saturnum. Til¹⁰⁾ de [sic] incomparabel Chr. Hugenius has put the last hand to this affair and in his ingenious Treatise, Systema Saturnium, Hag Com. 1659, 4^o, has published to the world a complete history of all observations of this Planets appearances, with a most ingenious Theory for their explication. In the beginning of the year 1655 his excellent Person first discovered de biggest of Saturns Satellites with a telescope of 12 feet. charged with an eyeglass of 3 inches. afterwards an. 1656 he doubled that length, retaining the same eyeglas &c. addit Halleium correxisse motum mei comitis Saturnij¹¹⁾, nescio quam bene, nam ab eo Cassinus dissentit. ego medius ut puto inter utrumque¹²⁾. Galletij ineptam hypothesin qua ad Saturni annulum exprimendum usus est refellit, quae hoc non meretur¹³⁾.

Pag. 271 refert observationem suam qua satellites Jovis omnes latuerint nempe a^o. 1681. nov. 2. hora 10 p.m. Dublinii St. Vet. quod Flamstedium suis numeris convenire invenerit. 2^dus post Jovem, reliqui ante discum.

Pag. 270, rationem periodorum ac distantiarum commemorat, quam debuisset Ceplero referre acceptam¹⁴⁾.

10) Voici ce qui précède le passage cité: ‘Galileo was the first that observed any thing extraordinary in Saturns Appearance An. 1610. Octob. as he tells us in some of his Italian Letters: But his Glasses were too short to give the true Shape of this Planet. All that he descry'd was something appendent on each side of him, which he took to be two Globes much less than Saturns own Body.....But when the Telescope was better advanced....the true and genuine Appearance of Saturn began to shew it self, and its regular Changes were taken notice of. But though several Authors writ Treatises of this surprising Appearance, and particularly the celebrated Hevelius (de nativa Saturni facie) Hodierna, &c. yet all their Observations were imperfect and deficient; and chiefly for want of excellent Glasses: Till the’, etc.

11) Voici, en effet, la suite du passage en question ‘The Satellit he discover'd, is the Fourth from Saturn; and in the forenamed Treatise, he gives us the Epochae and Tables of its Motion; But our most ingenious Countryman, Mr. Halley, deservedly celebrated for his Astronomical Labours, discovered in the year 1682. that Hugenius's Numbers were considerably run out; and therefore he set himself to correct the Period of this Satellit, which he has done accordingly, Num. 145. Pag. 82. Philosoph. Transact. And in Num. 187. Pag. 299, we shall find Mons. Cassini's Tables of the Motions of all Saturns Satellites, together with their distances from Saturn correspondent to their Periodical Times’.

12) Contrairement à la pensée de Huygens, Halley et Cassini arrivent tous les deux, aux lieux cités dans le note précédente, à un mouvement moyen journalier de 22^o34′38″, c'est-à-dire à une durée de la révolution sidérale du satellite de Huygens de 15^j 22^h 41^m. Huygens dans le ‘Systema Saturnium’ avait trouvé 15^j 22^h 39^m. Ajoutons que les observations modernes confirment les résultats de Halley et de Cassini.

13) Voir sur Gallet et sur son hypothèse les pp. 46, note 4, et 494 du T. VIII. Molyneux n'emploie pas moins de quatre pages (p. 265-269) à la réfutation de cette hypothèse.

14) Voici ce passage, où, en effet, Kepler n'est pas nommé: ‘But before I leave Saturn and Jupiter, I cannot but take notice of one admirable Property for the Knowledge whereof, we are beholden to the Telescope; and that is, the wonderful Agreement which is found in all the several Systems of our Vortex; as well between the General System of the Sun and Primary Planets with the particular System of Saturn's or Jupiter's Planets, as between the particular Systems themselves, in this single Property, That the Periodical Times of the Planets Revolutions are in a sesquialtera Ratio of their Distances from the Centre of the Planet about which they revolve.... This holds most exquisitely true in Jupiter's Satellites, as is noted by the admirably learned Mr. Newton, in his incomparable Treatise, Philosophiae Naturalis Principia Mathematica, Lib. 3. Hypoth. 5. And the same Law os Motion is strictly observed by the five Primary Planets, and the Earth about the Sun. As he notes, Hypoth. 7, 8. This is also verifyed by Mons. Cassini in the five Satellites of Saturn; as appears by his Account of them in the Philosoph. Transact. Num. 92. P. 5178. N. 133. P. 831. N. 181. P. 79’.

[p. 842]

Allusiunculas inserit de Martis robore, de Veneris pulchritudine, quae frivolae¹⁾.

The Heer Leeuwenhoeck of Delft in Holland. hujus diligentiam microscopicam celebrat. eumque se vidisse ait, et celasse exquisitiorem microscopij usum. quippe quem sibi reservet²⁾. Credo nihil aliud esse quam lucis usum in res visas subtiliter inductae.

Nihil mirabilius aut jucundius sibi visum ait quam sanguinis circuitum in Lacerta aquatica (anguilla)³⁾ (apud Leeuwenh. puto) de qua observatione ait

1) ‘Mars offers himself next; who, trusting in his own Strength, is attended by no Guards; But the Prying Telescope discovers in his Face Scars, Spots and Ruggedness’ (p. 274). ‘Venus, the brightest Planet in the Heavens. She fears not sometimes even at Noon-day to display her Beauty; and in this Armour reposing an entire Confidence, performs her Course alone, and free from all other Attendants’ (p. 275). ‘Mercury's wit and Quickness secures him, therefore he has no Train, but generally shelters himself under the Beams of his potent Lord the Sun’ (p. 276). Dans le même esprit Molyneux écrivait à propos du phénomène mentionné un peu plus haut ‘Jupiter there stood by himself, in all Appearance, without his Guards; and a bold Lucian might have pull'd him from his Throne without Resistance’ (p. 271).

2) ‘The Heer Lewenhoeck os Delft in Holland, has lately apply'd himself with great Diligence to the use os Microscopes: of which Instrument he thinks he has a better kind than was ever yet known. When I visited this Gentleman at Delft, he shew'd me several that indeed were very curious; but nothing more than what I had ordinarily seen before; being composed only os one single, very minute Glass-Sphere or Hemisphere, placed between two very thin pierced Laminae, or Plates of Brass, and the Object was brought to its due distance before the Glass by a fine Screw: But for his best sort, he beg'd our Excuse in concealing them’ (p. 281).

3) ‘I have been often delighted with the curious Appearance of many Objects seen through the Microscope. But none ever surprised me more, than the visible Circulation of the Blood in Water-Newts (Lacerta aquatica) to be seen as plainly as Water running in a River, and proportionately much more rapid’ (p. 281).

[p. 843]

se retulisse ad Soc. Reg. Et allegat Transact. Philos. num. 177. Pag. 1236⁴⁾. videndum apud fratrem⁵⁾.

de libella nostra⁶⁾ nihil⁷⁾.

de usu telescopij in metiendis ex una statione distantijs, ait sub finem anni 1665 (ut patet ex Philos. transact. Num. 7, P. 123) Auzotium permutationem arcani optici sui obtulisse Hookio. alterius quod Hookius habuerit, obtulisse. atque Auzotij fuisse hoc ipsum de distantijs metiendis⁸⁾. an habuerit igitur jam tunc Auzotius meum theorema de punctis conjugatis ad lentem convexam⁹⁾. Si

4) Celles pour le mois de décembre 1685. D'après cette communication, datée du 27 octobre 1685, il avait découvert lui-même ce phénomène depuis deux ans et demi et en avait envoyé le 12 mai 1683 une description détaillée à son frère qui se trouvait alors à Leiden.

5) Le frère Constantyn, qui recevait régulièrement les ‘Phil. Trans’.

6) Voir la note 1 de la p. 2.

7) C'est-à-dire à propos des applications du Télescope, dont Molyneux n'en traite que deux: ‘To view nigh Objects therewith’ et ‘To Measure the Distance os an Object at one Station by a Telescope’ (p. 281-287).

8) Il s'agit de l'article suivant, qu'on trouve dans les ‘Phil. Trans’. du 4 décembre 1665: ‘The instance of the Same Person’ [Auzout] ‘to Mr. Hook, for communicating his Contrivance of making, with a Glass of a Sphere of 20 or 40 foot diameter, a Telescope drawing several hundred foot; and his offer os recompensing that Secret with another, teaching To measure with a Telescope the Distances of Objects upon the Earth’. D'après cet article le secret d'Auzout, qu'il possédait depuis longtemps et qu'il était prêt à échanger contre celui de Hooke, consistait dans ceci: ‘Locorum distantias ex unica statione, absque ullo Instrumento Mathematico, metiri’. Si Hooke acceptait l'échange il lui découvrirait ce secret en y joignant les tables nécessaires. Or, Oldenburg, le secrétaire de la Société Royale, ajoutait à l'article d'Auzout la remarque ‘That the Secret he mentions.... is a thing allready known (if I am not mis-informed) to some Members of our Society; who have been a good while since considering of it, and have contrived ways for the doing of it: Whether the same with those of Auzout, I know not. Nor have I (at the distance that I am now from them) opportunity of particular Information’.

9) Molyneux, après avoir remarqué qu'Auzout n'a jamais publié sa méthode, expose la sienne comme il suit (p. 285 de son livre): ‘As the Micrometer is contrived to open and close in the Focus of the Object-Glass.... So we may adapt an Instrument, which may advance or withdraw the curious point of a slender Needle to or from the Object-Glass. And an Index (after the manner of the Micrometer) may shew how much the slender Point is withdrawn from the Object-Glass. Then looking through the Telescope at the Object, whose Distance we measure, let us withdraw the Needle, till by moving the Eye before the Eye-Glass, we perceive the Needle, as it were, fixt upon the Object.... Then is the Needle in the Respective Focus. And by observing the Index afore mentioned, we have the Measure of this Respective Focus from the Object-Glass: And consequently the Difference between it and the Solar Focus. With which we are to work according to the Rule, and we obtain what was required, viz. the Distance of the Object’.
Or, il est clair que, si la méthode d'Auzout, ce qui est probable, reposait sur ce même principe, la règle pour trouver les points correspondants lui était nécessaire, si du moins les tables en question n'étaient pas composées d'après l'expérience ou d'après une règle approximative, valable seulement pour des distances suffisamment grandes.

[p. 844]

habuit forsan ejus est demonstratio per angulos de qua Picartus¹⁾ mihi olim. Dimensio autem haec exigui usus.

Pag. 290. Gassendum²⁾ refutat, qui uno oculo nos uti putabat³⁾, inepte. Recte adfert author⁴⁾ argumentum a lusu pilae, in quo si oculus alter vel peritissimo lusori obtegatur, fiet hebes plane et infimis inferior.

1) Voir sur Jean Picard la note 8, p. 50 du T. VI. Nous n'avons trouvé dans la ‘Correspondance’ aucune allusion à cette communication de Picard à Huygens.

2) Voir sur Pierre Gassendi la note 8, p. 342 du T. I.

3) Voici ce qu'on trouve dans l'ouvrage de Molyneux sur cette conception bizarre, presque oubliée maintenant. Il en parle à la p. 290 comme d'une ‘opinion first as I think started by the celebrated Gassendus and since embraced by many, viz. that we see but with one Eye at once one and the same Point of an Object, otiante alio, (as they term it) whilst the other is idle and does nothing.... Against our seeing with two Eyes at once one and the same Point of an Object, it is commonly objected, that if it were so, every Object would seem in two places at once, vide Gassendi Epist. 4 de Magnit. Solis humilis & sublimis, & Taqueti, Opt. lib. 1. Prop. 2’. Ajoutons que, d'après Tacquet, ce serait l'oeil gauche dont la plupart des personnes se servent ordinairement et que l'on croyait que pendant la vision tous les esprits visuels délaissent l'oeil inoccupé pour suppléer l'oeil qui voit.

4) Après avoir indiqué des expériences dans lesquelles l'on voit effectivement deux images d'un même objet, Molyneux fait suivre: ‘And as a Conclusion to the whole’ [I] ‘shall only add one Experiment that Demonstrates we see with both Eyes at once; and 'tis, that which is commonly known and practised in all Tennis-Courts, that the best Player in the World Hoodwinking one Eye shall be beaten by the greatest Bungler that ever handled a Racket; unless he be used to the Trick, and then by Custom he gets an Habit of using one Eye only’ (p. 293).