Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 737]
| |
[Les Compléments à la Dioptrique]Premier Complément à ‘La Dioptrique’.
| |
[pagina 738]
| |
perfecta fuerit, hoc enim vere dicere possumus. Combien doit on penser qu'il aie estè au dessus de l'intelligence des hommes de concevoir et la forme et l'assemblage requis de verres qui devoient augmenter et comme approcher les objets eloignez, ou faire discerner d'autres invisibles a raison de leur petitesse, comme nous voions que font les telescopes et les microscopes. | |
§ 2.
| |
[pagina 739]
| |
maintenant encore perfectionnèGa naar voetnoot8). 2 autres compagnons de SaturneGa naar voetnoot6). Encore ira plus loin si la difficultè de s'en servir n'empeschoitGa naar voetnoot9). Usage des lunettes aux instrumens d'observation. Des microscopes. Cette science explique l'IrisGa naar voetnoot10). Et les ParéliesGa naar voetnoot11), Je ne m'arresteray pas beaucoup a une quantitè de Problemes et theoremes qu'on peut former. mais je me propose principalement a expliquer l'effect des lunettes d'approche, ce que personne n'a fait suffisamment jusqu'icy. Je traite seulement des surfaces spheriques et planes, qui seulement servent jusqu'icy et dont la theorie seroit encore necessaire pour expliquer l'effect des hyperboliques et elliptiques, si on les pouvoit formerGa naar voetnoot12), ce que je crois impossible et ceux qui scavent par exper. la difficultè de faire les spheriques seront de mon avis. Autre difficultè contre les hyperboliques a cause de l'inclinaison des surfacesGa naar voetnoot13).
Refraction comment expliquée par PardiesGa naar voetnoot14). lumiere comparée au sonGa naar voetnoot15). transparence sans penetration de rayons. difficultè du cristal ou talc de IslandeGa naar voetnoot16). sa description. figure. proprietezGa naar voetnoot17). | |
[pagina 740]
| |
Chap. 1Ga naar voetnoot1).
| |
[pagina 741]
| |
inutiles a construire des lunettes d'approche. a la fin j'adjouteray l'explication de ce meteore admirable qui a donnè de la peine a plusieurs philosophesGa naar voetnoot6). Sur les parelies et couronnesGa naar voetnoot7) dont j'ay trouvè une explication qui convient si bien avec tous les phenomenes que je ne crois pas qu'on doutera beaucoup que ce ne soit la veritè mesme. Ciceron 1 lib. de divinat. qu'on consultoit les livres des Sibilles quand il avoit paru deux soleils ou 3 lunesGa naar voetnoot8). | |
Chap. 2.Kepler le premier a expliquè la maniere de voir. Kepler a cherchè avec grand soin les loix de la refraction, mais ne les a point trouveesGa naar voetnoot9). a presque trouvè la figure hyperbolique pour les refr.Ga naar voetnoot10) Attribuees à des Cartes. Snellius avoit a peu pres les mesmes. ne parle point des sinus. manuscrit que j'ay vu. quantitè d'experiences. vu par des CartesGa naar voetnoot11). Loix de la refraction. ses differences dans differants corps. moyens de l'observer. en sortant et entrantGa naar voetnoot12).
Quoy qu'il suffise de poser ces loix pour principes de cette doctrine, comme estant tres certains par l'experience, il ne sera pas hors de propos de rechercher plus profondement la cause de la refractionGa naar voetnoot13) pour tascher de donner encore cette satisfaction a la curiositè de l'esprit qui aime a scavoir raison de toute chose. Et d'avoir au moins les causes possibles et vraysemblables que de demeurer dans une entiere ignorance. | |
[pagina 742]
| |
RefractionGa naar voetnoot1) comment expliquee par PardiesGa naar voetnoot2). Comparée au son. ondes en l'air. comparées a celles de l'eau. la pesanteur est cause de celles cy comme le ressort des autres. transparence sans penetration. corps capable de ce mouvement successif. Propagation perpendiculaire aux cercles. difficultez contre des CartesGa naar voetnoot3). d'où viendrait l'acceleration. il fait la lumiere un conatus movendi, selon quoy il est malaisè d'entendre la refraction comme il l'expliqueGa naar voetnoot4), a mon avis au moins. Cause de la reflexion a angles egaux. lumiere s'estend circulairement et non dans l'instant, au moins dans les corps icy bas. car pour la lumiere des astres il n'est pas sans difficultè de dire qu'elle ne seroit pas instantaneeGa naar voetnoot5). Cette explication convient avec les Experiences. pour les sinus. pour le rayon entrant et sortant. pour celuy qui ne peut penetrer. pour le verre. dans l'eau. maniere de Rohaut de faire voir les conveniencesGa naar voetnoot6). | |
[pagina 743]
| |
Chap. [3.]Cristal d'IslandeGa naar voetnoot7). | |
Chap. 4.de la refraction des surfaces planes et spheriques et du point de concours des rayons paralleles devant l'incidence. Que je ne traiteray que des surfaces planes et spheriques qui seules servent jusqu'icy et dont la theorie seroit necessaire pour expliquer l'essect des Hyperboliques et Elliptiques que M. des Cartes a tres subtilement inventèGa naar voetnoot8), si elles se pouvoient former, ce que ne peuvent esperer que ceux qui n'ayant point de pratique dans cet art, ignorent la dissicultè qu'il y a a former seulement les spheriques. l'avantage de la figure spherique et plane. Ce que j'ay dit de la necessitè de la theorie des spheriques est si vrai, que Des Cartes pour ne l'auoir point examinée n'a sceu determiner la chose la plus importante dans l'effect des lunettes qui est la proportion de leur grossissement, car ce qu'il en dit ne signifie rien; ce que je dis afin d'espargner la peine à ceux qui peutestre tascheront de l'entendre a cet endroitGa naar voetnoot9).
Concours des paralleles determinè et demontrè par approximation. dire sans | |
[pagina 744]
| |
demonstration si les rayons tombent de ca ou de la. haec etiam accurate demonstrata habemus sed ijs morari lectorem nolumusGa naar voetnoot1). | |
Chap. 5.Du concours et divergence des rayons qui sortant d'un point ou tendant vers un point rencontrent des surfaces planes ou spheriquesGa naar voetnoot2). | |
Chap. 6.Des points de concours et de divergence des rayons qui passent par les 2 surfaces d'une lentille convexe ou caveGa naar voetnoot3). Qu'on peut trouver ces points par les theoremes precedens des surfaces simples. mais qu'il y a des abregez. Et principalement quand on conte pour rien l'espesseur de la lentille. Problemes des foiers. | |
Chap. 7.des divers point de concours quand il y a divers points rayonnants. l'avantage de cecy dans les spheriquesGa naar voetnoot4). | |
Chap. [8.]Construction de l'oeilGa naar voetnoot5). admirable de ce qu'un si petit mouvement se fait sentir sur la choroide. que ce mouvement se communique par de si grands espaces. que les objects ne se confondent point quoyque envoyant les rayons les uns a travers les autres et directement contraires aucunement explique dans ce que j'ay dit des refr. que l'on juge de la figure distance et de la position d'une chose | |
[pagina 745]
| |
eloignee de nous. Qu'on admire pourquoy on voit les choses droitesGa naar voetnoot6) quoyque tournees dans nostre oeil a l'envers. que ce n'est que l'accoustumance de juger, et que si nous avions veu toute nostre vie toutes choses et mesme le mouvement de nos mains par un verre qui renverse les objects comme un convexe nous dirions encore que nous voions toutes choses directes et ne nous tromperions point en montrant le haut et le bas de nos mains. Voiez vos dioptriques. du lieu de l'imageGa naar voetnoot7). l'Erreur de plusieurs en cecyGa naar voetnoot8). Qu'on ne juge point la distance d'un seul oeil, les boites paintes en dedans le font voir ou on regarde par un trou. la difficultè qu'un autre aura a rencontrer vostre doit avec un oeil fermè. Embarras de BarrowGa naar voetnoot9). le nommer a la marge. Expliquer dans le miroir, dans une sphere refleschissante, et dans une transparente. | |
§ 3Ga naar voetnoot10) [1682?]Ga naar voetnoot11)Peut estre dans la 1e PartieGa naar voetnoot12), confirmer la proportion des sinus parce que je vois que quelques uns en doutent encore, FabriusGa naar voetnoot13). Que l'academie en a fait | |
[pagina 746]
| |
des experiences fort exactes. Experience de Kepler qui ignoroit cette proportionGa naar voetnoot1). de SnelliusGa naar voetnoot2) dont j'ay vu le manuscrit qui ne traitoit que de cela. que des Cartes l'a aussi vu. soit de la qu'il l'ait prise ou qu'il l'ait sceur auparavant c'est luy qui l'a publiée le premier.
Plusieurs de ces chosesGa naar voetnoot3) escrites desia par d'autres, que j'omettray ou que je passeray legerement. Laissez au petits geometres les choses faciles a trouver et laborieuses a demontrerGa naar voetnoot4). Il suffit de mettre certaines choses seulement en passant pour faire voir que vous les auez scues. Evitez les petitesses. Premierement des surfaces convexes et caves, les rayons incidents estant parallelesGa naar voetnoot5). Puis des plattes pour les rayons convergents et divergensGa naar voetnoot6). Puis le theoreme general der 4 proport.lesGa naar voetnoot7). le cas parfaitGa naar voetnoot8). Puis le theor. gen. des convexes lentilles et cavesGa naar voetnoot9). Que sans la theorie des verres spheriques on ne peut point expliquer l'effect du grossissementGa naar voetnoot10). | |
[pagina 747]
| |
que personne n'a bien expliquè le grossissement des lunettes surtout avec un cave.
Alhazen qui a vescu vers l'an.... a estè le premier que l'on sache qui ait commencè a mesurer les angles de la refractionGa naar voetnoot11). Et apres luy PortaGa naar voetnoot12), MaurolicusGa naar voetnoot13) et KeplerusGa naar voetnoot1) ont eu la mesme curiositè, voyant qu'il estoit necessaire de les scavoir pour rendre raison des refractions de l'atmosphere de l'arc en ciel et autres meteores, comme aussi pour expliquer l'effect des lunettes convexes et concaves dont se servent les viellards et ceux qui ont la vue courte, et dont l'invention fut trouvée vers l'an 1200, comme nous l'apprend mr. RediGa naar voetnoot14). mais personne d'eux tous n'auoit trouvè la veritable mesure des refractions. Et ce fut Willebr. Snellius Professeur des mathem. a LeidenGa naar voetnoot15).
Jusqu' icyGa naar voetnoot16) j'ay traitè des causes physiques des regles qu'observe la lumiere, et ce qui peut servir a confirmer nostre theorie en cela. maintenant je passe a l'explication des effects des lentilles de verre pour ce qui regarde l'assemblage des rayons et leur differentes inclinaisons, de ces grandes inventions qu'a produit nostre siecle pour augmenter le sens de la vue en nous representant les objets tant distans que fort proches beaucoup plus grands que les yeux seuls ne les appercoivent. Comme personne jusqu'icy n'a bien expliquè. Je me propose cela princi- | |
[pagina 748]
| |
palement dans cette partie, sans vouloir m'arrester a beaucoup de choses qui sont desia connues pour avoir estè escrites par d'autres, car y ayant fort long temps que j'avois fait ce traitèGa naar voetnoot1) il est arrivè qu'une partie de bien de choses qui y estoient contenues ont estè occupees par d'autres, les quelles je veux omettre maintenant ou passer dessus legerement. Pour ce qui est de l'inventeur des lunettes qui decouvrent de loin, il est certain que Bapt. PortaGa naar voetnoot2) qui vivoit a Naples en 1590 en a trouvè les premiers commencemens puis que son livre de la magie naturelle est imprimè plusieurs annees devant que cette invention fust trouvée en Hollande ou Zelande, dans lequel il parle de la jonction d'un verreconvexe avec un concave pour approcher les objects distants et les voir distinctement en mesme temps. Ce qu'il avait decouvert devoit pourtant estre peu de chose. Et cette invention estoit demeurée obscure jusqu'a ce que Metius ou ce Hollandois inconnu qui fit faire des verres à Middelbourg en ZelandeGa naar voetnoot3) dont parle SirturusGa naar voetnoot4) l'ont donnè du lustre et de la renommee en l'amenant a un degrè de perfection beaucoup plus grand que n'avoit fait Porta. Elle futGa naar voetnoot5) ensuite encore augmentée considerablement par l'industrie de Galilée, qui eust le bonheur de faire par son moyen ces celebres observations connues de tout le monde. Et si les nouvelles decouvertes que l'on fait au ciel de choses que l'on n'avoit pu voir auparavant sont des marques de l'avancement de cet art, je puis dire y avoir aussi contribuè quelque chose a cause du planete observè aupres de Saturne et de la forme de l'anneau qui l'environne, a quoy je me suis servi de verres que j'auois faits moi mesme dans des tubes de 22 pieds. Mais l'on a encore augmentè du depuis cette longueur jusqu' a 36 et 45 pieds, non pas sans succes comme font voir les decouvertes de 2 satellites de Saturne, outre celui dont je viens de parler, et celle des taches dans Jupiter et Mars par le moyen desquelles M. Cassini, premier observateur de ces dernieres nouveautez, a reconnu le temps de la revolution de ces planetes sur leur axe. Cette invention des lunettes qui decouvrent de loin fut bientost suivie de celle, qui lesGa naar voetnoot6) applique a des objects prochains et fait voir ce qui sans cela est invisible. | |
[pagina 749]
| |
l'on n'en sait pas bien le premier autheurGa naar voetnoot7), mais cette invention a estè aussi perfectionnée avec le temps et encore notablement dans ces dernieres anneesGa naar voetnoot8), par l'employ des boulettes de verres de la derniere petitesse de l'effect desquelles et des admirables decouvertes faites par ce moyen je parleray cy apresGa naar voetnoot9). Il est constant que ces inventions ont estè premierement trouvees par hazard, et qu'elles ont estè en suite accrues de beaucoup apres.
J'ay taschè dans le livre precedentGa naar voetnoot10) d'expliquer les causes et la nature de la Refraction et il me semble par le raport des plus considerables phenomenes a nos hypotheses qui sont simples etGa naar voetnoot11). difficile de dire la constitution des corps du verre et de l'eau. Nous ne scavons pas cette composition du tout. J'en diray ce qui me parait le plus probable quoyque je ne me puisse satisfaire entierement sur toutes les difficultez que j'en prevois. Il me paroit vraisemblable que la matiere etheree traverse ces corps et qu'elle en occupe une grande partie du dedans soit dans le verre ou l'eau. en entrant ellesGa naar voetnoot12) trouvent quelques particules plus grosses, qui reflechissent une partie du mouvement. Et entre ces particules elles trouvent beaucoup de passages et des espaces remplis de matiere etherée comme elles. par laquelle matiere passe le mouvement, mais a cause de tant de detours, il passe un peu plus lentement. Au sortir cette matiere etheree trouve derechef quelques parties plus grossieres meslees parmy la matiere etheree. On objectera contre le premier que le corps transparent ayant par tout au dedans de ces mesmes particules qui a la surface ont reflechi le mouvement de la matiere etheree, comment la lumiere ne se reflechit pas aussi au dedans de la masse du corps en sorte qu'on l'appercoive. Resp. Il se fait bien des reflexions contre ces particules grosses qui composent le corps au dedans, mais il ne s'en engendre point d'ondes. et que dans l'air et mesme dans l'ether icy bas il se fait aussi de telles reflexions particulieres. Objection 2. Contre quoy se fait la reflexion intrinseque des surfaces. C'est | |
[pagina 750]
| |
contre des particules grossieres. InstantGa naar voetnoot1). Ce sont donc celles qui ne traversent point le verre ou l'eauGa naar voetnoot2). Mais quand on aura ostè ces particules grossieres comme dans le tuyau de Torricelle, comment est ce que la reflexion interieure s'y fait pourtant, n'y ayant rien que ce qui a penetrè le verre ou l'eau?Ga naar voetnoot3) | |
§ 4Ga naar voetnoot4). [1684?]0Ga naar voetnoot5) de excellentiaGa naar voetnoot6). 1 de inventoreGa naar voetnoot7). 2 genera telescopiorum quaeGa naar voetnoot8). cavoconvexaGa naar voetnoot9). convexa solaGa naar voetnoot10). de alijs postGa naar voetnoot11). 3 ratio ac proportio augendi in singulis duorumGa naar voetnoot12). | |
[pagina 751]
| |
6 quod apertura objectivae nihil facit ad campum sed ad lucemGa naar voetnoot13). 4 amplitudo campi unde pendent in utrisqueGa naar voetnoot14). spatium comprehensum, quod includitGa naar voetnoot15). 5 cur major in convexis solis. propterea sola haec ad magna telescopia usurpanda. cavis ad minima relegatisGa naar voetnoot16). 7 cur ocularis convexior obscurius efficit telescopiumGa naar voetnoot17). 8 impossibile esse ut parva apertura objectivae multum amplificet telescopiumGa naar voetnoot18) quidquid machinemurGa naar voetnoot19). 16Ga naar voetnoot20) de hyperbolicis aut ellipticis vitris. confici non posse, et quare. prerogativa sphaericae et planae fig. Etsi possit nihil aut exiguum quid profuturus [sic]. quia aliud multo magis quam figura obstat radiorum collectioni exactae. Etenim si nihil nisi figura obstaret, lens planoconvexa &c. 9 telescopium e quatuor convexis interdiu optimumGa naar voetnoot21). cur meliora ijs quae tribus constantGa naar voetnoot22). 10 horum explicatio et augendi proportioGa naar voetnoot23) diaphragma a nobis inventumGa naar voetnoot24). 11 mutandam longitudinem telescopij ad propinqua conversiGa naar voetnoot25) myopi omnia contractioraGa naar voetnoot26). | |
[pagina 752]
| |
13 obscuritas in tubo requisita. crassiores proinde parandiGa naar voetnoot1). sed ad celestia tubo non opus per nostrum inventumGa naar voetnoot2). 14 Tabula aperturarum et ocularium et amplificationisGa naar voetnoot3) posse intendi oculalaria. sed interdiu duplo minus convexis utendumGa naar voetnoot4). ratio quod oculi in tenebris aliter affecti ac in luceGa naar voetnoot4). 15 Proportio subdupla longitudinum in aperturis demonstrataGa naar voetnoot5). ex supposita velut duplici refractionis proport.e Et convenit cum exper. ad maculas solisGa naar voetnoot6). ad instrumenta observationum. astrosc. compendiariaGa naar voetnoot7). de libellaGa naar voetnoot8). | |
§ 5Ga naar voetnoot9). [1684?]Ga naar voetnoot10).TuncGa naar voetnoot11) non pigebat ita minutatim persequi. Nunc piget laborem suscipere reformandi aut contrahendi. si non essent, non nunc liberet. dedisse me legenda haec Parisijs. Multa horum non ignorari viris Clariss. Newtono, Voldero, FullenioGa naar voetnoot12). Contra neglectum demonstrationum evidentium. et obscuritatem, quibus fit ut amittatur illa voluptas geometriae propria, ex clara perceptione probationum. Quin imo et in errorem ducunt. metaphy sica ista, et processus ad minima, recte ad inveniendum adhibentur. Inventa vero claris et evidentibus demonstrationibus comprobanda sunt, quatenus id fieri potest. Ita ArchimedemGa naar voetnoot13) fecisse apparet, | |
[pagina 753]
| |
cui istae occultiores viae non erant incognitaeGa naar voetnoot14). nec CavalerijGa naar voetnoot15) quidem compendia. sed in demonstrationibus summam evidentiam quaesivit, idque apud temporis illius geometros necessarium erat. CononGa naar voetnoot16) deceptus fuerat. neque tamen postulandum hoc aevo arbitror ut quaecunque de figurarum planarum et solidarum, atque etiam linearum magnitudinibus geometrae invenerunt Archimedeis demonstrationibus probentur. Tediosum enim id esset. Omninò tamen curandum ut planum fiat ea quae breviter dicuntur reduci posse ad cognitas absolutasque seu veterum seu recentiorum demonstrationes. Non jam de mechanicis alijsque dico ubi geometricae demonstrationes adhibentur ubi praecipue in principijs ponendis peccatur, tum inter demonstrandum tacite multa assumuntur, ut cum ad finem perveneris dubites rectene propositio comprobata sit an secus. atque ita quaedam quasi demonstrationes obtinentur, ac saepe falsa theoremata pro veris.
addenda Pareliorum explicatioGa naar voetnoot17).
Addenda libellae descriptio et demonstratioGa naar voetnoot17).
Addenda item Astroscopia compendiariaGa naar voetnoot18). commodè excercenda in 50 et 80 pedum longitudine. si excedatur difficultas praecipue in luna propter circulum radios laterales excludentemGa naar voetnoot19). | |
[pagina 754]
| |
§ 6Ga naar voetnoot1). [1687].OPTIQVE.
I Partie.
Ou il est traitè des causes naturelles de ce qui arrive a la Lumiere, tant simplement estendue que Reflechie, et Rompue, Et De la Refraction estrange du Cristal d'Islande. | |
§ 7Ga naar voetnoot2). [1690]Ga naar voetnoot3)Commencement du Traitè de ma Dioptrique en François que j'avois dessein de joindre au Traitè de la Lumière, ce qui est changèGa naar voetnoot4). | |
[pagina 755]
| |
[Sommaire.] [Fig. 1.]
les surfacesGa naar voetnoot5) spheriques estant les seules qui soient emploiees dans toutes les compositions de lunettes et telescopes, et j'ose dire les seules que l'on emploiera jamais, il faut en toutes manieres connoistre les loix de leur refraction et c'est ce que nous allons entreprendre maintenant. | |
[pagina 756]
| |
| |
[pagina 757]
| |
l'object sur toute l'estendue de l'objectif se reunissent dans un point au fond de l'oeuil nous pouvons pour determiner la grandeur de cette image considerer un seul de ces rayons, et il est libre de prendre celuy qui passe par le centre du verre objectifGa naar voetnoot10). J'ay traitè dans le livre precedentGa naar voetnoot12) des causes de la reflexion et de la refraction et des loix que la nature y observe. La certitude des quelles comme j'ay desia dit est d'ailleurs fondée sur des experiences tres exactes et tres souvent verifiées. Je passe maintenant aux effects merveilleux qui procedent de ces proprietez de la lumiere et cela principalement par le moyen des verres convexes et concaves, de la composition desquels naissent ces belles inventions des Lunettes d'approche et de celles qu'on appelle microscopes. Je feray voir la raison de tout ce qui s'y observe, et sur tout les proportions de leur grossissement qui a mon avis n'ont pas encore estè assez bien expliqueesGa naar voetnoot13). Et je raporteray leur divers usages et la maniere de s'en servir commodement. J'adjouteray aussi a la fin les causes du phenomene des Couronnes et Parelies ou faux soleilsGa naar voetnoot14), qui naissent certainement de la refraction et de la reflexion, mais d'une toute autre maniere que des personnes fort celebres ont cru. Je commenceray par les refractions des surfaces simples spheriques et planes, a l'explication desquelles nous avons besoin d'une prop. fort cognue d'ApolloniusGa naar voetnoot15), | |
[pagina 758]
| |
ou plustot de certaines consequences qui s'en tirent, c'est pourquoy je les feray icy preceder. La proposition est que si l'on divise une ligne droite AB inegalement en C, faisant la partie CB moindre que CA; et que l'on prolonge AB du costè B jusques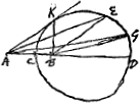 [Fig. 3.]
en D en sorte que comme AC a CB ainsi soit AD a DB, et que l'on descrive un cercle ayant CD pour diametre, alors si des points A, B, l'on mene des lignes diverses a quelque point de la circonference, comme AE, BE; elles auront entre elles la mesme raison que AC a CB. Plusieurs ont demontrè cette proposition apres Eutocius dans ses commentaires sur les Coniques, ou il fait voir de plus que si l'on mene de A et B deux lignes a quelque point qui ne soit pas dans la circonference susdite, elles ne pourront pas avoir la mesme raison que AC et CB. Lemme 1. Apres quoy l'on peut facilement demontrer cette autre propos.Ga naar voetnoot1) scavoir que, s'il y a deux triangles ayant des bases egales, et les autres costez proportionaux, et que dans chaque Δ l'un des angles sur la base soit obtus, mais plus dans l'un que dans l'autre, alors celuy dont l'angle obtus sera plus grand, ou dont l'autre angle sur la base sera plus petit aura chacun des deux costez qui sont proportionaux plus grands que ceux de l'autre. Car soit l'un de ces triangles AEB, et sur la mesme base AB soit fait le triangle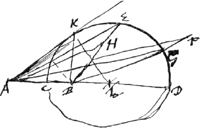 [Fig. 4.]
AGB pareil a l'autre qui est proposè. Et que AC a CB et AD a DB ayent la mesme raison que celle de AE a EB ou AG a GB. Il est certain par les choses demontrees auparavant que les sommets des triangles E, G seront dans la circonference CED descrite au diametre CD. Et que si des deux angles obtus, ABG est plus grand que ABE; la ligne BG approchera plus de BD, qui passe par le centre, que ne fait BE. d'ou s'ensuit que BG sera plus grande que BEGa naar margenoot* et par consequent aussi AG plus grande que AE, puisque AG, BG et BE, AE sont proportionnelles. Il reste a demontrer que le mesme arrivera | |
[pagina 759]
| |
si dans le triangle GAB l'angle aigu sur la base est moindre que l'angle aigu sur la base du triangle EAB. Ayant fait BK perpend. sur AB qui rencontre la circonference en K soit tiree AK, qui touchera la circonference au mesme point K. car puis que AK est a KB comme AD a DB aussi AK sera a AD comme KB a BD, c'est-à-dire comme CB a BK ou comme AC a AKGa naar voetnoot3). donc AC, AK, AD sont proportionelles, et partant AK touche la circonference en K. Puis que donc les angles ABE, ABG sont tous deux obtus et pour cela plus grands que ABK il paroit que les lignes AE, AG sont menees du point A a la partie concave de la circonference CED, et que par consequent celle des deux qui approche le plus de AD qui passe par le centre, c'est-à-dire qui fait avec AD le plus petit angle, sera la plus longueGa naar margenoot*. donc AG icy est plus grande que AE, et par consequent aussi BG plus grande que BE. Lemme 2. Il paroit aussi que si AG est a GB comme AD a DB, jamais AG ne peut egaler la longueur de la ligne AD, ni BG la longueur de BD, puis que l'intervalle DB est plus grand que le desmidiametre mais qu'elles peuvent approcher infiniment pres de cette longueur. | |
De la Refraction des Surfaces simples Spheriques et Planes.
| |
[pagina 760]
| |
Cecy s'ensuit de la proprietè fondamentale des refraćtions scavoir la proportionalitè des sinus. Car le sinus de l'angle DCE ayant au sinus de l'angle GCH cette proportion certaine que nous appellons la proportion de la refraction le costè CG dans le ΔCGF est a GF comme le sinus de l'angle GFC ou de son complement a 2 angles droits au sinus de l'angle GCF, c'est a dire comme le sinus de l'angle GFH ou DCE au sinus de l'angle GCF. | |
Prop. 2Ga naar voetnoot1). [Fig. 6.]
Que si le rayon DC passe d'un diaphane plus dense dans un autre qui l'est moins, en menant, comme devant, la parallele GF, la ligne CG a GF aura derechef la proportion de la refraction; c'est a dire celle que constituent les sinus des angles DCF, GCE; mais renversee en sorte que CG qui represente icy, aussi bien que dans le cas precedent, la penetrabilite du diaphane d'ou sort le rayon, soit moindre que GF, qui represente la penetrabilite de l'autre diaphane ou le rayon entre apres estre rompu. Car derechef dans le triangle CGF, le costè CG est a GF comme les sinus des | |
[pagina 761]
| |
angles qui leur sont opposez, c'est a dire comme le sinus de l'angle GFC ou FCD au sinus de l'angle GCF, ou de son complement a 2 droits, GCE.
En parlant de surface convexe ou concave je veux qu'on entende tousjours que cette surface est celle du diaphane plus dense, c'est-à-dire qui detourne les rayons entrants vers la perpendiculaire. | |
Propos. 3Ga naar voetnoot2).Trouver le point de concours des rayons paralleles apres leur refraction dans une surface sphérique convexe.Que AB soit la section de la surface convexe, ayant le centre C; sur la quelle tombent des rayons paralleles a la droite AC, ainsi que OB. Si l'on prolonge AC  [Fig. 7.]
jusqu'en Q, en sorte que AQ a QC ait la proportion qui mesure la refraction du diaphane proposè. Je dis alors que le point Q sera le point de concours des rayons avec l'axe AC apres estre rompus. Non pas qu'il le soit precisement, mais en sorte que tous les concours avec l'axe tombent en dedans du point Q, et qu'ils en approchent d'autant plus que les refractions viennent de rayons plus proches a l'axe. Et cela jusqu'a des distances moindres qu'aucune donnée. Ou il est a noter que dans la construction de lunettes de toute sorte l'on emploie de si petites portions de surfaces spheriques, que ce concours imparfait peut passer pour parfait en ce qui est de l'effect qu'en ressent nostre vue. Pour prouver ce qui a estè dit du point Q, soit du rayon OB la refraction BL, et soit menèe CBG, qui comme l'on sçait coupe la surface à angles droits. OBG est donc l'angle que le rayon incid. fait avec la perpendiculaire et LBC l'angle que fait le rayon rompu avec la mesme. d'ou, par la prop. prec.-la raison de BL a LC sera la mesme que celle qui mesure les refractions c'est-a-dire la mesme que de AQ a QC, ou bien, en faisant BCH egale a AQ, la mesme que BH a HC. Il s'ensuit donc par le lemme 2.eGa naar voetnoot3) que CL est moindre que CH c'est-a-dire moindre que CQ. Il s'en suit aussi que d'autant que le rayon OB tombera plus proche de l'axe AC, l'angle BCA, et partant aussi LCH sera plus petit, et BCL d'autant plus grand, et partant par le lemme 1.erGa naar voetnoot4) la ligne CL d'autant plus longue, et qu'enfin CL approchera de la longueur CQ jusqu'a des differences infiniment petites, par le lemme 2.me. | |
[pagina 762]
| |
Prop. 4Ga naar voetnoot1). [Fig. 8.]
Soit derechef la surface spherique convexe AB; mais que les rayons paralleles a l'axe comme OB, soient au dedans du corps diaphane, et qu'ils se rompent en sortant. Icy si l'on prolonge l'axe CA du costè A et que l'on fasse que la raison de CQ a QA soit celle de la refraction; le point Q sera le point de concours de la maniere que dans le cas precedent. Car si BL est la refraction du rayon OB, et que l'on mene la droite CBH, c'est icy OBC l'angle que fait le rayon incident avec la perpend. a la surface AB, et LBH l'angle que fait avec le mesme le rayon rompu BL donc par la Prop. [2] la raison de CL a LB est celle de la refraction, c'est a dire la mesme que de CQ a QA, ou, en faisant CBH egale a CQ, la mesme que de CH a HB. mais l'angle CBL est necessairement obtus. donc CL est moindre que CH c'est-a-dire que CQGa naar margenoot*. L'on voit aussi que plus le rayon OB passera proche de l'axe CA, plus l'angle BCA sera petit, et pour cela la ligne CL plus grandeGa naar margenoot* et qu'en fin la longueur de CL approchera infiniment pres de celle de CQGa naar margenoot*.
Nous considererons souvent dans la suite ces points Q comme si le concours de rayons paralleles s'y faisoit parfaitement, ayant egard alors au rayons qui sont fort proches de l'axe de la surface ou de la lentilleGa naar voetnoot4). | |
Propos. 5Ga naar voetnoot5).Ainsi AB estant une surface spherique concave sur laquelle tombent des rayons paralleles a son axe CA tels que NB; si l'on prolonge le demidiam. AC en Q faisant que AQ a QC ait la proport. de la refraction l'on prouvera que Q est le point d'ecart ou de divergence de ces rayons apres leur refraction, tellement que le rayon NB estant rompu en BD, cette ligne repondra au point Q.  [Fig. 9.]
Car considerant BQ comme estant la refraction du rayon OB, au cas que le corps diaphane fust du costè C, il s'en suit que le diaphane | |
[pagina 763]
| |
estant de l'autre costè qui est vers O, la refraction du rayon NB sera BD faisant une ligne droite avec BQ, parce que NB fait une droite avec OB. Car NB estant inclinée sur la surface AB, lors que le corps diaphane est vers O, d'un mesme angle que OB y est inclinée, lors que le corps diaphane est vers C, il faut qu'aussi leurs refractions soient pareilles, c'est a dire qu'elles fassent de pareils angles avec la surface AB ce que l'on scait estre ainsi quand BD fait une ligne droite avec BQ. | |
Prop. 6Ga naar voetnoot6).De mesme si AB est une surface concave qui borne le diaphane vers N, sur laquelle tombent des rayons paralleles a son axe AC, tels que NB si l'on prolonge le demidiam. CA en Q, faisant que CQ à QA ait la proport. de la Refr. l'on fera voir que Qest le point de divergence de ces rayons apres leur refraction, tellement que le rayon estant rompu en BD, elle sera en ligne droite avec BQ.  [Fig. 10.]
Et le raisonnement sera le mesme que dans le cas precedent en considerant qu'icy selon la propos. [4] le rayon OB auroit son point de concours en Q, si le corps diaphane estoit du costè C.
Ayant expliquè tout ce qui regarde les rayons paralleles, je passe aux refractions de ceux qui appartiennent a un point. J'appelle appartenir a un point quand les rayons sortent d'un point ou tendent vers un point, ou bien quand ils s'ecartent comme s'ils sortoient ou concourent comme s'ils alloient vers un pointGa naar voetnoot7). | |
Propos. 7Ga naar voetnoot8).La proposition generale est qu'une surface spherique convexe ou concave estant rencontréeGa naar voetnoot9) par des rayons appartenant à quelque point donnè; si de ce point et dans l'axe qui le | |
[pagina 764]
| |
joint avec le centre de la sphere l'on pose une quatrieme proportionnelle à trois distances du mesme point, dont la premiere soit au point auquel appartiendroient les refractions des rayons paralleles a l'axe venants du costè opposè; la seconde a la surface mesme qui est proposee; la troisieme au centre de la sphere. alors le point ou se termine cette quatrieme proportionnelle sera celuy auquel appartiendront les rayons rompus. En observant de la prendre en sorte, que toutes les distances soient ou d'un mesme costè a l'egard du point donnè, ou deux d'un costè et deux de l'autre. Cette proposition a plusieurs cas, parce que la surface est ou convexe ou concave; et sur chacune les rayons tombent en dehors ou en dedans; et ils sortent d'un point ou ils tendent vers un pointGa naar voetnoot1).  [Fig. 11.]
 [Fig. 12.]
 [Fig. 13.]
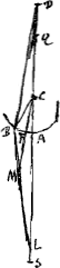 [Fig. 14.]
 [Fig. 15.]
 [Fig. 16.]
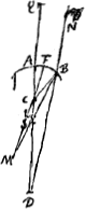
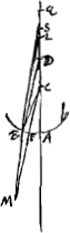
Je mettray premierement ceux qui concernent les surfaces convexes, soit que les rayons rencontrent la surface du diaphane en dehors ou en dedans dont la plus part est representee par ces figuresGa naar voetnoot2). Soit la circonference AB la section d'une surface convexe du corps diaphane, | |
[pagina 765]
| |
son centre C, et soit donnè le point D, du quel viennent ou vers le quel tendent les rayons qui vont rencontrer la surface AB. Dans la droite par DC soit trouvè Q le point de concours des rayons paralleles qui viendroient du costè opposè sur AB, en faisant suivant ce qui a estè montre dans les Prop. precedentesGa naar voetnoot3) que CQ a QA ait la proportion de la refr. directe ou renversée. Que si le point D estoit le mesme que Q, les rayons apres la refraction deviendroient paralleles a l'axe DC parce que les rayons paralleles venant du costè opposè ont leur point de concours, car cela s'ensuit de la refraction reciproque. Soit donc le point D different de Q. Et aux trois distances DQ, DA, DC soit trouvèe la quatrieme proportionnelle DS, scavoir que comme DQ a DA ainsi soit DC a DS, et que DS soit prise en sorte que toutes les quatre distances soient du mesme costé de D ou deux de l'un et deux de l'autre. Je dis que S sera le point auquel appartiendront les rayons rompus qui en venant appartiennent au point D. Car qu'un de ces rayons soit DB [Fig. 11, 12, 14 et 15] ou NB [Fig. 13 et 16], et sa refraction BL; qui rencontre l'axe DC en L et la droite FCM parallele a DB en M. Puisque donc BM est la refraction du rayon DB, et que FCM est parallele a ce rayon, les lignes BM, MC auront entre elles la proportion de la refr.Ga naar voetnoot4). Mais si l'on imagine l'arc AB extremement petit, et par la aussi l'arc BF; l'on peut considerer la raison de FM a MC comme estant la mesme que celle de la refractionGa naar margenoot* c'est a dire que celle de CQ a QA, et qu' ainsi CM est comme egale à AQ, de plus a cause de la petitesse de l'arc AB, l'on peut aussi considerer DB comme egale a DA. La raison donc de DB a CM, ou de DL a LC, sera comme la mesme que de DA à AQ. Et partant celle de DC a CL comme la mesme que de DQ à QA, c'est a dire que de DC a CS; puis que DQ, DA; DC, DS, | |
[pagina 766]
| |
sont proportionelles d'ou il paroit que le point L approchera si pres que l'on voudra du point S. Je pourrois faire voir dans quels de ces cas toutes les refractions concourent avec l'axe en dedans du point S a l'egard a la surface proposee, ou bien quand elles concourent toutes au delà du mesme point. mais trouvant que cette connoissance est fort peu importanteGa naar voetnoot1), par les raisons que l'on verra cy apres, je ne mettray point icy les demonstrations que j'en avois autrefois escritesGa naar voetnoot2), qui en quelques cas estoient assez longues. J'ay seulement marquè dans les figures les differences de ces concours, par la situation des points S et L. Ou il y a à noter dans le troisième des cas rapportez [Fig. 13] qui si la raison de DC a CA est plus grande que celle de la refraction, toutes les refractions concourent en dedans du point S, mais si cette raison est plus petite, elles tombent toutes en dehorsGa naar voetnoot3). Mais si la raison DC a CA est la mesme que celle de la refraction, alors toutes les refractions precisement au point S. Et c'est icy le mesme cas dont nous avons parle au livre preced.Ga naar voetnoot4) en traitant les ovales propres a la refraction. J'adjoute la demonstration que j'en escrivis autrefoisGa naar voetnoot5). Le point D estant placè de la sorte soit PB un rayon tendant vers D. Et qu'on 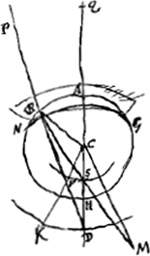 [Fig. 17.]
joigne BS. Je dis qu'elle sera la refraction du rayon PB. Car ayant menè CM parall. a PB, qu'elle rencontre BS prolongee en M et que l'on joigne CB. Puis que donc DC est a CH ou CA, comme CQ a QA, il s'ensuit que toute la DQ sera a toute la QC comme CQ a QA. Mais comme DQ a QC ainsi DA à AS, parce que nous avons fait comme DQ a DA ainsi DC a DS. donc DA sera a AS comme CQ a QA, c'est a dire comme DC a CH. donc si de DA on oste DC, et que de AS on oste CH ou CA, le reste CA ou CH sera au reste CS comme DC a CH. donc aussi BC a CS comme DC a CH, c'est a dire comme DC a CB. les triangles donc DCB, BCS sont semblables. C'est pourquoy aussi le costè DB sera au costè BS comme DC a CB, et l'angle BDC sera egal a l'angle SBC. d'icy il paroit qu'aussi dans les triangles DBS, BMC, l'angle MBC sera egal a BDS. Et puisque de plus l'angle BMC est egal a DBS, il s'en suit que les | |
[pagina 767]
| |
triangles DBS, BMC sont semblables. Et partant BM a MC, comme DB a BS, c'est a dire comme DC a CB ou CH, qui est la prop. de la refraction. C'est pourquoy BSM sera la refraction du rayon PBGa naar margenoot*. ce qu'il faloit prouver. D'icy l'on voit qu'on peut faire une lentille avec des surfaces spheriques qui assemble parfaitement en un point les refractions des rayons, qui tendent vers un autre pointGa naar voetnoot7). Car en joignant avec la surface convexe AB une surface concave NG qui ait pour centre le point S, il est evident que les rayons qui tendent vers D, tel que PB estant detournez par la surface AB vers le point S, ne soufriront plus aucune refraction à la surface NG, et qu'ainsi ils concourront tous a ce point. Il paroit aussi que la mesme lentille detournera les rayons venant du point S comme s'ils venoient du point D. l on peut encore faire une lentille creuse sur ce mesme fondementGa naar voetnoot8) qui ait une pareille perfection, mais ni en l'une ni en l'autre je ne trouve guere d'utilitè. Il reste a voir les cas au quels la surface AB est concave qui s'expliquent facilement par les precedentes. Car en faisant derechef que CQ a QA ait la prop. de  [Fig. 18.]
 [Fig. 19.]
 [Fig. 20.]
 [Fig. 21.]
 [Fig. 22.]
| |
[pagina 768]
| |
 [Fig. 18.]
 [Fig. 19.]
 [Fig. 20.]
 [Fig. 21.]
 [Fig. 22.]
la refraction directe dans les cas ou les rayons tombent sur la surface en dehors, et renversée dans ceux ou ils la rencontrent en dedans, il est constant que Q seroit le point de divergence des rayons paralleles qui viendroient de son costèGa naar margenoot*, qui est opposè a celuy que l'on considere icy. Il faut derechef trouver au 3 distances DQ, DA, DC, la 4.e proportionnelle DS, et la placer suivant ce qui a estè dit au commencement. Et le point S sera celuy auquel appartiendront les refractionsGa naar voetnoot2). Car en faisant que DBN, SBL soient des lignes droites, il est certain par ce qui a este demontrè des cas precedents que s'il venoit des rayons du costè Q comme NB ou DB qui tendissent vers D ou qui en sortissent, et que la surface AB fust convexe ils se romproient en sorte qu'ils appartiendroient au point S. mais les rayons qui viennent maintenant de l'autre costè estants en ligne droite avec ceux la, ils font avec la surface creuse AB les mesmes angles que ceux la faisaient avec la convexe. donc aussi en se rompant ils doivent faire avec ces surfaces des angles egaux; ce qui ne se peut que leur refractions ne soient en ligne droite avec ces premieres, et que partant elles n'appartiennent aussi au point SGa naar voetnoot3). C'est a dire qu'elles iront par BL si elles devienent divergentes, ou par BS si elles deviennent convergentes. | |
[pagina 769]
| |
Parce que l'on fait des lentilles, dont l'une des surfaces est plane, il est necessaire d'examiner aussi quels sont les points de concours ou de divergence dans ces surfaces, lors que les rayons qui les rencontrent viennent d'un point ou tendent vers un pointGa naar voetnoot4). 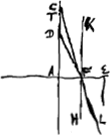 [Fig. 23.]
Soit une surface plane AE, sur laquelle tombe par dehors les rayons venants du point D. Si l'on mene DA perp. sur la surface AE et qu'on la prolonge du costè D jusqu'en T, en sorte que TA à AD ait la prop. de la refr. je dis que T sera le point de divergence des rayons rompus. C'est a dire de la maniere que nous avons considerè ces points dans les surfaces spheriquesGa naar voetnoot5). Car soit l'un des rayons incidents DF et sa refraction FL, et que LF prolongée rencontre la droite AT en C. Puis que donc la raison du sinus de l'angle DFK au sinus de l'angle LFH est celle des refractions, et que l'angle DFK est egal a FDA et l'angle LFH egal a FCD, donc aussi le sinus de l'angle FDA ou de FDC qui est son compl. a deux angles droits aura au sin. de l'angle FCD cette mesme prop. des refr.. mais dans le triangle FCD les costez CF a FD ont la mesme raison entre eux que les sinus de leur costez [sic] opposez. donc la raison de CF a FD sera encore la mesme que celle des refr. c'est a dire que celle de TA a AD. Or il paroit qu'en approchant le point d'incidence F vers A la ligne DF differera si peu que l'on voudra de DA. donc aussi la longueur de FC sera comme la mesme que de AT. mais celle de CF approchera en mesme temps autant qu'on voudra de celle de CA. donc aussi CA sera comme la mesme que TA. d'ou il paroit que le point T doit estre considerè comme le point de divergence des rayons qui venoient du point D, ayant egard aux rayons fort proches de DA. au reste dans la veritè toutes ces refractions concourrent au dela du point T, comme il est aisè de prouver. Car CF estant a FD comme TA a AD aussi le quarrè de CF sera au quarrè de FD comme le quarrè de TA au quarrè de AD. mais ostant le qu. FA de chacun des quarrez CF, FD la raison des restes c'est a dire du quarrè CA au qu.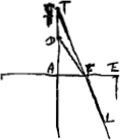 [Fig. 24.]
AD sera plus grande que n'estoit celle du quarrè CF au qu. FD, c'est a dire que celle du qu. TA au qu. AD. Et partant aussi la ligne CA aura plus grande raison a AD que TA a AD, d'ou il paroit que le point C est au de la de T. Les autres trois cas s'expliquent facilement par celuy cy. Car s'il y avoit des rayons tendans vers le point T, tel qu'est LF, et qu'ils fussent rompus en sortant du corps diaphane, il paroit que leur point de concours seroit D, ayant fait que TA a AD ait la prop. de la refraction. Car la refraction du rayon | |
[pagina 770]
| |
DF est FL selon ce qui vient d'estre montrè, aussi la refraction du rayon LF sera FD, a cause de la reciprocation connue de la refraction qui a estè remarquée au premier livreGa naar voetnoot1). Il est de plus aisè a comprendre que toutes les refractions concoureront icy en dedans du point D, par ce qui a estè montrè au cas precedent. Que s'il y a des rayons tendant vers un point D qui rencontrent le diaphane par dehors ainsi que NF. alors si l'on fait que TA a AD ait la prop.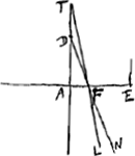 [Fig. 25.]
de la refr. le concours des rayons rompus sera au point T. Car, ayant menè la droite TFL, puis que du rayon DF la refraction estoit FL, lors que le diaphane estoit du costè L; il s'ensuit, qu'estant du costè D, la refraction du rayon NF sera FT, par la raison que nous avons alleguèe plus d'une foisGa naar voetnoot2), scavoir que les angles d'incidence estant egaux, ceux de la refraction le doivent estre de mesme. Et il est aisè de voir en considerant ce qui a estè montrè au premier cas, que toutes les refractions concoureront au dela du point T. Enfin si les rayons sortant d'un point T sont rompus par la surface AE en sortant du diaphane, et que l'on fasse que TA a AD ait la prop. de la refraction leur point de divergence sera D, par la reciprocation de la refraction, car si la refraction du rayon NF est FT, aussi celle du rayon TF sera FN. Et toutes les refractions regarderont icy en dedans du point D devers AGa naar voetnoot3). | |
§ 8Ga naar voetnoot4).
| |
[pagina 771]
| |
regularum abbreviantium inventionesGa naar voetnoot8) et prius theorema Cepleri [sic] de crassitudine lentium et inde pendentibus foci distantijsGa naar voetnoot9). quae sit lens optimaGa naar voetnoot10). Ubi telescopiorum et microscopij casus ostensi fuerint in Prop. pag. 77Ga naar voetnoot11) (adde) haec sigillatim postea et absque tot compositarum rationum ambagibus ostensum iri. Hic jam sequi possunt Theorema de transposito oculo et visibiliGa naar voetnoot12). Et quae de maximo et minimoGa naar voetnoot13). rejectâ propositione de telescopio solidoGa naar voetnoot14). Post haec propositio de anguli vitrei penetratione, &c.Ga naar voetnoot15) et de manente magnitudine cum paralleli ad oculum veniuntGa naar voetnoot16). tum de Telescopijs rursusGa naar voetnoot17). tum de composito ex 3 et 4 lentibusGa naar voetnoot18). Tum de aperturis telescopiorumGa naar voetnoot19). tum de curvatione rectarum apparenteGa naar voetnoot20). de loco imaginisGa naar voetnoot21). hunc in lentibus non mereri ut solicitè inquiraturGa naar voetnoot22). Sed magis in speculis. difficultas Newtoni et Molinetij resolutaGa naar voetnoot23). objectum ab oculo diversum pone. tunc distantia ex parallaxi oculi | |
[pagina 772]
| |
moti. Tum de utilitatibus ad Solis maculas et EclipsesGa naar voetnoot1) ad instrumenta seu paradigmata applicita telescopia. ad LibellamGa naar voetnoot2). an et Laterna magica?Ga naar voetnoot3) parva telescopiola magnis aperturis, vel an haec omittemus?Ga naar voetnoot4). Tum de microscopijs, simplicibus compositisGa naar voetnoot5). Tum de eorum aperturis primo simpliciumGa naar voetnoot6). fortasse et de distinctionis profunditateGa naar voetnoot7). Tum de speculari telescopio NewtoniGa naar voetnoot8) et quae sit ejus apertura. Quomodo duplex imaginis repercussio vitari possitGa naar voetnoot9).
de Parelijs et coronisGa naar voetnoot1).
Principium mutandumGa naar voetnoot10), dicendumque nos causas physicas refracti radij exposuisse alio libroGa naar voetnoot11). item cur rectis lineis radij feranturGa naar voetnoot12), item cur reciprocentur radij et eorum fractionesGa naar voetnoot13), de atmospherae item refractioneGa naar voetnoot14), et de Crystallo Islandica, quae caetera confirmentGa naar voetnoot15), de ArchimedeGa naar voetnoot16) et AristoteleGa naar voetnoot17), AlhazenoGa naar voetnoot18), VitellioneGa naar voetnoot18), SnellioGa naar voetnoot19), CartesioGa naar voetnoot20). Breviter refractionis lex in vitro et aqua ponaturGa naar voetnoot21).
Substitutum pag. 81 dioptricesGa naar voetnoot22). pro Quando autem punctum K &c.Ga naar voetnoot23) quae 3bis versibus ibi sequantur. Porro potest etiam cadere punctum K in centrum lentis A uti in fig. [18] et | |
[pagina 773]
| |
[19]Ga naar voetnoot24); quo casu etiam punctum L eodem incidere necesse est. ratioque magnitudinis apparentis ad veram componetur ex rationibus AB ad BC et CE ad EA. quod hoc modo tunc ostenditur. Nempe cum ratio apparentis ad veram sit ut semper ea quae BN ad BOGa naar voetnoot25), haec vero ratio componatur ex rat. BN ad ED, et ex rat. ED seu FE ad OB, quarum BN ad ED est eadem quae AB ad AE; altera vero FE ad OB eadem quae EC ad CB, componetur ergo ratio BN ad BO, quae est magnitudinis apparentis ad veram ex ratione AB ad BC et EC ad EA, ut dicebamus. Et haec quidemGa naar voetnoot26) &c.
mettre la Prop. pag. 77Ga naar voetnoot27). Et y adjouterGa naar voetnoot28). Et ostendere in Telescopijs ex convexa et cava lente compositis res visas longinquas augeri secundum rationem foci distantiae lentis convexae ad distantiam puncti dispersus lentis cavae. In telescopijs vero è duabus convexis compositis amplificationem eam fieri secundum rationem foci distantiae lentis convexae exterioris ad foci distantiam interiorisGa naar voetnoot29). Ainsi | |
[pagina 774]
| |
l'amplification des 2 lunettes sera prouvéeGa naar voetnoot1) sans avoir besoin de l'expédient de F.Ga naar voetnoot2) et mesme plus generalement a cause de la place de l'oeil libre. Puis les demonstrations plus simples et sans proportions composees pour les cas des telescopesGa naar voetnoot3). posset simpliciter sic, l'oeil contre le verre concave, et puis en l'eloignant et ouvrant l'oeilGa naar voetnoot4). peut-estre icy l'erreur de des CartesGa naar voetnoot5). Puis les deux convexesGa naar voetnoot6), et premierement dans la position ou la proportion de l'augmentation est la plus aisée a montrer. puis faire voir qu'elle est la mesme en transportant l'oeilGa naar voetnoot7). Microscope, plus simple demonstration premierement de 2 convexesGa naar voetnoot8) car d'un cave et convexe fait voir un trop petit champ. Puis des petites boules et simples convexesGa naar voetnoot9). observations remarquablesGa naar voetnoot9). Proposition, que quelque nombre de verres compose un telescope ou microscope, si les rayons sortent paralleles vers l'oeil, on verra l'objet egalement grand, quelque part qu'on place l'oeilGa naar voetnoot7). peut estre on pourra la mettre comme une consequence de ce qui a estè montrè du telescope de 2 verres. Telescope de 3 qui renverse et fait voir grand champGa naar voetnoot10). Telescope de 3 qui redresseGa naar voetnoot11). qu'on fera voir que celuy de 4 vaut mieuxGa naar voetnoot12). Telescope de 4Ga naar voetnoot13).
reflexio non videtur latinum.
de excludenda luce et reflexu ejus à telescopij tubisGa naar voetnoot14). de ijs quae sine tubisGa naar voetnoot15). addenda difficultas de circulo quo objectiva lens cingi debetGa naar voetnoot16). Diaphragma primus adhibere docuiGa naar voetnoot17). Hinc utilitas telescopiorum plurimum crescit. qui ad organa observationum quadrantes sextantes adhibentur. PicardusGa naar voetnoot18) in dimens. Terrae solertia egregia. descriptio Libellae nostraeGa naar voetnoot19). ad diametros planetarumGa naar voetnoot20) et exiguas fixarum et comitum distantiasGa naar voetnoot21). ad ascensiones | |
[pagina 775]
| |
rectas. La HireGa naar voetnoot22) laudandus. Utilitas ad observandas eclipses, maculas solis. transitus mercurij et veneris in loco tenebroso, quae in hoc lentium dispositio. Presbutae oculi dispositio in his pro vitio non est habenda. quae enim illis conveniunt telescopia ac lentium dispositio, eadem quoque optime constitutis oculis  [Fig. 26.]
conveniuntGa naar voetnoot23). Telescopium Newtoni, ejus augmentum explica, quod est secundum rationem foci distantiae speculi seu ¼ diametri, ad foci distantiam ocularis lentis convexaeGa naar voetnoot24). de caeteris quae ad specula convexa non persequor. quia non magni usus. tantum ad imaginum locum, quandoque extra speculum. Idem continget in sphaera vitrea vel aqua plena. Voiez la difficultè de BarrowGa naar voetnoot25). Essaier avec un miroir concave. Cum uno oculo locum ac distantiam imaginis putaverit dicerni posse, impegit in scopulum istum. Ubi locus imaginis nec binis oculis nec motu unius judicatur. binis enim duplex objectum cernitur isto casu. Et motus unius | |
[pagina 776]
| |
 [Fig. 27.]
 [Fig. 28.]
 [Fig. 29.]
 [Fig. 30.]
non facit parallaxin, sed plus movetur objectum quam ipse oculus. Unde ergo locus imaginis aliquo modo percipitur? Sola apparentia magnitudine notae rei. | |
[pagina 777]
| |
voir RohautGa naar voetnoot1), explication du telescope. il ne l'a pas. voiez les transactions, ce que Newton dit de la differente refraction des couleursGa naar voetnoot2). aberrationis diameter esset 1/50 diametri lentisGa naar voetnoot3) aperturae sed color ruber cum flavo tantum lucidi, praesertim radij non a sole sed alijs rebus manantibusGa naar voetnoot4). Et istorum colorum exigua tantum diffusio. nec puto major aberratio inde orta quam 1/200 apertura lentisGa naar voetnoot5). probatur picturae nitore ac subtilitate in loco clauso. Coupper le cristal de roche perpendiculairement à l'axe, pour voir si alors il ne doublera pas les objets, ou lors que les deux plans du prisme couperont l'axe a angles egaux contrairesGa naar voetnoot6). arcesso non accerso. Graevius in SuetonioGa naar voetnoot7). Correspondens punctumGa naar voetnoot8). definitiones quaedam scribendae. quid axis duarumGa naar voetnoot9) et uniusGa naar voetnoot10). | |
[pagina 778]
| |
quid focus. punctum dispersusGa naar voetnoot1). de multum aperienda lente majori ad observationes satellitum 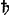 et stellularumGa naar voetnoot2). et stellularumGa naar voetnoot2).
| |
§ 9Ga naar voetnoot3).
| |
[pagina 779]
| |
refractione mirabili Islandicae crystalliGa naar voetnoot6). Cujus causas mirabor si quis alia ulla ratione explicit. De angulis aequalibus in reflexione frustra sunt EuclidesGa naar voetnoot7) AlhazenqueGa naar voetnoot8) alijGa naar voetnoot9). Item de loco imaginisGa naar voetnoot10). Et hic quoque Cartesius, Barrovius nam cum uno oculo distantiam judicari voluntGa naar voetnoot11), quod et Keplerus pag. 63 Para- | |
[pagina 780]
| |
lip.Ga naar voetnoot1), incidunt in difficultatem in qua haerere se fatetur BarroviusGa naar voetnoot2). Keplerus ibidem aliter quoque et rectè ex intuitu utriusque oculi imaginem definire docetGa naar voetnoot3). Keplerus ijsdem paralip.is pag. 105 et seqq. enixe quaerit figuram lentis quae à puncto venientes radios parallelos reddatGa naar voetnoot4), postquam refractionis leges quaesivit sed non reperit verasGa naar voetnoot5). Quibus postea per Snellium Cartesiumque constitutis, quam plana ac perspicua nunc evaserunt tum quae ad figuras istas refractioni idoneas, tum ad caeterum dioptricen spectant. Keplerus a vera lege refr.m non multum aberat, ejusque diligentiam aemulatus ac vestigijs insistens Snellius fere rem absolvitGa naar voetnoot6). Cum Porta picturam in lente crystallini fieri putaretGa naar voetnoot7), Keplerus primus ut puto ad fundum retinae eam transtulit. pag. 211Ga naar voetnoot8). Cum Porta scriptum reliquisset, si utramque recte componere noveris, &c.Ga naar voetnoot9) mirum est Keplerum nihil ejusmodi expertum. Scribit enim hoc Porta in magicae natur.lis libris, quos viderat Keplerus, nam opticen ejusGa naar voetnoot10) ait se non vidisseGa naar voetnoot11). | |
[pagina 781]
| |
RepercussosGa naar voetnoot12) radios dici vult non reflexos, et repercussum pro reflexione usurpat, rectè. repelluntur. retroaguntur. speculum remittit radios. a speculo resiliunt. prope intueri. i.e. ex propinquo. concursus radiorum, rectè. quo defluunt vel affluunt radij, quo tendunt, feruntur, deferuntur, coeunt, conveniunt, contendunt, diriguntur. infractio radiorum melius quam refractio, illud invenitur hoc non. franguntur radij. deflectunt. detorquentur. inflectuntur. obliquantur, in obliquum flectuntur. rumpuntur. deflexus radius. decussantur radij, bene. decussatio, potest usurpari. a puncto manant, exeunt. feruntur, promanant, effunduntur, prodeunt, se expandunt, discedunt (divergunt non bene.) oriuntur, veniunt, emittuntur. ad punctum pertinent radij. ad punctum colliguntur. Extensio, non latinum. visio, bonum. Excessus non significat ὑπεροχην. sed abitum aut mortem.
nisi relationem diversorum punctorum conjugatorum ad eandem superficiem, itemque ad eandem lentem pertinentium consideremus, nihil explicari potest de | |
[pagina 782]
| |
effectu telescopij nec microscopij. hoc autem nemo fecit, non Cartesius, BarroviusGa naar voetnoot1), nec Jac. GregoriusGa naar voetnoot2). 'E pulcherrimis naturae operibus, corpora diaphana cum liquida tum solida. Molineux dioptricaGa naar voetnoot3). | |
§ 10Ga naar voetnoot4).
|
|