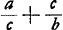Oeuvres complètes. Tome XIII. Dioptrique

[p. 621]

Appendice VIII¹⁾
À la troisième Partie de la Dioptrique ‘De Telescopiis et Microscopiis’.
[1684.]

[Premières recherches sur le rôle de l'aberration chromatique dans les lunettes et dans les microscopes.]

1) L'Appendice présent est emprunté aux p. 183-185 du Manuscrit F et doit être daté, d'après le lieu qu'il y occupe, des premiers mois de 1684. Nous l'avons divisé en paragraphes.

§ 1.

[Fig. 1.]

[Fig. 2.]

Aperturarum diametri in subdupla ratione foci distantiarum; posita radij dispersione velut ex diversis duabus refractionibus minimum quid discrepantibus²⁾.

Haec ut intelligantur videnda quae in dioptricis de aperturarum ratione quaesivi³⁾ quibusque fundamentum erat aberratio ob figuram sphaericam. quae jam inutilia.

Hic vitium et aberratio ex figura sphaerica non attenditur, utpote nullius momenti prae illa quae ex dispersione radij newtoniana⁴⁾.

Itaque duplex veluti refractio consideratur, quarum alterâ radij paralleli in lentem AC [Fig. 1] incidentes ponuntur convenire accuratè in F, alterâ in B, unde extremi radij in A cadentis aberratio ex dispersione erit FQ. Et est CB ad BF ut cb [Fig. 2] ad bf quia utrobique sunt duae diversae proportionis refractiones. nam si ex. gratia, sit CF ∞

2) Comparez la proposition qui commence en bas de la p. 487.

3) Comparez les p. 339-353 des ‘Rejecta’.

4) Comparez les p. 485-487. On lit encore ailleurs sur la même page du Manuscrit présent: ‘Concursus perfectus ponitur rubrorum ad F. Caeruleorum ad B cum aberratio ob figuram nullius hic sit momenti, si ad eam quae ex coloribus comparetur, ut calculo probari potest.’

[p. 622]

[Fig. 1.]

[Fig. 2.]

∞ duplum radij Cα quo superficies AC descripta est:et CB ∞ 21/10Cα. Erit et cf ∞ duplum radij δc, et cb ∞ 21/10δc. Hinc est quod dixi CA ad QF ut ca ad qf.

F focus communis lentium AC, DP. qui ex F in D, pergit in DE parallelus axi. Ergo BD per DK, ut sit ang. EDK ∞ FDB, per theorema...¹⁾.

FD quidem rubri coloris, sed ponitur lens PD tanquam hoc vitio colorum carens ex theoremate simili ei quod pag. 32 in Rejectis²⁾. hic nempe rubri et caesij³⁾ eadem ponitur refr.^o4).

ET est pupilla oculi, in quo aberratio NM⁵⁾, quae tunc utrobique aequalis erit si anguli QDF, qdf sint aequales.

Nam oculi constitutio est ea ut radij in pupillam paralleli axi, ut lk, conveniant omnes ad unum punctum n. ang.ⁱ aequales sunt fdq, kde, dkl; cujus dkl certa pars est nkm⁶⁾, nec refert quanta. si igitur QDF, qdf aequales erunt et aberrationes in fundo oculi aequales NM, nm.

ptn est recta.

ut amplificatio minoris telescopij (b/c) ad amplif. majoris (d/y) ita ½ diam. aperturae in minori (a) ad ½ diam. aperturae in majori x⁷⁾.

1) Voir la Prop. VI, Part. III, p. 475.

2) Voir la p. 341; mais consultez aussi le dernier alinéa du paragraphe présent.

3) Deux pages plus loin on trouve l'annotation suivante: Caesius, caeruleus. caesius purpurascens caeruleum mare, Cicer.’ Ajoutons que dans le texte de la ‘Dioptrique’ on trouve partout: ‘violaceus’; voir les pp. 483, 485, etc.

4) Plus bas la même hypothèse est faite implicitement pour la matière de l'oeil. Voir à ce propos la note 2, p. 491.

5) À la même page du manuscrit on trouve encore: ‘Concursus rubrorum esset in N’.

6) Comparez le deuxième alinéa de la p. 345.

7) C'est-à-dire, afin que la clarté des images soit la même dans les deux télescopes.

[p. 623]

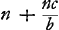⁸⁾⁹⁾ [CF] b ad [CF+FP] (b+c) ut QF (n) ad GH¹⁰⁾ seu ; et ita ∠FDQ ad GDQ. hoc est [ut n ad] n+minimo quod recte potest negligi. imo tantum negligitur quod non eadem ratio BF ad FG quae bf ad fg. nam BF ad bf ut b ad d, sed FG ad fg ut c ad y, seu c ad adc/bx seu bx ad ad seu a√bd ad ad seu √bd ad d.

8) Cette proportion résulte de l'égalité des angles QDF et qdf.

9) Il en résulte x:a = √d:√b; ce qu'il fallait démontrer.

10) Évidemment G représente le foyer de la lentille DP pour les rayons violets; comparez la p. 489 et la Fig. 25 de cette page, où G a la même signification. Par conséquent, puisque les aberrations sur l'axe des rayons de la même couleur sont comme les distances focales, on aura, b:c = BF:GF; donc .

[p. 624]

§ 2.

[Fig. 3.]
[Fig. 4.]

[Microscope simple.]¹⁾

ed [Fig. 3]²⁾ pergens in db rubrum. ed in df caeruleum.

ergo bd in de rubrum. ergo ruber ex f per fd in dk ut ang. kde ∞ fdb³⁾. Sed fd in de caeruleum, ergo radius lucidus per fd spargitur angulo edk ∞ fdb⁴⁾.

[PF] [Fig. 4] (b) ad [FB] (o) ut [pf] d
ad fb(od/b),
[pf] (d) ad [dp] (x) ut [fb] (od/b)
ad fq(ox/b)
[PF] (b) ad [DP] (a) ut [FB] (o) ad FQ (ao/b)
fq(ox/b) ad [pf] d ut FQ(ao/b) ad FP (b)⁵⁾
ox ∞ dao/b; x ∞ da/b
tout cecy convient aussi à l'aberration ancienne⁶⁾.

1) Comparez avec ce qui suit les p. 531-533 du texte de la ‘Dioptrique.’

2) ed est supposée parallèle à l'axe ntpfb.

3) Voir la Prop. VI, Part. III, p. 475.

4) Afin que dans les cas des Fig. 3 et 4 l'aberration chromatique mn ou MN soit la même au fond de l'oeil, c'est-à-dire pour que la vision soit également distincte, il faudra donc que les angles fdb et FDB soient égaux. C'est là la base des calculs qui suivent.

5) C'est-à-dire, afin que les angles qpf et QPF soient égaux, lesquels, eux-mêmes, égalent par approximation les angles bdf et BDF.

6) En effet, supposons que les lentilles dp et DP soient de figure semblable, que f et F soientleurs foyers et b et B les points où les rayons réfractés, provenant de ed et de ED, coupent l'axe. Alors les rayons partant de f qui suivent l'axe bn de très près se réuniront au point n; mais le rayon fd, qui passe par le point d du bord de la lentille, suivra la route fdkm. Or, si l'on néglige l'aberration sphérique de l'oeil, la distance mn ne dépendra que de l'angle kde == fdb. La première proportion PF:FB = pf:fb est donc vraie parce que les aberrations sphériques de lentilles semblables sont proportionnelles à leurs distances focales; la seconde et la troisième sont évidentes; la quatrième exprime l'égalité des angles qdf et QDF, c'est-à-dire des angles kde et KDE; d'où il s'ensuit que la vision sera, en effet, également distincte quand on aura x = da/b, ou x:a = d:b, c'est-à-dire, quand les largeurs des lentilles sont proportionnelles à leurs distances focales; mais consultez sur une démonstration bien plus simple, valable pour les deux aberrations, la note 3 de la p. 532.
D'ailleurs cette phrase en italiques a été ajoutée après coup à une époque inconnue, probablement en 1692.

[p. 625]

ut aeque distincta sit visio in microscopijs simplicibus, debent aperturarum diametri esse ut foci distantiae⁷⁾.

Hinc autem lumina quibus visibile nitescit ut qu.^a foci distantiarum. quia amplificatio in ratione contraria foci distantiarum.

Ergo acutioribus lentibus lux praestanda alio convexo⁸⁾ in rem visam derivata.

[Fig. 5.]

ruber⁹⁾ per edb [Fig. 5] caeruleus per edf ergo ruber in bde ergo caeruleus in bdk ut ang. edk ∞ fdb.

sic optimè.

P.S.¹⁰⁾ Il ne faut pas considérer icy l'aberr ation de Newton, selon laquelle les ouvertures des lentilles pourroient estre extremement grandes¹¹⁾, ce qu'il faut supputer en considérant que l'angle d'aberration dans les Telescopes se souffre jusqu'a environ d'un degrè¹²⁾. Mais dans ces lentilles l'aberration a cause de la figure spherique devient beaucoup plus considerable que l'autre de Newton, et oblige a etrecir les ouvertures.

7) Comparez la règle de la p. 531.

8) Voir la lentille dessinée au côté droit de la Fig. 4.

9) Dans ce qui va suivre il s'agit d'une légère simplification des considérations qu'on rencontre dans les deux premiers alinéa's de ce paragraphe. Or, cette simplification a été adoptée dans la rédaction définitive, p. 531-533 du Tome présent.

10) Ce postscriptum est sans doute postérieur aux autres parties de la pièce présente. Il date probablement de 1692.

11) Comparez le § 5 de l'Appendice IX, p. 634.

12) Lisez plutôt ‘d'un demi-degrè’ et consultez le § 4 de l'Appendice IX, p. 633. En effet, nous n'avons rencontré nulle part dans les manuscrits de Huygens un calcul de l'augle d'aberration chromatique admissible, qui permettrait de le porter jusqu'à la valeur d'un degré.

[p. 626]

§ 3.

In composito microscopio inquiritur quantitas sparsionis radiorum Newtoniana.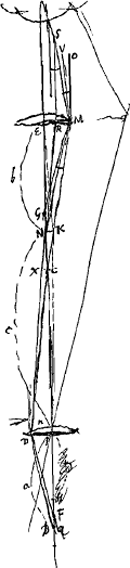

[Fig. 6.]

^{1)2)3)4)5)6)4) 7)8)9)}

1) Puisque SR est supposée parallèle à l'axe EP, N est le foyer de la lentille oculaire EM pour les rayons rouges.

2) Ainsi F est le point qui pour les rayons violets correspond au point N.

3) Plus tard, en 1692, Huygens formulera un lemme qui aura cette portée; voir l'avant-dernière ligne de la p. 665, § 21 de l'Appendice IX, ou la p. 551 du texte de la ‘Dioptrique’.

4) Voir la Prop. VI, Part. III, p. 475.

5) G est donc le foyer de l'oculaire pour les rayons violets.

6) Pour arriver à cette proportion on doit supposer que le rapport entre l'aberration chromatique longitudinale et la distance à la lentille DP est le même pour le point B, correspondant au point N, que pour le foyer de cette lentille; dans ce cas la proportion est une conséquence immédiate des considérations qu'on trouve à la p. 485, premier alinéa; mais en vérité cette supposition est en contradiction avec le lemme cité dans la note 3. D'après ce lemme on aurait, en représentant (comme dans la Fig. 42, p. 560) par H le foyer de la lentille DP et par HO l'aberration au foyer, BF:HO = BP²:HP² (voir le commencement de la note 4, p. 561, où l'on peut substituer à cause du lemme: ∠FDB = ∠HDO); mais puisque HO:HP = NG:NE, on en déduit, NG:NE = BF×HP:BP². Ce n'est donc que dans le cas où la distance PN est suffisamment grande pour pouvoir considérer comme égales HP et BP que la proportion du texte pourrait être admise.

4) Voir la Prop. VI, Part. III, p. 475.

7) Le point K est obtenu en tirant NK perpendiculairement à l'axe EPB.

8) À cause de l'égalité des angles BDF et NDC; les angles DBQ et DNK pouvant être considérés comme droits.

9) Plus tard, en 1692, (voir les p. 535-585 qui précèdent, ou l'Appendice IX, p. 629-673) Huygens reprendra l'étude de cet angle SMO = CMG, qu'il appellera alors l'angle d'aberration du microscope et sur la considération duquel, dans les cas des deux aberrations, chromatique et sphérique, il fondera sa théorie entière du microscope; mais pour le moment il semble que Huygens n'a pas eu d'autre but que de comparer l'aberration chromatique du microscope composé avec celle du microscope simple formé par la seule lentille DP. En effet, puisque les rayons rouges partant du point B finiront par prendre la direction RS parallèle à MO, tandis que les rayons violets, provenant du même point, prendront à la sortie de l'oculaire la direction MS, il est évident que l'aberration du microscope composé sera mesurée par l'angle SMO et, de même, celle du microscope simple par l'angle NDC = FDB, qui, d'après la note 3, sera censé ne pas changer quand l'objet est déplacé vers le foyer de la lentille DP comme cela devra avoir lieu quand cette lentille servira comme microscope simple. Par conséquent, le rapport cherché se trouve être de à 1.

[p. 627]

Semper cum b minor vel aequa c, erit ang. OMS major quam FDB seu δ.

Si b ∞ c est oculus superior lente E per EP, et tunc augmentum non majus quam sola lente P et oculo ad eam applicato¹⁰⁾.

Quando ergo erit ? cum bc ∞ ba+cc, cum cum b pauxillo major quam c.

Une¹¹⁾ lentille simple d'un pouce de foci dist. avec une ligne d'ouverture multiplie tant. Je veux une multiplication 4 fois plus grande en diam. Je prendray pour cela une lentille de ¼ de pouce de foyer, et ¼ de ligne d'ouverture.

10) Comparez la p. 529.

11) Peut-être l'annotation qui va suivre a-t-elle été ajoutée à une époque postérieure. Toutefois elle ne contient aucune considération qui, en 1684, était nécessairement étrangère à Huygens.

[p. 628]

Elle multipliera comme il faloit¹⁾, et fera voir autant distinctement que l'autre, mais 16 fois plus obscurement, ce qui ne se peut remedier qu'en augmentant la lumiere sur l'objet. de sorte qu'on ne peut pas effectuer autant de multiplication qu'on veut, si non en renforcant la lumiere. Si on veut faire la mesme multiplication en adjoutant a la premiere lentille un convexe oculaire, on verra aussi 16 fois plus obscurement, et de plus moins distinctement, parce que c sera ∞ 4b²⁾, et partant ∠CMG [Fig. 6] sera plus que 4δ ou 4 fois l'angle NDK, avec NMG. pour cela il faut faire l'ouverture de DP moindre que quand cette lentille est seule. toutefois cette composition de 2 lentilles est meilleure que de prendre une seule de ¼ de pouce pour la commoditè de voir et d'esclairer à costè et un grand champ distinct. et les tres petites lentilles malaisement sont si bien formées que les moins petites.

1) Comparez la p. 515.

2) C'est-à-dire pour avoir le même grossissement qu avec la nouvelle lentille simple; voir la p. 529.