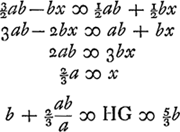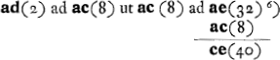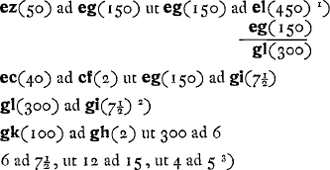Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 598]
| |||||
Appendice VI.
|
| 1. | 16 pedes longum, 3 lentibus. ejusdem effectus atque vulgare pedum 30 constat. 110 ducatis. |
| 2. | 10 vel 12 pedum, 7 vitris ad solem contuendum et terrestria quoq. 75 ducatis, ni fallor. |
| 3. | 7 vel 8 p. 5 vitris, ad astra. 70 aureis n.f. |
| 4. | 4 vel 5 pedum eidem usui. 4 vitris. 40 aureis, puto. |
Semidiameter patinae majoris 6 voet min 1 7/10 duym.
Semidiam. minoris, 2 6⅓/10 duijmGa naar voetnoot4).

Ga naar voetnoot5)Ga naar voetnoot6)Ga naar voetnoot7)Ga naar voetnoot8)Ga naar voetnoot9)
§ 2Ga naar voetnoot1). [1655.]Ga naar voetnoot2)
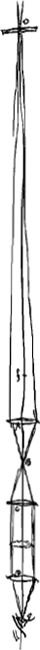
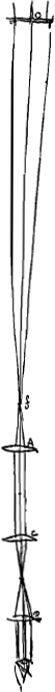
[Instruction pour l'usage des lunettes à miroir.]Ga naar voetnoot3)
Pour veoir les objects prochains il faut allonger la lunette.
La lunette estant tirée jusques aux cercles marquez sur le fer blanc, elle sera propre pour veoir les objets eloignez, mais pour veoir distinctement ceux qui ne sont qu'a cent pas ou a moindre distance il la faut racourcir de la largeur d'un doigt ou encore d'avantage selon qu'ils seront plus proches.
Pour regarder a la lune et aux planetes il faut oster le petit miroir, et regarder a travers de la lunette, comme l'on se sert des vulgaires. mais auparavant il sera bon de faire approcher vers l'oeil le verre qui est de ce coste la environ de la largeur d'une paille. La lune requiert aussi la lunette tant soit peu plus longue que les autres planetes et estoiles a cause de sa clartè.
§ 3Ga naar voetnoot4). [1666.]
AB [Fig. 1] hic paulo major quam foci distantia.
f [Fig. 1 et 2] focus communis lentis O et A.
distantiae AC, CD aequales et singulae duplae Af.
Convexa A, C, D aequalia.
DE ∞ AFGa naar voetnoot5).
§ 4Ga naar voetnoot6). [1668.]

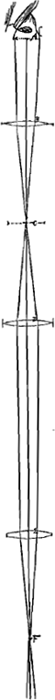
Telescopium Jos. Campani ped. 3. poll. 3Ga naar voetnoot7).
A amplitudo foraminis ad oculum.
AB ab initio tubi ad lentem primam ocularem
C locus et amplitudo foraminis sine lente.
D lens secunda.
E lens tertia, paulo minor reliquis duabusGa naar voetnoot8).
lentes 3 B, D, E, foci distantias omnino aequales habent poll. 1 et 10/12Ga naar voetnoot9). Pedis Rhenol.
Objectivum foci distantiam habet 2 ped. 5 poll.Ga naar voetnoot10).
Ejus dispositio ut focus incidat in punctum F.
Pars GGG intrat tubum HH, portatque lentem B, quam tenet cochlea K lignea. Ipsaque pars G tenetur cochlea L.
Tubus M intrat ab altera parte tubum H, portatque ab una
parte lentem D, firmatam cochlea buxea N. ab altera parte insertum habet tubulum O, qui portat lentem E, firmatam cochlea P.
QQ est operculum quod imponitur arcendo pulveri.

aperturae objectivi diameter 72/100 poll.Ga naar voetnoot1).
§ 5Ga naar voetnoot2). [1673.]
[Grandeur des objets visibles dans la lune avec une lunette de 60 pieds.]
de 60 pieds ouverture de 6 p. 81.Ga naar voetnoot3) 240 fois.
fait 60 pieds ouverture de 4 p. 200 foisGa naar voetnoot4) avec un oculaire de 3⅗ pouce. fait voir le diam. de la lune de 100 degr. puisqu'elle est d'un ½ degr. c'est a dire 500 lieues d'allemagne sous l'angle de 100 degr. ou 5 lieues sous 1 degr. ou 1 lieue sous 12 min.
1 degrè est la 1/57 partie de sa distance de l'oeuil donc a la distance de 57 pouces, c'est pres de 5 pieds, l'on verra un rond d'un pouce de diametre de mesme qu'une tasche de la lune qui a 5 lieues de diametre. Et 2⅖ lignes, a cette mesme distance de 5 pieds, comme une chose dans la lune de l'estendue de 1 lieue. Et une chose de ½ lieue, comme seroit la ville de Paris, comme 1⅕ lignes a la distance de 5 pieds.

§ 6Ga naar voetnoot5). [1683].
[Sur les diaphragmes qui doivent empêcher la lumière qui tombe sur les parois du tube d'atteindre l'oeil de l'observateur]Ga naar voetnoot6).

lunette de 12 pieds. ouvertureGa naar voetnoot1) de 1½ pouce. diaphragme de 9/10 d'un pouce. oculaires de 2 pouces de foier.
Si elle consiste en 4 pieces et que la separation en D ait une ouverture de 1 pouce; la grosseur de la lunette au bout A devra estre environ de 2½ pouces. Et a l'autre bout E environ de 2 pouces, alors elle sera obscure parfaitement, c'est à dire le tuyau en dedans; ce qui est très necessaire.
[Deuxième Partie.]Ga naar voetnoot2)
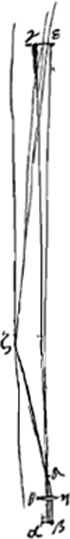
γε apertura objectivae lentis. δ focus ejus, idemque lentis ocularis θη.
Propter latitudinem pupillae αβ, non tantum radij γδ, εδ, qui per totam aperturam lentis majoris transeunt, ad ipsam deferuntur, sed et qui a tubi latere egrediuntur ut ζδ, nisi annulis impediantur ita ut punctum ζ, illustratum radio εζ, lucem projicere possit in lentem θη.
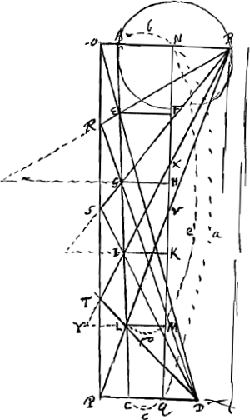
NQ axis telescopij [Fig. 7].
AB apertura lentis objectivae; CD apertura ocularis sive potius diaphragmatisGa naar voetnoot3).
Sit tubus ex quinque partibus compositus, in quarum singulis foramina aperta quorum semidiametri AN, EF, GH, IK, LM; quae definit recta AC, quia ab omnibus punctis aperturae AB ad omnia puncta CD radij pervenire debent.
BL, DC conveniant in P, idem BA, DE conveniant in O. Erit NOGa naar voetnoot4) dimidia crassitudo ejus tubi ex illa parte, QP ex alteraGa naar voetnoot5); quantae ad minimum requiruntur, ut tubus intus plane obscurus fiat; quantacunque fuerit tubi longitudo.
Rectae BE, BG, BI, BL productae usque in latus tubi OP, referunt radios lucis; et apparet lucem inde ortam non posse percipi ab ullo puncto aperturae seu lentis CD, ductis DEO, DGR, DIS, DLT quae cum prioribus conveniunt in ipsa linea OP. quod tamen demonstrandum superestGa naar voetnoot6).
Fit QP ∞ QC + ½NAGa naar voetnoot5). Et NO ∞ NA + ½QCGa naar voetnoot4). quae regula observanda cum 5 partibus tubus constat. at si 4 partibus, sit QP ∞ QC+⅔NA, et

et NO ∞ NA+⅔ QC. Si vero 3 partibus, fit QP ∞ QC+NA et NO ∞ NA+QC. Si duabus, fit QP ∞ QC+2NA. NO ∞ NA+2QC.
[NQ ∞ a; AN ∞ NB ∞ b; CQ ∞ ∞ QD ∞ c.]Ga naar voetnoot1)
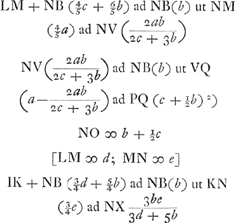
Ga naar voetnoot2)
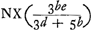 ad NB(b) ut
ad NB(b) ut 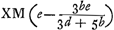 ad MY (d+⅔b) imo facile erat videre LY esse ∞ ⅓AB sive ⅔AN quia AI ad IL ut 3 ad 1.
ad MY (d+⅔b) imo facile erat videre LY esse ∞ ⅓AB sive ⅔AN quia AI ad IL ut 3 ad 1.
§ 7. [1683.]
[Oculaire d'une lunetteGa naar voetnoot3) de Huygens qui se trouve à l'Observatoire de Leyde.]
§ 8Ga naar voetnoot1). [1683.]
[Sur une lunette de Coveri.]Ga naar voetnoot2)
25 marsGa naar voetnoot3) Vu une lunette de 6 pieds 10 pouc. de Stefano Coueri a Livorno à 4 verres. l'ouverture de l'objectif estoit celle cy scavoir d'un pouce, et ½ ligne. la distance du foier des oculaires depuis le milieu du verre, 2 pouces 4/10. l'ouverture du diaphragme 10½ ligne. la grandeur des oculaires presque la moitie de leur distance de foier.

§ 9Ga naar voetnoot4). [1684.]
[Manière d'observer les satellites de Saturne et d'autres petites étoiles.]Ga naar voetnoot5)
Ad comites Saturni aliasque minimas stellulas conspiciendas posset apertura telescopij multo amplior solita usurpari, quia enim tantum ut puncta apparent istae stellulae nihil prodest earum diametros amplificari telescopio, sed oportet ut quanta possunt luce clarescant. Ideo augeatur apertura vel ad duplam solitae latitudinem, simulque lens ocularis assumatur dupla majori foci distantia. Sic fiet ut stellulae istae quadruplo clariores appareant, et tamen aeque distinctae seu terminatae. Sane duplo minus amplificabuntur; sed hoc nihil hic refert. Hac ratione possemus aucta apertura in telescopio 30 pedum, satellites Saturnios aeque ac nunc 120 pedes longo intueri, quia in quadrupla longitudine dupla tantum adhibetur aperturae diameterGa naar voetnoot6). Unde patet eandem tunc fore in telescopio 30 ped. quae alias 120 pedali convenit.
CF [Fig. 11], cf [Fig. 10] sint aequales foci distantiae. Aperturae AC, ac inaequales.
Cum aberrationes extremorum radiorum FQ. fq sint inter se ut semidiam.i


aperturarum AC, ac. nam BF, bf sunt aequales, (ut patet ex ijs quae pag. sequ. dicta suntGa naar voetnoot1)) sicut autem FQ ad fq ita debeat esse FD ad fd, seu FP ad fp, ut fiant anguli aequales FDQ, fdq; unde aeque perfecta terminatio consequitur; Ergo sicut AC ad ac, ita debet esse FP ad fp quae sunt ocularium lentium foci distantiae.
Parandae igitur lentes 20 vel 30 pedum sed tam amplae ut possint aperturas habere 4 9/10 et 6 pollicum. Sunt enim expeditiora ad usum breviora telescopia.
Ut ne noceat Saturni claritas, potest virgula papyracea per mediam lentem ocularemGa naar voetnoot2), vel potius in foco lentis majoris apponi quae Saturni corpus tegat, dum satellites quaeruntur.
Videri posset sexdecuplo clariora omnia apparituraGa naar voetnoot3), quia imagines ad quadruplo minus spatium arctantur in fundo oculi, et hoc ita erit, praeterquam in comitibus Planetarum et stellis fixis quia cum tantum velut puncta sint in oculo earum imagines telescopio utroque visae, unice attendendum est quantum lucis colligatur ad ista puncta illustranda. quanto enim plus colligitur tanto melius cernentur hujusmodi stellulae, nec refert fere qualis sit lens ocularis.
§ 10Ga naar voetnoot4). [1686.]
[Considérations sur la grandeur du champ de vision; la pupille de l'oeil étant considérée comme réduite à un seul pointGa naar voetnoot5).]
[Deuxième Partie.]
Apertura objectivi ponitur aequalis foci dist.ae lentis ocularisGa naar voetnoot4). apertura ocularis ponitur 4/9 suae foci distantiae. Hinc posito oculo in foco ocularis d, fit angulus campi tantillo minor tantum quam si in a oculus ponatur ita ut radius if per margines utriusque vitri transiens cadat in a, fit enim ad minor quam 1/120 dcGa naar voetnoot5), ratio autem campi ex d et a, sicut angulus fdc ad fac, hoc est proximè ut ac ad dc.
Sit cz 3 poll. item cd. zg 460 poll. sive 30 ped. [sic!] ig 1½ poll. fc ⅔ poll. ∞ ∞ hg. Ergo ih ∞ ⅚ poll.
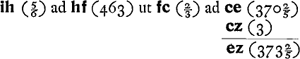
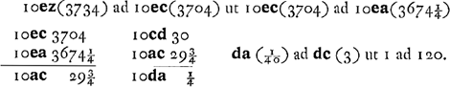
§ 11Ga naar voetnoot6). [1692.]

Ad pag. 86 dioptricesGa naar voetnoot7).
G focus lentis magnae; KV ∞ a foci dist. lentis K; GK ∞ ⅓a; KS ∞ ∞ ½a; HS ∞ ¼a foci dist. lentis S; SM ∞ ⅙a oculi dist.a ad quem pervenient radij paralleli; A lens magna; ratio augmenti quae AG ad GKGa naar voetnoot8).
in tabula ratio augmenti est ut 310 ad 1Ga naar voetnoot9). Sed sit ratio augmenti 300 ad 1.
300 ad 1 ut 200 (pedes foci dist.ae seu long.do telesc.) ad 20/30 (KG); KV ∞ 3KG ∞ 2 ped.; ¼KV ∞ SH ∞ ½, foci dist. lentis EF seu S.
In telescopio 200 ped. lens ad K erit 2 pedum foci dist.; lens ad S erit ½ ped. foci dist.
ratio augm.Ga naar voetnoot10) 250 ad 1 ut 130 (ped. foci dist. magnae lentis teu long.o telesc. ad 13/25 (KG); pedes 39/25 ∞ KV ∞ a; 4⅔ [poll.] fere SH lent.
ad S foc. dist. cujus diam. circiter 2⅖ poll.; 18¾ poll. fere lens ad K sive dist. KV cujus diameter circiter 6 poll.
Ut fiat EF ad SM ut 4 ad 5Ga naar voetnoot1).
§ 12Ga naar voetnoot2). [1692.]
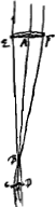
lens major 30 ped. foci dist. habet aperturam 3 poll.Ga naar voetnoot3) et ocularem cujus foci dist. poll. 3.
AB foc. dist. lentis magn. 360 ad BH foc. dist. oculi 3 ut EF apert. 3 ad CD 9/360 latit.do quam in lente oculari et in pupilla occupant radij a puncto visibilis egressi. vocetur Latitudo ad oculum.
CD 1/40 pollicis, seu minus quam ⅓ lineae.
120 pedis foci dist. lentis maj.
1440 ad 6 f.d. ocul.Ga naar voetnoot3) ut 6 apert. ad 1/40 latitudo ad pupillam eadem. aperturae et foci distantiae ocularium in duobus telescopijs sunt in subdupla ratione foci distantiarum lentium magnarumGa naar voetnoot4).
§ 13Ga naar voetnoot5). [1692.]
minus distat claritas telescopij a claritate oculi in aere aperto quam intra aedes, quia illic minor apertura pupillae nudae quam hic. hinc quae intra aedes sunt obscure cernuntur teles.o. Tamen obscurius videtur telescopium in aere aperto, quia oculi multa luce hebetiores fiunt ad conspicienda obscuriora.
foci dist. ocularium in diurno (1 8/10 poll.) cujus exterior habet f. dist. 30 poll. seu 2½ ped. sed eidem ex tabula debetur oculare cujus f. dist. 86/100 poll.Ga naar voetnoot6) nempe ad nocturnas. multiplicatio ut 16⅔ ad 1Ga naar voetnoot7). Ergo ocularis 4 1/10 poll. debetur objectivae 13 ped. ad diurnaGa naar voetnoot8) quia objectivae
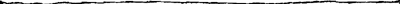
13 ped. ex tabula debetur ocularis 197/100 poll.Ga naar voetnoot3) (utor 2 2/10 poll. nempe secundum correctam tabulam)Ga naar voetnoot9).
Sed dedi oculare ad diurna 2 8/10 poll. Ergo non respondet claritas ei quae in minori telescopio diurno, sed duplo et amplius minor est. 2 8/10 ad 4 1/10; 28 ad 41 prox. ut 2 ad 3 claritas ut 4 ad 9 prox.
§ 14Ga naar voetnoot10). [1692.]
Cur tribus ocularibus nihilo magis curventur lineae rectae quam una.
Si nulla esset aberratio radius à laevo rei visae (lunae puta) puncto, iret per HKLMNCGa naar voetnoot11) [Fig. 15] ad oculum C et semidiam. lunae videretur ang.o NCV.
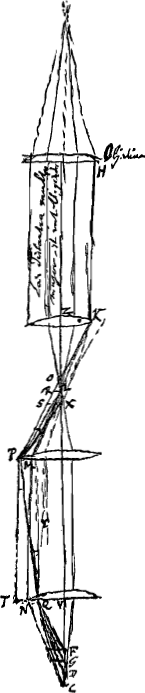
Nunc propter aberrationem fertur per HKRPQFGa naar voetnoot1). hoc est si ponatur oculus ad F videbitur lunae semidiameter angulo QFV. Ideoque et posito oculo in C videbitur idem semidiam. ang.o qui sit aequalis QFV, per prop. [XIII, Part. I, Lib. II]Ga naar voetnoot2). Cognoscenda est igitur differentia inter angulos NCV, QFV. quam dico aequalem esse angulo simplicis aberrationis LKO, ac propterea nihilo magis curvari lineas rectas (hujus causa bene exponenda estGa naar voetnoot3)) positis 3 ocularibus quam uno.
Nam posita LX ∞ LO; quia radius XP iret in PT axi parallelusGa naar voetnoot4), ibit KOP per PQ, ut sit ang. TPQ ∞ OPX. Sit QY parall. PT. Jam rad. YQ iret per QD, faciens aberrationem CD ∞ OL. Ergo rad. PQ ibit per QF, ut sit ang. FQD ∞ YQP. Jam ang. NCQ est aequ. PLMGa naar voetnoot5), hoc est duplo RKL. ang. vero CQF ∞ 3 ang. CQDGa naar voetnoot6) sive 3 ang. RKL. atqui ang. NCQ+QCV est aequ. NCV. Et ang. CQF+QCV est aequ. QFV. Ergo QFV superat NCV quantum CQF superat NCQ hoc est angulo RKL. Ergo seu tribus ocularibus seu uno apparebit ½ diam. Lunae ang.o NCV+RKL cum debuerit videri ang.o NCV seu ZLK absque aberratione. nam circa lunae medium fit ampliatio quasi absque aberratione.
Causa curvaturae.
Partes rei visae quae prope axem sunt minus augentur quam quae remotiores ab eo; quod fit ex aberratione lentiumGa naar voetnoot7).
CA augetur 1/18 sui, ut A sit in R.
CP augetur 1/36 sui, ut P sit in Q.
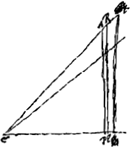
Ergo AP curvatur in RQ.
- voetnoot1)
- Sous cette suscription nous avons réuni plusieurs pièces qui se rapportent aux lunettes; toutes empruntées aux manuscrits de Huygens et écrites de sa main à l'exception de celle qu'on trouve au § 7 (p. 607), où nous donnons le dessin et la description d'une lunette de Huygens en possession de l'Observatoire de Leyde. Nous avons arrangé ces pièces chronologiquement, chacune d'elles constituant un paragraphe de l'Appendice présent.
- voetnoot2)
- Ce paragraphe est emprunté aux p. 93-95 du ‘boeckje’; manuscrit dont il est question à la p. 4 du T. XI.
- voetnoot3)
- On peut consulter sur ces télescopes les pp. 215, 308-310 et 424 du T. I, la p. 294 du T. III et la p. 125 du T. IV. Ajoutons qu'à la p. 86 du Manuscrit C on trouve encore la description suivante d'un petit télescope de Wiselius de 3 pouces: ‘Verkijckertie van Wiselius, van 3 duijm. het voorglas aen wedersijden in een schoteltie van 3½ duijm radius. het oogglas aen wedersijden op een bol van 6½/10 van een duijm radius. distantie tusschen beijde glazen 2½ duijm. opening 34/100 van een duijm.’ De la description il s'ensuit donc que l'objectif, dont l'ouverture mesurait 0,34 pouce, et l'oculaire étaient formés par des lentilles biconvexes symétriques avec rayons de courbure de 3½ et de 0,65 pouce placées à une distance l'une de l'autre de 2½ pouce. Ajoutons que cette description est accompagnée d'un petit dessin qui ne fait connaître que la forme extérieure du télescope. Elle doit dater de l'année 1666 d'après le lieu où elle se trouve.
- voetnoot4)
- Nous ne savons pas à quelles lunettes ces données se rapportent.
- voetnoot5)
- Traduction: ‘Lunette de Keffelaer - quatre pieds moins 2 pouces. Verre concave comme le mien.’ Probablement il s'agit d'une lunette fabriquée par Wiselius mais en possession de Keffelaer. L'ouverture en est représentée en vraie grandeur par le cercle à côté.
- voetnoot6)
- Traduction: ‘lunette de Wiselius, de 4½ pied en 7 pièces’. On trouve une description détaillée d'une telle lunette en sept pièces aux p. 308-309 du Tome 1.
- voetnoot7)
- Traduction: ‘[distance] entre l'oeil et le premier verre’.
- voetnoot8)
- Traduction: ‘du premier jusqu'au deuxième [verre]’
- voetnoot9)
- Traduction: ‘distance focale du premier [verre]’.
- voetnoot1)
- La pièce était écrite sur une des pages d'une feuille séparée de quatre pages.
- voetnoot2)
- On lit sur la même feuille, écrit avec la même plume et la même encre, très reconnaissables, le bout de phrase que voici: ‘Quae circa Saturni stellam prioribus ignota batavici tubi ope’. Il faut donc que la pièce ait été rédigée après le 25 mars 1655, date de la découverte du satellite de Saturne.
- voetnoot3)
- Consultez sur ces lunettes les p. 265-269 du Tome présent.
- voetnoot4)
- La pièce est empruntée à la p. 93 du Manuscrit C. D'après le lieu qu'elle occupe elle doit dater de 1666. Le système de lentilles est identique à celui de Campani décrit dans le paragraphe qui suit et dans la Prop. V, p. 469-473 du Tome présent. La sigure à gauche montre comment le champ de vision ne dépend que de l'ouverture de la première des trois lentilles oculaires qui se trouve le plus près de l'objectif; voir le dernier alinéa de la p. 471. La figure à droite correspond entièrement à la fig. 14, p. 469.
- voetnoot5)
- Lisez: Af.
- voetnoot6)
- La pièce occupe une feuille séparée.
- voetnoot7)
- Il s'agit sans aucun doute de la lunette de Campani qui appartenait à l'Abbé Charles de Bryas et dont les mesures furent prises par Christiaan Huygens en mai 1668 et communiquées le même mois à son frère Constantyn; voir la lettre du 11 mai 1668, p. 213 du T. VI. C'était la lunette dont il est fait mention dans la lettre de Petit à Huygens, p. 266 du T. IV, lettre qui doit être datée du 28 novembre 1664 (et non de 1662 comme elle l'est au lieu cité). Et l'on peut ajouter qu'au mois de novembre 1664 elle fut éprouvée par Auzout contre une lunette à miroir de Huygens, comme on peut le lire à la p. 145 du T. V.
- voetnoot8)
- Le dessin ne donne que les trois oculaires; l'objectif est supposé se trouver à une distance de 2 pieds 5 pouces plus bas que le point F.
- voetnoot9)
- C'est-à-dire à peu près 4,80 centimètres, le pouce Rhinlandais égalant 2,616 cm. La distance BD = DE devrait donc être égale à environ 9,60 cm.; or, en mesurant ces distances sur le dessin on trouve BD = 9,00 cm., DE = 9,80 cm. Le dessin que nous reproduisons ici à mi-grandeur était donc fait à vraie grandeur, mais pas avec beaucoup de soin.
- voetnoot10)
- Le grossissement serait donc de 29:1⅚, c'est-à-dire à-peu-près seize fois. Auzout trouvait environ 14 fois; voir la p. 145 du T. V.
- voetnoot1)
- Nous reproduisons ce dessin à sa vraie grandeur.
- voetnoot2)
- La pièce est empruntée à une feuille séparée collée dans le Manuscrit E près de la dernière page. Elle a servi de brouillon à une partie de la lettre du 9 août 1673 à Colbert. Comparez la p. 351 du T. VII.
- voetnoot3)
- C'est-à-dire 6 pouces 8 lignes. On peut constater que cette mesure de même que le grossissement s'accorde avec le tableau qu'on trouve à la p. 353 des ‘Rejecta’.
- voetnoot4)
- Grossissement intermédiaire entre celui de 241 du tableau mentionné dans la note précédente et celui de 170 du tableau de la p. 499.
- voetnoot5)
- La pièce occupe les p. 165-167 du Manuscrit F et doit, d'après le lieu qu'elle occupe, dater de 1682 ou de 1683.
- voetnoot6)
- De tels diaphragmes furent employés p.e. en assez grand nombre dans les grandes lunettes de Hevelius, et, d'après les p. 227 et 228 du T. IV et la p. 417 du T. VIII, ils existaient aussi dans les grandes lunettes anglaises et dans les lunettes des frères Huygens. La première partie du paragraphe présent traite le cas d'un tube cylindrique (voir la Fig. 5). On doit la considérer comme un premier essai. La deuxième partie, qui est plus achevée, s'occupe du cas d'un tube de forme conique. Et il paraît que de tels tubes pourvus de diaphragmes ont, en effet, été construits par les frères Huygens, mais ils ont abandonné cette construction à la suite d'un accident survenu à une lunette de Constantyn, qu'il décrit dans une lettre à Christiaan du 25 mars 1683 (p. 413 du T. VIII). La lunette étant placée dans un coin, l'objectif en bas, les pièces du tuyau, plus minces en haut qu'en bas, tombèrent avec un grand fracas sur l'objectif qu'elles faillirent écraser, mais qui résista heureusement au choc.
- voetnoot7)
- Dans cette première partie Huygens suppose connues les ouvertures des diaphragmes, égales entre elles et à celle, se trouvant en E qui semble représenter l'ouverture de l'oculaire (voir toutefois la note 3 de la p. 604), et il se propose de calculer la largeur qu'on doit donner au tube pour qu'aucune lumière réfléchie par la paroi ne puisse atteindre l'oculaire. Or, il est évident qu'une des parties du tube, qui peuvent être éclairées par la lumière qui passe par le diaphragme en C, commence en G. Il faut donc faire en sorte que la lumière partant du point G, ou des points voisins de la partie éclairée du tube, soit empêchée par le diaphragme en D d'atteindre l'oculaire en E et pour cela il suffira que le point G se trouve sur la droite KN. C'est là la base des calculs qui suivent; toutefois les lignes tirées dans la figure montrent que Huygens n'a pas manqué d'examiner également l'effet des parties de la paroi éclairées par la lumière passant par les ouvertures des diaphragmes en D et en B. Alors ces calculs lui auront appris que la même largeur HG == 5/3 b est nécessaire et suffisante pour empêcher toute lumière venant de ces parties de la paroi de parvenir à l'oculaire en E.
- voetnoot1)
- Lisez plutôt ‘largeur du tube’; alors on aurait, en effet, 2HG = 3/2 pouce et 2b == ⅗×2HG = 9/10.
- voetnoot2)
- Dans cette deuxième partie il s'agit de construire un tube à diaphragmes qui se rétrécit du côté de l'oculaire, de manière qu'aucune lumière venant des parties éclairées de la paroi ne puisse passer par les ouvertures des diaphragmes; consultez sur la réalisation pratique d'un tel tube de forme conique la note 6, p. 603, qui précède.
- voetnoot3)
- Il s'agit donc du dernier diaphragme qui précède à l'oculaire. Or, ces mots ‘sive potius diaphragmatis’ font supposer que peut-être on doit s'imaginer qu'aussi dans la Fig. 5, p. 603, on n'a pas affaire en E avec l'oculaire mais avec le diaphragme qui le précède. Dans ce cas le diamètre des diaphragmes pourrait excéder celui de l'oculaire, ce qui n'apporterait aucun changement dans les calculs, puisqu' il s'agit alors d'empêcher la lumière, qui tombe sur les parois, de passer par ce dernier diaphragme en E.
- voetnoot4)
- Posant AN = b, CQ = c on trouve, pour le cas de n diaphragmes,
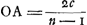 ; puisque OA:CD(2c) = AE:EC = NF:FQ = 1:n-1. Donc
; puisque OA:CD(2c) = AE:EC = NF:FQ = 1:n-1. Donc 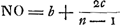 .
.
- voetnoot5)
- Au cas général
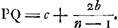 .
.
- voetnoot6)
- Il n'en est rien. Huygens s'est laissé tromper par les apparences. Toutefois la construction est bonne. En effet, il est clair d'abord que le tube ne peut pas être rétréci ni à l'un ni à l'autre bout sans manquer le but proposé. Ensuite nous montrerons qu'aucune lumière ne peut pénétrer dans l'oeil par l'intermédiaire de la paroi. Soit à cet effet S le point d'intersection de DI avec la paroi et S' celui de BG avec la même paroi. Il suffira alors de démontrer que dans tous les compartiments du tube la somme des distances de S au plan CD et de S' au plan AN dépasse ou égale la longueur NQ = l du tube. Soit donc QK = p/n l et, par conséquent, IK =
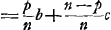 ; si nous prenons alors QN et QP pour l'axe des x et des y d'un système de coordonnées, on trouvera
; si nous prenons alors QN et QP pour l'axe des x et des y d'un système de coordonnées, on trouvera 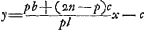 pour l'équation de la droite DI et y =
pour l'équation de la droite DI et y = 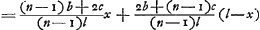 pour celle de la droite OP. Il en résulte xS =
pour celle de la droite OP. Il en résulte xS = 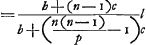 . Si nous remplaçons dans cette formule b par c, c par b et p
par n-p-1, on aura
. Si nous remplaçons dans cette formule b par c, c par b et p
par n-p-1, on aura 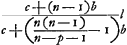 pour la distance de S' au plan AN. Or, l'excès sur l de la somme de xS et de cette dernière distance se trouve être égal à
pour la distance de S' au plan AN. Or, l'excès sur l de la somme de xS et de cette dernière distance se trouve être égal à 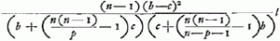 , expression essentiellement positive excepté pour le premier et le dernier compartiment, où elle devient égale à zero, puisqu' alors on a respectivement p = o, et p = n-1.
, expression essentiellement positive excepté pour le premier et le dernier compartiment, où elle devient égale à zero, puisqu' alors on a respectivement p = o, et p = n-1.
Remarquons encore que pour b = c, c'est-à-dire pour un tube cylindrique, les points S et S' se confondent pour tous les compartiments. C'est le cas de la figure 5 de la première partie dans laquelle on aura donc, au cas général,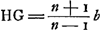 .
.
- voetnoot5)
- Au cas général
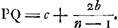 .
.
- voetnoot4)
- Posant AN = b, CQ = c on trouve, pour le cas de n diaphragmes,
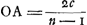 ; puisque OA:CD(2c) = AE:EC = NF:FQ = 1:n-1. Donc
; puisque OA:CD(2c) = AE:EC = NF:FQ = 1:n-1. Donc 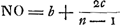 .
.
- voetnoot1)
- Dans ce qui suit Huygens a évidemment voulu déterminer la position des points d'intersection R, S, T, mais il n'a pas achevé le calcul.
- voetnoot2)
- Comparez les notes 4 et 5 de la p. 605, qui précède.
- voetnoot3)
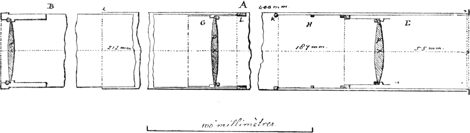
- La lunette en question porte un objectif sur lequel Huygens écrivit, avec un diamant, sur l'un des côtés sa signature caractéristique ‘Chr. Hugenius f.’ et sur l'autre ‘Ped. 12 Opt.’ Le tube en fer blanc est composé de 5 pièces, entrant l'une dans l'autre, sans compter l'oculaire terrestre qui contient trois lentilles, disposées d'après les indications données dans la Prop. V, p. 469.
La figure ci-jointe fait connaître en détail la disposition de cet oculaire, qui nous semble être identique avec celui qui est mentionné dans les lettres échangées par les frères Huygens en mars et avril 1683; voir les pp. 411, 412, 415, 416, 417, 419 et 420 du T. VIII.
On distingue dans la figure le tube A d'une longueur de 400 mM., dans lequel se trouve du côté de l'objectif un tube B contenant deux lentilles biconvexes C et D de 38 et de 40 mM. de diamètre, ayant des distances focales de 104 et de 106 mM., et du côté de l'oeil un tube E contenant la lentille biconvexe F ayant un diamètre de 38 mM. et une distance focale de 77 mM. La lentille C a une position in variable dans le tube B, tandis que la lentille D, fixée dans un petit tube G qui glisse dans B, peut être rapprochée ou éloignée de C; la plus grande distance entre les deux, telle qu'elle est indiquée dans la figure, étant de 212 mM.
La lentille F est fixée dans le tube E qu'on peut enfoncer dans A, jusqu'à ce qu'il butte contre l'extrémité d'un autre tube H qui peut glisser aussi dans A mais qui est retenu en place par un anneau ressort K.
Quand, du côté de l'objectif, on enfonce le tube B autant que possible dans le tube A, c'est-à-dire jusqu'à ce qu'il touche l'anneau L, et que du côté de l'oeil on enfonce entièrement le tube E, comme nous l'avons indiqué dans la figure, la distance des lentilles D et F est de 187 mM. Celle de F jusqu'au bord du tube, où l'on place l'oeil, est de 55 mM.
Ajoutons qu'on n'aperçoit nulle part une trace de diaphragmes.
A fin que cette combinaison de lentilles satisfasse aux conditions exposées dans la Prop. V citée, il faut que les distances focales de C et D soient les mêmes, ce qui est le cas à fort peu près, et que la distance de ces deux lentilles (212 mM.) soit égale à la somme (210 mM.) de leurs distances focales. Quant à la troisième lentille F, sa distance focale de 77 mM. diffère sensiblement de celles des autres, mais la condition que les rayons venant d'un point à distance infinie redeviennent parallèles entre eux après leur sortie de la lentille F peut être remplie à peu près, puisqu'elle exige que la somme des distances focales des lentilles D et F, laquelle est de 183 mM., soit égale à leur distance mutuelle qu'on peut réduire à 187 mM. D'ailleurs il est clair qu'on peut obtenir un parallélisme complet p.e. en diminuant un peu la distance entre l'objectif et le système des trois oculaires.
En écartant le tube B on peut obtenir une lunette astronomique avec une seule lentille oculaire, donnant le même grossissement.
On trouvera encore d'autres détails sur cette lunette avec une exposition des résultats d'une investigation de ses qualités optiques aux pp. 409-412 et 423-429 d'un article de feu l'astronome de Leyde F. Kaiser ‘Iets over de kijkers van de gebroeders Christiaan Huygens’ dans les ‘Verslagen en Mededeelingen van het Koninklijk Nederlandsch Instituut’ de l'année 1846.
- voetnoot1)
- La pièce se trouve à la p. 169 du Manuscrit F.
- voetnoot2)
- On peut consulter sur cette lunette les pp. 415 et 420 du T. VIII, d'après lesquelles elle grossissait 31 fois et fut jugée par Huygens ‘tres excellente et bien ordonnée.’
- voetnoot3)
- Sans doute le 25 mars 1683 d'après le lieu que la pièce occupe au Manuscrit F.
- voetnoot4)
- Ce paragraphe est emprunté à la p. 182 du Manuscrit F. D'après le lieu où il se trouve, il doit dater d'un des premiers mois de 1684.
- voetnoot5)
- Comparez le dernier alinéa de la p. 511.
- voetnoot6)
- Voir la règle qui commence en bas de la p. 487.
- voetnoot1)
- Il s'agit du § 1 de l'Appendice VIII; voir la p. 621 qui suit. Comparez encore les p. 483-485, où l'aberration chromatique des lentilles est traitée plus amplement.
- voetnoot2)
- En effet, si l'on a égard aux petites dimensions, lorsqu'ils traversent l'oculaire, des faisceaux de lumière (voir les p. 507-509) qui partent des différents points d'un objet éloigné, on voit que de cette manière on peut écarter la lumière venant de Saturne sans affaiblir la clarté des images des satellites.
- voetnoot3)
- Comparez toujours le dernier alinéa de la p. 511.
- voetnoot4)
- La pièce est empruntée à la p. 251 du Manuscrit F et doit dater de 1686 ou 1687.
- voetnoot5)
- La pupille étant considérée comme un point unique, Huygens va comparer les champs de vision qu'on obtient en plaçant l'oeil au foyer d de l'oculaire et en le plaçant au point a où le diamètre de ce champ est un maximum. Pour trouver ce dernier point on doit chercher l'intersection avec l'axe el du rayon lifa dont la partie qui se trouve entre les lentilles passe par les contours de l'objectif gi et de l'oculaire cf. Or, puisque khfd représente le rayon qui passe par le foyer d de l'oculaire, il est clair que le rapport cherché des diamètres des deux champs de vision est égal à celui des angles hkg et ilg, c'est-à-dire, par approximation, au rapport de hg/gk et de ig/gl; c'est la méthode suivie dans la première partie. Posons, pour la rendre plus générale, dc = cz = f, gz = gk = F, 2fc = 2hg = δ, 2gi = d, ac = x, ec = y, gl = z, on trouve alors successivement
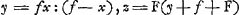
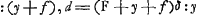 . On en déduit,
. On en déduit,
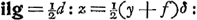
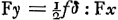 , mais hkg = ½δ:F, donc hkg:ilg = x:f.
, mais hkg = ½δ:F, donc hkg:ilg = x:f.
Or, ce résultat simple: que les diamètres des champs de vision en d et en a sont dans le rapport de ac à dc, se laisse déduire d'une autre façon si l'on considère fdc et fac comme des angles très petits, ce qu'on doit supposer aussi pour pouvoir appliquer les formules qui précèdent. Dans cette supposition il est clair que les angles qui déterminent les champs de vision se trouveront en divisant les angles fdc et fac par les grossissements correspondants; mais ces grossissements sont égaux d'après la Prop. XIII, Part. I, Liv. II, p. 233, les diamètres des champs de vision sont donc proportionnels à ces derniers angles, qui, eux-mêmes, sont évidemment inversement proportionnels aux distances df et af, c'est-à-dire qu'ils sont dans le rapport de ac à cd. C'est le résultat de ce raisonnement qu'on retrouvera dans la deuxième Partie.
- voetnoot6)
- Voir la Prop. XX, Part. I, Liv. I, p. 99; a et e sont des points correspondants par rapport à l'oculaire.
- voetnoot1)
- Détermination du point l qui correspond au point e par rapport à l'objectir.
- voetnoot2)
- gi:gl mesure le champ de vision dans le cas que l'oeil est placé en a.
- voetnoot3)
- Rapport des diamètres des champs de vision en d et en a.
- voetnoot4)
- Comparez la note 2 de la p. 496.
- voetnoot5)
- Avec les notations de la note 5, p. 610 on a
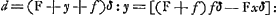 :fx. On en déduit:
:fx. On en déduit: 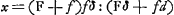 . On a donc en général:
. On a donc en général:
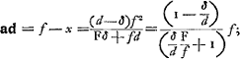
ce qui donne dans les suppositions introduites ici, où δ = 4/9f et d = f,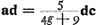 , où g = F:f représente le grossissement. Tout dépend donc de ce grossissement. Or, il est clair que Huygens a en vue ici le cas numérique qui va suivre et où, en effet, les conditions δ = 4/9f et d = f se trouvent réalisées. Dans ce cas ou a g = 460/3; donc
, où g = F:f représente le grossissement. Tout dépend donc de ce grossissement. Or, il est clair que Huygens a en vue ici le cas numérique qui va suivre et où, en effet, les conditions δ = 4/9f et d = f se trouvent réalisées. Dans ce cas ou a g = 460/3; donc 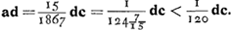 .
.
- voetnoot6)
- La pièce est empruntée à la p. 47 du Manuscrit H et doit être datée de 1692 d'après le lieu où elle se trouve. Elle donne deux nouveaux exemples de lunettes construites d'après les règles exposées dans la Prop. IV, p. 461 et appliquées aux fig. 11 et 12 de la p. 462. Et il nous semble que du moins le deuxième exemple, où les dimensions des lentilles sont indiquées, a dû correspondre à une lunette employée par Huygens.
- voetnoot7)
- C'est la page dont il est question dans la note 2 de la p. 463 du Tome présent.
- voetnoot8)
- Comparez pour ce qui précède le deuxième alinéa de la p. 463.
- voetnoot9)
- Voir le Tableau de la p. 499. Il s'agit d'un télescope de 200 pieds.
- voetnoot10)
- Voir dans le même Tableau les données pour un télescope de 130 pieds.
- voetnoot1)
- On a EF = 2⅖ pouce, SM = ⅙a = 7/2 8/5 pouce; donc, en réalité, EF:SM = 4:5⅕.
- voetnoot2)
- La pièce est empruntée à la p. 55 du Manuscrit H. Sur son contenu ou peut consulter les p. 507-509.
- voetnoot3)
- Comparez le Tableau de la p. 499.
- voetnoot3)
- Comparez le Tableau de la p. 499.
- voetnoot4)
- Comparez la règle qui commence en bas de la p. 487.
- voetnoot5)
- Les annotations qui suivent se trouvent aux pp. 56 et 62 du Manuscrit H. Elles traitent les conditions différentes de l'emploi des lunettes dans la maison et en plein air, pendant le jour et pendant la nuit. Comparez la p. 505.
- voetnoot6)
- Le Tableau de la p. 497 donne 0,77 pour 2 et 0,95 pour 3 pieds, dont la moyenne égale 0,86; toutefois un petit calcul à part montre que Huygens a employé la règle de la note 2, p. 496, pour trouver 0,86.
- voetnoot7)
- C'est-à-dire pour un oculaire de la distance focale de 1 8/10 pouces, qu'on trouve tracée à côté. La distance de 0,86 pouces donne un grossissement de presque 35 fois.
- voetnoot8)
- C'est-à-dire en supposant que les distances focales à employer pendant le jour sont proportionnelles à celles qui peuvent servir la nuit.
- voetnoot3)
- Comparez le Tableau de la p. 499.
- voetnoot9)
- Il s'agit d'un tableau calculé d'après la règle du texte de la p. 495; c'est-à-dire en ajoutant un dixième à la distance focale indiquée par le Tableau de la p. 497.
- voetnoot10)
- La pièce qui suit est empruntée aux pp. 64 et 65 du Manuscrit H.
- voetnoot11)
- Parmi tous les rayons qui partent du point indiqué, Huygens choisit celui qui passe par le foyer de l'objectif, qu'on doit supposer se trouver à grande distance du premier oculaire ZK qui appartient à un système de trois lentilles oculaires, tel que celui considéré dans la Prop. V. p. 469. Comparez la Fig. 15 de cette page.
- voetnoot1)
- Il est vrai que HKRPQF ne représente qu'un seul des rayons qui, partant du point donné de l'objet, atteignent l'objectif de la lunette et pénètrent dans l'oeil de l'observateur; mais on sait que le faisceau formé par ces rayons se réduit dans les lunettes employées par Huygens à des dimensions très petites lorsqu'il tombe sur la première lentille de l'oculaire (voir la p. 509). On peut donc suivre à volonté un de ces rayons et choisir celui qui, entre l'objectif et la première lentille de l'oculaire, prend exactement la direction de l'axe; cela est d'autant plus permis parce que tous ces rayons qui, en traversant les lentilles de l'oculaire, parcourent à peu près la même route deviendront par première approximation parallèles entre eux avant d'entrer dans la pupille (voir la fig. 14 de la p. 472).
- voetnoot2)
- Voir la p. 233.
- voetnoot3)
- Voir plus bas sous l'en-tête ‘causa curvaturae’.
- voetnoot4)
- Puisque les lentilles ZK et PM sont de dimensions égales et qu'ainsi leurs aberrations sphériques sur l'axe, OL et LX, doivent être les mêmes.
- voetnoot5)
- Les distances mutuelles des trois lentilles étant égales, on a approximativement PT = 2PS, donc TQ = 2SX, puisque ∠TPQ = ∠OPX. Mais
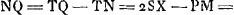
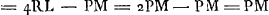 , donc enfin ∠NCQ = ∠PLM; c'est-à-dire par approximation, de même que toutes les égalités traitées ici.
, donc enfin ∠NCQ = ∠PLM; c'est-à-dire par approximation, de même que toutes les égalités traitées ici.
- voetnoot6)
- Puisque
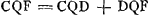 et DQF = YQP = TPQ = OPX = 2OPL = 2RKL, tandis que RKL = CQD puisque CD = OL, LK = ZL = CV = CQ, et puisqu'enfin ZK ne diffère pas sensiblement de QV.
et DQF = YQP = TPQ = OPX = 2OPL = 2RKL, tandis que RKL = CQD puisque CD = OL, LK = ZL = CV = CQ, et puisqu'enfin ZK ne diffère pas sensiblement de QV.
- voetnoot7)
- On rencontre une sigure tout-à-fait semblable à la Fig. 16 dans le Manuscrit D à la p. 406, où elle est accompagnée de la seule phrase ‘de deformatione specierum per lentes visarum, et cur rectae lineae curvae appareant’; annotation qui doit dater de 1673.