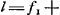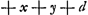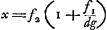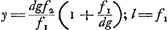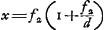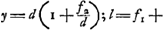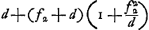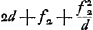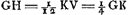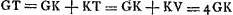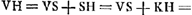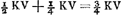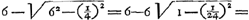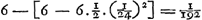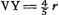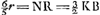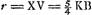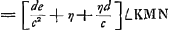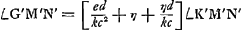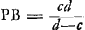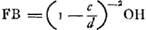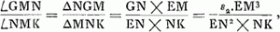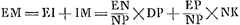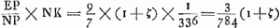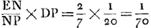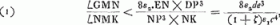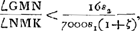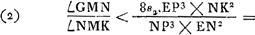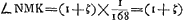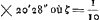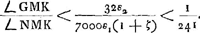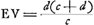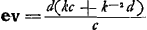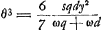Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 434]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
La Dioptrique.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 435]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Dioptrica.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 436]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Quelques-uns attribuent l'honneur de la première invention, due d'ailleurs au hasard comme je l'ai dit, à Jacob Metius, hollandais et citoyen d'Alkmaar. Mais, quant à moi, je sais certainementGa naar voetnoot1) qu'avant lui, vers la neuvième année de ce siècle, un artisan habitant Middelbourg en Zélande a fabriqué des télescopes, soit que ce fût celui dont Sirturus fait mentionGa naar voetnoot2), savoir Joh. Lippersheim, ou bien celui auquel Borellus décerne la palme dans son opuscule sur le véritable inventeur du télescopeGa naar voetnoot3), savoir Zacharias. Les plus grands tubes fabriqués par ces artisans à cette époque n'étaient que d'un pied et demi. Mais longtemps avant ces deux in venteurs Joh. Bapt. Porta de Naples avait suggéré les rudiments de cet art: il existe de cet auteur un ouvrage sur la Dioptrique et la Magie NaturelleGa naar voetnoot5) publié pas moins de 15 ans avant que les télescopes surgirent dans notre patrie, les Pays-Bas. Dans cet ouvrage il est fait mention de ses lentilles (qu'il appelle ‘specilla’) qui font voir les objets éloignés comme s'ils se trouvaient à petite distance, et il parle de la combinaison des lentilles concaves et convexesGa naar voetnoot7). Mais que Porta n'avait pas fait de grand progrès, cela est prouvé par le fait qu'en tant d'années l'art dont les premiers commencements avaient été trouvés ne s'est pas développé et que Porta lui même n'a observé au ciel aucun des phénomènes qui y ont été vus plus tard. Ceci doit être attribué, fans doute, au fait que l'invention était due à des expériences fortuites. Car quoique Porta possédât quelques connaissances mathématiques, il n'avait pas saisi cependant les théories fort subtiles sur lesquelles l'art optique est basé, de sorte qu'il ne pouvait parvenir à cet art par la méditation; à plus forte raison cela devait être impossible aux artisans peu instruits dont j'ai parlé plus haut. Mais qu'on ait fait cette invention par un heureux hasard, cela n'a rien d'étonnant, attendu qu'on faisait depuis plus de trois siècles un fréquent usage des deux espèces de lentilles, à l'aide desquelles, prises séparément, les défauts des yeux peuvent être corrigés. Il y a plutôt lieu de s'étonner qu'une chose si aisée à découvrir soit restée cachée si longtemps. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 437]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sunt qui inventionis, sed uti dixi fortuitae, primae laudem Jacobo Metio Batavo Alcmariae civi tribuant. Mihi vero certo compertum estGa naar voetnoot1) ante ipsum telescopia fabricasse artificem quendam Medioburgensem apud Zelandos circa annum hujus saeculi 9. sive is fuerit cujus Sirturus meminitGa naar voetnoot2) Joh. Lippersheim nomine, sive cui Borellus in libello de vero Telescopij repertore primas defertGa naar voetnoot3) Zacharias. Hi tunc non majores sesquipedalibus tubos factitabant. Utroque vero multo prior rudimenta artis suggesseratGa naar voetnoot4) Joh. Bapt. Porta Neapolitanus, cujus exstant de rebus dioptricis, et Magia Naturali, libriGa naar voetnoot5) totis 15 annis ante editi quam in Belgio nostro telescopia exorirentur. In quibus libris de specillis (ut vocat) suis memorat res procul positas quasi propinquae essent referentibusGa naar voetnoot6), deque conjunctione cavarum et convexarum lentiumGa naar voetnoot7). Nihil tamen magnopere eum profecisse, hoc ipsum probat quod tanto tempore ars jam coepta non ultra inclaruit, neque ipse Porta quidquam in caelo observavit eorum quae postea apparuerunt. Hoc inde est quod fortuitis experimentis originem inventi deberi constat. Neque enim hic vir licet mathematicarum aliquatenus gnarus subtilissimasGa naar voetnoot8) rationes quibus ars ea pro fundamentis utitur comprehenderat, ut meditatione eam eruere posset, multoque minus illi quos ante memoravi homines opifices ac scientiarum rudes. Fortuna vero et casu eodem perventum nihil mirum est, cum frequens usus esset jam a trecentis atque amplius annis utriusque generis lentium quibus seorsim adhibitis vitia oculorum emendantur. ut potius mirandum sit tam diu rem obviam latuisse. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 438]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
D'ailleurs, aussitôt que le bruit de l'invention des télescopes hollandais s'était répandu, Galilée en construisit de semblables et bientôt après de beaucoup meilleurs, à l'aide desquels il observa le premier les célèbres phénomènes célestes qu'on connaît: il aperçut les montagnes et les vallées de la Lune, les taches du Soleil et à l'aide de celles-ci la rotation du Soleil sur lui-même, les planètes satellites de Jupiter, les phases de Vénus semblables à celles de la Lune, et la diversité des grandeurs apparentes de cette planète; la Voie lactée remplie d'une multitude de petites étoiles qui lui donnent son éclat; la différence entre les diamètres des étoiles fixes et ceux des planètes et un nombre d'étoiles surpassant de beaucoup celui de celles qu'on connaissait dans les temps anciensGa naar voetnoot3). Le même savant avait observé aussi les phénomènes de Saturne aussi bien qu'il le pouvait avec ses télescopes de petites dimensions, mais il n'était pas parvenu à reconnaître les véritables figures de cette planète, et pendant bien des années après lui personne n'y a mieux réussi. Car quoique les télescopes fussent devenus beaucoup plus grands, leur qualité et leur puissance étaient restées à peu près les mêmes. C'est nous qui avons eu le bonheur d'attaquer ce problème sous de meilleurs auspices: ayant accompli une étude approfondieGa naar voetnoot4) de la théorie de la réfraction des rayons et construit nous-mêmes à notre propre usage des lentilles et des télescopes longs de vingt pieds et davantageGa naar voetnoot5). Àleur aide nous avons découvert des formes non encore remarquées de Saturne et leur cause, un anneau entourant le globe tel qu'il ne s'en rencontre chez aucune autre planète, et nous avons trouvé aussi un petit satellite de la planète Saturne tournant autour d'elle en une période de seize jours. Tout ceci a été écrit par nous dans un livre destiné à ce sujet et publié il y a 26 ansGa naar voetnoot6). Excités par nos observations, des astronomes et des artisans ont construit bientôt après de plus grands télescopes, parmi lesquels ceux qui ont été fabriqués à Rome par Joseph CampaniGa naar voetnoot7) sont les meilleurs. À l'aide de ces instruments le sieur Cassini a réussi heureusement à observer, dix ans après, deux nouveaux satellites de SaturneGa naar voetnoot8) outre celui que nous avions trouvé. Le même savant a découvert à la surface des planètes Jupiter et Mars certaines taches et a pu conclure de leurs mouvements aux périodes de révolution de ces planètesGa naar voetnoot9). Voilà jusqu'où cette noble invention nous a conduits; voilà le résumé des merveilles célestes que le télescope a révélées aux habitants de la terre. Quel homme, à moins qu'il ne soit absolument stupide, ne reconnaît pas la grandeur et l'importance de ces découvertes? Et quelle personne initiée aux études philosophiques ne comprend pas combien ces nouvelles connaissances ont jeté une vive clarté sur nos conceptions de la nature de l'univers? Certes, nous pouvons être reconnaissants envers le siècle où nous vivons pour la connaissance de choses si importantes acquise seulement en ce dernier temps. Quel prix ces savants illustres, qui par un espace | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 439]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Caeterum ut primum Telescopiorum Belgicorum fama sparsa erat continuo Galileus similia illis, ac brevi multo praestantiora paravitGa naar voetnoot1), quibus celeberrima illa caeli phaenomena omnium primus deprehenditGa naar voetnoot2): Lunae montes vallesque, Solis maculas, et ex his conversionem ejus in semet ipsum, Planetas Jovis comites, Phases Veneris quales Lunae, variasque ad aspectum magnitudines; Viam lacteam minutis stellulis refertam, unde candoris causa. Differentiam stellarum inerrantium inter et planetarum diametros, atque illarum numerum antiquitus cognito multo majoremGa naar voetnoot3). Idem Galileus Saturni quoque phaenomena observaverat, quà licebat in illa perspicillorum suorum parvitate, veras autem planetae figuras adsecutus non erat, sed neque quisquam alius multis post ipsum annis. Etsi enim magnitudine multum creverant tubi, parum tamen virtute et efficacia processerant. Nos autem magis auspicato rem eandem aggressi, cum quae ad refractiones radiorum attinent studiose investigassemusGa naar voetnoot4), ipsique nobis lentes effecissemus ac telescopia pedes viginti et amplius longaGa naar voetnoot5), his Saturni formas non ante visas deprehendimus causamque earum annulum globo circundatum, nullo in caeteris planetis exemplo. item comitem Saturno planetam exiguum reperimus dierum sexdecim periodo circumeuntem, quae omnia ante annos 26 libro singulari conscripta edidimusGa naar voetnoot6). Nostris autem observationibus excitati astronomi atque artifices majora subinde telescopia paraverunt, in quibus optima quae a Josepho CampanoGa naar voetnoot7) Romae fabricata. Quorum opera feliciter usus decennio post duos alios praeter nostrum illum comites apud Saturnum reperit dom. CassinusGa naar voetnoot8). Idemque in Jovis ac Martis sideribus maculas quasdam observavit, ex quarum motu etiam globorum quibus inerant conversiones statis temporibus definitasGa naar voetnoot9). Et hactenus quidem adhuc processit nobile hoc artificium, haecque summa est eorum quae de rebus caelestibus terrarum incolis revelavit. Quae magna ac praeclara esse quis nisi plane stupidus non agnoscit? Quanta vero ad naturae contemplationem lux hinc exorta sit, quis non philosophiae studijs initiatus intelligit? Certe gratari saeculo huic nostro possumus propter tantarum rerum nunc demum acquisitam scientiam: quam quo non pretio redemissent viri illi eximij, non | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 440]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
de peu d'années en ont été exclus, Copernic, Régiomontanus, Brahé n'auraientils pas voulu payer pour entrer en possession de ces connaissances! Et les anciens cultivateurs de la science, Pythagore, Démocrite, Anaxagore, Philolaüs, Platon, Hipparque, combien de terres étrangères n'eussent-ils pas parcourues poussés par le désir d'apprendre à connaître de tels secrets de la nature et de pouvoir jouir de pareils spectacles! Mais peut-être devons-nous nous attendre à contempler bientôt, outre ceux dont nous avons parlés, encore d'autres spectacles nouveaux et nombreux, depuis que nous avons réussi, il y a peu de temps, à faire disparaître par notre inventionGa naar voetnoot1) le grand inconvénient résultant du trop grand poids et des trop fortes dimensions des tubes; en effet, nous avons supprimé entièrement ces tubes, de sorte que des télescopes de 100 ou de 200 pieds peuvent maintenant être maniés aussi aisément qu'autresois ceux de dix pieds; et surtout depuis que plusieurs personnes ont commencé à cultiver l'art de polir de fort grandes lentilles, laquelle étude, après un long intervalle, nous avons aussi repris nous-mêmesGa naar voetnoot2) avec tant de succès que nous ne nous en sommes pas repentis. Mais venons-en aux causes et aux propriétés de cet oeil factice, dont nous ne possédons pas jusqu'ici une explication assez claire. En effet, on n'est pas parvenu jusqu'à ce jour à ce qui est le plus important dans cette matière, c'est-à-dire à la connaissance de la nature et de la grandeur du grossissement de l'objet visé, érant données la forme et la position des lentilles. Kepler n'a point enseigné cela, quoiqu'il soit digne de beaucoup de louanges à cause des explications de phénomènes dioptriques qu'il a données le premier. Descartes ne fut pas plus heureux que lui; en vérité il s'écarta plutôt de la bonne route dans les démonstrations qu'il voulut donner de la nature et de l'effet du télescopeGa naar voetnoot3). Ceci est à peine croyable d'un homme si intelligent et si versé dans ces choses; il fallait néanmoins le dire afin que personne n'essaye vainement de comprendre des phrases dont on ne peut tirer aucun sens raisonnable. Beaucoup d'autres auteurs après lui se sont donné de la peine pour arriver au même but; cependant ils n'ont pas réussi mieux que lui à résoudre le problème en question qui est ici d'une importance fondamentale. Nous commencerons donc maintenant par la discussion de ce problème; nous le traiterons séparément pour chaque espèce de télescope. Nous avons démontré généralement dans ce qui précèdeGa naar voetnoot3) comment on peut calculer le grossissement lorsque la forme et la position de deux lentilles quelconques sont données ainsi que l'endroit où se trouve l'oeil. Mais puisqu'il ne s'agit actuellement que de considérer les cas qui se présentent chez les télescopes, nous pourrons arriver plus rapidement aux mêmes résultats. Nous parlerons d'abord des télescopes composés d'une lentille convexe et d'une lentille concave, lesquels | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 441]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
longo annorum intervallo hinc exclusi Copernicus, Regiomontanus, Braheus. Veteres autem illi sapientiae cultores Pythagoras, Democritus, Anaxagoras, Philolaus, Plato, Hipparchus quas non exteras terras peregrinando pervagati essent hujusmodi naturae secretorum noscendi amore, utque talibus frui possent spectaculis. Fortasse autem et alia plura ac nova praeter ea quae diximus propediem exspectanda sint, postquam nupero invento nostroGa naar voetnoot1) in gens incommodum ex nimia tuborum mole ac pondere ortum, atque adeo ipsos tubos, sustulimus, ut nihilo difficilius nunc centenum vel ducentorum pedum telescopia quam antea decempedalia tractentur. utique cum et expoliendarum amplissimarum lentium artem plures jam excolere coeperint, cujus nos quoque studium longo tempore intermissum repetijmus, nec poenitendo successuGa naar voetnoot2). Sed jam ad caussas proprietatesque factitij hujus oculi pergamus, quas non satis feliciter hactenus expositas habemus. Quod enim hic prae caeteris requirebatur ut data lentium forma ac positu ex his modus mensuraque amplificandae rei visae definiretur, id hactenus praestitum non est. Nam neque Keplerus hoc docuit, etsi multa laude dignus ob ea quae in dioptricis primus explicuit, neque illo felicior fuit Cartesius, imo ut vere dicam a via potius aberravit in his quae de ratione et effectu telescopij demonstranda susceperatGa naar voetnoot3). Quod vix credibile de tanto viro, tamque in his rebus versato, tamen dicendum fuit, ne quis frustra ea intelligere laboret e quibus nulla aptaGa naar voetnoot4) sententia elici potest. Cum vero alij multi post eum in eodem argumento operam insumserint, nihilo magis tamen idem problema quod in his omnium praecipuum est absolverunt. Ab eo nunc nos ordiemur idque in singulis telescopiorum generibus expediemus. Ostendimus autem in superioribusGa naar voetnoot5) in universum data forma et positu duarum quarumlibet lentium, itemque oculi loco, quomodo augmenti ratio cognoscatur. At quia nunc illos tantum casus quos telescopia requirunt exequi necesse estGa naar voetnoot6), brevius idem conficiemus. Ac primum quidem in illo telescopiorum genere quod è convexa et cava lente componitur omniumque primum fuit inventum. Requi- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 442]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
furent inventés les premiers de tous. Or, tous les télescopes exigent en premier lieu une telle position des lentilles qu'il en résulte une vision distincte. Mais pour qu'ils grossissent les objets, il faut pour ces télescopes composés de deux lentilles que la lentille extérieure soit convexe et que la lentille oculaire ait des surfaces convexes ou concaves faisant partie d'une plus petite sphèreGa naar voetnoot1). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition IGa naar voetnoot2).Le télescope composé d'une lentille convexe et d'une lentille concave fait apercevoir les objets éloignés distinctement et debout; il les grossit dans un rapport égal à celui de la distance focale de la lentille convexe à la distance du point de dispersion de la lentille concaveGa naar voetnoot3). SoitGa naar voetnoot4) AO [Fig. 1] l'axe commun des deux lentilles, A la lentille convexe extérieure et O son point de concours pour les rayons parallèles provenant d'un objet situé à grande distance. Supposons que D représente la lentille concave placée de telle manière entre la lentille A et son foyer O que le point de dispersion des rayons parallèles, arrivant sur elle du côté où se trouve le point O, tombe précisément en O. Et puissel'oeil du spectateur se trouver d'abord fort près de cette lentille concave. Les rayons issus d'un point de l'objet situé à grande distance sont censés tomber parallèlement sur la lentille A et ceux en particulier qui proviennent d'un point situé sur le prolongement de l'axe seraient dirigés vers le point O; toutefois ils sortiront de nouveau parallèles à cause de la réfraction due à la lentille D placée comme nous l'avons dit, ainsi que cela résulte des démonstrations antérieures. Nous voulons, en effet, obtenir que les rayons arrivent parallèlement à l'oeil, afin que le télescope s'adapte à ceux qui jouissent d'une bonne constitution de l'oeil; car plus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 443]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
runt vero primo eam lentium positionem telescopia omnia, ut distincta visio sequatur. ut vero auctiora referant quae spectantur, necesse est in his quae duabus lentibus constituuntur ut exterior convexa sit, ejus vero quae est oculo propiore minori sphaera sit sive convexitas sive cavitasGa naar voetnoot1). 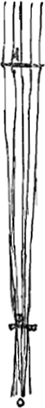 [Fig. 1.]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio I.]Ga naar voetnoot2)Telescopium ex convexa et cava lente compositum visibilia longinqua, distinctè ac recto situ videri facit, amplificatque secundum rationem focidistantiae lentis convexae ad distantiam puncti dispersus lentis cavaeGa naar voetnoot3). SitGa naar voetnoot4) utriusque lentis axis communis AO; lens verò exterior convexa A, cujus punctum concursus radiorum parallelorum, à visibili longè remoto venientium, ponatur O punctum. Cava autem sit D, quae sic collocetur inter lentem A et focum ejus O, ut punctum dispersus radiorum parallelorum à parte ea ubi est O in ipsam incidentium, cadat in idem punctum O. Et huic lenti proximus primò statuatur spectantis oculus. Radij igitur a puncto rei longinquae egressi censentur paralleli incidere in lentem A, ij quidem qui ex puncto in axe producto procedunt cogerentur ad punctum O; sed rursus paralleli evadent opera lentis D, ita ut dictum est collocatae, uti ex supra demonstratis constat. Parallelos enim radios ad oculum pervenire volumus, ut bona oculi constitutione fruentibus telescopium aptetur; nam de myope | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 444]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
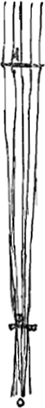 [Fig. 1.]
loin nous parlerons du myope. Or, de la même manière les faisceaux de rayons provenant de points fort éloignés placés hors de l'axe se réuniraient aux points correspondants près de O, si, par la réfraction due à la lentille D, les rayons de chaque faisceau n'étaient pas de nouveau rendus parallèles entre eux, quoique obliques par rapport à l'axe AD; comme cela résulte de la Prop. XXII, Part. I, Liv. IGa naar voetnoot1). Nous n'avons pas tracé ces rayons dans la figure pour éviter la confusion. Or, il est évident d'après ce qui a été démontré à la Prop. I, Part. I, Liv. IIGa naar voetnoot2) que le grossissement et la position de l'image, lorsque les deux lentilles sont en place, seront les mêmes qu'au cas où, au lieu de la lentille D, il y aurait une petite ouverture; mais dans ce dernier cas le rapport de la grandeur apparente à la grandeur vraie est égal au rapport des longueurs AO et OD, comme cela a été démontré à la Prop. II, Part. I, Liv. IIGa naar voetnoot3). Et d'après la même proposition l'objet est vu debout. La même chose aura donc lieu dans le cas du télescope composé des lentilles A et D. Mais lorsque l'oeil s'éloigne de la lentille D, la grandeur apparente de l'objet demeure la même d'après la Prop. XIII, Part. I, Liv. IIGa naar voetnoot4), et la vraie grandeur ne change pas non plus puisque l'objet se trouve par hypothèse à grande distance. Le grossissement reste donc le même qu'auparavant. Or, la position de l'image reste également la même d'après la proposition citée. Mais s'il s'agit d'adapter un télescope de ce genre à l'oeil d'un myope, on a vuGa naar voetnoot5) qu'il faut rapprocher la lentille oculaire D, et avec elle l'oeil de l'observateur, un peu plus de la lentille A; parce qu'on obtiendra ainsi que les rayons n'arrivent plus à l'oeil parallèlement mais en divergeant. Il en résulte que le grossissement sera un peu moindre pour l'oeil myope qu'au cas précédent, vu que le point O reste en place et qu'en conséquence l'intervalle DO devient plus grand, tandis que le grossissement est toujours exprimé par le rapport AO:OD. C'est làGa naar voetnoot6) la démonstration la plus courte du théorème principal. Nous prouverons encore d'une autre façon la partie de ce théorème qui se rapporte au grossissement de l'objet, de sorte qu'il ne sera pas nécessaire de recourir à la Prop. V, Part. I, Liv. IIGa naar voetnoot7). Supposons donc que les lentilles AC et D et le point O | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 445]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
dicemus postea. Similiter vero a punctis longinquis extra axem positis manantes colligerentur quique ad puncta sua prope O, sed et hi lentis D refractione evadent denuo paralleli quamvis ad axem AD obliqui, secundum prop. [XXII, Part. I, Lib I]Ga naar voetnoot1) quos radios tamen in figura non expressimus, vitandae confusionis gratia. Jam ex demonstratis prop. [I, Part. I, Lib. II]Ga naar voetnoot2) patet eandem fore amplificationem et positum, manente lente utraque, atque cum loco lentis D foramen exiguum statuetur; tunc vero magnitudinis apparentis ad veram ea est ratio quae AO ad OD, ut ostensum prop. [II, Part. I, Lib. II]Ga naar voetnoot3), et ex eadem visibile erectum spectatur. Ergo eadem hîc fiunt telescopio ex lentibus A, D composito. Quod si vero retrocedat oculus ab lente D, eadem remanet rei visae magnitudo apparens ex prop. [XIII, Part. I, Lib. II]Ga naar voetnoot4). nec vera mutatur, quia visibile longinquum ponitur. Ergo eadem quae prius manet amplificatio. Sed et positus idem ex eadem prop. [XIII]. Quod si myopi aptandum sit hujusmodi telescopium, paulo propius admovendam esse constatGa naar voetnoot5) lenti A lentem ocularem D unàque oculum spectatoris; quoniam sic fiet ut non jam paralleli ut antea radij perveniant ad oculum, sed divergentes. Hinc vero paulo minus augmentum continget myopi quam prius cum punctum O maneat, eoque intervallum DO crescat, ratio vero augmenti sit semper ea quae AO ad OD. EtGa naar voetnoot6) haec quidem primarij theorematis brevissima est demonstratio. Cujus partem eam quae ad amplificationem rei visae attinet aliter quoque demonstrabimus, ut nihil opus sit prop. [V, Part. I, Lib. II]Ga naar voetnoot7). Positis igitur ut ante | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 446]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
soient situés comme auparavant, construisons une troisième proportionnelle DP [Fig. 3] aux deux lignes DO et DA, et portons-la dans le même sens que DO. Des rayons quelconques tels que ECP, se dirigeant vers le point P, et réfractés par la lentille AC seront amenés, d'après la Prop. XX, Part. I, Liv. IGa naar voetnoot1), à se réunir au point D, centre de la lentille placée là. Supposons que ce rayon ECP fasse partie d'un faisceau provenant du bord gauche de la lune, le centre de la lune se trouvant sur le prolongement de l'axe DA. Il paraît que ce rayon atteindra la pupille de l'oeil en suivant la droite CDF, attendu qu'il passe par le centre D de la lentille dont l'épaisseur est négligée et dont les deux surfaces près de leurs points centraux sont considérées comme parallèlesGa naar voetnoot3). Or, nous avons dit que tous les rayons provenant de ce point de la lune arrivent parallèlement à l'oeil. L'oeil les reçoit donc tous parallèles au rayon CDF; il voit, par conséquent, ce point, situé sur le bord de la lune, à l'endroit vers lequel se dirige la droite DC; et comme cette droite est située du côté de l'axe où se trouve le point de la lune d'où les rayons sont partis, il paraît que les objets seront vus debout. Or, l'angle ADC correspond au demi-diamètre de la lune grossie par le télescope. Mais l'angle CPA est celui qui correspond au même demi-diamètre vu à l'oeil nu, puisque le rayon ECP, comme nous l'avons dit, part du bord gauche de la lune, tandis que le rayon HAP part du centre; car, à cause de la distance très grande, la lune apparaît sous le même angle, soit qu'on la contemple à l'oeil nu du point P, soit du point G. Le grossissement a donc lieu suivant le rapport de l'angle ADC à l'angle APC, lequel est ici considéré comme égal au rapport de la droite PA à DA. Mais comme on a d'après la construction DO:DA = DA:DP, on aura, par inversion et par composition, AO:OD = PA:AD. Le rapport qui exprime le grossissement a donc la valeur AO:OD; ce qu'il fallait démontrer. On voit de plus que le grossissement ne dépend aucunement du choix de l'endroit derrière la lentille où l'oeil est placé. ConsidéronsGa naar voetnoot4) de nouveau les lentilles AC [Fig. 4] et D, placées comme | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 447]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lentibus AC et D et puncto O, fiat duabus DO, DA, tertia proportionalis DP [Fig. 3], ponenda in eandem partem ac DO. Jam radij quilibet ad punctum P
 [Fig. 2.]
 [Fig. 3.]
tendentes ut ECP et a lente AC refracti, cogentur ad punctum D lentis hic positae centrum ex prop. [XX, Part. I, Lib. I]Ga naar voetnoot1). Ponamus istum ECP radium esse unum ex ijs qui a dextroGa naar voetnoot2) lunae latere egrediuntur, cum centrum Lunae sit in producto axe DA. Et constat quidem hunc recta linea CDF ad oculi pupillam perventurum, quia per centrum lentis D transit, cujus mediae crassitudo pro nulla habetur, et duae ejus superficies ibidem pro parallelisGa naar voetnoot3). Diximus autem omnes a puncto illo lunae procedentes inter se parallelos ad oculum deferri. Itaque sic omnes recipit oculus ut radio CDF paralleli incedant; ac propterea punctum illud in lunae latere videt eo loco quo tendit recta DC, quae cum in eandem partem axis tendat ad quam situm est punctum lunae unde radij advenere, apparet erectas exhiberi res visas. Porro angulus ADC definit semidiametrum lunae telescopio auctae. Sed angulus CPA est is quo nudo oculo iste semidiameter comprehenditur, quia radium ECP à dextroGa naar voetnoot2) lunae latere exire diximus, radium vero HAP, a centro ejus, nam sive e puncto P, sive ex G luna spectetur nudo oculo eodem angulo apparet propter maximam distantiam. Itaque amplificatio contingit secundum rationem anguli ADC ad APC, quae censetur hic eadem ac rectae PA ad DA; sed quia ex constructione est DO ad DA ut DA ad DP, erit invertendo et componendo AO ad OD ut PA ad AD. Ergo jam amplificationis ratio est quae AO ad OD; quod erat demonstrandum. Apparet autem hic nihil referre quantum ad amplificationem quo loco post lentem oculus constituatur. PonanturGa naar voetnoot4) rursus lentes AC [Fig. 4] et D ut ante, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 448]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
auparavant et supposons que AQ sur le prolongement de leur axe soit égale à AO. Prenons parmi les rayons qui nous arrivent d'un point du bord droit de la lune le rayon RQC qui, passant par le point Q (car il doit y avoir un rayon passant par ce point), rencontre la lentille AC au point C. Ce rayon deviendra ensuite parallèle à l'axe AD et après avoir été réfracté de nouveau par la lentille concave D il divergera comme s'il provenait d'un point L, et se dirigera vers l'oeil en suivant la droite LIF, de sorte que la distance LD sera égale à la distance DO, parce qu'alors L est le point de dispersion des rayons parallèles tombant sur la lentille D. Or, le rapport du grossissement se calcule dès lors facilement. Attendu que les rayons issus d'un point situé sur le bord droit de la lune arrivent parallèlement à la pupille GF après avoir traversé les deux lentilles et qu'ils deviennent donc tous parallèles au rayon LIF que nous favons faire partie de ce faisceau, le point considéré de la lune sera aperçu suivant la droite IL et l'angle ILD correspondra par conséquent au demi-diamètre de la lune. Mais l'angle sous lequel on verra ce demi-diamètre à l'oeil nu, soit du point D, soit du point Q, est RQH ou CQA. Le rapport du grossissement est donc celui de l'angle DLI à l'angle AQC, c'est-à-dire, de la droite AQ à la droite LD, à cause de l'égalité des longueurs AC et DI. Mais AQ est égale à AO et LD est égale à DO. Le grossissement est donc exprimé par le rapport AO:OD; ce qu'il fallait démontrer.  [Fig. 5.]
Le même théorème peut encore être démontré par la considération des rayons qui se coupent au centre A de la lentille ACGa naar voetnoot1). Il suffit de suivre la marche du rayon RA, qui représente dans la figure [Fig. 5] un des rayons qui proviennent du bord droit de la lune; ce rayon, d'après la Prop. XXIII, Part. I, Liv. IGa naar voetnoot2), traversera la lentille nommée sans changer de direction, attendu que nous négligeons son épaisseur. Rencontrant ensuite la lentille concave au point I, le rayon divergera, après avoir été réfracté par cette lentille, comme s'il provenait du point M qu'on trouve en construisant une troisième proportionnelle AM aux deux longueurs AO et AD, comme cela ressort de la Prop. XX, Part. I, Liv. IGa naar voetnoot3). Par conséquent, les rayons qui nous arrivent d'u point situé sur le bord droit de la lune devront de nouveau tous se mouvoir parallèlement à MIF, parce que, comme nous l'avons remarqué plus haut, ces rayons arrivent parallèlement à l'oeil après avoir été réfractés par les deux lentilles. Il s'ensuit que ce point devra être aperçu suivant la droite FIM. On en conclut que le grossissement sera exprimé par le rapport de l'angle DMI à l'angle DAI ou HAR. Or, le rapport des angles DMI à DAI est égal à l'inverse du rapport AD:DM lequel est égal au rapport AO:OD, puisque les trois longueurs AO, AD et AM forment une proportion. Le théorème est donc de nouveau démontré. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 449]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 4.]
et sit AQ in axe earum producto aequalis AO. Accipiamus jam ex radijs ijs qui a puncto lateris dextri lunae adveniunt radium RQC qui per Q punctum transiens (aliquis enim eo transibit) occurrat lenti AC in C. Is hinc parallelus fiet axi AD, et refractione altera lentis cavae D diverget ac si veniret a puncto L, et ad oculum feretur secundum rectam LIF, ut nempe distantia LD sit aequalis DO, quia tunc L est punctum dispersus parallelorum in lentem D incidentium. Proportio autem auctae magnitudinis facile jam hic colligitur. Quia enim radij a puncto in latere lunae dextro egressi perveniunt paralleli ad pupillam GF, postquam utramque lentem pervasere, omnesque propterea paralleli fiunt radio LIF, quem constat esse eorum unum; percipietur illud lunae punctum secundum rectam IL, ac proinde angulo ILD semidiameter lunae comprehendetur. At vero angulus quo semidiameter spectabitur oculo nudo sive ex D sive ex Q, est RQH, sive CQA. Ergo ratio augmenti est ea quae anguli DLI ad AQC, hoc est, quae rectae AQ ad LD, propter aequales AC, DI. Sed AQ est aequalis AO, et LD aequalis DO. Est ergo ratio augmenti ea quae AO ad OD; quod erat ostend. Potest idem rursus demonstrari ex interfectione radiorum quae in A centro lentis AC contingitGa naar voetnoot1). Sequendo nimirum radium RA unum in hac figura [Fig. 5] eorum qui ex lunae dextro latere adveniunt, qui recto cursu lentem hanc penetrabit, cum pro nulla habeatur cjus crassitudo, per prop. [XXIII, Part. I, Lib. I]Ga naar voetnoot2). Deinde occurrens lenti cavae in I ita ejus refractione diverget, ac si a puncto M exiret, quod invenitur ponendo duabus AO, AD tertiam prop. AM ut constat ex prop. [XX, Part. I, Lib. I]Ga naar voetnoot3). Itaque rursus hic radij qui a puncto in latere dextro lunae adveniunt, quoniam, post utriusque lentis refractionem, paralleli ad oculum feruntur, ut supra fuit animadversum, debebunt omnes ipsi MIF paralleli ferri, eoque punctum illud conspici secundum rectam FIM. Unde jam intelligitur rationem amplificationis fore eam, quae anguli DMI ad DAI seu HAR. Est autem ang. DMI ad DAI reciproce ut AD ad DM, hoc est ut AO ad OD, quia proportionales factae AO, AD, AM. Itaque rursus constat propositum. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 450]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De cette manière Descartes aurait pu établir la théorie du télescope mieux que par la considération de l'intersection des rayons qui a lieu à la surface de la lentille extérieure; intersection dont il croyait devoir se servirGa naar voetnoot1), ce qui n'est pourtant nullement nécessaire, comme cela se voit bien d'après les démonstrations données ici. Il faut dire aussi que l'exposition qu'on lit dans sa DioptriqueGa naar voetnoot3) est entachée de plusieurs erreurs de même que sa figure: jamais il n'aurait pu conclure de là à la valeur du grossissement. Ignorant cette valeur il a aussi conçu, au sujet de l'efficacité du télescope, une espérance beaucup plus grande que ne le permet la nature des choses. En effet, il estimait que si l'industrie des artisans parvenait à exécuter ce qu'enseigne la théorie nous serions en état d'observer sur les corps célestes des choses aussi particulières et aussi petites que celles que nous voyons autour de nous sur la terre. Il n'était pas pourtant sans savoir que le diamètre de la lentille extérieure doit surpasser la largeur de la pupille dans un rapport égal au grossissement, afin que tous les objets soient vus par le télescope aussi bien éclairés qu'à l'oeil nuGa naar voetnoot5). Or je trouve que, lors même qu'on se contenterait du quart de la clarté primitive, l'ouverture de la lentille extérieure devrait surpasser le diamètre de la terre, si l'on exige que les objets situés sur Jupiter nous apparaissent comme s'ils se trouvaient à une distance de 40 piedsGa naar voetnoot6). Il en résulte qu'il y a ici une difficulté dont on ne peut pas triompher par le travail des mainsGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition II.Faire connaître l'amplitude de l'angle visuel, c'est-à-dire de l'espace aperçu d'un seul regard, par un télescope composé d'une lentille convexe et d'une lentille concave. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 451]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Hac via causas telescopij melius investigasset Cartesius, [quam] ex intersectione radiorum quae fit in superficie lentis exterioris, quâ intersectione ille utendum putabatGa naar voetnoot1); quod tamen haudquaquam necesse esse ex ijs quae hic ostensa sunt satis liqueet. At nunc multiplici errore implicita estGa naar voetnoot2) ejus expositio quae in dioptricis legiturGa naar voetnoot3), uti et schema ipsum, neque ex ijs unquam proportionem amplificationis colligereGa naar voetnoot4) potuit. Cujus ignoratione majorem quoque multo quam rei natura patitur de telescopij efficacia spem concepit. Putabat enim si artificum industria praestare posset quod ars docet, fore ut res tam particulares et minutas in astris videremus, quam sunt eae quas vulgo in terra percipimus. Cum tamen non nesciverit eadem proportione qua res visae amplificantur, etiam diametrum lentis exterioris superare debere pupillae latitudinem, ut lucida omnia telescopio aeque ac nudo oculo spectenturGa naar voetnoot5). Nam, licet jam quarta parte hujus claritatis contenti simus, invenio tamenGa naar voetnoot6) aperturam illam lentis exteriorem Terrae diametro majorem esse debere, si res in Jove tanquam 40 pedibus distantes spectandas praebere postuletGa naar voetnoot6). Ut appareat aliud quam manuum industriam hic requiriGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio II.]Quaenam sit amplitudo anguli visorij seu spatij quod uno intuitu exhibet telescopium ex convexa et cava lente constructum. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 452]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L'amplitude de l'angle visuel dans ces télescopes dépend surtout de la grandeur de la pupille, comme on peut s'en convaincre par l'expérieuce. En effet, si l'on ferme d'abord l'oeil placé devant le télescope ce qui donne lieu à une grande dilatation de la pupille comme cela arrive généralement dans l'obscurité, et qu'on ouvre l'oeil ensuite, on embrassera du premier regard un champ circulaire plus vaste que bientôt après, attendu que ce cercle se rétrécira immédiatement, la pupille devenant plus petite par l'éclat de la lumière qu'elle reçoit. Et si l'on place devant l'oeil une lamelle percée d'un petit trou on apercevra encore moins d'objets. Toutefois si l'on rend ce trou fort petit, la grandeur du cercle éclairé ne sera pas diminuée proportionnellement à la petitesse du trou; dans ce cas c'est l'ouverture de la lentille convexe qui détermine le diamètre du cercle en question, et, par conséquent, ce diamètre ne deviendra pas inférieur à une certaine grandeur à moins que la lentille convexe elle aussi ne soit rendue plus petite. Il est facile d'expliquer la cause de ces phénomènes. En esset, supposons que EF [Fig. 6]Ga naar voetnoot1) soit la lentille convexe, B la lentille concave, et que la pupille appliquée à cette dernière ait en premier lieu le diamètre CD; tirons à partir des points opposés C et D, situés sur le bord de la pupille, les droites CAH et DAG passant par le centre de la lentille convexe A; ces droites détermineront l'angle visuel GAH dans lequel on apercevra d'un seul regard tous les objets qui se présentent à la vue, puisque les rayons venant des points G et H et passant par le centre de la lentille A arrivent aux points C et D sans avoir été réfractés; par conséquent, les objets situés à l'intérieur de l'angle GAH ne peuvent manquer d'émettre des rayons qui atteignent l'oeil. CelaGa naar voetnoot2) sera vrai même dans le cas où la pupille a une largeur un peu inférieure à DBC; en effet, tirons GAK de manière que AK soit égale à AO et joignons E et K: pourvu que EK atteigne la pupille, on verra chaque objet qui se trouve à l'intérieur de l'angle GAH. Mais les points extrêmes vers lesquels se dirigent les droites AG et AH seront vus obscurément, parce qu'une partie minimum seulement des rayons qu'ils envoient vers la lentille EF atteignera la pupille. Il en résulte que quelque petite que devienne l'ouverture de la lentille EF, l'amplitude de l'angle visuel ne diminue cependant de rien ou de fort peu seulement, pourvu que le cercle de la pupille ne se contracte pas. Mais lorsque la largeur de la pupille a diminué et qu'elle s'est réduite pour ainsi dire à un seul point, l'amplitude de l'angle visuel devient égale à celle de l'angle EPF, EF représentant l'ouverture de la lentille convexe et le point P étant trouvé comme dans la Prop. II, Part. I, Liv. IIGa naar voetnoot3), c'est-à-dire, en rendant proportionnelles les longueurs BO, BA et BP, où BO représente la distance de la lentille concave au foyer de la lentille convexe. En effet, aucun des rayons qui traversent la lentille A ne peut parvenir au point B de l'oeil à moins qu'avant de tomber sur cette lentille il ne se dirigeât vers le point P. Et l'amplitude du plus grand angle EPF formé par ces rayons est déterminée par l'ouverture de la lentille A. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 453]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
A pupillae magnitudine praecipuè pendet amplitudo anguli visorij in hisce telescopijs, idque experiri licet, nam si oculum telescopio admotum claudas primum, quo pupilla multum dilatetur ut in tenebris solet, deinde aperias, primo intuitu latiori orbe visibilia comprehendes quam paulo post, quia statim contrahetur orbis ob arctatum fulgore lucis pupillam. Quod si lamellam cum exiguo foramine oculo opponas, minori etiam copia rerum visibilium frueris. 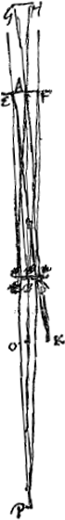 [Fig. 6.]
Veruntamen si minimum foramen efficias non pro ratione ejus exilitatis orbis lucidus arctabitur, sed tunc apertura lentis convexae amplitudinem ejus definit, quae proinde non ultra certam quantitatem decrescet nisi et lens convexa amplius coarctetur. Quorum ratio explicatu facilis est. Si enim lens convexa sit EF [Fig. 6]Ga naar voetnoot1), cava B, cui applicata pupilla primò latitudinem habeat CD, ducanturque ab oppositis punctis C, D, quae sunt in pupillae circumferentia, rectae CAH, DAG, per centrum lentis convexae A transeuntes; hae definient angulum visorium GAH, quo, quicquid rerum visibilium comprehenditur, uno obtutu conspicietur, quoniam per centrum lentis A radij a punctis G, H venientes absque inflexione penetrant ad C et D; ideoque aspectabilia intra angulum GAH comprehensa non possunt quin ad oculum radios emittant. ImoGa naar voetnoot2) etiamsi pupilla pauxillo angustior sit quam DBC, nam ductâ GAK ut AK sit aequalis AO, junctaque EK: dummodo EK in pupillam incidat, cernetur visibile comprehensum angulo GAH. obscurè vero puncta extrema quo tendunt rectae AG, AH, quia particula tantum radiorum quos in lentem EF mittunt, pupillam ingreditur. Atque hinc fit ut quantumvis in angustum apertura lentis EF contrahatur, nihil aut minimum tantum diminuatur anguli visorij amplitudo, dummodo pupillae orbis non coarctetur. Diminuta autem hac pupillae latitudine, atque ad unum velut punctum redacta, anguli visorij amplitudo fit ea quae anguli EPF, posita EF apertura lentis convexae, et puncto P invento, ut in prop. [II, Part. I, Lib. II]Ga naar voetnoot3), ut nempe BO, (ea est distantia lentis cavae a foco convexae) BA, et BP sint proportionales. Nulli enim radij, per lentem A transmissi, ad punctum oculi B pervenire possunt, nisi qui priusquam in lentem illam inciderent tendebant ad punctum P. Eorum vero maximus angulus EPF apertura lentis A praefinitur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 454]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition III.Un télescope composé de deux lentilles convexes fait voir les objets éloignés distinctement mais renversés; il les grossit dans un rapport égal à celui de la distance focale de la lentille extérieure à la distance focale de la lentille intérieure. Soit AC la lentille convexe extérieure, D la lentille intérieure, la droite AD l'axe commun des deux lentilles, O le foyer de la lentille AC. Supposons l'autre lentille convexe D placée de telle manière que le même point O soit pour elle le foyer ou point de concours des rayons parallèles à l'axe AD venant du côté où se trouve l'oeil G. Il faut démontrer que dans ces conditions les objets fort éloginés sont aperçus distinctement et renversés et qu'ils sont grossis dans un rapport égal à AO:OD. Il fautGa naar voetnoot1) construire de nouveau deux figures. Dans la première [Fig. 7] les rayons venant du dehors et parallèles à l'axe HA sont amenés par la réfraction due à la lentille AC à se réunir dans son foyer O et, après avoir continué leur route jusqu'à la lentille D, deviennent de nouveau parallèles à l'axe AD de sorte qu'ils parviennent dans cet état à l'oeil placé au point G. Il faut aussi, comme dans la proposition précédenteGa naar voetnoot2), se figurer que ce faisceau de rayons parallèles émane d'un seul point de l'objet situé à grande distance, point qui se trouve sur l'axe HAD et qui peut être, par exemple, le centre de la lune, et que des autres points, par exemple d'un point situé sur le bord droit de la lune, partent semblablement vers la lentille AC des faisceaux de rayons parallèles qui sont inclinés par rapport au premier faisceau; il s'en suit qu'après avoir été réfractés, ces rayons sont amenés à se réunir en un point situé en-dehors de l'axe près de O; ensuite, après s'être coupés en ce point et avoir atteint la lentille D, ils en sortent de nouveau parallèles, je veux dire parallèles entre eux mais non pas à l'axe AD; c'est ainsi qu'ils parviennent à l'oeil. Ces considérations font voir que la vision est distincte. L'autre figure [Fig. 8] démontrera la position renversée de l'image et la grandeur du rapport qui exprime le grossissement. On y a tracé, comme plus haut, les lentilles convexes AC et D et entre elles leur foyer commun O; supposons en outre, comme dans la deuxième démonstrationGa naar voetnoot3) ayant rapport au télescope précédent, que la distance AQ soit égale à la distance AO. Le reste de la démonstration procédera aussi à peu près de la même façon. En effet, choisissons parmi les rayons qui nous arrivent d'un point situé sur le bord droit de la lune, le rayon RQC qui passe par le point Q. Après avoir été réfracté par la lentille AC, ce rayon suivra la voie CI | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 455]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio III.] [Fig. 7.]
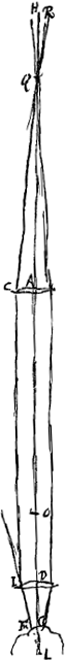 [Fig. 8.]
Telescopium e duabus convexis lentibus compositum procul posita distinctè sed eversa ostendit, amplificatque secundum rationem foci distantiae lentis exterioris ad foci distantiam interioris. Sit lens exterior convexa AC, interior D, axis communis utrique recta AD. Focus lentis AC sit O. Altera vero convexa D ita collocata intelligatur ut idem punctum O sit ipsi focus seu punctum concursus radiorum axi AD parallelorum qui venirent a parte ea ubi est oculus G. Ostendendum est his positis res longe dissitas distincte et eversas spectari et augeri secundum rationem AO ad OD. DuplexGa naar voetnoot1) autem rursus describenda est figura, in quarum altera [Fig. 7] radij extrinsecus venientes, axi HA paralleli, refractione lentis AC cogantur ad focum ejus O, atque inde ulterius tendentes ad lentem D, denuo paralleli fiant axi AD, atque ita ad oculum in G positum perveniant. Rursus etiam sicut superiori propositioneGa naar voetnoot2) cogitandum hunc parallelorum complexum ab uno rei procul dissitae puncto venire, quod sit in axe HAD, velut à centro Lunae, ab alijs vero punctis ejus similes manare radiationes parallelas in lentem AC velut è latere Lunae dextro, qui ad priores inclinentur, et hinc refracti cogantur ad punctum extra axem juxta O, ubi sese intersecantes, atque ad lentem D delati denuo paralleli evadant, inter se nempe non autem axi AD, atque ita ad oculum perveniant. Hinc itaque constat visionem distinctam fieri. Altera porro figura [Fig. 8], situm visibilis eversum, et rationem augmenti ostendet. Ubi positis ut ante, lentibus convexis AC et D, et inter ipsas foco utriusque communi O; sit porro, ut in secundaGa naar voetnoot3) demonstr.e Telescopij superioris, Distantia AQ aequalis AO. Et reliqua quoque demonstratio fere eodem modo procedet. Seligatur enim ex radijs qui e puncto in latere lunae dextro adveniunt radius RQC qui per punctum Q transit. Is | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 456]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
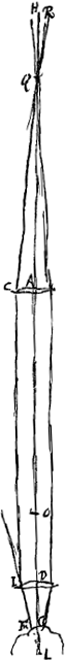 [Fig. 8.]
parallèle à AD; réfracté de nouveau par la lentille D il se dirigera suivant la droite IFL vers le point L pris de telle manière que la distance DL est égale à DO. Mais comme les rayons issus du bord droit de la lune, après avoir traversé les deux lentilles, arrivent parallèlement à l'oeil, comme nous l'avons dit plus haut, et que IFL est un de ces rayons, il s'ensuit que tous ces rayons atteignent l'oeil parallèlement à IFL. Par conséquent, ce point de la lune sera aperçu suivant la droite FI, et comme cette droite se dirige vers le côté opposé à celui d'où sont venus ces rayons il apparaît que l'image de la lune sera renversée, de sorte que le côté droit prendra la place du côté gauche et pareillement le bord supérieur celle du bord inférieur. Et comme le centre de la lune est vu suivant la droite DA, l'angle apparent sous lequel on voit le demidiamètre de la lune sera l'angle ILD. Mais lorsqu'on regarde à l'oeil nu onaperçoit le même demi-diamètre sous l'angle HQR ou AQC. Legrossissement est donc exprimé par le rapport de l'angle AQC à l'angle DLI, c'est-à-dire de DL à AQ, à cause de l'égalité de AC et de DI, ou encore par le rapport de DO à OA. La proposition est donc démontrée. Ici aussi il apparaît que la grandeur apparente est indépendante de la place de l'oeil derrière la lentille DGa naar voetnoot2). Mais pour que l'oeil embrasse un vaste champ d'un seul regard le mieux sera de le placer au point L ou près de ce point, puisqu'il apparaît que, même lorsque la largeur de la pupille est fort petite, toute la lentille D, du moins lorsque son ouverture ne surpasse pas celle de la lentille AC (et on a coutume de la construire plus petite), est vue remplie d'imagesGa naar voetnoot3). En effet, nous ferons voir par la démonstration suivante qu'il existe un point un peu plus éloigné de la lentille D que le point L, tel que si l'on y place l'oeil on verra toute la lentille D briller d'images, même au cas où l'ouverture de la pupille ainsi que celle de la lentille AC sera fort petiteGa naar voetnoot5). Disposons, par suite, les lentilles AC et D [Fig. 9] comme dans les cas précédents, de sorte que le point O soit leur foyer commun. Construisons une troisième proportionnelle AG aux deux longueurs AO et AD. Le point G sera donc situé à une plus grande distance de la lentille D que le point L, attendu que DL et DO sont égales. C'est au point G qu'il faudra placer l'oeil pour obtenir le résultat dont nous avons parlé. Car si nous suivons de nouveau, comme dans la troisième démonstrationGa naar voetnoot6) ayant rapport au télescope composé d'une lentille convexe et d'une lentille concave, le rayon RA, l'un de ceux qui nous arrivent d'un point situé sur le bord droit de l'objet, et qui passe par le centre de la lentille ACGa naar voetnoot7), | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 457]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
refractione lentis AC ibit per CI parallelam AD, et rursus a lente D refractus tendet secundum rectam IFL ad punctum L, ita sumtum ut distantia DL sit aequalis DO. Quia autem radij a latere lunae dextro, postquam per utramque lentem transierunt, paralleli perveniunt ad oculum, ut antea diximus, eorum vero unus est IFL, sequitur eos omnes ipsi IFL parallelos in oculum incidere, eoque illud lunae punctum percipietur secundum rectam FI; quae cum ad partem oppositam vergat ejus unde hi radij advenere apparet situm lunae inverti, ut dextra sinistris, eoque et supera inferis mutentur. Porro cum centrum Lunae secundum rectam DA conspiciatur, erit apparens angulus semidiametri lunae ILD. Nudo autem oculo idem semidiameter angulo HQR seu AQC comprehenditur. Ergo ratio amplificationis est quae anguli AQC ad DLI, hoc est quae AQ ad DLGa naar voetnoot1), propter aequales AC, DI, hoc est, ea quae AO ad OD; quare constat propositum.  [Fig. 9.]
Hic vero nihil quoque referre apparet quantum ad apparentem magnitudinem quo loco post lentem D oculus colloceturGa naar voetnoot2). Sed ut multa uno intuitu oculus comprehendat ad punctum L vel prope ipsum optimè constituetur, quoniam apparet, etiamsi minima sit pupillae latitudo, totam tamen lentem D quatenus aperturam lentis AC non excedit (solet autem intra hanc mensuram consistere), imaginibus plenam spectariGa naar voetnoot3). Ostendemus autem sequenti demonstratione dari punctum paulo ultra L à lente D distans, ubi si collocetur oculus totam lentem D pictura lucentemGa naar voetnoot4) aspiciet, etiamsi minimae fuerint tum pupillae tum lentis AC aperturaGa naar voetnoot5). Dispositis enim sicut ante lentibus AC, D [Fig. 9], ut focus earum communis sit punctum O. Statuatur duabus AO, AD tertia proportionalis AG, unde punctum G ultra L distabit a lente D, cum DL, DO sint aequales. Erit autem ad G ponendus oculus, ut fiat quod dictum est. Si enim, ut in tertiaGa naar voetnoot6) demonstratione telescopij ex convexa et cava compositi, sequamur rursus radium RA unum eorum qui ex puncto in dextro rei visae latere adveniunt quique incidit in centrum lentis ACGa naar voetnoot7), | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 458]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 9.]
ce rayon traversera la lentille en ligne droite d'après la prop. XXIII, Part. I, Liv. IGa naar voetnoot1), attendu que nous négligeons l'épaisseur de la lentille. Rencontrant ensuite la lentille D au point I et réfracté par cette lentille, le rayon considéré sera dirigé vers le point G, centre de la pupille, attendu que les longueurs AO, AD et AG forment une proportionGa naar voetnoot2). Par conséquent, tout ce qu'on aperçoit à l'oeil nu sous l'angle DAI ou HAR sera aperçu dans la lentille D; de sorte que l'amplitude du champ (comme on dit) dépend de la largeur de la lentille D quand même les ouvertures de la lentille A et de la pupille sont pour ainsi dire des points et pareillement dans le cas où les deux ouvertures sont plus grandes. Il faut savoir pourtant qu'il n'est pas bon d'employer une lentille D trop large à cause de l'inconvénient des couleurs dues à une trop grande réfraction, inconvénient dont nous parlerons plus loinGa naar voetnoot3). Il ne faut pas non plus diminuer trop l'ouverture de la lentille AC, afin que l'image ne devienne pas obscure; nous ferons connaître ailleursGa naar voetnoot4) la dimension qu'il est bon de lui donner. Mais si la pupille est contractée considérablement, comme si elle était placée devant une lamelle percée d'un trou tel qu'on peut le faire avec une épingle, la clarté de l'image s'en trouve à peine diminuée, puisque les faisceaux de rayons ou cônes lumineux partant de chaque point de l'objet sont extrêmement minces en tombant sur la lentille D et qu'ils restent tels en se dirigeant parallèlement vers l'oeilGa naar voetnoot5). Et on conclut ici aisémentde nouveau que le grossissement est égal au rapport de l'angle DGI à l'angle HAR ou DAI, c'est-à-dire, de AD à DG ou de AO à OD, attendu qu'on a DA:AO = GA:AD. Cette même proposition peut être prouvée d'une autre façon encore, analogue à celle de la première démonstrationGa naar voetnoot6) ayant rapport au télescope composé d'une lentille concave et d'une lentille convexe: c'est-à-dire, en suivant la marche du rayon qui, issu d'un point de l'objet situé en dehors de l'axe du télescope, est conduit par la réfraction due à la lentille AC au centre de la lentille oculaire D. Cela est évident si l'on considère la figure ci-jointe [Fig. 10]; sa construction et la démonstration qui s'y rapporte sont les mêmes ici et au lieu indiquéGa naar voetnoot7). Les considérations précédentes font voir aussi combien les télescopes composés de deux lentilles convexes surpassent ceux dont la lentille oculaire est concave, puisqu'ils embrassent d'un seul regard un champ beaucoup plus étendu. En effet, cette étroitesse du champ est désagréable et absolument incommode surtout lorsque les tubes ont une longueur supérieure à trois ou quatre pieds. C'est pourquoi, bien que ce télescope excellent, et célèbre à cause de tant de découvertes nouvelles, que possédait Galilée fut composé d'un verre convexe et d'un verre con- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 459]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
is recta linea hanc penetrabit secundum prop. [XXIII, Part. I, Lib. I]Ga naar voetnoot1) cum pro nulla habeatur ejus crassitudo. Deinde lenti D occurrens in I, cogetur hujus refractione ad punctum G, quod est pupillae medium, propterea quod proportionales sunt AO, AD, AGGa naar voetnoot2). Itaque quicquid angulo DAI sive HAR oculo nudo comprehenditur spectabitur in lente D; adeo ut campi (ut vocant) amplitudo jam pendeat a latitudine lentis D, licet aperturae lentis A et pupillae sint veluti puncta. atque ita quoque omnino si utraque magis pateat. Sciendum vero neque lentem D nimis amplam esse adhibendam, propter incommodum colorum ex nimia refractione, de quo in sequentibus diceturGa naar voetnoot3); nec [nimis] arctandam aperturam lentis AC, ne obscuritas inducatur. certa autem mensura ejus alibi docebiturGa naar voetnoot4). Pupilla vero licet apposita lamellae cum foramine, quantum acus
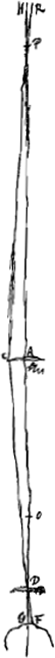 [Fig. 10.]
facere potest, in angustum contrahatur, nihil fere lucis aufert, quoniam coni radiosi a singulis rei visae punctis manantes insigni tenuitate sunt cum incidunt in lentem D, quam retinentes inde paralleli ad oculum perguntGa naar voetnoot5). Porro facile rursus hic intelligitur proportionem ampliationis esse eam quae anguli DGI ad HAR sive DAI, hoc est eam quae AD ad DG, sive quae AO ad OD, quia DA ad AO ut GA ad AD. Atque haec proportio aliter rursus, ut in demonstratione primaGa naar voetnoot6) ex cavo et convexo comprobari potest, sequendo radium illum qui a puncto rei visae extra axem telescopij posito manans deducitur lentis AC refractione ad centrum lentis ocularis D. Hoc enim patet ex inspecta figura [Fig. 10] hic adscripta, in qua eadem est constructio ac demonstratio quae fuit illicGa naar voetnoot7). Hinc porro apparet quanto praestent Telescopia ex convexis duobus composita ijs quorum lens ocularis cava est, cum tanto amplius spatium uno intuitu comprehendant. Est enim angustia illa spectaculi injucunda et prorsus incommoda praesertim si ultra tres quatuorve pedes tubi extendantur. Quare etsi Galilei egregium illud perspicillum ac tot novis | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 460]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
cave, aujourd'hui on n'emploie aucun télescope de ce genre ni pour observer les corps célestes ni pour regarder les objets terrestres: on se sert, en effet, uniquement de lunettes composées de verres convexes. Seules les lunettes fort courtes composées d'un verre convexe et d'un verre concave sont restées en usage; c'est-à-dire celles qui ont une longueur de 4 ou 5 pouces; pour des lunettes si courtes l'amplitude de l'angle visuel qu'on trouve est tolérable. Dans de telles lunettes le grossissement peut être exprimé environ par le nombre 4. Mais on se sert même avec avantage d'un grossissement qui n'est que double: dans ce cas on aperçoit tous les objets bien éclairés même à l'intérieur d'une maison. Et l'on voit les étoiles mieux qu'à l'oeil nu, et beaucoup d'étoiles simultanément, attendu que dans un télescope de ce genre l'ouverture de la lentille extérieure peut atteindre un pouce et demi. L'on peut, il est vrai, choisir deux lentilles convexes et les combiner de telle manière qu'elles représentent debout les objets éloignés; mais on n'obtiendra pas de cette manière un bon télescope, puisque les rayons issus d'un même point de l'objet ne peuvent pas parvenir parallèlement à l'oeil, que les objets ne peuvent être agrandis considérablement, et qu'on ne peut pas non plus voir simultanément un grand nombre d'objets. Il y a en outre cet inconvénient que le tube doit inutilement être rendu fort longGa naar voetnoot1). Mais à l'aide de trois lentilles convexes on peut voir les objets debout et distinctementGa naar voetnoot2). Le champ toutefois est plus petit que lorsqu'on se sert de quatre lentillesGa naar voetnoot3), à moins que, lorsqu'on en prend trois, la lentille la plus proche de l'oeil n'ait à peu près un diamètre d'ouverture double de celui qu'il faut dans des oculaires de ce genreGa naar voetnoot4); et ce diamètre ne peut être rendu si grand sans que les couleurs de l'arc-en-ciel apparaissent aux bords. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition IVGa naar voetnoot5).Faire voir comment on peut, en prenant trois lentilles convexes au lieu de deux, agrandir le champ du télescope dont nous nous servons pour observer les corps célestes. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 461]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
repertis celebre ex convexo et cavo fuerit conjunctum, nunc tamen ejus generis nulla nec ad syderum observationes nec ad res in Terra spectandas adhibentur, sed tantum è convexis composita. Unicus vero usus cavoconvexorum in minima longitudine relictus est, 4 nempe aut 5 digitorum, in qua brevitate tolerabilis jam latitudo anguli istius visorij reperitur. In hujusmodi perspicillis ratio incrementi facienda est quadrupla circiter. Sed et dupla non majorem utiliter adhibere solemus. quo fit ut lucida etiam intra aedes omnia spectentur. Et stellae melius quam oculo nudo, multaeque simul, quoniam in tali perspicillo apertura exterioris lentis vel ad sesquipollicem patere potest. Ac possunt quidem binae convexae lentes parari tales, atque ita inter se componi, ut erecta referant visibilia longinqua; nec tamen quicquam boni inde obtinebitur, quod nec paralleli ad oculum tunc radij pervenire possunt qui e singulis rei visae punctis emanant, neque eae multum amplificari, nec magna copia simul conspici, praeterquam quod tubi longitudo sine utilitate multum producenda essetGa naar voetnoot1). Tribus vero lentibus convexis et recto positu et distincta possunt videriGa naar voetnoot2), sed non tam lato campo quam quaternisGa naar voetnoot3), nisi lens oculo propior duplam fere aperturae diametrum habeat ejus quae in similibus ocularibus requiriturGa naar voetnoot4), cum tria adhibentur, quod fieri nequit quin colores iridis circa margines existant. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Propos [itio IV]Ga naar voetnoot5).Quomodo pro duobus convexis tria adhibendo amplior fiat telescopij prospectus, quo ad sidera spectanda utimur. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 462]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 11.]
 [Fig. 12.]
Quoique les lentilles ne doivent pas être multipliées sans nécessité parce que beaucoup de lumière est perdue à cause de l'épaisseur du verre et par les réflexions répétées, cette multiplication peut cependant avoir l'avantage d'agrandir le champ du télescope et faire ainsi qu'on s'en sert avec plus de plaisir. Car si nous ajoutons à la grande lentille deux oculaires ayant entre eux un certain rapport et une certaine distance, l'aberration des rayons qui se dirigent vers l'oeil à partir des différents points de l'objet devient beaucoup moindre que lorsqu'on prend une lentille oculaire unique donnant le même grossissementGa naar voetnoot1), et l'on peut ainsi embrasser d'un seul regard un bien plus grand nombre d'objets. De plus, les bulles et impuretés de toute espèce que renferment les lentilles oculaires disparaissent entièrement, tandis que, lorsqu'on ne se sert que d'une seule lentille, elles ne sont paspeu gênantes. Supposons que le grossissement qu'on se propose d'obtenir soit représenté par le rapport P:Q. Soit L [Fig. 11 et 12] la lentille extérieure, G son foyer. Prenons un point K tel que P:Q = LG:GK; ce point tombant entre L et G. Plaçons en K une lentille convexe dont la distance focale KV soit le triple de KG; divisons KV en deux parties égales par le point S et plaçons-y l'autre lentille EF, dont ½ SK représente la distance focale SH. Supposons l'oeil placé en M, la distance SM étant prise égale à ½ KG. On aura obtenu alors ce qu'on cherchaitGa naar voetnoot2). Nous nous servons de deux figures pour la démonstration. Dans la première [Fig. 12] nous avons tracé les rayons venant d'un point unique de l'objet; lequel point nous voulons qu'on considère comme | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 463]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Quanquam lentes non frustra sint multiplicandae, quod et vitri crassitudine et iteratis reflexionibus non parum lucis depereat; hanc tamen utilitatem praebere potest, ut latior evadat eoque jucundior telescopij prospectus. Adsumtis enim praeter magnam lentem ocularibus duobus certam inter se rationem distantiamque habentibus, tunc multo minor fit aberratio radiorum à diversis punctis rei visae ad oculum tendentium, quam si unica lens ocularis adhibeatur, quae eandem amplificationem efficiatGa naar voetnoot1), atque ita multo plura longe unico intuitu comprehendere licet, ac praeterea naevi ac impuritas omnis lentium ocularium plane evanescit, cum alioqui in una lente non parum adferat incommodi. Sit ratio augmenti proposita ea quae P ad Q. Lens exterior L [Fig. 11 et 12]. focus ejus G. Et ut P ad Q ita sit LG ad GK, cadente puncto K inter L et G. Et in K lens convexa statuatur cujus foci distantia KV sit tripla ad KG, et divisa KV aequaliter in S, statuatur ibi lens altera EF cujus foci distantia SH sit ½ SK. Oculus vero sit in M, posita SM distantia ∞ ½ KG. Erit factum quod quaeriturGa naar voetnoot2). Demonstrationem vero duplici figura explicamus. In quarum priori [Fig. 12] expendimus radios ab uno aliquo rei visae puncto manantes, quod punctum in axe telescopij positum intelligi volumus. Qui itaque radij velut axi paralleli in | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 464]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
situé sur l'axe du télescope. Ces rayons sont donc censés tomber sur la lentille L parallèlement à l'axe. Ils doivent donc ensuite se diriger vers le foyer G de cette lentille. Mais nous démontrerons que par la réfraction due à la lentille K ils seront dirigés vers le point H, et qu'ensuite, se coupant et tombant sur la lentille S, ils deviendront parallèles pour continuer ainsi leur route jusqu'à M, la pupille de l'oeil. En effet, si l'on prend KT = KV (distance focale de la lentille K), on aura, vu que nous avons posé KG = ⅓ KV et KH = ¼ KVGa naar voetnoot1), GH:GK = 1:4Ga naar voetnoot2). Mais on a aussi GK:GT = 1:4Ga naar voetnoot3). Les longueurs GH, GK et GT forment donc une proportion; par consequent, les rayons qui tendent vers le point G seront amenés par la réfraction due à la lentille K à se diriger vers HGa naar voetnoot4), foyer de la lentille S, laquelle rendra donc les rayons parallèles. Arrivant ensuite à l'oeil M ces rayons y produiront donc une vision distincte, ce qui est l'une des choses qu'il s'agissait de démontrer. Nous ferons voir maintenant dans la seconde figure [Fig. 11] le grossissement, qui possède la valeur donnée, et l'amplitude de l'angle visuel. En effet, prenons sur le prolongement de l'axe la longueur LN égale à la distance focale LG. Traçons des rayons venant de points fort éloignés, passant ensuite par le point N, et tombant de part et d'autre sur la lentille extérieure L. Soient NO et NP ces rayons. Il est évident que par la réfraction due à cette lentille ils deviennent parallèles à l'axe et qu'ils suivent alors les droites OC et PD jusqu' à ce qu'ils tombent sur la lentille K. Nous savons qu'ils tendront ensuite vers le point V suivant les droites CV et DV. Mais lorsqu'ils auront été interceptés par la lentille S, je dis qu'ils seront dirigés vers le point M, où nous avions placé la pupille de l'oeil. En effet, comme SV = ½ KV et SM = ½ KG, c'est-à-dire = ⅙ KV, on aura SM:SV = 1:3 et, par conséquent, VM:VS = 2:3. Mais on a aussi VS:VHGa naar voetnoot5) = 2:3. Par conséquent, VM, VS et VH forment une proportion, et comme H est le foyer de la lentille S, il résulte de la Prop. XX, Part. I, Liv. I.Ga naar voetnoot6) que les rayons qui tendent vers le point V sont réfractés par la lentille | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 465]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 11.]
 [Fig. 12.]
lentem L incidere censentur. Unde porro tendere debent ad hujus lentis focum G. Sed refractione, quae fit in lente K, ostendemus eos mitti ad punctum H; atque inde sese intersecantes atque in lentem S incidentes, reddi parallelos, itaque ad oculi pupillam M pergere. Positâ enim KT aequali KV, quae erat foci distantia lentis K, quia KG dicta est esse ⅓ KV; KH vero ¼ KVGa naar voetnoot1). Erit GH ad GK ut 1 ad 4Ga naar voetnoot2); sed et GK ad GT erit ut 1 ad 4Ga naar voetnoot3). Ergo proportionales GH, GK, GT, ac proinde radij ad G tendentes flectentur refractione lentis K ad HGa naar voetnoot4), cum sit H focus lentis S, faciet haec ut a puncto H pergentes paralleli fiant, qui proinde oculo ad M occurrentes distinctam visionem efficient, quod unum est eorum quae demonstrare oportebat. Jam in altera figura [Fig. 11] ratio amplificationis eadem datae ostendetur et amplitudo anguli visorii. Ponatur enim LN in producto axe aequalis foci distantiae LG. Et a punctis longinquis venientes radij expendantur per punctum N transeuntes atque in lentem L extremam utrimque incidentes, qui sint NO, NP. quos constat refractione ejus effici axi parallelos, atque ita incedant per OC, PD, donec incidant in lentem K. Unde porro scimus pervecturos rectis CV, DV ad punctum V. Sed a lente S interceptos ajo detorqueri ad punctum M, ubi oculi pupilla posita fuit. Quia enim SV est ½ KV; et SM ∞ ½ KG, hoc est ∞ ⅙ KV; erit SM ad SV ut 1 ad 3, ac proinde VM ad VS ut 2 ad 3. Sed et VS ad VHGa naar voetnoot5) est ut 2 ad 3. Ergo proportionales VM, VS, VH et quia H est focus lentis S, constat ex propos. [XX, Part. I, Lib. I]Ga naar voetnoot6) radios ad V tendentes ita frangi a lente S ut tendant ad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 466]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 11.]
S de telle manière qu'ils se dirigent ensuite vers le point M. Tirons donc, à partir des points E et F, dans lesquels les droites CV et DV coupent la lentille S, les droites EM et FM. AinsiGa naar voetnoot1) l'objet sera vu à travers les lentilles sous l'angle EMF qui est à l'angle ONP comme LG est à KG, c'est-à-dire, comme P est à Q. En effet, comme le rapport EMF:ONP ou EMS:ONL est composé des rapports EMS:EVS et EVS:ONL, tandis que le rapport EMS:EVS est égal au rapport VS:MS ou VS:½KG, et le rapport EVS:ONL au rapport NL (ou LG):KV (ou 2VS), le rapport EMF:ONP sera composé des rapports 2VS:KG et LG::2VS, c'est-à-dire, EMF sera à ONP comme LG est à KG ou comme P est à Q. Ce qu'il fallait démontrer. OnGa naar voetnoot2) peut se demander quel est l'avantage de cet arrangement et si l'effet n'est pas le même que lorsqu'on se borne à un seul oculaire α [Fig. 13], dont la distance focale Gα est égale à KG [Fig. 11], c'est-à-dire à ⅓aGa naar voetnoot3), attendu qu'alors l'angle αMβ sera égal à l'angle KGD ou SMF, parce que KD = 2SFGa naar voetnoot4) et KG = 2SMGa naar voetnoot5). Réponse: Le grossissement sera en effet le même dans les deux cas. Mais la lentille S pourra avoir une ouverture supérieure à la moitié de celle de la lentille α, d'abord parce que la distance focale de la lentille S est ¼a, c'est-à-dire plus que la moitié de la distance focale de la lentille αGa naar voetnoot6) qui est ⅓a, en second lieu parce que le rayon DF qui converge sera moins coloré en traversant la lentille S que s'il était parallèle à l'axe. Il est vrai qu'il a déjà été coloré au point D, mais faiblement, parce que KV est la distance focale de la lentille KGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 467]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
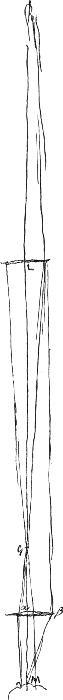 [Fig. 13.]
punctum M. A punctis igitur E et F, in quibus rectae CV, DV secant lentem S, ducantur rectae EM, FM. SicGa naar voetnoot1) visibile per lentes cernetur sub ang. EMF qui ad ONP habet proportionem, ut LG ad KG, id est, ut P ad Q. Quia enim ratio EMF ad ONP, id est, EMS ad ONL componitur ex rationibus EMS ad EVS, et EVS ad ONL; ratio vero EMS ad EVS eadem est, quae VS ad MS sive ½KG, item ratio EVS ad ONL eadem quae NL sive LG ad KV sive 2 VS. Erit ratio EMF ad ONP composita ex 2 VS ad KG, et LG ad 2 VS, id est, erit EMF ad ONP ita LG ad KG, ita P ad Q: quod erat dem. VidendumGa naar voetnoot2) an quid juvet. Et an non idem effectus sit, ac si ponatur sola ocularis α [Fig. 13], cujus foci distantia Gα ∞ KG [Fig. 11] hoc est ∞ ⅓ aGa naar voetnoot3); quum angulus αMβ sit futurus aequalis KGD, hoc est, SMF; nam KD ∞ 2 SFGa naar voetnoot4), et KG ∞ 2 SMGa naar voetnoot5). Resp [onsio]. Erit quidem amplificatio eadem utrobique, sed lens S majorem feret aperturam quam dimidiam lentis αGa naar voetnoot6), tum quia lentis S foci distantia est ¼a, eoque major quam ½ foci distantiae lentis α, quae est ⅓a; tum quia radius DF convergens, minus colorabitur in transitu per lentem S, quam si axi parallelus incederet. Sed in D jam aliquem colorem traxit, sed parum, quia lentis K foci distantia est KVGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 468]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VGa naar voetnoot1).Expliquer la construction d'un télescope composé de quatre verres convexes, à l'aide duquel on voit les objets debout et dont le champ est vaste. À cause de la position inverse qu'il donne aux objets, nous ne nous servons guère du télescope composé de deux verres convexes que pour contempler les étoiles, qui peuvent indifféremment être regardées dans l'une ou l'autre position. Nous dirons plus tard quels rapports il faut alors observerGa naar voetnoot2). Or, on a essayé de différentes manières, à l'aide de 3, 4, 5 ou plus de lentilles, de redresser de nouveau les images et de permettre en même temps au spectateur d'embrasser un vaste champ d'un seul regard. Sans doute, il ne faut pas multiplier les lentilles sans cause, parce que la matière dont chacune d'elles est formée ainsi que les réflexions dues aux surfaces dispersent une partie des rayons. Cependant on ne peut atteindre l'effet désiré avec un nombre de lentilles inférieur à 4. Car, quoique pour des télescopes de même longueur on puisse obtenir avec trois lentillesGa naar voetnoot3), aussi bien qu'avec quatre, la position droite de l'image, le même grossissement et un champ aussi vaste, la combinaison de trois lentilles est cependant inférieure à celle de quatre lentilles parce que dans la première les lentilles oculaires ou du moins l'une d'elles (celle qui est la plus proche de l'oeil) doivent être composées de portions plus grandes de surfaces sphériques, par rapport au diamètre ou plutôt à la distance focale, si l'angle visuel de l'instrument doit être le même dans les deux casGa naar voetnoot4): il s'ensuit que les objets semblent colorés et que les lignes droites auprès des bords de l'ouverture paraissent courbéesGa naar voetnoot5). Il faut donc se servir de quatre lentilles, avec lesquelles le télescope est composé de la façon suivante. A [Fig. 14 et 15] est la lentille extérieure, AB sa distance focale; sur le même | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 469]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio V.]Ga naar voetnoot1)Telescopij ex quatuor convexis compositi constructionem explicare, quo res visae erectae spectantur et magna copia. 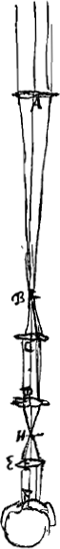 [Fig. 14.]
 [Fig. 15.]
Propter inversam positionem rei visae vix aliter utimur composito è duobus convexis quam ad sidera, quae non refert quo positu spectentur. Quaenam verò tunc proportio servanda sit postea diceturGa naar voetnoot2). Quomodo autem erigantur rursus imagines magnaque simul earum copia uno intuitu comprehendatur diversimode quaesitum fuit 3, 4, 5, et pluribus lentibus. Quae sine causa non sunt multiplicandae, quod et singularum materia et superficierum reflexiones radiorum partem intervertant. Paucioribus tamen quam quaternis optatum effectum consequi non licet. Etsi enim in eadem telescopij longitudine et situs erectus et eadem amplificatio et eadem copia simul visorum obtineri potest tribusGa naar voetnoot3) aequè ac quatuor lentibus, deterior tamen est trium compositio quam quaternarum, quia in illa lentes oculares, aut unam certe earum oculo proximam, e majoribus superficiei sphaericae portionibus constare necesse est ratione diametri aut foci distantiae, si eadem anguli visorij magnitudo praestanda sitGa naar voetnoot4). Hinc vero colore inficiuntur res visae et lineae rectae circa aperturae margines curvae apparentGa naar voetnoot5). Quaternis igitur utendum est, ex quibus telescopium hoc modo componitur. Lens exterior est A [Fig. 14 et 15], cujus foci distantia | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 470]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
axe sont placées trois lentilles oculaires C, D et E, tout-à-fait identiques entre elles, et dont celle qui est située le plus à l'intérieur est placée au-delà du foyer B à une distance égale à sa propre distance focale. La distance qui sépare les lentilles C et D l'une de l'autre est double de la distance BC; la distance de la lentille D à la lentille E est égale à l'intervalle CD; enfin la distance qui sépare la lentille E de l'oeil F est de nouveau égale à l'intervalle BCGa naar voetnoot1). Il faut de nouveau deux sigures dans ce cas. Dans la première [Fig. 14] nous traçons les rayons émanant d'un seul point de l'objet fort éloigné; or, il apparaît aisément à celui qui a compris les raisonnements précédents que ces rayons tombent d'abord à fort peu près parallèlement sur la lentille A, qu'ensuite ils se réunissent au point B, son foyer, et que, puis après, divergeant à partir de ce point, ils tombent sur la lentille C qui les rend de nouveau parallèles et les dirige vers la lentille D laquelle les réunit en son foyer H qui divise en deux parties égales l'intervalle DE. Tendant ensuite, à partir du point H, vers la lentille E ils deviennent parallèles pour la troisième fois après avoir traversé cette lentille, et, tombant dans cet état sur l'oeil F, ils causent une vision distincte, attendu qu'au fond de l'oeil ils se rassemblent en un seul point. Dans la seconde figure [Fig. 15] on considère le grossissement; il est égal au rapport de AB, distance focale de la lentille extérieure, à la distance focale BC d'une des lentilles oculaires. On y fait voir aussi la grandeur de l'angle visuel. En effet, en supposant aux trois oculaires des ouvertures égales et qui ne surpassent pas celle de la lentille extérieure A, traçons les droites MQ et NR parallèles à l'axe commun et comprenant entre elles les diamètres de l'ouvertures des lentilles E et D; traçons de même KO et LP parallèles au même axe et comprenant entre elles l'ouverture de la lentille KL. Posant ensuite AG = AB, tirons les droites OGV et PGT qui se coupent en G. Il est évident alors que la largeur d'un objet situé à grande distance qui à l'oeil nu serait vu du point G, donc aussi du point F, sous l'angle TGV, occupe l'angle MFN lorsqu'on regarde cet objet par le télescope. Par conséquent, le grossissement est égal au rapport de l'angle MFN à l'angle TGV ou PGO, c'est-à-dire au rapport de l'intervalle AG à l'intervalle EF, attendu que PO et MN sont égales; ou bien encore au rapport de la distance focale AB à la distance focale BC. Ce qu'il fallait démontrer. Il apparaît en outre que l'angle visuel MFN comprend aussi une même latitude d'objets qu'un télescope composé des deux lentilles A et C, puisque l'objet compris dans l'angle TGV serait aperçu dans ce télescope sous l'angle KSL égal à l'angle MFN. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 471]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
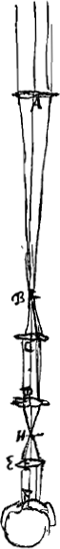 [Fig. 14.]
 [Fig. 15.]
AB, in eodem vero axe positae sunt lentes oculares tres C, D, E prorsus aequales inter se, quarumque interior intervallo BC quantum est sua foci distantia ultra focum B removetur, ejusque intervalli duplum est a lente C ad lentem D, ac tantundem ab hac ad lentem E, ac denique ab hac ad oculum F rursus, quantum inter B et CGa naar voetnoot1). Rursus autem binis figuris hic opus est, in quarum priore [Fig. 13] radij ab uno puncto rei longe distantis manantes exhibentur, quos facile apparet, si quis praecedentia perceperit, primum tanquam parallelos incidere in lentem A, inde colligi in B foco ejus, ac inde divergentes in lentem C incidere, quae denuò parallelos efficiat, mittatque ad lentem D, quae congreget eos ad focum suum H qui medium dividit intervallum DE. Tum denique ex H puncto ad lentem E tendentes ab ea tertiò parallelos reddi atque ita ad oculum F accidentes distinctam visionem efficere cum in fundo ejus ad punctum unum cogantur. In secunda figura [Fig. 15] consideratur ratio amplificationis quae est ea quae AB, foci distantiae lentis exterioris, ad foci distantiam BC, unius ex ocularibus. Ac praeterea anguli visorij amplitudo hic demonstratur. Positis enim ocularium trium aperturis aequalibus quae non majores sint apertura lentis exterioris A, ducantur MQ, NR axi communi parallelae et aperturae diametros lentium E et D comprehendentes. itemque KO, LP eidem axi parallelae et comprehendentes aperturam lentis KL, et posita AG aequali AB, ducantur rectae OGV, PGT quae sese intersecent in G. Jam patet latitudinem rei visae longinquae quae oculo nudo ex puncto G, ideoque et ex F, cerneretur in angulo TGV, hanc oculo per telescopium intuenti, occupare angulum MFN, ideoque augmenti rationem esse eam quae anguli MFN ad ang. TGV sive PGO, hoc est, eam quae intervalli AG ad intervallum EF, cum PO, MN, sint aequales; hoc est, eam quae foci distantia AB ad foci distantiam BC. quod erat dem. Apparet porro angulum visorium MFN eandem quoque visibilium latitudinem comprehendere ac telescopium quod binis lentibus A et C constaret, cum res visa quae angulo TGV intercipitur, in illo telescopio spectetur in angulo KSL ipsi MFN aequali. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 472]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
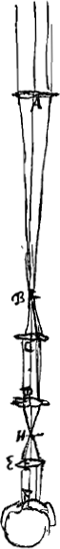 [Fig. 14.]
 [Fig. 15.]
Cette excellente combinaison de lentilles a été inventée la première fois à Rome; je ne sais par quiGa naar voetnoot1). Il faut ajouter cependant qu'elle doit une grande partie de sa supériorité à l'anneau ou diaphragme qu'on introduit dans le tube au point H, situé au milieu entre les lentilles E et D, ou au point B, foyer commun des lentilles A et C; nous avons expliqué dans le livre sur les causes des phénomènes que présente SaturneGa naar voetnoot2) l'usage de ce diaphragme, qui était auparavant inconnu. Cet usage est de la plus grande utilité, tant pour la mesure des diamètres des planètes comme je l'ai dit à l'endroit désigné, que pour autre chose dont je parlerai plus loinGa naar voetnoot3). Mais dans les télescopes considérés l'effet de cet anneau est de donner au champ une limite circulaire nette: en effet, les objets placés auprès de H ou de B y sont aperçus distinctement par l'oeil F, vu que les rayons provenant de H ou de B y entrent parallèlement. Et en même temps les couleurs aux bords disparaissent par l'effet du diaphragme, couleurs qu'il était impossible d'éviter entièrement avant cette invention. Quant à l'ouverture du diaphragme, elle doit être un peu plus petite que celles des lentilles oculaires ellesmêmes, et son diamètre doit avoir à la distance focale des lentilles oculaires un certain rapport qui est environ de .... à ...., comme l'expérience nous l'enseigneGa naar voetnoot4). Nous déterminerons plus loin la valeur que doit avoir le rapport de la distance focale de la lentille extérieure à celle des lentilles oculaires et à l'ouverture par laquelle elle peut laisser entrer la lumièreGa naar voetnoot5). Il semble étrange que dans ce télescope les couleurs de l'arc-en-ciel, résultant de la réfraction due à plusieurs lentilles oculaires, n'apparaissent pas plus que lorsqu'on se sert d'une seule lentille oculaire. Mais la raison en est que la lentille QR corrige l'effet de la lentille KL en détruisant les couleurs produites par elle. En effet, ce qui est arrivé au rayon OKRN [Fig. 15] qui passe par des surfaces inclinées à K et ensuite à R, est comparable à ce qui lui serait arrivé s'il avait traversé deux coins SS et TTGa naar voetnoot6) placés en sens opposés avec des faces parallèles. Dans ce dernier cas le rayon n'est pas coloré, aussi peu que s'il passait par une plaque de verre. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 473]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Haec egregia lentium compositio Romae nescio à quoGa naar voetnoot1) primum fuit inventa, multum tamen adjuta annulo seu diaphragmate quod ad H, loco medio inter lentes ED, vel ad B focum communem lentium A et C inseritur, cujus usum non ante cognitum explicuimus in libro de causis phaenomenon SaturniGa naar voetnoot2). Est vero longe praecipuus, cum in metiendis planetarum diametris ut ibi docui, tum ad alia de quibus agam in sequentibusGa naar voetnoot3). In hisce vero telescopijs circulum apparentium imaginum praeciso ambitu iste annulus ideo circumscribit, quod quae circa H vel B collocantur distincte cernuntur oculo F, cum radij ab H vel B egressi paralleli ad eum deferantur. Simul vero colores circa margines ejus opera resecantur, qui non bene antea vitari poterant. Ponenda autem apertura annuli ipsarum lentium ocularium aperturis paulo minor, diameterque ejus ad ocularium foci distantiam certa ratione referendus, quae circiter ea est, quae.... ad......Ga naar voetnoot4) docente nimirum experientia. Quaenam vero sit ponenda proportio foci distantiae lentis exterioris ad foci distantiam ocularium quantâque aperturâ lucem admittere possit lens illa in sequentibus definieturGa naar voetnoot5). Mirum videtur in hoc telescopio colores iridis oriri plurium ocularium refractione, non magis quam cum una ocularis adhibetur. Sed ratio haec est quod lens QR corrigit et aufert colores quas lens KL produxit. Idem enim accidit radio OKRN [Fig. 15] per superficies inclinatas ad K ac deinde ad R, transeunti, ac si per cuneos binos contrariè positos SS, TTGa naar voetnoot6) transiret parallelis lateribus, qui colore non inficitur, non magis quam si per l[aminam vitream incederet]Ga naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 474]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemme.Les angles qui ne surpassent pas 30o peuvent être considérés comme proportionnels à leurs sinus. D'autres auteurs en matière d'optique avaient déjà adopté ce lemmeGa naar voetnoot1) parce qu'il s'écarte extrêmement peu de la vérité. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VI.Soit BAC un angle solide en verre, inférieur à 19o. Si deux rayons tombent sur le verre en un même point de telle manière que l'inclinaison de chacun d'eux soit inférieure à 29o du côté opposé au point A, la différence entre les inclinaisons des rayons incidents sera égale à celle des inclinaisons des rayons qui quittent le verre après la réfractionGa naar voetnoot2). 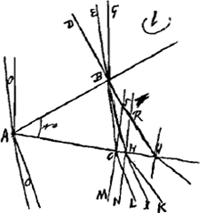 [Fig. 16.]
Supposons que l'angle BAC entre deux plans qui terminent un angle solide en verre soit inférieur à 19o. Supposons de plus que dans le plan passant par ABC il y ait une ligne droite DBV qui coupe le plan AB normalement au point B et qu'avec elle les rayons EB et GB fassent des angles inférieurs à 29o du côté opposé au point A, de sorte que le rayon EB lequel fait le plus petit angle avec DBV, suive dans le corps transparent la voie BH et le quitte selon HK; tandis que GB suit dans le corps transparent la voie BC et le quitte selon CL. Je dis qu'on peut considérer comme égal à l'angle EBG des rayons incidents l'angle que forment entre eux les rayons HK et CL sortant du corps diaphane, c'est-à-dire, l'angle KHI, si HI est menée parallèlement à CL. En effet, construisons à AC les normales MCS et NHR coupant DBV aux points S et R. Il y a cinq cas [Fig. 16-20], puisque les angles BCA et BHA peuvent être chacun inférieur, ou chacun supérieur à un angle droit; ou bien l'angle BCA peut être supérieur et l'angle BHA inférieur à un angle droit, ou bien BCA ou BHA peut être droit. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 475]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemma.Angulos 30 gradus non excedentes proportionales centeri suis Sinibus. Hoc jam ante ab alijs quoque opticorum scriptoribus assumtum fuitGa naar voetnoot1), quia exigua prorsus a vero est differentia. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio VI.][Posito angulo vitri solido 19 gradibus minore BAC si duo radij in unum vitri punctum incidant, ita ut singulorum inclinatio sit minor 29 gradibus in partem ab A puncto aversam, erit differentia inclinationum radiorum incidentium aequalis differentiae inclinationum radiorum qui post refractionem e vitro exeunt.]Ga naar voetnoot2) Si sit angulus BAC, [Fig. 16] quo duo plana angulum ex vitro solidum terminantiaGa naar voetnoot3) inclinantur minor grad. 19.i, sitque praeterea in plano per ABC etiam recta linea DBV, quae planum AB normaliter secet in B, et ad eam inclinentur radij EB, GB, angulis minoribus quam gr. 29 in partem ab A puncto aversam, quorum interior EB intra diaphanum feratur per BH, atque exeat in HK; GB vero feratur intra diaphanum per BC, exeat vero in CL. Dico angulo EBG radiorum incidentium aequalem censeri posse eum quo egressi HK, CL inter se inclinantur, hoc est, angulum KHI, si fiat HI parallela CL. Ducantur enim rectae ad AC normales MCS, NHR, quae secent DBV in punctis S, R. Sunt autem casus quinque [Fig. 16-20], possunt enim anguli BCA, BHA, vel uterque esse minor recto, vel uterque major, vel angulus BCA major recto, et BHA minor. Vel BCA vel BHA rectus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 476]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Je démontrerai d'abord que dans tous ces cas chacun des angles formés par les rayons BH, HK; BC et CL avec les droites perpendiculaires à AH est inférieur à 30o. En effet, puisque dans le premier cas [Fig. 16] l'angle A du triangle BAH est inférieur à 19o, et l'angle ABH à l'angle droit ABV, l'angle BHA sera nécessairement plus grand que 71o; retranchant cet angle de l'angle droit AHR on trouve donc un angle BHR inférieur à 19o. Or, le sinus de cet angle, qui donc est inférieur à 32557 parties lorsque le rayon de la circonférence en a 100000, est au sinus de l'angle NHK comme 2 est à 3 d'après la loi de la réfraction dans le verreGa naar voetnoot1). Par conséquent, le sinus de l'angle NHK est inférieur à 48836 et l'angle NHK lui-même est inférieur à 30o; parce que le sinus de 30o est 50000. On démontrera de la même manière que l'angle MCL lui aussi est inférieur à 30o. Deuxième cas [Fig. 17]. Comme l'angle DBG est inférieur à 29o et que son sinus est à celui de l'angle VBC comme 3 est à 2, l'angle VBC sera inférieur à 19⅓o, d'après le lemme précédent. Mais l'angle VBC est égal à la somme des angles BSC et BCS. L'angle BCS est donc à plus forte raison inférieur à 19⅓o, et son sinus à 33107. Mais comme 2 est à 3, ainsi est le sinus de l'angle BCS à celui de l'angle MCL. Par conséquent, le sinus de l'angle MCL est inférieur à 49662, et l'angle MCL lui-même à 30o. On démontrera de la même manière que l'angle NHK est inférieur à 30o. Troisième cas [Fig. 18]. On démontrera que l'angle NHK est inférieur à 30o de la même manière qu'au premier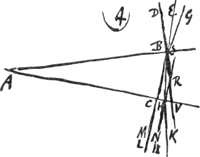 [Fig. 19.]
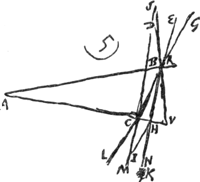 [Fig. 20.]
cas; et la même chose pour l'angle MCL comme au deuxième cas. Quatrième cas [Fig. 19]. On donnera pour l'angle NHK la même démonstration qu'au premier cas. Cinquième cas [Fig. 20]. Même démonstration pour l'angle MCL qu'au deuxième cas. Ceci étant établi, la démonstration procédera comme il suit. Dans tous les cas il faut considérer l'angle VBC comme égal aux deux tiers de l'angle DBG, parce que ce rapport est celui des sinus de ces angles. De même il faut considérer l'angle VBH comme égal aux deux tiers de l'angle DBE. Par conséquent, l'angle HBC sera censé égal aux deux tiers de l'angle EBG. En outre, dans les trois premiers cas [Fig. 16-18] il faut considérer l'angle SCB comme égal aux deux tiers de l'angle MCL. De même l'angle RHB comme égal aux deux tiers de l'angle NHK. Il s'ensuit que dans le premier et dans le deuxième cas la différence des angles SCB et RHB doit être censée égale aux deux tiers de la différence des angles MCL et NHK, c'est- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 477]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
In his omnibus ostendam primò, angulos singulos quos radij BH, HK; BC, CL constituunt cum rectis perpendicularibus ad AH, minores esse 30 gradibus. Nam 1.o casu [Fig. 16] cum sit in triangulo BAH ang. A minor 19 gr. et ABH minor recto ABV, erit necessario BHA major gr. 71, qui proinde ablatus ab recto AHR relinquit ang. BHR minorem gr. 19. Hujus vero sinus, qui igitur minor est quam partium 32557 qualium radius circuli est 100000, est ad sinum ang. NHK ut 2 ad 3 ex lege refractionis vitriGa naar voetnoot1). Ergo sinus anguli NHK minor quam 48836, et ang. ipse NHK minor ang.o 30 gr. quippe cujus sinus est 50000. Eadem ratione et ang. MCL minor probabitur quam 30 gr.  [Fig. 16.]
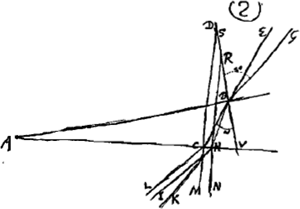 [Fig. 17.]
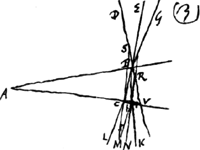 [Fig. 18.]
Casu 2.o [Fig. 17] quoniam ang. DBG minor est quam 29 gr. sinus vero ipsius ad sinum ang.i VBC ut 3 ad 2, erit per lemma praec. angulus VBC minor gradibus 19⅓. Sed ang. VBC aequalis est summae ang. BSC et BCS. Ergo BCS omnino minor quam 19⅓ gr. Et sinus ejus minor quam partium 33107. Sicut autem 2 ad 3 ita sinus ang. BCS ad sinum ang. MCL. Ergo sinus ang. MCL minor quam partium 49662. et angulus ipse MCL minor itaque quam gr. 30. Eadem ratione ostendetur ang. NHK minor 30 gr. Casu 3.o [Fig. 18] ang. NHK minor ostendetur 30 gr. eodem modo quo in casu primo. angulus vero MCL eodem modo atque in casu secundo. Quarto casu [Fig. 19], de ang.o NHK demonstratur eodem modo atque in casu primo. Item quinto casu [Fig. 20] de ang. MCL eodem modo atque in casu secundo. His ostensis sic procedet demonstratio. Omnibus casibus anguli DBG angulus VBC duabus tertijs aequari censendus, quia haec est sinuum ipsorum ratio. itemque anguli DBE duabus tertijs angulus VBH. ergo et anguli EBG duae tertiae censebitur angulus HBC. Rursus tribus casibus prioribus [Fig. 16-18] anguli MCL duabus tertijs aequalis censendus ang. SCB, itemque ang.i NHK duabus tertijs aequalis ang. RHB. Quare et casu 1.o et 2.o duabus tertijs differentiae angu- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 478]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
-à-dire aux deux tiers de l'angle KHI, vu que nous avons menée HI parallèlement à CL. Mais dans le troisième cas [Fig. 18] la somme des angles SCB et RHB doit être considérée comme égale aux deux tiers de la somme des angles MCL et NHK, c'est-à-dire ici aussi aux deux tiers de l'angle KHI. Or, dans ce cas il apparaît facilement que cette somme est égale à l'angle HBC, tandis que dans les deux premiers cas [Fig. 16-17] la différence des mêmes angles SCB et RHB est égale au même angle HBC. Par conséquent, dans ces trois cas l'angle HBC doit être considéré comme égal aux deux tiers de l'angle KHI. Mais le même angle HBC fut considéré comme égal aux deux tiers de l'angle EBG. Il s'ensuit que l'angle KHI doit être censé égal à l'angle EBG; ce qu'il fallait démontrer. Et dans le quatrième cas [Fig. 19], [Fig. 19.]
 [Fig. 20.]
où l'angle BCA est droit, CL coïncide avec CM et HI avec HN; et comme, d'après ce qui a été démontré plus haut, l'angle HBC doit être censé égal aux ⅔ de l'angle EBG, et de même l'angle BHR ou HBC égal aux ⅔ de l'angle IHK, il s'ensuit qu'ici aussi les angles IHK et EBG doivent être considérés comme égaux. Enfin dans le cinquième cas [Fig. 20], où HK coïncide avec HN, il apparaît que l'angle BCS doit de nouveau être considéré comme égal aux deux tiers de l'angle MCL ou KHI. Mais ce même angle BCS, ou CBH qui lui est égal, fut considéré comme égal aux deux tiers de l'angle EBG. Il apparaît donc que dans ce cas aussi les angles KHI et EBG doivent être estimés égaux; ce qui restait à démontrer. Or, si les rayons EB et GB ou d'autres rayons parallèles à eux [Fig. 16] tombent pour ainsi dire précisément sur l'angle A du corps transparent, il est évident qu'au même sommet A deux angles égaux (désignés par la lettre o) seront formés, l'un par les deux rayons incidents, l'autre par les deux rayons réfractés. D'ailleurs on voit aisément comment ce même théorème peut être adapté à un indice de réfraction quelconque. Du reste, vû que, ordinairement, lorsque dans la suite nous ferons usage de ce théorème, l'angle BAC, ainsi que les autres angles sous lesquels les rayons incidents et les rayons réfractés sont inclinés par rapport aux droites perpendiculaires à la surface réfringente, sera beaucoup plus petit que ceux que nous avons définis ici, et que de même les angles des rayons incidents EBG seront toujours très petits, il faut observer que les angles ou inclinaisons des rayons qui sortent du verre tendront d'autant mieux vers l'égalité parfaite avec les angles correspondants des rayons incidents, puisque le rapport des angles correspond alors plus précisément à celui des sinus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 479]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lorum MCL, NHK, quae differentia est angulus KHI, (nam HI parallelam duximus CL) aequalis censebitur differentia angulorum SCB, RHB. Casu 3.o vero [Fig. 18], duabus tertijs summae angulorum MCL, NHK, quae summa rursus est angulus KHI, aequalis censebitur summa angulorum SCB, RHB. Atqui hoc casu summam
 [Fig. 16.]
 [Fig. 17.]
 [Fig. 18.]
hanc facile apparet aequari angulo HBC. Casibus vero 1.o et 2.o [Fig. 16 et 17] differentiam eorundem angulorum SCB, RHB aequari eidem angulo HBC. Ergo his tribus casibus angulus HBC aequalis censendus duabus tertijs anguli KHI. Idem vero ang. HBC aequalis census fuit duabus tertijs anguli EBG. Ergo angulus KHI aequalis censendus ang.o EBG, quod erat dem. Casu vero 4.o [Fig. 19], ubi ang. BCA est rectus, incidit CL in CM, et HI in HN; cumque angulus HBC sit aequalis censendus ⅔ ang. EBG, ex ante demonstratis, et angulus BHR qui aequalis HBC, aequalis censendus ⅔ anguli IHK. Sequitur et hic aequales esse censendos angulos IHK, EBG. Denique casu 5.o [Fig. 20], ubi HK cadit in HN, apparet rursus angulum BCS aequalem censendum duabus tertijs ang.1 MCL seu KHI; idem vero BCS seu ipsi aequalis CBH census fuit duas tertias facere anguli EBG. Igitur apparet rursus aequales censendos angulos KHI, EBG. quae supererant demonstranda. Quod si radij EB, GB, vel ipsis paralleli [Fig. 16], incidant in ipsum velut angulum diaphani A, manifestum est ad eundem verticem A conventuros angulos duos aequales notatos o, quos bini incidentes radij ac bini refracti efficient. Facile autem perspicitur quomodo idem hoc Theorema ad quamlibet refractionis proportionem accommodari possit. Sciendum etiam, quia cum in sequentibus eo utemur, tam angulus BAC, quam caeteri quibus radij incidentes et refracti inclinantur ad rectas superficiei refringenti perpendiculares longe minores plerumque erunt ijs quos hic definivimus. itemque anguli radiorum incidentium EBG semper exigui, eò propius ad horum perfectam aequalitatem accessuros angulos seu inclinationes radiorum e vitro egredientium, quia tanto propius angulorum ratio sinuum rationi respondet. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 480]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VII.Déterminer l'ouverture des lentilles dans les télescopes. Comme il a été démontréGa naar voetnoot1) que le grossissement dans les télescopes munis de deux lentilles est égal au rapport de la distance focale de la lentille extérieure à celle de l'oculaire, ou bien, si ce dernier est concave, à la distance de son point de dispersionGa naar voetnoot2), il pourrait sembler qu'avec un télescope, si court qu'il soit, il doive être possible d'obtenir un grossissement quelconque. Mais il y a deux raisons pour lesquelles il n'en est pas ainsi. La première c'est que, lorsque l'ouverture de la lentille extérieure reste constante, le télescope donnera des images d'autant plus obscures que son grossissement, par l'emploi d'une lentille oculaire plus forte, sera plus considérable. La seconde c'est qu'il donnera en même temps des images moins nettes. Et si l'on cherche à obtenir un meilleur effet en augmentant l'ouverture, la confusion deviendra d'autant plus grande. Ce qui se rapporte à la clarté et à l'obscurité des imagesGa naar voetnoot3) sera compris si nous faisons attention à l'image de l'objet qui se forme sur le fond de l'oeil; plus celle-ci deviendra grande, soit par la réfraction due aux lentilles soit seulement par la diminution de la distance, plus grande aussi sera la quantité des rayons partant de chaque point de l'objet qui devront pénétrer dans l'oeil pour que la clarté reste la même. En effet, lorsque, en regardant à l'oeil nu, on s'approche de l'objet jusqu'à ce que la distance est devenue la moitié de ce qu'elle était, l'image formée sur le fond de l'oeil acquiert un diamètre double, par conséquent une surface quadruple. Mais d'autre part quatre fois plus de rayons, partant d'un point quelconque de l'objet, entrent dans la pupille, puisque l'angle du cône lumineux devient double. Par conséquent, on aperçoit l'objet également éclairé à l'une et à l'autre distance; c'est là une loi de la nature. Mais s'il faut construire un télescope qui augmente dix fois le diamètre des objets et qui en même temps donne des images aussi lumineuses que lorsqu'on regarde à l'oeil nu, le diamètre de l'ouverture de la lentille extérieure devra être dix fois plus grand que celui de la pupille, même dans le cas où aucune partie des rayons ne serait interceptée ni par la réflection due aux deux surfaces de la lentille ni par la couleur du verre. Ainsi, en effet, tandis que la surface de l'objet est agrandie cent fois, la pupille recevra aussi cent fois plus de lumière que lorsqu'on regardait à l'oeil nu. Mais une bien plus faible quantité de lumière suffit pour les télescopes: ceux dont nous nous servons le jour ne sont pas trop obscurs lorsque leurs images possèdent seulement la sixième ou la septième partie de la clarté qu'on perçoit ordinairement avec les yeux. Et les télescopes plus longs, avec lesquels nous observons la lune et les planètes, exigent encore deux fois moins de lumière, parce que dans les ténèbres les yeux réagissent sur une plus faible lumière que pendant le jour. C'est ainsi que dans un télescope long de 30 pieds qui agrandit | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 481]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio VII.]Lentium Aperturas in Telescopijs definire. Cum ratio augmenti in duarum lentium telescopijs ea esse ostensa sitGa naar voetnoot1) quae foci distantiae lentis exterioris ad ocularis foci distantiam; aut si haec cava lens fuerit, ad distantiam puncti dispersusGa naar voetnoot2), videatur forsan quamvis brevi telescopio quantumlibet aucta visibilia spectari posse. Sed duplex causa est quae hoc impediat. Altera quod, manente eadem lentis exterioris apertura, quanto magis res visas amplificarit telescopium adhibita oculari lente acutiori tanto quoque obscuriores videri faciet. Altera quod et minus distinctas eas referet. Si vero augenda apertura remedium quaeratur, eo magis augebitur confusio. Quae ad lucem obscuritatemque attinentGa naar voetnoot3) intelligentur si attendamus ad picturam illam rei visae quae in fundo oculi formatur; quae quanto major efficietur, sive id refractione lentium fiat, sive solum propius accedendo, tanto majore copia a singulis rei punctis radij intra oculum recipiendi sunt, ut eadem claritas maneat. Si enim nudo oculo intuens duplo propius ad visibile accedas, fit ejus pictura in fundo oculi duplo quam fuerat major secundum diametrum, quadruplo secundum aream. Sed et quadruplo plures radij pupillam ingrediuntur ab unoquoque ejus puncto manantes, quia coni radiosi angulus duplus fit. Itaque eadem lux picturae in utraque distantia percipitur, idque ita natura comparatum est. Si vero telescopium parandum sit decuplo augens visibilia ratione diametri, quodque tam lucida omnia referat atque cum nudo visu spectantur, debebit et in lente exteriori diameter aperturae ad pupillae diametrum decupla esse, etiamsi nec repercussu superficierum utriusque lentis, nec vitri colore pars ulla radiorum interciperetur. Sic enim cum rei visae superficies centuplo augeatur, habebitur et lux centupla ejus quam nuda pupilla admittebat. Sed multo minor lucis mensura telescopijs sufficit. Nam quibus interdiu utimur, non nimis obscura sunt si modo sextam vel septimam partem habeant claritatis quae solet oculis percipi. Longiora vero, quibus luna ac Planetae spectantur, duplo minori adhuc luce indigent, quod oculi per tenebras minore luce moveantur quam interdiu. Ita in telescopio 30 pedes longo, quod Planetas amplificat centies novies ratione diametri, eoque latitudinem aperturae posceret, quae ad eam quae pupillae | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 482]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
109 fois le diamètre des planètes et qui exigerait donc une largeur d'ouverture ayant à celle de la pupille le rapport 109:1, c'est-à-dire qui serait environ de 11 pouces, la largeur de la pupille étant considérée comme égale à 1/10 pouce, on trouve qu'une ouverture de 3 pouces suffit, quoique cette ouverture ne recueille pas la treizième partie de la lumière qui serait reçue par une ouverture de 11 pouces. Mais la largeur de la pupille n'est pas exactement déterminée, ni toujours la même et encore ne sait-on exactement quelle est la clarté suffisante. Quant aux planètes plus éloignées et à cause de cela plus obscures, il faut leur donner une clarté un peu plus grande qu'aux plus proches du soleil pour une raison dont je parlerai dans la suiteGa naar voetnoot1). Ce qu'il faut chercher surtout c'est ceci: étant donné un télescope convenablement arrangé comme l'expérience l'a montré, pour lequel on connaît les distances focales de ses deux lentilles et la plus grande ouverture de la lentille extérieure que ce télescope peut supporter, comment peut-on à l'aide de celui-ci déterminer les dimensions d'un nombre quelconque d'autres télescopes de longueurs donnéesGa naar voetnoot2), produisant des images également lumineuses et également nettes? En effet, c'est par la solution de ce problème qu'on arrive à la connaissance de la nature et de la grandeur de l'avantage qu'on peut tirer d'un allongement des télescopes. C'est de cette manière aussi qu'on peut examiner si les lentilles ont été travaillées et polies d'une manière convenable ou non. Mais pour pouvoir tenir compte de la netteté de l'image, il faut savoir que deux causes contribuent à gâter cette netteté, dont la première est que la figure sphérique des lentilles ne réunit pas en un seul point les rayons émanant d'un point de l'objet, mais leur donne une légère aberration, comme nous l'avons démontré plus hautGa naar voetnoot4). La seconde est qu'un rayon tombant obliquement sur la surface d'un corps transparent plus dense, lequel rayon soit considéré comme une ligne droite, ne se meut plus suivant une ligne droite après la réfraction, mais est divisé, pour ainsi dire, en plusieurs rayons colorés formant entre eux de petits angles. Par exemple, lorsque le rayon CA [Fig. 21] tombe sur la surface AB du verre, ce rayon sera dispersé, après la réfraction, à travers un petit angle DAE, dont le côté AD qui s'écarte le plus de la perpendiculaire GAF sera porteur d'une couleur rouge, tandis que la couleur violette foncée appartiendra à l'autre rayon extrême AE et qu'entre D et E apparaîtront le jaune, le vert et le bleu dans le même ordre dans lequel on les voit ordinairement dans l'arc-en-ciel. M. Is. Newton a le premier découvert cette propriété et ses conséquencesGa naar voetnoot6); et recevant en un lieu obscur les rayons du soleil réfractés par un prisme de verre [Fig. 22], il a observé que cette dispersion du rayon a lieu d'une telle manière: comme si les indices de réfraction des différents rayons colorés étaient différents, et que le rayon CA contenait tous ces rayons colorés. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 483]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
se haberet ut 109 ad 1; hoc est quae pollicum esset fere 11, posita nempe pupillae latitudine 1/10 poll., sufficere invenitur apertura 3 pollicum latitudine. quae minus quam decimam tertiam partem colligit ejus lucis quae contingeret apertura pollicum 11. Sed nec pupillae latitudo certa est aut semper eadem, nec praecise definiri potest, quae claritas sufficiat. Et planetis remotioribus atque eo obscurioribus aliquanto amplior danda est, quam soli propioribus ob causam in sequentibus dicendamGa naar voetnoot1). Illud vero omnino quaerendum est, quomodo dato uno telescopio quod experientia docente rectè sit ordinatum, cujusque lentium duarum foci distantiae datae sint, et apertura lentis exterioris quantam maximam pati potest; quomodo inquam ex hoc alia quotvis quarumcunque longitudinum definianturGa naar voetnoot2), ita ut visibilia aeque lucida, et aeque distincta ostendantGa naar voetnoot3). Hinc enim cognoscitur quid quantumque longitudine telescopiorum producenda profici possit. Item an recte elaborati expolitique sint orbes vitrei an secus. Distinctae vero visionis ratio ut habeatur, sciendum est ex duplici causa eam vitiari, quarum altera est, quod sphaerica lentium convexitas non ad punctum unum cogat radios a puncto rei visae manantes, sed aliquantulum aberrare faciat, ut in superioribus ostensum fuitGa naar voetnoot4). Altera, quod radius in superficiem densioris diaphani oblique incidens, ac velutGa naar voetnoot5) recta linea habitus, postquam refractus fuerit non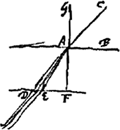 [Fig. 21.]
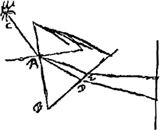 [Fig. 22.]
amplius in linea feratur, sed velut in plures spargatur exiguis angulis dissidentes, coloribusque infectos. Veluti si in superficiem vitri AB [Fig. 21] incidat radius CA is refractus spargetur angulo exiguo DAE, cujus latus AD à perpendiculo GAF magis recedens colorem rubrum deferet, alterum extremum AE violaceum obscurum; inter D et E vero apparebunt flavus, viridis, caeruleus, eodem ordine ut in Iride spectari solent. Hoc ita esse et quidnam ex eo sequeretur, pridem advertit V. CI. Is. NewtonusGa naar voetnoot6); ac prismate vitreo radios solis refractos in loco obscuro excipiens [Fig. 22] observavit ea lege hanc radij dissipationem contingere ac si variae essent variè coloratorum radiorum refractiones, aliae alijs majores, radiusque CA omnes | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 484]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Et il a trouvé que les rayons extrêmes sont réfractés de telle façon en AD et en AE que sin GAC:sin FAD = 68:44, et sin GAC:sin FAE = 69:44Ga naar voetnoot1). Ensuite il en a conclu que dans toute lentille en verre telle que AB [Fig. 23] possédant l'axe CD, où la partie la moins réfractée, portant la couleur rouge, des rayons extrêmes parallèles à l'axe KA et LB rencontre l'axe en D, tandis que la partie violette la plus réfractée le rencontre au point E, ED sera égale à 1/50 CD; et que, par conséquent, si l'on prolonge AE et BE jusqu'à ce qu'elles rencontrent en F et en G la droite menée par D parallèlement à la lentille AB, la ligne GF, diamètre du cercle d'aberration, devient égale à la cinquantième partie du diamètre ABGa naar voetnoot3). L'angle DAF sera donc aussi considéré comme égal à la cinquantième partie de l'angle ADC. La raison de ces énoncés apparaît aisément lorsqu'on considère la lentille AB comme planconvexe, la surface convexe ACB faisant partie d'une sphère de rayon CN. En effet, comme 68 est à 44, ainsi sera ND à DCGa naar voetnoot4), mais comme 69 est à 44, ainsi sera NE à CE. C'est pourquoi NC sera à CD comme 24 est à 44 et NC:CE = 25:44, et par suite DC:CE = 25:24, ou CD:DE = 25:1. Mais ce que nous avons démontré ici à propos de la lentille planconvexe, s'applique également à toute autre lentille, attendu que pour des lentilles de même épaisseur les distances focales sont égalesGa naar voetnoot5). Or, cette dernière aberration est d'une autre nature que celle due à la forme sphérique des lentilles; elle est en géneral beaucoup plus grande. Car, considérons par exemple la lentille AB possédant une surface plane et une surface convexe, cette dernière étant exposée aux rayons incidents; supposons la distance focale HD égale à 1 pied ou 12 pouces et l'ouverture AB égale à un demi-pouce, ce qui est environ l'ouverture qu'il faut donner à cette lentille dans un télescope d'un pied; alors HC, l'épaisseur de la lentille, est égale à 1/192 pouceGa naar voetnoot6) et les 7/6 de cette longueurGa naar voetnoot7), c'est-à-dire 1/164 pouce, indiquent la grandeur de l'aberration totale DE provenant de la figure sphérique. Mais pour l'aberration Newtonienne on aura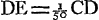 Ga naar voetnoot8), c'est-à-dire aux 12/50 d'un pouce. Elle est donc ici à la première aber- Ga naar voetnoot8), c'est-à-dire aux 12/50 d'un pouce. Elle est donc ici à la première aber-
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 485]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
istos contineret. Extremos autem in AD, AE ita refringi ut quidem sinus anguli GAC, ad sinum anguli FAD, esset ut 68 ad 44, ad sinum vero anguli FAE ut 69 ad 44Ga naar voetnoot1). atque hinc porro collegit, in quavis lente vitrea, ut AB [Fig. 23], cujus axis CD, si radiorum extremorum axi parallelorum KA, LB pars levius refracta ac rubrumGa naar voetnoot2) colorem deferens conveniat cum axe in D, maxime vero refracta ac violacea in E, tunc esse ED aequalem
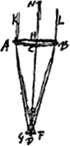 [Fig. 23.]
1/50 CD, ac proinde si producantur AE, BE donec occurrant in F et G rectae per D ductae ac lenti AB parallelae, fieri GF, diametrum circelli aberrationis aequalem parti quinquagesimae diametri ABGa naar voetnoot3). Unde et ang. DAF censebitur efficere 1/50 ang.o ADC. Quorum ratio facile apparet posita lente AB planoconvexa, cujus convexa superficies ACB sit a sphaera cujus semidiameter CN. Sicut enim 68 ad 44 ita erit ND ad DCGa naar voetnoot4), sicut vero 69 ad 44 ita NE ad EC. Quare NC ad CD ut 24 ad 44 et NC ad CE ut 25 ad 44 ac proinde DC ad CE ut 25 ad 24. Et CD ad DE ut 25 ad 1. Quod autem de lente hac planoconvexa ostendimus, omni quoque alij convenit, quia in aeque crassis aequales sunt foci distantiaeGa naar voetnoot5). Est autem aberratio haec et alius naturae et plerumque longissime superat eam quae ratione figurae sphaericae contingit. Nam si sit ex. gr. lens AB, cujus altera superficies plana sit, altera convexa, atque ea radijs incidentibus exposita, foci vero distantia HD sit ped. 1, seu poll. 12, apertura AB dimidij pollicis, quanta circiter huic lenti in pedali telescopio danda est; fit HC crassitudo lentis 1/192 poll.Ga naar voetnoot6) cujus 7/6Ga naar voetnoot7), hoc est 1/164 poll. definit aberrationem totam DE, quae ex figura sphaerica oritur. Sed ex Newtoniana aberratione erit DE 1/50 CDGa naar voetnoot8), hoc | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 486]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
artion comme 39 est à 1. Et plus les télescopes sont longs, plus grande sera cette différence des aberrations. Mais comme il pourrait sembler qu'un si grand défaut de la réfraction devrait gâter absolument l'effet des télescopes, tandis que l'expérience nous apprend le contraire, nous devons rendre raison de cette contradiction apparente. Il faut donc remarquer que cette image colorée du soleil telle que Newton l'a observéeGa naar voetnoot1) réunit de beaucoup la plus grande partie de la lumière là où brille la couleur jaune, à côté de la couleur rouge; mais qu'elle devient beaucoup plus obscure du côté où elle tend vers le violet. Et il est hors de doute que lorsque les rayons proviennent d'une source de lumière autre que le soleil, la plus grande partie des rayons aberrants ne peuvent être aperçus. Il s'ensuit que les rayons issus des différents points d'un objet éloigné forment au foyer d'une lentille convexe une image suffisamment nette et à contours distincts quoique enveloppée d'une certaine luminosité comme d'une vapeur, laquelle provient de cette aberration, c'est-à-dire de la dispersion des différents rayons. Il faut remarquerGa naar voetnoot2) que la proposition VIGa naar voetnoot3) peut être étendue à des rayons dispersés en couleurs diverses. En effet, il en résulte qu'on observe la même loi pour les rayons dispersés que pour les rayons blancs; puisse, par exemple, le rayon SD [Fig. 24] se dissiper en DO rouge et DR violet; et de même le rayon ND en DB rouge et DF violet. On conclut, dis-je, de cette proposition VI que les angles BDO déterminé par les rayons rouges et FDR déterminé par les rayons violets seront l'un et l'autre égal à l'angle SDN. Nous pourrons encore en déduire non inopportunément le lemme suivant: L'aberration NDM appartenant au rayon incident BD sera égale à l'aberration BDF qui correspond au rayon réfracté ND. En effet, comme au rayon incident BD correspond l'aberration NDM ou, ce qui est la même chose, au rayon incident SD l'aberration ODR = NDM, et comme d'autre part l'aberration BDF correspond au rayon incident ND, les angles BDO déterminé par la couleur rouge et FDR déterminé par la couleur violette seront l'un et l'autre égal à l'angle SDN et, par conséquent, égaux entre eux; en d'autres termes, on aura ∠BDO = ∠FDR, et si l'on retranche l'angle commun FDO, ou obtiendra que l'angle restant BDF est égal à ODR, c'est-à-dire à NDM; ce qu'il fallait démontrer.
Je procéderai maintenant à la détermination des ouvertures des télescopes et je démontrerai que: Les diamètres des ouvertures doivent être | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 487]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
est 12/50 pollicis. Quae itaque ad priorem se hic habet ut 39 ad 1. Quo longiora vero telescopia, eo major erit haec aberrationum differentia. Quia autem tanto refractionis vitio videri posset penitus corruptum iri omnem telescopiorum effectum, quod tamen contra evenire experimur; omnino exponenda est hujus rei ratio. Sciendum itaque imaginem illam Solis coloratam qualem Newtonus observavitGa naar voetnoot1), longe maximam lucis partem colligere ubi flavus color effulget, rubro proximus. Eandem vero multo fieri obscuriorem qua parte ad violaceum tendit. Nec dubitandum, quin si ab alia quam a Solis luce radij adveniant, major pars aberrantium sentiri nequeat. Ita fit ut qui a singulis visibilium punctis manant, lentis convexae opera picturam rei procul positae satis distinctam ac circumscriptam in foco exhibeant, etsi luce quadam, veluti nebula, aspersam, quae ab ista aberratione seu radiorum singulorum dispersu oritur. NotandumGa naar voetnoot2) autem Propos. VIGa naar voetnoot3) ad radios in varios colores dissipatos, extendi posse. Ex ea enim sequitur, eandem observari legem in radijs dissipatis, quae in puris; ex gr. SD [Fig. 24] radius dissipetur in DO colorem rubrum et DR violaceum; itemque radius ND in rubrum DB et violaceum DF, sequitur inquam, ex hac prop. VI angulos BDO a radijs coloris rubri et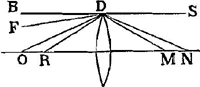 [Fig. 24.]
FDR a radijs coloris violacei descriptos singulos fore aequales angulo SDN. Unde non incommode et illud ad modum Lemmatis deduci potest: Aberrationem NDM per radium incidentem BD productam, fore aequalem aberrationi BDF genitae per refractum ND. Quia enim a radio incidente BD fit NDM aberratio, vel quod idem est, ab incidente SD aberratio ODR ∞ NDM, rursus quia ex incidente ND sit aberratio BDF, erunt anguli BDO a colore rubro, et FDR a violaceo descripti, singuli aequales ang. SDN, ergo etiam inter se aequales id est, ang. BDO ∞ FDR, unde demto communi ang. FDO, erit reliquus BDF ∞ ODR id est NDM, q.e.d.
Nunc ad aperturas telescopiorum definiendas pergam, ostendamque, diametros aperturarum in subdupla ratione foci distantiarum lentis | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 488]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
pris dans un rapport égal à la racine carrée du rapport des distances focales de la lentille extérieure; et de même aussi les distances focales des lentilles oculairesGa naar voetnoot1). Considérons un télescope composé des lentilles AC et DP [Fig. 25], dont la première est la lentille extérieure et la seconde l'oculaire. Soit CP l'axe du télescope passant par les deux lentilles à leur milieu; puisse cet axe couper la pupille de l'oeil au point T et son fond au point N. Prenons CF comme distance focale de la lentille AC, et PF comme distance focale de la lentille DP. Soit AC la largeur de la moitié de l'ouverture. Supposons ce télescope bien construit par rapport à la clarté et à la netteté des images, de sorte qu'il ne puisse supporter ni une plus grande ouverture de la lentille extérieure ni une plus forte lentille oculaire. Qu'il s'agisse maintenant de construire un autre télescope plus long et grossissant plus fortement, dont la lentille ac [Fig. 26] ait une distance focale cf d'un rapport donné à CF. On demande de calculer à l'aide du télescope donné le diamètre de l'ouverture aa ainsi que la distance focale pf de la lentille oculaire, de telle sorte que le deuxième télescope donne des images aussi lumineuses et aussi nettes que le premier, composé des lentilles AC et PD. Indiquons dans les deux cas toutes les parties de la figure par les mêmes lettres, mais de forme différente, les deux figures étant construites de la même manière. Soit F le point de concours des rayons parallèles à l'axe qui amènent la couleur rouge, tant pour ceux qui tombent du dehors sur la lentille AC que pour ceux qui arriveraient du côté de l'oeil pour tomber sur la lentille PD. Mais supposons que le point de concours des rayons parallèles venant de la lentille AC qui nous font voir la couleur violette soit le point B; tandis que G représente le point de concours des rayons parallèles qui conduisent cette couleur à travers la lentille PD. Or, la constitution de l'oeil soit par hypothèse telle qu'il réunit en un point unique de son fond les rayons rouges tombant sur lui parallèlement à l'axe. Nous négligeons ici l'aberration provenant de la forme sphérique, attendu que cette aberration, comme nous l'avons déjà dit, n'a aucune importance comparée à celle qui provient des couleurs. Par conséquent, si du bord de l'ouverture AA on trace les droites ABDGa naar voetnoot2) et AFO rencontrant la lentille PD en D et en O, ces droites représenteront les rayons colorés extrêmes provenant d'un seul rayon parallèle à l'axe par suite de la réfraction due à la lentille AC. Traçons les droites DF, FA et DG et supposons que l'axe CP prolongé coupe la pupille de l'oeil au point T et atteigne le fond de l'oeil au point N. Menons la droite DE parallèlement à l'axe depuis la lentille oculaire jusqu'à la pupille et joignons les points E et N. Du reste, l'angle | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 489]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
exterioris esse ponendos. atque ita quoque foci distantias lentium oculariumGa naar voetnoot1). Sit telescopium ex lentibus AC, DP [Fig. 25] compositum, AC exteriori, DP oculari, axis telescopij per utramque mediam lentem [Fig. 25.]
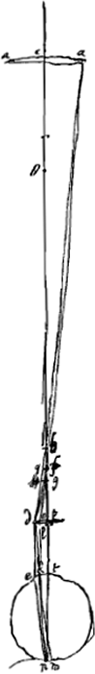 [Fig. 26.]
transiens sit CP, qui pupillam oculi secet in T puncto, ejusque fundo occurrat in N. Foci distantia lentis AC sit CF, lentis DP foci distantia PF. dimidiae aperturae latitudo sit AC. Ponatur vero telescopium hoc recte ordinatum, quantum ad lucem ac distinctam visionem attinet, ut nec majorem aperturam in exteriori lente ferre possit, nec acutiorem lentem ocularem; jamque aliud sit construendum, longius ac majoris amplificationis, cujus lens ac, habeat foci distantiam cf, datae rationis ad CF, quaeraturque hinc diameter aperturae aa, itemque foci distantia lentis ocularis pf, quibus fiat aeque lucidum hoc telescopium, et aeque distincte res visas exhibens, atque illud ex lentibus AC, PD. Sint omnia ejusdem nominis sed diversae figurae literis utrobique notata, et constructio eadem. Intelligatur nempe F esse punctum concursus radiorum axi parallelorum qui rubrum colorem adferunt, tam in lentem AC extrinsecus advenientium, quam qui in lentem PD caderent à regione oculi. Sed B esse concursum parallelorum lentis AC, qui violaceum exhibent. G concursum parallelorum qui colorem hunc ducunt per lentem PD. Oculi vero ea sit constitutio, ut radios rubros axi parallelos excipiens perducat ad punctum unum fundi sui. Aberrationem quae ex figura sphaerica oritur pro nulla hic habemus, quippe quae ut jam diximus nullius momenti sit ad hanc quae fit ex coloribus, ac proinde si ab extrema apertura AA ducantur rectae ABDGa naar voetnoot2), AFO quae lenti PD occurrant in D et O, eae referent radios coloratos extremos quos ex uno axi parallelo radio fecit refractio lentis AC. Jungantur DF, FA, DG, et productus axis CP secet oculi pupillam in puncto T, ejusque fundo incidat in N. Sitque recta DE axi parallela a lente oculari ad pupillam ducta, et jungatur EN. Caeterum angulus BDF, a cujus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 490]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
BDF, de la grandeur duquel dépend, comme nous le montrons, l'aberration au fond de l'oeil, peut être appelé l'angle d'aberration. Comme donc un rayon violet allant de G à D se dirigerait [Fig. 25.]
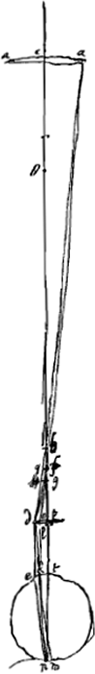 [Fig. 26.]
suivant DE parallèlement à l'axe, le rayon ABD de la même couleur ne pourra être réfracté selon DE, mais se rendra à la pupille en suivant, d'après la proposition VIGa naar voetnoot1), une droite DK plus rapprochée de l'axe de telle manière que les angles BDG et EDK deviendront égaux. Traçons KL parallèle à l'axe. Parce que l'oeil, comme nous l'avons supposé, est construit de telle manière que des rayons rouges parallèles DE et LK viendraient se réunir en un point N du fond de l'oeil, le rayon DK, même s'il est rouge, ne se rendra pas au même point (et encore moins, s'il est violet), mais se mouvra plus près de l'axe selon KM de telle manière que les angles NKM et DKL, ou leurs sinus, auront entre eux un rapport déterminéGa naar voetnoot2) dont la grandeur n'a pour le moment aucune importance. Or, il faut que dans les deux télescopes les angles NKM soient égaux pour que les images soient également nettes; car lorsqu'il en est ainsi, l'aberration NM au fond de l'oeil sera aussi la même dans les deux cas. En effet, nous savons que le rayon rouge AFO après avoir traversé la lentille PD sera parallèle à l'axe et descendra donc au point N du fond de l'oeil. Il est donc nécessaire que les angles DKL ou KDE ou BDG soient égaux dans les deux cas. Ou bien les angles BDF. Car alors on pourra à bon droit considérer les angles BDG comme égaux, puisque dans les deux cas les angles FDG (quoiqu'inégaux entre eux) sont fort petits par rapport à ceux-là. En effet, on a CF:FB = PF:FG d'après la nature de l'aberration que nous considéronsGa naar voetnoot3); d'où l'on tire par permutation CF:FP == FB:FG. Mais CF surpasse de beaucoup FP; dans le télescope de 30 pieds, par exemple, le rapport de ces deux longueurs est de 120Ga naar voetnoot4) à 1. Par conséquent, FB surpasse FG dans le même rapport, et il en est à-peu-près de même pour l'angle BDF et l'angle FDG. Ceci étant établi, nous continuerons le calcul de la manière suivante. Posons dans le cas du premier télescope CF = b, FP = c, AC = a, et dans le cas du | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 491]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
magnitudine pendere ostendimus aberrationem in fundo oculi, vocetur angulus aberrationis. Quum igitur radius qui ex G in D ferretur violaceo colore tinctus abiturus sit in DE axi parallelam, non poterit radius hujus coloris ABD in DE refringi, sed ex propos. [VI]Ga naar voetnoot1) interius feretur ad pupillam per DK, ut fiant anguli aequales BDG, EDK. Sit KL axi parallela, quia itaque ea est oculi constitutio ut radij rubri paralleli DE, LK, conveniant in fundo ad punctum N, non conveniet eodem radius DK, etiamsi ruber, ac minus etiam cum sit violaceus, sed interior feretur secundum KM, ut angulus NKM ad DKL seu sinus ad sinum certam rationem habeatGa naar voetnoot2), quae cujusmodi sit scire nihil interest. Sed in utroque telescopio aequales esse oportet angulos NKM, ut aeque distincta visio existat; quia sic aberratio quoque NM in fundo oculi utrobique aequalis erit. Constat enim radium rubrum AFO penetrata lente PD futurum axi parallelum, eoque descensurum ad punctum in oculi fundo N. Oportet itaque et angulos DKL, seu KDE, seu BDG, utrobique aequales esse. Sive etiam angulos BDF. Tunc enim et anguli BDG pro aequalibus rectè habebuntur, quia utrobique minimi sunt horum respectu (licet inaequales inter se) anguli FDG. Sicut enim CF ad FB ita est PF ad FG, ex natura hujus aberrationisGa naar voetnoot3); unde permutando ut CF ad FP ita FB ad FG. Atqui CF superat longissime FP, ut in telescopio ex. gr. pedum 30, sit earum ratio quae 120Ga naar voetnoot4) ad 1. Ergo ita quoque FB superat FG, et ita fere angulus BDF angulum FDG. Ex his jam calculum prosequemur hoc modo. Sit in priore telescopio CF ∞ b; FP ∞ c; AC ∞ a: in posteriore cf ∞ d, fp ∞ y;ac ∞ x. Et fiat sicut CF ad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 492]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
deuxième cf = d, fp = y, ac = x. Prenons un point θ tel qu'on ait CF::FP = θf:fp. On aura donc θf = by/c. Comme donc le grossissement dû au premier telescope est égal à CF:FP, ou à θf:fp, et le grossissement dû au deuxième télescope à cf:fp, les diamètres des images produites par les deux télescopes seront entre eux comme θf est à cf. Mais AC doit avoir à ac le même rapport, puisque nous voulons que les deux télescopes donnent des images également lumineuses; ce qui arrivera lorsque, plus l'un des deux grossit les objets, plus aussi est grande l'ouverture avec laquelle il assemble les rayons issus d'un même point de ces objets. AC est donc à ac, c'est à-dire a est à x, comme θf est à cf, c'est-à-dire, d'après ce que nous avons dit plus haut, comme by/c est à d. Il s'ensuit que y ou fp est égale à adc/bx.
 [Fig. 27.]
Traçons FQ perpendiculairement à l'axe, et supposons qu'elle coupe la droite DA au point Q. Comme on a alors CB:BF = cb:bf (car BF est égale à 1/50 CB dans les deux figures, comme nous l'avons montré plus hautGa naar voetnoot1)), on aura aussi CA:FQ = ca:fq. Et, par permutation, CA:ca = FQ:fq. Mais puisque, comme nous l'avons dit, les angles d'aberration BDF et bdf doivent être égaux, on aura DF:FQ = df:fq, ou PF:FQ = pf:fq, attendu que dans les deux cas PF et DF peuvent être censées égales à cause de la petitesse de leur différence. Par conséquent, on aura aussi, par permutation, PF:pf == FQ:fq, ou = CA:ca. Or, PF = c, pf = adc/bx et CA = a. Par conséquent, ca ou x = aad/bx et bxx = aad, c'est-à-dire, xx:aa = d:b, ou x:a = √d:√b; ce qu'il fallait démontrer. On prouve ensuite de la manière suivante que les distances focales des lentilles PD et pd sont entre elles comme les diamètres des ouvertures AA et aa. Comme, d'après ce que nous avons dit, a:x = by/c:d, on aura aussi aa:xx = bbyy/cc:dd. Mais nous avions aa:xx = b:d. Par conséquent, bbyy/cc:dd = b:d. Il s'ensuit que byy = ccd et cc:yy = b:d, c'est-à-dire = aa:xx; donc aussi c:y = a:x, c'est-à-dire le rapport des distances focales FP et fp est égal au rapport des rayons des ouvertures AC et ac. Pour les télescopes composés d'une lentille convexe et d'une lentille concave [Fig. 27] on peut prouver les mêmes choses par une démonstration entièrement analogue, avec cette différence seulement que la distance du | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 493]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
FP ita linea θf ad fp, eritque θf ∞ by/c. quia igitur ratio augmenti in priore telescopio
 [Fig. 25.]
 [Fig. 26.]
est ea quae CF ad FP, seu θf ad fp; in posteriore vero ea quae cf ad fp, erunt in utroque magnitudines apparentes secundum diam. inter se ut θf ad cf. quam eandem rationem habere debet AC ad ac; quia aeque lucidum esse volumus telescopium utrumque: quod ita fiet, si quanto magis alterum res visas auget, tanto majori apertura radios colligat ab earum singulis punctis profectos. Est igitur AC ad ac, hoc est, a ad x, ut θf ad cf, hoc est, ex ante dictis, ut bt/c ad d. unde fit y seu fp ∞ ∞ adc/bx. Ducatur FQ axi perpendicularis, quae rectae DA occurrat in Q. Quia itaque ut CB ad BF ita cb ad bf (nam utrobique BF est 1/50 CB, ex supra expositisGa naar voetnoot1)); erit et CA ad FQ ut ca ad fq. Et permutando CA ad ca ut FQ ad fq. Quia vero, ut dictum fuit, aequales debent esse anguli aberrationis BDF, bdf, erit DF ad FQ ut df ad fq, sive PF ad FQ ut pf ad fq, cum utrobique pro ijsdem haberi possint PF et DF, propter minimam differentiam. Proinde et permutando PF ad pf ut FQ ad fq, hoc est, ut CA ad ca. Est autem PF ∞ c; pf ∞ adc/bx; CA ∞ a. Ergo ca sive x ∞ aad/bx. Et bxx ∞ ∞ aad. hoc est xx ad aa ut d ad b. sive x ad a in subdupla ratione d ad b, quod erat ostendendum. Quod autem et lentium PD, pd, foci distantiae sunt sicut aperturarum diametri AA, aa, hinc ita probatur. Cum dictum fuerit esse a ad x ut by/c ad d. Erit et aa ad xx ut bbyy/cc ad dd. Erat autem aa ad xx ut b ad d. Ergo bbyy/cc ad dd ut b ad d. unde byy ∞ ccd. Et cc ad yy ut b ad d, hoc est ut aa ad xx; ac proinde etiam c ad y ut a ad x hoc est, ratio foci distantiarum FP, fp eadem quae semidiametrorum aperturae AC, ac. In telescopijs ex convexa et cava lente compositis [Fig. 27] eadem ostendi | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 494]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
point de dispersion correspondra alors à ce qui était ici la distance focale de l'oculaire convexe. Mais on ne se sert guère de ces lentilles concaves dans les combinaisons, à cause de l'étroitesse du champ qu'elles permettent aux télescopes d'embrasserGa naar voetnoot1). Du reste, pour trouver et les ouvertures et les lentilles oculaires qui conviennent à chaque lentille extérieure, nous avons établi la règle suivante à l'aide des considérations qui précèdent et en supposant en même temps que le télecope de 30 pieds soit une fois pour toutes construit d'une façon déterminée. On multipliera par 3000 le nombre de pouces que contient la distance focale de la lentille extérieure; la racine carrée du produit représentera en centièmes de pouces le diamètre de l'ouverture cherchée. La même racine augmentée d'une dixième partie de sa valeur donnera la distance focale de la lentille oculaire exprimée également en centièmes de pouces. Et les dimensions latérales des images sont entre ellescomme les diamètres des ouvertures. Tout ceci est démontré de la manière suivante. L'expérience nous apprend qu'à une lentille de 30 pieds convient une ouverture de 3 pouces. Si donc on se propose une autre lentille dont la distance focale contient un nombre b de pieds; alors, d'après ce qui précède, le rapport 30:√30b, c'est-à-dire le rapport des racines carrées des distances focales, sera égal au rapport des 3 pouces de l'ouverture donnée (ou de 300 centièmes de pouces) à l'ouverture cherchée de la lentille. Par permutation, on trouve que 30 est à 300, c'est-à-dire 1 à 10, comme √30b est à l'ouverture cherchée en centièmes de pouces. Cette ouverture sera donc de √3000b centièmes de pouces, comme la règle l'annonce. Nous trouvons en outre qu'à cette même lentille de 30 pieds convient un oculaire dont la distance focale est de 3 3/10 pouces. Or, les distances focales sont entre elles comme les ouvertures. Par conséquent, la distance focale de 3 3/10 pouces ou de 330 centièmes de pouces est à la distance focale cherchée comme l'ouverture de 3 pouces ou de 300 centièmes de pouces est à l'ouverture de √3000 b centièmes de pouces. Ou bien, par permutation, comme 300 est à 330, c'est-à-dire comme 1 est à 1 1/10, ainsi est l'ouverture √3000 b à la distance focale cherchée Enfin les considérations suivantes feront voir que les grossissements, en d'autres termes que les grandeurs apparentes des objets aperçus à l'aide des télescopes, sont entre elles comme les diamètres des ouvertures. Dans chaque télescope la grandeur apparente est à la grandeur vraie, c'est-à-dire à celle qu'on aperçoit à l'oeil nu, comme la distance focale de la lentille extérieure est à la distance focale de l'oculaire. Par conséquent, dans l'un des deux télescopes considérés dans la présente proposition, ce rapport des grandeurs sera celui de CF à FP ou de b à c; mais dans l'autre [Fig. 26] celui de cf à fp, c'est-à-dire de d à adc/bx ou de bx/a à c. Mais la grandeur | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 495]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
possunt, simili plane demonstratione, nisi quod distantia puncti dispersus in lente cava tunc erit quod hic fuit convexi ocularis foci distantia. Sed horum cavorum in compositione jam nullus fere est usus, propter angustiam spatij, quam telescopiorum prospectui relinquuntGa naar voetnoot1). Caeterum ad inveniendas tum aperturas, tum lentes oculares cuique lenti exteriori convenientes, ex jam dictis et semel constituto 30 pedum telescopio, hanc effecimus regulam. Foci distantia lentis exterioris quem numerum pedum habebit, is numerus ducatur in 3000; facti radix erit diameter aperturae quaesitae in cente simis pollicum. Eadem si augeatur decima sui parte, dabit foci distantiam lentis ocularis ijsdem centesimis expressam. Apparentes vero rei visae latitudines sunt sicut diametri aperturarum. quae omnia sic probantur. Lenti 30 pedum experimur convenire aperturam 3 pollicum. Si igitur proponatur lens alia cujus foci distantia contineat numerum pedum b, erit ex supra expositis sicut 30 ad √30b, quae est ratio subdupla rationis foci distantiarum, ita 3 pollices aperturae seu 300 centesimae pollicis ad aperturam lentis quaesitam; vel permutando erit ut 30 ad 300, hoc est, 1 ad 10 ita ram lentis quaesitam; vel permutando erit ut 30 ad 300, hoc est, 1 ad 10 ita √30b ad aperturam in centesimis pollicum, quae itaque erit √3000b, qualem regula statuit. Lenti quoque eidem 30 pedum convenire invenimus ocularem, cujus foci distantia 3 3/10 pollicis. Sunt autem foci distantiae sicut aperturae. Ergo ut apertura 3 poll. seu 300 centesimarum ad aperturam √3000b, ita foci distantia 3 3/10 poll., sive 330 centesimarum, ad foci distantiam quaesitam. Sive permutando ut 300 ad 330, hoc est ut 1 ad 1 1/10 ita apertura √3000b ad istam foci distantiam. Denique proportionem amplificationis, seu apparentes rerum magnitudines telescopijs perceptas esse, ut aperturarum diametros, sic manifestum fiet. In unoquoque telescopio magnitudo apparens ad veram, sive quae nudo oculo percipitur, est ea quae foci distantiae lentis exterioris ad foci distantiam ocularis. Ergo in telescopio altero propositionis....Ga naar voetnoot2) erit haec magnitudinum ratio quae CF ad FP, seu b ad c. in altero vero [Fig. 26] quae cf ad fp, hoc est, quae d ad adc/bx, seu bx/a ad c. Sed magnitudo vera utrobique est eadem. Ergo magnitudo apparens in telescopio priore ad eam quae in altero se habebit ut b [ad bx/a, hoc | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 496]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
vraie est la même dans les deux cas. Par conséquent, la grandeur apparente dans le premier télescope est à celle dans l'autre comme b est à bx/a, c'est-à-dire comme a est à x, ou comme l'un des diamètres des ouvertures est à l'autre; ce qu'il fallait démontrer. Il s'ensuit qu'en partant du grossissement, qui, dans le cas du télescope de 30 pieds, s'exprime par le rapport 109:1, on a putrouver tous les autres grossissements d'après le rapport des ouvertures. Ces grossissements sont portés dans le tableau suivantGa naar voetnoot2).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 497]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
est, ut a ad x]Ga naar voetnoot1), sive ut aperturarum diametri, [quod erat probandum]Ga naar voetnoot1). [Quare ex]Ga naar voetnoot1) amplificatione quae est [in]Ga naar voetnoot1) 30 pedum telescopio [ut 109 ad 1, caeterae omnes ex]Ga naar voetnoot1) proportione aperturarum repertae sunt [et in Tabulam sequentemGa naar voetnoot2) relatae]Ga naar voetnoot1).
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 498]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 499]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 500]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition VIII.Si dans deux télescopes possédant des lentilles extérieures égales, mais dont les ouvertures sont différentes, tandis que les diamètres de ces ouvertures et les distances focales des lentilles oculaires sont entre eux dans un même rapport, on apercevra tous les objets avec une netteté égale à l'aide de chacun d'eux, et les largeurs apparentes des objets seront entre elles dans le rapport inverse, tandis que les clartés seront entre elles dans un rapport égal à la quatrième puissance du rapport direct. Supposons égales, pour les rayons rouges parallèles à l'axe, les distances focales CF [Fig. 28], cf [Fig. 29] des lentilles AA et aa, et de même, pour les rayons violets, les distances focales CB, cb. Mais supposons inégales les ouvertures, dont les diamètres sont AA et aa respectivement. Et puissent les distances focales FP, fp des lentilles oculaires être entre elles dans le même rapport. Ensuite, après avoir tracé dans les deux cas, comme plus hautGa naar voetnoot1), les droites ABD, AF, FD et FQ, joignons aussi les points Q et P. Vu qu'alors CB et BF sont l'une et l'autre égales dans les deux cas, d'après la nature de l'aberration dont nous parlonsGa naar voetnoot2), nous aurons FQ:fq = AA:aa. Mais c'est là aussi, par supposition, le rapport FP:fp. Par conséquent, les angles FPQ, fpq, seront égaux; avec lesquels les angles FDQ, fdq sont considérés comme identiques, parce que les angles PFD sont supposés fort petits. Mais de cette égalité des angles FDQ et fdq l'on conclut, comme à propos de la proposition précédenteGa naar voetnoot3), que la même aberration a lieu dans les deux cas au fond de l'oeil, et qu'on aperçoit l'image de l'objet avec une netteté égale lorsqu'on se sert de l'un ou de l'autre télescope. Ensuite, d'après ce que nous avons démontréGa naar voetnoot4), la vérité de la deuxième partie de la proposition est manifeste, savoir que les grandeurs des images seront entre elles dans le rapport inverse de celui des distances focales, dans le cas bien entendu où les lentilles extérieures sont les mêmes dans les deux télescopes. Enfin ce qui est dit du rapport des clartés des images sera démontré comme il suit. Comme les distances focales des lentilles AA, aa sont égales, la grandeur apparente des images serait la même dans les deux cas, si les lentilles PD et pd elles aussi étaient égales. La clarté de la première image serait alors | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 501]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio VIII.]Si in Telescopijs duobus, aequales exteriores lentes habentibus, differant inter se aperturarum diametri, et eadem quoque proportione foci distantiae lentium ocularium; aeque distinctè ijs omnia conspicientur; apparentesque visibilium latitudines ejus proportionis contrariam habebunt. claritates vero directae quadruplicatam.  [Fig. 28.]
 [Fig. 29.]
Sint lentium AA [Fig. 28], aa [Fig. 29] aequales foci distantiae CF, cf ex radijs axi parallelis coloris rubri, itemque aequales CB, cb foci distantiae ex radijs coloris violacei. aperturae autem inaequales quarum diametri AA, aa. eandemque his proportionem habeant lentium ocularium foci distantiae FP, fp. Porro ductis utrobique, ut supraGa naar voetnoot1), rectis ABD, AF, FD, FQ, jungantur etiam QP. Quia ergo tam CB quam BF sunt utrimque aequales, ex natura aberrationis, de qua agimusGa naar voetnoot2); erit FQ ad fq ut AA ad aa. Sed ita quoque est, ex hypothesi, FP ad fp. Ergo aequales erunt anguli FPQ, fpq, a quibus nihil differre censentur FDQ, fdq. quia anguli PFD minimi esse intelliguntur. Ex hac vero aequalitate angulorum FDQ, fdq, conficitur, sicut prop. praecedentiGa naar voetnoot3), eandem utrobique in oculi fundo fieri aberrationem, [atque] aeque distinctam utroque telescopio cerni rei visae imaginem. Porro secunda pars propositionis ex supra demonstratisGa naar voetnoot4) manifesta est, nempe latitudines rei visae fore in proportione contraria foci distantiarum quae in lentibus ocularibus, quum nempe lentes exteriores utrobique eaedem. De claritatis vero proportione sic probabitur. Cum aequales sint lentium AA, aa foci distantiae, si aequales quoque essent lentes PD, pd eadem utrimque appareret rei visae magnitudo; claritas autem esset ad claritatem, sicut quadr. ex AA ad qu. ex aa, hoc est, sicut circuli aperturarum, quia hanc rationem habet | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 502]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
à celle de la deuxième, comme le carré de AA est à celui de aa, c'est-à-dire comme les cercles des ouvertures sont entre eux, parce que c'est là le rapport des quantités de rayons reçus de chaque point de l'objet. Mais dans le cas présent l'image produite au fond de l'oeil par le télescope CP est à celle produite par le télescope cp comme le carré de fp est au carré de FP; par conséquent, la clarté du télescope CP serait à celle du télescope cp dans le rapport inverse, c'est-à-dire de FP2 à fp2, si seulement la même quantité de lumière était repanduc sur les deux images. Mais en vérité le télescope CP reçoit plus de lumière que le télescope cp dans ce même rapport, à cause de la plus grande ouverture. Par suite, la clarté donnée à l'image par ce télescope sera à celle de l'image de l'autre télescope comme la quatrième puissance de AA est à celle de aa. C'est ce qu'il restair à démontrer. Par conséquent, si nous supposons égales les distances focales CF et cf, et si le diamètre de l'ouverture AA est le double du diamètre aa, et de même la distance focale FP le double de la distance focale fp, la clarté du télescope CP sera seize fois plus grande que celle du télescope cp. Cependant ce qui a été démontré à propos de l'égalité dans les deux cas de la netteté de l'image, ne s'accordera pas entièrement avec l'expérience: en effet, lorsque la clarté sera plus grande, l'inconvénient du brouillard qui résulte de l'aberration sera plus grand; la raison en est la même que celle dont nous avons parlé un peu plus haut en comparant les observations diurnes aux observations de nuitGa naar voetnoot1). Et on trouvera qu'il en est ainsi aussi bien lorsqu'on regarde avec les deux télescopes que lorsqu'on contemple le même objet avec le même télescope en lui donnant des ouvertures différentes. Mais si l'on se sert de la même ouverture pour regarder des objets de clarté différente, cette cause là aussi donnera lieu à un plus fort nuage dans le cas où la lumière est la plus forte. Il paraît donc que pour observer les planètes plus obscures il faut se servir d'une ouverture un peu plus grande que pour contempler les planètes plus lumineusesGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition IX.Appliquer les télescopes du tableau précédent à tous les objets soit pour des observations diurnes soit pour des observations nocturnesGa naar voetnoot3). Il faut savoir que les télescopes déterminés par les nombres du tableau donné plus hautGa naar voetnoot4) doivent être employés à l'observation des étoiles. Or, je viens de direGa naar voetnoot5) qu'il faut une plus grande quantité de lumière dans le cas de ceux dont nous | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 503]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
copia radiorum ab unoquoque visibilis puncto receptorum. at nunc imago in fundo oculi ex telescopio CP, ad eam quae ex telescopio cp est, ut qu. fp ad qu. FP, ideoque hanc proportionem inversam, hoc est, quam qu. FP ad quad. fp haberet claritas telescopij CP ad claritatem telescopij cp, si tantùm lux aequalis in utramque effunderetur. nunc vero secundum eandem proportionem plus lucis excipitur telescopio CP quam cp, propter majorem aperturam. Ergo claritas imaginis per hoc intromissa erit ad alteram in ratione quadratoquadratorum AA ad aa. quod ostendendum supererat. Si ergo positis foci distantijs aequalibus CF, cf, aperturae diameter AA sit dupla aa, itemque foci distantia FP dupla fp, erit telescopij CP claritas sexdecupla ejus quae telescopij cp. Quod autem de distincta visione utrobique aequali demonstratum est, non exacte ita experimento conveniet, sed in majori claritate majus erit nebulae incommodum quae ex aberratione oritur, ob eandem quam paulo ante attulimus causam cum diurnas observationes nocturnis conferremusGa naar voetnoot1). Et hoc quidem ita invenitur si utroque telescopio, sive eodem cum diversis aperturis idem visibile inspectetur. Quod si ad visibilia diversae claritatis eadem apertura adhibeatur, rursus ex illa causa major nebula orietur ubi major erit lux. ac propterea obscurioribus Planetis paulo major apertura quam illustrioribus danda videturGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio IX].[Tabulae praecedentis telescopia visibilibus omnibus sive diurnis sive nocturnis applicare.]Ga naar voetnoot3) Quae in Tabula superioreGa naar voetnoot4) exhibentur telescopia, ad siderum observationes adhiberi sciendum. Dixi vero non multo antèGa naar voetnoot5), plus lucis requiri in ijs quibus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 504]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nous servons le jour; car, lorsque les yeux ont été éblouis par la grande clarté du jour et qu'on les applique ensuite au télescope, on voit obscurément ce qui paraîtrait lumineux à travers les ténèbres de la nuit. En effet, en me servant pour des observations de jour des télescopes décrits dans le tableau, j'ai constaté expérimentalement qu'il fallait y changer les lentilles oculaires en appliquant d'autres de distance focale à peu près doubleGa naar voetnoot1). La clarté deviendra ainsi quatre fois plus grande, parce que la surface des images sera réduite dans la même proportion; car la quantité des rayons restera la même, attendu que l'ouverture de la lentille extérieure n'a pas été changée, et les rayons éclaireront donc davantage un espace plus restreint. Or, si l'on ne change pas la lentille oculaire mais qu'on augmente l'ouverture, la clarté deviendra, il est vrai, plus grande, mais l'image sera plus voilée à cause de la plus grande aberration; c'est pourquoi il ne faut pas vouloir remédier à l'obscurité de l'image de cette façon. Mais on pourrait se demander à cette occasion pourquoi, lorsque nous substituons une lentille oculaire moins forte et que l'aberration examinée jusqu'ici est donc diminuée, on ne pourrait augmenter en même temps l'ouverture de la lentille extérieure jusqu'à ce que l'aberration est de nouveau devenue la même que celle qui correspond au télescope construit d'après le tableau. Car de cette façon on augmentera la clarté sans pourtant diminuer aucunement la netteté de la visionGa naar margenoot*. Mais il faut répondre à cette question en se basant sur une remarque déjà faite plus hautGa naar voetnoot5), savoir que le nuage provenant de l'aberration Newtonienne nuit d'autant plus à la netteté que l'image formée sur le fond de l'oeil est plus lumineuse, puisqu'en même temps ce nuage devient plus lumineux. Et l'expérience nous fait voir qu'il en est ainsi: nous observons que dès qu'on augmente de cette sorte l'ouverture des télescopes diurnes, le nuage provenant de l'aberration commence à nuire à la netteté de l'image devenue plus lumineuse. Il ne faut donc rien changer aux ouverturesGa naar voetnoot6). On peutGa naar voetnoot7) demander en outre, s'il n'est pas utile, lorsqu'un télescope adapté | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 505]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
interdiu utimur, quia scilicet multa diei. claritate praestinctis oculis atque inde telescopio admotis obscurum videtur, quod per noctis tenebras lucidum esset. Eadem itaque telescopia quae in Tabula descripta sunt cum ad diurnas observationes adhiberem, experiendo comperi mutandas in ijs oculares lentes, appositis quarum foci distantiae duplae circiter sint priorumGa naar voetnoot1); ita claritas fiet quadrupla, quia eadem proportione diminuentur imagines ratione superficiei; manebit enim eadem radiorum quantitas, ob nihil mutatam aperturam lentis exterioris, ac proinde clarius efficient angustius spatium. Quod si non mutata oculari lente apertura augeatur, augebitur quidem claritas sed fiet nebula major ex majori aberrationeGa naar voetnoot2), eoque hoc remedio non est utendum. Hinc veroGa naar voetnoot3) quaeri potest, cum substituta lente oculari minus acutâ, minuatur aberratio ea quam hactenus examinavimus, cur non simul eousque augeri queat apertura lentis exterioris quoad eadem rursus aberratio existat, quae secundum tabulam ordinato telescopio inerat. Sic enim plus lucis accrescet, nec tamen quidquam decedet visioni distinctaeGa naar margenoot*. Responsum vero inde petendum quod superius jam attigiGa naar voetnoot5) nebulam nempe illam ex aberratione Newtoniana magis nocere si lucidior in fundo oculi imago pingatur; simul enim et nebulae lux increscet. et hoc reipsa experimur, simul ac augetur diurnorum hujusmodi apertura nebulam ex aberratione in lucidiore visibili nocere incipere. Itaque nihil mutandae sunt aperturaeGa naar voetnoot6). RursusGa naar voetnoot7) quaeri potest, si Telescopium Saturni observationibus aptum, ad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 506]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
aux observations de Saturne est dirigé vers la Lune qui est cent fois plus lumineuse (je ne parle pas de la quantité totale de lumière, mais de celle émise par les diverses parties), vu qu'elle est dix fois plus près du Soleil, s'il n'est pas utile, dis-je, de diminuer la largeur de l'ouverture et en même temps la distance focale de la lentille dans la même proportion, de sorte que la clarté des régions de la Lune ne devienne pas plus grande que celle de l'image de Saturne, mais que le grossissement soit beaucoup plus fort. Dans le télescope de 30 pieds on pourrait par exemple réduire à √9/10 pouce le diamètre de l'ouverture qui est maintenant de 3 poucesGa naar voetnoot1), ce diamètre serait donc réduit au tiers à peu près de sa valeur primitive; et en même temps on pourrait diminuer dans la même proportion la distance focale de la lentille oculaire. En effet, de cette façon, pour un observateur regardant le même objet, la clarté serait réduite dans un rapport égal à la quatrième puissance du rapport 3:√9/10, d'après la proposition VIIIGa naar voetnoot2); c'est-à-dire dans le rapport 100:1. Et comme les parties de la Lune sont cent fois plus lumineuses que celles de Saturne, l'image de la Lune resterait également lumineuse que celle de Saturne obtenue antérieurement. Mais d'après la même proposition l'aberration au fond de l'oeil sera aussi la même dans les deux cas, et le grossissement de la Lune surpassera celui de Saturne dans le rapport 3:√9/10, qui est supérieur à 3. Il semble ainsi que ce changement de l'ouverture et de la lentille oculaire serait fort avantageux. Mais en réalité il en est tout autrement. Il faut donc indiquer la cause de ce phénomène. Je dis que cette cause est double. D'abord chaque petite partie du disque lunaire sera vue mieux et plus exactement si l'on laisse au télescope toute sa lumière que si on la réduit à sa centième partie, quoique cet effet ne soit pas en rapport avec une si grande différence. La seconde cause c'est que, lorsqu'on rétrécit trop l'ouverture, la pureté du contour des images disparaît. Il faut considérer ceci soigneusement et apprendre à connaître les limites fixées ici par la nature. En effet, plus l'ouverture est diminuée, plus minime aussi devient le diamètre du petit cylindre suivant lequel les rayons issus d'un point quelconque de l'objet parviennent à l'oeil; dans la figure 25 appartenant à la proposition VIIGa naar voetnoot4) le rayon de ce petit cylindre est PO; or, si le double de ce rayon, en d'autres termes le diamètre entier, est long de ⅕ à ⅙ ligneGa naar voetnoot5), c'est-à-dire moindre que 1/60 ou 1/72 pouce, le contour net des images disparaît par une cause inconnue, inhérente à la constitution naturelle de l'oeil, soit qu'il faille chercher cette cause dans la choroïde ou dans la rétine, soit qu'elle provienne de la nature des humeurs de l'oeil. Car aussi, lorsqu'on place devant l'oeil nu une lamelle munie d'une ouverture large de moins de ⅕ ou ⅙ ligne, les bords des objets commencent à paraître moins nets, et la confusion deviendra plus grande plus on diminue la largeur de l'ouverture. Or, on démontre aisément dans le cas de l'exemple considéré que le petit cylindre qui pénètre dans l'oeil devient plus étroit qu'il ne devrait l'être. En effet, d'après la règle des ouverturesGa naar voetnoot6), la distance focale de la lentille oculaire devient égale à 11/10 √9/10 ligne. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 507]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lunam convertatur, quae centuplo lucidior est (non tota inquam sed partibus singulis) quippe decuplo Soli propinquior, an non utiliter aperturae latitudo imminui possit, simulque eadem proportione lentis ocularis foci distantia; ut fiat regionum Lunae claritas non major quam quae erat in Saturno, amplificatio vero multo major evadat. Velut in telescopio 30 pedum, si diameter aperturae 3 pollicumGa naar voetnoot1) reducatur ad √9/10 pollicis, quae paulo minus efficiunt quam partem tertiam prioris, simulque foci distantia lentis ocularis eadem proportione diminuatur; hic enim idem visibile respicienti esset claritatis proportio quadruplicata ejus quae 3 ad √9/10, ex propos. [VIII]Ga naar voetnoot2) hoc est, ea quae 100 ad 1; cumque Lunae regiones sint centuplo clariores quam Saturni, maneret eadem claritas in Luna quae prius fuerat in Saturno. sed ex eadem prop. et aberratio quoque in fundo oculi utrobique aequalis erit, et amplificatio in Luna quam Saturno major secundum rationem 3 ad √9/10, quae major est tripla. Itaque plurimum profutura haec aperturae et ocularis lentis variatioGa naar voetnoot3) videtur. at reipsa secus accidit. Igitur causa cur ita fiat dicenda est. quam duplicem esse ajo. prima enim quod melius accuratiusque cernantur partes minimae quaeque in orbe Lunari, si tota lux telescopio relinquatur, quam si centuplo minor fiat, etsi non pro hac tanta ratione differentiae. altera est, quod nimium arctata apertura pereat nitida imaginum circumscriptio, quod diligenter est notandum, et quinam hic a natura constituti sint termini noscendum. Fit nempe ut quanto magis contrahitur apertura, tanto exiliori cylindrulo ad oculum accidant radij ab uno quopiam rei visae puncto manantes, cujus cylindruli semidiameter in fig. [25] prop. [VII]Ga naar voetnoot4) est PO. Quod si duplum ejus sive diameter totus sit intra ⅕ vel ⅙ lineaeGa naar voetnoot5), hoc est, minor quam 1/60 vel 1/72 pollicis deperit illa imaginum circumscriptio, ob causam in oculi naturali constitutione latentem, sive ea in choroide aut retina quaerenda sit, sive in ipsis oculi humoribus. namque et ad nudum oculum oppositâ laminâ cum foramine quod sit infra ⅕ aut ⅙ lineae partem minus distincti visibilium termini apparere incipiunt, ac tanto confusiores quanto ulterius minuetur foramen. Facilè vero ostenditur in adducto exemplo justo angustiorem fieri cylindrulum ad oculum. Fit enim ex regula aperturarumGa naar voetnoot6), foci distantia lentis ocularis 11/10 √9/10 lineae. Sicut autem | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 508]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Mais, comme la distance focale de la lentille extérieure est à celle de la lentille intérieure, c'est-à-dire comme, dans la figure 25 de la proposition VIIGa naar voetnoot1), CF est à FP, ainsi est le diamètre de l'ouverture AA au double de PO, en d'autres termes au diamètre de ce petit cylindre. Autrement dit, comme 30 pieds ou 360 pouces sont à 11/10 √9/10 pouce ainsi est √9/10 pouce à une longueur un peu inférieure à 1/30 ligne et, par conséquent, beaucoup inférieure à ⅙ ligne. Mais dans la construction primitive et ordinaire du télescope, on avait que comme 360 pouces étaient à 3 3/10 pouces, ainsi 3 pouces à 11/400 pouce ou ⅓ ligne à-peu-près; cette dernière grandeur représentant le diamètre du petit cylindre, dont l'étroitesse n'était donc pas telle qu'elle pouvait être nuisible. Mais le diamètre de l'ouverture et en même temps la distance focale de la lentille oculaire ne pourraient être diminués de beaucoup plus d'un tiers de leur grandeur, parce que déjà alors la largeur du cylindre près de l'oeil excède à peine ⅕ ligneGa naar voetnoot3). Et c'est ce qui arrive pour chaque longueur du télescope; attendu que dans notre tableau les télescopes ont des dimensions telles que pour chacun d'eux cette largeur auprès de l'oeil est la même, comme je le démontrerai un peu plus loin. Par conséquent, même si nous voulions tourner le télescope de Saturne à Vénus, dont la clarté est 225 fois plus grande, il ne faudrait pas diminuer l'ouverture de plus d'un tiers; mais s'il reste une trop grande clarté, il faut y remédier à l'aide d'un verre couvert d'une légère couche de noir de fumée. La diminution de l'ouverture nuit encore d'une autre façon. En effet, chacune des taches et des petites bulles qui se trouvent dans la lentille oculaire apparaît alors plus nettement, attendu que chacune d'elles intercepte toute la largeur ou une partie de la largeur du petit cylindre dont nous avons parlé et, par conséquent, une petite partie de l'objet. QuantGa naar voetnoot4) à mon assertion, d'après laquelle la largeur du petit cylindre lumineux tombant sur l'oeil se trouve être égale pour tous les télescopes de notre tableau, elle peut être prouvée brièvement comme il suit. Dans les figures appartenant à la proposition VIIGa naar voetnoot5) les rayons des petits cylindres de cette espèce dans deux télescopes de longueur différente sont PO et po. Et comme FC:CA = FP:PO, on aura PO = ac/b; de même, comme fc:ca = fp::po, tandis que fc = a et ca = x et que nous avons trouvé fp = adc/bxGa naar voetnoot6), on obtiendra po = ac/b. Par conséquent, po sera égale à PO, ce qu'il fallait démontrer. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 509]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
foci distantia lentis exterioris ad interioris, hoc est, sicut in fig. [25] Prop. [VII]Ga naar voetnoot1) CF ad FP, ita est diameter aperturae AA ad duplam PDGa naar voetnoot2), seu ad diametrum istius cylindruli. hoc est, sicut 30 ped. seu 360 poll. ad 11/10 √9/10 unius pollicis ita sunt √9/10 ad non totam 1/30 unius lineae, longe nempe minorem quam ⅙. Sed in priore atque ordinaria telescopij constitutione, erat sicut 360 poll. ad pollices 3 3/10 ita 3 poll. ad 11/400 pollicis, seu ferè ⅓ lineae, cylindruli diametrum, cujus itaque nequaquam ea est angustia quae nocere possit. Non multo amplius vero quam tertia sui parte diameter aperturae ac simul lentis ocularis foci distantia diminui possent, quia jam hinc fit latitudo ad oculum quae vix excedat ⅕ lineaeGa naar voetnoot3); idque in omni telescopij longitudine locum habet; quandoquidem in Tabula nostra ita ordinata sunt ut in omnibus Latitudo ista ad oculum sit eadem, ut paulo post demonstrabo. Etiamsi igitur a Saturno ad Venerem convertere telescopium velimus, cujus claritas major est 225 vicibus, non tamen ulterius contrahenda est apertura quam parte tertia; sed si nimia claritas supersit ea leviter infecto fuligine vitro est auferenda. Nocet enim alia quoque ratione diminutio aperturae, quod nimirum naevi et bullae quaeque exiguae quae lenti oculari insunt magis apparent, quippe totam cylindruli de quo diximus latitudinem vel partem ejus intercipientes, eoque et particulam rei visae. QuodGa naar voetnoot4) autem dixi latitudinem cylindruli radiosi oculo incidentis in omnibus Tabulae nostrae Telescopijs eandem reperiri, paucis ostendi potest. Sunt enim in schemate prop. [VII]Ga naar voetnoot5) ejusmodi cylindrulorum in duobus diversae longitudinis telescopijs semidiametri PO, po. Cumque sit ut FC ad CA ita FP ad PO, erit PO ∞ ac/b. ac similiter cum sit ut fc ad ca ita fp ad po; fc vero sit ∞ d; ca vero ∞ x, et fp sit inventa ∞ adc/bxGa naar voetnoot6), fiet po ∞ ac/b, ideoque aequalis PO, quod erat ostendendum. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 510]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
J'en conclus enfin que rien ne nous empêche d'allonger indéfiniment les télescopes, et cela avec un effet toujours plus grand, pourvu que nous observions les lois du tableau antérieur. En effet, et la clarté et la netteté restent alors partout les mêmes comme cela résulte de la proposition VIIGa naar voetnoot1) sur laquelle le tableau est fondé; et l'inconvénient dont nous avons parlé en dernier lieu, qui résulte de l'étroitesse du faisceau lumineux auprès de la pupille, est absent dans chaque casGa naar voetnoot2). Maisavant de quitter les télescopesGa naar voetnoot3), je montrerai comment on peut observer les petites étoiles et surtout les satellites de Jupiter et de Saturne, en augmentant beaucoup et plus que de coutume l'ouverture de la lentille extérieure et en même temps la distance focale de l'oculaireGa naar voetnoot4). En effet, comme ces corps célestes quoique observés à l'aide du télescope, n'apparaissent que comme des points, à rien ne sert d'augmenter leurs diamètres: il faut plutôt qu'ils deviennent brillants de lumière autant que possible. Or, c'est ce qu'on obtient ici surtout en augmentant les ouvertures. Car lorsque l'ouverture est rendue deux fois plus grande selon le diamètre, on recueille une quantité de lumière quatre fois plus grande provenant du corps céleste. Or, si l'on double en même temps la distance focale de la lentille oculaire, la netteté sera la même que primitivement; pourtant la clarté ne deviendra pas 16 fois plus grande, comme cela résulterait du calcul fait plus hautGa naar voetnoot5) mais restera quadruple; parce que, comme je l'ai déjà dit, l'image du corps céleste sur le fond de l'oeil est pour ainsi dire un point et qu'il suffit, par conséquent, de considérer la quantité de lumière tombant sur l'oeil: plus cette quantité sera grande, plus le corps céleste lui-même sera aperçu clairement et aisément. Il en est autrement si l'on observe avec ce télescope la lune ou une des planètes primairesGa naar voetnoot7), dont les différentes parties recevront chacune une quantité de lumière seize fois plus grande. Or, nous pourrons par cette amplification de l'ouverture augmenter beaucoup la force du télescope pour l'observation des étoiles fort petites ou des satellites de SaturneGa naar voetnoot8). Et peut-être pourrons-nous avec un télescope long de 30 pieds ayant une ouverture deux fois plus grande que de coutume, c'est-à-dire une ouverture de 6 pouces, obtenir les mêmes résultats qu' autrement avec un télescope de 120 pieds, auquel fut attribué dans le tableau antérieurGa naar voetnoot9) une telle largeur d'ouvertureGa naar voetnoot10). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 511]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Atque hinc denique concludo nihil obstare quin servatis Tabulae superioris legibus quousque lubet Telescopiorum longitudines producamus, idque semper majore cum effectu. Quandoquidem et claritas et distinctio eadem ubique manet ut patet ex Prop. [VII]Ga naar voetnoot1) quam Tabula pro fundamento habet; et hoc quoque posterius incommodum, ex angustia radiationis ad pupillam, peraeque abestGa naar voetnoot2). Priusquam vero a Telescopijs discedamusGa naar voetnoot3), ostendam quomodo observari possint stellulae exiguae ac praecipue satellites Jovis ac Saturni, aucta insigniter ac praeter solitum apertura exterioris lentis, simulque ocularis foci distantiaGa naar voetnoot4). Quia enim velut puncta tantum apparent haec sidera, licet telescopio spectata; nihil prodest eorum diametros augeri, sed oportet quanta possunt luce clarescant. Hoc autem praecipue hic fit auctis aperturis. Duplicata enim apertura secundum diametrum, quadrupla lux à sidere profluens colligitur. Quod si simul lentis ocularis foci distantia duplicetur, orietur distinctio eadem quae ab initio, non tamen fiet claritas sexdecupla, quanta ex superiore ratiocinioGa naar voetnoot5), sed quadrupla manebit; quoniam ut jam dixi imago sideris in fundo oculi est instar puncti, eoque tantùm lucis quantitas in ipsum derivata considerandaGa naar voetnoot6) est; quae quantò major, tantò clarius faciliusque sidus ipsum conspicietur. quod aliter est si lunam aut planetarum primariorumGa naar voetnoot7) aliquem hoc telescopio intueamur, quorum partes singulae sexdecuplam lucem accipient. Poterimus autem hac aperturae ampliatione plurimum augere vim telescopij in deprehendendis stellis minimis aut Saturni ComitibusGa naar voetnoot8), ac forsan 30 pedibus longo cum apertura solitae dupla seu 6 poll. lata tantundem efficere quantum alias telescopio pedum 120 cui in superiore TabulaGa naar voetnoot9) tanta aperturae latitudo attributa fuitGa naar voetnoot10). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 512]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Des Microscopes.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 513]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
De Microscopiis.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 514]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
D'ailleurs les microscopes simples dont j'ai parlé et qui étaient autrefois réputés moins bons, ont été améliorés il y a peu de temps à ce point qu'ils surpassent tous les autres dans la puissance d'agrandir. Ils se composent soit d'une seule petite lentille convexe soit d'une petite sphère en verre placée près de l'oeil; nous exposerons d'abord les raisons et les causes de chacune de ses dispositions. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Proposition X.]Exposer la construction et l'emploi des microscopes simplesGa naar voetnoot2). L'effet de la petite lentille se conçoit aisément d'après ce que nous avons écrit en général à la Prop. III, Livre II, Part. IGa naar voetnoot3) sur le grossissement dû à une lentille convexe. En effet, soit N la lentille (fig. 30), supposons l'objet placé en R, son foyer, et l'oeil O fort près de la lentille. Les rayons issus du point R et réfractés se rendront parallèlement à l'oeil O et donneront lieu à une vision distincte. Or, l'objet QRQ sera aperçu en même grandeur que si la lentille N était absente et qu'au lieu d'elle il y avait une lamelle percée d'une petite ouvertureGa naar voetnoot4), c'est-à-dire il sera vu sous l'angle QNQ. De sorte que la lentille interposée n'a ici d'autre effet que de rendre distincte la vision qui sans la lentille serait confuseGa naar voetnoot5). Mais comme la vision ne devient distincte pour l'oeil nu que lorsque celui-ci est à une certaine distance, de 8 pouces par exemple, on pourra dire que l'image apparente est maintenant grossie dans un rapport égal à celui de ces 8 pouces au petit espace NR, c'est-à-dire à la distance focale de la petite lentille N; de sorte que si cette distance est égale à la cinquième partie d'un pouce, le grossissement linéaire sera 40:1. Plus donc la distance focale de la petite lentille N est petite, plus grand aussi sera son pouvoir de grossir l'image d'un petit objetGa naar voetnoot6); toutefois il se | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 515]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Caeterum simplicia quae dixi microscopia, cum ante hac minoris fierent haud pridem eo perducta fuere ut caeteris omnibus in augendis virtuteGa naar voetnoot1) antecellant. Fiunt autem vel lenticula una convexa, vel sphaerula vitrea prope ad oculum admota, quorum utriusque rationes causasque hic primum exponemus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio X.][Simplicium microscopiorum rationes et usus exponere.]Ga naar voetnoot2)Lenticulae effectus ex ijs facile intelligitur, quae de amplificatione convexae lentis in universum scripsimus Prop. [III, Lib. II, Part. I]Ga naar voetnoot3). Sit enim lens N  [Fig. 30.]
[Fig. 30], res visa ad R focum nempe ejus, oculus O proxime lenti admotus. Jam radij ex R egressi ac refracti mittentur ad oculum O paralleli, distinctamque visionem efficient. Visibile autem QRQ eadem magnitudine cernetur ac si lens N abesset, et in locum ejus lamina cum exiguo foramine constituereturGa naar voetnoot4), nempe angulo QNQ. ut proinde nihil aliud hic praestet interposita lens, quam ut distincta fiat visio, quae absque lente confusa foretGa naar voetnoot5). Sed cum nudo oculo ita demum distincta fiat si spatio aliquo, puta 8 pollicum, oculus distet; tanto nunc auctior imago apparens dici poterit quanto 8 pollices isti majores sunt spatiolo NR, seu foci distantiâ lenticulae N, quae si pollicis quintam partem aequet, erit augmentum velut 40 ad 1, ratione diametri. Quanto igitur minor erit foci distantia lenticulae N, tanto major erit effectus ejus in dilatanda rei minutae specieGa naar voetnoot6); quamquam obstacula quaedam hic sese | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 516]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
présente ici certains obstacles que nous devons mentionner plus tard et qui empêchent de dépasser certaines limitesGa naar voetnoot1). Et la même chose a lieu dans le cas des petites sphères qui, comme nous l'avons dit, peuvent être employées ici en guise de lentilles; lesquelles d'ailleurs peuvent aisément être fabriquées aussi petites qu'on le désire. Ces sphères ne sont inférieures aux petites lentilles, si les unes et les autres sont en verre, que sous un seul rapport: pour un même grossissement les petites lentilles sont trois fois plus distantes de l'objet; elles laissent donc libre un espace à travers lequel la lumière peut être admise latéralement. De cette façon on peut observer les couleurs des objets, tandis qu'autrement il faut tourner le microscope vers la lumière directe et contempler seulement des objets si minces qu'ils sont transparents. L'effet obtenu avec la petite sphère, et ce que nous avons dit de la distance trois fois moindre, est démontré de la façon suivanteGa naar voetnoot3): Considérons une sphère en verre à centre K (fig. 31) et à axe AB; plaçons sur cet axe, prolongé des deux côtés, l'oeil en D et l'objet en C; les distances AD et BC étant chacune égale au quart du diamètre AB. Le point C est donc le point de concours des rayons parallèles à l'axe AB qui tombent sur la surface AHGa naar voetnoot4). C'est pourquoi l'objet placé en C enverra, par suite de la réfraction due à la sphère, des rayons parallèles à l'oeil situé au point D; par conséquent, la vision deviendra distincte. Si l'on prolonge BD jusqu' en L, de sorte que AL soit égale au diamètre AB, et si, d'après la proposition XII, Liv. I, Part. IGa naar voetnoot5), on choisit le point F de telle manière que DL:DK = DA:DF, D sera le point de concours des rayons qui dans la sphère correspondent au point F, tels que GH. Or, de même que DL et DK sont égales, de même aussi DA et DF le seront. Supposons maintenant GE parallèle à l'axe et puisse ce rayon intercepter la ligne CE de l'objet. Tirons en outre la droite ED. Le rayon EG, réfracté au point G, se meut donc selon GH et, réfracté de nouveau au point H, il continue sa route et atteint l'oeil au point D. C'est pourquoi la ligne CE est vue sous l'angle ADH, tandis que, contemplée à l'oeil nu, elle occuperait l'angle CDE, que je dis être la moitié de l'angle précédent. En effet, comme AF est le double de AD, l'angle ADH sera le double de l'angle AFH. Or, DE est parallèle à FG, parce que GE est d'abord parallèle à FD et peut être considérée comme égale à cette dernière droite ou à la droite BC, attendu que la petite ligne CE est, par hypothèse, de fort petite dimension par rapport au diamètre de la sphère. Par conséquent, l'angle ADH sera aussi double de l'angle CDE; l'angle ADH est donc égal à l'angle CKE. Il s'ensuit que, l'oeil étant placé au point D (ou en un autre point quelconque sur le prolongement de l'axe BA d'après la prop. XIII du Livre II, Part. IGa naar voetnoot7)), la ligne CE apparaîtra sous le | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 517]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
afferunt in sequentibus memoranda, quae ultra certos terminos progredi vetantGa naar voetnoot1). Atque idem in sphaerulis accidit quae ut diximus pro lentibus hic adhiberi possunt; quas alioqui quantumvis exiguas facile parare licet. Hae vero hoc uno lenticulis cedunt si utraeque sint vitreae, quod in pari amplificatione triplo amplius a visibili lenticulae distent, eoque spatium praebeantGa naar voetnoot2), quo lateralis lux immittatur. Sic enim rerum colores conspicere licet, cum alioqui directae luci obvertendum sit microscopium, et tantum quae tenuitate sua pellucent intuenda. Effectus vero sphaerulae, atque hoc quod diximus de triplo minore distantia sic [Fig. 31.]
 [Fig. 32.]
demonstranturGa naar voetnoot3): Sit sphaera vitrea cujus centrum K [Fig. 31], axis AB, in quo utrimque producto statuatur oculus ad D; visibile ad C; positis distantijs singulis AD, BC diametri AB quadrantibus. Est ergo punctum C concursus radiorum axi AB parallelorum qui incidunt in superficiem AHGa naar voetnoot4); quare visibile in C positum, mittet radios ex refractione sphaerae parallelos ad oculum in D, eoque fiet visio distincta. Producta autem BD ad L, ut AL sit diametro AB aequalis, si fiat secundum propos. [XII, Lib. I, Part. I]Ga naar voetnoot5) ut DL ad DK, ita DA ad DF, erit in puncto D concursus radiorum intra sphaeram positorumGa naar voetnoot6) et ad punctum F pertinentium, qualis GH. Sicut autem aequales DL, DK, ita quoque erunt DA, DF. Sit jam GE axi parallela, atque intercipiat rei visae lineam CE, ac ducatur recta ED. Radius ergo EG, fractus ad G, incedit secundum GH, et rursus fractus ad H, pergit ad oculum in D. quamobrem linea CE spectatur angulo ADH, quae nudo oculo occuparet ang.m CDE. quem dico illius esse dimidium. Quia enim AF dupla ad AD, erit angulus ADH duplus AFH. Est autem DE parallela FG, quia GE et parallela est FD, et huic ipsi sive rectae BC aequalis censenda, quia CE lineola velut minima habetur ratione sphaerae diametri. Erit ergo anguli quoque CDE duplus ADH; qui aequalis proinde angulo CKE. Unde liquet oculo ad D collocato, (sive utcunque alibi in producto axe BA per prop. [XIII, Lib. II, Part. I]Ga naar voetnoot7) apparituram lineam | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 518]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
même angle sous lequel cette ligne serait vue à l'oeil nu par un observateur regardant du point KGa naar voetnoot1). Si donc le diamètre AB de la petite sphère est de 1/12 pouceGa naar voetnoot2), et c'est de sphères de cette grandeur que nous nous servons habituellementGa naar voetnoot3), KC devient égale à 1/16 pouce, distance qui est à celle de 8 pouces comme 1 est à 128. Par conséquent, dans ce cas le grossissement est exprimé par le rapport 128:1; il est donc sans doute fort considérable. Mais si la distance focale NR de la lentille N [Fig. 32] est égale à la droite KC, l'objet RQ, comme nous l'avons dit, sera vu à travers cette lentille en même grandeur que lorsque l'oeil avait été placé en N et que la lentille était absente; et la grandeur apparente ne change pas en quelque endroit de l'axe prolongé RN que l'on place l'oeil. Il s'ensuit donc que le même grossissement et en général le même effet est obtenu par la lentille N et par la sphère AB. Il est établi en outre que la distance RN est égale à trois fois la distance BC; ce qu'il fallait démontrer. Nous avons négligé ici l'épaisseur de la lentille NQ ce qui est permis lorsque la distance focale NR est égale à un pouce ou n'est pas beaucoup plus petite. Mais comme les lentilles très menues sont pratiquement les meilleures, par exemple celles qui sont formées des deux côtés dans une cavité sphérique dont le demidiamètre ne surpasse pas le douzième d'un pouce, il faut nécessairement leur laisser une certaine épaisseur, afin qu'elles ne deviennent pas incapables d'être maniées à cause de leur extrême petitesse et qu'elles ne prennent pas moins bien la forme sphérique. Il en résulte que la distance, dont j'ai parlé, de la lentille à l'objet s'amoindrit. Considérons par exemple (Fig. 33) une petite lentille ST, dont la surface coupée par un plan donne des arcs SXT et SVT égaux au tiers d'une circonférence, c'est-à-dire décrits des centres X et V avec le rayon XV. Pour que cette lentille produise le même grossissement de l'objet que la petite sphère AB [Fig. 31], il faut que XV devienne égale au rayon KB augmenté d'un quartGa naar voetnoot4); d'où il s'ensuit que la distance focale VY est égale au double de BCGa naar voetnoot5) ou à ⅔ NR. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 519]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 31].
 [Fig. 32.]
CE angulo eodem quo nudo oculo appareret intuenti ex puncto KGa naar voetnoot1). Unde si diameter sphaerulae AB sit 1/12 pollicisGa naar voetnoot2), qualibus uti solemusGa naar voetnoot3), fit KC ∞ 1/16 pollicis cujus ad distantiam 8 pollicum ea est ratio quae 1 ad 128; adeo ut amplificationis ratio tunc sit quae 128 ad 1, quae sane insignis admodum. atqui si lentis N [Fig. 32] foci distantia NR aequalis sit rectae KC, diximus ejus opera visibile RQ eadem magnitudine cerni ac si, absque lente, in N oculus poneretur; neque etiam hic mutatur apparens magnitudo ubicunque in axe producto RN oculus statuatur. Ergo sequitur eandem multiplicationem, eundemque prorsus effectum praestari lente N et sphaera AB. Et constat porrò distantiam RN triplam esse BC, quae fuerant demonstranda. Hic crassitudinem lentis NQ pro nulla habuimus, qualis censeri potest, cum foci distantia NR pollicaris est vel non multo minor; Sed quum usu praestent exiles lenticulae, velut quae utrinque formantur cavo sphaerico, cujus ½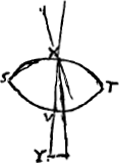 [Fig. 33].
diameter duodecimam pollicis non excedit, necessario relinquenda est ijs crassitudo aliqua, ne ob nimiam parvitatem intractabiles fiant, neve minus bene sphaericam formam induant. Hinc vero minuitur illa quam dixi distantia vitri a subjecto visibili. Velut si sit lenticula ST [Fig. 33] cujus superficies plano secta faciat arcus SXT, SVT circumferentiae trientes, nempe descriptos centris X, V, radio XV. Haec ut idem praestet augendo visibili ac sphaerula AB [Fig. 31]; debet XV radio KB et quartae ejus parti aequalis poniGa naar voetnoot4); unde oritur foci distantia VY dupla BCGa naar voetnoot5), seu ⅔ NR. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 520]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XI.Expliquer comment on fabrique les petites sphères et lentilles et de quelle façon on s'en sert. Plus les sphères sont petites, plus il est aisé de les fabriquer, et cela de la façon suivanteGa naar voetnoot1). On introduitGa naar voetnoot2) de très menus fragments de verre dans la partie inférieure de la flamme d'une lampe là où l'on observe la couleur bleue, de sorte que le verre rougit au feu. On touche le fragment de verre, de manière à l'y faire adhérer, avec un fil de fer étiré, aussi mince que possible, et on le fait adroitement tourner; le verre en découle ainsi en petites boules qui seront suffisamment grandes si elles sont égales à un grain de moutarde. Parmi plusieurs boulettes ainsi préparées vous en trouverez quelques bonnes; vous pourrez le constater après les avoir enchâssées dans une lame d'airain. Cela se fait ainsi. Vous plierez en deux une lame d'airain très mince de la largeur d'un doigt et d'une longueur double; vous percerez le carré ainsi obtenu en son milieu avec la pointe d'une aiguille, vous polirez avec une pierre de touche les trous opposés pour enlever toute inégalité aux bords, et vous couvrirez la surface de noir de fumée afin qu'il ne reste aucune partie brillante à l'intérieur. Vous introduirez ensuite la boulette encore attachée au fil de fer entre les deux parties de la lame et vous la placerez entre les deux ouvertures; vous la retiendrez dans cette position par la pression, plaçant autour d'elle trois petits clous d'airain coupés d'un fil et les rivant à l'aide d'un marteau. Vous construirez ainsi avec peu de peine plusieurs microscopes dont vous choisirez les meilleursGa naar voetnoot4). Comme je l'ai dit, le principal usage qu'on peut faire de ces microscopes est d'observer de petits corps transparents. Les petits appareils ainsi construits sont montés de telle manière que par la rotation d'une vis on peut les faire approcher ou s'écarter de l'objet; on peut ainsi les placer à la distance requise et rendre la vision distincteGa naar voetnoot5). À cet effet il est aussi fort utile d'écarter le surplus de lumière et de n'admettre celle-ci que par un trou éloigné de l'objet à une distance à peu près égale à quatre fois son diamètreGa naar voetnoot6). On peut mieux définir | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 521]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Proposition XI.]Quomodo sphaerulae et exiguae lentes parentur atque usui aptentur exponere. Sphaerulae quo minores eo facilius conficiuntur, hoc modoGa naar voetnoot1). FragminaGa naar voetnoot2) vitri minima ad imam lucernae flammam qua parte caeruleus color conspicitur admoventur ut candescant atque ita filo ferreo, quantum tenuissimum duci potest excepta, ac porro dextrè versata, in globulos abeunt, qui satis magni si granum sinapi aequaverint. E pluribus ita paratis aliquos probos reperies, idque experieris postquam lamellae aereae eos incluseris. Quod ita fit. Lamellam ex aere tenuissimo digiti latitudine, longitudine duplâ, complicabis, tum medium hoc quadratum acus cuspide perforabis, foramina opposita coticula laevigabis ne quid scabri circa margines adhaereat et flammae fuligine inficies, ne quid fulgidum intus remaneatGa naar voetnoot3). Inde sphaerulam adhuc filo ferreo haerentem intra lamellam atque ad ipsa foramina inseres; pressamque continebis adactis circum aeneis tribus claviculis ex filo desectis malleoque firmatis. Sic levi opera plura microscopia efficies, e quibus quae optima seligesGa naar voetnoot4). Horum uti dixi praecipuus est usus ad pellucida quaeque corpuscula inspicienda. Imponuntur vero machinulae ita constructae ut cochleolae conversione accedant recedantque a visibili, atque ita ad requisitam distantiam deducantur fiatque distincta visioGa naar voetnoot5). cui porro plurimum conducit, ut lux nimia coërceatur, nec nisi per foramen admittatur quod circiter quaternis suis diametris a visibili distetGa naar voetnoot6). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 522]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
de cette façon l'ouverture qui convient à la boulette que par la largeur du trou contigu qu'il n'y a aucun avantage à rétrécir. L'oeil doit être placé fort près de la boulette afin qu'il puisse embrasser un plus grand espace. D'ailleurs les petits corps solides ou liquides qu'on veut examiner doivent être placés sur une petite plaque de verre ronde et plane laquelle doit, pendant l'observation, être mobile dans tous les sensGa naar voetnoot2). Quelques observateurs attirent le fluide par des tubes de verre si étroits qu'on peut à peine y faire entrer un seul cheveuGa naar voetnoot3); mode d'opérer qui a aussi ses avantages. Mais si l'on se sert des petites lentilles dont nous avons parlé et si l'on place latéralement une deuxième lentille pour éclairer l'objet d'en hautGa naar voetnoot4), il faut prendre soin de donner les dimensions convenables au petit trou qui sert d'ouverture, essayant quel diamètre il peut avoir sans que la vision devienne moins distincte. En effet, dans ce cas les points des corpuscules rayonnent eux-mêmes, ce qui n'a pas lieu chez les corps transparents qu'on observe à travers les boulettes: dans ce dernier cas l'objet intercepte de la lumière mais n'en émet pas. L'effet qu'on obtient ainsi de ces petites lentilles et boules est admirable, comme on peut s'en convaincre d'après les expériences publiéesGa naar voetnoot5), par lesquelles la connaissance des choses naturelles a fait de grands progrès. Parmi celles-ci il y a l'observation nette du mouvement circulaire du sang, lequel nous avons vu avec délice dans la queue d'une anguille, où il nous fut montré par notre célèbre compatriote Leeuwenhoek, investigateur fort zélé de ces phénomènesGa naar voetnoot6). En effet, cette queue est transparente; et le sang, composé de globules légèrement colorées en rouge, circule rapidement par les petits canaux des artères qui aboutissent dans les veines. Sans doute on observerait la même chose dans les autres animaux; seulement on ne trouve pas aisément chez eux des parties transparentes. Or, Leeuwenhoek avait plongé une petite anguille vivante dans un tube de verre à moitié rempli d'eau, auquel il appliquait extérieurement le microscope là où l'extrémité de la queue touchait le verreGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 523]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Etenim hoc pacto melius apertura sphaerulae conveniens definitur quam latitudine foraminis contigui, quod hic arctari nihil necesse est. Oculus sphaerulae proxime admovendus est quo majus spatium complectatur. Caeterum quae visui proponuntur corpuscula, aut liquorum guttulae, orbiculo vitreo plano imponuntur qui inter aspiciendum in omnem partemGa naar voetnoot1) mobilis sit oportetGa naar voetnoot2). Sunt et qui vitreis tubulis liquorem attrahant, tam angustis ut vix pilos singulos admittantGa naar voetnoot3). quae ratio suos quoque usus habet. lenticulis autem quas diximus utendo, ac lente aliâ à latere appositâ, lucem rei visae desuper affundendoGa naar voetnoot4), curandum est ut aperturae minimum foramen exactè temperetur, experiendo quantum patere possit sine distinctae visionis detrimento. radiant enim hic corpusculorum puncta, quod aliter est in pellucidis quae per sphaerulas spectantur, ubi lucem intercipit res objecta, non emittit. Mirabilis autem est lenticularum ac sphaerularum ejusmodi effectus, ut ex editis in publicum experimentis cognoscere licetGa naar voetnoot5), quibus naturalium rerum cognitio plurimum lucis accepit. In his est observatio manifesta circularis motus sanguinis, quem, monstrante N. Lewenhoukio nostro, diligentissimo horum investigatoreGa naar voetnoot6), in anguillae cauda, summa cum voluptate conspeximus. Est enim perlucida; ac sanguis globulis subrubentibus constans, celeri motu per cananiculos arteriarum, qui venis continuantur, discurrit. quod haud dubie in caeteris quoque animalibus animadverteretur, sed non facile partes luci perviae in his reperiuntur. Anguillulam vivam in tubum vitreum demiserat aqua semiplenum cui extrinsecus microscopium applicabat ea parte qua cauda extrema vitrum tangebatGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 524]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Il est également intéressant d'observer les animalcules nageant dans des gouttes d'eau, dans lesquelles du gingembre ou du poivre ou quelque autre substance possédant une odeur plus ou moins prononcée a séjourné durant quelques joursGa naar voetnoot1). Ces animalcules sont de formes diverses et plus petits les uns que les autres. Leurs mouvements assez rapides eu égard à leur propre grandeur sont étranges: en effet, on ne peut voir aucun agencement qui leur permette d'avancer, attendu qu'ils ne possèdent ni pieds ni branchies et qu'ils ne fléchissent pas le corps comme le font les poissons. Car les petites anguilles du vinaigreGa naar voetnoot2), beaucoup plus grandes que ces animalcules, nagent de la même manière que les poissons des fleuves; ces anguilles ont ceci de remarquable qu'elles donnent naissance à des petits vivantsGa naar voetnoot3). En effet, j'ai vu une anguille qui en contenait quatre autres plus petites (car elles sont entièrement transparentes) et comme elle fut soigneusement gardée dans un petit tube, elle leur a donné le jour après quelques heures, et les petites anguilles nageaient chacune séparément. Mais il est vraisembable que les animalcules dont j'ai dit qu'ils se meuvent dans l'eau, viennent de l'air et sont attirés dans l'eau par l'odeur. En effet, des substances diverses ayant été macérées dans l'eau, on y trouve les mêmes formes d'animalculesGa naar voetnoot4). Mais lorsque le vase est fermé, il n'en apparaît aucunGa naar voetnoot5). Or, ils planent aisément dans l'air à cause de leur extrême petitesse, attendu qu'ils sont beaucoup plus menus que les moindres grains de poussière. Il est donc fort possible que, sans le savoir, nous en faisions entrer dans nos poumons bien des milliers. Et il ne serait pas inutile d'observer dans quels saisons il en apparaît davantage, et si leur nombre augmente lorsque l'air est vicié. Il apparaîtGa naar voetnoot6) que le lait consiste dans de petits globules transparents nageant dans un liquide également transparent mais de pouvoir réfringent différent; par conséquent, le lait paraît blanc quoiqu'il ne contienne que des matières absolument diaphanes et incolores. Je ne parle pas de tant de formes admirables de menus insectes. Des ailes des papillons et des cousins, recouvertes de plumes extrêmement petitesGa naar voetnoot7). Des grains de poussière attachés aux étamines au milieu des fleursGa naar voetnoot8), lesquels ne sont autre chose que des follicules transparents remplis de cette matière dont les abeilles font la cire, et qu'elles emportent à leurs ruches attachée à leurs pieds. Mais il faut considérer comme la découverte la plus admirable et la plus impor- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 525]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Jucunda etiam est animalculorum observatio aquae guttulis innatantium, in quam zinziber, aut piper, aut aliud odoris acrioris diebus aliquot demersum fueritGa naar voetnoot1). Variae sunt formae aliaeque alijs minores, miri etiam motus pro modulo ipsorum satis celeres quorum instrumentum nullum animadverti potest, cum pedibus branchijsque careant, nec corpora ut pisces inflectant. Nam anguillulae acetiGa naar voetnoot2), quae istis longe majores sunt, eadem ratione ac fluviatiles natant, in quibus hoc mirum quod ex se foetus generent. Vidi enim quae parvulas quaternas intra se contineret (sunt enim perlucidae totae) cumque in tubulo asservaretur, post horas aliquot eas enixa est, quae seorsim quaeque natabant. Sed ista quae dixi in aqua discurrentia animalcula veri simile est ex aere in aquam allici propter odorem. Varijs enim rebus in aqua maceratis eaedem formae eorum reperiunturGa naar voetnoot4). at caluso vasculo nulla comparentGa naar voetnoot5). Facile autem ob insignem parvitatem in aere sustinentur, cum minimis pulvisculis multo minora sint. Ita multa ipsorum millia forsan in pulmones dimittimus ignari. nec inutile esset observare quibus anni tempestatibus plura appareant, et num aere vitiato augeantur. Lac exiguis globulis pellucidis constare apparetGa naar voetnoot6). in liquore item pellucido sed diuersae refractionis natantibus; hinc album videtur cum tamen non aliam materiam quam prorsus diaphanam contineat, coloreque carentem. Mitto insectorum minimorum tot mirabiles formas. Alas papilionum et culicum, plumulis exiguis obsitasGa naar voetnoot7). Pulvisculos in medijs florum apicibus inhaerentesGa naar voetnoot8), qui nil aliud sunt quam folliculi transparentes materia ea pleni ex qua ceram apes conficiunt, quamque pedibus suis affixam in alvearia deferunt. Omnium | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 526]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tante de toutes ce qu'on a observé dans la semence des animaux mâlesGa naar voetnoot1), savoir qu'il y nage en guise de petits poissons une immense multitude d'animalcules ayant à peu près la même forme que les grenouilles qui viennent de naître et qui ne possèdent pas encore de pattes. Il ne me paraît guère douteux que ces animalcules entrent dans les oeufs féminins et constituent le commencement des animaux qui en naîtrontGa naar voetnoot3). En effet, il y a plusieurs raisons qui nous portent à croire qu'il en est ainsi, et ce n'est pas une grande objection que de dire que souvent parmi une si grande multitude ce ne sont que quelques-uns ou même un seul qui arrive à grandir jusqu'à devenir un animal, attendu que nous observons la même abondance, la même fécondité superflue, dans la plupart des semences des arbres et des herbes, par exemple dans les semences du sapin, du pavot, etc. À cause de leur extrême petitesse (car même dix mille de ces animalcules ne sont pas égaux en grandeur à un petitgrain de sableGa naar voetnoot4)), il faut les observer avec ces petites boules de verre, dont le pouvoir grossissant est le plus grand. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XII.Expliquer la construction des microscopes composésGa naar voetnoot5). Nous parlerons maintenant des microscopes composés, à l'aide desquels on observe les objets qui ne transmettent pas la lumière et où leurs couleurs vraies apparaissent, et cela mieux et plus commodément qu'avec des lentilles uniquesGa naar voetnoot6). Soit A [Fig. 34 et 35] la plus petite lentille du microscope, et B la plus grande. Nous ferons voir plus loin la cause pour laquelle elles doivent être placées ainsiGa naar voetnoot7). Et supposons B la plus proche de l'oeil qui se trouve au point C, tandis que A est située du côté de l'objet placé en E. ABC est l'axe commun aux deux lentilles. Il faut considérer la question de deux manières que nous écluciderons par deux figures. Dans la première les rayons émanant d'un seul point E de l'objet et tombant sur la lentille A sont réunis par la réfraction due à cette lentille en un point P; | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 527]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
vero mirabilissimum ac praecipuum putandum, quod in semine animalium marium est observatumGa naar voetnoot1), nempe in eo animalculorum immensam multitudinem pisciculorum more natare, ejus fere formae quam ranae habent nuper natae ac nondum pedibus praeditaeGa naar voetnoot2). Quae animalcula, intrare ova foeminarum, atque esse ipsorum animalium inde excludendorum initia, vix mihi dubitandum videturGa naar voetnoot3). Plurima enim hoc suadeant, nec multum obstat quod e tanta multitudine saepe vel pauca vel unum duntaxat in animal excrescant, cum eadem abundantia ac superflua faecunditas in plerisque arborum et herbarum seminibus conspiciatur, velut abietis, papaveris etc. Haec vero animalcula propter miram parvitatem (nam vel decem millia eorum exiguum arenae granum non aequantGa naar voetnoot4)) globulis istis vitreis inspicienda sunt, quorum in augendo praecipua est virtus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio XII.]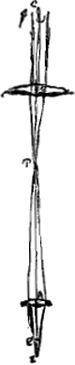 [Fig. 34.]
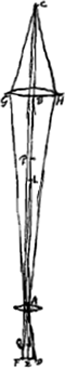 [Fig. 35.]
[Microscopiorum compositorum rationes explicare.]Ga naar voetnoot5) Nunc de compositis microscopijs dicemus, quorum opera spectantur quae lucem non transmittunt, verique eorum colores apparent, idque melius commodiusque quam lenticulis singulisGa naar voetnoot6). Sint lentes microscopij A [Fig. 34 et 35] minor, et B major, cur autem ita ponendae causam postea demonstrabimusGa naar voetnoot7). sitque B oculo propior, qui sit ad C punctum; A vero ad rem visam obversa, quae sit ad E, axis communis lenti utrique ABC. duplex autem adhibenda est observatio, quam duplici schemate designamus. In priore radij ex uno rei visae puncto E manantes in lentem A, conveniunt hujus refractione ad punctum P, atque ibi sese intersecantes, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 528]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
se coupant en ce point et continuant leur route jusqu'à la lentille B, ils sont rendus parallèles par cette dernière et parviennent ainsi à l'oeil placé au point C; de cette façon la vision devient distincte. Il faut donc que la distance AE soit plus grande que AQ, distance focale de la lentille A. Et les longueurs EQ, EA, EP doivent former une proportionGa naar voetnoot1). Mais la lentille B doit être placée de telle manière que son foyer qui se trouve du côté de A, tombe précisément au point P. Tout ceci est évident d'après ce qui a été démontré plus haut. La deuxième figure montre les rayons DAG, FAH, EAB émanant chacun d'un autre point de l'objet. Or, le point A est le centre de la lentille, et, pour déterminer la place C de l'oeil, on fait en sorte que les grandeurs AP, AB et AC forment une proportionGa naar voetnoot2). En effet, de cette façon on obtient que, quelque petite que soit l'ouverture de la lentille A, la lentille B est pourtant remplie toute entière par l'image de l'objet, puisque les rayons issus du point A et tombant sur la lentille B toute entière sont amenés à se réunir au point C. On apprendra à connaître le grossissement en traçant dans la seconde figure la droite CF; en effet, il sera égal au rapport de l'angle BCH à l'angle ECF, lequel est égal au produit du rapport de l'angle BCH à l'angle BAH et de celui de l'angle BAH ou EAF à l'angle ECF. Mais le premier de ces rapports est égal au rapport de la droite AB à la droite BC, et le deuxième au rapport CE:EA, attendu que pour ces petits angles le rapport des angles est considéré comme égal au rapport des tangentes. Par conséquent, le grossissement sera composé des rapports AB::BC ou AP:PB (car AP, AB et AC forment une proportion) et CE:EA. Mais pour pouvoir mieux juger de l'effet du microscope, il faut plutôt comparer l'angle BCH à l'angle sous lequel l'on verrait la droite EF si celle-ci était située à une distance de 8 pouces de l'oeil, c'est-à-dire à l'angle ELF, LE étant prise égale à 8 pouces d'après ce que nous avons dit plus hautGa naar voetnoot3) à propos du grossissement dû à une petite lentille simple. Le grossissement doit donc ici être considéré comme composé du rapport de l'angle BCH à l'angle BAH, et de BAH ou EAF à ELF; c'est-à-dire du rapport AP:PB et du rapport de la ligne EL, longue de 8 pouces, à la droite EA. En effet, si le microscope avait une longueur telle que, par exemple, CE était de deux pieds, c'est-à-dire égale à trois fois LE et qu'on avait trouvé d'après le premier calcul un grossissement 90:1, il ne faudrait cependant considérer le grossissement que comme égal à 30:1, parce que la ligne EF regardée à travers le microscope ne paraîtrait que 30 fois plus longue que cette même ligne regardée à l'oeil nu d'une distance de 8 pouces. Car il ne s'agit pas de calculer combien le microscope grossit un objet situé à une distance de deux pieds, mais seulement de savoir dans quel rapport est grossi | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 529]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
atque in lentem B pergentes, hujus opera paralleli redduntur atque ita ad oculum in C perveniunt, eoque distincta fit visio. Oportet itaque distantiam AE majorem esse quam sit AQ foci distantia lentis A. Et proportionales esse debent EQ, EA, EPGa naar voetnoot1). Lens vero B ita collocanda ut ejus focus qui versus A, cadat in ipsum punctum P. quae omnia ex supra demonstratis manifesta sunt. Altera figura radios singulos exhibet à diversis rei visae punctis fluentes DAG, FAH, EAB. Est autem punctum A medium lentis, ponunturque AP, AB, AC proportionales, ad definiendum oculi locum CGa naar voetnoot2); ita enim fit ut quamlibet exiguo foramine pateat lenticula A, tota tamen lens B imagine rei visae impleatur, quoniam radij ex A in totam lentem B cadentes coguntur ad punctum C. Proportio autem magnitudinis apparentis ad veram cognoscetur ductâ in secunda figura rectâ CF. Erit enim ea quam habet angulus BCH ad angulum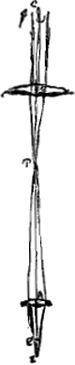 [Fig. 34.]
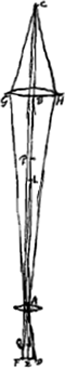 [Fig. 35.]
ECF. quae ratio componitur ex ratione anguli BCH ad angulum BAH et anguli BAH seu EAF ad angulum ECF. Sed prior harum est eadem quae rectae AB ad BC, et posterior ea quae CE ad EA, quia in exiguis angulis hisce eadem censetur ratio angulorum quae tangentium. Ergo ratio apparentis ad veram magnitudinem erit composita ex rationibus AB ad BC seu AP ad PB (nam proportionales sunt AP, AB, AC) et CE ad EA. Sed ut rectius aestimetur microscopij effectus, comparandus est potius angulus BCH cum angulo, quo cerneretur recta EF si ab oculo 8 pollices distaret, hoc est cum ang.o ELF; positâ LE pollicum 8, secundum ea quae de simplicis lenticulae multiplicatione superius dicta fuereGa naar voetnoot3). atque ita ratio amplificationis censenda hic componi ex ratione anguli BCH ad BAH, et BAH seu EAF ad ELF; hoc est ex ratione AP ad PB, et lineae EL, 8 pollices longae, ad rectam EA. Si enim tantae longitudinis esset microscopium ut ex. gratia CE esset duorum pedum, hoc est, tripla LE, repertaque esset priori ratiocinio magnitudo apparens ad veram quae 90 ad 1, tamen non nisi quae 30 ad 1 censenda esset, quia tantum trigecuplo major appareret linea EF microscopij opera quam nudo oculo ex octo pollicum distantia spectata. Non enim considerandum quantum microscopio amplificemus rem duobus pedi- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 530]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
l'objet regardé de la distance à laquelle nous avons coutume de placer l'oeil, lorsque nous voulons voir distinctement. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XIII.De la clarté des images formées par les microscopes et de leurs ouvertures. De même que nous avons auparavant discuté les ouvertures des télescopesGa naar voetnoot2), de même aussi nous nous occuperons maintenant de ce qui se rapporte aux petites lentilles des microscopes situées du côté des objets; desquelles dépend toute leur puissance et tout leur effet, à tel point qu'on peut conclure de la nature de ces lentilles jusqu'à quelle limite on peut pousser le grossissement; ce que personne, que je sache, n'a encore exposé. Or, on rencontrera ici, comme cela a été démontré dans le cas des télescopes, une progression pour ainsi dire infinie, non pas il est vrai dans le microscope simple, contenant une seule lentille, mais dans ceux qui en comprennent deuxGa naar voetnoot3). Pour les microscopes composés d'une seule lentille, il faut observer que dans ceux qui possèdent une distance focale d'un demi-pouce ou davantage, il n'est pas du tout nécessaire de diminuer l'ouverture afin de rendre la vision distincte, attendu que l'étroitesse de la pupille a précisément l'effet d'exclure, pour autant qu'il en est besoin, les rayons qui seraient nuisibles et cela absolument de la même manière que si la lentille ne possédait qu'une ouverture de cette même grandeur. Mais dans le cas des lentilles plus petites, où il est nécessaire de limiter les ouvertures, il faut que leurs diamètres aient entre eux un rapport égal à celui des distances focales, afin de donner des objets des images également nettes. Mais la clarté sera alors dans le même rapport élevé au carré; de sorte que plus les lentilles dont on se servira seront fortes, plus grande, mais aussi plus obscure, sera l'image qu'elles donneront de chaque objetGa naar voetnoot4). Considérons une petite lentille P [Fig. 36], dont l'axe est TBF et PD le rayon de la plus grande ouverture que l'expérience a montré qu'elle peut avoir, rayon inférieur à celui de la pupille. Soit le foyer extrême des rayons rouges qui proviennent de rayons parallèles à l'axe, au point F, où l'objet lui-aussi est placé, tandis que le foyer des rayons violets provenant de ces mêmes rayons parallèles à l'axe, se trouve en B. En supposant aussi toutes les mêmes choses au sujet de la plus petite lentille p [Fig. 37], dont le rayon de l'ouverture pd soit à la distance focale pf dans le même rapport que chez la plus grande lentille, je dis qu'on aperçoit l'objet avec une netteté égale à travers chacune des deux lentilles. En effet, comme dans l'un et l'autre cas le rayon ED, s'il tombe parallèlement | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 531]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
bus distantem, sed quanto major efficiatur quam cum ex eo spectatur intervallo, quo solemus oculum admovere cum distincteGa naar voetnoot1) intueri cupimus. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio XIII.]De Microscopiorum luce et aperturis. Sicut antea de Telescopiorum aperturis inquisivimusGa naar voetnoot2), ita nunc ea quoque expendemus quae Microscopiorum lenticulis ad res visas obversis conveniunt; unde omnis eorum pendet vis et effectus, adeo quidem ut hinc discendum sit quousque visibilium amplificatio perduci possit: quod hactenus a nemine, quod sciam, fuit definitum. Invenietur autem et hic progressus quidam infinitus qualis in Telescopijs ostensus fuit, non quidem in simplici unius lenticulae Microscopio, sed in ijs quae ex binis componunturGa naar voetnoot3). Si singulis lentibus microscopia constituantur, sciendum est in ijs quae circiter semipollicarem habent aut majorem foci distantiam, nihil opus esse moderanda apertura distinctam visionem efficere; quoniam ipsa pupillae angustia radios nocituros quantum opus est excludit, atque ita prorsus ac si non majori foramine lens adaperta foret. In minoribus vero lenticulis ubi aperturarum circumscriptio necessaria est, oportet harum diametros eandem rationem servare quae est foci distantiarum, ut aeque distincte res visas referant. claritas vero tunc erit in eadem ratione duplicata, ut proinde quo acutiores lenticulae adhibebuntur eo majora quidem sed et obscuriora omnia videri faciantGa naar voetnoot4). 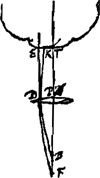 [Fig. 36.]
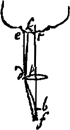 [Fig. 37.]
Sit lenticula P [Fig. 36], cujus axis TBF, semidiameter aperturae PD, quantam maximam experientia ferri posse ostendit, eaque pupillâ minor. focus extremus radiorum rubrorum qui ab axi parallelis procedunt, in F puncto, ubi et visibile collocatum sit. focus violaceorum ab ijsdem axi parallelis procedentium, in B. Positis item ijsdem omnibus in minore lenticula p [Fig. 37], cujus aperturae semidiameter pd sit ad foci distantiam pf sicut in majore. dico utraque aeque distinctè visibile conspici. Cum enim utrobique si radius ED axi parallelus in lentem P incidat, idem | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 532]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
à l'axe sur la lentille P, est dispersé également par l'angle FDB, de sorte qu'il conduit l'extrême couleur rouge au point F, et l'extrême couleur violette au point B, il arrivera réciproquement que le rayon FD émanant de l'objet, sera dispersé par l'angle EDK, de telle manière que l'angle EDK sera égal à l'angle FDB, d'après la proposition...Ga naar voetnoot1) L'angle d'aberration est donc dans les deux cas l'angle FDB et c'est de lui que dépend l'aberration des rayons au fond de l'oeil, comme nous l'avons démontré lorsque nous traitions du télescopeGa naar voetnoot2). Mais comme, d'après la nature de cette aberration, PF:FB = pf:fb, et qu'on a de même, par hypothèse, PD:PF = pd:pf, il est évident que les angles PFD, pfd d'une part et les angles PBD, pbd d'autre part sont égaux et que, par conséquent, la différence des deux premiers est égale à celle des deux derniers, c'est-à-dire ∠FDB = ∠fdb. Par suite, les aberrations au fond de l'oeil sont égales dans les deux cas, et il en résulte que la vision est dans les deux cas également distincteGa naar voetnoot3). De plus, comme les angles PFD et pfd sont égaux, il apparaît que dans les deux cas la même quantité de rayons issus des points F, f, et d'autres points quelconques, atteint les lentilles et, par conséquent, aussi la pupille de l'oeil. Mais la largeur de l'image au fond de l'oeil est d'autant plus grande dans le cas de la petite lentille, que PF est plus grande que pf, comme cela a été démontré plus hautGa naar voetnoot4); et les surfaces apparentes sont entre elles comme les carrés de leurs largeurs. Par conséquent, la même quantité de rayons de lumière employée pour illuminer l'une et l'autre surface, rendra la plus petite plus lumineufe dans un rapport égal à celui des deux surfaces, c'est-à-dire au carré du rapport PF:pf; ce qui restait à démontrer. Comme donc dans les petites lentilles plus fortes la perfection de la vision telle qu'on la trouve dans de plus grandes ne peut être conservée sans que l'obscurité augmente, il s'ensuit qu'il n'est pas permis de pousser le grossissement aussi loin qu'on le voudrait, à moins que, pour éclairer l'objet, une lumière plus abondante ne soit procurée d'autre partGa naar voetnoot5). Mais même de cette façon nous n'avançons guère, parce que la largeur auprès de la pupille, c'est-à-dire celle du petit cylindre lumineux émanant des différents points de l'objet, duquel nous avons parlé dans l'explication des télescopesGa naar voetnoot6) et qui possède ici une largeur précisément égale à celle de l'ouverture, ne peut être diminuée de manière à devenir inférieur à ⅕ ou ⅙ ligne; de sorte que de toutes façons un terme est posé à l'efficacité de ces petites lentilles. Ainsi nous examinerons dans la suite ce que l'on peut obtenir par la combinaison de deux lentilles: nous démontrerons en premier lieu que l'on peut avoir un plus grand effet avec les microscopes plus courts qu'avec ceux qui sont plus longs. Nous démontrerons mêmeGa naar voetnoot7) qu'il existerait une progression pour ainsi dire | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 533]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
spargatur per angulum FDB, ita ut rubrum colorem extremum deferat ad F, violaceum extremum ad B. fiet vicissim ut radius a visibili manans FD, spargatur per angulum EDK, ita ut angulus EDK sit aequalis FDB, ex prop...Ga naar voetnoot1) Est itaque utrobique aberrationis angulus FDB, a quo pendet aberratio radiorum in oculi fundo, ut ostensum cum de Telescopijs agebaturGa naar voetnoot2). Quia vero ex natura aberrationis hujus, ut PF ad FB, ita est pf ad fb; itemque ex hypothesi, PD ad PF ut pd ad pf, manifestum est aequales esse tam angulos PFD, pfd, quam PBD, pbd, quare et differentia priorum, aequalis differentiae posteriorum, hoc est ang. FDB aequalis angulo fdb. ac proinde aberrationes in fundo oculi utrimque aequales, eoque visio aeque distinctaGa naar voetnoot3). Porro quia anguli PFD, pfd aequales, apparet eandem quantitatem radiorum utrobique a punctis rei visae F, f et alijs quibusvis ad lentes manare, eoque et ad oculi pupillam. Latitudo vero rei visae in fundo oculi tanto major fit minori lenticula, quanto major est PF quam pf, ut in superioribus demonstratum estGa naar voetnoot4); et superficies apparentes sunt in duplicata ratione latitudinum. Ergo eadem radiorum lucidorum quantitas utrique superficiei illustrandae impensa, clariorem efficiet minorem secundum rationem quâ ab altera superficie superatur, hoc est secundum duplicatam rationem PF ad pf, quod demonstrandum supererat. Cum itaque servari non possit eadem visionis perfectio in acutioribus lenticulis quae reperitur in majoribus, quin crescat obscuritas, sequitur non licere amplificando quousque libet progredi, nisi lux major illustrando visibili aliunde arcessaturGa naar voetnoot5). Nec sic quoque multum proficimus, quoniam latitudo ad pupillam, seu cylindrulus radiosus à singulis rei visae punctis affluens de quo in telescopiorum explicatione dictum fuitGa naar voetnoot6), quique hic ipsam aperturae latitudinem habet, non infra quintam sextamve lineae partem contrahi potest, adeo ut undique terminus praescriptus sit harum lenticularum efficaciae. Jam porro quid binis lentibus componendis fieri possit investigabimus, atque inprimis ostendemus plus praestari posse brevioribus quam longioribus microscopijs. Quin etiam infinitum quendam ampliationis progressum dari demonstrabimusGa naar voetnoot7) nisi obstaret lenticularum parvitas, quae continuo tanta fit, ut nec veras sphaerae | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 534]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
infinie du grossissement, si la petitesse des lentilles n'y faisait obstacle, laquelle devient bientôt telle que nous ne pouvons ni leur donner des formes sphériques parfaites ni nous en servir assez aisément, attendu qu'elles finissent par échapper même aux regards. OrGa naar voetnoot1), la proposition suivante sera également vraie pour chacune des deux aberrations des rayons. Car nous montrerons plus loinGa naar voetnoot2) qu'il faut ici tenir compte aussi de l'aberration qui provient de la forme de la lentille. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XIV.Lorsqu'un microscope quelconque composé de deux lentilles, tel que nous l'avons décritGa naar voetnoot3), est donné, on peut, en conservant la lentille oculaire, trouver un autre microscope plus court, pour lequel la grandeur apparente de l'objet et la clarté sont les mêmes, tandis que la vision est plus nette, ou bien la netteté la même et la clarté plus grandeGa naar voetnoot4). Considérons un microscope composé de la lentille oculaire EZ [Fig. 38] et de la lentille PD se trouvant du côté de l'objet, desquelles l'axe commun est VE PB. Supposons l'objet placé au point B; soit O, entre P et B, le foyer de la lentille PD, N, entre E et P, le foyer de la lentille EZ. L'oeil se trouve au point V et la disposition soit la même que plus hautGa naar voetnoot5), c'est-à-dire telle que BO, BP et BN forment une proportion, et de même PN, PE, PV. Ensuite, ayant pris une lentille oculaire ez [Fig. 39] possédant une distance focale en égale à EN, joignons-y une deuxième lentille pd, dont la distance focale po soit inférieure à PO. Or, comme PO est à po, ainsi soit PN à pn et ainsi aussi PB à pb. Par conséquent, de même que les rayons émanant d'un point B de l'objet, se réunissent au point N par la réfraction due à la lentille PD, de même aussi les rayons qui viennent du point b se réunissent en n par la réfraction due à la lentille pd; ensuite ils deviendront parallèles par la réfraction due à la lentille ez, et c'est dans cet état qu'ils parviendront à l'oeil placé en v, point qu'on trouve en formant une proportion des trois grandeurs pn, pe et pv; il en résultera que l'oeil verra toute la lentille ez remplie de l'image de l'objet, d'après ce que nous avons | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 535]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
superficies ijs inducere, nec satis commode ipsas tractare possimus, quippe quae et visum denique effugiant. SequensGa naar voetnoot1) vero propositio aeque vera erit in utraque radiorum aberratione. Namque hic ejus quoque rationem habendam esse quae ex figura nascitur, postmodum ostendemusGa naar voetnoot2). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Propos [itio XIV]. [Fig. 38.]
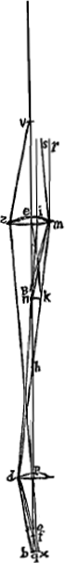 [Fig. 39.]
Dato quocunque Micro scopio ex binis lentibus quomodo diximusGa naar voetnoot3) composito, potest aliud brevius reperiri, servata eadem lente oculari in quo eadem fiat rei visae magnitudo apparens, eadem claritas, visio autem distinctior, vel servata eadem distinctione, major claritasGa naar voetnoot4). Sit microscopium ex lentibus EZ [Fig. 38] oculari et PD ad visibile obversa compositum, quarum axis communis VEPB; Sit visibile ad B; focus lentis PD inter P, B, sit O. focus lentis EZ inter E, P, sit N. Oculus ad V. dispositio autem qualis supraGa naar voetnoot5), ut nempe BO, BP, BN sint proportionales, itemque PN, PE, PV. Porro adsumta lente oculari ez [Fig. 39] quae foci distantiam en aequalem habeat EN, jungatur ei lens altera pd, cujus foci distantia po minor sit quam PO. Sicut autem PO ad po, ita sit PN ad pn, et ita quoque PB ad pb. Itaque quemadmodum radij a puncto rei visae B manantes, refractione lentis PD conveniunt in N, ita quoque qui a puncto b veniunt, refractione lentis pd convenient in n, atque inde refractione lentis ez fient paralleli atque ita ad oculum ferentur qui sit in v, positis proportionalibus pn, pe, pv, unde fiet ut totam lentem ez imagine rei visae | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 536]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
expliqué plus hautGa naar voetnoot1). Or, je dis maintenant que dans les deux microscopes les objets auront la même grandeur apparente. Et, si, de plus, les ouvertures des lentilles PD et pd sont prises proportionnelles à leurs distances focales, je dis qu'on obtient avec les deux microscopes la même clarté, mais qu'avec le plus court on voit tous les objets plus distinctement, en d'autres termes que l'angle d'aberration dans l'oeil y devient plus petit. Supposons que les petites lignes BX et bx, perpendiculaires à l'axe et égales entre elles, représentent les largeurs de l'objet, et traçons par les centres des lentilles P et p les droites XPZ et xpz coupant les lentilles EZ et ez aux points Z et z; menons à partir de ces points les droites ZV et zv aux points où se trouve l'oeil. Les petites lignes égales BX et bx seront donc vues sous les angles EVZ et evz et si nous démontrons que celles-ci sont égales entre elles, c'est-à-dire, que le rapport VE:EZ est égal au rapport ve:ez, la grandeur apparente sera la même dans les deux casGa naar voetnoot2). Or, le rapport VE:EZ est composé des rapports VE:EP et EP:EZ. Mais le rapport VE:EP est égal au rapport EN:NP, parce que VP, EP et NP forment une proportion. Et le rapport EP:EZ est le même que PB:BX. Par conséquent, le rapport VE:EZ est composé des rapports EN:NP et PB:BX, et sera donc égal au rapport des rectangles EN, PB et NP, BX, lequel se compose aussi des rapports PB:NP et EN:BX. On démontre de même que dans le plus petit microscope le rapport ve:ez est composé des rapports pb:np et en:bx. Mais le rapport pb:np est, par hypothèse, égal au rapport PB:NP, comme cela se voit aisément. De même le rapport en:bx est égal au rapport EN:BX, parce que en et EN sont égales entre | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 537]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
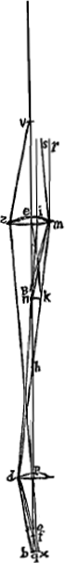 [Fig. 39.]
plenam spectet, per ea quae superius explicata suntGa naar voetnoot1). dico jam utroque microscopio apparentes rei visae magnitudines fore aequales. Quod si et aperturae lentium PD, pd, proportionales ponantur ipsarum fòci distantijs. dico utroque microscopio eandem haberi claritatem, sed breviori omnia distinctius cerni, sive angulum aberrationis in oculo hic minorem fieri. Sint rei visae latitudines lineolae BX, bx, axibus perpendiculares et inter se aequales, et per centra lentium P, p, ducantur rectae XPZ, xpz, lentibus EZ, ez occurrentes in Z, z, atque hinc ducantur ZV, zv, ad puncta oculi. Spectabuntur itaque lineolae aequales BX, bx, angulis EVZ, evz, qui si inter se aequales esse ostendantur, hoc est si eadem sit ratio VE ad EZ quae ve ad ez, erit utrobique magnitudo apparens eademGa naar voetnoot2). Componitur autem ratio VE ad EZ ex rationibus VE ad EP et EP ad EZ. Sed ratio VE ad EP est eadem quae EN ad NP, quia proportionales sunt VP, EP, NP. Et ratio EP ad EZ est eadem quae PB ad BX. Ergo ratio VE ad EZ componitur ex EN ad NP et PB ad BX, ac propterea eadem erit quae rectang.i EN, PB ad rectang. NP, BX; quae etiam componitur ex rationibus PB ad NP et EN ad BX. Eodem modo in minore microscopio ostenditur ratio ve ad ez componi ex rationibus pb ad np et en ad bx. Sed ratio pb ad np est eadem ex hypothesi quae PB ad NP ut facile perspicitur. Itemque ratio en ad bx eadem quae | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 538]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
elles et bx et BX de même. Par conséquent, les rapports VE:EZ et ve:ez sont composés des mêmes rapports; il s'ensuit qu'ils sont égaux entre eux; il en est donc aussi de même des grandeurs apparentes de la petite ligne BX ou bx. Si nous prenons ensuite les ouvertures PD et pd dans le même rapport que les distances focales PO et po, c'est-à-dire dans celui des droites PB et pb, il apparaît que la même quantité de rayons, provenant des points quelconques B et b de l'objet, entrera dans chacun des deux microscopes; il en sera, par conséquent, de même de la lumière provenant de la surface tout entière, laquelle quantité de lumière étant distribuée dans les deux instruments sur des images égales, il s'ensuit que leur clarté devient la même. Ensuite on démontre facilement que l'angle d'aberration qui résulte de la dispersion du rayon est plus petit dans le microscope le plus court. En effet, si BF et bf représentent ces aberrations pour les rayons venant des points N et n, on conçoit aisémentGa naar voetnoot1) qu'elles seront entre elles comme les distances BP et bp; et le rapport de ces distances est égal à celui des ouvertures ou de leurs moitiés PD et pd. Il s'ensuit, si l'on trace FD et fd, que BDF et bdf deviennent des triangles semblables et que leurs angles D et d deviennent égaux. Et comme donc les rayons ND et nd sont dispersés de telle manière, par la réfraction due aux lentilles PD et pd, que DB et db portent la couleur rouge et DF et df la couleur violette, et que, par conséquent, les rayons violets FD et fd seraient réciproquement transformés en DN et dn, il arrivera que les rayons violets contenus dans les rayons BD et bd se transforment en DM et dm, de telle sorte que les angles MDN et mdn seront égaux aux angles BDF et bdfGa naar margenoot* Or, ces deux derniers sont égaux entre eux; il en est donc de même des angles MDN et mdn. Et comme PN est plus grande que pn (en effet, ces droites sont entre elles comme les distances focales PO et po), si l'on trace NK et nk perpendiculairement à l'axe et rencontrant les droites DM et dm, on aura que NK est plus grande que nk; et, si l'on trace NM et nm, ainsi que KE et ke, l'angle nek sera plus petit que l'angle NEK, vu que NE et ne sont égales. Par conséquent, nmk sera aussi plus petit que NMK, parce que ces angles sont considérés comme égaux respectivement aux angles précédents. Or, si l'on suppose ensuite que les points G et g sont les foyers des rayons violets qui tombent parallèlement à l'axe sur les lentilles EZ et ez, de même que N et n sont les foyers des rayons rouges (car nous définissons toujours les distances focales par le concours des rayons rouges), il s'ensuivra que si les rayons violets se meuvent par GM et gm ils deviendront des rayons parallèles à l'axe, comme MR et mr, et que, par conséquent, les rayons violets DM et dm ne seront pas parallèles à l'axe après la réfraction mais qu'ils seront inclinés du côté de l'axe de telle manière que les angles RMS et | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 539]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
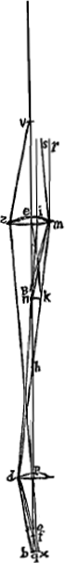 [Fig. 39.]
EN ad BX, quia aequales inter se en et EN itemque bx et BX. Ergo rationes VE ad EZ, et ve ad ez ex ijsdem rationibus componuntur, eoque inter se aequales sunt; ac proinde et apparentes magnitudines lineolae BX, vel bx. Porro positis aperturis PD, pd in eadem ratione quae est foci distantiarum PO, po, hoc est quae rectarum PB, pb, apparet eandem radiorum quantitatem ex punctis singulis B et b, rei visae, microscopio utroque hauriri; ac proinde et à tota ipsarum superficie. Quae lux cum utrobique aequalibus in oculo imaginibus impendatur, sequitur harum claritatem aequalem fieri. Denique angulum aberrationis a diffusione radij minorem esse in breviori microscopio facile quoque ostenditur. Si enim aberrationes istae sint BF, bf radiorum ex N et n venientium, facile intelligiturGa naar voetnoot1) eas fore inter se sicut distantiae BP, bp; quam eandem rationem quoque habent aperturae sive earum dimidiae PD, pd. Unde junctis FD, fd, apparet triangula similia fieri BDF, bdf. eorumque angulos ad D et d aequales. Cum igitur radij ND, nd, refractione lentium PD, pd ita dissipentur, ut DB, db rubrum colorem deferant; DF, df vero violaceum, ac proinde vicissim violacei FD, fd abirent in DN, dn; fiet ut qui in radijs BD, bd violacei continentur, abeant in DM, dm, ita ut anguli MDN, mdn sint aequales angulis BDF, bdfGa naar margenoot*. Hi autem duo inter se aequales sunt, ergo etiam aequales anguli MDN, mdn. Cumque PN sit major quam pn (sunt enim inter se ut foci distantiae PO, po) si ducantur axi perpendiculares NK, nk, rectis DM, dm, occurrentes, erit major NK quam nk; et junctis NM, nm, itemque KE, ke, quia aequales sunt NE, ne, erit ang. nek minor quam NEK, ideoque et nmk minor quam NMK, quia hi singuli istis singulis aequales censentur. Quod si porro ponatur puncta G, g esse focos radiorum violaceorum qui axi paralleli in lentes EZ, ez incidunt, sicut rubrorum sunt foci N et n; (nam per rubrorum radiorum concursum semper foci distantias definimus) sequetur jam, si violacei per GM, gm ferantur eos axi parallelos evasuros, puta in MR, mr, ac proinde violaceos DM, dm, post refractionem non fore axi parallelos, sed ita introrsum declinaturos ut anguli RMS, rms fiant aequales angulis GMK, gmk. Quia autem aequales sunt EN, en, minor | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 540]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
rms deviendront égaux aux angles GMK et gmk. D'ailleurs, comme EN et en sont égales, tandis que em est plus petite que EM, comme nous le montrerons bientôt, on aura que, dans le cas de l'aberration qui provient de la forme des lentilles, gn sera plus petite que GNGa naar voetnoot1), mais que dans celui de l'autre aberration ces deux longueurs seront égales. Par conséquent, l'angle nmg sera toujours plus petit que l'angle NMG. Mais l'angle nmk était, lui aussi, plus petit que NMK, par conséquent l'angle entier gmk est plus petit que GMK. Or, l'angle rms était égal à l'angle gmk, et l'angle RMS à l'angle GMK; par conséquent, rms est plus petit que RMS. Mais c'est de ces angles que dépend l'aberration à l'intérieur de l'oeil comme nous l'avons démontré lorsque nous nous occupions des ouvertures des télescopesGa naar voetnoot2). L'aberration sera donc plus petite dans le microscope plus court que dans le plus long; ce qu'il fallait démontrer en troisième lieu. On peut ajouter que le rapport de ces deux aberrations sera à-peu-près égal à celui des droites NK et nk, c'est-à-dire à celui des distances focales PO et po, en tant que les angles NMG et nmg sont négligeables à cause de leur petitesseGa naar voetnoot3). Quant à notre affirmation, d'après laquelle em est plus petite que EM, elle peut être démontrée comme suit. Supposons qu'en H et h se trouvent les points où les droites DM et dm coupent les axes. On conclut aisément de ce qui a été exposé plus haut que les angles NDP et ndp d'une part, HDP et hdp d'autre part sont égaux; et comme dp est plus petite que DP, ph sera aussi inférieure à PH. Et dans la même proportion hn sera inférieure à HN. Mais ne est égale à | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 541]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
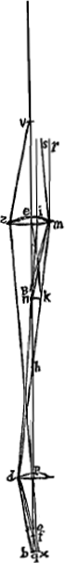 [Fig. 39.]
vero em quam EM, ut mox ostendemus, erit in aberratione quae ex figura oritur, minor gn quam GNGa naar voetnoot1), in altera vero aberratione hae erunt aequales. Itaque semper angulus nmg minor quam NMG. Erat autem et nmk minor quam NMK, ergo totus gmk minor quam GMK. Atqui angulo gmk aequalis erat rms, et angulo GMK aequalis RMS. Ergo et rms minor quam RMS; ab his vero angulis pendet aberratio intra oculum uti ostensum fuit cum de telescopiorum aperturis ageremusGa naar voetnoot2). Ergo minor haec erit breviori huic quam longiori microscopio; quod tertio loco erat demonstrandum. Caeterum eadem fere proportione sese superabunt, qua rectae NK, nk, hoc est, qua foci distantiae PO, po, quatenus anguli NMG, nmg, ob parvitatem negligipossuntGa naar voetnoot3). Quod autem dictum fuit minorem esse em quam EM, sic ostendetur. Sint puncta quibus rectae DM, dm axes intersecant ad H, h. Facile itaque ex superius expositis intelligitur tam angulos NDP, ndp, quam HDP, hdp esse aequales; cumque minor sit dp quam DP, erit et ph minor quam PH. Eademque proportione hn minor quam HN. Sed | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 542]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
NE. Par conséquent, he est plus petite que HE. Et comme les angles ehm et EHM sont égaux, em sera plus petite que EM, ce qui restait à démontrer. Or, comme la netteté de l'image se trouve être plus grande dans le plus court des microscopes, et que la clarté est la même dans ces deux instruments, il s'ensuit que l'ouverture de la lentille pd peut être augmentée quelque peu jusqu'à ce que l'angle d'aberration rms devient égal à l'angle RMS, et qu'ainsi, le reste étant le même, le microscope plus court donnera des images plus lumineuses. Il y a donc ici une progression infinie de clartéGa naar voetnoot1). En effet, la clarté devient d'autant plus grande que la petite lentille pd considérée est plus forte. La largeur auprès de la pupille, dont nous avons parlé plus hautGa naar voetnoot2), n'y fera pas d'obstacle; au contraire, dans les microscopes plus courts cette largeur augmentera aussi. En effet, si l'on prend d'abord, comme ci-devant, les ouvertures proportionnelles aux distances focales, et si l'on prolonge les droites DN et dn jusqu'à ce qu'elles coupent les lentilles EZ et ez aux points I et i, EI et ei seront les demi-largeurs auprès de la pupille, parce qu'à partir des points I et i les rayons qui ont suivi les chemins BD, DI et bd, di, tendront parallèlement vers la pupille. Mais ces longueurs EI et ei seront évidemment égales, parce que les distances focales NE et ne sont égales, ainsi que les angles ENI et eni; en effet, les angles DNP et dnp, opposés à ces derniers, sont égaux. Mais si l'ouverture pd devient plus large, il apparaît que ei deviendra aussi plus grande que EIGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XV.Après avoir expliqué ceci nous examinerons ensuite comment on peut rendre les microscopes plus courts et plus grossissants, en conservant la même clarté et la même netteté, ainsi que la même largeur auprès de la pupille, qu'on trouve dans un microscope donné et aussi la même valeur du rapport BP:PNGa naar voetnoot4). Dans cet examen nous traiterons séparément l'aberration qui résulte de la dispersion du rayon et celle qui provient de la sphéricité de la figure et en premier lieu celle provenant de la dispersion. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 543]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
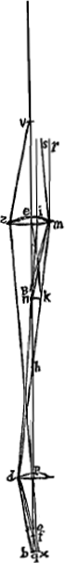 [Fig. 39.]
ne est aequalis NE. Ergo he minor quam HE. Et quia anguli aequales ehm, EHM erit em minor quam EM, quod ostendendum supererat. Cum autem magis distincta visio breviori hoc microscopio obtingat quam longiori, sitque claritas in utroque eadem, sequitur aperturam lentis pd aliquantum augeri posse, donec aberrationis angulus rms fiat aequalis RMS, atque ita caeteris paribus, clarius fieri brevius microscopium. Est ergo progressus claritatis hic infinitusGa naar voetnoot1), quippe quae eo magis augetur quo acutior ponetur lenticula pd. Neque vero obstabit Latitudo ad Pupillam superius explicataGa naar voetnoot2). sed contra haec quoque in brevioribus augebitur. Primum enim positis ut ante aperturis proportionalibus ad foci distantias, productisque rectis DN, dn, donec lentibus, EZ ez, occurrant in punctis I, i. Erunt EI, ei, latitudines ad pupillam dimidiae, quia à punctis I, i radij ad pupillam paralleli pergunt per BD, DI et bd, di, advenientes, quas quidem EI, ei aequales esse constat, quia aequales sunt foci distantiae NE, ne, itemque aequales anguli ENI, eni; quia nempe ipsis oppositi DNP, dnp sunt aequales. Quod si jam igitur latior fiat apertura pd, apparet et ei majorem fieri quam EIGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio XV.]His explicatis inquiremus jam porro quomodo servata eadem claritate et distinctione, itemque latitudine ad pupillam quae est in microscopio dato, nec non ratione BP ad PN, breviora fieri possint, quaeque simul res visas magis amplificentGa naar voetnoot4). Qua in re aberrationes quae ex dissipatione radij, quaeque ex figura sphaerica oriuntur, seorsim adhibebimus, et prius illam, quae ex dissipatione. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 544]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Supposons de nouveau que nous ayons affaire à deux microscopes [Fig. 38 et 39] et que tout soit comme dans le cas de la proposition précédente, à cela près que, dans le plus petit, le rapport de pb à la demi-ouverture pd soit inconnu, ainsi que la distance focale ne de la lentille oculaire. Mais tout le reste sera construit comme auparavant. Soit en outre dans le plus grand microscope la distance PB = b, c'est-à-dire celle de la petite lentille P à l'objet; de plus PN = c, NE = d, PD (largeur de la demi-ouverture) = a; BX (longueur de l'objet) = h, NK = n. Supposons toutefois que les distances PN et PB des points conjugués soient entre elles dans un rapport plus grand que de 6 ou 7 à 1, et que la distance focale EN soit plus grande que la distance focale PO, comme on a coutume, et à bon droitGa naar voetnoot1), d'arranger les choses dans les microscopes de ce genre. Mais dans le plus petit microscope prenons la distance pb = f, et pd (la demi-ouverture cherchée) = x. On aura pn = cf/b, puisque nous prenons proportionnelles entre elles les grandeurs PB, PN; bp, pn. Or, si l'on avait eu BP:PD = bp:pd, il apparaît que l'on aurait pd = fa/b, et que l'angle d'aberration bdqGa naar voetnoot2) du rayon venant du point n et tombant sur la lentille p serait égal à l'angle d'aberration BDQ du rayon venant du point N et tombant sur la lentille P, parce qu'ici, comme dans le cas de la proposition précédente, NP:np = PB:pb et que le rapport des distances focales PO:po a aussi la même valeur. Mais maintenant, puisque je pose la demi-ouverture pd = x et non pas = fa/b, l'angle BDQ sera à l'angle bdq comme fa/b est à x. En effet, d'après la loi de l'aberration que nous considérons ici, bq a toujours le même rapport à pdGa naar voetnoot3); par conséquent, l'angle bdq est censé croître ou diminuer proportionnellement à l'ouverture pd. D'autre part, si les angles NDK et ndk étaient égaux, le rapport NK:nk serait jugé égal au rapport PN:pn. Mais maintenant le rapport NK:nk sera considéré comme composé du rapport PN:pn et du rapport des angles NDK et ndk, en d'autres termes du rapport PB:pb ou b:f, et du rapport des angles BDQ et bdqGa naar voetnoot4), lequel, comme nous l'avons dit, est égal à celui des grandeurs fa/b et x. Par conséquent, le rapport | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 545]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
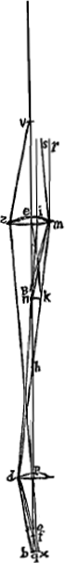 [Fig. 39.]
Ponantur bina rursus microscopia [Fig. 38 et 39], atque omnia eadem quae propos. praecedenti, nisi quod incerta sit, in minori, ratio pb ad semiaperturam pd; itemque incerta lentis ocularis foci distantia ne. caetera vero omnia eodem modo construantur. Porro in majori microscopio distantia PB sit ∞ b, quâ nempe lenticula P abest à visibili. PN ∞ c; NE ∞ d. semiaperturae latitudo PD ∞ a. BX longitudo rei visae ∞ h, NK ∞ n. Ponamus autem distantias punctorum conjugatorum PN ad PB esse in ratione majori quam 6 vel 7 ad 1, et foci distantiam EN majorem esse foci distantiâ PO. quemadmodum haec in hujusmodi microscopijs rectèGa naar voetnoot1) statui solent. at in minori microscopio assumatur distantia pb ∞ f; semiapertura quaesita pd ∞ x. Erit autem pn ∞ cf/b quia proportionales ponimus PB, PN; bp, pn. Quod si fuisset ut BP ad PD ita bp ad pd, apparet futuram pd ∞ fa/b, et angulum aberrationis bdqGa naar voetnoot2), radij ex n venientis in lentem p, aequalem futurum angulo aberrationis BDQ radij ex N venientis in lentem P: quia sicut prop. praecedenti ita hic quoque ut NP ad np, ita PB ad pb, et ita quoque foci distantia PO ad po. Nunc vero quia semi-aperturam pd pono ∞ x, non autem ∞ fa/b, erit ut fa/b ad x ita angulus BDQ ad angulum bdq. Semper enim, ex lege aberrationis quam hic consideramus, bq ad pd eandem rationem servatGa naar voetnoot3), ac proinde quoque censetur angulus bdq proportionaliter crescere aut minui cum apertura pd. Rursus si aequales essent anguli NDK, ndk, censeretur esse NK ad nk ut PN ad pn, nunc vero ratio NK ad nk componi censebitur ex rationibus PN ad pn, et ea quae anguli NDK ad ndk. hoc est ex rationibus PB ad pb, seu b ad f, et anguli BDQ ad bdqGa naar voetnoot4), quam diximus esse eandem quae fa/b ad x; ac proinde ratio NK ad nk erit quae rectanguli fa ad | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 546]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
NK:nk sera égal à celui des rectangles fa et fx, ou bien à a:x. Et comme NK = n, on aura nk = nx/a. Pour que, en premier lieu, l'angle d'aberration à l'intérieur de l'oeil devînt égal dans les deux cas, les angles KMG et kmg devraient être égaux, ce que l'on peut conclure de ce qui a été dit plus hautGa naar voetnoot1). Mais au lieu de ceux-ci nous admettrons que les angles KMN et kmn doivent être égaux, où l'on néglige les accroissements NMG et nmg, attendu qu'ils sont fort petits en comparaison de ces angles eux-mêmes, comme cela apparaîtra dans la description et dans le calcul, qui suit, de notre microscopeGa naar voetnoot2). Comme donc NK est à NM ou NE, c'est-à-dire comme n est à d, ainsi sera approximativement nk ou nx/a à nm ou ne, laquelle est donc égale à dx/a. Ensuite, comme la même longueur, celle des petites lignes BX, bx, est vue dans le microscope donné sous l'angle EVZ, et dans l'autre sous l'angle evz, l'angle PBD doit être à l'angle pbd comme l'angle EVZ est à l'angle evz. En effet, de cette façon la quantité de lumière qui entre dans chacun des deux microscopes sera proportionnelle à la grandeur apparente; et par suite la clarté sera pour chacun d'eux la même. Par conséquent, en permutant, on aura aussi que l'angle EVZ est à PBD comme evz est à pbd. Or, le rapport des angles EVZ et PBD est composé des rapports EVZ:EPZ (ou BPX) et BPX:PBD; lesquels sont ici considérés comme égaux respectivement à PE:EV, ou bien (à cause de la proportion formée par les trois grandeurs PN, PE et PV) PN:NE et BX:PD, en d'autres termes à c:d et h:a; l'angle EVZ sera donc à l'angle PBD comme ch est à da. C'est pourquoi l'angle evz aura à l'angle pbd ce même rapport. Mais le rapport de l'angle evz à l'angle pbd est composé des rapports des angles evz et epz (ou bpx) et des angles bpx et pbd, lesquels rapports sont considérés ici comme égaux respectivement à pe:ev, ou pn:ne, et bx:pd, en d'autres termes à cf/b:dx/a et h:x; il s'ensuit que le rapport composé de cf/b:dx/a et de h:x, en d'autres termes le rapport cfh/b:dxx/a, sera égal au rapport ch:da. On en tire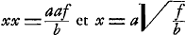 . .
On trouve donc ici, comme chez les télescopesGa naar voetnoot3), que lorsque la clarté reste la même ainsi que l'aberration provenant de la dispersion, les ouvertures des len- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 547]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
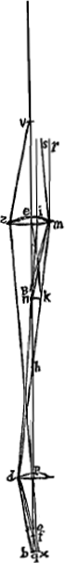 [Fig. 39.]
rectang. fx seu quae a ad x. cumque NK sit ∞ n, erit nk ∞ nx/a. Jam quo aberrationis angulus utrobique intra oculum aequalis fiat, deberent esse aequales anguli KMG, kmg; ut ex superioribus intelligi potestGa naar voetnoot1). Sed pro his ponemus aequales esse debere angulos KMN, kmn, neglectis accessionibus angulorum NMG, nmg; quia minimi sunt illorum respectu, ut apparebit in descriptione et calculo sequenti microscopij nostriGa naar voetnoot2). Sicut igitur NK ad NM seu NE, hoc est sicut n ad d, ita censebitur esse nk, hoc est nx/a ad nm seu ne, quae itaque ∞ dx/a. Jam porro quia eadem longitudo lineolarum BX, bx, in dato quidem microscopio spectatur angulo EVZ, in altero autem percipitur angulo evz; debet esse ut angulus EVZ ad evz ita PBD ad pbd; sic enim lux hausta utroque microscopio erit ut apparens magnitudo; ac proinde eadem utrique claritas. Itaque permutando etiam erit angulus EVZ ad PBD ut evz ad pbd. anguli autem EVZ ad PBD ratio componitur ex rationibus EVZ ad EPZ sive BPX, et BPX ad PBD; quae censentur hic eaedem ac PE ad EV, sive (ob proportionales PN, PE, PV) PN ad NE, et BX ad PD. hoc est, eaedem quae c ad d, et h ad a; ac proinde erit angulus EVZ ad PBD ut ch ad da. quare et angulus evz ad pbd hanc eandem habebit rationem. Atqui ratio anguli evz ad pbd, componitur ex rationibus ang. evz ad epz, sive bpx, et bpx ad pbd; quae censentur hic eaedem ac pe ad ev, sive pn ad ne, et bx ad pd. hoc est eaedem quae cf/b ad dx/a, et h ad x. ac proinde ratio composita ex cf/b ad dx/a et h ad x, hoc est ratio cfh/b ad dxx/a, erit eadem quae ch ad da. Unde fit xx ∞ aaf/b; et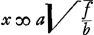 . .
Invenitur itaque hic, sicut in TelescopijsGa naar voetnoot3), ut si maneat eadem claritas eademque aberratio ex dissipatione, prodeant aperturae lentium quae rei visae obvertuntur, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 548]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tilles qui se trouvent du côté de l'objet sont proportionnelles aux racines carrées des distances focales, car comme √b est à √f ainsi le demi-diamètre a de l'ouverture est ici à x. Or, b et f sont proportionnelles aux distances focales PO et po. Ensuite comme, d'après ce que nous avons dit, l'angle DBP est à l'angle dbp dans un rapport égal à celui des grandeurs apparentes correspondant aux deux microscopes, c'est-à-dire à celui des angles ZVE et zve, il s'ensuit que si l'on veut que le grossissement soit deux fois plus grand dans le microscope composé des lentilles e et p que dans l'autre, l'angle dbp doit être deux fois plus grand que l'angle DBP, afin que la clarté demeure la même pour l'un et pour l'autre. Il en résulte encore, puisque BP:PD = b:a, que l'on aura bp:pd (c'est-à-dire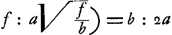 . On aura donc f = ¼b et, par suite, x . On aura donc f = ¼b et, par suite, x 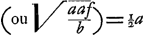 . Et la distance focale ne, qui était dx/a, devient égale à ½d. . Et la distance focale ne, qui était dx/a, devient égale à ½d.
Supposons donc un microscope tel que le nôtre, dans lequel la distance focale PO de la petite lentille est de 7/10 pouce, celle EN de la lentille oculaire = 2, la distance NP = 7 pouces, et par conséquent la distance PB de l'objet = 7/9 pouce d'après la proposition XX, Part. I, Liv. IGa naar voetnoot2), attendu que les points N et B sont conjugués entre eux par rapport à la lentille P. On a encore EV (distance de l'oeil à la lentille E) = 18/7, parce que les points P et V sont conjugués entre eux par rapport à cette lentille. De même PD, le demi-diamètre de l'ouverture, est égal à 1/20. Ceci étant supposé, on construira à l'aide de ce microscope un autre grossissant les objets deux fois plus, la clarté et la netteté demeurant les mêmes, pour lequel on aura po = 7/40, en = 1, la distance np = 7/4, pb = 7/36, ev = 11/7, pd = 1/40, et dont la longueur totale vb est donc de 4½ pouces environ, tandis que VB, la longueur du nôtre, est de 12⅓ pouces environ, c'est-à-dire trois fois plus grande. Or, dans notre microscope le grossissement linéaire est de 36:1, c'est-à-dire que, d'après ce que nous avons dit à la proposition. XIIGa naar voetnoot3), la largeur de l'objet paraîtra dans cette mesure plus grande que lorsqu'on le considérerait à l'oeil nu à une distance de 8 pouces; parce que, comme cela a été démontré à l'endroit cité, ce rapport est composé du rapport PN:NE et de celui de la longueur de 8 pouces à PB, c'est-à-dire, des rapports 7:2 et 8:7/9, lesquels produisent le rapport 36:1. Cependant nous démontrerons que la largeur auprès de la pupille, dont nous avons parlé plus hautGa naar voetnoot4), est la même chez les deux microscopes. En effet, dans le plus grand on a NP (ou c):PD (ou a) = NE (ou d):EI; EI, la largeur | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 549]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
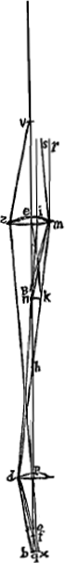 [Fig. 39.]
in subduplicata ratione foci distantiarum. nam ut √b ad √f, ita hic aperturae semidiameter a ad x. Sunt autem b et f foci distantiae PO et poGa naar voetnoot1). Porro quoniam, sicut magnitudines apparentes in utroque microscopio, hoc est sicut angulus ZVE ad zve, ita diximus esse angulum DBP ad dbp, sequitur si multiplicatio duplo major postuletur in microscopio ex lentibus e et p composito quam in altero; debere angulum dbp duplo majorem esse quam DBP, ut eadem in utroque servetur claritas. Ac proinde cum BP sit ad PD, ut b ad a, fore bp ad pd, hoc est f ad 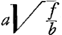 ut b ad 2a. Unde fit f ∞ ¼b, atque hinc x sive ut b ad 2a. Unde fit f ∞ ¼b, atque hinc x sive 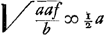 . Et foci distantia ne, quae erat dx/a, ∞ ½d. . Et foci distantia ne, quae erat dx/a, ∞ ½d.
Sic, posito microscopio quale est nostrum, in quo lenticulae foci distantia PO est 7/10 partium qualium pollex est 1, lentis ocularis foci distantia EN ∞ 2, distantia NP ∞ 7; ac proinde distantia rei visae PB ∞ 7/9, ex propos. [XX, Part. I, Lib. I]Ga naar voetnoot2), quia nempe ad lentem P conjugata sunt puncta N et B. Item EV ∞ 18/7, distantia nempe oculi a lente E, quia ad eam conjugata sunt puncta P et V. Item semidiameter aperturae PD ∞ 1/20. His inquam positis, fiet hinc aliud duplo magis res visas amplians microscopium servata eadem claritate ac distinctione, in quo po erit 7/40; en ∞ 1; distantia np ∞ 7/4; pb ∞ 7/36; ev ∞ 11/7; pd ∞ 1/40. Cujus itaque longitudo tota vb circiter 4½ pollicum cum nostri longitudo VB sit circiter 12⅓ poll. eoque fere triplo major. Est autem in nostro amplificatio ratione diametri, ea quae 36 ad 1, ut nempe secundum ea, quae propos. [XII]Ga naar voetnoot3) diximus, tanto auctior appareat rei visae latitudo quam si ab octo pollicum distantia nudo oculo spectaretur; quoniam, ut ibi ostensum fuit, proportio haec componitur ex rationibus PN ad NE, et ea quae longitudinis 8 poll. ad PB, hoc est, ex rationibus 7 ad 2 et 8 ad 7/9, quae efficiunt rationem 36 ad 1. Latitudo autem ad pupillam, de qua in superioribusGa naar voetnoot4), in utroque microscopio eadem esse probatur. Quia cum in majore sit ut NP ∞ c ad PD ∞ a ita | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 550]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
auprès de la pupille, sera donc égale à ad/c. Et de même, dans le plus petit, puisque 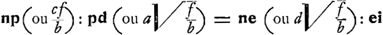 , on trouve que ei a également la valeur ad/c.
Ces considérations seront justes s'il est permis de ne tenir compte que de l'aberration résultant de la dispersion, et il y aura pour ainsi dire une progression infinie à des microscopes plus puissants, puisqu'on peut poser , on trouve que ei a également la valeur ad/c.
Ces considérations seront justes s'il est permis de ne tenir compte que de l'aberration résultant de la dispersion, et il y aura pour ainsi dire une progression infinie à des microscopes plus puissants, puisqu'on peut poser  comme b est à une autre grandeur quelconqueGa naar voetnoot1). Mais, en vérité, il faut examiner si l'autre aberration, celle qui provient de la forme des lentilles, ne peut pas déranger plus ou moins ces conclusions. À cet effet, il est nécessaire que nous commencions par soumettre au calcul chacun des deux angles d'aberration dans notre microscope dont nous venons de parler et où, comme nous le savons, ni l'une ni l'autre aberration n'est encore nuisibleGa naar voetnoot2). Mais nous voulons d'abord démontrer le lemme suivant: comme b est à une autre grandeur quelconqueGa naar voetnoot1). Mais, en vérité, il faut examiner si l'autre aberration, celle qui provient de la forme des lentilles, ne peut pas déranger plus ou moins ces conclusions. À cet effet, il est nécessaire que nous commencions par soumettre au calcul chacun des deux angles d'aberration dans notre microscope dont nous venons de parler et où, comme nous le savons, ni l'une ni l'autre aberration n'est encore nuisibleGa naar voetnoot2). Mais nous voulons d'abord démontrer le lemme suivant:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemme 1Ga naar voetnoot3).Soit NPB [Fig. 40] l'axe, O le foyer d'une lentille convexe PD; SD un rayon parallèle à l'axe, lequel envoie donc, après avoir été dispersé par la réfraction, un rayon rouge selon DO; supposons en outre que le rayon violet extrême coupe l'axe au | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 551]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
NE ∞ d ad EI, erit EI latitudo ad pupillam ∞ ad/c. at in minore similiter, quia ut np, hoc est cf/b, ad pd, hoc est 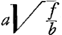 , ita , ita 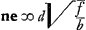 , ad ei, invenitur et haec ∞ ad/c.
Haec itaque sic se habebunt si tantum aberrationis ejus quae ex dissipatione ratio ineunda sit. eritque progressio velut infinita ad majores microscopiorum effectus obtinendos, quoniam poni poterat f ad , ad ei, invenitur et haec ∞ ad/c.
Haec itaque sic se habebunt si tantum aberrationis ejus quae ex dissipatione ratio ineunda sit. eritque progressio velut infinita ad majores microscopiorum effectus obtinendos, quoniam poni poterat f ad 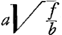 ut b ad aliam quamlibetGa naar voetnoot1). Sed verò examinandum est, an non altera aberratio quae ex figura oboritur aliquid turbare possit. Quem in finem oportet ut utriusque aberrationis angulum in nostro illo quod diximus microscopio, ubi neutram adhuc nocere scimus, primum calculo investigemusGa naar voetnoot2). Praemittimus vero Lemma hujusmodi. ut b ad aliam quamlibetGa naar voetnoot1). Sed verò examinandum est, an non altera aberratio quae ex figura oboritur aliquid turbare possit. Quem in finem oportet ut utriusque aberrationis angulum in nostro illo quod diximus microscopio, ubi neutram adhuc nocere scimus, primum calculo investigemusGa naar voetnoot2). Praemittimus vero Lemma hujusmodi.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemma 1Ga naar voetnoot3).Sit lentis convexae PD [Fig. 40] axis NPB. focus in O, radius axi parallelus SD, qui itaque ex refractione dissipatus mittit radium rubrum in DO, sed violaceum extremum ponamus convenire cum axe in R. Quod si jam a puncto in axe N, fera- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 552]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
point R. Or, si du point N, situé sur l'axe, part le rayon ND qui tombe sur cette même lentille et qui, dispersé par la réfraction, envoie son rayon rouge au point B et son rayon violet extrême au point F, je dis qu'on pourra considérer l'angle BDF comme égal à l'angle ODR; et la différence sera d'autant plus faible que les surfaces de la lentille se couperont en D sous un plus petit angle et que les points B et O seront moins éloignés l'un de l'autre. En effet, comme le rayon rouge, contenu dans le rayon incident SD, continue sa route suivant DO, tandis que le rayon rouge, contenu dans le rayon ND, prend le chemin DB, l'angle BDO sera, d'après la proposition VIGa naar voetnoot1), à-peu-près égal à l'angle SDN. De la même façon, comme le rayon violet, contenu dans SD, continue sa route suivant DR, et le rayon violet, contenu dans ND, suivant DF, l'angle FDR sera, d'après la même proposition VI, estimé égal à l'angle SDN. Par conséquent, les angles BDO et FDR sont aussi considérés comme égaux entre eux, et lorsqu'on en retranche la partie commune FDO, les parties restantes BDF et ODR seront pareillement égales, et cela d'autant plus exactement que l'angle en D sous lequel les deux surfaces de la lentille seront inclinées l'une par rapport à l'autre sera plus petit, que les rayons SD et ND tomberont plus normalement sur ces surfaces, et que ces rayons intercepteront entre eux un plus petit angle SDN, comme on le comprendra d'après ce que nous avons ditGa naar voetnoot2) à propos de la proposition VI. Or, il est évident que SDN est d'autant plus petit que le point B est moins distant du point O; en effet, alors PN est d'autant plus grande, parce que BO, BP et BN forment une proportion d'après la proposition XXGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XVI.Calculer dans notre microscope l'angle de l'aberration provenant de la dispersion, et examiner quelle peut être sa grandeur dans les télescopes et dans les microscopes, sans que cette aberration soit nuisibleGa naar voetnoot4). Nous effectuerons maintenant de la façon suivante le calcul dont nous avons parléGa naar voetnoot5). La distance focale de la lentille P [Fig. 41], dont nous négligeons l'épaisseur, était PO = 7/10 pouceGa naar voetnoot6). Mais PD était égale à 1/20 pouce. Joignons les | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 553]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
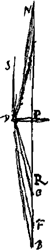 [Fig. 40.]
tur in lentem eandem radius ND, qui ex refractione dissipatus, mittat radium rubrum in B, violaceum extremum in F. dico angulum BDF aequalem censeri posse angulo ODR, tantoque propius quanto inclinatio superficierum lentis in D erit minore angulo, quantoque minus distabunt puncta B, O. Cum enim radius ruber qui inest incidenti radio SD, eat in DO; ruber vero qui in radio ND eat in DB, erit ex propos. [VI]Ga naar voetnoot1) angulus BDO proxime aequalis SDN. Similiterque cum radius violaceus qui inerat in SD, abeat in DR; itemque violaceus qui in ND, abeat in DF; censebitur ex eadem prop. VI ang. FDR aequalis SDN: Itaque aequales inter se censentur et BDO, FDR, et ablato communi FDO, erunt similiter aequales BDF, ODR. ac tanto propius quanto et angulus inclinationis superficierum lentis in D erit minoris anguli, et rectiores radij SD, ND in superficies illas incident, radijque ipsi minorem intercipient ang. SDN, ut ex ijs intelligitur quae ad prop. [VI] supra dicta fueruntGa naar voetnoot2). patet autem tanto minorem esse SDN quanto punctum B minus distat ab O, tanto enim major PN, quia proportionales sunt BO, BP, BN ex prop. [XX]Ga naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio XVI.][Angulum aberrationis ex dissipatione in nostro microscopio, et quantus in Telescopijs et Microscopijs nocere non possit, per calculum inquirere.]Ga naar voetnoot4) Jam calculum quem diximusGa naar voetnoot5) sic prosequemur. Erat lentis P [Fig. 41], cujus crassitudinem pro nulla habemus, foci distantia PO ∞ 7/10 poll.Ga naar voetnoot6) PD vero | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 554]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
points D et O. Il est déjà établi que si un rayon tombe parallèlement à l'axe sur la lentille au point D, ce rayon doit être dispersé par un angle ODβ égal à 1/50 de l'angle DOP, comme nous l'avons dit en parlant de la dispersion du rayonGa naar voetnoot1). Soit Oβ perpendiculaire à l'axe et puisse Dβ couper cet axe en δ. Par conséquent, Oβ sera estimée égale à 1/50 PD, mais PD était égale à 1/20 pouce. Oβ sera donc égale à 1/1000, et OD ou OP, qui était égale à 7/10, sera à Oβ comme 700 est à 1. Mais, d'après le lemme précédent, le rayon incident ND serait dispersé par un angle égal à ODβ et cet angle serait BDQ, attendu que ND envoie, par supposition, un rayon rouge selon DB. Par conséquent, ∠BDQ = ∠ODβ. Mais comme d'autre part le rayon incident BD est dispersé par un angle NDK égal à BDQ pour la raison donnée plus hautGa naar voetnoot2), c'est-à-dire égal à l'angle ODβ, on aura aussi DN (ou PN):NK = DO (ou PO):Oβ, c'est-à-dire = 700:1. Mais EN:NP == 2:7 = 200:700. Par conséquent, EN (ou MK):NK = 200:1, c'est-à-dire comme 100000, le rayon de la table, est à 500, c'est-à-dire à la tangente de 17′12″Ga naar voetnoot3); et par conséquent l'angle NMK de cette aberration sera dans notre microscope à peu près égal à 17′12″Ga naar voetnoot4). Cet angle sera de la même grandeur dans le microscope plus court, c'est-à-dire dans celui de 4½ poucesGa naar voetnoot5), et pareillement dans tous les microscopes plus petits construits successivement, parce que cette condition d'une aberration égale a été présupposée dans notre investigationGa naar voetnoot6). Or, si à l'angle NMK nous ajoutons l'angle NMG, que nous avons négligé auparavant à cause de sa petitesse, l'angle d'aberration deviendra ici de 17′42″ environGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 555]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
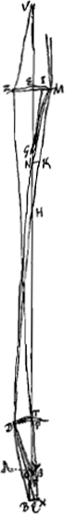 [Fig. 41.]
1/20. Jungatur DO. Constat jam, si radius axi parallelus desuper in D incidat, eum spargi debere angulo ODβ, qui sit 1/50 anguli DOP, uti diximus cum radij dissipationem exponeremusGa naar voetnoot1). Sit Oβ axi perpendicularis quem secet Dβ in δ. igitur Oβ censebitur ∞ 1/50 PD. sed PD erat 1/20 poll. Ergo Oβ ∞ 1/1000, et OD seu OP, quae erat 7/10, erit ad Oβ, ut 700 ad 1. Sed per lemma praemissum, radius incidens ND dissiparetur angulo qui esset aequalis ODβ. isque angulus esset BDQ, quandoquidem ND ponitur mittere radium rubrum per DB. Itaque ang. BDQ ∞ ODβ. Quia vero vicissim radius incidens BD dissipatur angulo NDK, aequali BDQ ex causa in superioribus explicataGa naar voetnoot2), hoc est angulo ODβ; erit et DN, seu PN, ad NK, ut DO seu PO ad Oβ, hoc est ut 700 ad 1. Sed EN est ad NP ut 2 ad 7, sive ut 200 ad 700. Ergo EN seu MK ad NK ut 200 ad 1, hoc est ut radius tab. 100000 ad 500 tangentem 17′.12″Ga naar voetnoot3); ac proinde angulus aberrationis hujus NMK erit in nostro microscopio proximè 17′.12″Ga naar voetnoot4). Idemque erit in breviori illo pollicum 4½Ga naar voetnoot5), et in omnibus deinceps diminutis, quia haec conditio aberrationis aequalis in investigatione posita fuitGa naar voetnoot6). Quod si angulo NMK addamus ang. NMG, quem ibi ob parvitatem negleximus, fiet hic ang. aberrationis 17′.42″ circiterGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 556]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
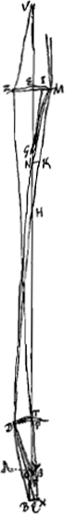 [Fig. 41.]
Mais si dans les télescopes nous demandons la grandeur permise de l'angle de cette aberration, nous trouverons pour les nocturnes un angle de 31′⅓ environGa naar voetnoot1), et pour les diurnes la moitié ou 15′⅔, ce qui ne diffère pas beaucoup de la valeur 17′42″ trouvée plus haut. En effet, dans la figure de la Prop. VIIGa naar voetnoot2), si la distance focale CF de la lentille AC est prise égale à 30 pieds, CA, comme nous l'avons dit, est égale à 3/2 poucesGa naar voetnoot3). D'où l'on conclut FQ = 1/50 CA, c'est-à-dire == 3/100 pouce. Mais QD, ou la distance focale FP, était alors de 3 3/10 pouces. Par conséquent QD:QF = 3 3/10:3/100, c'est-à-dire = 110:1, c'est-à-dire comme le rayon 100000 d'un cercle est à 909, tangente de l'angle 31′20″Ga naar voetnoot4), lequel est égal à-peu-près à l'angle d'aberration QDFGa naar voetnoot5), auquel nous avons attribué cette valeur. Ces considérations feront voir pourquoi ni dans notre microscope, ni dans un autre autant qu'on le veuille plus petit et par conséquent plus grossissant dans la même mesure, s'il fut construit d'après le nôtre selon la règle trouvée, cette aberration provenant de la dissipation du rayon ne peut être nuisibleGa naar voetnoot6). Mais examinons maintenant l'aberration qui résulte de la forme sphérique des lentilles. À cet effet, il faut de nouveau commencer par établir un lemme tel que le suivantGa naar voetnoot7): | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 557]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Sed in Telescopijs si quaeramus quantus aberrationis hujus angulus ferri possit, inveniemus in nocturnis quidem 31′⅓ circiterGa naar voetnoot1), in diurnis vero dimidium sive 15′⅔. quod ab illis 17′.42″ non multum discrepat. Etenim in figura propos. [VII]Ga naar voetnoot2). posita lentis AC foci distantia CF pedum 30, diximus CA esse 3/2 poll.Ga naar voetnoot3) unde FQ ∞ 1/50 CA hoc est 3/100 poll. Sed QD seu foci distantia FP tunc erat 3 3/10 poll. Ergo QD ad QF ut 3 3/10 ad 3/100 hoc est ut 110 ad ad 1, hoc est ut semidiameter circuli 100000 ad 909 tangentem anguli 31′.20″Ga naar voetnoot4), qui est proximè angulus aberrationis QDFGa naar voetnoot5), quantum esse diximus. Ex his intelligitur cur nec in nostro microscopio neque in alio quamlibet breviori eoque magis amplificante, quod secundum inventam regulam ex nostro ordinatum fuerit, haec aberratio ex radij dissipatione nocitura sitGa naar voetnoot6). Nunc vero de aberratione quae ex figura lentium sphaerica oritur examen instituamus. Ubi rursus lemma praemittendum est hujusmodiGa naar voetnoot7). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 558]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemme 2Ga naar voetnoot1).Soit NPB [Fig. 42] l'axe de la lentille convexe PD. Supposons le foyer en O. SD représente un rayon parallèle à l'axe qui, après la réfraction, se meut selon DH, faisant l'aberation OH. Or, supposons que d'un point N situé sur l'axe parte un rayon ND vers cette même lentille, lequel, après avoir été réfracté, coupe l'axe au point F, et soit B le point conjugué avec N, et FB, par conséquent, l'aberration du rayon ND. Je dis que HO sera à FB à-peu-près comme PO2 est à PB2, et cela d'autant plus exactement que la distance NP sera plus grande en comparaison de la distance POGa naar voetnoot2).En effet, prenons PV sur l'axe égale à PO, et soit HL perpendiculaire à l'axe. Posons PO (ou PV) = c, PD = a, NP = d, HO = n. Alors, comme NV, NP, PO et PB forment une proportion d'après la prop. XXGa naar voetnoot3), on aura 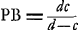 . Mais comme l'angle LDH est estimé égal à l'angle SDN d'après la proposition VIGa naar voetnoot4), c'est-à-dire égal à l'angle DNP, on aura approximativement que NP = d est à PD = a, comme DL (qui est censée égale à PH, c'est-à-dire à c-n) est à LH qui aura la valeur . Mais comme l'angle LDH est estimé égal à l'angle SDN d'après la proposition VIGa naar voetnoot4), c'est-à-dire égal à l'angle DNP, on aura approximativement que NP = d est à PD = a, comme DL (qui est censée égale à PH, c'est-à-dire à c-n) est à LH qui aura la valeur 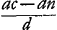 . Et parce que PD:LH = PF:FH, DP-LH,
c'est-à-dire . Et parce que PD:LH = PF:FH, DP-LH,
c'est-à-dire 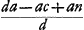 , sera à DP = a, comme PH = c-n est à PF qui aura la valeur , sera à DP = a, comme PH = c-n est à PF qui aura la valeur 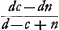 ; en soustrayant cette dernière de ; en soustrayant cette dernière de 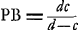 , on obtient , on obtient 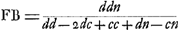 , grandeur qui est à HO = n, comme dd est à dd-2dc++cc+dn-cn; or, ce rapport peut être censé égal au rapport de dd à dd-2dc++cc puisque la quantité n est fort petite par rapport aux autres. Mais comme dd est à dd-2dc+cc, c'est-à-dire, comme NP2 est à NV2, ainsi est PB2 à PO2; parce que, comme nous l'avons dit, NV est à NP, comme PO est à PB. Par conséquent, FB sera à HO à fort peu près comme PB2 est à PO2, et cela d'autant plus exactement que l'angle SDN sera plus petit, comme cela ressort de ce que , grandeur qui est à HO = n, comme dd est à dd-2dc++cc+dn-cn; or, ce rapport peut être censé égal au rapport de dd à dd-2dc++cc puisque la quantité n est fort petite par rapport aux autres. Mais comme dd est à dd-2dc+cc, c'est-à-dire, comme NP2 est à NV2, ainsi est PB2 à PO2; parce que, comme nous l'avons dit, NV est à NP, comme PO est à PB. Par conséquent, FB sera à HO à fort peu près comme PB2 est à PO2, et cela d'autant plus exactement que l'angle SDN sera plus petit, comme cela ressort de ce que
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 559]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Lemma 2.]Ga naar voetnoot1)Sit lentis convexae PD [Fig. 42] axis NPB. Focus in O. Radius axi parallelus SD, qui refractus eat per DH, faciens aberrationem OH, a puncto autem in axc, N, feratur ad lentem eandem radius ND, qui refractus conveniat cum axe in F, sitque B punctum conjugatum ipsi N, adeoque radij ND aberratioSumatur enim PV in axe aequalis PO, sitque HL axi perpend. Et PO sive PV sit ∞ c; PD ∞ a; NP ∞ d; HO ∞ n. Jam quia proportionales sunt NV, NP; PO, PB ex prop. [XX]Ga naar voetnoot3), erit 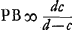 . Quia vero angulus LDH aequalis censetur SDN ex propos. [VI]Ga naar voetnoot4), hoc est angulo DNP, erit proxime ut NP ∞ d, ad PD ∞ a, ita DL quae censetur aequalis PH, hoc est c-n, ad LH, quae erit . Quia vero angulus LDH aequalis censetur SDN ex propos. [VI]Ga naar voetnoot4), hoc est angulo DNP, erit proxime ut NP ∞ d, ad PD ∞ a, ita DL quae censetur aequalis PH, hoc est c-n, ad LH, quae erit 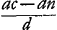 . Et quia PD ad LH ut PF ad FH, erit DP minus LH, hoc est . Et quia PD ad LH ut PF ad FH, erit DP minus LH, hoc est 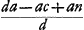 ad DP ∞ a, ut ad DP ∞ a, ut
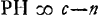 ad PF, quae erit ad PF, quae erit 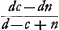 quae subtracta a quae subtracta a 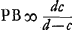 fit fit 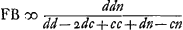 quae ad HO ∞ n, ut dd ad dd-2dc+cc+dn-cn; haec autem ratio eadem censeri potest quae dd ad dd-2dc+cc, quia quantitas n minima est caeterarum respectu. Sicut autem dd ad dd-2dc+cc, hoc est ut quadratum NP ad quadratum NV ita est quadratum PB ad quadratum PO; quia diximus esse ut NV, NP, ita PO ad PB; Ergo erit FB ad HO proxime ut quadratum PB ad quadratum PO, ac tanto quidem magis quanto angulus SDN minor erit, quae ad HO ∞ n, ut dd ad dd-2dc+cc+dn-cn; haec autem ratio eadem censeri potest quae dd ad dd-2dc+cc, quia quantitas n minima est caeterarum respectu. Sicut autem dd ad dd-2dc+cc, hoc est ut quadratum NP ad quadratum NV ita est quadratum PB ad quadratum PO; quia diximus esse ut NV, NP, ita PO ad PB; Ergo erit FB ad HO proxime ut quadratum PB ad quadratum PO, ac tanto quidem magis quanto angulus SDN minor erit,
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 560]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
nous avons annoté à la proposition VIGa naar voetnoot1); en d'autres termes d'autant plus exactement que le rapport NP:PO a une plus grande valeur. La proposition est donc démontréeGa naar voetnoot2). De cette proposition on tire le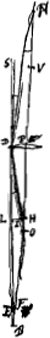 [Fig. 42.]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemme 3Ga naar voetnoot3).Lorsqu'on trace les droites DO et DB, les angles HDO et FDB seront égaux.Ga naar voetnoot4). En effet, supposons que DO coupe HL en I, et que FE, perpendiculaire à l'axe, rencontre la droite DB en E. Le rapport BF:HO est composé des rapports BF:FE, FE:HI et HI:HO. C'est-à-dire des rapports BP:PD, FE:HI et PD:PO, ou bien des rapports FE:HI et BP:PO. Or, le rapport BF:OH est égal à BP2:PO2, d'après ce que nous avons démontré plus hautGa naar voetnoot5). Il résulte de tout ceci que le rapport FE:HI est égal au rapport BP:PO, ou FP:PH, parce que FB et HO sont fort petites; ou bien au rapport FD:HD. L'angle FDE est donc censé égal à l'angle HDI à cause de la petitesse des angles DFP et DHP. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XVII.Calculer l'angle d'aberration sphérique dans notre microscopeGa naar voetnoot6). Nous venons maintenant au calcul dans lequel nous nous proposons de tenir compte de l'épaisseur de la petite lentille P, représentée par TP dans la figure précédenteGa naar voetnoot7). Or, cette petite lentille possède dans notre microscope une surface plane, savoir la surface inférieure. Et comme la distance focale PO est de 7/10 pouce, et qu'elle peut être estimée égale au diamètre de courbure de la surface convexe TDGa naar voetnoot8), on aura que comme PO, ou 7/10, est à PD, ou 1/20, ainsi cette dernière | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 561]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ut patet ex ijs quae ad propos. [VI] annotavimusGa naar voetnoot1); hoc est quanto major ratio NP ad PO. Itaque patet propositumGa naar voetnoot2). Hinc vero sequitur, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Lemma 3.]Ga naar voetnoot3)Ductis DO, DB, angulos aequales fore HDO, FDBGa naar voetnoot4). Ponatur enim DO secare HL in I, et FE axi perpendicularem occurrere rectae DB in E. Quia ergo ratio BF ad HO componitur ex rationibus BF ad FE, et FE ad HI et HI ad HO. Hoc est ex rationibus BP ad PD, et FE ad HI, et PD ad PO; hoc est, ex rationibus FE ad HI et BP ad PO. Ratio autem eadem BF ad OH est ea quae quadrati BP ad quadratum PO, ex ante demonstratisGa naar voetnoot5); necesse est rationem FE ad HI eandem esse quae BP ad PO, sive quae FP ad PH, quia FB et HO sunt minimae; sive quae FD ad HD. Unde angulus FDE censetur aequalis HDI propter parvitatem angulorum DFP, DHP. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio XVII.]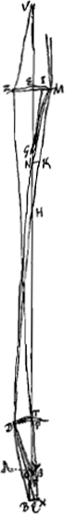 [Fig. 41.]
[Angulum aberrationis ex figura in nostro microscopio per calculum investigare.]Ga naar voetnoot6) Hinc ad calculum accedimus in quo jam crassitudo lenticulae P consideranda est, quae sit TP, in figura superioriGa naar voetnoot7). Habet autem lenticula haec in nostro microscopio superficiem alteram planam quae deorsum conversa est. Cumque foci distantia PO sit 7/10 pollicis eademque aequalis censeri possit diametro convexitatis superficiei TDGa naar voetnoot8); erit ut PO, sive 7/10 ad PD ∞ 1/20, ita haec ad TP, quae fiet 1/280. Hujus vero 7/6 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 562]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
sera à TP, laquelle aura donc la valeur 1/280. Mais les 7/6 de cette dernière longueur sont égales à l'aberration Oδ qui appartient au rayon parallèle à l'axe tombant sur la lentille au point D, parce que la surface plane de la petite lentille est tournée de l'autre côtéGa naar voetnoot1). Par conséquent Oδ = 7/1680, ou = 1/240. Mais comme δP ou OP, est à PD, c'est-à-dire comme 7/10 est à 1/20, ou 14 à 1, ainsi est δO à Oβ. Il
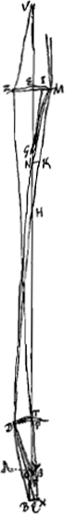 [Fig. 41.]
s'ensuit que Oβ acquiert la valeur 1/3360, et l'on a DO (ou PO):Oβ == 7/10:1/3360 = 2352:1. Mais d'après le Lemme 3 le rayon incident ND ferait un angle d'aberration BDQ égal à l'angle ODβ; réciproquement le rayon BD fera donc un angle d'aberration NDK égal à BDQGa naar voetnoot2), ou ODβ. Par conséquent, comme DO, ou PO, est à Oβ, c'est-à-dire comme 2352 est à 1, ainsi sera DN, ou PN, à NK. Mais comme 2 est à 7, ou comme 672 est à 2352, ainsi est EN à NPGa naar voetnoot3). On trouve donc, par la règle de la proportion dérangéeGa naar voetnoot4), le rapport EN:NK, ou MK:NK, = 672:1, c'est-à-dire égal au rapport du rayon 100000 des Tables à 149, tangente de l'angle 5′8″ qui est l'angle NMKGa naar voetnoot5). Tel est donc dans notre micro scope l'angle d'aberration sphériqueGa naar voetnoot6). Que la vue en peut supporter sans inconvénient un plus grand, cela résulte de ce que, lorsqu'on retourne la petite lentille PD de sorte que | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 563]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
aequantur aberrationi Oδ quam facit radius axi parallelus in D incidens, quia lenticulae plana superficies in partem alteram obversa estGa naar voetnoot1). Ergo Oδ ∞ 7/1680 sive 1/240. Sicut autem δP seu OP ad PD, hoc est, sicut 7/10 ad 1/20, sive ut 14 ad 1, ita est δO ad Oβ. Ergo fit Oβ ∞ 1/3360; et DO seu PO ad Oβ ut 7/10 ad 1/3360, sive ut 2352 ad 1. Sed per Lemma [3] radius incidens ND faceret angulum aberrationis BDQ aequalem ODβ: ac proinde vicissim radius BD faciet angulum aberrationis NDK aequalem BDQGa naar voetnoot2) seu ODβ. Ergo ut DO, seu PO, ad Oβ, hoc est, ut 2352 ad 1, ita erit DN, seu PN, ad NK. Sed ut 2 ad 7, sive ut 672 ad 2352, ita est EN ad NPGa naar voetnoot3). Ergo ex aequoGa naar voetnoot4) EN ad NK, seu MK ad NK, ut 672 ad 1, hoc est ut in Tabulis semidiameter 100000 ad 149, tangentem anguli 5′.8″, qui est angulus NMKGa naar voetnoot5). Hic igitur in microscopio nostro est angulus aberrationis ex figuraGa naar voetnoot6). Quo majorem ferri posse absque visionis incommodo inde apparet, quod inversâ lenticulâ PD, ut pars convexa deorsum spectet, quadruplo fere major fit iste aber- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 564]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
son côté convexe est dirigé vers le bas, cet angle d'aberration devient environ quatre fois plus grand, parce qu'alors l'aberration du rayon qui tomberait parallèlement à l'axe sur la lentille au point D est égale à 9/2 fois l'épaisseur PT d'après la proposition IV, Part. IIGa naar voetnoot1), aberration qui dans le cas considéré n'était que de 7/6 PT, c'est-à-dire seulement d'un quart à peu près de la valeur trouvée en dernier lieu. Il s'ensuit que l'angle d'aberration NMK lui aussi se trouve être alors à peu près quatre fois plus grand que celui pour lequel nous venons de trouver la valeur de 5′. Mais, la lentille étant ainsi retournée, on observe à peine quelque affaiblissement de la vision distincte. L'angle de cette aberration peut donc être porté jusqu' à 20 minutes à peu près; quoique l'angle de l'aberration provenant de la dissipation, qui était de 18′ environGa naar voetnoot2), s'y ajoute. En effet, on comprend aisément que dans tous les cas cette dernière aberration s'ajoute à la précédenteGa naar voetnoot3). Or si, dans le microscope plus court, long de 4½ poucesGa naar voetnoot4), nous cherchons de la même manière l'angle de l'aberration sphérique, nous trouverons que cet anglelà est également de 20′ à peu prèsGa naar voetnoot5). Par conséquent, cet angle sera lui aussi à peine assez grand pour nuire; de sorte que l'effet obtenu avec un microscope de ce genre sera excellent. Mais si nous construisons, d'après la formule de la règle trouvée plus hautGa naar voetnoot6), des microscopes encore plus courts et plus grossissants, cet angle d'aberration croîtra toujours; et cette cause empêche donc que, en nous basant sur cette règle, nous ne puissions augmenter indéfiniment la puissance des microscopes. Toutefois, ce qui semblera peut-être merveilleux, nous démontrerons qu'il existe une autre règleGa naar voetnoot7), qui permet d'obtenir un tel progrès à l'infini. À cet effet nous commençons par établir un Lemme de la forme suivante: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemme 4Ga naar voetnoot8).Si sur une lentille convexe tombent des rayons parallèles à l'axe ou émanant d'un point situé sur l'axe et éloigné de la | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 565]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
rationis angulus; quia tunc aberratio radij qui parallelus axi incideret in D aequat 9/2 crassitudinis PT, ex propos. [IV, Part. II]Ga naar voetnoot1) quae aberratio hic erat tantum 7/6 PT, hoc est fere pars quarta tantum istius. Unde et angulus aberrationis NMK fere quadruplus tunc invenitur ejus qui nunc inventus est 5′. Atqui sic inversâ lenticulâ, vix percipitur aliquid distinctae visioni decedere. Itaque 20 circiter scrupulorum primorum ferri potest angulus istius aberrationis; accedente licet angulo aberrationis quae ex dissipatione, qui erat fere 18′Ga naar voetnoot2). Semper enim hanc aberrationem alteri superaddi facile intelligi potestGa naar voetnoot3). Quod si in breviori illo 4½ pollicum microscopioGa naar voetnoot4), quaeramus eodem modo angulum aberrationis quae ex figura, inveniemus eum quoque 20′ circiterGa naar voetnoot5); qui proinde vix quoque nocere poterit; ut proinde eximius futurus sit ejusmodi perspicilli effectus. Si vero breviora etiam, ac magis amplificantia moliamur ex praescripto Regulae superius inventaeGa naar voetnoot6) crescet semper iste aberrationis angulus. adeoque haec causa impedit quo minus Regulam istam sequentes, infinito progressu microscopiorum virtutem augere possimus. Sed quod mirum fortasse videbitur, aliam suppetere ostendemus RegulamGa naar voetnoot7), per quam ejusmodi progressus concedatur. Praemittimus autem Lemma ejusmodi. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Lemma [4]Ga naar voetnoot8).Si in lentem convexam radij incidant axi paralleli, vel a puncto in axe ultra focum distante manantes, efficient ij | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 566]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
lentille à une distance plus grande que la distance focale, ils formeront après la réfraction des angles d'aberration sphérique à peu près proportionnels à la troisième puissance des distances des points d'incidence à l'axe. Nous démontrerons ce Lemme d'abord pour les rayons parallèles. Soit PB [Fig. 43] l'axe, G le foyer d'une lentille PS, c'est-à-dire, celui des rayons parallèles à l'axe et situés fort près de lui. L'épaisseur de la lentille soit négligée, puisque la distance entière PS est supposée fort petite en comparaison de PB. Supposons de plus que le rayon parallèle qui tombe sur la lentille au point D se meuve ensuite selon DH, faisant l'aberration GH, mais que celui qui tombe parallèlement sur la lentille au point S se meuve selon SI, faisant l'aberration GI. Lorsqu'on trace les droites DG et SG, les angles d'aberration dont nous voulons parler sont GSI et GDH. Je dis que ces angles sont entre eux à peu près comme les troisièmes puissances de SP et de DP. En effet, soit GC perpendiculaire à l'axe et puissent les droites DH et SI prolongées couper cette perpendiculaire aux points K et C. Les angles GSC et KDG sont donc censés être entre eux dans le rapport CG:GK, attendu que DP et SP sont fort petites par rapport à PG. Or, le rapport CG:KG est égal à celui composé des rapports CG:GI, GI:GH et GH:GK, dont le premier, CG:GI, est égal à SP:PI ou à SP:PG, parce que IG est fort petite par rapport à PG. D'autre part le deuxième rapport GI:GH est égal au rapport PS2:PD2, d'après la prop. VII, part. IIGa naar voetnoot1). Et le troisième rapport GH:GK est égal à HP:PD, c'est-à-dire à GP:PD, parce que HG est fort petite par rapport à GP. Par conséquent, le rapport CG:KG sera composé des rapports SP:PG, PG:PD et PS2::PD2. Mais de ceux-ci les deux premiers forment le rapport SP:PD. Le rapport composé des trois rapports en question sera donc égal à SP3:PD3. Ainsi nous avons démontré que le rapport CG:KG, ou bien celui des angles d'aberration CSG et KDG, est à peu près égal à SP3:PD3, c'est-à-dire au cube du rapport SP:PD. Supposons maintenant que les rayons incidents tombant sur la lentille aux points D et S viennent d'un point auquel le point B est conjugué, et que BF représente l'aberration du rayon tombant sur la lentille au point D, tandis que BL est l'aberration du rayon qui tombe sur la lentille au point S. Puisque, d'après le lemme 2Ga naar voetnoot2), on a donc que PG2 est à PB2 comme GH est à BF, et de même comme IG à LB, on obtiendra, par permutation et conversion, IG:GH == LB:BF. Mais nous avions IG:GH = SP2:DP2, donc aussi LB:BF == SP2:DP2Ga naar voetnoot3). En partant de là on démontrera de la même manière qu' on l'a | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 567]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
refracti angulos aberrationis ex Figura, qui proximè triplicatam rationem habeant ejus, quam distantiae punctorum incidentiae ab axe. Primo vero de parallelis ostendemus. Sit lentis PS [Fig. 43] axis PB, focus G, radiorum nempe axi parallelorum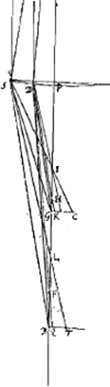 [Fig. 43.]
ab eoque minimo distantium. Lentis crassitudo pro nulla habeatur, quia tota PS valde exigua intelligitur ad PB comparata. Porro radius parallelus qui in D punctum incidit feratur in DH, faciens aberrationem GH. qui vero in S incidit parallelus feratur in SI, faciens aberrationem GI. Junctis igitur DG, SG, erunt anguli aberrationis quos hic intelligimus GSI, GDH. Quos dico proximè triplicatam rationem habere ejus quae SP ad DP. Sit enim GC ad axem perpendicularis, cui occurrant productae DH, SI in K et C. Censentur igitur anguli GSC, KDG eam habere rationem quae CG ad GK, cum DP, SP sint minimae respectu PG. Est autem ratio CG ad KG eadem compositae ex rationibus CG ad GI, et GI ad GH, et GH ad GK. quarum prima ratio CG ad GI, eadem est quae SP ad PI, vel quae SP ad PG, quia IG minima est respectu PG. Item ratio altera GI ad GH est eadem quae quadrati PS ad qu. PD, per prop. [VII, Part. II]Ga naar voetnoot1). Et tertia GH ad GK eadem quae HP ad PD, hoc est, quae GP ad PD, quia HG est minima respectu GP. Itaque ratio CG ad KG, componetur ex rationibus SP ad PG, et PG ad PD, et quadrati PS ad quadratum PD. Sed harum priores duae efficiunt rationem SP ad PD. Ergo ex tribus composita erit eadem quae cubi SP ad cubum PD. Itaque ostensum est rationem CG ad KG, sive anguli aberrationis CSG ad KDG, proxime esse eam quae cubi SP ad cubum PD, hoc est triplicatam rationis SP ad PD. Ponamus jam radios incidentes in D et S, venire à puncto cui conjugatum sit punctum B, atque esse radij in D cadentis aberrationem BF; ejus vero qui in S cadit, aberrationem BL. Cum igitur ex lemmate [2]Ga naar voetnoot2) sit ut quadratum PG ad quadratum PB, ita GH ad BF; atque ita quoque IG ad LB, erit permutando, et convertendo, ut IG ad GH ita LB ad BF. Sed IG erat ad GH ut quadratum SP ad quadratum DP, ergo et LB ad BF ut quadratum SP ad quadratum DPGa naar voetnoot3). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 568]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
fait antérieurement pour les angles GSI et GDH que les angles BSL et BDF sont entre eux comme les troisièmes puissances des distances SP et PD. En effet, ces angles, ou bien BST et BDQ sont censés être entre eux comme BT est à BQ, parce que DP et SP sont fort petites par rapport à BP. Or, le rapport BT:BQ est égal a celui composé des rapports TB:BL, BL:BF et BF:BQ. De ceux-ci le premier, TB:BL, est égal à SP:PL, ou à SP:PB, parce que LB est fort petite par rapport à PB. De même le deuxième rapport, BL:BF, est égal à PS2:PD2, comme nous l'avons démontré un peu plus haut. Et le troisième, BF:BQ, est égal à FP:PD, c'est-à-dire à BP:PD, parce que FB est fort petite par rapport à BP. Par conséquent, le rapport BT:BQ sera composé des rapports SP:PB, PB:PD et PS2:PD2; et parce que de ceux-ci les deux premiers forment le rapport SP::PD, le rapport BT:BQ, c'est-à-dire le rapport de l'angle BSL à l'angle BDF, sera égal à PS3:PD3; ce qui restait à démontrer. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XVIIIGa naar voetnoot1).Comment on peut construire des microscopes plus courts et plus grossissants, dans lesquels on conserve la même clarté et la même netteté, et qui cependant ne sont pas sujets à l'inconvénient nommé plus haut qui résulte d'une plus grande aberration sphériqueGa naar voetnoot2). SupposonsGa naar voetnoot3) de nouveau que nous ayons affaire à deux microscopes et que tout soit comme dans le cas de la proposition XIVGa naar voetnoot4) à cela près que, dans le plus petit microscope, le rapport de pb à la demie-ouverture pd soit inconnu, ainsi que la distance focale ne de la lentille oculaire. Mais tout le reste soit construit comme auparavant. Soit en outre dans le plus grand microscope la distance PB = b, c'est-à-dire celle de la petite lentille P à l'objet; de plus PN = c, NE = d, PD (largeur de la demi-ouverture) = a; BX (longueur de l'objet) = h, NK = n. Supposons toutefois que les distances PN et PB des points conjugués soient entre elles dans un rapport plus grand que de 6 ou 7 à 1, et que la distance focale EN soit plus grande que la distance focale PO, comme on a cou- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 569]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Unde jam, sicut ante de angulis GSI, GDH, ostendetur eadem ratione angulos BSL, BDF esse in ratione triplicata distantiarum SP, PD. Hi enim anguli, sive BST, BDQ censentur esse inter se ut BT ad BQ, quia DP, SP sunt minimae respectu BP. Est autem ratio BT ad BQ eadem compositae ex rationibus TB ad BL, et BL ad BF, et BF ad BQ. Quarum prima TB ad BL est eadem quae SP ad PL, seu quae SP ad PB, quia LB est minima respectu PB. Item ratio altera BL ad BF est eadem quae quadrati PS ad quadratum PD, ut paulo ante est ostensum. Et tertia BF ad BQ est eadem quae FP ad PD, hoc est quae BP ad PD, quia FB est minima respectu BP. Itaque ratio BT ad BQ componetur ex rationibus SP
 [Fig. 38.]
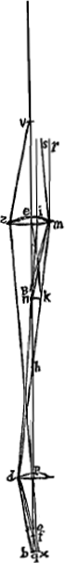 [Fig. 39.]
ad PB, et PB ad PD, et quadrati PS ad quadratum PD. quarum duae priores cum efficiant rationem SP ad PD, erit ratio BT ad BQ, hoc est anguli BSL ad BDF, ea quae cubi PS ad cubum PD, quod supererat demonstrandum. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio XVIII.]Ga naar voetnoot1)[Quomodo breviora fieri possint microscopia et magis amplificantia, in quibus servetur eadem claritas et distinctio, nec tamen priori incommodo a majori aberratione ex figura fiant obnoxia.]Ga naar voetnoot2) PonanturGa naar voetnoot3) bina rursus microscopia, atque omnia eadem quae propositione [XIV]Ga naar voetnoot4), nisi quod incerta sit, in minori, ratio pb ad semiaperturam pd; itemque incerta lentis ocularis foci distantia ne. caetera vero omnia eodem modo construantur. Porro in majori microscopio distantia PB sit ∞ b, quâ nempe lenticula P abest a visibili. PN ∞ c; NE ∞ d. semiaperturae latitudo PD ∞ a. BX longitudo rei visae ∞ h. NK ∞ n. Ponamus autem distantias punctorum conjugatorum PN ad PB, esse in ratione majori, quam 6 vel 7 ad 1, et foci distantiam EN majorem esse foci distantiâ PO. quemadmodum haec in hujusmodi micro- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 570]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
tume, et à bon droit, d'arranger les choses dans les microscopes de ce genre. Mais dans le plus petit microscope posons la distance pb = f, et pd (la demi-ouverture cherchée) = x. Onaura pn = cf/b, puisque nous prenons proportionnelles entre elles les grandeurs BP, PN; bp, pn. Mais si l'on avait eu BP:PD = bp:pd, il apparaît que l'on aurait pd = fa/b et que l'angle d'aberration bdq du rayon venant du point n et tombant sur la lentille p serait égal à l'angle d'aberration BDQ du rayon venant du point N et tombant sur la lentille P; parce qu'ici, comme dans le cas de la proposition XIVGa naar voetnoot1), NP:np = PB:pb et que le rapport des distances focales PO et po a aussi la même valeur. Mais maintenant, puisque je pose la demi-ouverture pd = x et non pas = fa/b, on aura, d'après le lemme précédentGa naar voetnoot2), que comme le cube de fa/b, c'est-à-dire f3a3/b3, sera à x3 ainsi l'angle BDQ sera à l'angle bdq. D'autre part, si les angles NDK et ndk étaient égaux, NK serait censé être à nk comme PN est à pn. Mais maintenant le rapport NK:nk sera censé être composé du rapport PN:pn et de celui des angles NDK et ndk, c'est-à-dire, du rapport PB:pb (ou b:f) et de celui de l'angle BDQ à l'angle bdq, que nous avons dit être égal á f3a3/b3:x3, c'est-à-dire à f3a3:b3x3. Par conséquent, on aura NK::nk = bf3a3:fb3x3, c'est-à-dire = ffa3:bbx3. Et comme NK = n, on aura nk == nbbx3/ffa3. Or, pour que l'angle d'aberration à l'intérieur de l'oeil devînt égal dans les deux cas, les angles KMG et kmg devraient être égaux; mais nous pouvons remplacer ces angles par KMN et kmn en négligeant, comme plus hautGa naar voetnoot3), les accroissements NMG et nmg de ces angles, attendu qu'ils sont extrêmement petits par rapport à eux, et cela avec encore plus de droit que dans la recherche précédenteGa naar voetnoot4). Comme donc NK est à NM, ou NE, c'est-à-dire, comme n est à d, ainsi, estimons-nous, sera nk à nm (ou ne), c'est-à-dire nbbx3/ffa3 à ne, laquelle aura donc la valeur dbbx3/ffa3. Ensuite, comme les longueurs égales des petites lignes BX, bx sont vues par le microscope donné sous l'angle EVZ, par l'autre sous l'angle evz, PBD doit être à pbd comme l'angle EVZ est à l'angle evz. En effet, de cette façon les quantités de lumière qui entrent dans l'un et l'autre microscope seront entre elles comme les grandeurs apparentes, et, par conséquent, la clarté sera la même dans les deux | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 571]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
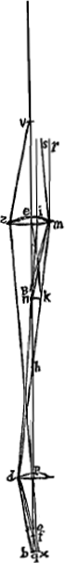 [Fig. 39.]
scopijs rectè statui solent. at in minori microscopio assumatur distantia pb ∞ f; semiapertura quaesita pd ∞ x. Erit autem pn ∞ cf/b, quia proportionales ponimus BP, PN; bp, pn. Quod si fuisset ut BP ad PD ita bp ad pd, apparet futuram pd ∞ fa/b, et angulum aberrationis bdq, radij ex n venientis in lentem p, aequalem futurum angulo aberrationis BDQ radij ex N venientis in lentem P: Quia sicut prop. [XIV]Ga naar voetnoot1) ita hic quoque ut NP ad np, ita PB ad pb, et ita quoque foci distantia PO ad po. Nunc vero quia semi-aperturam pd pono ∞ x, non autem ∞ fa/b, erit ex lemmate praemissoGa naar voetnoot2) ut cubus ex fa/b, hoc est, ut f3a3/b3 ad x3, ita angulus BDQ ad angulum bdq. Rursus si aequales essent anguli NDK, ndk, censeretur esse NK ad nk ut PN ad pn. Nunc vero ratio NK ad nk componi censebitur ex rationibus PN ad pn, et ea quae anguli NDK ad ndk; hoc est ex rationibus PB ad pb seu b ad f, et anguli BDQ ad bdq; quam diximus esse eandem quae f3a3/b3 ad x3, sive quae f3a3 ad b3x3, ac proinde erit NK ad nk ut bf3a3 ad fb3x3, hoc est ut ffa3 ad bbx3. Cumque NK sit ∞ n, erit nk ∞ nbbx3/ffa3. Jam quo aberrationis angulus utrobique intra oculum aequalis fiat, deberent esse aequales anguli KMG, kmg; sed pro his ponemus KMN, kmn, neglectis ut supraGa naar voetnoot3) accessionibus angulorum NMG, nmg, quia exigui prorsus sunt illorum respectu, ac magis etiam quam in disquisitione praecedentiGa naar voetnoot4). Sicut igitur NK ad NM seu NE, hoc est sicut n ad d, ita censebitur esse nk ad nm seu ne, hoc est, nbbx3/ffa3 ad ne, quae itaque erit ∞ dbbx3/ffa3. Jam porro quia eadem longitudo lineolae BX, bx, in dato quidem microscopio spectatur angulo EVZ, in altero autem angulo evz; debet esse ut angulus EVZ ad evz ita PBD ad pbd. Sic enim lux hausta utroque microscopio erit ut apparens magnitudo, ac proinde eadem utrique claritas. Ergo et permutando, angulus | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 572]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
cas. On aura donc aussi, par permutation, que l'angle EVZ est à l'angle PBD comme evz est à pbd. Or, le rapport des angles EVZ à PBD se compose du rapport des angles EVZ à EPZ (ou BPX) et BPX à PBD, c'est-à-dire des rapports PE:EV, ou PN:NEGa naar voetnoot1), et BX:PD, en d'autres termes, des rapports c:d et h:a; il a, par conséquent, la valeur ch:da. Donc aussi le rapport des angles evz et pbd doit avoir cette même valeur. Mais ce rapport de l'angle evz à l'angle pbd est composé du rapport de l'angle evz à l'angle epz, ou bpx, et de celui de l'angle bpx à pbd; c'est-à-dire, des rapports pe:ev, ou pn:ne, et bx:pd; en d'autres termes, des rapports cf/b:dbbx3/ffa3 et h:x. Ce rapport est donc égal à hcf/b:dbbx4/ffa3. Par conséquent, le rapport ch:da doit être égal au rapport hcf/b::dbbx4/ffa3. Il en résulte x4 =
f3a4/b3, et 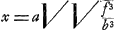 Ga naar voetnoot2).
Si nous exigeons maintenant que le microscope trouvé grossisse les objets deux fois plus que le microscope donné, il faut pour la raison que nous avons exposée dans la recherche précédente, que l'angle dbp soit deux fois plus grand que DBP, et puisque BP est à PD comme b est à a, il faudra que bp soit à pd, c'est-à-dire f à Ga naar voetnoot2).
Si nous exigeons maintenant que le microscope trouvé grossisse les objets deux fois plus que le microscope donné, il faut pour la raison que nous avons exposée dans la recherche précédente, que l'angle dbp soit deux fois plus grand que DBP, et puisque BP est à PD comme b est à a, il faudra que bp soit à pd, c'est-à-dire f à 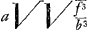 , comme b est à 2a. On en conclut , comme b est à 2a. On en conclut 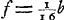 , partant x ou , partant x ou 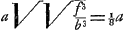 . Et la distance focale en qui était dbbx3/ffa3 acquiert la valeur ½d. . Et la distance focale en qui était dbbx3/ffa3 acquiert la valeur ½d.
D'après ces considérations, l'on pourra, en partant de notre microscope, dont nous avons indiqué les dimensions dans une investigation antérieureGa naar voetnoot3), en construire un autre d'un grossissement linéaire double (la clarté et la netteté restant les mêmes), dans lequel po sera de 7/160 pouce, en = 1, la distance np = 7/16, pb = = 7/144, ev = 23/7Ga naar voetnoot4), le rayon de l'ouverture pd = 1/160. Et en poursuivant le procédé de la règle en question, l'on pourra de la même façon aller plus loin et prendre la distance focale po de la petite lentille aussi petite que l'on veut. En effet, ni l'aberration sphérique, ni l'obscurité ne seront jamais nuisi- | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 573]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
EVZ ad PBD ut evz ad pbd. Ratio autem anguli EVZ ad PBD componitur ex rationibus anguli EVZ ad EPZ seu BPX, et BPX ad PBD; hoc est ex rationibus PE ad EV, seu PN ad NEGa naar voetnoot1), et BX ad PD; hoc est ex rationibus c ad d, et h ad a,
 [Fig. 38.]
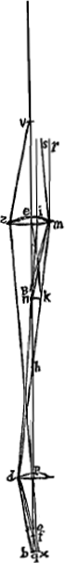 [Fig. 39.]
ac proinde est ea quae ch ad da. Ergo et ratio anguli evz ad pbd debet esse ea quae ch ad da. Haec autem ratio anguli evz ad pbd componitur ex rationibus anguli evz ad epz seu bpx, et bpx ad pbd; hoc est, ex rationibus pe ad ev, seu pn ad ne, et bx ad pd; hoc est, ex rationibus cf/b ad dbbx3/ffa3, et h ad x:ac proinde est ea quae hcf/b ad dbbx4/ffa3. Igitur eadem ratio ch ad da quae hcf/b ad dbbx4/ffa3. Unde fit x4 ∞ ∞ f3a4/b3. Et 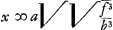 Ga naar voetnoot2).
Quod si jam velimus ut microscopium inventum duplo magis amplificet res visas quam quod erat datum: oportet eandem ob causam, quam exposuimus in praecedenti inquisitione, ut angulus dbp duplo major sit quam DBP, cumque BP ad PD sit ut b ad a, debebit esse bp ad pd, hoc est f ad Ga naar voetnoot2).
Quod si jam velimus ut microscopium inventum duplo magis amplificet res visas quam quod erat datum: oportet eandem ob causam, quam exposuimus in praecedenti inquisitione, ut angulus dbp duplo major sit quam DBP, cumque BP ad PD sit ut b ad a, debebit esse bp ad pd, hoc est f ad 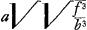 ut b ad 2a. Unde fit ut b ad 2a. Unde fit 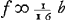 . atque hinc x, sive . atque hinc x, sive 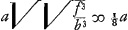 . Et foci distantia en, quae erat dbbx3/ffa3 ∞ ½d. . Et foci distantia en, quae erat dbbx3/ffa3 ∞ ½d.
Secundum quae ex nostro microscopio cujus mensuras in priori disquisitione posuimusGa naar voetnoot3), fiet aliud duplo magis amplificans ratione diametri (servata eadem claritate ac distinctione,) in quo po erit 7/160 poll. en ∞ 1. distantia np ∞ 7/16, pb ∞ 7/144, ev ∞ 23/7Ga naar voetnoot4), semidiameter aperturae pd ∞ 1/160. atque ita ulterius progredi licet ex hujus regulae praescripto, ponendo lenticulae foci distantiam po quamlibet exiguam. nec enim aberratio ex figura, nec obscuritas unquam nocebunt, | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 574]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
bles, attendu qu'elles restent toujours les mêmesGa naar voetnoot1). Et l'autre aberration, celle qui résulte de la dispersion du rayon, ne nuira pas non plus, vu qu'elle devient chaque fois plus petiteGa naar voetnoot2). Mais la largeur auprès de la pupille restera la même que dans notre microscope, car cette largeur ei y avait la valeur ad/c, comme nous l'avons démontré plus hautGa naar voetnoot3), tandis qu'ici, puisqu'on a 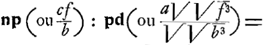 , on obtient de nouveau ei = ad/c. , on obtient de nouveau ei = ad/c.
D'après cette règle il existe donc une progression infinieGa naar voetnoot4) dans l'augmentation des pouvoirs du microscopeGa naar voetnoot5), si nous admettons qu'il est possible de fabriquer des lentilles arbitrairement petites. Or, dans ces recherches nous supposions que le rapport BP:PN, c'est-à-dire celui des distances des deux points conjugués à la lentille P, garde toujours la même valeur. Mais nous pouvons aussi, sans faire cette supposition, trouver des règles générales, assez différentes des précédentes, mais tendant toutefois au même but; nous énoncerons ces règles en peu de mots, sans indiquer la voie par laquelle elles ont été trouvées pour ne pas nous attarder plus longtemps sur ce sujet. D'ailleurs elles s'appuient sur les mêmes fondements que nous avons déjà fait connaître. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 575]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
quippe semper eaedem manentesGa naar voetnoot1). neque etiam aberratio altera quae ex radij dissipatione
 [Fig. 38.]
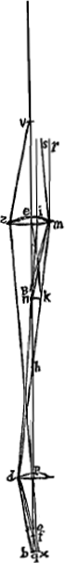 [Fig. 39.]
oritur obstabit, cum continuè minuaturGa naar voetnoot2). Latitudo vero ad pupillam eadem quae in nostro manebit, erat enim ibi ista latitudo ei ∞ ad/c, ut supra demonstratumGa naar voetnoot3). Hic vero quia ut np, hoc est cf/b, ad pd, hoc est 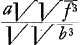 , ita ne, hoc est , ita ne, hoc est 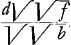 , ad ei, fit rursus ei ∞ ad/c. , ad ei, fit rursus ei ∞ ad/c.
Est igitur ex hac Regula progressio infinitaGa naar voetnoot4) in propagandis microscopij viribusGa naar voetnoot5) si lenticulas quamlibet exiguas parari posse ponamus. In hisce vero disquisitionibus eandem semper servari statuimus rationem BP ad PN, quam nempe habent distantiae punctorum conjugatorum ab lente P. Possumus autem et absque eo regulas generales invenire, nonnihil à prioribus diversas, atque eodem tamen tendentes, quas breviter perscribemus, omissa investigandi ratione, ne nimis diutius hic obhaereamus. Nituntur autem ijsdem, quae jam exposuimus, fundamentis. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 576]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Proposition XIX.Étant donc reproduite la figure de la proposition XIVGa naar voetnoot1), si l'on demande de construire un microscope composé de deux lentilles convexes e et p (Fig. 39), lequel possède une distance focale donnée de la lentille oculaire e, et de même un grossissement donné, et pour lequel microscope l'angle de l'aberration provenant de la dispersion du rayonGa naar voetnoot2) ainsi que la clarté soientles mêmes que pour un autre microscope donné composé des lentilles E et P [Fig. 38], la distance focale de la petite lentille inférieure p, sa position et son ouverture seront trouvées de la manière suivante. Supposons la distance focale donnée en de la lentille oculaire e égale à la ligne d, et soit demandé de faire en sorte que la grandeur apparente soit à celle qu'on apercevrait à une certaine distance, par exemple de 8 poucesGa naar voetnoot3) (distance que nous appellerons ω), comme ω est à une ligne donnée q. On exige en outre que l'angle d'aberration, que nous avons dit être nmkGa naar voetnoot4), soit égal à l'angle NMK dans l'autre microscope qui est donné; angle que nous définissons par le rapport de la ligne KM à KN ou EN à KN, qui soit égal au rapport de ω à une ligne donnée s; c'est-à-dire, nous voulons que le rapport en à nk ait la même valeur. Supposons de plus qu'une même clarté doive être obtenue que dans le microscope donné, il en sera ainsi si, prenant la largeur bx de l'objet égale à BX, nous rendons le rapport de l'angle zve à l'angle dbp égal au rapport des angles ZVE et DBP, comme cela s'entend par ce qui a été exposé plus hautGa naar voetnoot5). Or, soit ce rapport égal à celui de ω à une ligne g; on en trouve la valeur en remarquant qu'il est composé du rapport des angles ZVE à ZPE ou BPX, et celui de BPX à PBD; c'est-à-dire des rapports PE:EV, ou PN:NE (à cause de la proportionalité de PN, de PE et de PVGa naar voetnoot6)), et BX:PD. Appelons de plus h la ligne BX, y la distance focale po de la petite lentille cherchée et x la distance pb de l'objet. La règle sera exprimée par la formule 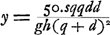 Ga naar voetnoot7). Lorsque y sera connue, on trouvera x qui aura la valeur 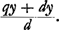 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 577]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[Propositio XIX.] [Fig. 38.]
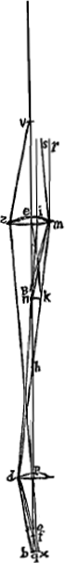 [Fig. 39.]
Repetita igitur figura Propos. [XIV]Ga naar voetnoot1), si microscopium è duobus convexis e et p compositum [Fig. 39] quaeratur, quod datam habeat lentis ocularis e foci distantiam, itemque datam amplificationem, et in quo angulus aberrationis ex dissipatione radijGa naar voetnoot2), ut et claritas sit eadem quae in aliodato microscopio ex lentibus E et P composito [Fig. 38]; invenietur foci distantia lenticulae inferioris p, ejusque positus et apertura hoc modo.Sit lentis ocularis e foci distantia en data aequalis d lineae. postuletur vero ut magnitudo apparens sit ad eam quae ex certa distantia, puta 8 pollicumGa naar voetnoot3), spectaretur, (quae distantia vocetur ω) ut ω ad q lineam datam. Angulus vero aberrationis, quem diximus esse nmkGa naar voetnoot4), requiratur aequalis angulo NMK, in altero dato microscopio; quem definimus proportione lineae KM ad KN seu EN ad KN, quae sit ea quae ω ad datam s. ut nempe eandem hanc habeat en ad nk. Claritas denique eadem quoque praestanda sit quae in microscopio dato, quod fiet si, posita rei visae latitudine bx ∞ BX, eadem sit ratio anguli zve ad dbp, quae anguli ZVE ad DBP, ut ex superioribus intelligiturGa naar voetnoot5). Sit autem haec ratio ea quae ω ad g, quae inde invenitur quod composita sit ex rationibus anguli ZVE ad ZPE seu BPX, et BPX ad PBD; hoc est, ex rationibus PE ad EV, seu PN ad NE (propter proportionales PN, PE, PVGa naar voetnoot6)), et ratione BX ad PD. Porro BX dicatur h, lenticulae verò quaesitae foci distantia po ∞ y; distantia rei visae pb ∞ x. Eritque regula hujusmodi 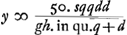 Ga naar voetnoot7). Cognita vero y
invenietur et x quae erit Ga naar voetnoot7). Cognita vero y
invenietur et x quae erit 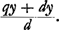 Semidiameter vero aperturae pd Semidiameter vero aperturae pd
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 578]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Et le rayon de l'ouverture sera 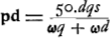 Ga naar voetnoot1). Il faut savoir que dans ces formules le nombre 50 provient de ce que dans le cas de cette aberration causée par la dispersion on pose toujours 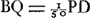 , comme nous l'avons dit plus hautGa naar voetnoot2). , comme nous l'avons dit plus hautGa naar voetnoot2).
Enfin pnGa naar voetnoot3) aura la valeur 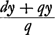 Ga naar voetnoot4). Or, il apparaît, attendu que la valeur de y peut aussi être exprimée par la formule 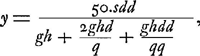 que, plus on suppose petite la valeur de q, c'est-à-dire plus on suppose grand le grossissement ω:q, plus le diviseur de cette quantité sera grand et plus petite sera, par conséquent, la longueur y, c'est-à-dire la distance focale po. On voit donc que de cette façon on peut, en diminuant les dimensions de la petite lentille p, augmenter autant qu'on le désire le pouvoir du microscope, du moins en tant que l'autre aberration, celle qui provient de la sphéricité, ne s'y oppose pas; pour laquelle nous indiquerons un peu plus loin une autre règle. Mais si nous supposons donnée la petite lentille p et non pas l'oculaire e, nous trouverons que dans ce cas le grossissement ne peut être augmenté que fort peuGa naar voetnoot7). En effet, si nous appelons r la distance focale donnée po, tandis que les autres lettres ont la même signification qu' auparavant, on trouve: 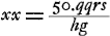 Ga naar voetnoot8), | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 579]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
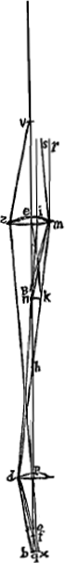 [Fig. 39.]
erit 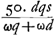 Ga naar voetnoot1). in quibus sciendum est numerum 50 inde esse quod in hac aberratione quae ex dissipatione est ponitur semper Ga naar voetnoot1). in quibus sciendum est numerum 50 inde esse quod in hac aberratione quae ex dissipatione est ponitur semper 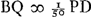 , ut in superioribus dictum fuitGa naar voetnoot2); pnGa naar voetnoot3) denique erit , ut in superioribus dictum fuitGa naar voetnoot2); pnGa naar voetnoot3) denique erit 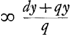 Ga naar voetnoot4). Apparet autem quia hic valor y etiam sic exprimi potest, y ∞ Ga naar voetnoot4). Apparet autem quia hic valor y etiam sic exprimi potest, y ∞ 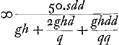 , quanto minor ponetur q, hoc est quanto major ratio multiplicationis ω ad q, tanto minoremGa naar voetnoot5) fore divisorem quantitatis hujus, ac tanto majoremGa naar voetnoot6) proinde longitudinem y, seu foci
distantiam po. atque ita, diminuenda lenticula p, posse quantum libet augeri microscopij virtutem, nisi quatenus altera aberratio obstabit, quae ex figura superficiei sphaericae pendet, cui paulo post aliam regulam applicabimus.
Sed si datam ponamus lenticulam p, non autem ocularem e, inveniemus non posse tunc augeri amplificationem nisi paulò tantumGa naar voetnoot7). Si enim foci distantia data po vocetur r, caeteris eadem, quae prius significantibus, invenitur xx ∞ , quanto minor ponetur q, hoc est quanto major ratio multiplicationis ω ad q, tanto minoremGa naar voetnoot5) fore divisorem quantitatis hujus, ac tanto majoremGa naar voetnoot6) proinde longitudinem y, seu foci
distantiam po. atque ita, diminuenda lenticula p, posse quantum libet augeri microscopij virtutem, nisi quatenus altera aberratio obstabit, quae ex figura superficiei sphaericae pendet, cui paulo post aliam regulam applicabimus.
Sed si datam ponamus lenticulam p, non autem ocularem e, inveniemus non posse tunc augeri amplificationem nisi paulò tantumGa naar voetnoot7). Si enim foci distantia data po vocetur r, caeteris eadem, quae prius significantibus, invenitur xx ∞ 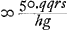 Ga naar voetnoot8). ubi apparet, quanto minor ponetur q, hoc est, Ga naar voetnoot8). ubi apparet, quanto minor ponetur q, hoc est,
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 580]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d'où il résulte que, plus on suppose q petite, c'est-à-dire, plus on suppose grand le grossissement ω:q, plus petit aussi devient la longueur x. Mais x, ou pb, doit être plus grande que r, ou po. Par conséquent, si dans un microscope de ce genre on prend au commencement pb plus petite que 2 po (ce qu'il saut faire dans tous les cas, comme dans notre microscope décrit plus hautGa naar voetnoot1), où le rapport pb:po n'a que la valeur 10:9), on ne pourra pas donner à q une valeur deux fois plus petite qu'auparavant; c'est-à-dire le grossissement ne pourra pas être doublé, parce qu'alors la nouvelle valeur de x serait égale à la moitié de la première, donc inférieure à r. Toute la perfection d'un microscope de ce genre doit donc être cherchée dans la petitesse de la lentille inférieure; il faut en calçuler les dimensions d'après la formule donnée un peu plus haut, jusqu'au point où l'aberration sphérique commencerait à être nuisible; c'est-à-dire aussi longtemps que l'angle NMK de cette aberration aura une valeur inférieure à 20′Ga naar voetnoot2). Mais si l'on exige un grossissement plus fort, il faut, en partant du microscope donné, où cet angle ne sera pas plus grand que 20′, en trouver un autre d'après une règle exprimée par la formule suivante: 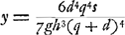 Ga naar voetnoot3); et dans ce cas l'on aura de nouveau: 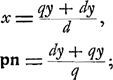 mais pd aura ici la valeur 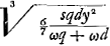 Ga naar voetnoot4) Et il faut savoir en outre que le rapport de l'angle ZVE à l'angle DBP dans le microscope donné est maintenant supposé égal au rapport ∛ω:∛g. Et de cette façon q peut être diminuée autant qu'on veut, c'est-à-dire le grossissement peut être rendu toujours plus fort, tandis que la lentille oculaire ainsi que la netteté et la clarté de l'image restent les mêmes. Mais la distance focale de la petite lentille diminuera davantage. Quant au nombre 6/7 qui figure comme facteur dans ces formules, il provient de ce que nous supposons la petite lentille p planconvexe, la surface plane étant tournée vers le dessous; l'aberration sphérique pour un rayon extrême parallèle à l'axe est pour cette lentille égale à 7/6 fois son épaisseur, comme nous l'avons démontré plus hautGa naar voetnoot5). Ainsi, si nous supposons la petite lentille p également convexe de part et d'autre, le facteur numérique sera ⅗, parce que l'aberration due à une lentille de ce genre est égale à 5/3 fois son épaisseurGa naar voetnoot6). Du reste, afin que nous donnions un exemple de l'une et de l'autre règle, et | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 581]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
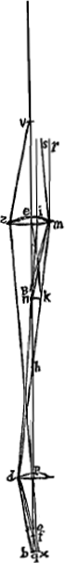 [Fig. 39.]
quo major ratio amplificationis ω ad q, eo minorem fieri x. atqui x, seu pb, debet esse major quam r, seu po. Ergo si in hujusmodi microscopio ponatur ab initio pb minor quam dupla po; (ut omnino faciendum, et in nostro superius descriptoGa naar voetnoot1) est pb ad po tantum ut 10 ad 9) non poterit q duplo minor quam prius adsumi; hoc est, non poterit duplicari ampliatio, quia x fieret dimidia prioris, ac proinde minor quam r. Omnis igitur microscopij hujusmodi perfectio in lenticulae inferioris parvitate quaerenda est; computando ex praescripto regulae modo traditae, quoad aberratio ex figura non oberit; hoc est, quoad ejus angulus NMK infra 20′ consistetGa naar voetnoot2). Sed si major ampliatio postuletur, oportet ex dato microscopio in quo angulus hic non erit major quam 20′, invenire aliud ex regula, quae est hujusmodi,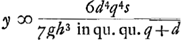 Ga naar voetnoot3), ubi rursus erit Ga naar voetnoot3), ubi rursus erit 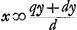 , , 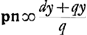 , sed pd fit hic , sed pd fit hic 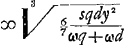 Ga naar voetnoot4). Et sciendum est insuper rationem anguli ZVE ad DBP in microscopio dato eam nunc poni quae ∛ω ad ∛g. Atque hoc modo quousque lubet diminui potest q, hoc est, augeri amplificatio, manente lente oculari eadem, nec non distincta visione et claritate, sed magis decrescet lenticulae foci distantia. Numerus autem 6/7 quantitati huic praepositus inde oritur quod lenticulam p planoconvexam ponimus, superficie plana deorsum spectante; cujus aberratio ex figura pertinens ad radium extremum axi parallelum, est 7/6 suae crassitudinis, ut ante hoc
ostensumGa naar voetnoot5). Sic si utrimque aequaliter convexa lenticula p poneretur, esset numerus praefixus ⅗, quia aberratio ejusmodi lentis efficit 5/3 suae crassisitudinisGa naar voetnoot6). Ga naar voetnoot4). Et sciendum est insuper rationem anguli ZVE ad DBP in microscopio dato eam nunc poni quae ∛ω ad ∛g. Atque hoc modo quousque lubet diminui potest q, hoc est, augeri amplificatio, manente lente oculari eadem, nec non distincta visione et claritate, sed magis decrescet lenticulae foci distantia. Numerus autem 6/7 quantitati huic praepositus inde oritur quod lenticulam p planoconvexam ponimus, superficie plana deorsum spectante; cujus aberratio ex figura pertinens ad radium extremum axi parallelum, est 7/6 suae crassitudinis, ut ante hoc
ostensumGa naar voetnoot5). Sic si utrimque aequaliter convexa lenticula p poneretur, esset numerus praefixus ⅗, quia aberratio ejusmodi lentis efficit 5/3 suae crassisitudinisGa naar voetnoot6).
Caeterum ut utriusque regulae exemplum demus, ac primò prioris, ubi | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 582]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
d'abord de la première où 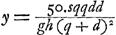 , on doit savoir qu'il faut commencer par calculer la longueur des lignes s et g dans le microscope donné; on aura de fait s = 1/25 pouce, parce que le rapport EN (ou MK):NK, c'est-à-dire ω:s, fut trouvé pour ce microscope égal à 200:1Ga naar voetnoot1). En effet, nous prenons ω = 8 poucesGa naar voetnoot2), et 200:1 = 8:1/25. Mais g se calcule être égale à 16/7, parce que, comme nous l'avons ditGa naar voetnoot2), le rapport ω:g est composé des rapports PN:NE et BX:PD; or, ce rapport composé se réduit au rapport unique PN:NE, ou 7:2, si BX ou h (ce qui est permis) est supposée égale à PD qui était ici de 1/20; en effet, 7:2 == 8:16/7. Mais quelle que soit la valeur qu'on donne à la quantité h, la quantité gh sera toujours la même pour un microscope donnéGa naar voetnoot3). Si donc nous supposons, en premier lieu, que d ait la même valeur dans le microscope cherché qu'elle avait dans notre microscopeGa naar voetnoot4), savoir d = 2; mais que nous exigeons que le grossissement ω:q soit égal à 72:1,
c'est-à-dire, qu'il soit le double du grossissement de notre microscope, d'où l'on tire q = 1/9Ga naar voetnoot5); on trouvera d'après la règle, en partant de ces données, y = 70/361, et les autres grandeurs d'après la détermination que nous en avons donnée dans l'exposition de la règleGa naar voetnoot6). Mais si, en supposant les mêmes choses, on prend d = 1 pouce, on trouve y = = 7/40 et pd = 1/40, absolument comme dans la première rechercheGa naar voetnoot7) où l'on conservait la même valeur du rapport BP:PN; ce qui confirme la vérité de la présente règle. , on doit savoir qu'il faut commencer par calculer la longueur des lignes s et g dans le microscope donné; on aura de fait s = 1/25 pouce, parce que le rapport EN (ou MK):NK, c'est-à-dire ω:s, fut trouvé pour ce microscope égal à 200:1Ga naar voetnoot1). En effet, nous prenons ω = 8 poucesGa naar voetnoot2), et 200:1 = 8:1/25. Mais g se calcule être égale à 16/7, parce que, comme nous l'avons ditGa naar voetnoot2), le rapport ω:g est composé des rapports PN:NE et BX:PD; or, ce rapport composé se réduit au rapport unique PN:NE, ou 7:2, si BX ou h (ce qui est permis) est supposée égale à PD qui était ici de 1/20; en effet, 7:2 == 8:16/7. Mais quelle que soit la valeur qu'on donne à la quantité h, la quantité gh sera toujours la même pour un microscope donnéGa naar voetnoot3). Si donc nous supposons, en premier lieu, que d ait la même valeur dans le microscope cherché qu'elle avait dans notre microscopeGa naar voetnoot4), savoir d = 2; mais que nous exigeons que le grossissement ω:q soit égal à 72:1,
c'est-à-dire, qu'il soit le double du grossissement de notre microscope, d'où l'on tire q = 1/9Ga naar voetnoot5); on trouvera d'après la règle, en partant de ces données, y = 70/361, et les autres grandeurs d'après la détermination que nous en avons donnée dans l'exposition de la règleGa naar voetnoot6). Mais si, en supposant les mêmes choses, on prend d = 1 pouce, on trouve y = = 7/40 et pd = 1/40, absolument comme dans la première rechercheGa naar voetnoot7) où l'on conservait la même valeur du rapport BP:PN; ce qui confirme la vérité de la présente règle.
Dans la deuxième règle suivant laquelle 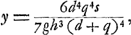 en cherchant d'abord les valeurs de s et de g dans le microscope donné quand on tient compte de l'aberration sphérique, on trouvera de fait s = 1/84 pouce, parce que dans ce cas nous avions trouvé que le rapport EN (ou MK):NK, c'est-à-dire ω:s, avait la valeur 672:1Ga naar voetnoot8); car 672:1 = ω (ou 8):1/84. Mais g est trouvée égale à 64/343, parce que le rapport ∛ω:∛g, c'est-à-dire le rapport des angles | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 583]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 [Fig. 38.]
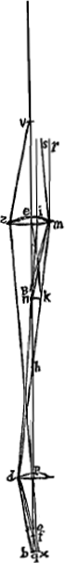 [Fig. 39.]
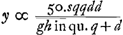 , sciendum est hinc incipiendum, ut lineae s et g inveniantur quantae sunt in microscopio dato. ac fit quidem s ∞ 1/25 poll. quia ibi ratio EN seu MK ad NK, hoc est ω ad s, fuit inventa quae 200 ad 1Ga naar voetnoot1). Ponitur enim ω ∞ 8 poll.Ga naar voetnoot2) et ut 200 ad 1, ita 8 ad 1/25. at g invenitur ∞ 16/7, quia ratio ω ad g dicta fuitGa naar voetnoot2) componi ex rationibus PN ad NE, et BX ad PD; quae composita redit ad solam rationem PN ad NE, sive 7 ad 2, si BX seu h (quod licet) ponatur aequalis PD, quae ibi erat 1/20. nam ut 7 ad 2 ita est 8 ad 16/7. quaecunque vero ponatur h erit semper quantitas gh eadem in dato microscopioGa naar voetnoot3). Quod si jam d eandem esse ponamus in eo quod quaerimus, quae erat in nostroGa naar voetnoot4), nempe d ∞ 2; sed rationem amplificationis ω ad q eam velimus esse quae 72 ad 1, hoc est duplo majorem quam in nostro, unde q fit ∞ 1/9Ga naar voetnoot5); ex his jam secundum regulam, invenietur y ∞ 70/361, et reliqua prout fuere in expositione regulae definitaGa naar voetnoot6). Quod si his ijsdem positis, statuatur d ∞ 1 poll. invenitur y ∞ 7/40 et pd 1/40, prorsus ut in priori disquisitione, ubi servabatur ratio eadem BP ad PNGa naar voetnoot7); quod veritatem regulae hujus comprobat.
In posteriori regula ubi , sciendum est hinc incipiendum, ut lineae s et g inveniantur quantae sunt in microscopio dato. ac fit quidem s ∞ 1/25 poll. quia ibi ratio EN seu MK ad NK, hoc est ω ad s, fuit inventa quae 200 ad 1Ga naar voetnoot1). Ponitur enim ω ∞ 8 poll.Ga naar voetnoot2) et ut 200 ad 1, ita 8 ad 1/25. at g invenitur ∞ 16/7, quia ratio ω ad g dicta fuitGa naar voetnoot2) componi ex rationibus PN ad NE, et BX ad PD; quae composita redit ad solam rationem PN ad NE, sive 7 ad 2, si BX seu h (quod licet) ponatur aequalis PD, quae ibi erat 1/20. nam ut 7 ad 2 ita est 8 ad 16/7. quaecunque vero ponatur h erit semper quantitas gh eadem in dato microscopioGa naar voetnoot3). Quod si jam d eandem esse ponamus in eo quod quaerimus, quae erat in nostroGa naar voetnoot4), nempe d ∞ 2; sed rationem amplificationis ω ad q eam velimus esse quae 72 ad 1, hoc est duplo majorem quam in nostro, unde q fit ∞ 1/9Ga naar voetnoot5); ex his jam secundum regulam, invenietur y ∞ 70/361, et reliqua prout fuere in expositione regulae definitaGa naar voetnoot6). Quod si his ijsdem positis, statuatur d ∞ 1 poll. invenitur y ∞ 7/40 et pd 1/40, prorsus ut in priori disquisitione, ubi servabatur ratio eadem BP ad PNGa naar voetnoot7); quod veritatem regulae hujus comprobat.
In posteriori regula ubi 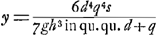 quaesitis prius s et g quantae sunt in dato microscopio, habita ratione aberrationis ex figura, invenitur quidem s ∞ 1/84 poll. quia ibi ratio EN seu MK ad NK, hoc est, ω ad s, fuit inventa quae 672 ad 1Ga naar voetnoot8); nam ut 672 ad 1 ita ω seu 8 ad 1/84. at g invenitur ∞ 64/343, quia ratio ∛ω ad ∛g hoc est ratio quaesitis prius s et g quantae sunt in dato microscopio, habita ratione aberrationis ex figura, invenitur quidem s ∞ 1/84 poll. quia ibi ratio EN seu MK ad NK, hoc est, ω ad s, fuit inventa quae 672 ad 1Ga naar voetnoot8); nam ut 672 ad 1 ita ω seu 8 ad 1/84. at g invenitur ∞ 64/343, quia ratio ∛ω ad ∛g hoc est ratio
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 584]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ZVE et DBP, est composé, comme nous l'avons ditGa naar voetnoot1), des rapports PN:NE et BX:PD; lequel rapport composé se réduit, comme un peu plus haut, au seul rapport PN:NE ou 7:2. Mais comme 7 est à 2, ainsi est ∛ω, ou 2, à 4/7, fraction qui est donc égale à ∛g; d'où l'on tire g = 64/343. Or, quelle que soit la valeur donnée à h, la quantité gh3 aura ici toujours la même valeur pour le microscope donnéGa naar voetnoot3). Si nous voulons maintenant que d ait la même valeur pour le microscope cherché que pour notre microscope donné, savoir d = 2 pouces, mais que le grossissement ω:q soit le double du nôtre, c'est-à-dire 72:1, on aura q = 1/9; et en partant de ces données l'on trouvera suivant la formule à peu près y = 1/19Ga naar voetnoot4), et les autres grandeurs d'après la détermination qui en fut donnée dans l'exposition de la règle. Mais si, les mêmes choses étant posées, on prend d égale à 1 pouce, on trouvera y = 7/160 et pd = 1/160, absolument comme dans la deuxième recherche précédenteGa naar voetnoot5), où le rapport BP:PN gardait sa valeur; ce qui confirme la vérité de cette deuxième règle.
FIN DE LA TROISIÈME PARTIE.
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
[pagina 585]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
anguli ZVE ad DBP, dicta fuitGa naar voetnoot1) componi ex rationibus PN ad NE et BX ad PBGa naar voetnoot2), quae composita redit, ut paulo ante, ad rationem solam PN ad NE, seu 7 ad 2. Ut autem 7 ad 2 ita ∛ω seu 2, ad 4/7; quod ergo aequale ∛g, ideoque g ∞ 64/343. quaecunque vero ponatur h, erit hic semper in microscopio dato eadem quantitas gh3Ga naar voetnoot3). Quod si jam d eandem esse velimus in microscopio quaesito ac in dato nostro, nempe d ∞ 2 poll., rationem vero amplificationis ω ad q duplam nostrae, hoc est, quae 72 ad 1; erit q ∞ 1/9; et ex his jam secundum hanc regulam invenietur y proxime ∞ 1/19Ga naar voetnoot4). Et reliqua ut fuere in expositione regulae definita. Quod si his ijsdem positis, statuatur d ∞ 1 poll. invenietur y ∞ 7/160 et pd ∞ ∞ 1/160 prorsus ut in secunda superiori disquisitioneGa naar voetnoot5), ubi servabatur ratio BP ad PN, quod posterioris hujusce regulae veritatem comprobat.
[FINIS PARTIS TERTIAE.] |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||