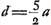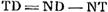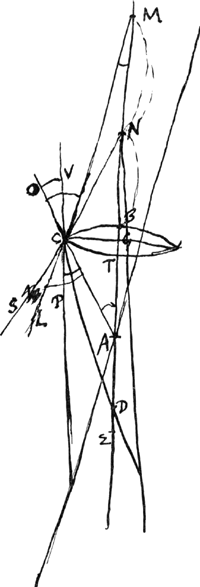
[Fig. 3.]
NC, NT, AC, AB 10000000
ut 72 ad 5 Ga naar voetnoot2) ita AC ad CG ∞ sin. ∠CAG Ga naar voetnoot3); AG ∞ s. compl. ∠CAG; 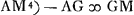 Ga naar voetnoot4) Ga naar voetnoot4); ∠CAG + CMG Ga naar voetnoot5); ⅔sin.OCM ∞ s.ACP Ga naar voetnoot6) sive OCV; 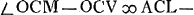 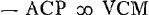 ; 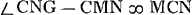 ; 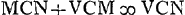 ; 3/2 sin.VCN ∞ sin.SCD Ga naar voetnoot7) vel sin.NCD; 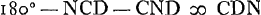 ; s.CDN ad CN ut sin.NCD ad ND; TE Ga naar voetnoot8) ∞ 2AB vel 2NT Ga naar voetnoot9). |
-
voetnoot1)
- La pièce est empruntée aux pp. 162-167; 177-180 et 182 du Manuscrit D. Elle suit donc de bien près, dans ce manuscrit, l'Appendice VII et doit avoir été composée quelques jours ou quelques semaines plus tard. Nous l'avons divisée en paragraphes dont le premier se rapporte aux p. 162-167, le second aux p. 177-180 et le troisième à la p. 182.
-
voetnoot2)
- Il s'agit du § 4 (p. 420-422) de l'Appendice VII qui précède. Aussi la figure présente correspond-elle à la fig. 3 de la p. 420 et les lettres ont-elles la même signification.
-
voetnoot3)
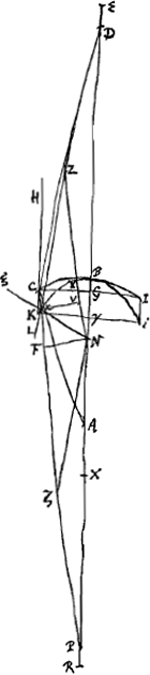
- Huygens se propose donc de calculer, pour un exemple numérique, la différence qu'il y a entre la vraie aberration NE du rayon extrême d'un faisceau émanant du point M et tombant sur le côté plan d'une lentille planconvexe et celle qu'on obtient par l'application de la règle de la p. 422. À cet effet il commence par calculer la position exacte du point N où le rayon extrême coupe l'axe après avoir subi les réfractions à la surface plane et à la surface courbe de la lentille en question.
-
voetnoot4)
- À propos des dimensions choisies on peut remarquer que le diamètre de 10 pouces de la grande lentille excède plus de quatre fois celle qui d'après la table de la p. 353 correspond à la distance focale du système composé, laquelle est de 15 pieds suivant les nombres proportionnels qu'on trouve, p. 424, à la fin du § 5 de l'Appendice VII.
-
voetnoot5)
- LC représente la direction du rayon MC après la première réfraction à la surface plane. Huygens applique donc ici la Prop. II, Part. I, Liv. I, p. 15.
-
voetnoot6)
- C'est la formule déduite à la p. 285. En effet, on peut considérer LC comme un rayon parallèle à l'axe d'une lentille dont la moitié est représentée par la figure CHD.
-
voetnoot7)
- En exécutant les calculs indiqués, que nous ne reproduisons pas, Huygens trouve BN = 711,75429.
-
voetnoot8)
- Par la Prop. V, Part. I, Liv. I, p. 23.
-
voetnoot9)
- Huygens prépare l'application de la Prop. XII, Part. I, Liv. I, p. 41. O est le point de concours de rayons venant de la direction EB et réfractés à la surface CB.
-
voetnoot10)
- E est donc le point correspondant au point M par rapport à la lentille planconvexe. Huygens trouve BE = 718,15187 et il en déduit (voir la note 7) NE = 6,39758.
-
voetnoot11)
- Voir la règle de la p. 422, où l'on a maintenant
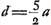 , b = BG. , b = BG.
-
voetnoot12)
- Dans le cours du calcul Huygens a trouvé BG = 0,17382, mais NE = 6,39758 (voir la note 10); il en déduit par division NE = 36,80 BG.
-
voetnoot13)
- Peut-être parce que la différence ne lui semblait pas sansimportance, Huygens a essayé encore de prendre en considération quelques termes contenant bb qu'il avait écrits, mais biffés, dans les calculs qui accompagnent le texte du § 4, p. 420, de l'Appendice précédent; mais nous supprimons ces calculs numériques.
-
voetnoot14)
- Dans ce paragraphe Huygens va calculer l'aberration sphérique exacte de la lentille auxiliaire, trouvée capable, d'après les calculs de la p. 424 du § 5 de l'Appendice précédent, à compenser en première approximation l'aberration sphérique de la lentille planconvexe dont il est question dans le § 1 qui précède.
-
voetnoot15)
- Comparez les nombres proportionnels de la p. 424. Le rayon de courbure de la surface convexe de la lentille planconvexe y est représenté par le nombre 10000. Or, dans le paragraphe précédent ce rayon égalait 72 pouces, il s'agit donc de trouver les rayons de courbure de la lentille auxiliaire à l'aide des nombres proportionnels correspondants. Mais on pourrait s'étonner que Huygens, n'ayant calculé ces nombres proportionnels que jusqu'à quatre chiffres, va pousser ici et plus loin les calculs, que nous avons supprimés, jusqu'à six chiffres et plus encore. Toutefois ce procédé se laisse justifier jusqu'à un certain point et on peut même dire que Huygens aurait dû l'appliquer d'une manière plus suivie (comparez la note 11 de là p. 431). En effet, en partant des nombres proportionnels 9191 et 7764, on peut calculer l'aberration DE en trois ou quatre chiffres, mais pour cela il est nécessaire d'en avoir un plus grand nombre dans les valeurs de BE et de BD, dont la différence donnera DE. Il faut donc faire le calcul comme si les longueurs de AB et de NB fussent connues en six ou sept chiffres. Bien entendu, les derniers chiffres dans les nombres qu'on trouve pour BE et BD dépendront aussi bien des chiffres qu'on a ajoutés, en poussant les opérations arithmétiques du calcul de AB et NB plus loin que de raison, que de ceux dont on est sûr, mais l'influence des premicrs disparaîtra dans le résultat de la soustraction finale.
-
voetnoot1)
- Puisque les valeurs de CG doivent se correspondre dans les deux lentiles.
-
voetnoot2)
- Voir la p. 287. CκP est la direction du rayon HC après la réfraction à la surface CB.
-
voetnoot3)
- Par la Prop. II, Part. I, Liv. I, p. 14.
-
voetnoot4)
- R est le foyer de la surface CB pour les rayons ayant la direction EB.
-
voetnoot5)
- Voir la p. 285. DZκ représente la direction du rayon CκP après la nouvelle réfraction à la surface κY; NYZ est tirée parallèle à PFκC; Nζ à DZκ.
-
voetnoot6)
- Préparation à l'application de la Prop. XII, Part. I, Liv. I, p. 41 pour trouver le point E correspondant
à R par rapport à la surface KκBi; X est le point de dispersion des rayons arrivant dans la direction RB après leur réfraction à la surface KκBi.
-
voetnoot7)
- Lisez ‘RX ad XN (∞ 2BN) ut RB ad BE’; proportion qu'on déduit facilement de celle (RX:RB = RN:RE) qu'on obtient par l'application de la proposition citée dans la note précédente.
-
voetnoot10)
- Les calculs, que nous avons supprimés, ont été exécutés d'après la deuxième méthode, indiquée dans le ‘Aliter’. Ils amènent successivement: CAG = 4o20′⅓″; ACP = 2o53′14″; APC = 1o26′46″⅓; AP = 132,08267; NP = 142,35707; NκP = 3o41′5″; NκD = 174o28′4″; κND = 5o7′51″; κDN = 24′″; ND = 769,24304; BD = 713,34224. Et ensuite BR = 198,52560; Bκ = 167,70240; RX = 30,82320; BE = 720,09005.
-
voetnoot10)
- Les calculs, que nous avons supprimés, ont été exécutés d'après la deuxième méthode, indiquée dans le ‘Aliter’. Ils amènent successivement: CAG = 4o20′⅓″; ACP = 2o53′14″; APC = 1o26′46″⅓; AP = 132,08267; NP = 142,35707; NκP = 3o41′5″; NκD = 174o28′4″; κND = 5o7′51″; κDN = 24′″; ND = 769,24304; BD = 713,34224. Et ensuite BR = 198,52560; Bκ = 167,70240; RX = 30,82320; BE = 720,09005.
-
voetnoot11)
- C'est la valeur trouvée au paragraphe précédent pour l'aberration de la lentille planconvexe (voir la note 10 de la p. 429), laquelle, si l'on désire une compensation à peu près parfaite, devrait égaler la valeur de DE trouvée ici. Comme la différence excède considérablement l'épaisseur de la
lentille planconvexe, mentionnée dans la note 12 de la p. 429, et que l'aberration d'une telle lentille, employée sans lentille auxiliaire, n'est que 7/6 fois cette épaisseur, le résultat a dû paraître très peu satisfaisant à Huygens. Mais en réalité la compensation est un peu meilleure. En effet, il est clair que le calcul de Huygens, par lequel il n'a trouvé la valeur de l'angle κDN qu'en secondes entières, c'est à dire à peine en quatre chiffres, ne permet pas de calculer avec une approximation suffisante la petite différence entre BE et BD. C'est pourquoi nous avons refait les calculs, qui nous ont donné successivement CAG = 4o19′59″,62; ACP = 2o53′14″,23; APC = 1o26′45″, 39; AP = = 132,0981; NP = 142,3725; NκP = 3o41′5″,23; NκD = 174o28′4″,94; κDN = 24′4″,44; ND = 769,536; BD = 713,635; ce qui amène DE = 6,455. Par conséquent, la différence entre l'aberration, que nous avons calculée ici, du rayon extrême de la lentille auxiliaire, et celle 6,398, que nous avons vérifiée et trouvée exacte, du rayon extrême de la lentille planconvexe se réduit à 0,057; ce qui est un peu moins que le tiers de l'épaisseur de la lentille planconvexe, c'est-à-dire, que les cinq douzièmes de l'épaisseur d'une lentille qui possèderait la même distance focale que le système composé formé par la lentille planconvexe et la lentille auxiliaire.
-
voetnoot1)
- Ce paragraphe fait connaître la méthode pour calculer exactement l'aberration sphérique du rayon MC qui tombe sur une lentille biconvexe symétrique en partant d'un point M situé sur l'axe de la lentille à une distance donnée. Il est évident que ce calcul devait servir pour vérifier par un exemple numérique jusqu' à quel point on pouvait réussir à compenser l'aberration sphérique d'une telle lentille de la manière décrite aux §§ 6 et 7, p. 424-427, de l'Appendice précédent. Mais ce calcul n'a pas été entrepris.
-
voetnoot2)
- Ces nombres indiquent les dimensions à choisir pour la lentille biconvexe. Comparez, à la p. 428, celles de la lentille planconvexe du § 1.
-
voetnoot3)
- C'est-à-dire, dans une table où le rayon du cercle est représenté par 10000000.
-
voetnoot5)
- ∠CMG se calcule facilement puisque MG et CG sont connues.
-
voetnoot6)
- VCP est la direction du rayon MC après sa réfraction à la surface CB.
-
voetnoot7)
- CD est la direction du rayon VCP après la réfraction à la surface CT.
-
voetnoot8)
- E est l'image de M dans la supposition faite au § 6 de l'Appendice précédent, d'après laquelle MB = 2AB. Alors, comme nous l'avons remarqué dans la note 4 de la p. 425, les rayons qui émanent de M peuvent être considérés à l'intérieur de la lentille comme parallèles à l'axe et ils se réuniront donc de nouveau après la sortie de la lentille dans un point E pour lequel TE = MB = 2AB = 2NT.
-
voetnoot9)
- TE est
donc connue, mais
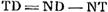 de même; donc aussi DE, c'est-à-dire, l'aberration cherchée. de même; donc aussi DE, c'est-à-dire, l'aberration cherchée.
|
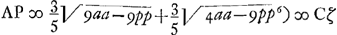 Ga naar voetnoot6);
Ga naar voetnoot6); 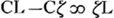 ; ζL ad LA ut CL ad LN;
; ζL ad LA ut CL ad LN; 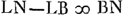 Ga naar voetnoot7).
Ga naar voetnoot7).
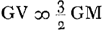 Ga naar voetnoot8);
Ga naar voetnoot8); 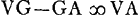 ; AO ∞ 2ABGa naar voetnoot9);
; AO ∞ 2ABGa naar voetnoot9); 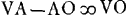 ; VA+
; VA+ 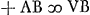 ; VO ad VA ut VB ad VE;
; VO ad VA ut VB ad VE; 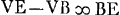 Ga naar voetnoot10);
Ga naar voetnoot10); 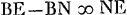 .
.
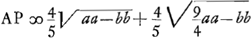 Ga naar voetnoot2). Sed
Ga naar voetnoot2). Sed 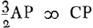 Ga naar voetnoot3). datur vero et AR ∞ 2ABGa naar voetnoot4). Ergo et
Ga naar voetnoot3). datur vero et AR ∞ 2ABGa naar voetnoot4). Ergo et 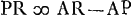 . Est vero BR ∞ 3AB;
. Est vero BR ∞ 3AB; 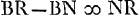 ;
; 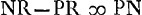 ; ut PC ad CG ita PN ad NF; qu.Nκ (seu NB ∞ n)-qu.NF ∞ ∞ κF; ut PC ad PG (quae data est propter datas AB, AG) ita PN ad PF;
; ut PC ad CG ita PN ad NF; qu.Nκ (seu NB ∞ n)-qu.NF ∞ ∞ κF; ut PC ad PG (quae data est propter datas AB, AG) ita PN ad PF; 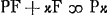 . Ex datis NY ∞ NB et κV ∞ ∞ NF, quae dicatur p, datur NZ sive
. Ex datis NY ∞ NB et κV ∞ ∞ NF, quae dicatur p, datur NZ sive 
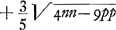 Ga naar voetnoot5).
Ga naar voetnoot5). 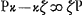 ; ut ζP ad PN ita κP ad PD;
; ut ζP ad PN ita κP ad PD; 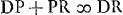 ; BX ∞ 3BNGa naar voetnoot6);
; BX ∞ 3BNGa naar voetnoot6); 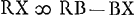 ; RX ad XB ut RB ad BEGa naar voetnoot7);
; RX ad XB ut RB ad BEGa naar voetnoot7); 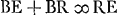 ;
; 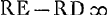 DE, quae est aberratio quaesita.
DE, quae est aberratio quaesita.
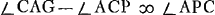 Sin.APC ad AC ut Sin.ACP ad AP;
Sin.APC ad AC ut Sin.ACP ad AP; 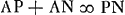 ; Nκ ad Sin.NPκ sive APC ut NP ad Sin.NκP; unde ∠NκP; 3/2 Sin.NκP ∞ Sin.ξκD, sive NκD;
; Nκ ad Sin.NPκ sive APC ut NP ad Sin.NκP; unde ∠NκP; 3/2 Sin.NκP ∞ Sin.ξκD, sive NκD; 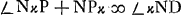 ; 2 recti -
; 2 recti - 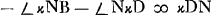 ; Sin.κDN ad κN utSin.NκD ad ND; ND -
; Sin.κDN ad κN utSin.NκD ad ND; ND - 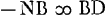 ; BR ∞ 3AB; BX ∞ 3BN;
; BR ∞ 3AB; BX ∞ 3BN; 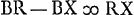 ; RX ad XN ut RB ad BEGa naar voetnoot9);
; RX ad XN ut RB ad BEGa naar voetnoot9); 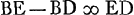 .
.


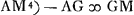 Ga naar voetnoot4); ∠CAG + CMGGa naar voetnoot5); ⅔sin.OCM ∞ s.ACPGa naar voetnoot6) sive OCV;
Ga naar voetnoot4); ∠CAG + CMGGa naar voetnoot5); ⅔sin.OCM ∞ s.ACPGa naar voetnoot6) sive OCV; 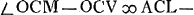
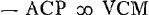 ;
; 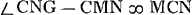 ;
; 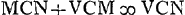 ; 3/2 sin.VCN ∞ sin.SCDGa naar voetnoot7) vel sin.NCD;
; 3/2 sin.VCN ∞ sin.SCDGa naar voetnoot7) vel sin.NCD; 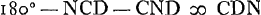 ; s.CDN ad CN ut sin.NCD ad ND; TEGa naar voetnoot8) ∞ 2AB vel 2NTGa naar voetnoot9).
; s.CDN ad CN ut sin.NCD ad ND; TEGa naar voetnoot8) ∞ 2AB vel 2NTGa naar voetnoot9).