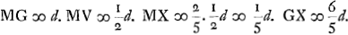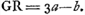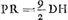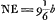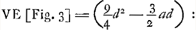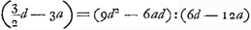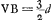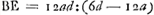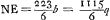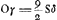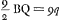Oeuvres complètes. Tome XIII. Dioptrique
(1916)–Christiaan Huygens–
[pagina 418]
| |
Appendice VIIGa naar voetnoot1)
| |
[pagina 419]
| |
§ 2Ga naar voetnoot6).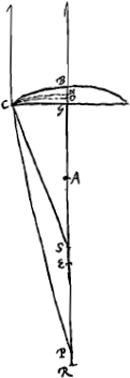 [Fig. 2.]
Aberratio axi parallelorum superficiei convexae BC. Sit rad. AB ∞ a. BR ∞ 3aGa naar voetnoot7). Crassit. BG ∞ b. Sit CP radius refractus. Et sit centro P radio PC descriptus arcus CO. Quia ergo PC vel PO proxime aequalis RB sive 3a, hoc est triplae BA. Erit GO ∞ ⅓ BGGa naar voetnoot8). Sed CP ad PA ut 3 ad 2Ga naar voetnoot9). Ergo et OP ad PA ut 3 ad 2. Ergo OA ad AP ut 1 ad 2. Sed OA ∞ AB - BO ∞ a-⅔b 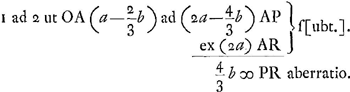 | |
§ 3.Aberratio axi parallelorum, lentis planoconvexae, convexo exteriore. Sit CS refractio radij CP à superficie plana CG exeuntis. Et centro S sit descriptus arcus CN. Quia ergo CS vel SN proxime aequalis 2a, erit GN ∞ ½ BGGa naar voetnoot8) ∞ ½b. Sed PC ad CS ut 3 ad 2Ga naar voetnoot10). Ergo et PC ad SN ut 3 ad 2. 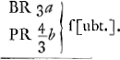 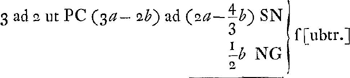 | |
[pagina 420]
| |
§ 4.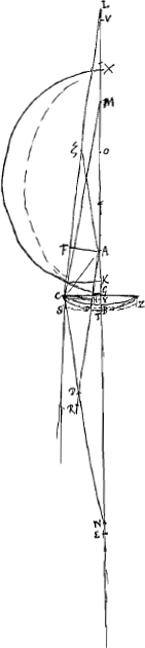 [Fig. 3.]
Aberratio lentis planoconvexae radiorum a puncto venientium in superficiem planam. AB ∞ a; BG ∞ b; MG ∞ d, M punctum radians; MV ∞ ½dGa naar voetnoot2), V punctum disp. superf.ei planae CG; MX ∞ ⅖MV ∞ ⅕dGa naar voetnoot2); BO ∞ 3aGa naar voetnoot3). ½ XG (⅗d) ad AB (a) ut BG (b) ad GK (5/3 ab/d)Ga naar voetnoot4) 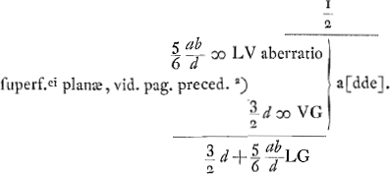 Ga naar voetnoot2) LC ∞ LG + min. (3/2d + minima) ad AB (a) ut BGb 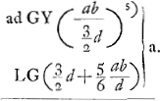 Ga naar voetnoot5) | |
[pagina 421]
| |
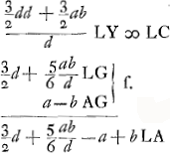 qu. 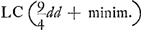 ad qu. ad qu. 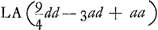 sive ut qu. CG ad qu. AFGa naar voetnoot6) vel CHGa naar voetnoot7) ita BG (b) ad DHGa naar voetnoot8). sive ut qu. CG ad qu. AFGa naar voetnoot6) vel CHGa naar voetnoot7) ita BG (b) ad DHGa naar voetnoot8).
Hic minimum primi termini negligitur rectè, quia tertius terminus b minimus est. nam etsi non negligeretur, id in quarto termino DH inconsiderabile augmentum efficeret. 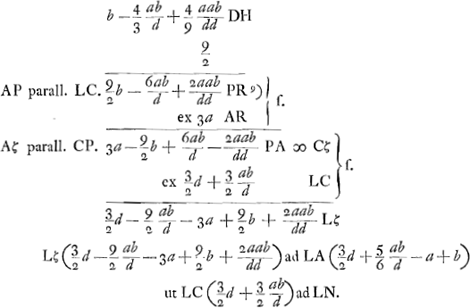 Ga naar voetnoot9) | |
[pagina 422]
| |
Hic nihil omittendum ex minimis primi et secundi et tertij termini, quia quartus est magnus.  Ga naar voetnoot1)Ga naar voetnoot2)Ga naar voetnoot1)Ga naar voetnoot1) ut auferatur LN ex LE alternis multiplicantur numeratores et divisores, et differentia productorum dividitur per productum denominatorum, in quo minima negliguntur quia NE est minima. Sed et in illa productorum differentia negliguntur in quibus bb, quia hae quantitates respectu caeterarum, in quibus tantum b sunt minimae. Tollunt porro se mutuo omnes, in quibus nullum b, necessario. 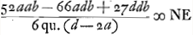 Ga naar voetnoot3). Regula aberr.is Ga naar voetnoot3). Regula aberr.is
| |
§ 5Ga naar voetnoot4).Ex aberratione cognita lentis planoconvexae radiorum a puncto venientium alia methodus suppetit lentem compositam perfectam construendi. Oportet enim tantum cavoconvexam adjungere STZ [Fig 3], quae radios parallelos excipiens inflectit quasi venirent a puncto E, habeatque aberrationem aequalem aberrationi lentis planoconvexae radiorum ex puncto M venientium quam invenimus. Ex. gr. | |
[pagina 423]
| |
sit MB dupla foci dist.ae lentis CGB. Erit BE ipsi MB aequalisGa naar voetnoot5). Debebitque crassitudo cavae lentis CST esse dimidia crassitudinis BG ut radios parallelos dispergat quasi ex E veniant, ut facile est probareGa naar voetnoot6). Atqui lentis CGB aberratio tunc invenitur noncupla proximè suae crassitudinisGa naar voetnoot7). Ergo aberratio cavae debet esse octodecupla suae crassitudinis. Unde per regulam aberrationis menisci caviGa naar voetnoot8) invenitur proportio radiorum ad describendas superficies CT et ST, debere esse proximè ut 303 ad 155Ga naar voetnoot9). foci distantia autem sive potius puncti dispersus datur BE ∞ 4a. Unde ipsi radij inveniuntur per regulam in dioptr. traditamGa naar voetnoot10), quia ut diff. radiorum ad alterutrum ita duplum reliqui ad distantiam puncti dispersus. hic fiunt 296/303a et 296/155aGa naar voetnoot11).  [Fig. 4.]
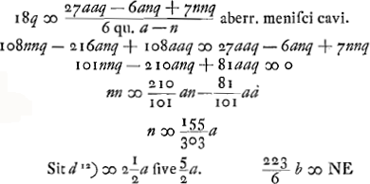 Ga naar voetnoot12) | |
[pagina 424]
| |
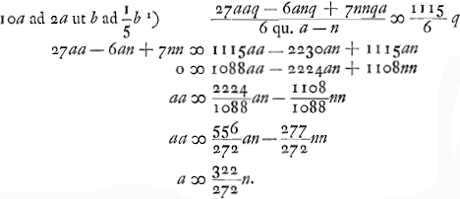 Ga naar voetnoot1) Radij: plana; 10000 conv.; 7764 cav. auxil.ae 9191 conv. auxil.ae; 25000 foci dist. compositaeGa naar voetnoot2). bon. | |
§ 6Ga naar voetnoot3).Aberratio in lente aequaliter convexa cum radius a puncto venit, distante duabus semidiametris convexi. Fit aberratio 9/2 crassitudinis. ut debebat ex eo quod sint quasi duae planoconvexae, | |
[pagina 425]
| |
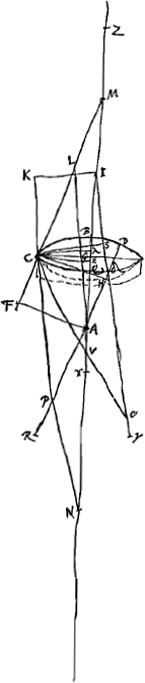 [Fig. 5.]
in quibus singulis aberratio parallelorum planam incidentium est9/2 crassitudinisGa naar voetnoot4). AB ∞ IQ ∞ a; BG ∞ GQ ∞ b; MB ∞ 2a, M punctum radians. QY ∞ 2a. 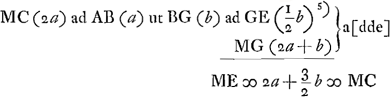 Ga naar voetnoot5) qu. MC (4aa+min) ad qu. MA (9aa) sive ut qu. CG ad qu. AF [sive CH] ita BG (b) ad DH (9/4b)Ga naar voetnoot6) 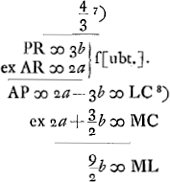 Ga naar voetnoot7)Ga naar voetnoot8) 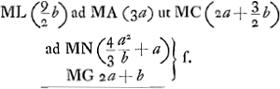 | |
[pagina 426]
| |
 [Fig. 5.]
 Ga naar voetnoot1)Ga naar voetnoot2)Ga naar voetnoot3) 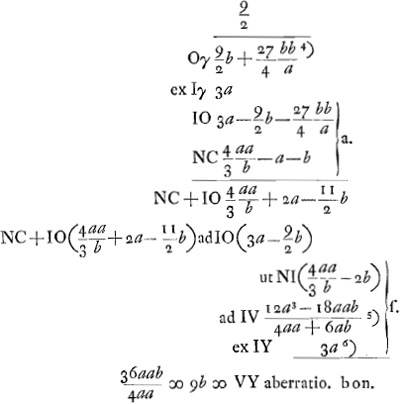 Ga naar voetnoot4)Ga naar voetnoot5)Ga naar voetnoot6) Ergo aberratio VY aequatur 4½ crassitudinis BQ. | |
[pagina 427]
| |
§ 7Ga naar voetnoot7). [Fig. 6.]
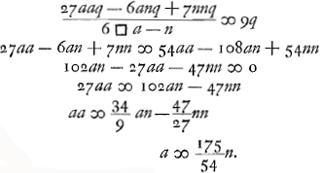 Radij { 10000 convexi Radij { idem convexi alterius Radij { 6920 cavi auxiliariae Radij { 23972 convexi auxil. 20000 longit.o telesc.ij seu foci distantia compositae lentisGa naar voetnoot8). |
|


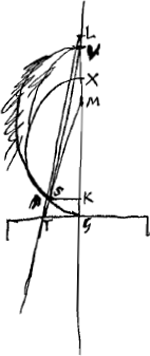
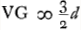 ; V punctum dispersus
; V punctum dispersus